 Open Access Article
Open Access ArticleThe effect of morphology and particle–wall interaction on colloidal near-wall dynamics†
J. Alejandro
Rivera-Morán
 a,
Yi
Liu
a,
Samuel
Monter
a,
Yi
Liu
a,
Samuel
Monter
 ab,
Chiao-Peng
Hsu‡
ab,
Chiao-Peng
Hsu‡
 c,
Pia
Ruckdeschel
d,
Markus
Retsch
c,
Pia
Ruckdeschel
d,
Markus
Retsch
 d,
Maciej
Lisicki
d,
Maciej
Lisicki
 e and
Peter R.
Lang
e and
Peter R.
Lang
 *a
*a
aForschungszentrum Jülich, IBI-4, Jülich, Germany. E-mail: p.lang@fz-juelich.de
bUniversität Konstanz, Germany
cETH-Zürich, Switzerland
dUniversität Bayreuth, Germany
eUniversity of Warsaw, Poland
First published on 29th September 2021
Abstract
We investigated the near-wall Brownian dynamics of different types of colloidal particles with a typical size in the 100 nm range using evanescent wave dynamic light scattering (EWDLS). In detail we studied dilute suspensions of silica spheres and shells with a smooth surface and silica particles with controlled surface roughness. While the near wall dynamics of the particle with a smooth surface differ only slightly from the theoretical prediction for hard sphere colloids, the rough particles diffuse significantly slower. We analysed the experimental data by comparison with model calculations and suggest that the deviating dynamics of the rough particles are not due to increased hydrodynamic interaction with the wall. Rather, the particle roughness significantly changes their DLVO interaction with the wall, which in turn affects their diffusion.
1 Introduction
The low Reynolds-number dynamics of particles near a flat interface is generally slower than in bulk and directionally anisotropic due to an increased flow resistance caused by hydrodynamic interaction between particles and the interface. The first theoretical investigations of this effect date back to the early twentieth century,1,2 while the first experimental verifications3 only became available in the 1980s. With the modern microscopy and evanescent wave scattering methods4 that are now available, there have been numerous investigations of colloidal dynamics in the ultimate vicinity of glass surfaces during the last three decades.5–20 With a few exceptions,7,8,18 in most of these investigations, data-analysis and interpretation is based on the assumption of particles with smooth surfaces and no static interaction with the wall other than excluded volume. Similarly, in most studies concerning static particle–particle or particle–wall interactions, flat and homogeneous surfaces are assumed.21–24 Only since synthesis methods have been available, which allow the batch production of particles with controlled surface roughness,25–27 have systematic studies on the effect of particle roughness become possible.The rheological behaviour and particle deposition on various kinds of surfaces have been intensively investigated. It was found that in suspensions of rough particles the onset of discontinuous shear thickening is shifted towards lower volume fractions and critical stresses as compared to particles with smooth surfaces.26,28,29 This effect is commonly attributed to additional tangential stresses caused by hydrodynamic interaction or solid contacts of asperities. The deviation between experientially observed particle deposition rates and values predicted assuming DLVO interaction between bodies with smooth surfaces has been attributed to the neglect of roughness for a long time. Analytical expressions for the interaction potential between rough particles are not available, but simulations suggest that the stabilization barrier of DLVO potentials is significantly reduced by surface roughness.30,31 An analytical approximation for the interaction energy between a rough particle and a flat surface was given by Suresh et al.32 and verified by total internal reflection microscopy experiments.33 Jin et al.34 provided the first numerical model for particle deposition including the impact of surface roughness, merging modified expressions for DLVO interactions between rough surfaces and hydrodynamic interaction.
So-called hairy colloids, i.e. core–shell particles consisting of a hard particle core carrying polymer brushes, may be regarded as a limiting case of rough particles with extremely pointed asperities and high surface coverage. However, such particles show a qualitatively different rheology, e.g., the presence of the brushes suppresses shear thickening.35,36 This is attributed to the fact that the brush behaves like a porous shell, reducing the flow resistance as compared to a compact sphere with the same outer radius. The hydrodynamics of such particles can be described by invoking a hydrodynamic penetration length which reduces the effective hydrodynamic radius to a value smaller than the outer radius of the core shell particle.37–39 The same concept can be generally applied to flows past rough surfaces at low Reynolds numbers.8,40,41 Consequently, rough particles and porous shell particles are expected to show faster near-wall dynamics as compared to smooth particles with the same outer radius.
In our investigation we employed full spherical particles with a smooth surface, micro-porous spherical shells and spherical particles with surface roughness to test this prediction. We used evanescent wave dynamic light scattering (EWDLS) experiments supported by numerical model calculations to study the Brownian particle dynamics parallel to a flat glass wall. After a thorough introduction to the materials and methods in Section 2 and the numerical model in Section 3, we discuss our findings in Section 4.
2 Experimental
2.1 Materials
We investigated three different types of silica particles, namely standard spheres with a smooth surface (SSi), spherical hollow shells (HSi) and spheres with controlled surface roughness (RSi). The HSi particles were synthesized in a three-step procedure consisting of the synthesis of a monodisperse polystyrene latex core by emulsifier-free emulsion polymerisation which was covered by a silica shell applying a Stöber synthesis protocol. After purification and drying the resulting core–shell particles were calcined to burn off the core. The RSi were produced through hetero-aggregation of small particles onto the surface of a large core. Here we used a combination of particles of 150 nm and 8 nm in diameter. In a second step, a smoothing layer was applied to adjust the height of the asperities. The coverage of the RSi was determined by the number ratio of core and asperity particles. The roughness was controlled by adjusting the thickness of the smoothing layer, which also prevents the detachment of asperity particles. Here we applied a 5 nm thick smoothing layer. The synthesis routes to these particles are described in the literature for the HSi42 and RSi,25,28 while the SSi are the same as the large particles used in the first step of the two-step procedure leading to the RSi.All colloids were suspended either in pure (Mili-Q grade) water which has an approximate electrolyte concentration of cS ≈ 10−5 mol L−1 due to carbon dioxide absorption, corresponding to a Debye screening length of λD−1 ≈ 100 nm. At larger electrolyte concentrations, all types of particles would aggregate inevitably. To exclude distortions and misinterpretation of evanescent wave DLS data by the formation of aggregates over the experiment duration and their preferred sedimentation, all samples were characterized by bulk DLS before and after the EWDLS experiments. In no case did we find variations of the hydrodynamic radius, beyond experimental error. Prior to DLS and EWDLS measurements, all sample solutions were centrifuged at 800 rpm for about 16 hours to spin down dust and potential aggregates as far as possible.
The particle size parameters and their standard deviations measured with different methods are listed in Table 1.
| Particle type | Smooth, full silica | Hollow silica | Rough silica |
|---|---|---|---|
| Acronym | SSi | HSi | RSi |
| 〈RH〉 | 77 | 154 | 86 |
| 〈RG〉 | 55 | (176) | 74 |
| 〈R〉SLS | 69 | 142 | — |
| σ SLS | 0.05 | 0.02 | — |
| 〈RC〉SLS | — | 128 | — |
| 〈R〉TEM | 65 | 142 | 65 |
| σ TEM | 0.08 | 0.03 | 0.15 |
| 〈RC〉TEM | — | 132 | — |
2.2 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ/2)/λ0 with the solvent refractive index, nS, and the laser vacuum wavelength λ0. To determine the particles' Stokes–Einstein diffusion coefficient, D0, the initial slope of the correlation function Γ = −D0Q2 was identified by a non-linear least squares fit to a stretched exponential and plotted vs. Q2. The initial slope of this representation is 2D0. The particles' hydrodynamic radii, 〈RH〉, were calculated via the Stokes–Einstein relation, 〈RH〉 = kBT/6πη〈D0〉 using T = 293 K and η = 1.0 mPa s for the solvent viscosity, where kBT is the thermal energy unit. It is understood that for polydisperse samples 〈RH〉 is the z-average of the radius distribution and 〈D0〉 is the corresponding averaged diffusion coefficient.
sin(θ/2)/λ0 with the solvent refractive index, nS, and the laser vacuum wavelength λ0. To determine the particles' Stokes–Einstein diffusion coefficient, D0, the initial slope of the correlation function Γ = −D0Q2 was identified by a non-linear least squares fit to a stretched exponential and plotted vs. Q2. The initial slope of this representation is 2D0. The particles' hydrodynamic radii, 〈RH〉, were calculated via the Stokes–Einstein relation, 〈RH〉 = kBT/6πη〈D0〉 using T = 293 K and η = 1.0 mPa s for the solvent viscosity, where kBT is the thermal energy unit. It is understood that for polydisperse samples 〈RH〉 is the z-average of the radius distribution and 〈D0〉 is the corresponding averaged diffusion coefficient.
2.3 Evanescent wave dynamic light scattering
The reciprocal penetration depth of the evanescent field is determined by the angle of incidence αi, the refractive index of the glass n1 and that of the suspension n2 as  . The magnitude of the scattering vector component parallel to the interface is given by
. The magnitude of the scattering vector component parallel to the interface is given by  while the normal component is Q⊥ = 2πn2
while the normal component is Q⊥ = 2πn2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αr/λ0. Here θ is the in-plane and αr the off-plane angle defining the position of the detector unit with respect to the reflecting interface. The two scattering vector components can be varied independently of each other by changing θ and αr. To determine the particle dynamics parallel to the interface at a given penetration depth, a series of correlation functions is recorded at a fixed αr varying Q‖ by changing θ. The initial slopes of the correlation functions Γ are determined by converting the experimental curves to field correlation functions, g1(t), and fitting their short time parts repeatedly with a single exponential starting from a manually chosen number of data points, Np. When a single fit has converged, Np is reduced by two and the remaining data are fitted again. With this procedure it is possible to identify a limited range of Np's where the best fitting values are essentially independent of Np.14 The Γ-values from these ranges are plotted versus Q‖2 to yield a linear slope which according to eqn (6) is the diffusion coefficient parallel to the interface 〈D‖〉(κ). The latter is a function of the penetration depth, since the experiment integrates over the z-coordinate, normal to the interface, as indicated by the angle brackets. Examples of original correlation functions and data analysis are presented in the ESI.†
αr/λ0. Here θ is the in-plane and αr the off-plane angle defining the position of the detector unit with respect to the reflecting interface. The two scattering vector components can be varied independently of each other by changing θ and αr. To determine the particle dynamics parallel to the interface at a given penetration depth, a series of correlation functions is recorded at a fixed αr varying Q‖ by changing θ. The initial slopes of the correlation functions Γ are determined by converting the experimental curves to field correlation functions, g1(t), and fitting their short time parts repeatedly with a single exponential starting from a manually chosen number of data points, Np. When a single fit has converged, Np is reduced by two and the remaining data are fitted again. With this procedure it is possible to identify a limited range of Np's where the best fitting values are essentially independent of Np.14 The Γ-values from these ranges are plotted versus Q‖2 to yield a linear slope which according to eqn (6) is the diffusion coefficient parallel to the interface 〈D‖〉(κ). The latter is a function of the penetration depth, since the experiment integrates over the z-coordinate, normal to the interface, as indicated by the angle brackets. Examples of original correlation functions and data analysis are presented in the ESI.†
3 Model for numerical calculations
3.1 Near wall dynamics
Suspended particles close to a solid interface show slower Brownian dynamics than in bulk suspension due to hydrodynamic interaction with the wall. Approximations for the resulting friction coefficients in the low Reynolds number limit parallel and normal to the wall were published by Brenner and co-workers.45,46 Although there are more accurate, but non-analytical expressions e.g. ref. 37, we use here the closed approximation to calculate the diffusion coefficient parallel to the wall | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 | (6) |
3.2 Particle–wall interactions
The interaction potential of the investigated particles with the adjacent glass wall is modelled as a superposition of three contributions,| Φ(z) = ΦvdW(z) + Φer(z) + Φg(z) | (7) |
The strength of the van der Waals attraction is given by the Hamaker constant, AH, and the dependence on separation distance can be calculated for the sphere wall geometry48 to yield
 | (8) |
To model the electrostatic repulsion we exploited the linear superposition approach by Lin et al.49
 | (9) |
Here, ε = εrε0 where ε0 is the vacuum permittivity and εr is the relative permittivity of the medium, Z is the valency of a single charged site (assumed to be Z = 1 in the following), e is the electron unit charge and γp,w = tanh(ZeΨp,w/4kBT) where Ψp,w is the surface potential of the particle and the wall, respectively. Since we have no means to assess the surface potential of the wall, we used an effective value γ2 = γpγw.
The expression of Lin et al. is more accurate for the given sphere–wall geometry for all values of λDR than the expression which can be derived using Derjaguin's approximation. It is however worthwhile to note that the two expressions differ only by a constant in λDR. The ratio of the two expressions is given by 1 − 1/λDR + (1 + 1/λDR)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{−2λDR}.
exp{−2λDR}.
The gravitational contribution to the potential is determined by the buoyancy corrected particle mass
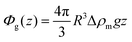 | (10) |
For all the calculated data presented in Sections 4.1.2 and 4.2 we replaced the particle radius by the hydrodynamic radius as determined by dynamic light scattering, since for the particles with surface roughness (RSi) a radius cannot be defined meaningfully.
3.3 Particle shape and polydispersity
If the investigated particles have a size distribution, P(R), with a significant width, the expression for the initial slope of the correlation function becomes more complex than eqn (5). In this case the near wall form amplitude B(Q, R)nw does not cancel from the expression for Γ as in the monodisperse case, and an integration over the size distribution of the numerator and denominator is required to obtain the expression for the size averaged initial slope | (11) |
Due to the exponential illumination profile, the form amplitude of a spherical particle cannot be written in a closed analytical form, it is rather given by
 | (12) |
where J0 refers to the zero order Bessel-function of the first kind. For a spherical core–shell particle with a core radius, RC, outer radius, R, and scattering length densities of the core, ρC, and of the shell, ρS, the form amplitude is given by
 | (13) |
4 Results and discussion
4.1 Experimental findings
From the 3-D reconstructions, it is evident that SSi particles are, although not perfectly, to a good approximation spherical. The RSi particles consist of spherical main bodies carrying asperities on their surface which are irregularly distributed but approximately equal in height. TEM and SEM images from the HSi particles indicate a perfectly spherical shape and a narrow distribution of radii and shell thicknesses. The geometrical parameters and their relative standard deviation are listed in Table 1 together with the results from light scattering measurements. In all cases we observed that the hydrodynamic radius, 〈RH〉, is larger than the radius measured in TEM, 〈R〉TEM. For the rough particles this is intuitively understood, as the TEM radius is that of the central spherical body, which is identical with the SSi radius. The hydrodynamic radius is expected to be larger since the asperities will contribute to the hydrodynamic drag, additionally. In the case of SSi and HSi the discrepancy is explained in part by the fact that the two methods measure different averages of the size distribution. For a Gaussian distribution the ratio of both quantities is related to the relative standard deviation σ by 〈RH〉/〈R〉TEM= (1 + 3σ2)/(1 + σ2), since TEM measures the number average and DLS the z-average of a size distribution. However, for the SSi sample this would account only for about a two percent discrepancy, based on the relative standard deviation observed in TEM. For the HSi sample the expected difference is even smaller. Most likely the discrepancy is explained by the presence of a small fraction of aggregates. In the case of HSi the presence of aggregates with a hydrodynamic radius of 2 × 〈R〉TEM, the same relative standard deviation as the main population and a relative volume fraction of 5% would account for the deviation.
The electron microscopy and DLS findings were further underpinned by static light scattering measurements. The radius of gyration, 〈RG〉, for the three particle types listed in Table 1 were obtained from Guinier extrapolations. For the HSi particles the ratio ρ = 〈RG〉/〈RH〉 = 0.71, which is about ten percent smaller than the expected value for a perfect sphere of  . While for the RSi particles we found an intermediate value of ρ = 0.86, the value for HSi ρ = 0.91, which is about ten percent smaller than expected for an infinitely thin shell. Although these ratios appear reasonable, it has to be noted that the particles sizes (in particular for HSi) are beyond the limits where Guinier's approximation can be safely applied and the values for 〈RG〉 should be taken with care. More detailed information can be obtained from the SLS data by analysing the particle form factor. In Fig. 3 we present the experimentally determined P(Q) vs. Q data for the SSi and HSi. While the SSi form factor is featureless, the data from the HSi particles show a distinct minimum around Q ≈ 0.022 nm−1. Non-linear least squares fitting with the form factor for polydisperse spheres and spherical shells50 resulted in values for radius, shell thickness and relative standard deviations, which are in very good agreement with the TEM data.
. While for the RSi particles we found an intermediate value of ρ = 0.86, the value for HSi ρ = 0.91, which is about ten percent smaller than expected for an infinitely thin shell. Although these ratios appear reasonable, it has to be noted that the particles sizes (in particular for HSi) are beyond the limits where Guinier's approximation can be safely applied and the values for 〈RG〉 should be taken with care. More detailed information can be obtained from the SLS data by analysing the particle form factor. In Fig. 3 we present the experimentally determined P(Q) vs. Q data for the SSi and HSi. While the SSi form factor is featureless, the data from the HSi particles show a distinct minimum around Q ≈ 0.022 nm−1. Non-linear least squares fitting with the form factor for polydisperse spheres and spherical shells50 resulted in values for radius, shell thickness and relative standard deviations, which are in very good agreement with the TEM data.
 | ||
| Fig. 4 Normalized parallel diffusion coefficients versus normalized penetration depth for three types of particles as indicated in the legend. The symbols are the experimental data and the error bars represent standard deviations from three consecutive experiments. The full line is the prediction for hard sphere particles according to ref. 46. | ||
The data from the SSi particles may be considered to agree, except for one outlier at high penetration depth, with the theoretical reference curve for hard spheres (HS)46 within experimental scatter. The HSi data are systematically, though not much, smaller than the HS-prediction, while the RSi particles show a significantly slower near wall diffusion than hard sphere particles. While the HSi data follow the trend of the HS-predictions at a somewhat lower level, the RSi data show a qualitatively different behaviour. Except for the outlier at the highest penetration depth, the gradient of the experimental data is always larger than that predicted for the reference system. It is tempting to assign this observation to the particle shape, i.e. the surface roughness. However, hydrodynamic theory predicts that surface roughness will reduce the wall drag effect as compared to smooth spherical particles with the same hydrodynamic radius.37–39
An alternative interpretation is based on the static interaction between the particles and the glass surface. The theoretical prediction for the near-wall dynamics of hard sphere particles shown in Fig. 4 is based on the assumption that the particle number density, n(z), is constant throughout the entire sample down to the wall. This assumption is invalid, if static interactions other than the excluded volume are effective, as the density depends on the potential by Boltzmann's law. The effect of a DLVO interaction potential plus a gravitational contribution between monodisperse spheres and the wall on n(z) is demonstrated in Fig. 5 for particles with 100 nm radius and fixed Hamaker constant AH = 0.5kBT. For Ber > AH the near surface region is significantly depleted of particles up to a range of about three particle radii, while an enrichment of particles occurs, if Ber is of the order of or smaller than the Hamaker constant. Since the near wall diffusion coefficient increases with separation distance according to eqn (1) it is expected that the experimental values for 〈D‖〉(κ)/D0 are larger than those predicted for hard spheres, if the static interaction with the wall is mainly repulsive and vice versa. We will discuss this effect quantitatively in Section 4.2.
 | ||
| Fig. 5 Left: Sphere-wall interaction potentials calculated with eqn (7) for R = 100 nm, AH = 0.5kBT, λD−1 ≈ 100 nm, Δρm = 1 g mL−1 and amplitudes of the electrostatic repulsion Ber as indicated in the legend. The inset highlights the shallow minimum, marked by the vertical line for the potential with Ber = 0.5kBT which is due to the gravitational contribution. Right: Particle number densities normalized by the value for hard spheres versus separation distance, calculated with Boltzmann's law, using the potentials shown in the left panel. | ||
It is worth noting that the gravitational contribution to the interaction potential (i.e. sedimentation) causes a shallow (secondary) minimum in the potential, which causes a small (secondary) maximum in the particle density distribution. However, for the particle sizes and density mismatches considered here, the effect of sedimentation on the particle dynamics is negligible as compared to the DLVO interactions.
There are two further effects which might cause the observed deviations of our experimental dynamic data from the hard sphere prediction, i.e. particle polydispersity and the resulting influence of the particle form amplitude on the experimental 〈Γ〉-values according to eqn (11) and particle aggregation in combination with enhanced sedimentation of the aggregates. Both effects will also be analysed in detail in Section 4.2.
4.2 Numerical calculations
 | ||
| Fig. 6 Normalized parallel diffusion coefficients versus normalized penetration depth for hollow shells interacting only by excluded volume, with a constant shell thickness of 20 nm and a Gaussian distribution of the outer radius with μ = 150 nm and relative standard variations as indicated in the legend. Inset: Dependence of the initial relaxation rate on Q‖2. Symbols are the data calculated using eqn (1), (2), (6), (11) and (13). The full line is the prediction for monodisperse hard sphere particles according to Brenner.46 | ||
In all calculations concerning polydisperse or aggregating (Section 4.2.2) systems a density mismatch of Δρm = 1 g mL−1 was incorporated to consider the enhanced sedimentation of larger particles. At low penetration depths systematic deviations from the prediction for monodisperse hard spheres towards slower dynamics are observed. However, the deviation is smaller than typical experimental scatter. Only at the largest polydispersity, and high penetration depths a significant deviation towards faster diffusion coefficients occurs. Similarly small effects are observed for spherical particles, where generally, the effect of polydispersity becomes larger with decreasing particle size, which is shown in the ESI.†
An analytical expression for B(Q) of rough particles is in general not available. However, assuming that the asperities are small compared to the overall particle size, their average separation distance is small compared to the laser wavelength and they are randomly distributed, the form amplitude can be approximated by that of a spherical core particle plus a thin shell with the scattering length density of the asperities and an effective thickness which is very small compared to the reciprocal scattering vector. We may therefore assume that the effect of form amplitude and polydispersity is similarly small as observed for spheres and spherical shells.
Calculated data of the normalized diffusion coefficients vs. normalized penetration depth are shown in Fig. 7 for a system consisting of a major population with μ = 100 nm and minor populations with μagg varying up to 1000 nm and ϕagg = 0.05 (left panel). Obviously, the presence of aggregates causes a strong slowing down of the system's near wall dynamics, even if the average hydrodynamic radius of the aggregates is only twice the size of the single particles. Data for this size ratio and varying relative volume fraction of the minor population is shown in the right panel of Fig. 7. The dynamics of the system with μagg = 2μ and ϕagg ≈ 0.03 shows a similar deviation from the monodisperse reference system as the experimental HSi data. However, in all cases the calculated data show a smaller gradient than the reference systems which is clearly different from the trend of the experimental RSi data.
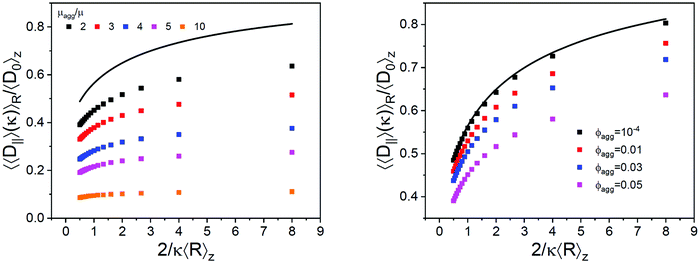 | ||
| Fig. 7 Normalized parallel diffusion coefficients versus normalized penetration depth for systems of spheres with a bimodal Gaussian size distribution. The major population has a number average size of μ = 100 nm and both populations have a relative standard deviation of σ = 0.05. Left panel: The minor population has a relative volume fraction of ϕagg = 0.05 and their mean size μagg is varied as indicated in the legend. Right panel: The minor population has a number average size of μagg = 2μ and varying relative volume fractions as indicated in the legend. Symbols are the data calculated using eqn (1), (2), (6), (11) and (12). The full line is the prediction for monodisperse hard sphere particles according to Brenner.46 | ||
 | ||
| Fig. 8 Normalized parallel near wall diffusion coefficients versus normalized penetration depth for spherical particles interacting with the wall by the potentials displayed in Fig. 5 (left) and with Ber = 1kBT (right) and varying Hamaker constants as indicated in the legend. In all cases the excess mass density was chosen Δρm = 1 g mL−1. Symbols are data calculated using eqn (1), (2), (6), (11) and (12). The full line represents the prediction for the hard sphere reference system according to Brenner.46 | ||
In the right panel of Fig. 8 we show the influence of varying Hamaker constants at a constant moderate electrostatic repulsion on the near-wall dynamics. At finite Hamaker constants, the calculated values are slower than those of the reference system, for almost all penetration depths. Only at the largest penetration depth investigated, the calculated dynamics appear to converge towards the reference data. At Hamaker constants AH ≥ Ber the calculated data deviate from the reference data similarly to the experimental data of the RSi system.
 | ||
| Fig. 9 Normalized parallel diffusion coefficients versus normalized penetration depth. Symbols are experimental data from the SSi-, the HSi- and the RSi-system, as indicated in the legend. Full lines represent data calculated using eqn (1), (2), (6), (11) and (12) and the parameters listed in Table 2. | ||
| Particle type | 〈RH〉z (nm) | σ | B er (kBT) | A H (kBT) | ϕ agg |
|---|---|---|---|---|---|
| SSi | 71 | 0.05 | 1.5 | 0.5 | 5 × 10−3 |
| HSi | 154 | 0.05 | 1.0 | 0.25 | 0.03 |
| RSi | 80 | 0.05 | 1.5 | 2.75 | 5 × 10−3 |
For the SSi- and HSi-system we could obtain a reasonable match of calculated with experimental data using an amplitude of the electrostatic repulsion of the order of kBT and some fraction of kBT for the Hamaker constant. The electrostatic amplitude of the particle–wall interaction corresponds to an effective surface potential Ψp,w ≈ −2 mV which is about an order of magnitude smaller than that reported in the literature51–53 based on total reflection microscopy measurements of the interaction potential between 2 μm Stöber–Silica particles and fused silica microscopy slides. Similarly, the ζ-potentials of all three systems are in the range of −30 to −40 mV. However it is important to note that the value of Ber is determined by the product of the particle's and wall's surface potentials. In the present case, the wall consists of a special high refractive index quartz glass (SF10) and there are indications in the literature that the surface charge density of quartz may54 be one to two orders of magnitude lower than that of silica.55 We therefore reckon that the small value of Ber is due to the low surface potential of the wall. Finally, the Ber-values for all three systems investigated here are about equal, which makes us confident that they are reliable. The found Hamaker constants of order AH ≤ kBT are in the range expected for non-retarded van der Waals interactions calculated based on the Lifshitz theory56 for silica interacting with quartz across water.
In the case of the HSi-system, we had to allow for a higher relative volume fraction of “aggregates” to obtain a satisfying match of the calculated data with experiments. This is probably due to the fact that HSi particles were calcined and thus dried during synthesis to remove the organic core onto which the silica shell had been grown.42 The probability of aggregates, which were not properly dispersed, being present is therefore higher than in samples which were never dried. Furthermore, spinning down aggregates is less effective than with full body particles due to the reduced excess mass density.
The most striking finding is, however, that for the RSi-particles the Hamaker constant required to allow for a match of calculated with experimental data is an order of magnitude larger than for the HSi- and SSi-systems. This implies that surface roughness plays an important role for the particle wall interaction and the resulting near wall dynamics. It is known from simulation work that surface roughness will enhance both electrostatic repulsion and van der Waals attraction, simply because the effective surface to surface separation is reduced by asperities. Walz et al. reported a lowering of the stabilisation barrier of the resulting DLVO-potential by about 10 to 15%, due to the different distance dependence of attraction and repulsion.31 A similar reduction of the stabilization barrier was reported by Bhattacharjee et al.30 Furthermore, these authors observe that the primary minimum of the DLVO interaction potential completely vanishes due to asperities. This might explain why our rough particles do not stick irreversibly to the glass surface, despite the large Hamaker constant. In this respect our findings may be regarded as additional experimental evidence for the predicted roughness effects on DLVO interaction energies. The resulting deviation of the dynamic data from the predictions for the reference hard sphere system are a mere consequence of the particle wall interaction potential and the resulting variation of number density with separation distance over which EWDLS inherently integrates.
Our findings might pave the way to a new method for the measurement of static particle wall interactions. Although the technique, especially the data analysis by comparison to model calculations, is cumbersome and not very efficient at this time, it might provide an extension of the classical total internal reflection microscopy (TIRM) technique.57 While TIRM requires particle sizes which are typically in the range of several micrometres, EWDLS allows measurements on particles as small as 30 nm in radius.14
5 Conclusions
The Brownian near wall dynamics of different types of suspended silica particles were examined by evanescent dynamic light scattering. While the experimental averaged diffusion coefficients parallel to the wall for smooth full spheres (SSi) and hollow spherical porous shells (HSi) might be considered to be in qualitative agreement with theoretical predictions for the hard sphere reference system, particles with a rough surface (RSi) show significant deviations. The averaged diffusion constants are significantly smaller than for smooth non-interacting particles which is in conflict with hydrodynamic theory.37–39 To interpret these observations, systematic numerical calculations were performed to investigate the effect of particle polydispersity, the presence of aggregates and static particle–wall interactions on the dynamics. By comparison with experimental data we found that for the SSi and HSi systems very good agreement can be obtained by including a small fraction of aggregates and a particle–wall DLVO interaction, with a Hamaker constant and an amplitude of the electric double layer repulsion, both in the range of ≈kBT. For the RSi system, at least a five times higher Hamaker constant needs to be taken into account to match the calculated data to the experimental results. Despite the high Hamaker constant the rough particles do not adsorb to the wall irreversibly. Both findings are consistent with the simulation results, which show that the DLVO stabilization barrier is significantly reduced by surface roughness31 and that the primary DLVO minimum completely vanishes for rough particles.30 We conclude that particle near wall dynamics are very sensitive to surface roughness where the theoretically predicted reduction of the flow resistance can be largely overcompensated by the effect of static particle wall interaction and the resulting particle number density profile.Author contributions
J. Alejandro Rivera-Morán: investigation, formal analysis, writing – review and editing; Yi Liu: investigation, formal analysis, validation, writing – review and editing; Samuel Monter: investigation, formal analysis, software, validation, writing – review and editing; Chiao-Peng Hsu: resources, writing – review and editing; Pia Ruckdeschel: resources; Markus Retsch: resources, writing – review and editing; Maciej Lisicki: funding acquisition, conceptualization, writing – review and editing; Peter R. Lang: conceptualization, funding acquisition, software, supervision, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Sara Bals, Qiongyang Chen and Hans Vanrompay from EMAT at the University of Antwerp for the TEM-investigation of the SSi and RSi particles and we gratefully acknowledge helpful discussions with Jan Dhont, Gerhard Nägele and Gunwoo Park from Forschungszentrum Jülich GmbH, IBI-4. This work has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 731019 (EUSMI).Notes and references
-
H. A. Lorentz, Abhandlung über Theoretische Physik: Ein allgemeiner Satz, die Bewegung einer reibenden Flüssigkeit betreffend, nebst einigen Anwendungen desselben, B.G. Teubner, Leipzig and Berlin, 1907 Search PubMed
.
- H. Faxén, Ark. Mat. Astron. Fys., 1923, 17, 1 Search PubMed
.
- Z. Adamczyk, M. Adamczyk and T. van de Ven, J. Colloid Interface Sci., 1983, 96, 204–213 CrossRef CAS
.
- K. H. Lan, N. Ostrowsky and D. Sornette, Phys. Rev. Lett., 1986, 57, 17–20 CrossRef PubMed
.
- B. Lin, J. Yu and S. A. Rice, Colloids Surf., A, 2000, 174, 121–131 CrossRef CAS
.
- B. H. Lin, J. Yu and S. A. Rice, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 3909–3919 CrossRef CAS PubMed
.
- H. B. Eral, F. Mugele and M. H. G. Duits, Langmuir, 2011, 27, 12297–12303 CrossRef CAS PubMed
.
- J. Y. Walz and L. Suresh, J. Chem. Phys., 1995, 103, 10714–10725 CrossRef CAS
.
- L. Joly, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2006, 96, 046101 CrossRef CAS PubMed
.
- M. Hosoda, K. Sakai and K. Takagi, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 6275–6280 CrossRef CAS
.
- M. I. Feitosa and O. N. Mesquita, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 6677–6685 CrossRef CAS PubMed
.
- N. Garnier and N. Ostrowsky, J. Phys. II, 1991, 1, 1221–1232 CrossRef CAS
.
- P. Holmqvist, J. K. G. Dhont and P. R. Lang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021402 CrossRef PubMed
.
- P. Holmqvist, J. K. G. Dhont and P. R. Lang, J. Chem. Phys., 2007, 126, 044707 CrossRef PubMed
.
- M. Lisicki, B. Cichocki, J. K. G. Dhont and P. R. Lang, J. Chem. Phys., 2012, 136, 204704 CrossRef PubMed
.
- M. Lisicki, B. Cichocki, S. A. Rogers, J. K. G. Dhont and P. R. Lang, Soft Matter, 2014, 10, 4312–4323 RSC
.
- Y. Liu, J. Blawzdziewicz, B. Cichocki, J. K. G. Dhont, M. Lisicki, E. Wajnryb, Y.-N. Young and P. R. Lang, Soft Matter, 2015, 11, 7316–7327 RSC
.
- Y. Liu, N. Claes, B. Trepka, S. Bals and P. R. Lang, Soft Matter, 2016, 12, 8485–8494 RSC
.
- V. N. Michailidou, G. Petekidis, J. W. Swan and J. F. Brady, Phys. Rev. Lett., 2009, 102, 068302 CrossRef CAS PubMed
.
- V. N. Michailidou, J. W. Swan, J. F. Brady and G. Petekidis, J. Chem. Phys., 2013, 139, 164905 CrossRef CAS PubMed
.
- D. Grasso, K. Subramaniam, M. Butkus, K. Strevett and J. Bergendahl, Rev. Environ. Sci. Biotechnol., 2002, 1, 17–38 CrossRef CAS
.
- D. Kleshchanok, R. Tuinier and P. R. Lang, Smart Colloidal Mater., 2008, 20, 073101 Search PubMed
.
- Q. Li, U. Jonas, X. S. Zhao and M. Kappl, Asia-Pac. J. Chem. Eng., 2008, 3, 255–268 CrossRef CAS
.
- V. Dahirel and M. Jardat, Curr. Opin. Colloid Interface Sci., 2010, 15, 2–7 CrossRef CAS
.
- M. Zanini, C.-P. Hsu, T. Magrini, E. Marini and L. Isa, Colloids Surf., A, 2017, 532, 116–124 CrossRef CAS
.
- L. C. Hsiao, S. Jamali, E. Glynos, P. F. Green, R. G. Larson and M. J. Solomon, Phys. Rev. Lett., 2017, 119, 158001 CrossRef PubMed
.
- L. C. Hsiao and S. Pradeep, Curr. Opin. Colloid Interface Sci., 2019, 43, 94–112 CrossRef CAS
.
- C.-P. Hsu, S. N. Ramakrishna, M. Zanini, N. D. Spencer and L. Isa, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5117–5122 CrossRef CAS PubMed
.
- D. Lootens, H. van Damme, Y. Hémar and P. Hébraud, Phys. Rev. Lett., 2005, 95, 268302 CrossRef PubMed
.
- S. Bhattacharjee, C.-H. Ko and M. Elimelech, Langmuir, 1998, 14, 3365–3375 CrossRef CAS
.
- J. Y. Walz, Part. Surf., 2002, 7, 151–169 Search PubMed
.
- L. Suresh and J. Y. Walz, J. Colloid Interface Sci., 1996, 183, 199–213 CrossRef CAS
.
- L. Suresh and J. Y. Walz, J. Colloid Interface Sci., 1997, 196, 177–190 CrossRef CAS PubMed
.
- C. Jin, T. Glawdel, C. L. Ren and M. B. Emelko, Sci. Rep., 2015, 5, 17747 CrossRef CAS PubMed
.
- N. J. Wagner and J. F. Brady, Phys. Today, 2009, 62, 27–32 CrossRef CAS
.
- B. Schroyen, C.-P. Hsu, L. Isa, P. van Puyvelde and J. Vermant, Phys. Rev. Lett., 2019, 122, 218001 CrossRef CAS PubMed
.
- B. Cichocki and R. B. Jones, Phys. A, 1998, 258, 273–302 CrossRef CAS
.
- G. C. Abade, B. Cichocki, M. L. Ekiel-Jeżewska, G. Nägele and E. Wajnryb, J. Chem. Phys., 2012, 136, 104902 CrossRef PubMed
.
- J. Riest, T. Eckert, W. Richtering and G. Naegele, Soft Matter, 2015, 11, 2821–2843 RSC
.
- C. Kunert, J. Harting and O. I. Vinogradova, Phys. Rev. Lett., 2010, 105, 016001 CrossRef PubMed
.
- O. I. Vinogradova and A. V. Belyaev, J. Phys. Condens. Matter, 2011, 23, 184104 CrossRef PubMed
.
- P. Ruckdeschel, M. Dulle, T. Honold, S. Förster, M. Karg and M. Retsch, Nano Res., 2016, 9, 1366–1376 CrossRef CAS
.
- P. A. Midgley and M. Weyland, Ultramicroscopy, 2003, 96, 413–431 CrossRef CAS PubMed
.
- T. K. Moon, IEEE Signal Process. Mag., 1996, 13, 47–60 CrossRef
.
- A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 637–651 CrossRef CAS
.
- H. Brenner, Chem. Eng. Sci., 1961, 16, 242–251 CrossRef CAS
.
- M. A. Bevan and D. C. Prieve, J. Chem. Phys., 2000, 113, 1228–1236 CrossRef CAS
.
- H. C. Hamaker, Physica, 1937, 4, 1058–1072 CrossRef CAS
.
- S. Lin and M. R. Wiesner, Langmuir, 2010, 26, 16638–16641 CrossRef CAS PubMed
.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171–210 CrossRef CAS
.
- H.-J. Wu and M. A. Bevan, Langmuir, 2005, 21, 1244–1254 CrossRef CAS PubMed
.
- H.-J. Wu, T. O. Pangburn, R. E. Beckham and M. A. Bevan, Langmuir, 2005, 21, 9879–9888 CrossRef CAS PubMed
.
- T. D. Iracki, D. J. Beltran-Villegas, S. L. Eichmann and M. A. Bevan, Langmuir, 2010, 26, 18710–18717 CrossRef CAS PubMed
.
- X. Shen, A. E. Wang, R. M. Sankaran and D. J. Lacks, J. Electrost., 2016, 82, 11–16 CrossRef CAS
.
- S. H. Behrens and D. G. Grier, J. Chem. Phys., 2001, 115, 6716–6721 CrossRef CAS
.
- B. Lennart, Adv. Colloid Interface Sci., 1997, 70, 125–169 CrossRef
.
- D. C. Prieve, Adv. Colloid Interface Sci., 1999, 82, 93–125 CrossRef CAS
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01191j |
| ‡ Present address: Technische Universität München, Germany. |
| This journal is © The Royal Society of Chemistry 2021 |




