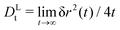Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tracer dynamics in crowded active-particle suspensions
Julian
Reichert
a and
Thomas
Voigtmann
 *ab
*ab
aInstitut für Materialphysik im Weltraum, Deutsches Zentrum für Luft- und Raumfahrt (DLR), 51170 Köln, Germany. E-mail: thomas.voigtmann@dlr.de
bDepartment of Physics, Heinrich-Heine Universität Düsseldorf, Universitätsstr. 1, 40225 Düsseldorf, Germany
First published on 9th November 2021
Abstract
We discuss the dynamics of active Brownian particles (ABPs) in crowded environments through the mean-squared displacement (MSD) of active and passive tracer particles in both active and passive host systems. Exact equations for the MSD are derived using a projection operator technique, extending to dense systems the known solution for a single ABP. The interaction of the tracer particle with the host particles gives rise to strong memory effects. Evaluating these approximately in the framework of a recently developed mode-coupling theory for active Brownian particles (ABP-MCT), we discuss the various dynamical regimes that emerge: While self-propelled motion gives rise to super-diffusive MSD, at high densities, this competes with an interaction-induced sub-diffusive regime. The predictions of the theory are shown to be in good agreement with results obtained from an event-driven Brownian dynamics (ED-BD) simulation scheme for the dynamics of two-dimensional active Brownian hard disks.
1 Introduction
The observation of active motion of self-propelled micro-organisms and the peculiar collective effects that it gives rise to, is a fascinating topic of biophysics that has stipulated a vast, rapidly growing research field in soft matter and non-equilibrium statistical physics.1,2 Since microswimmers are subject to both passive Brownian motion as well as to active driving, the active Brownian particle (ABP) model3 has emerged as a convenient model system to study the interplay of the two kinds of forces. Interest in the ABP model is further stirred by the experimental realization through colloidal Janus particles.4 Direct observation in quasi-two-dimensional (2D) setups makes the mean-squared displacement (MSD) a key quantity to discuss.5 The MSD of a single ABP can be obtained analytically, and this already displays some interesting features: After a short-time asymptote that is passive-diffusive, ∼t, a cross-over to a super-diffusive transient, ∼t2, signals persistent swimming, before Brownian rotational diffusion leads to a long-time asymptote that is again diffusive, but with an activity-enhanced diffusion coefficient. The appearance of a super-diffusive regime in the MSD also signals the non-equilibrium nature of the motion.Analytical solutions for interacting ABP are not available. Yet the motion of both active and passive colloids in a crowded host suspension (passive or active) is of high interest. Active tracer particles in passive suspensions can potentially be exploited as heat engines.6 Recent observations specifically focussed on how a single Janus colloid changes its dynamics when embedded in a glass-forming suspension of passive colloids,5 and how colloidal motion is influenced by bacterial baths.7 The latter case, that of a passive colloid in an active fluid, is a widely used micro-rheology technique to infer properties of the host medium through the tracer-particle motion.8 The MSD of a passive tracer in active suspension shows clear signs of the non-equilibrium bath dynamics.9–16 The passive tracer thus acts as a “thermometer” to define an effective activity-induced temperature17–19 and to quantify the deviations from equilibrium.19,20 In general this poses the question how the activity of the host suspension “transfers” to the probe.21
Here we derive evolution equations to describe the MSD of ABP in dense systems. We demonstrate the general structure of the evolution equations, where the effect of the surrounding bath is “integrated out” to appear in a set of well-defined memory kernels. The equations are derived rigorously within the Mori–Zwanzig projection-operator approach for the angle-resolved tagged-particle density correlation function, to obtain in the limit q → 0 two coupled integro-differential equations that contain the coupling to the dense host system in three memory kernels corresponding to translational (angular mode l = 0) and dipolar-like (l = ±1) couplings. The equations reduce to ordinary differential equations whose solution is the well known analytical result for a single ABP, if these memory kernels are dropped. The memory kernels have explicit microscopic expressions, and are the target of approximation schemes. Modeling the memory kernels by a recent extension of the mode-coupling theory of the glass transition, the mode-coupling theory for active Brownian particles (ABP-MCT),22–24 we obtain theoretical predictions for the MSD in the various cases of active and passive tracers in active and passive host systems, and we compare those results to event-driven Brownian dynamics (ED-BD) computer simulation. As one nears kinetic arrest in the host system, there emerges an interplay between the time scales of the free active motion, and that of steric-hindrance induced caging provided by the host particles.
2 Theory
We consider the active Brownian particle (ABP) equations of motion in 2D,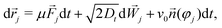 | (1a) |
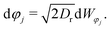 | (1b) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) j =
j = ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) j(φj) = (cos
j(φj) = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φj,sin
φj,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φj)T evolves purely through rotational diffusion, where translational and rotational diffusion are driven by independent Wiener processes d
φj)T evolves purely through rotational diffusion, where translational and rotational diffusion are driven by independent Wiener processes d![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) j and d
j and d![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) φj. The
φj. The ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) j = −∇jU({
j = −∇jU({![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) k}) are potential interaction forces that are taken to be steeply repulsive to model hard-disk behavior. In absence of active driving, the system is in thermal equilibrium, thus the mobility obeys the fluctuation–dissipation theorem, μ = Dt. In the active system, each particle experiences a constant self-propulsion force given by the swimming speed v0, along its current director
k}) are potential interaction forces that are taken to be steeply repulsive to model hard-disk behavior. In absence of active driving, the system is in thermal equilibrium, thus the mobility obeys the fluctuation–dissipation theorem, μ = Dt. In the active system, each particle experiences a constant self-propulsion force given by the swimming speed v0, along its current director ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) j.
j.
Into the N-particle system of ABP with self-propulsion velocity v0, we embed a single tracer particle (position ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) s, orientation φs) with self-propulsion velocity vs0, whose equations of motion are again given by the equivalent of eqn (1). We allow for the case of a tracer of different interactions than among the host particles, and also different short-time diffusion coefficients Dst and Dsr, although in the discussion we will focus on otherwise identical particles that merely differ in their self-propulsion speeds. In particular this covers the experimentally relevant cases of a passive tracer in an active host system (vs0 = 0, v0 ≠ 0) and the reversed case of a single ABP that is embedded in a passive glass-forming fluid (vs0 ≠ 0 but v0 = 0).
s, orientation φs) with self-propulsion velocity vs0, whose equations of motion are again given by the equivalent of eqn (1). We allow for the case of a tracer of different interactions than among the host particles, and also different short-time diffusion coefficients Dst and Dsr, although in the discussion we will focus on otherwise identical particles that merely differ in their self-propulsion speeds. In particular this covers the experimentally relevant cases of a passive tracer in an active host system (vs0 = 0, v0 ≠ 0) and the reversed case of a single ABP that is embedded in a passive glass-forming fluid (vs0 ≠ 0 but v0 = 0).
The MSD is defined by
δr2(t) = 〈|![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) s(t) − s(t) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) s(0)|2〉, s(0)|2〉, | (2) |
Without interactions, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) j = 0, eqn (1) are readily solved3 to provide δr2(t) for a single, non-interacting ABP. Our aim is to extend this solution to interacting particles, encoding the interactions in retarded-friction memory kernels akin to a GLE description of the motion in a fluctuating environment.
j = 0, eqn (1) are readily solved3 to provide δr2(t) for a single, non-interacting ABP. Our aim is to extend this solution to interacting particles, encoding the interactions in retarded-friction memory kernels akin to a GLE description of the motion in a fluctuating environment.
2.1 Transient correlation functions
Eqn (1) describe a Markov process with configuration space elements Γ = ({![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j},{φj}) whose probability distribution p(Γ,t) evolves through the Smoluchowski equation ∂tp = Ωp, with the Smoluchowski operator
j},{φj}) whose probability distribution p(Γ,t) evolves through the Smoluchowski equation ∂tp = Ωp, with the Smoluchowski operator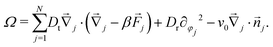 | (3) |
Microscopic observables of interest to describe the motion of the ABP are the angle-resolved fluctuating particle densities to wave vector ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) (of magnitude q = |
(of magnitude q = |![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) |) and angular-mode index l,
|) and angular-mode index l,
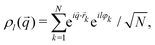 | (4) |
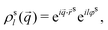 | (5) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) s,φs) is understood to be excluded from the sum over the N particles comprising the host system.
s,φs) is understood to be excluded from the sum over the N particles comprising the host system.
The ABP-MCT is built on the integration-through transients (ITT) framework25 that allows to treat formally the dynamical evolution of a non-equilibrium system with arbitrarily strong perturbation, and provides a starting point for approximations. In this framework, quantities of particular interest are the transient dynamical density correlation functions. In a spatially homogeneous system they are diagonal in ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) and read
and read
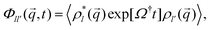 | (6) |
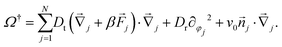 | (7) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ,0) = Sll′(q), where in the particular case of particles that interact through a spherically symmetric interaction potential,
,0) = Sll′(q), where in the particular case of particles that interact through a spherically symmetric interaction potential,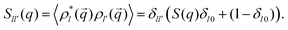 | (8) |
In a system that remains statistically isotropic, the dynamical correlation functions obey specific transformation rules under rotation. Introducing matrix notation for angular indices,
Φ(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ′,t) = u†·Φ( ′,t) = u†·Φ(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ,t)·u, ,t)·u, | (9) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ′ is the vector obtained by rotating
′ is the vector obtained by rotating ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) by an angle ψ, and ull′ = δll′
by an angle ψ, and ull′ = δll′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[ilψ]. In particular, letting θq be the angle of
exp[ilψ]. In particular, letting θq be the angle of ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) with the x-axis normal
with the x-axis normal ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) x, we define
x, we define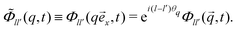 | (10) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ,t) are isotropic even functions of
,t) are isotropic even functions of ![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) . In particular the positional density-correlation function Φ00(q,t) is isotropic, even in q and real-valued.
. In particular the positional density-correlation function Φ00(q,t) is isotropic, even in q and real-valued.
The tracer motion is characterized by the tagged-particle correlation function,
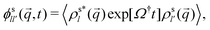 | (11) |
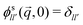 . Of particular interest here is the (00) element of that correlation function in the limit q → 0: it is by the rotation-transformation property an isotropic, real-valued even function of q and linked to the MSD; in two spatial dimensions,
. Of particular interest here is the (00) element of that correlation function in the limit q → 0: it is by the rotation-transformation property an isotropic, real-valued even function of q and linked to the MSD; in two spatial dimensions,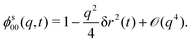 | (12) |
2.2 Mori–Zwanzig evolution equations
An exact evolution equation for the density-correlation functions can be obtained through a projection operator scheme. In essence, one rewrites the propagator exp[Ω†t] in terms of its action on the projected subspace![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) spanned by the fluctuating densities, and a remainder within the orthogonal projection
spanned by the fluctuating densities, and a remainder within the orthogonal projection ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) = 1 −
= 1 − ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) that gives rise to a non-Markovian evolution of the projected variables expressed through memory integrals. Specifically, we project onto all angle-resolved density fluctuations,
that gives rise to a non-Markovian evolution of the projected variables expressed through memory integrals. Specifically, we project onto all angle-resolved density fluctuations, 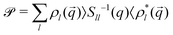 . Rewriting ∂t
. Rewriting ∂t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[Ω†t] = Ω†(
exp[Ω†t] = Ω†(![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) +
+ ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) )exp[Ω†t] and employing a Dyson decomposition for the second part,
)exp[Ω†t] and employing a Dyson decomposition for the second part, 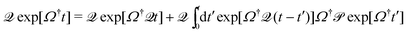 , this yields and expression for the evolution of density fluctuations that takes the form of a GLE, with a memory kernel given by the projected dynamics. After taking care to transform the memory kernel into a form that is one-particle irreducible, one obtains thus for the density-correlation function22,24
, this yields and expression for the evolution of density fluctuations that takes the form of a GLE, with a memory kernel given by the projected dynamics. After taking care to transform the memory kernel into a form that is one-particle irreducible, one obtains thus for the density-correlation function22,24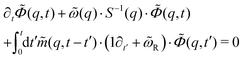 | (13) |
![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) (q,t) =
(q,t) = ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) (q,t)·
(q,t)·![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) T−1(q) is given by the formally exact expression
T−1(q) is given by the formally exact expression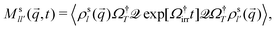 | (14) |
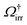 (see ref. 22 and 24 for details).
(see ref. 22 and 24 for details).
An important quantity here and in the following is the frequency matrix
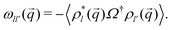 | (15) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) = ωT(
) = ωT(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) + ωR, where ωR,ll′ = δll′l2Dr and ωT(
) + ωR, where ωR,ll′ = δll′l2Dr and ωT(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) is given by the tri-diagonal matrix
) is given by the tri-diagonal matrix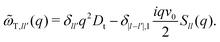 | (16) |
An equation analogous to eqn (13) can be derived for the tagged-particle correlator,
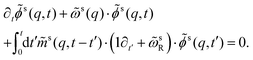 | (17) |
![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) is the analog of eqn (15) for the tagged particle (for which formally Sll(q) = 1).
) is the analog of eqn (15) for the tagged particle (for which formally Sll(q) = 1).
Eqn (13) and (17) constitute the starting point of our discussion of the MSD of active Brownian particles. According to eqn (12), the MSD is obtained from the q → 0 limit of eqn (17). In practice, evaluation of the memory kernel appearing in this equation, will also require knowledge of the collective dynamics in the form of eqn (13).
2.3 Low-density solution
We first recapitulate the solution at vanishing host-system density n. Since eqn (13) and (17) have been written such that the corresponding memory kernels are irreducible, these memory kernels are at least of![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (n), and can be dropped in the dilute limit. The low-density theory is thus given by
(n), and can be dropped in the dilute limit. The low-density theory is thus given by∂t![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (q,t) + (q,t) + ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (q)·S−1(q)· (q)·S−1(q)·![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (q,t) = 0, (q,t) = 0, | (18) |
![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) (q,t) = exp[
(q,t) = exp[![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (q)·S(q)−1t]S(q), and the corresponding expression holds for
(q)·S(q)−1t]S(q), and the corresponding expression holds for ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s(q,t). We note in passing that an alternative representation of the exact low-density solution is in terms of suitable eigenfunctions of the Smoluchowski operator for a free ABP,26,27 the Mathieu functions in 2D. It can be shown that the two representations are indeed equivalent.24
s(q,t). We note in passing that an alternative representation of the exact low-density solution is in terms of suitable eigenfunctions of the Smoluchowski operator for a free ABP,26,27 the Mathieu functions in 2D. It can be shown that the two representations are indeed equivalent.24
Specializing the tagged-particle equivalent of eqn (18) to the positional density correlator ϕs00(q,t), making use of the tri-diagonal structure of ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) s(q), we get
s(q), we get
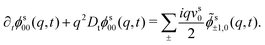 | (19) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s±1,0(q,t) is similarly given by
s±1,0(q,t) is similarly given by∂t![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s±1,0(q,t) + s±1,0(q,t) + ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) s±1,±1(q) s±1,±1(q)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s±1,0(q,t) + s±1,0(q,t) + ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) s±1,0(q) s±1,0(q)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s00(q,t) + s00(q,t) + ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) s±1,±2(q) s±1,±2(q)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s±2,0(q,t) = 0. s±2,0(q,t) = 0. | (20) |
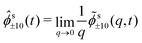 | (21) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (q) by the rotation property eqn (9). In leading order for q → 0, we can replace
(q) by the rotation property eqn (9). In leading order for q → 0, we can replace ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s00(q,t) = 1 and drop the last term in eqn (20), because
s00(q,t) = 1 and drop the last term in eqn (20), because ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s±2,0(q,t) =
s±2,0(q,t) = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (q2) due to the rotation property. Inserting the explicit expressions of
(q2) due to the rotation property. Inserting the explicit expressions of ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) s(q), one obtains finally the coupled differential equations that determine the MSD,
s(q), one obtains finally the coupled differential equations that determine the MSD,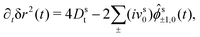 | (22a) |
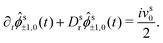 | (22b) |
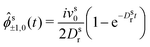 | (23) |
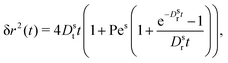 | (24) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) includes all angular-index values l. In principle, one could aim to derive an evolution equation for the MSD by projecting only on the l = 0 density fluctuations, but then a memory kernel would appear that does not vanish in the low-density limit.
includes all angular-index values l. In principle, one could aim to derive an evolution equation for the MSD by projecting only on the l = 0 density fluctuations, but then a memory kernel would appear that does not vanish in the low-density limit.
It is worth recalling the typical time- and length-scales that are inherent in eqn (24). After a short-time passive-Brownian regime, δr2 ≃ 4Dstt for t ≪ τv, a ballistic regime, δr2 ≃ (vs0)2t2 for τv ≪ t ≪ τl is followed by a final cross-over to an activity-enhanced diffusive regime, δr2 ≃ 4Dst(1 + Pes)t for t ≫ τl. Here, τv and τl mark the characteristic time scales of the free ABP, and they are associated with length scales 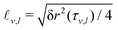 . From balancing the asymptotic expressions against each other, one obtains (dropping s superscripts for convenience)
. From balancing the asymptotic expressions against each other, one obtains (dropping s superscripts for convenience)
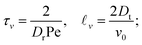 | (25a) |
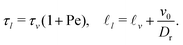 | (25b) |
2.4 General equations for the MSD
To derive expressions for the MSD, eqn (17) needs to be evaluated in the limit q → 0. This requires an expression for the inverse of the frequency matrix ωsT(![[q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0071_20d1.gif) ) that appears in the definition of the memory kernel. The simple tri-diagonal structure,
) that appears in the definition of the memory kernel. The simple tri-diagonal structure,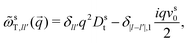 | (26) |
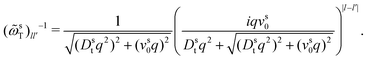 | (27) |
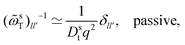 | (28) |
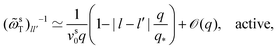 | (29) |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) sT(q) needs to be performed on the infinite-dimensional algebra of matrices labeled by angular-mode indices. Care has to be taken when introducing a cutoff for the angular modes, as is customary in numerical implementations: the cutoff matrix
sT(q) needs to be performed on the infinite-dimensional algebra of matrices labeled by angular-mode indices. Care has to be taken when introducing a cutoff for the angular modes, as is customary in numerical implementations: the cutoff matrix ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) sT(q) has an inverse that has the wrong q → 0 asymptote (either ∼ 1/q2 or constant for the (00) element, depending on whether the cutoff is performed at even or odd angular modes). The recognition that the inverse has to be performed before introducing a cutoff is crucial in deriving the correct MSD equations of motion.
sT(q) has an inverse that has the wrong q → 0 asymptote (either ∼ 1/q2 or constant for the (00) element, depending on whether the cutoff is performed at even or odd angular modes). The recognition that the inverse has to be performed before introducing a cutoff is crucial in deriving the correct MSD equations of motion.
To complete the derivation, the q → 0 limits of the memory kernels ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) s(q,t) are needed. Note first the case of a passive tracer: there,
s(q,t) are needed. Note first the case of a passive tracer: there, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) s(q,t) and
s(q,t) and ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) s(q) remain diagonal matrices, and
s(q) remain diagonal matrices, and ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) s00(q,t) =
s00(q,t) = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (q2). Hence, only the memory integral involving
(q2). Hence, only the memory integral involving ![[m with combining tilde]](https://www.rsc.org/images/entities/i_char_006d_0303.gif) s00 remains in the equation determining the MSD. For an active tracer, one needs to recognize that for l > 0,
s00 remains in the equation determining the MSD. For an active tracer, one needs to recognize that for l > 0, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) sl0(q,t) =
sl0(q,t) = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) ((iqvs0)|l|), and that the memory kernels
((iqvs0)|l|), and that the memory kernels ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) s(q,t) are of at least
s(q,t) are of at least ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (q0). Combined with the terms 1/q and 1/q2 that appear in
(q0). Combined with the terms 1/q and 1/q2 that appear in ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) T−1(q), the potentially relevant terms are
T−1(q), the potentially relevant terms are 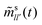 for l′ = ±1. In the q → 0 limit the powers of q stemming from
for l′ = ±1. In the q → 0 limit the powers of q stemming from ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) sl0(q,t) leave the quantities
sl0(q,t) leave the quantities 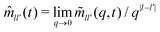 for |l − l′| ≤ 1 as the relevant memory kernels.24
for |l − l′| ≤ 1 as the relevant memory kernels.24
Hence, we arrive at the coupled integro-differential equations that describe the time-evolution of the ABP-MSD in a crowded environment,
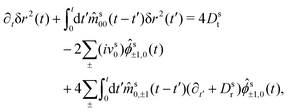 | (30a) |
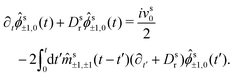 | (30b) |
Further evaluation requires specific expressions for the memory kernels. In principle, these have exact microscopic expressions as derived above. Due to the appearance of the irreducible projected dynamics, they are not straightforward to evaluate, but one could in principle use any suitable microscopic dynamic theory of the system (such as dynamic density functional theory) to approximate them. The results that we discuss in the following are obtained by employing ABP-MCT. This theory approximates the memory kernel ![[M with combining tilde]](https://www.rsc.org/images/entities/b_i_char_004d_0303.gif) s(q,t) as a bilinear functional involving the density correlation functions,
s(q,t) as a bilinear functional involving the density correlation functions,
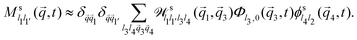 | (31) |
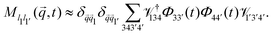 | (32) |
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) ,
, ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) †, and
†, and ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) are given in terms of the equilibrium static structure factor S(q) of the passive system; the ABP-MCT expressions can be found in ref. 24. As also shown there, a somewhat tedious procedure confirms that the MCT approximation preserves the correct low-q behavior of the memory kernels, so that the correct q → 0 limit of the evolution equations, eqn (30), is obtained within ABP-MCT.
are given in terms of the equilibrium static structure factor S(q) of the passive system; the ABP-MCT expressions can be found in ref. 24. As also shown there, a somewhat tedious procedure confirms that the MCT approximation preserves the correct low-q behavior of the memory kernels, so that the correct q → 0 limit of the evolution equations, eqn (30), is obtained within ABP-MCT.
The first line of eqn (30a) corresponds to the expression derived earlier for the MSD of a passive tracer in a dense system.28,29 In a passive host system, the memory kernel ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) s00(t) is a completely monotone function, i.e., it is positive and a continuous superposition of purely relaxing exponentials; as a consequence, the MSD of a passive tracer in a passive host system is always slowed down compared to free diffusion, and it follows an increasingly pronounced sub-diffusive regime with increasing host-system density. Within ABP-MCT, the effect of activity in the host system enters through a modification of the dynamics in the collective density correlation function
s00(t) is a completely monotone function, i.e., it is positive and a continuous superposition of purely relaxing exponentials; as a consequence, the MSD of a passive tracer in a passive host system is always slowed down compared to free diffusion, and it follows an increasingly pronounced sub-diffusive regime with increasing host-system density. Within ABP-MCT, the effect of activity in the host system enters through a modification of the dynamics in the collective density correlation function ![[capital Phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0db.gif) 00(p,t), cf.eqn (31). Since within the theory, the collective density correlations decay faster with increasing activity,22,24 this suggests enhanced diffusivity for the tracer particle due to active host-particle motion. However, there is also an explicit dependence of the coupling vertices
00(p,t), cf.eqn (31). Since within the theory, the collective density correlations decay faster with increasing activity,22,24 this suggests enhanced diffusivity for the tracer particle due to active host-particle motion. However, there is also an explicit dependence of the coupling vertices ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) on the host-system activity, whose structure admits more complex solutions; in particular, as we will discuss below, there appears a super-diffusive regime in the MSD even of a passive tracer particle. This is remarkable since it demonstrates the non-equilibrium nature of the motion: For dynamics driven by the equilibrium Smolchowski operator, it can be shown exactly, that there can be no superdiffusive regimes in the MSD. A brief proof for this statement is given in Appendix A.
on the host-system activity, whose structure admits more complex solutions; in particular, as we will discuss below, there appears a super-diffusive regime in the MSD even of a passive tracer particle. This is remarkable since it demonstrates the non-equilibrium nature of the motion: For dynamics driven by the equilibrium Smolchowski operator, it can be shown exactly, that there can be no superdiffusive regimes in the MSD. A brief proof for this statement is given in Appendix A.
2.5 Numerics and simulation
In the following, we discuss exemplary features of the solutions of eqn (30) for the case of 2D hard disks of diameter σ. The single control parameter for the passive system is then the dimensionless number density n, or the packing fraction φ = (π/4)nσ2. The size σ sets the unit of length, and σ2/Dt the unit of time. We consider tracer particles that are of the same size as the host particles, and unless otherwise noted, Dt = Dst = 1 and Dr = Dsr = 1 are chosen. We briefly outline the numerical evaluation of eqn (30) within ABP-MCT, and the ED-BD simulation scheme whose results we discuss in the following. Further details can be found in ref. 24 and 30.The ABP-MCT expressions for the memory kernels were discretized on an equidistant grid of 128 points in wave numbers q, with cutoff 40σ. A cutoff of L = 1 was used for the angular-mode indices, which allows to study the regime of not too large self-propulsion velocities in the theory. The current implementation suffers from numerical instabilities at large vs0 that arise from the specific details of the implementation of the integral solver, and the prohibitive memory and runtime requirements for matrices with larger cutoff L. We thus restrict the discussion of the theory to vs0 ≤ 8Dt/σ. To obtain the dynamics, ABP-MCT requires as input quantity the equilibrium static structure factor of the system, for which we use a recent result from density-functional theory (DFT).31
Simulations were carried out with N = 625 particles with uniform size polydispersity to avoid crystallization (standard deviation 0.2σ). The ED-BD scheme is essentially a rejection-free Monte Carlo approach32 where random Gaussian displacements are chosen at every time step in order to implement Brownian motion, and potential particle overlaps are resolved by performing elastic collisions between the particles. The inclusion of a suitable drift in the Gaussian displacements implements the active motion.33–35 Simulation trajectories were equilibrated for at least 104 time steps, and averaged over at least 200 realizations, and over initial times in the stationary regime.
3 Results
3.1 Passive tracer in passive bath
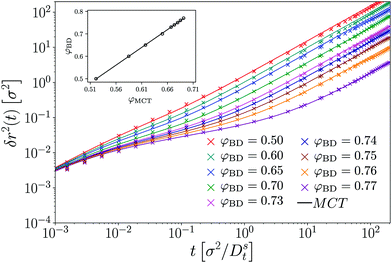
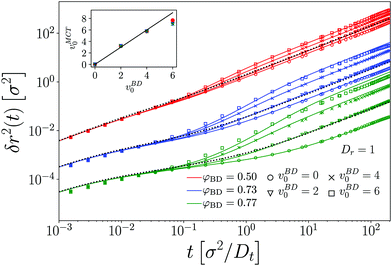
To establish a baseline for the comparison of MCT with our simulation data, we first briefly demonstrate the results obtained for a passive tracer particle in a passive host system (Fig. 1). In this comparison, we follow a well-established procedure to account for the fact that the theory predicts dynamical arrest at a packing fraction φc whose numerical value is different from the one seen in simulation. In particular, with the specific choice of numerical parameters and DFT static structure factor in our MCT calculations, we obtain φc,MCT ≈ 0.699 in close agreement with the result obtained from a modified hypernetted-chain (MHNC) approximation of S(q) and a somewhat different numerical integration scheme for the memory kernel.29 From the ED-BD simulations we estimate φc,BD ≈ 0.78.Since the relevant parameter describing the long-time dynamics in MCT is asymptotically linearly related to the control-parameter distance ε = φ − φc, up to a prefactor of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1), one expects that the theory describes the dynamics of the system after mapping the packing fraction φBD asymptotically linearly to a (smaller) packing fraction φMCT that enters the MCT calculations. This has been discussed in detail for three-dimensional (3D) hard spheres.36 Note that the mapping of packing fractions that we use here differs somewhat from the one that gives best agreement between theory and simulation for the density correlation functions at finite q;24 this also has previously been discussed in the 3D system36 and is attributed to a further quantitative error of the MCT approximation in the low-q regime of the memory kernel.
(1), one expects that the theory describes the dynamics of the system after mapping the packing fraction φBD asymptotically linearly to a (smaller) packing fraction φMCT that enters the MCT calculations. This has been discussed in detail for three-dimensional (3D) hard spheres.36 Note that the mapping of packing fractions that we use here differs somewhat from the one that gives best agreement between theory and simulation for the density correlation functions at finite q;24 this also has previously been discussed in the 3D system36 and is attributed to a further quantitative error of the MCT approximation in the low-q regime of the memory kernel.
Keeping this caveat in mind, we find (cf.Fig. 1) that after the adjustment of packing fractions, MCT provides an excellent quantitatively accurate description of the MSD obtained from our ED-BD simulations in the regime of packing fractions approaching φc.
The MSD show the typical features known from glass-forming Brownian systems: after a short-time diffusive asymptote, δr2 ≃ 4Dtt (in our systems where hydrodynamic interactions are absent), a regime of subdiffusive motion, i.e., of sublinear growth in δr2(t) as a function of time, marks the transient cageing of particles by their neighbors. On the fluid side of the glass transition that we study here, φ < φc, the MSD eventually crosses over to a long-time diffusive asymptote, δr2 ≃ 4DLtt, where DLt(φ) is the long-time translational self-diffusion coefficient that decreases strongly as φ is increased and is predicted by MCT to vanish at φc. Hence, as the density of the system is increased, the cageing regime extends to increasingly long times, and in the ideal glass predicted by MCT the MSD arrests to a finite plateau value, δr2(t) ≃ 4![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c2 as t → ∞ for φ ≥ φc. The length scale
c2 as t → ∞ for φ ≥ φc. The length scale ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c quantifies a typical “cage size” in the glass, and by a simple argument due to Lindemann is expected to be some fraction of the particle size, typically around 10%. Indeed, from inspection of Fig. 1 we estimate
c quantifies a typical “cage size” in the glass, and by a simple argument due to Lindemann is expected to be some fraction of the particle size, typically around 10%. Indeed, from inspection of Fig. 1 we estimate ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c ≈ 0.087σ in our system, in excellent agreement with the MCT prediction.
c ≈ 0.087σ in our system, in excellent agreement with the MCT prediction.
We restrict the discussion in the following to densites φBD ≤ 0.77, where the system still represents a fluid. At larger densities, the simulated MSD do not show the kinetic arrest in our 2D system that is predicted by MCT. This is a known effect from passive MCT in 3D.36 Although our systems should be small enough to observe kinetic arrest, in principle the effect of 2D-specific Mermin–Wagner fluctuations should also be taken into consideration, for example by studying the cage-relative MSD.37–41
3.2 Active tracer in passive bath
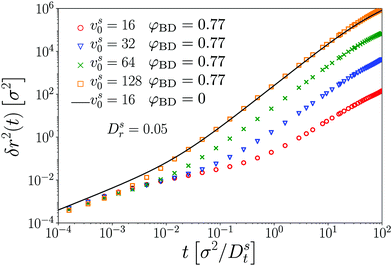
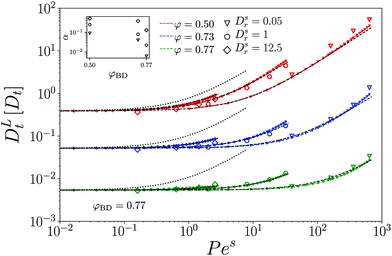
Having established the accuracy of MCT for the passive system after a suitable mapping of densities, we now turn to the dynamics of a single active tracer in a system of passive hard disks. The ED-BD simulation results and the predictions of MCT without further adjustment of parameters again are in very good agreement (Fig. 2), in the parameter range of vs0 within which we can obtain numerically stable solutions of the MCT equations of motion.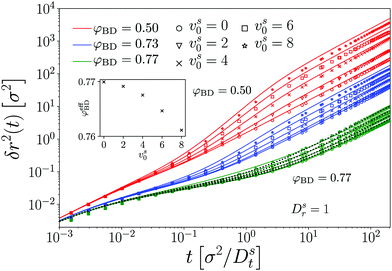 | ||
| Fig. 2 MSD δr2(t) of a single active Brownian particle in a bath of passive hard disks. Symbols are results from Brownian-dynamics simulations at packing fraction φBD as labeled (color-coded), for different self-propulsion velocities vs0 of the tracer (as labeled, increasing from bottom to top in each group of curves). Lines are results from MCT, with the adjustment of packing fractions shown in Fig. 1. Dotted lines for φ = 0.77 show fits using the MSD of a passive tracer at a reduced host-packing fraction φeff(vs0) (inset). | ||
We exemplarily discuss the case vs0 = 8 for the densities φ = 0.50 and φ = 0.77. Recall from eqn (25) that for a free ABP with vs0 = 8, a ballistic regime appears in the MSD for 4![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) v2 = 1/4 ≪ δr2 ≪ 1089/4 = 4
v2 = 1/4 ≪ δr2 ≪ 1089/4 = 4![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) l2. In the case of a moderately dense host system, φ = 0.50, the MSD or the ABP tracer still evidences this regime of persistent active motion. Yet, as the density of the passive host system is increased to φ = 0.77, both our simulations and theory indicate that a superdiffusive regime is not encountered any more. Here, the strong influence of the cage effect that is responsible for the glassy dynamics suppresses the persistent motion of the single active tracer particle.
l2. In the case of a moderately dense host system, φ = 0.50, the MSD or the ABP tracer still evidences this regime of persistent active motion. Yet, as the density of the passive host system is increased to φ = 0.77, both our simulations and theory indicate that a superdiffusive regime is not encountered any more. Here, the strong influence of the cage effect that is responsible for the glassy dynamics suppresses the persistent motion of the single active tracer particle.
Recall that ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c ≈ 0.087 ≪
c ≈ 0.087 ≪ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) v for the choice of parameters that we discuss here. It is thus plausible that the passive-host dynamics suppresses the persistent active motion of the tracer at sufficiently high densities, and as a result, the MSD at φ = 0.77 qualitatively appear as one would also observe for a passive tracer particle; the activity in this regime is only seen through an enhanced long-time diffusion. In fact, the data for φ = 0.77 can be fit with the MSD of a passive tracer, at an effectively reduced host-system packing fraction φeff(vs0) (dotted lines in Fig. 2). The φeff-vs.-vs0 relation (inset of the figure) shows the expected quadratic dependence on vs0 that conforms to the vs0 → –vs0 symmetry of the ensemble. In this system of active hard disks, where temperature is irrelevant (and only sets an overall time scale of the motion), φeff can be seen as the analog of an effective temperature, Teff(vs0) − T0 ∝ (vs0)2 in the sense that active motion reduces the coupling strength to the bath. From the low-density solution, eqn (24), one would identify Teff − T0 = Pe, and the corresponding enhancement of diffusivity for the parameters exemplified in Fig. 2 is a factor of 32. For the passive long-time dynamics, a change in (effective) temperature would bring about an even larger change in the long-time diffusivity, while the enhancement seen in Fig. 2 for φ = 0.77 is only around a factor 2. This clearly indicates the limitations of the effective-temperature picture42 for an ABP in a crowded medium.
v for the choice of parameters that we discuss here. It is thus plausible that the passive-host dynamics suppresses the persistent active motion of the tracer at sufficiently high densities, and as a result, the MSD at φ = 0.77 qualitatively appear as one would also observe for a passive tracer particle; the activity in this regime is only seen through an enhanced long-time diffusion. In fact, the data for φ = 0.77 can be fit with the MSD of a passive tracer, at an effectively reduced host-system packing fraction φeff(vs0) (dotted lines in Fig. 2). The φeff-vs.-vs0 relation (inset of the figure) shows the expected quadratic dependence on vs0 that conforms to the vs0 → –vs0 symmetry of the ensemble. In this system of active hard disks, where temperature is irrelevant (and only sets an overall time scale of the motion), φeff can be seen as the analog of an effective temperature, Teff(vs0) − T0 ∝ (vs0)2 in the sense that active motion reduces the coupling strength to the bath. From the low-density solution, eqn (24), one would identify Teff − T0 = Pe, and the corresponding enhancement of diffusivity for the parameters exemplified in Fig. 2 is a factor of 32. For the passive long-time dynamics, a change in (effective) temperature would bring about an even larger change in the long-time diffusivity, while the enhancement seen in Fig. 2 for φ = 0.77 is only around a factor 2. This clearly indicates the limitations of the effective-temperature picture42 for an ABP in a crowded medium.
The appearance and disappearance of superdiffusive motion is best seen by the effective power-law exponents associated to the MSD. Recall that for any function that is a power law, its logarithmic derivative α(t) = d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δr2(t)/d
δr2(t)/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t will be constant and equal to the power-law exponent. The effective exponents α(t) corresponding to the MSD shown in Fig. 2 confirm the interplay between subdiffusive cage motion, α < 1, and super-diffusive persistent active motion, α > 1, for the active tracer in the dense passive host system (Fig. 3). For the choice of parameters represented in the figure, the cage effect sets in at times earlier than the free-particle crossover to persistent motion, since
t will be constant and equal to the power-law exponent. The effective exponents α(t) corresponding to the MSD shown in Fig. 2 confirm the interplay between subdiffusive cage motion, α < 1, and super-diffusive persistent active motion, α > 1, for the active tracer in the dense passive host system (Fig. 3). For the choice of parameters represented in the figure, the cage effect sets in at times earlier than the free-particle crossover to persistent motion, since ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c ≪
c ≪ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) v. As a result, the effective exponent in all cases follows an S-shaped curve that first drops to values below unity, and increases to values above unity in the time window τv ≪ t ≪ τl that follows the cageing dynamics. The cross-over where the subdiffusive cage motion is modified by the tracer activity is, even at the density φ = 0.73, well predicted by τv (vertical dashed lines in Fig. 3).
v. As a result, the effective exponent in all cases follows an S-shaped curve that first drops to values below unity, and increases to values above unity in the time window τv ≪ t ≪ τl that follows the cageing dynamics. The cross-over where the subdiffusive cage motion is modified by the tracer activity is, even at the density φ = 0.73, well predicted by τv (vertical dashed lines in Fig. 3).
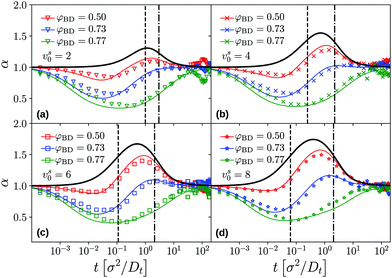 | ||
Fig. 3 Effective exponents α(t) = d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δr2(t)/d δr2(t)/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t obtained from the MSD of an active tracer in a passive host system, corresponding to the data shown in Fig. 2. Panels (a)–(d) show the results for the different self-propulsion velocities vs0 of the tracer. Symbols are BD simulation results, lines are MCT results. Thick black lines correspond to the analytical solution for a free active particle. Vertical dashed and dot-dashed lines indicate the time scales τv and τl characterizing the free-particle MSD, cf.eqn (25). t obtained from the MSD of an active tracer in a passive host system, corresponding to the data shown in Fig. 2. Panels (a)–(d) show the results for the different self-propulsion velocities vs0 of the tracer. Symbols are BD simulation results, lines are MCT results. Thick black lines correspond to the analytical solution for a free active particle. Vertical dashed and dot-dashed lines indicate the time scales τv and τl characterizing the free-particle MSD, cf.eqn (25). | ||
At very large vs0, one expects the transition to persistent motion (on time scale τv, respectively length scale ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) v) to occur even before cageing becomes effective. Currently, the required large vs0 do not allow us to solve the MCT equations reliably. We thus turn to ED-BD simulations in this regime (Fig. 4). Indeed, even at the density φ = 0.77 for which the passive host system induces subdiffusive cageing motion over about three decades in time for the passive or moderately active tracers, we observe in our ED-BD simulations for large vs0 an increasingly rapid cross-over to superdiffusive motion that replaces the subdiffusive regime entirely once
v) to occur even before cageing becomes effective. Currently, the required large vs0 do not allow us to solve the MCT equations reliably. We thus turn to ED-BD simulations in this regime (Fig. 4). Indeed, even at the density φ = 0.77 for which the passive host system induces subdiffusive cageing motion over about three decades in time for the passive or moderately active tracers, we observe in our ED-BD simulations for large vs0 an increasingly rapid cross-over to superdiffusive motion that replaces the subdiffusive regime entirely once ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) v ≪
v ≪ ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) c. This is exemplified for vs0 ≳ 32 by the ED-BD data (Fig. 4; where we have also set Dsr = 0.05Dt/σ2 to emphasize the effect). In essence, strong activity of sufficiently large persistence length eliminates the cage effect for the active tracer. In the simulations it appears that as vs0 is further increased, one essentially observes the motion of a free ABP, with a density-renormalized swim speed. To exemplify this, we compare the ED-BD results for vs0 = 128 with the free-particle MSD for vs0,eff = 16; both curves agree closely (Fig. 4).
c. This is exemplified for vs0 ≳ 32 by the ED-BD data (Fig. 4; where we have also set Dsr = 0.05Dt/σ2 to emphasize the effect). In essence, strong activity of sufficiently large persistence length eliminates the cage effect for the active tracer. In the simulations it appears that as vs0 is further increased, one essentially observes the motion of a free ABP, with a density-renormalized swim speed. To exemplify this, we compare the ED-BD results for vs0 = 128 with the free-particle MSD for vs0,eff = 16; both curves agree closely (Fig. 4).
It would be worth further investigation whether the active tracer undergoes a delocalization transition even in the passive glass. For a tracer that is driven by an external force of fixed direction, this effect is known43 and has been studied in the framework of MCT.44–47 Here, the theory predicts that above a certain threshold force, the tracer motion delocalizes (as indicated by an MSD that grows without bound even when the host system is glassy). However, in the present theory the situation is less obvious, because the active tracer always has a finite persistence time if Dr > 0, and the limit Dr → 0 does not necessarily commute with the long-time limit of interest in studying glassy dynamics.
For the regime of moderate activity, the active tracer becomes, within the theoretical idealization, trapped in the passive host system at densities φ ≥ φc. This is expected because the cages possess a finite microscopic yield strength,44 and if the self-propulsion velocity vs0 translates into a force exerted by the active tracer that is below this threshold (and also not infinitely persistent for finite Dr), cages will not yield due to activity.
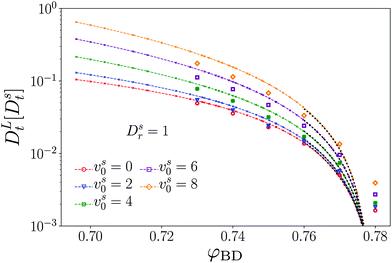
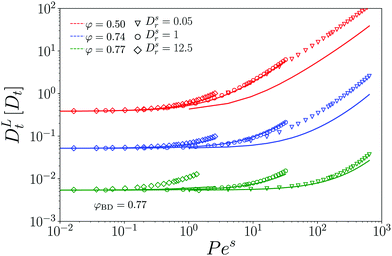
Approaching the glass transition, one thus expects the long-time motion of the tracer to be quantified by a long-time diffusion coefficient DLt(φ) that approaches zero at φ = φc, and, by bona fide extension of the well established asymptotic results of MCT for passive systems, vanishes as a power law close to the transition, DLt(φ) ∼ |φ − φc|γ for φ → φc from below. The exponent γ is a non-universal exponent emerging from the asymptotic solution of the MCT equations. In practice, the MCT description of the glass transition is an idealized one, and one observes in simulations deviations from the power-law behavior close to and above φc, rendering DLt finite also there.
Our EDBD simulations confirm this expectation (Fig. 5). In the density window 0.76 ≲ φ ≲ 0.77, the long-time self-diffusion coefficient 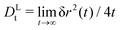 follows the power-law expected from MCT. Deviations are seen for our simulations at φ = 0.78; as mentioned above, the appearance of long-range fluctuations in the 2D system likely affects the data here, and we exclude this point from our discussion.
follows the power-law expected from MCT. Deviations are seen for our simulations at φ = 0.78; as mentioned above, the appearance of long-range fluctuations in the 2D system likely affects the data here, and we exclude this point from our discussion.
As anticipated from Fig. 2, increasing the self-propulsion velocity of the tracer enhances its long-time diffusion. The quantitative agreement with MCT deteriorates with increasing vs0, but the qualitative behavior remains the same. With our choice of parameters, discussing a change in vs0 at fixed φ and fixed Dsr, we observe only a monotonic increase of DLt with increasing vs0. One should note that theory and simulations on a different model of active particles, the active Ornstein–Uhlenbeck particles (AOUP), demonstrate a non-monotonic variation with activity48 that has also been reported from some experiments.49,50
In the low-density regime, eqn (24) establishes that in the long-time diffusive regime of the ABP, activity only enters through the dimensionless Péclet number Pes = (vs0)2/2DsrDst. In particular, one obtains DLt = Dst(1 + Pes). At high densities, this simple relation cannot be expected any more, because the cage effect provides a further scale for the problem, so that out of the two parameters that quantify the active motion of the ABP, vs0 and Dsr, two independent dimensionless numbers can be formed.
It is nevertheless instructive to check the scaling with Pes. Indeed, both theory and simulation demonstrate that for any fixed Dsr the long-time diffusion coefficients are of the form const.+Pes (symbols in Fig. 6). This quadratic dependence on the self-propulsion velocity is also expected from the symmetry of the ensemble under mapping vs0 → –vs0. Yet, the prefactors depend on both Dsr and the packing fraction. A simple-minded rescaled description that takes into account the reduced diffusivity in the passive system, DLt = DL,0t(ϕ)(1 + Pes) with DL,0t(ϕ) the density-renormalized free diffusion of the passive particle, still fails (dotted lines in Fig. 6). An empirical rescaling, DLt = DL,0t(φ)(1 + α(φ,Dsr)Pes) describes the data (dashed lines), and reveals two trends for the rescaling factor α: it decreases with increasing host-system density, i.e., the enhancement of long-time diffusion at given tracer-Péclet number becomes weaker. The prefactor α also increases with increasing Dsr at fixed packing fraction. This appears compatible with the intuition that for Dsr → ∞ at fixed Pes (implying also vs0 → ∞), the active tracer recovers effectively-free motion with a renormalized Brownian diffusion coefficient due to the dense host system. It is also compatible with the limit Dsr → 0, which at fixed Pes implies vs0 → 0 and therefore recovers the case of a passive tracer particle.
A common approach in developing coarse-grained theories of ABP is to account for a density-renormalized swim velocity: Due to interactions, the average velocity characterizing the particle motion is no longer the bare self-propulsion speed vs0 of an individual ABP, but a density-dependent effective swim velocity vs(φ).51 The quantity vs(φ) is in principle a non-equilibrium transport coefficient onto which the ITT framework provides a useful handle. One can derive, using ITT, a generalized Green–Kubo formula for vs(φ), relating it to the microscopic correlation function of the particles' orientation-projected forces.52 We have recently obtained a ABP-MCT expression for the swim velocity30 that was shown to be in reasonable qualitative agreement with simulation data.23 Qualitatively, vs(φ)/vs0 decays from unity at low densities towards zero at the glass transition, and thus qualitatively explains the density-dependent reduction of the empirical prefactor α used in Fig. 6.
A direct comparison of the ABP-MCT results for the active-tracer long-time diffusion DLt with the expression DLt ≈ DL,0t(φ)(1 + Peseff(φ)) (lines and symbols in Fig. 7) demonstrates reasonable agreement especially at the highest density studied (φ = 0.77) and not too large Dsr. Here, Peseff(φ) = vs(φ)2/2DsrDst is the effective Péclet number formed with the density-dependent swim speed. The latter has been evaluated from the theory using the ITT expression,
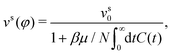 | (33a) |
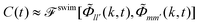 where only terms involving l,l′,m,m′ ∈ {−1,0,1} enter. For a derivation and more detailed expressions of the swim-speed functional we refer to ref. 23 and 30. Note that the swim velocity depends on Dsr implicitly, however, it does not capture the complete dependence on rotational diffusion for the active tracer that is displayed by the results for the long-time diffusivity in Fig. 6 and 7. In principle, one would also expect a description in terms of the swim velocity to only hold on sufficiently coarse-grained scales, while ABP-MCT provides a microscopic approach for which the bare model coefficients are the relevant parameters.
where only terms involving l,l′,m,m′ ∈ {−1,0,1} enter. For a derivation and more detailed expressions of the swim-speed functional we refer to ref. 23 and 30. Note that the swim velocity depends on Dsr implicitly, however, it does not capture the complete dependence on rotational diffusion for the active tracer that is displayed by the results for the long-time diffusivity in Fig. 6 and 7. In principle, one would also expect a description in terms of the swim velocity to only hold on sufficiently coarse-grained scales, while ABP-MCT provides a microscopic approach for which the bare model coefficients are the relevant parameters.
 | ||
| Fig. 7 Long-time diffusion coefficient DLt(φ) of an active tracer in a passive hard-disk system, as a function of the tracer Péclet number Pes, for the parameters shown in Fig. 6. Solid lines repeat the ABP-MCT results from Fig. 6. Symbols show DLt = DL,0t(1 + Peseff) were the effective tracer-Péclet number Peseff = (vs(φ))2/2DsrDst is evaluated with the density-renormalized effective swim velocity vs(φ) (see text). | ||
3.3 Tracer motion in the active bath
We continue by discussing the tracer motion in an active host system. One interesting case here is exemplified by the MSD of a passive tracer in a host system of ABP (Fig. 8). Again, for the range of v0 similar to what we discussed in the reverse case of an active tracer in the passive host, the MSD show a succession of subdiffusive cage motion followed by super-diffusive escape from the cageing plateau. It is a clear signature of the non-equilibrium character of the host system dynamics, that even for the passive tracer, the MSD grows faster than diffusive. This implies that a description of the active host fluid in an effective-equilibrium framework (such as assigning an elevated effective temperature to a thermalized fluid with added activity42) cannot capture this dynamics. Only for the weakly active host system (v0 = 2Dt/σ in Fig. 8) do we find a reasonable description of the MSD in terms of the fully passive-dynamics MSD at an effective reduced packing fraction similar to what was discussed in connection with Fig. 2 (dotted lines in Fig. 8).Qualitatively, the regime of superdiffusion in the case of the passive tracer, Fig. 8, appears more pronounced the denser is the host system; compare this to the reversed case of an active tracer in a passive bath, Fig. 2, where an increased host-system density serves to more strongly suppress superdiffusive motion. This is of course intuitive, since in the latter case, the tracer activity is suppressed by the passive caging, while in the former case, activity modifies the effective cage motion that is seen by the tracer.
ABP-MCT is again able to account for this nontrivial dynamics qualitatively. The comparison in Fig. 8 becomes even quantitatively satisfactory if one allows for a further empirical mapping of parameters besides the density mapping that was fixed in the fully passive system: We find that the influence of host-system activity on the relaxation dynamics is stronger in the ED-BD simulations than it is predicted by MCT. The quantitative error can be absorbed in a rescaling of the self-propulsion velocity vMCT0 that enters the theory calculation. We find reasonable agreement with a linear rescaling, vMCT0 ≈ 1.5vBD0 (inset of Fig. 8).
The fact that the effect of the nonequilibrium perturbation on the glassy dynamics of the host system, in fluidizing that system, is underestimated by MCT is in line qualitatively with previous applications of the theory to, for example, sheared colloidal suspensions25 or active microrheology;44–47 also there, the introduction of an empirical scaling factor allowed to bring the theory in quantitative agreement with simulation data. In general, one finds that MCT overestimates the glassiness of the relaxation dynamics, and hence it predicts too slow relaxation for a fixed density φ and fixed self-propulsion strength v0. Since the effects of both parameters on the structural relaxation are opposite (increasing density slows down, increasing activity speeds up the dynamics), it is plausible that the theory curves for a decreased ϕ and an increased v0 match the simulation data. The mapping of v0 has also been successful in a description of the relaxation of density fluctuations at finite q.24
As before, an examination of the effective power-law exponent, α(t) = d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δr2(t)/d
δr2(t)/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t extracted from the logarithmic derivative of the MSD, allows to study in detail the succession of sub- and super-diffusive regimes (Fig. 9). It becomes apparent that as a general trend, MCT overestimates the extent and strength of both regimes; in particular for the highest self-propulsion velocity studied here, v0 = 6, the theory predicts a pronounced super-diffusive regime around t = 1 at densities close to the glass transition; the ED-BD simulations show superdiffusion to a lesser extent. This possibly indicates that the simple-minded mapping of vBD0 to an increased vMCT0 does not account for all observations equally well. (We also expect such mapping to only work in a limit range of v0 and, in particular, Dr, but this requires further investigation.) Close to φc, the exponents reveal that the MSD remains subdiffusive at all times only for up to v0 = 2Dt/σ; this confirms that only for this weakly active host system, an effective-density passive description can work.
t extracted from the logarithmic derivative of the MSD, allows to study in detail the succession of sub- and super-diffusive regimes (Fig. 9). It becomes apparent that as a general trend, MCT overestimates the extent and strength of both regimes; in particular for the highest self-propulsion velocity studied here, v0 = 6, the theory predicts a pronounced super-diffusive regime around t = 1 at densities close to the glass transition; the ED-BD simulations show superdiffusion to a lesser extent. This possibly indicates that the simple-minded mapping of vBD0 to an increased vMCT0 does not account for all observations equally well. (We also expect such mapping to only work in a limit range of v0 and, in particular, Dr, but this requires further investigation.) Close to φc, the exponents reveal that the MSD remains subdiffusive at all times only for up to v0 = 2Dt/σ; this confirms that only for this weakly active host system, an effective-density passive description can work.
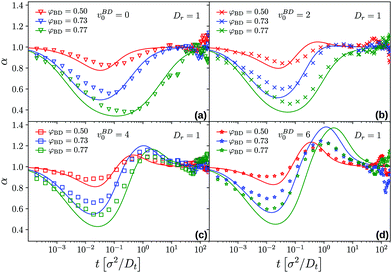 | ||
Fig. 9 Effective exponents α(t) = d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δr2(t)/d δr2(t)/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t for the MSD of a passive tracer in a host system of active Brownian hard disks, corresponding to the data shown in Fig. 8. Symbols are BD simulation results, lines are from the MCT fits. t for the MSD of a passive tracer in a host system of active Brownian hard disks, corresponding to the data shown in Fig. 8. Symbols are BD simulation results, lines are from the MCT fits. | ||
Finally, we turn to the MSD of an active tracer in a system of ABP (Fig. 10). The results are qualitatively quite similar to the ones that we have discussed before; intuitively one expects an addition of the effects discussed in connection with the active tracer in a passive system, Fig. 2, and with the passive tracer in the active system, Fig. 8. Indeed, we observe in the fully active system (Fig. 10) pronounced superdiffusion succeeding the subdiffusive cage motion at all the densities that are shown, for sufficiently large v0: at low host system density, it stems from the activity of the tracer itself, while at high host system density, even the passive tracer acquires induced superdiffusive motion. To emphasize the similarity, we compare the MSD for the active tracer in the active host system with those of the passive tracer in that system (different colored symbols in Fig. 10). Indeed, at the density φ = 0.77 close to the glass transition, both quantities are nearly identical in our simulations, indicating that here, the dominant effect comes from the host system activity, and any tracer effectively follows the collective dynamics. At the lower density φ = 0.50, the passive tracer shows a far less enhanced superdiffusive regime, since here the active bath is not yet as effective in transmitting its activity to the passive tracer. Note that for sufficiently high density, the MSD remains nearly diffusive and acquires a more pronounced superdiffusive regime when decreasing the density; this has been also discussed in simulations of a system of active dumbbells.53
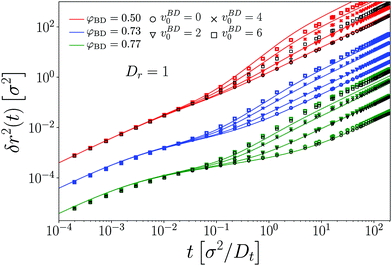 | ||
| Fig. 10 Mean-squared displacements δr2(t) of an active tracer particle in a host suspension of active Brownian disks, at packing fraction φ and self-propulsion velocities as indicated. Colored symbols are results from BD simulations, lines are MCT fits with empirically mapped densities and velocities as in Fig. 8. For clarity, groups of curves corresponding to fixed φ are shifted downward by one decade each. Black symbols repeat our simulation results for a passive tracer in the active host system from Fig. 8 (shown only for φ = 0.77 and for v0 = 0, 6 for φ = 0.50 for clarity). | ||
The theory correctly captures these two effects: up to the velocity mapping that is required to quantitatively describe the host system activity, as described above, both the passive (lines in Fig. 8) and the active tracer dynamics (lines in Fig. 10) are quantitatively well described by ABP-MCT. As anticipated from the previous discussion, some systematic deviations set in for the largest v0 that we have studied here. It remains a question for future work to assess the quality of ABP-MCT for very large self-propulsion velocities, once better numerical integration schemes are available for the theory.
4 Conclusions
We have derived equations to describe the mean-squared displacement (MSD) of active and passive tracer particles in dense systems of passive or active Brownian particles. The description is based on the integration-through transients (ITT) framework, a non-equilibrium statistical physics framework that allows to treat the activity of active Brownian particles (ABPs) as an arbitrarily strong perturbation to the passive-equilibrium Brownian dynamics. While the formulas, eqn (30), are exact in principle, their evaluation requires knowledge of memory kernels that encode the interaction with the host particles in terms of positional and dipolar orientational density fluctuations.The dynamics at high densities is qualitatively well predicted when the relevant memory kernels are evaluated using the mode-coupling theory for active Brownian particles (ABP-MCT), as our comparison with event-driven Brownian dynamics (ED-BD) computer simulations demonstrates. The good qualitative agreement holds for the range of densities close to the glass transition and for not too large self-propulsion velocities, even if the transient correlation functions evaluated within the theory are compared to the stationary correlations obtained in the simulation. To achieve quantitative agreement between theory and simulation, two parameters have to be adjusted: the overall density entering the mode-coupling theory of the glass transition (MCT) equations is lower than the one in the simulation, which accounts for the fact that the theory predicts kinetic arrest at too low density. This appears already in the passive system and is not a feature of the extension to ABP. Secondly, the theory underestimates the speedup of the collective dynamics of ABP, so that in the case of an active bath, quantitative agreement is obtained when the theory is evaluated with a self-propulsion velocity that is higher than the one in the simulation.
The most prominent feature of the MSD including activity is the appearance and, at high densities, disappearance of a ballistic regime of persistent active motion. For a free ABP, superdiffusion appears in a regime set by time and length scales connected to the self-propulsion velocity and the reorientational diffusion coefficient. Close to the glass transition, these time scales compete with the relevant time scales of structural relaxation, and hence in the MSD we observe a typical sequence of initial passive diffusion, glassy sub-diffusion, followed by super-diffusive cage breaking at large enough activity, and finally long-time diffusion. The simulations also demonstrate that for very large activity, the sub-diffusive cageing regime can be entirely suppressed by the active motion. These findings are in qualitative agreement with recent experimental data on the MSD of a single active particle in a colloidal glass former,5 as we discuss in detail elsewhere.23
In the low-density regime, absorbing the translational diffusion coefficient Dst in the units of time, the two parameters that quantify active motion, viz. its velocity vs0 and its persistence time 1/Dsr, only enter in a specific combination through a dimensionless group, the Péclet number Pes. The appearance of a further length scale through the cage effect at high densities change this, and as a result the motion of the active tracer depends on both vs0 and Dsr separately.
From discussing the various cases of active/passive tracers in active/passive host systems it emerges that the active motion of the tracer is responsible for super-diffusive motion as long as the host system is not yet too dense; in very dense host systems, it is the activity of the host particles that drive super-diffusive motion even for a passive tracer.
The fact that the extension of MCT can describe superdiffusive MSD at all is not trivial. Theories where the angular dynamics is integrated out, and hence the dynamics of the active particles is mapped onto one described by an effective Smoluchowksi operator are not a priori able to capture this. Especially, for the case of a passive tracer in an active bath, a naive application of the theory would just assume the standard form of the passive-MSD equations of motion, coupled to enhanced relaxation dynamics in the bath. Instead, a superdiffusive regime appears in our theory, in good agreement with simulation.
Conflicts of interest
There are no conflicts to declare.A Features of the passive-equilibrium MSD
Recall that for a colloidal system in equilibrium, the dynamics is described by a backward Smoluchowski operator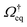 that is self-adjoint in the scalar product weighted with the equilibrium distribution, i.e.,
that is self-adjoint in the scalar product weighted with the equilibrium distribution, i.e., 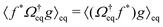 . The structure of
. The structure of 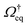 implies
implies 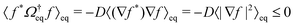 (assuming the diffusion coefficient to be positive), so that the operator
(assuming the diffusion coefficient to be positive), so that the operator 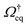 has non-positive real eigenvalues only.
has non-positive real eigenvalues only.
The density correlation functions are hence completely monotone functions,54,55i.e., they can be written in the form (specializing to the tagged-particle correlation function for the sake of the following argument) 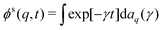 with some positive definite measure daq that is concentrated on the nonnegative real axis. For a completely monotone function, there holds (−)k∂ktϕs(q,t) ≥ 0.
with some positive definite measure daq that is concentrated on the nonnegative real axis. For a completely monotone function, there holds (−)k∂ktϕs(q,t) ≥ 0.
The MSD (in d spatial dimensions) follows from 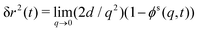 and thus ∂tδr2(t) again is a completely monotone function. (The MSD is thus confirmed to be a monotonically increasing function of time.) As a consequence, using the fact that δr2(t) itself is positive,
and thus ∂tδr2(t) again is a completely monotone function. (The MSD is thus confirmed to be a monotonically increasing function of time.) As a consequence, using the fact that δr2(t) itself is positive,
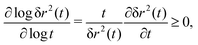 | (34) |
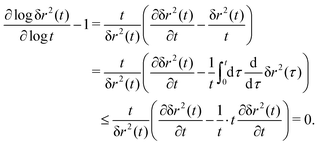 | (35) |
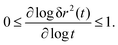 | (36) |
Acknowledgements
This project was funded through Deutsche Forschungsgemeinschaft (DFG), project within the SPP 1726 “Physics of Microswimmers”, project Vo 1270/7-2.Notes and references
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- S. Ramaswamy, J. Stat. Mech., 2017, 17, 054002 CrossRef.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- C. Lozano, J. R. Gomez-Solano and C. Bechinger, Nat. Mater., 2019, 18, 1118–1123 CrossRef CAS PubMed.
- D. Martin, C. Nardini, M. E. Cates and E. Fodor, EPL, 2018, 121, 60005 CrossRef.
- L. Ortlieb, S. Rafa, P. Peyla, C. Wagner and T. John, Phys. Rev. Lett., 2019, 122, 148101 CrossRef CAS PubMed.
- D. Wirtz, Annu. Rev. Biophys., 2009, 38, 301–326 CrossRef CAS PubMed.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017–3020 CrossRef CAS PubMed.
- A. Caspi, R. Granek and M. Elbaum, Phys. Rev. Lett., 2000, 85, 5655–5658 CrossRef CAS PubMed.
- D. T. N. Chen, A. W. C. Lau, L. A. Hough, M. F. Islam, M. Goulian, T. C. Lubensky and A. G. Yodh, Phys. Rev. Lett., 2007, 99, 148302 CrossRef CAS PubMed.
- C. Wilhelm, Phys. Rev. Lett., 2008, 101, 028101 CrossRef PubMed.
- N. Gal and D. Weihs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 020903(R) CrossRef PubMed.
- C. Valeriani, M. Li, J. Novosel, J. Arlt and D. Marenduzzo, Soft Matter, 2011, 7, 5228 RSC.
- A. Lagarde, N. Dagès, T. Nemoto, V. Démery, D. Bartolo and T. Gibaud, Soft Matter, 2020, 16, 7503–7512 RSC.
- S. Ye, P. Liu, F. Ye, K. Chen and M. Yang, Soft Matter, 2020, 16, 4655–4660 RSC.
- D. Loi, S. Mossa and L. F. Cugliandolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051111 CrossRef PubMed.
- D. Loi, S. Mossa and L. F. Cugliandolo, Soft Matter, 2011, 7, 10193 RSC.
- D. Levis and L. Berthier, EPL, 2015, 111, 60006 CrossRef.
- C. Maggi, M. Paoluzzi, L. Angelani and R. Di Leonardo, Sci. Rep., 2017, 7, 17588 CrossRef PubMed.
- C. Maes, Phys. Rev. Lett., 2020, 125, 208001 CrossRef CAS PubMed.
- A. Liluashvili, J. Ónody and Th. Voigtmann, Phys. Rev. E, 2017, 96, 062608 CrossRef PubMed.
- J. Reichert, L. F. Granz and Th. Voigtmann, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44, 27 CrossRef CAS PubMed.
- J. Reichert, S. Mandal and Th. Voigtmann, arXiv:2010.13763.
- M. Fuchs and M. E. Cates, J. Rheol., 2009, 53, 957–1000 CrossRef CAS.
- C. Kurzthaler, S. Leitmann and T. Franosch, Sci. Rep., 2016, 6, 36702 CrossRef CAS PubMed.
- C. Kurzthaler, C. Devailly, J. Arlt, T. Franosch, W. C. K. Poon, V. A. Martinez and A. T. Brown, Phys. Rev. Lett., 2018, 121, 078001 CrossRef CAS PubMed.
- M. Fuchs, W. Götze and M. R. Mayr, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 58, 3384–3399 CrossRef CAS.
- M. Bayer, J. M. Brader, F. Ebert, M. Fuchs, E. Lange, G. Maret, R. Schilling, M. Sperl and J. P. Wittmer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 011508 CrossRef CAS PubMed.
- J. Reichert, PhD thesis, Heinrich-Heine-Universität Düsseldorf, 2020.
- A. L. Thorneywork, S. K. Schnyder, D. G. A. L. Aarts, J. Horbach, R. Roth and R. P. A. Dullens, Mol. Phys., 2018, 116, 3245–3257 CrossRef CAS.
- A. Scala, Th. Voigtmann and C. De Michele, J. Chem. Phys., 2007, 126, 134109 CrossRef CAS PubMed.
- R. Ni, M. A. C. Stuart and M. Dijkstra, Nat. Commun., 2013, 4, 2704 CrossRef PubMed.
- D. Levis, J. Codina and I. Pagonabarraga, Soft Matter, 2017, 13, 8113–8119 RSC.
- N. de Macedo Biniossek, H. Löwen, Th. Voigtmann and F. Smallenburg, J. Phys.: Condens. Matter, 2018, 30, 074001 CrossRef CAS PubMed.
- F. Weysser, A. M. Puertas, M. Fuchs and T. Voigtmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 011504 CrossRef CAS PubMed.
- E. Flenner and G. Szamel, Nat. Commun., 2015, 6, 7392 CrossRef CAS PubMed.
- H. Shiba, Y. Yamada, T. Kawasaki and K. Kim, Phys. Rev. Lett., 2017, 117, 245701 CrossRef PubMed.
- B. Illing, S. Fritschi, H. Kaiser, C. L. Klix, G. Maret and P. Keim, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1856–1861 CrossRef CAS PubMed.
- S. Vivek, C. P. Kelleher, P. M. Chaikin and E. R. Weeks, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 1850–1855 CrossRef CAS PubMed.
- Y.-W. Li, C. K. Mishra, Z.-Y. Sun, K. Zhao, T. G. Mason, R. Ganapathy and M. Pica Ciamarra, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 22977–22982 CrossRef CAS PubMed.
- L. Berthier and J. Kurchan, Nat. Phys., 2013, 9, 310–314 Search PubMed.
- A. M. Puertas and T. Voigtmann, J. Phys.: Condens. Matter, 2014, 26, 243101 CrossRef CAS PubMed.
- I. Gazuz, A. M. Puertas, T. Voigtmann and M. Fuchs, Phys. Rev. Lett., 2009, 102, 248302 CrossRef CAS PubMed.
- I. Gazuz and M. Fuchs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032304 CrossRef.
- M. Gruber, G. C. Abade, A. M. Puertas and M. Fuchs, Phys. Rev. E, 2016, 94, 042602 CrossRef CAS PubMed.
- M. Gruber, A. M. Puertas and M. Fuchs, Phys. Rev. E, 2020, 101, 012612 CrossRef CAS PubMed.
- L. Berthier, E. Flenner and G. Szamel, J. Chem. Phys., 2019, 150, 200901 CrossRef PubMed.
- N. Klongvessa, F. Ginot, C. Ybert, C. Cottin-Bizonne and M. Leocmach, Phys. Rev. Lett., 2019, 123, 248004 CrossRef CAS PubMed.
- N. Klongvessa, F. Ginot, C. Ybert, C. Cottin-Bizonne and M. Leocmach, Phys. Rev. E, 2019, 100, 062603 CrossRef PubMed.
- M. E. Cates and J. Tailleur, Annu. Rev. Condens. Matter Phys., 2015, 6, 219–244 CrossRef CAS.
- A. Sharma and J. M. Brader, J. Chem. Phys., 2016, 145, 161101 CrossRef CAS PubMed.
- R. Mandal, P. J. Bhuyan, P. Chaudhuri, M. Rao and C. Dasgupta, Phys. Rev. E, 2017, 96, 042605 CrossRef PubMed.
- G. Gripenberg, S. O. Londen and O. Staffans, Volterra Integral and Functional Equations, Cambridge University Press, Cambridge, 1990, vol. 34 Search PubMed.
- D. V. Widder, The Laplace Transform, Princeton University Press, Princeton, 1946 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |