Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Migration of nanoparticles across a polymer–polymer interface: theory and simulation
Nigel
Gibbions
 *a,
Nigel
Clarke
a and
Didier R.
Long
*a,
Nigel
Clarke
a and
Didier R.
Long
 b
b
aDepartment of Physics and Astronomy, University of Sheffield, Sheffield S3 7RH, UK. E-mail: ngibbions1@sheffield.ac.uk
bLaboratoire Polymères et Matériaux Avancés, CNRS/Solvay, UMR 5268, 87 avenue des Frères Perret, 69192 Saint Fons Cedex, France
First published on 20th July 2021
Abstract
We proposed recently a theoretical description for hydrodynamic flows in inhomogeneous liquids in the vicinity of solid interfaces, consistent with current theoretical descriptions of the thermodynamical equilibrium of liquids in the vicinity of solid surfaces and with the Onsager formalism for linear response theory in out-of-equilibrium liquids. We showed that these equations allow for describing diffusio-osmosis along a capillary and also wetting/dewetting dynamics of liquids on a solid substrate. We now apply this physical model to the wetting/dewetting dynamics of nano-particles in polymer blends, showing how they reach equilibrium at the interface between two liquids at rest and how they migrate from the non-preferred polymer to the preferred one under applied flow.
1 Introduction
The behaviour of liquids in contact with solids is a field rich in theoretical interest and practical applications. These applications include the formulation of paints, the design of car windscreens, and the manufacture of contact lens solutions.1,2 Theoretical, computational, and experimental studies have explored the static equilibrium properties of droplets on solid substrates, and the dynamics of both wetting and dewetting. Such studies have examined the effects of physical defects or chemical impurities in the substrate on wetting behaviour,3,4 and the wetting properties of thin rubber films where dissipation due to viscoelastic effects may significantly modify the dynamics.5The starting point for any discussion of wetting is the equilibrium state of a liquid droplet on an ideal solid substrate, as depicted in Fig. 1. At equilibrium, the balance of forces in the x-direction leads to Young's equation:
γS = γSL + γL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe θe | (1) |
| S = γS − (γSL + γL) | (2) |
S = γL(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe − 1) θe − 1) | (3) |
 | ||
| Fig. 1 The balance of forces at the triple line of a liquid droplet on an ideal, solid substrate, showing the equilibrium contact angle θe. | ||
 | ||
| Fig. 2 Wetting regimes, from total wetting, to no wetting, characterised by the spreading parameter, S, and the equilibrium contact angle θe. | ||
The physical picture represented in Fig. 1 results from a virtual work principle applied by moving the contact line and considering the variation of the total interfacial energy considered at the coarse-grained level of surface tension description.1 It is a simplification since it ignores the effects of non-localised forces (e.g. van der Waals) in the vicinity of the interface. Although the range of these forces is small (up to tens of nanometres), their finite range is essential for describing diffusio-osmosis and wetting dynamics.6 The interfacial forces can be accounted for by body forces in the Stokes equations localized in the vicinity of interfaces. In ref. 6 we introduce an interaction potential Γ(ψ,r) localized in the vicinity of the solid interface, and show how the non-localised forces this gives rise to may be integrated over a region of size a in the z direction (perpendicular to the surface), and ξ in the x direction (parallel to the surface) to recover the net force γS − γSL, which acts close to the surface. In this integration, a represents the length scale over which the interfacial potential acts, ξ represents the interfacial width of the droplet, and we approximate the concentration profile at the droplet boundary to be a delta function. The net force due to the interaction potential, γS − γSL, combined with the −γL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe term from the surface tension of the liquid (contained in the body forces of the generalized Stokes equations), recovers the net force at the triple line, as represented in Young's equation. Instead of Fig. 1 where surface forces act at a well-define triple line, a more realistic physical description is that of Fig. 3, where surface forces are shown as acting over a finite region in the vicinity of a notional triple line.
θe term from the surface tension of the liquid (contained in the body forces of the generalized Stokes equations), recovers the net force at the triple line, as represented in Young's equation. Instead of Fig. 1 where surface forces act at a well-define triple line, a more realistic physical description is that of Fig. 3, where surface forces are shown as acting over a finite region in the vicinity of a notional triple line.
 | ||
| Fig. 3 The balance of forces in the vicinity of the triple line where a liquid droplet meets a solid substrate, taking into account non-localised forces arising from the interaction potential between the liquid and the solid substrate. These forces typically, have a range of up to tens of nanometres, thus the surface forces act over a more diffuse region than Fig. 1 suggests. For simplicity, we show the net effect of γS and γSL close to the solid surface, while γL is shown as acting at the triple line. | ||
When a liquid droplet is placed on a solid substrate, it is usually far from thermodynamic and mechanical equilibrium, and will relax towards equilibrium by wetting the surface, either totally or partially. Instead of an equilibrium contact angle, we observe a dynamic contact angle, θd > θe, and the radius of the droplet increases, potentially without limit when total wetting occurs, leaving a molecular scale film on the substrate. The dynamics of wetting is governed by the balance between capillary and viscous forces. For small contact angles, and low Reynolds number, the lubrication approximation applies, implying Poiseuille flow within the droplet, and the spreading velocity V is given by:1
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r ∼ 10). The dynamics of spreading resulting from interfacial tension effects has been the subject of intense research for many years.7,8
r ∼ 10). The dynamics of spreading resulting from interfacial tension effects has been the subject of intense research for many years.7,8
In contrast dewetting refers to the retraction of a droplet, far from equilibrium, to its equilibrium state, exposing a dry region of the solid substrate as it retreats. Dewetting is also observed when a thin liquid film on a solid substrate ruptures (creating, in effect, a droplet of semi-infinite extent), exposing a dry region, which then expands as the fluid retreats. In both cases, a fluid ridge forms at the solid–liquid boundary, due to conservation of matter and, in the early stages of dewetting, grows in volume (Fig. 4). At longer time scales, following the rupture of a thin film, the fluid ridge itself may break into droplets (due to the Rayleigh–Plateau instability), which then continue to dewet by retracting to form smaller droplets. Note that when the liquid interface is between two different liquids, liquid A and liquid B, wetting for one liquid is dewetting for the other. There is no fundamental difference between wetting and dewetting in this respect. It is essentially a matter of initial conditions seen from the point of view of liquid A or liquid B.
A closer analogy to dewetting is the spinodal decomposition of a binary system quenched below its critical point. Below this point, the system is unstable and local concentration fluctuations are amplified, giving rise to phase separated domains. Furthermore, exponential growth (in the linear regime typical of the early stages of spinodal decomposition) results in a favoured length-scale, which grows much more rapidly than its competitors. When the volume fraction ratio is close to 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, this gives rise to co-continuous regions of each phase, randomly orientated, but with a uniform width, determined by the favoured length scale.9–11 In a similar way, dewetting occurs when local fluctuations in the height of a thin film are amplified, and cause the film to rupture. The instability may be induced by local chemical impurities, or physical irregularities in the substrate or may arise spontaneously for films thin enough.12,13 The former situation arises when the film is in a metastable state, and is known as dewetting by nucleation and growth, while the latter is known as spinodal dewetting. Again, the analogy with binary systems in metastable and unstable regions of the phase diagram is apparent. The fact that spinodal dewetting has a characteristic length scale often results in patterns of small droplets, or other structures, with long range order, which may be fine-tuned by varying the thickness of the initial film. This ability to fine tune the resultant structure opens up the possibility of a range of applications in, for example, the surface treatment of materials, metallic film manufacturing, and the development of organic semiconductors.14
50, this gives rise to co-continuous regions of each phase, randomly orientated, but with a uniform width, determined by the favoured length scale.9–11 In a similar way, dewetting occurs when local fluctuations in the height of a thin film are amplified, and cause the film to rupture. The instability may be induced by local chemical impurities, or physical irregularities in the substrate or may arise spontaneously for films thin enough.12,13 The former situation arises when the film is in a metastable state, and is known as dewetting by nucleation and growth, while the latter is known as spinodal dewetting. Again, the analogy with binary systems in metastable and unstable regions of the phase diagram is apparent. The fact that spinodal dewetting has a characteristic length scale often results in patterns of small droplets, or other structures, with long range order, which may be fine-tuned by varying the thickness of the initial film. This ability to fine tune the resultant structure opens up the possibility of a range of applications in, for example, the surface treatment of materials, metallic film manufacturing, and the development of organic semiconductors.14
In addition to the macroscopic description discussed above, various approaches have been used for describing wetting dynamics. Molecular dynamics (MD) simulations is one of the leading approaches, but has the drawback of being computationally intensive: even on fast supercomputers, it has only been possible to simulate systems of billions of particles for a few hundred nanoseconds.15
Thus, many problems of great interest to interfacial science and the study of soft condensed matter are inaccessible to an MD approach. Dissipative particle dynamics and its refinements16–18 address this difficulty by coarse graining the system into a collection of point-like particles interacting via both conservative and dissipative forces, in a way that aims to maintain thermodynamic consistency. While such an approach improves computational efficiency it does so at the expense of artificiality, and the underlying physics is somewhat obscured. A similar criticism may be made of other modelling techniques, including the Lattice–Boltzmann method.
A more straightforward approach is to apply the familiar methods of continuum fluid mechanics to the problem of simulating the dynamics of wetting and dewetting. It has been known for some time19 that the continuum approximation remains valid at surprisingly short length scales. Thus, it becomes feasible to apply continuum fluid mechanics to problems involving the wetting and dewetting of a nanoparticle, and to the migration of that particle from one liquid phase to another. A persistent difficulty in simulating wetting and dewetting behaviour using fluid mechanical models is the treatment of boundary conditions in multi-phase systems and how to account for the interfacial forces. Specifically, how can the no-slip boundary condition commonly assumed in fluid dynamics be reconciled with the requirement of relative motion between the liquid and the solid substrate, at their interface, in both wetting and dewetting? Another issue is where the interfacial forces in the liquids should be located, and how they should be represented. The same no-slip condition also leads to a divergence in the energy dissipated by the flow close to the contact line, which forces us to truncate the relevant integral at both the lower limit (of molecular length scale) and the upper limit (the size of the droplet, say).4
In order to make progress, it is necessary to correctly describe the thermodynamics of a system consisting of two liquid phases in contact with a third solid phase. This entails showing how driving forces arise due to concentration gradients in the bulk and in the vicinity of the triple line, and how a non-zero slip-length emerges naturally when the system is described in the appropriate physical terms.
In ref. 6 we introduced a formalism regarding Stokes equations which allows us to describe diffusio-osmosis and wetting dynamics in a way which is consistent with the thermodynamical equilibrium state of a liquid in the vicinity of a solid interface. In particular our description is consistent with the contact value theorem of colloidal science.20–23 According to this theorem, there is no excess pressure in the vicinity of a flat surface immersed in a liquid which would result from the interaction between the surface and the liquid, whereas it was assumed by Derjaguin that such a pressure is the cause for diffusio-osmotic flows.24–26 Our description of the Stokes equation in inhomogeneous liquids in the vicinity of a solid interface is also consistent with the general formalism of out-of-equilibrium thermodynamics.27–29 Non-local contributions to the excess of Gibbs free energy give rise to body forces in the Stokes equation in the vicinity of an interface and therefore to convection. The same contributions to the Gibbs free energy on a more coarse-grained picture are responsible for the surface tension between two liquids or between a liquid and a solid surface. The Stokes equations describe then the convective contribution to the relaxation towards thermodynamic equilibrium. What is key in this picture is that the driving forces are purely transverse and have a spatial extension. They are not applied exactly where a no-slip boundary condition holds which allows these forces to give rise to a flow. This feature solves the apparent paradoxes regarding wetting when the forces are supposed to be applied on the very solid interface. The mobility is thus proportional either to the range of the interaction or to a slipping length and may be a combination of both in the general case.
Thus, this paper's approach is grounded in continuum fluid mechanics, supplemented with a diffuse interface approach, versions of which are also used by Araki & Tanaka, and Patrick Anderson among others.30 One of the key issues is to model the hydrodynamic forces in the liquid during wetting and dewetting, and to model the slipping that must occur at surfaces and interfaces for relative motion between the solid and the liquid phases to occur at all. The description of the thermodynamics of the problem with an appropriate Gibbs free energy functional resolves both of these difficulties and permits a de facto slip length of ∼0.5 nm (the monomer length scale) to emerge naturally. This enables coupled equations of motion for the concentration field and the velocity field to be solved numerically, thereby reproducing realistic wetting and dewetting dynamics.
Having established that the model realistically simulates the dynamics of wetting and dewetting in a quiescent system, we apply the model to a system subject to a constant external shear. The aim is to further explore the dynamics of dewetting, and to determine the conditions under which a particle may be induced to migrate across an interface between two liquid phases, a problem of great practical interest in the manufacture of composite materials. Anderson et al. have also addressed this problem in a series of papers. In ref. 31, a constant external force, acting on the particle, and perpendicular to the interface, is introduced to achieve the migration of the particle from one phase to the other. Without this external force, the particle remains stuck at the interface between the liquid phases. In a later paper32 the same effect is achieved by modelling the interface between a viscoelastic fluid and a Newtonian fluid, as shear is applied parallel to the interface. In this paper, we model the effect of shear perpendicular to the interface between the liquid phases, and show that no special assumptions about the rheological properties of the liquids are needed to model the migration of a particle from one phase to the other.
2 Physical model
Our starting point is a general expression for the total Gibbs free energy in a system in which concentration gradients are present: | (5) |
| g(ψ,∇ψ) = g(0)(ψ) + g(1)(∇ψ) | (6) |
 | (7) |
In ref. 6 we apply variational principles to eqn (7) to determine the evolution of such a three-phase system. Based on the generic free energy functional, the relationship between the Gibbs free energy and the chemical potential, and the equations of hydrodynamics, we obtain coupled equations of motion for the velocity field (a modified Stokes equation) and the concentration field (a modified Cahn–Hilliard equation):
| −∇p + ∇{η[∇v + (∇v)T]} + μ∇ψ = 0 | (8) |
 | (9) |
| ∇·v = 0 | (10) |
 | (11) |
Before describing the implementation and solution of our physical model, we note some ways in which it might be extended. Firstly, in many circumstances, nanoparticles are grafted with polymer chains to control their affinity with another polymer,33 or to prevent their aggregation due to van der Waals forces.21 The presence of such a polymer layer, or polymer brush may have several effects that should be taken into account in extending our model. As discussed in ref. 6, the hydrodynamic flow in the vicinity of the particle, in the presence of concentration gradients, is the consequence of localized tangential forces in the vicinity of the particle, as shown by eqn (8). The presence of a polymer brush may modify the spatial distribution of these forces but, if the density of the brush is relatively low, this effect should be small. On the other hand, the hydrodynamic flow created in the liquid by these tangential forces should be partially screened by the brush as discussed, for example, in the case of electro-osmosis along grafted solid interfaces in ref. 34. Another effect in the wetting/dewetting limit is the deformation of the soft polymer brush due to the liquid A/liquid B surface tension. This effect induces dissipation within the brush which may become the dominant factor for the wetting/dewetting dynamics.35 These kinds of effects would need to be taken into account in extending our model to polymer grafted nano-particles.
A second possible extension of our model is to systems containing multiple nanoparticles. This would enable us to, for example, investigate the mechanisms responsible for the formation of bicontinuous gels, as described in ref. 36, and has obvious relevance to the manufacturing of composite materials that incorporate nanoparticles. Our model may be adapted to describe such systems by the addition of a term representing the force field due to the particles to the Stokes eqn (8), and the inclusion of a suitable Lennard-Jones potential for the inter-particle interactions, as in ref. 37.
3 Implementation and solution
To implement and solve this physical model we adapt the fluid particle dynamics approach developed by Araki and Tanaka.38 In this approach, hard particles are modelled as highly viscous fluids (typically 50 times more viscous than the surrounding fluid). Thus it is an example of a diffuse interface method, as discussed in ref. 30 and 31, and avoids the difficulties with managing the boundary conditions associated with hard surfaces in fluid flows. The fluid particle dynamics approach has been applied to charged colloidal suspensions,39 colloidal aggregation in liquid crystals,40 and nanoparticles in a phase separating binary mixture37,41 but this is the first time it has been used to study the dynamics of wetting and dewetting under shear, and the shear induced migration of a particle from one fluid phase to another.To make progress we specify the form of each term in the free energy functional (7):
 | (12) |
Note that ϕ varies in value from 0 to 1, over a length scale equal to the width of the particle interface, e. Thus, |∇ϕ| is of order  . We assume the width of the interface to be the monomer length scale of approximately 0.5 nm, which we equate to 1, in the dimensionless units of the model (see Appendix A).
. We assume the width of the interface to be the monomer length scale of approximately 0.5 nm, which we equate to 1, in the dimensionless units of the model (see Appendix A).
The bulk free energy term is based on the Flory–Huggins free energy density for a binary polymer mixture:42
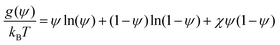 | (13) |
In fact, we use a modified version of the usual Flory–Huggins expression:
 | (14) |
The equations of motion, (8)–(10) are unchanged in form, but now the chemical potential μ is the functional derivative of the new free energy functional, eqn (12).
To solve the equations of motion, we use an FTCS (Forward-Time, Central-Space) finite difference scheme on a discrete two-dimensional lattice, with periodic boundary conditions. To avoid the numerical instability associated with logarithmic functions, we approximate the Flory–Huggins free energy density, eqn (14), with a 10th order polynomial in even powers of ψ:
| g(ψ) = a1ψ10 + a2ψ8 + a3ψ6 + a4ψ4 + a5ψ2 | (15) |
In outline, the numerical solution of the equations of motion proceeds by solving the Stokes equation without the pressure term, in order to calculate an uncorrected velocity field. It is then possible to take the divergence of both sides of the complete Stokes eqn (8), including the pressure term, and to apply the incompressibility condition to calculate the pressure field and thus the corrected velocity field. Having calculated the velocity field, it is straightforward to solve the modified Cahn–Hilliard eqn (9) to calculate the ψ field. The interior of the particle is the region of the system where the ψ field is near-zero and the ϕ field is near unity. The motion of the particle is tracked by integrating the velocity field within this region and averaging over the region's extent. The circularity of the particle boundary is enforced after each step in the simulation.
We choose a default lattice size of 256 × 256. The default particle radius is 25 lattice cells (∼12.5 nm) and the particle interface width is 1.0 (∼0.5 nm) throughout. The ratio of the particle “fluid” viscosity to the polymer viscosity is 50 in all simulations, and the particle interface energy barrier parameter, ζ = 10.0 to limit ingress of polymer fluid into the particle's domain. With this value of ζ, the order parameter field in the interior of the particle is typically ψ ∼ 10−4.
All simulations take place in the Rouse regime, where entanglement effects of polymer chains at the molecular scale may be neglected. In our model and, given the chosen time scale, this implies an effective diffusion coefficient of D = 1.0, and a fluid viscosity of η ∼ 1.0. In the simulations described in this paper, we assume strong segregation between the polymers and set the Flory–Huggins interaction parameter, χ = 4.0. For the wetting parameter, we typically assume a high intermediate value of W = 4.0; in other words, the particle has a marked preference for one phase over the other.
When the particle starts in the non-favoured polymer, its distance from the central interface is specified in lattice cell units. Physically, a lattice cell has dimensions comparable with a typical monomer length of 0.5 nm. In the dewetting simulations, the distance of the particle from the interface is varied from 2.5 nm to 10.0 nm. Both a quiescent system and a system subject to a shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 and
= 1.0 × 104 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 × 104 s−1 are simulated. The former shear rate implies 100 percent shear in 106 × Δt = 100 μs.
= 2.0 × 104 s−1 are simulated. The former shear rate implies 100 percent shear in 106 × Δt = 100 μs.
In Appendix A we discuss the mapping of dimensionless to physical quantities and show that, given the above parameter choices, a single simulation step equates to 10−10 s. When running simulations, snapshots of the system are taken after each 1000 simulation steps. Thus, the time resolution of the simulations is 10−7 s. This strikes a good balance between data storage capacity and computation time, and the ability to observe the system at short time scales.
4 Wetting
Our focus in this paper is on spinodal dewetting, which occurs when the film thickness is of the order of a few nanometres, and which we therefore expect to observe in our simulations of a particle close the interface of two liquid phases. The effect of shear on such a system, and in particular on whether shear promotes the migration of the particle from one liquid phase to the other, is also of great theoretical and practical interest. Additionally, we may also use our model to explore the dynamics of wetting. To do this, the particle is initially located symmetrically with respect to the polymer–polymer interface, and its position is fixed. Of course, this is an artificial constraint since a particle in a real system moves under the influence of hydrodynamic forces, but it enables us to treat the surface of the particle as analogous to the solid substrate in the above discussion. We vary the wetting parameter, W, from 1.0 to 8.0, and observe the evolution of the system in each case. The Flory–Huggins parameter, χ = 4.0 in all simulations, implying strong segregation between the two phases (in fact ψeq = ±0.9562). Denoting the favoured phase as A and the non-favoured phase as B, Young's equation becomes:γSB = γSA + γAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe θe | (16) |
| S = γSB − (γSA + γAB) | (17) |
To make further progress, we recall that the wetting parameter, W = 2(γSB − γSA), so the condition for total wetting becomes:
| W > 2γAB | (18) |
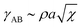 | (19) |
 . To be specific, if χ = 4.0, as it is in our simulations, γAB ∼ 2. Therefore, from eqn (18) and (19), we predict that total wetting will occur when W ≳ 4.
. To be specific, if χ = 4.0, as it is in our simulations, γAB ∼ 2. Therefore, from eqn (18) and (19), we predict that total wetting will occur when W ≳ 4.
We turn now to the results of our wetting simulations. Fig. 5 shows typical dynamics for the W = 4.0 case.
 | ||
| Fig. 5 Stages of wetting, with wetting parameter W = 4.0. The particle is initially located symmetrically at the interface and immobilised, allowing the preferred phase to wet its surface. | ||
We also show the state of system after 1.0 × 107Δt (equivalent to 1.0 ms), for values of W from 1.0 to 8.0 (Fig. 6).
Finally, we show the evolution of the mean free energy density (per lattice cell) of the system as the favoured phase wets the particle, for values of W from 1.0 to 8.0 (Fig. 7).
Note that in the early stages of the simulation (0.1–0.2 μs) the polymer–polymer interface rapidly equilibrates, and this effect is superimposed on the wetting dynamics. This is unavoidable, but occurs rapidly enough not to obscure the wetting dynamics. Thus our model is consistent with assumptions made in our previous paper6 about the relative time scales associated with local equilibration close to the solid surface and with the hydrodynamic flow itself.
From these results, we note that, qualitatively, the wetting behaviour appears physically realistic for all values of W. As W increases, the degree of wetting by the favoured polymer is greater, and the contact angle decreases.
Total wetting clearly occurs when W = 8.0. This seems to correspond to a kink in the free energy density plot at t ≈ 0.7 μs. From a video of the early stages of wetting when W = 8.0, we estimate that complete wetting occurs at t ∼ 0.9 μs, supporting this hypothesis. Although not so obvious in the snapshots of the system's evolution, it is possible that total wetting also occurs when W = 4.0, as marked by a similar kink in the free energy density plot, also at t ≈ 0.7 μs. The occurrence of total wetting at W = 8.0 and W = 4.0 is consistent with the condition for total wetting: W ≳ 4 derived above.
The characteristic time scale for wetting is ∼1.0 μs for all values of W considered. There is some evidence that higher values of W result in faster wetting:  is greater at low values of t, for higher values of W, although this is accompanied by greater relaxation time scales.
is greater at low values of t, for higher values of W, although this is accompanied by greater relaxation time scales.
5 Dewetting without shear
To observe the qualitative dynamics of dewetting at a higher spatial resolution, we choose a system size of 1024 × 1024 cells, and a particle of radius 100 lattice cells (∼50 nm). In this simulation, the particle is initially positioned at d = 4.0 nm from the central interface. Fig. 8 shows the state of the system in the early stages of its evolution, up to t = 80.0 μs.As expected, we observe the formation of a fluid rim, characteristic of dewetting at around t = 20.0 μs. At later times, the rim continues to grow and moves outwards towards the edge of the system, at constant speed. At longer time scales (not shown), the curvature of the interface becomes more uniform, and the interface is expected to flatten over time scales that are computationally inaccessible.
We also show the magnitude of the velocity field, at various times close to the dewetting point, in Fig. 9. The maximum speed of fluid flow is observed close to the surface of the particle, just after dewetting occurs, and is of order 1.0 ms−1.
To study the quantitative dynamics of dewetting, we vary the initial distance of the particle from the central interface and observe the time to the onset of dewetting. In the strong segregation regime (W = 4.0), all stages of dewetting occur in rapid succession: the time between the first sign of the interface distorting, and first contact of the favoured phase with the particle service is typically ≲1.0 μs. Thus, we take the dewetting point to be when the favoured phase first makes contact with the particle surface. This is quite straightforward to assess by inspection of snapshots of the system close to the dewetting point.
With these parameters, we observe (Table 1 and Fig. 12) that dewetting occurs in less than 1.0 μs when the particle starts at d = 2.5 nm from the central interface, and the dewetting time increases to ∼60 μs when d = 4.5 nm. At d = 5.0 nm dewetting is not observed, indicating a critical film thickness, dc ∼ 5 nm, given our assumptions about the strength and range of the intermolecular forces involved.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 and
= 1.0 × 104 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 × 104 s−1 as the distance of the particle from the interface varies from d = 2.5 nm to d = 10.0 nm
= 2.0 × 104 s−1 as the distance of the particle from the interface varies from d = 2.5 nm to d = 10.0 nm
| Distance [nm] | Dewetting time [μs] | ||
|---|---|---|---|
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 [×104 s−1] = 0 [×104 s−1] |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 [×104 s−1] = 1.0 [×104 s−1] |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 [×104 s−1] = 2.0 [×104 s−1] |
|
| 2.5 | 1.2 | 1.2 | 1.2 |
| 4.0 | 10.4 | 10.6 | 10.8 |
| 4.5 | 57.4 | 49.7 | 46.8 |
| 5.0 | — | 64.2 | 54.5 |
| 6.0 | — | 76.5 | 61.1 |
| 7.0 | — | 86.4 | 65.9 |
| 8.0 | — | 96.2 | 70.5 |
| 9.0 | — | 107.0 | 74.9 |
| 10.0 | — | 118.4 | 79.0 |
We end this section with a note about the dynamics of the polymer–polymer interface long after dewetting has occurred. To observe the behaviour of the interface over longer time scales, we used a smaller particle, of radius r = 5.0 nm, to reduce the computational load. In this simulation, the interface continues to flatten, carrying the particle with it, even after ∼2.2 ms, indicating that the system has not reached equilibrium. The final equilibrium state of the system, in which the interface is flat and meets the surface of the particle at the true contact angle implied by the a wetting parameter of W = 4.0, is inaccessible in the time scales of our simulations.
6 Dewetting with shear
The study of dewetting behaviour under shear has practical relevance to the manufacture of composite materials, where nanoparticles are often added to polymer blends to enhance the mechanical properties of the end product. During the manufacturing process, particles can migrate to the phase boundaries, where they can retard, or even halt, further phase separation, or remain embedded in one phase or the other. The final distribution of particles in the composite material contributes to its mechanical properties (toughness and elasticity, for example). Since the dispersion of nanoparticles within a blend is commonly achieved by shearing the mixture, there are potential practical benefits to understanding this process in a model system.The ability to model the behaviour of a particle near an interface under shear is an important first step in understanding the behaviour of such systems, and how to achieve the desired distribution of particles in the final product. In ref. 32 the behaviour of a single particle close to an interface under shear is studied, building on previous work on the dynamics of a particle near the interface between two fluids in ref. 31 and 45 The shear stress is applied parallel to the interface, which separates a viscoelastic fluid (where the particle starts), and a Newtonian fluid. Shearing the system induces a gradient in the normal stress close to the interface, and also creates a Laplace pressure as the interface is subtly distorted by the effect of shearing. The motion of the particle is determined by the balance of these forces which, in turn depend on dimensionless parameters in the model – chiefly the Weissenberg number, Wi (shear rate times relaxation time), and the Capillary number, Ca (the ratio of viscous stress and capillary stress). The simulations delineate four possible outcomes: migration of the particle away from the interface; movement towards the interface (which eventually stalls); adhesion to the interface; and migration across the interface into the Newtonian fluid. By varying Wi and Ca, the authors are able to produce morphology plots, showing the dependence of the final state of the particle on the dimensionless parameters. They also vary other parameters in the model – for example, the equilibrium contact angle (determined by W in our model) and the mobility of the particle (determined by D in our model) – and show how these changes modify the morphology plots.
In a similar vein37,41 considers the movement of multiple particles, under hydrodynamic forces caused by phase separation in a quenched homogeneous blend, and show how the resultant morphology of the system varies as the particle concentration and mobility is varied. In these simulations, there is no eternal shear on the system.
In contrast, the approach taken in this paper is to apply shear perpendicular to the interface between the two liquid phases, and to observe the behaviour of the particle at different shear rates: in particular, can the particle be induced to migrate to its preferred phase, or does it adhere to the interface and remain stuck? We begin by studying simple dewetting of a thin film of the preferred phase at the surface of the particle, before considering later stages of the expulsion process.
As before, we use a wetting parameter of W = 4.0 in all simulations. The particle is initially in the non-favoured phase, 4.5 nm, just less than the critical film thickness, from the interface between the liquid phases. We vary this distance up to 10 nm, and observe the dynamics of dewetting.
Initially, we consider the effect of two different shear rates on the dewetting behaviour of the system: ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 and
= 1.0 × 104 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 × 104 s−1. The former shear rate corresponds to a strain of 100% at 106 × Δt = 100 μs. In all cases, the dewetting time is estimated from snapshots of the system.
= 2.0 × 104 s−1. The former shear rate corresponds to a strain of 100% at 106 × Δt = 100 μs. In all cases, the dewetting time is estimated from snapshots of the system.
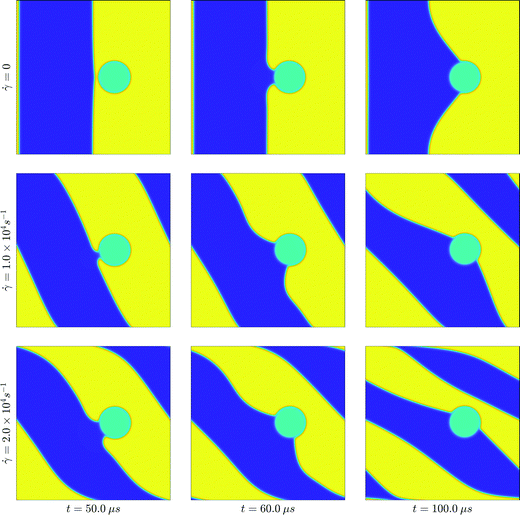
First, we illustrate the qualitative dynamics of dewetting at the chosen shear rates, compared with the dynamics of the quiescent system. Fig. 10 shows snapshots of the system near the point of dewetting, after dewetting, and at a later stage, for the two shear rates considered, and at zero shear.
We also show the magnitude of the fluid velocity field, close to the surface of the particle, at the dewetting point, and shortly afterwards (Fig. 11). As in the quiescent system, the maximum speed of fluid flow is observed close to the surface of the particle, just after dewetting occurs, and is of order 1.0 ms−1.
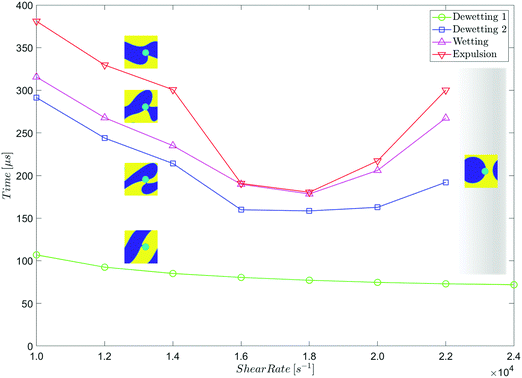
To quantify these observations, we plot the dewetting time, against the initial distance of the particle from the interface, which ranges from d = 2.5 nm to d = 10.0 nm, for the quiescent system and for the two shear rates used. Table 1 summarises the results, which are plotted in Fig. 12.
 | ||
| Fig. 12 Dependence of dewetting time on the initial distance of the particle from the interface, with and without shear. The uncertainty is ∼±0.5 μs so error bars are not shown. | ||
We note again a critical film thickness dc ∼ 5 nm. When d ≳ dc, dewetting only occurs under shear, as the externally imposed flow translates the interface between the liquid phases closer to the particle surface. This is consistent with the assumed range of the intermolecular forces in our model, and with the range of values for the critical film thickness seen in the literature.2 The dewetting time ranges from ∼1 μs to ∼100 μs. Again, this is consistent with our assumptions about the range of intermolecular forces, and the characteristic time scale chosen. It can be shown that the observed dewetting times are consistent with a simple model, in which the interface between the two liquid phases shears linearly with time and dewetting occurs almost instantaneously when the distance between the particle and the interface is small (less than ∼2.5 nm, say).
7 Expulsion under shear
Under shear, it is possible that the particle will be fully expelled from its non-preferred phase, after dewetting has occurred. In this section, we consider the status of the particle, beyond the dewetting point, at a range of constant shear rates. We take an initial state in which the particle begins d = 4.5 nm (i.e. just below the critical film thickness) from the central interface as our base case, and vary the shear rate from![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 to
= 1.0 × 104 s−1 to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.4 × 104 s−1 in steps of Δ
= 2.4 × 104 s−1 in steps of Δ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.2 × 104 s−1. In each case, the simulation runs long enough to observe the complete expulsion of the particle from its non-preferred phase or, if expulsion does not occur, any alternative steady state that may arise.
= 0.2 × 104 s−1. In each case, the simulation runs long enough to observe the complete expulsion of the particle from its non-preferred phase or, if expulsion does not occur, any alternative steady state that may arise.
When complete expulsion occurs, it is preceded by initial dewetting, breaking of the central interface under shear-induced stress, a second dewetting, and wetting of the particle by its preferred phase. Expulsion occurs when the last part of the non-preferred phase detaches completely from the surface of the particle. Some time after the particle is expelled, the system reaches its steady state. Fig. 13 illustrates the generic stages in the expulsion process.
However, in some cases, after the interface between the two liquids phases breaks, the second dewetting fails to occur because the moving region of the preferred phase does not make contact with the particle's surface. In this scenario, which occurs at lowest and highest shear rates in our simulations, an alternative steady state is reached in which the particle adheres to the surface of a droplet of the preferred phase, embedded in the non-preferred phase (Fig. 14).
Although the free energy changes associated with the later stages of expulsion are hard to discern, due to the much greater free energy changes associated with the breaking of the polymer–polymer interface, it is instructive to consider the evolution of the mean free energy density at various shear rates up to a point just after dewetting first occurs (Fig. 15).
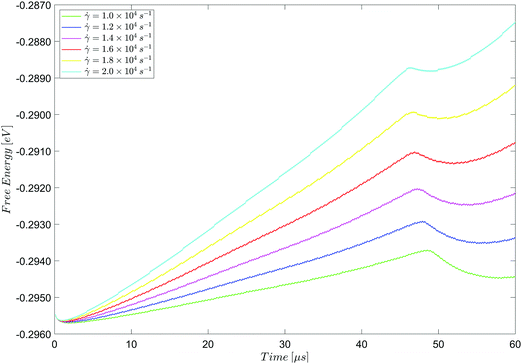 | ||
Fig. 15 Evolution of free energy under shear up to, and just after, the first dewetting point for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 to = 1.0 × 104 s−1 to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 × 104 s−1. = 2.0 × 104 s−1. | ||
Fig. 15 shows a period of very early, rapid equilibration at the interface (∼1.0 μs), during which the mean free energy density decreases slightly. This is followed by a steady increase in the mean free energy density due to the increased strain at the interface as the system is sheared at a constant rate. At all shear rates, dewetting occurs between 40 μs and 50 μs, and is accompanied by a temporary decrease in the mean free energy density, before it resumes its steady increase due to shear-induced strain at the interface between the two liquid phases.
Finally, we turn to the time scales over which the various stages of expulsion occur. Table 2 summarises the results of simulations in the Rouse regime at shear rates between ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 and
= 1.0 × 104 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.4 × 104 s−1. For completeness, we also show the dewetting time in the quiescent system, where the other stages of expulsion do not occur (instead, the particle adheres to the slowly flattening interface).
= 2.4 × 104 s−1. For completeness, we also show the dewetting time in the quiescent system, where the other stages of expulsion do not occur (instead, the particle adheres to the slowly flattening interface).
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 to
= 1.0 × 104 s−1 to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 × 104 s−1. In all simulations, the particle starts 4.5 nm from the central interface. A letter ‘A’ indicates that the alternative steady state in which the particle adheres to a droplet of its preferred phase is reached (i.e. after the initial dewetting, no further stages of the expulsion process are observed)
= 2.0 × 104 s−1. In all simulations, the particle starts 4.5 nm from the central interface. A letter ‘A’ indicates that the alternative steady state in which the particle adheres to a droplet of its preferred phase is reached (i.e. after the initial dewetting, no further stages of the expulsion process are observed)
| Shear rate [×104 s−1] | Dewetting 1 [μs] | Dewetting 2 [μs] | Wetting [μs] | Expulsion [μs] |
|---|---|---|---|---|
| No shear | 57.4 | — | — | — |
| 1.0 | 49.7 | A | A | A |
| 1.2 | 48.9 | A | A | A |
| 1.4 | 48.2 | 225.6 | 245.8 | 310.8 |
| 1.6 | 47.7 | 201.0 | 220.8 | 295.4 |
| 1.8 | 47.2 | 175.9 | 194.3 | 270.3 |
| 1.9 | 47.0 | 159.7 | 176.7 | 251.3 |
| 2.0 | 46.8 | 144.6 | 159.6 | 160.3 |
| 2.2 | 46.4 | A | A | A |
| 2.4 | 46.0 | A | A | A |
The expulsion data summarised in Table 2 is plotted in Fig. 16.
In these simulations, complete expulsion occurs at shear rates of 1.4 × 104 s−1 ≤ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 2.0 × 104 s−1. Outside of this range of shear rates, the system reaches an alternative steady state in which the particle adheres to a droplet of its preferred phase.
≤ 2.0 × 104 s−1. Outside of this range of shear rates, the system reaches an alternative steady state in which the particle adheres to a droplet of its preferred phase.
The second dewetting time decreases (approximately) linearly as the shear rate increases. Similarly, the wetting time decreases (approximately) linearly as the shear rate increases, and the time between second dewetting and wetting is roughly constant (∼20 μs) at all the shear rates at which complete expulsion occurs.
The relationship between expulsion time and shear rate is more complex. Between ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.4 × 104 s−1 and
= 1.4 × 104 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.9 × 104 s−1 the expulsion time decreases as the shear rate increases, but the relationship is notably less linear than that between the times of the earlier stages of expulsion, and the shear rate. At
= 1.9 × 104 s−1 the expulsion time decreases as the shear rate increases, but the relationship is notably less linear than that between the times of the earlier stages of expulsion, and the shear rate. At ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 2.0 × 104 s−1, there is a sudden decrease in the expulsion time, and the particle is expelled from its non-preferred phase very soon after wetting occurs, In fact, these two events are almost simultaneous.
≤ 2.0 × 104 s−1, there is a sudden decrease in the expulsion time, and the particle is expelled from its non-preferred phase very soon after wetting occurs, In fact, these two events are almost simultaneous.
Finally, although it is not obvious in Fig. 16, the initial dewetting time decreases as the shear rate increases. To highlight this point, we present the identical plot when the initial distance of the particle from the interface is d = 2 × dc = 9.0 nm (Table 3 and Fig. 17).
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 to
= 1.0 × 104 s−1 to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 × 104 s−1. In all simulations, the particle starts 9.0 nm from the central interface
= 2.0 × 104 s−1. In all simulations, the particle starts 9.0 nm from the central interface
| Shear rate [×104 s−1] | Dewetting 1 [μs] | Dewetting 2 [μs] | Wetting [μs] | Expulsion [μs] |
|---|---|---|---|---|
| No shear | — | — | — | — |
| 1.0 | 106.9 | 291.4 | 315.6 | 381.0 |
| 1.2 | 92.5 | 243.9 | 267.8 | 329.6 |
| 1.4 | 85.1 | 214.1 | 235.0 | 300.7 |
| 1.6 | 80.5 | 159.8 | 189.7 | 190.7 |
| 1.8 | 77.2 | 158.5 | 178.4 | 180.4 |
| 2.0 | 74.7 | 162.7 | 206.0 | 217.2 |
| 2.2 | 73.0 | 192.1 | 267.4 | 300.2 |
| 2.4 | 71.9 | A | A | A |
As expected, the decrease in the initial dewetting time as the shear rate increases is now observable, although the relationship is still quite weak due to the overall short time scales involved. In fact, by assuming that dewetting occurs almost instantaneously when the interface is less than a distance d ∼ 2.5 nm, and that the interface deforms linearly at a constant shear rate, it is possible to predict the initial dewetting time observed in all of our simulations quite accurately.
In contrast with simulations where the particle starts d = 4.5 nm from the interface, the particle is always expelled from its non-preferred phase. This indicates that the final state of the particle is determined by both the initial geometry of the system, and the applied shear rate.
For shear rates between ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.0 × 104 s−1 and
= 1.0 × 104 s−1 and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.4 × 104 s−1, Fig. 17 resembles the higher shear rate region of Fig. 16. That is, we observe a somewhat linear relationship between the time of the various stages of the expulsion process and shear rate. Again, the time between second dewetting and wetting is roughly constant at ∼20 μs in this range of shear rates.
= 1.4 × 104 s−1, Fig. 17 resembles the higher shear rate region of Fig. 16. That is, we observe a somewhat linear relationship between the time of the various stages of the expulsion process and shear rate. Again, the time between second dewetting and wetting is roughly constant at ∼20 μs in this range of shear rates.
At ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.6 × 104 s−1, there is a sudden decrease in the expulsion time, and the particle is expelled from its non-preferred phase very soon after wetting occurs (the two events are virtually simultaneous). This is similar to what we observe in the previous simulation with d = 4.5 nm at a shear rate of
= 1.6 × 104 s−1, there is a sudden decrease in the expulsion time, and the particle is expelled from its non-preferred phase very soon after wetting occurs (the two events are virtually simultaneous). This is similar to what we observe in the previous simulation with d = 4.5 nm at a shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2.0 × 104 s−1.
= 2.0 × 104 s−1.
At shear rates of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≥ 1.6 × 104 s−1, times of the later stages of expulsion (second dewetting, wetting, and expulsion) remain relatively constant as the shear rate increases, before beginning to increase when the shear rate is
≥ 1.6 × 104 s−1, times of the later stages of expulsion (second dewetting, wetting, and expulsion) remain relatively constant as the shear rate increases, before beginning to increase when the shear rate is ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 2.0 × 104 s−1. This rising trend in the times to second dewetting, wetting and expulsion continues up to a shear rate of
∼ 2.0 × 104 s−1. This rising trend in the times to second dewetting, wetting and expulsion continues up to a shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 2.4 × 104 s−1 when the system abruptly reverts to the alternative steady state illustrated in Fig. 14.
∼ 2.4 × 104 s−1 when the system abruptly reverts to the alternative steady state illustrated in Fig. 14.
The behaviour with a shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1.8 × 104 s−1 is unusual. Although the particle is initially expelled from the non-preferred phase at t = 180.4 μs (as plotted in Fig. 17), it then repeatedly adheres to, and detaches from, the interface between the liquid phases, before finally reaching the steady state observed in all other simulations (Fig. 18). The final expulsion of the particle from the non-preferred phase occurs at t ∼ 550 μs, much later than the initial expulsion time plotted in Fig. 17.
= 1.8 × 104 s−1 is unusual. Although the particle is initially expelled from the non-preferred phase at t = 180.4 μs (as plotted in Fig. 17), it then repeatedly adheres to, and detaches from, the interface between the liquid phases, before finally reaching the steady state observed in all other simulations (Fig. 18). The final expulsion of the particle from the non-preferred phase occurs at t ∼ 550 μs, much later than the initial expulsion time plotted in Fig. 17.
Regardless of the starting position of the particle, two steady states are observed: complete expulsion from the non-preferred phase; and adhesion to the interface of a droplet of the preferred phase, in a matrix of the non-preferred phase. Both of these regimes are seen in ref. 37, where the migration of multiple particles is promoted by hydrodynamic currents in a phase-separating blend. In contrast to ref. 32, we do not observe steady states in which the particle remains in the non-preferred phase. This is to be expected, since the effect of shear in our simulations is to move the interface between the two liquid phases closer to the surface of the particle, until the non-localised forces in the vicinity of the particle surface become sufficient to initiate dewetting.
Nevertheless, it is not necessarily the case that the particle cannot remain in the non-preferred phase, when the system is sheared. Plots of the particle position against time show that the particle initially moves away from the interface, under the influence of shear-induced flow. It is also possible that different parameter choices might lead to a wider variety of steady states, like those observed in ref. 32. In particular, we hypothesise that the strength of the particle's relative preference between the two phases, as represented by the W parameter, will determine the final steady state of the system under shear.
8 Conclusion
We have solved a physical model for the Stokes equations of a non-homogenous liquid in the presence of solid interfaces. This model has been introduced in ref. 6 and is consistent with the contact value theorem regarding thermodynamical equilibrium of liquids in contact with solid interfaces20–23 and with the general formalism of Onsager regarding the linear response theory of out-of-equilibrium systems.27–29 It allows us to describe how non-homogeneous liquids relax towards equilibrium by diffusion and convection. A key feature of our model is that the interfacial forces on solid interfaces are not located on the interface itself but are distributed in their vicinity and appear as body forces in the Stokes equations. To solve the physical model, we used a numerical approach introduced by Araki and Tanaka where the particle is described as a highly viscous liquid; this allows us to solve the Stokes equations in the whole system without managing complex boundary conditions. The model enabled us to describe wetting and dewetting of particles at or in the vicinity of liquid interfaces, at rest or in the presence of an imposed shear. It also enabled us to realistically model the migration of a particle from one liquid phase to another, via a process of first dewetting, second dewetting, wetting by the preferred phase, and expulsion, when shear is applied to the system, while enabling us to explore the factors which determine whether expulsion eventually occurs.Conflicts of interest
There are no conflicts to declare.Appendix: dimensionless quantities
We wish to make certain parameters in our simulations dimensionless, by choosing a suitable time scale, τ, length scale, a (which we take to be the monomer length scale (∼0.5 nm)) and energy scale, T (which we take to be the thermal energy at room temperature, 0.025 eV ≈ 4 × 1021 J). For the diffusion coefficient and viscosity, we then have: | (20) |
 | (21) |
Our aim is to determine the value of these quantities in the Rouse and the entangled regimes, along with the physical values of other important dimensionless quantities in our model (specifically, time and shear rate).
In the Rouse regime, which is the focus of the current paper, we have:42
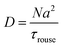 | (22) |
 | (23) |
Then, choosing  ensures that
ensures that ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = 1 and
= 1 and ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) = 1 also.
= 1 also.
We also have:
 | (24) |
In our computational model, this implies that a dimensionless time of ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 1 corresponds to a physical time of t = 10−7 s. Since our Rouse regime simulations use a dimensionless time step of Δ
= 1 corresponds to a physical time of t = 10−7 s. Since our Rouse regime simulations use a dimensionless time step of Δ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0.001. This implies that each step equates to Δt = 10−10 s in physical time.
= 0.001. This implies that each step equates to Δt = 10−10 s in physical time.
We will also be interested in the shear rate. Our model computes the displacement due to shear as follows:
 | (25) |
 is the dimensionless shear rate which, in our simulations, ranges from ∼0.001 to ∼0.002. Since Δ
is the dimensionless shear rate which, in our simulations, ranges from ∼0.001 to ∼0.002. Since Δ![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = 0.001 and taking, for example,
= 0.001 and taking, for example,  , we have:
, we have:| Δγ = n × L × 10−6 | (26) |
 | (27) |
 corresponds with a physical shear rate of
corresponds with a physical shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 2 × 104 s−1.
= 2 × 104 s−1.
Finally, we return to eqn (21) to calculate an order of magnitude estimate of the viscosity of our fluid in the Rouse regime. Rearranging, we obtain:
 | (28) |
 | (29) |
Acknowledgements
NC and NG thank Solvay and the EPSRC (grant number ST/N504282/1) for financial support.References
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
- P. G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena, Springer, New York, 2004 Search PubMed.
- M. Geoghegan and G. Krausch, Prog. Polym. Sci., 2003, 28, 261–302 CrossRef CAS.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- D. Long, A. Ajdari and L. Leibler, Langmuir, 1996, 12, 5221–5230 CrossRef CAS.
- N. Clarke, N. Gibbions and D. R. Long, Soft Matter, 2020, 16, 3485–3497 RSC.
- L. H. Tanner, J. Phys. D: Appl. Phys., 1979, 12, 1473–1484 CrossRef CAS.
- M. N. Popescu, G. Oshanin, S. Dietrich and A.-M. Cazabat, J. Phys.: Condens. Matter, 2012, 24, 243102 CrossRef CAS PubMed.
- J. W. Cahn, Acta Metall. Mater., 1961, 9, 795–801 CrossRef CAS.
- J. W. Cahn, Acta Metall. Mater., 1966, 14, 1685–1692 CrossRef CAS.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Ithaca, New York, 1980 Search PubMed.
- C. Bollinne, S. Cuenot, B. Nysten and A. M. Jonas, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 389–396 CrossRef CAS PubMed.
- R. Xie, A. Karim, J. F. Douglas, C. C. Han and R. A. Weiss, Phys. Rev. Lett., 1998, 81, 1251–1254 CrossRef CAS.
- D. Gentili, G. Foschi, F. Valle, M. Cavallini and F. Biscarini, Chem. Soc. Rev., 2012, 41, 4430–4443 RSC.
- A. Heinecke, W. Eckhardt, M. Horsch and H.-J. Bungartz, Supercomputing for Molecular Dynamics Simulations: Handling Multi-Trillion Particles in Nanofluidics, Springer, Berlin, 2015 Search PubMed.
- P. J. Hoogerbrugge and J. M. V. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- P. Espanol and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed.
- B. J. Alder and T. E. Wainwright, Phys. Rev. A: At., Mol., Opt. Phys., 1970, 1, 18–21 CrossRef.
- D. C. Grahame, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed.
- J. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 1991 Search PubMed.
- D. Ben-Yaakov, D. Andelman, D. Harries and R. Podgornik, J. Phys.: Condens. Matter, 2009, 21, 424106 CrossRef PubMed.
- R. M. Adar and D. Andelman, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 11 CrossRef PubMed.
- B. V. Derjaguin, G. P. Sidorenkov, E. A. Zubaschenkov and E. V. Kiseleva, Kolloidn. Zh., 1947, 9, 335–347 Search PubMed.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- S. Marbach, H. Yoshida and L. Bocquet, J. Chem. Phys., 2017, 146, 194701 CrossRef PubMed.
- S. R. de Groot and P. Mazur, Non-Equilibrium Thermodynamics, Dover, Mineola, 1984 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Statistical Physics, Part 2, Pergamon Press, New York, 1981 Search PubMed.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Elsevier, Amsterdam, 1987 Search PubMed.
- D. M. Anderson, G. B. McFadden and A. A. Wheeler, Annu. Rev. Fluid Mech., 1998, 30, 139–165 CrossRef.
- Y. J. Choi and P. D. Anderson, Int. J. Numer. Methods Fluids, 2011, 69, 995–1015 CrossRef.
- N. O. Jaensson, C. Mitrias, M. A. Hulsen and P. D. Anderson, Langmuir, 2018, 34, 1795–1806 CrossRef CAS PubMed.
- P. F. Green, Soft Matter, 2011, 7, 7914–7926 RSC.
- J. L. Harden, D. L. Long and A. Ajdari, Langmuir, 2001, 17, 705–715 CrossRef CAS.
- D. L. Long, A. Ajdari and L. Leibler, Langmuir, 1996, 12, 1675–1680 CrossRef CAS.
- K. Stratford, R. Adhikari, I. Pagonabarraga, J.-C. Desplat and M. E. Cates, Science, 2005, 309, 2198–2201 CrossRef CAS PubMed.
- T. Araki and H. Tanaka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 1–7 CrossRef PubMed.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS PubMed.
- T. Araki and H. Tanaka, Phys. Rev. Lett., 2004, 93, 015702 CrossRef.
- H. Kodama, K. Takeshita, T. Araki and H. Tanaka, J. Phys.: Condens. Matter, 2004, 16, L115–L123 CrossRef CAS.
- T. Araki and H. Tanaka, J. Phys.: Condens. Matter, 2008, 20, 072101 CrossRef.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, UK, 2003 Search PubMed.
- R. A. L. Jones and R. W. Richards, Polymers at Surfaces and Interfaces, Cambridge University Press, Cambridge, UK, 1999 Search PubMed.
- E. Helfand and Y. Tagami, J. Polym. Sci., Part B: Polym. Lett., 1971, 9, 741–746 CrossRef CAS.
- N. O. Jaensson, M. A. Hulsen and P. D. Anderson, Comput. Fluids, 2017, 156, 81–96 CrossRef.
| This journal is © The Royal Society of Chemistry 2021 |