Open Access Article
Open Access ArticleRotational diffusion and rotational correlations in frictional amorphous disk packings under shear†
Dong
Wang‡
 ab,
Nima
Nejadsadeghi‡
c,
Yan
Li‡
d,
Shashi
Shekhar
*d,
Anil
Misra
ab,
Nima
Nejadsadeghi‡
c,
Yan
Li‡
d,
Shashi
Shekhar
*d,
Anil
Misra
 *e and
Joshua A.
Dijksman
*e and
Joshua A.
Dijksman
 *f
*f
aDepartment of Physics & Center for Non-linear and Complex Systems, Duke University, Durham, North Carolina 27708, USA
bDepartment of Mechanical Engineering & Materials Science, Yale University, New Haven, Connecticut 06520, USA
cMechanical Engineering, University of Kansas, 1530 W. 15th St, Lawrence, KS 66045-7609, USA
dComputer Science & Engineering, University of Minnesota, Minneapolis, MS, USA. E-mail: shekhar@umn.edu
eCivil, Environmental & Architectural Engineering, University of Kansas, 1530 W. 15th St., Lawrence, KS 66045-7609, USA. E-mail: amisra@ku.edu
fPhysical Chemistry and Soft Matter, Wageningen University & Research, Stippeneng 4, 6708 WE Wageningen, The Netherlands. E-mail: joshua.dijksman@wur.nl
First published on 29th July 2021
Abstract
We show here that rotations of round particles in amorphous disk packing reveal various nontrivial microscopic features when the packing is close to rigidification. We analyze experimental measurements on disk packing subjected to simple shear deformation with various inter-particle friction coefficients and across a range of volume fractions where the system is known to stiffen. The analysis of measurements indicates that shear induces diffusive microrotation, that can be both enhanced and suppressed depending upon the volume fraction as well as the inter-particle friction. Rotations also display persistent anticorrelated motion. Spatial correlations in microrotation are observed to be directly correlated with system pressure. These observations point towards the broader mechanical relevance of collective dynamics in the rotational degree of freedom of particles.
Amorphous packings of particles occur in many contexts, ranging from glassy polymers to colloidal gels, geological sediments and active matter. These materials are well known to have complex mechanical behavior. For example, their mechanical response is often strain history dependent.1–4 Their phase behavior can also be complex, ranging from solid to liquid and gas-like, which is especially fascinating for purely athermal systems.5,6 The amorphous nature of the microstructure of these systems makes it notoriously challenging to understand the origin of such behavior in general.7 Notably, these “granular” material systems are characterized by a length-scale proportional to particle size, that makes their theoretical description using classical continuum physics concepts particularly challenging. For accurate descriptions of amorphous packing mechanics, in which various micro-scale mechanisms exist that give rise to non-standard kinematics, such as those resulting in vortex type structures,8,9 the traditional views of continuum mechanics desperately need updating. One route towards a more general continuum description considers material point rotations and has an origin in the work from the Cosserat brothers.10 Indeed, it has long been recognized that the rotational motion of particles in thermally driven amorphous packings can be linked to slowdown effects and glassy dynamics11–13 and are relevant for phase behavior of strongly driven granular systems.6,14,15 Nevertheless, much progress is needed to include (particle) rotational degrees-of-freedom in continuum mechanics approaches.16–19 There is ample evidence that particle rotations indeed contribute to the mechanical response of particle packings,20–23 although there is precious few systematic experimental data available that can disentangle the various mechanisms that drive rotational dynamics on the local scale. The purpose of this paper is to illustrate the diffusive and spatially correlated dynamics of particle rotations in a strain-history dependent material that undergoes a transition to rigidity when its particle volume fraction is varied. We make use of an athermal disk packing to avoid temperature and displacement-rotation couplings and invoke special boundary conditions that allow us to decouple shear from packing fraction-dependent effects.
Mechanical phases
Athermal granular material systems exhibit many non-standard physical phenomena, such as that of negative group velocity,24,25 frequency band gaps,26–29 chirality30 and load path dependency. The latter is the key physical phenomenon that underlies our results: collections of discrete athermal particles have the remarkable property that they can become rigid when assembled into certain arrangements. These loose particle packings can resist shear or compression when a sufficient number of them is present per unit volume, a feature commonly called jamming. Notably, even when not spatially confined, packing of particles can enhance its stiffness when the assembly is subject to shear strain. This shear deformation induced stiffening is known as shear jamming. With “shear” here we refer to system-level deformation unless otherwise noted.The role of rotation
To study the role of rotational degrees of freedom, decoupling rotation from translation is challenging. In many materials the involved particles (be it molecules, colloids or grains) are not spherically symmetric, hence their rotation requires also spatial displacement of their neighbors, particularly for high density, jammed granular materials. To probe the role of only the rotational degrees of freedom in the strain dependence of amorphous packings, athermal round particle systems are an optimal prototypical choice. Such particles can be designed to experience contact friction, which directly couples rotational degrees of freedom to displacements. In an athermal packing of frictional disks, shear for even circular particles is thus directly coupled to rotations without necessarily requiring particle displacements.While rotational dynamics of spherical particles in athermal packings has been probed via wave-propagation measurements31 and compression,32 particle-level experimental evidence that links rotational degrees of freedom directly to shear in amorphous packings has so far not been obtained. We use a unique set of experimental data to show that suppressing the particles' microrotation dynamics by making them more frictional induces a marked stress response in the packing. We will see that particle rotations display strain-induced diffusive behavior even at very small strain amplitudes. The diffusive behavior can be correlated with mechanical packing behavior as it depends on particle packing density and friction coefficient in manners consistent with previously observed mechanical packing properties.33–35 Additionally, particle rotations display non-local correlations as revealed by spatial auto-correlation measures36. These mesoscopic correlations change markedly when the packing becomes more jammed, suggesting that the non-local mechanical effects well known to exist in sheared glassy granular media and amorphous materials in general37–39 and mediated by displacement correlations, can be additionally mediated by correlated rotational dynamics.
Rotational dynamics across the phase boundary
We systematically vary the friction coefficient and packing density of the particles to capture the entire transition region of jamming and shear-induced jamming, known to exist for our model system. Our data reveals that in our completely athermal amorphous packing, suppressing rotational degrees-of-freedom directly coincides with a mechanical stiffening. More significantly, we observe that suppressing rotational diffusion also suppresses mesoscopic spatial anticorrelations in the microrotation field. Our work thus shows that shear jamming may be intricately related to the suppression of rotational degrees of freedom. Indeed, some work had already hinted at the relevance of rotational degrees of freedom of particles in loose particle assemblies for both slow,16,40–42 irreversibility43 and fast granular flows44–46 and recently also for the statistical mechanics of sheared packings.47,48 Our data is however the first that provides systematic experimental particle level statistics and correlation analysis across a range of friction coefficients and volume fractions. We also provide strong evidence that particle rotations are an essential kinematical quantity in the study of dense amorphous packings, as they are already in the field of active matter6 and metamaterials.30 More broadly, the spatial autocorrelation analysis of rotations that we employ may reveal essential features in materials science of a large variety of materials that exhibit the effects of intrinsic length scales.Methods
Experimental setup
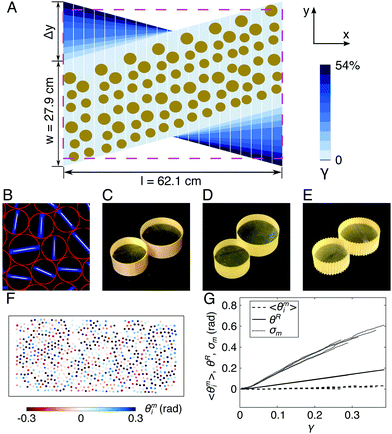
In our experiments, we analyze a series of experiments that allow for the tracking of rotation of every disk-shaped particle in a ∼1000-particles large simple shear geometry. In our experiments we have used quasi-two dimensional packings, as three dimensional shear experiments have the propensity for formation of finite shear localization bands into which the particle rotations typically concentrate.42,49–51 In contrast, our two dimensional geometry with articulated base allows us to suppress shear localization entirely, as reported elsewhere.33,34 Shear is applied quasi-statically from an isotropic stress free state and tracked during the initial shear transient up to a strain of 0.5. For a sketch of the setup, see Fig. 1a. The slats have a width of the diameter of a small particle. Previous experiments have described dilatancy and displacement dynamics in these packings.33,34 A fluorescent bar placed on the particles combined with UV imaging allows us to track the absolute orientation of every particle in the packing; see Fig. 1b.Particles with different friction
Having access to rotational dynamics of the particles, we can explore the effect of inter-particle friction using granular assemblies with controlled variations of inter-granular friction coefficient, as well as the effect of different initial packing fractions ϕ. Three sets of particles were used in our experiments. One set of particles was cut from photoelastic sheets,33 having an inter-particle friction coefficient μm of approximately 0.7. After conducting experiments with this set, we wrapped these particles with Teflon tape. Dry Teflon–Teflon contacts have a friction coefficient of μl ∼ 0.1535. A third set of data was obtained with photoelastic disks cut with fine teeth on their circumference so that particles will interlock when they come into contact. Such a particle shape mimics an extremely large friction coefficient; we refer to these particles as μh. Examples of these particle types are shown in Fig. 1c–e. The diameter ratio of big to small disks is 1.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (a small particle has a diameter of ∼1.3 cm), and the number ratio is roughly 1
1 (a small particle has a diameter of ∼1.3 cm), and the number ratio is roughly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.3 (big to small) for each packing. Although it is well-known that polydispersity affects packing mechanics,52–54 we did not vary the ratio of big to small particles for any μ or ϕ in the present study.
3.3 (big to small) for each packing. Although it is well-known that polydispersity affects packing mechanics,52–54 we did not vary the ratio of big to small particles for any μ or ϕ in the present study.
Experimental protocol
Particles were first randomly placed in the shear cell and manually relaxed until no inter-particle contact force was visible by eye. Then starting from either an initial parallelogram or a rectangular configuration, the shear cell was deformed by strain steps of 0.0027. The system was then relaxed for 10 seconds followed by taking three kinds of images: one with white light, one with polarized light, and one with UV light. These three images reveal particle positions, particle contact forces/pressure, and particle orientation, respectively. Such a process of shearing, relaxing and image taking was repeated until a certain total shear strain was achieved. For each packing fraction and friction coefficient, we repeated all the experiments five times with the exception of the lowest two density μl runs; they were repeated twice. Note that the analysis of the images acquired during the experiment reveals that not all the grains were detected in all frames, where some grains move out of or inside the boundaries of the images from one frame to another. As a result, for the analysis performed in the current paper, only grains common between all the frames were considered, and the grains present at one frame and not detected in another frame are excluded. Moreover, the grains on the boundary were removed from the analysis.Particle rotations under simple shear
We probe the dynamics of orientations obtained from image analysis of each frame. The observed grain rotations in simple shear experiments can be decomposed into two parts. One part of the rotation of each grain is a result of the imposed affine macro-scale deformation field, which contributes an overall rigid body rotation. In our calculations, the rigid body rotation between any two frames is not assumed from the imposed strain on the boundaries, but obtained as half of the difference in the slope of straight lines fitted to the coordinates of grains centroids in the two frames. We note that, in general, the relation between the measured change in slope and the rigid body rotation is nonlinear especially in finite deformation. However, a linear relation in the current analysis for the considered shear strain range is a good approximation. One can also extract the rigid body rotation on a local scale around every particle, for example from the Delaunay triangulation.55 Such a choice gives different scientific insights, just like one can compare the displacement field with a field imposed from the boundaries (globally) versus the one that emerges locally. However, it is not trivial to select which local region to analyze to find the local rigid body rotation. Moreover subtracting the local rigid body motion might also remove the vorticity we aim to analyze. The linear fit works because from previous work we know that in our particular shear geometry,35 grain displacements tend to follow the imposed macro-scale deformation field. While there exist fluctuations from the imposed linear macro-scale deformation field in the grain centroid displacements, we have shown previously that these fluctuations are small.Separating out microrotations
The second rotation contribution is due to the micro-scale phenomena of individual grain spin that we call microrotation. Denoting the rotation of grain i by θi and the macro-scale rigid body rotation by θR, the microrotation of grain i, is obtained as θmi = θi − θR. Fig. 1f gives the microrotation field for a μm packing. Additional examples of microrotation fields for different μ, are given in ESI† Fig. S1. The initial frame is taken as the reference configuration to obtain the evolution of the grain-spin measures as a function of imposed strain. The rigid body rotation θR grows linearly with strain as expected from the linearly increasing strain field imposed on the packing (see Fig. 1g). The mean of the microrotations 〈θmi〉 and the standard deviation of microrotations also change as a function of strain as observed in Fig. 1g for all five repeats done for μm at ϕ = 0.816. An overview of microrotation kinematics for several other μ and ϕ can be found in Fig. 2 in ESI.† Notably, the mean microrotation 〈θmi〉 is nearly zero for all the cases measured in this work: that is, there is no preferred direction in which grain microrotation fluctuations occur. Note that the slats on which the particles rest are likely to contribute to θi. It appears that the slats mechanism ensures that the mean particle rotations tracks the rigid body rotation on average. We have also examined many spatial plots and videos of the particle rotation θi and never noticed any signature of bias that the slats might induce; see Fig. 1f. The metrics derived from θi did not show any sign of structures that can be traced back to the slat geometry. For examples of typical microrotation trajectories, see Fig. S3 in ESI.† This null-result is highly reproducible between different repeats of the experiments and consistent with earlier numerical simulations.40,41,51,56,57 It is also noteworthy that the microrotations follow a nearly Gaussian distribution for all cases (see Fig. S4 in ESI†). However, the amplitude of grain microrotation fluctuations increases monotonically with strain. Note that some of such shear induced rotational fluctuations have been observed in the experimental work of Matsushima in ref. 16 on nonspherical particles.
also change as a function of strain as observed in Fig. 1g for all five repeats done for μm at ϕ = 0.816. An overview of microrotation kinematics for several other μ and ϕ can be found in Fig. 2 in ESI.† Notably, the mean microrotation 〈θmi〉 is nearly zero for all the cases measured in this work: that is, there is no preferred direction in which grain microrotation fluctuations occur. Note that the slats on which the particles rest are likely to contribute to θi. It appears that the slats mechanism ensures that the mean particle rotations tracks the rigid body rotation on average. We have also examined many spatial plots and videos of the particle rotation θi and never noticed any signature of bias that the slats might induce; see Fig. 1f. The metrics derived from θi did not show any sign of structures that can be traced back to the slat geometry. For examples of typical microrotation trajectories, see Fig. S3 in ESI.† This null-result is highly reproducible between different repeats of the experiments and consistent with earlier numerical simulations.40,41,51,56,57 It is also noteworthy that the microrotations follow a nearly Gaussian distribution for all cases (see Fig. S4 in ESI†). However, the amplitude of grain microrotation fluctuations increases monotonically with strain. Note that some of such shear induced rotational fluctuations have been observed in the experimental work of Matsushima in ref. 16 on nonspherical particles.
 | ||
| Fig. 2 Standard deviation of rotations as a function of imposed shear strain in three different packing fractions for the (A) μl, (B) μm, and (C) μh particles (solid lines). All experiments are repeated five times and each fit well to power law behavior σm ∝ Dγn (dashed lines). (D) and (E) show, respectively, the variation of the parameters D and n as a function of packing fraction of the sets in μl, μm, μh. The highlighted data in yellow are the data used in panels a–c and Fig. 3. Error bars indicate the range among the repeats. | ||
Diffusive microrotation
Focusing further on the growth of σm(γ) we see that its strong growth with γ and the reproducibility among different initial configurations is also observed for different ϕ over the entire range of relevant densities and μ as shown in Fig. 2a–c. Up to a strain of 0.15, σm can be well described by the empirical relation σm = Dγn + σ0 as shown by the good quality of the fits. We interpret prefactor D as (the square root of) a diffusion constant as done previously for rotations induced by thermal fluctuations.58,59 Power law index n indicates the (weakly) nonlinear strain dependence and σ0 is a possible offset that is negligible for all experiments. We see that the strength of the fluctuations captured by D(ϕ) and n(ϕ) is very sensitive to friction μ as shown in Fig. 2d and e. The friction dependence does however capture the mechanical performance of the packing as well: at large μ, particle interactions associated with rotation are stronger even at smaller ϕ, and this trend is observed in both D(ϕ) and n(ϕ). Considering D as a diffusion constant, its thermal analogue would be given by the ratio of thermal fluctuations and viscous damping. Such competition can also be seen in the rotational diffusion: both D and n indicate that there are two mechanisms that play a role in the rotational diffusion, which is especially visible for μm. Initially, D, n(ϕ) grows with ϕ, indicating the enhanced particle interactions that give more fluctuations in rotations. However, above a certain ϕc(μ), D decreases, and above the packing fraction, ϕ ≈ 0.80, trends in the parameters D, n seem to converge, although we do not have access to a large enough range of ϕ to show that the decreasing trend for D,n visible for μm and μh reaches the plateau visible for μl. The trends do indicate that competing mechanisms emerge in high packing fractions suppressing the growth of further rotational fluctuations. We naively expect that with increasing ϕ, the number of contact interactions between particles per unit of strain increases, hence increasing D. This effect cannot continue indefinitely, as also steric hindrance effects must be reducing the intensity of such contact interactions. Steric hindrance does play a role for μh, the gear-shaped particles, but less so for the much smoother μl,μm particles. The mechanisms that determine n are not as intuitive but note that if we consider γ as a time variable and as a displacement fluctuation metric, normal diffusive behavior would have n = 0.5. Consequently, all behavior observed in our experiment can be considered superdiffusive. Interestingly, the values for n(ϕ) converge above a volume fraction of about 0.81, although a decreasing trend persists. The value of n tends towards 1 at very high packing fraction, indicating a linear dependence of σm on strain. These trends are even more visible if we consider smaller strain, see Fig. S5 in ESI.†
as a displacement fluctuation metric, normal diffusive behavior would have n = 0.5. Consequently, all behavior observed in our experiment can be considered superdiffusive. Interestingly, the values for n(ϕ) converge above a volume fraction of about 0.81, although a decreasing trend persists. The value of n tends towards 1 at very high packing fraction, indicating a linear dependence of σm on strain. These trends are even more visible if we consider smaller strain, see Fig. S5 in ESI.†
Correlations in microrotations
The observed Gaussian nature of the particle microrotation fluctuations is accompanied by underlying correlations in particle microrotation, which can be expected to exist in dense amorphous packings where many grains are in contact. Indeed, there are long range correlations in particle microrotations as visible in our three-step approach to quantifying the spatial autocorrelation of microrotations, leading to a mathematically well defined quantitative system average signal called Moran's I, that is widely used for geographical data36.Average neighborhood variance
We first compute the particle average neighborhood microrotational variance Sn. The neighborhood variance of each particle refers to the product of its microrotation deviation from mean microrotation and the mean microrotation deviation of its Voronoi neighborhood from mean microrotation. We compute the “average neighborhood variance” by | (1) |
Physically, a positive/negative value of Sn means that in general a particle rotates in the same/opposite direction as its neighborhood. Trivially, for two touching gears, Sn should be negative. However, in a large packing of gear or disk-shaped particles, it is not obvious how Sn behaves as a function of strain or volume fraction. Fig. 3a shows the average neighborhood variance for three different packing fraction ϕ for different μ: μl; ϕ = 0.783,0.810,0.828; μm; ϕ = 0.692, 0.758, 0.816; μh; ϕ = 0.713, 0.744, 0.807. The average neighborhood variance is clearly monotonically dependent on both μ and ϕ and grows with γ. We observe that higher friction or density results in lower average neighborhood variance, which means greater difference between a particle's microrotation and its neighborhood's. As mentioned, this anticorrelation makes mechanical sense: gear-like motion forces rotation of opposite direction in interlocking particles.
Global Moran's I
A large absolute value of Sn may be caused by two effects: either there is a (dis)similarity between neighborhood particle microrotations, or there is a large variance in the microrotation. To focus only on the comparison of the dissimilarity among neighborhood particles microrotation across the packing, we normalize Sn by the variance of the particle microrotation, σm2. We have shown the dynamics of σm2 and its non-monotonic dependence on friction and packing fraction in Fig. 2. By computing Sn/σm2, we arrive immediately at the system wide spatial autocorrelation metric called Moran's I. For completeness, global Moran's I is defined as follows: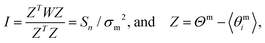 | (2) |
 , where N is the number of observations. In other words, the more observations there are, the closer the expectation to 0. Values of I usually range from −1 to +1. Values significantly below E(I) indicate negative spatial autocorrelation and values significantly above E(I) indicate positive spatial autocorrelation. A value of 0 for Moran's I implies that the neighbors are independent of each other, while positive values imply that neighbors are similar (e.g., smoothly varying field) and negative values imply that neighbors are dissimilar (e.g., a chessboard).
, where N is the number of observations. In other words, the more observations there are, the closer the expectation to 0. Values of I usually range from −1 to +1. Values significantly below E(I) indicate negative spatial autocorrelation and values significantly above E(I) indicate positive spatial autocorrelation. A value of 0 for Moran's I implies that the neighbors are independent of each other, while positive values imply that neighbors are similar (e.g., smoothly varying field) and negative values imply that neighbors are dissimilar (e.g., a chessboard).
Generally, the microrotations of the grains in all the materials in these analyses are negatively autocorrelated: the grains rotate like a chain of gears to some extent. Fig. 3b shows the trends of I as the shear strain increases. The differences in behavior for μl,μm,μh is evident: low friction particles have a weak spatial autocorrelation, whereas particles with higher friction coefficient develop stronger autocorrelations, with I decreasing to −0.3. The difference between the packings with a different ϕ is small but not insignificant. In general, anti-autocorrelations increase with larger packing fractions. Strikingly, also the rotational correlations are very strain sensitive, with 3% strain being enough to indicate significant difference between packings of the different ϕ and μ.
Local Moran's I
We go one step further and use the normalized neighborhood variance to gain insight into the local mechanics of sheared amorphous packings. There are cases where there is no global trend of spatial autocorrelation, but there are local communities where spatial autocorrelation is strong. Spatial autocorrelations as captured by I are thus not the same everywhere; in fact there are clusters of (anti)correlated rotations. We can quantify the local variability of these correlations by computing the standard deviation of what is called Local Moran's I and often used to represent the spatial autocorrelation within the local neighborhood of each observation. The formal definition is as follows: | (3) |
The standard deviation of Local Moran's I captures the rotational “floppiness” in the packing. With floppiness we refer to the presence of low-energy deformation modes as is typical,60 in this case deformations coming from rotations. A large σI signifies the presence of large relative rotations between neighboring particles, which are mechanically likely to occur when particles are not touching, hence “floppy”. At large ϕ in a highly overconstrained system, interlocking grains must all have the same rotational behavior so the variability of I in the packing should be small, hence σI should be small. At smaller ϕ, there are more ways to reach mechanical equilibrium, hence the variability among correlations should be higher. Similarly, σI should express the phenomena of shear jamming: at small strain, the shear jamming mechanisms has not been activated yet, so σI is small. We see in Fig. 3c that as strain increases, the packing moves from partially to completely constrained and should thus achieve a small σI. Finally, the role of μ should also be non-linear: at small and large μ, the rotational variability should be high as per previous arguments, so σI(μ) should have an optimum. We observe indeed all these mechanically reasonable trends in σI(ϕ, γ, μ). Ii standard deviation is strain dependent, exhibiting a distinct peak floppiness at about 3% strain (Fig. 3c). Note that at these strain levels, system level pressure is undetectable, highlighting again the sensitive nature of rotations.
The connection of spatial correlations to the rotational diffusion is also still visible in the fluctuations of the anticorrelated microrotation: observe how for ϕ > 0.80, σI is small for all μ, precisely where also the diffusivity of microrotation becomes independent of μ. Finally, we show two examples of the spatial distribution Ii(x, y) for two situations μl, ϕ = 0.828 and μh, ϕ = 0.807 in Fig. 3d and e. These examples clearly show clusters of isotropic and and anisotropic shapes emerging along boundaries and in the bulk of the packing. Examples can be seen in the highlighting in Fig. 3d and e; further evidence for string-like clusters can be seen in Fig. S6 in ESI,† especially at μh. The nine supplementary videos show the entire range of qualitative features in Ii(γ) for the three characteristic packing fractions for each μl, μm and μh. Spatial correlations can span up to ten particle diameters and can be string-like or globular, highlighting again the spatial anisotropy that can build up in the amorphous system. While the complete spatial dynamics of neighborhood microrotation similarity is challenging to interpret due to the dual and non-monotonic role of both friction and density, we can clearly see particle rotations becoming an essential parameter necessary to be included in both the statistical physics of and continuum modeling theories with non-local mechanical couplings inside sheared amorphous packing.
Relating microrotations to pressure
We evaluate the connection between the particle rotations and the mechanical response of the system by examining the packing pressure as a function of strain as obtained from the photoelastic signal of the particles. Fig. 4a gives the pressure P evolution with applied shear strain γ. We observe that for the selected data sets, pressure evolution at the low and high packing density ϕ are vastly different. At low density (for ϕ < 0.8), P is small for all μi. For the high density, we see that pressure grows strongly with γ in similar manner way for all μi, although it should be remarked that the similarity is fortuitous as the packing with μl is denser than that for μm and μh. The key points to note are two-fold. One, at low ϕ, regardless of friction, significant enduring normal forces are absent while particle rotations grow with deformation. However, for larger μ, there is an important difference: while enduring normal forces remain absent at ϕ < 0.8, we see an optimum for microrotation diffusion constant D and a clear difference in exponent n for both μm and μh, indicating that competing mechanisms drive the particle rotations. These may include rotations that result due to rolling friction versus those due to sliding friction. The results suggest that during brief particle contacts, one of these mechanisms (rolling or sliding) dominates for different packing densities ϕ. Two, in contrast to low ϕ, at large ϕ, both the pressure P and particle rotations grow with deformation with the particle microrotation standard deviation σm growing to greater than 0.2 rad for the three μi. It is noteworthy that the particle displacements are very much suppressed in this regime61 and hence rotations must be a significant source of sliding between particles and hence a dominant dissipation mechanism32. The sliding between particles must be especially strong at large ϕ as per the insights provided by Moran's I standard deviation σI, which is remarkably suppressed for the case of large ϕ, while the particle rotations continue to grow as seen from Fig. 2. Although anticorrelated motion should suppress rotational sliding, anticorrelations themselves are suppressed at large ϕ.The relevance of rotations for the mechanics of packings at large densities is further highlighted by considering Sn(P). The local neighborhood variance for μl is very small while P is large as shown in Fig. 4b. This indicates that particles are mostly sliding with respect to each other at this high density. It is clear that low friction is unlikely to induce anticorrelations among rotations. The situation is very different for μm and μh. For these, Sn(P) are clearly linear functions, indicating that for that particular ϕ pressure can be associated with a certain amount of anticorrelated motion of particles. We note again that the similarity of the data in Fig. 4b is probably due to a fortuitous choice of data. In general one might expect the slope in dSn/dP(ϕ) to have a sharp transition with ϕ for μl. On the other hand, it is reasonable to expect for μm, μh the slope change could have a smooth variation. Further investigations may be needed to verify this expectations. Nevertheless, the presented data shows unequivocally that local correlations in rotations can function as an indicator of the transition from a an unjammed to (shear)jammed solid.
Conclusions
We have shown that simple shear induces spatially correlated fluctuations in the a rotational dynamics of round, frictional particles. Individual particle rotational motion is diffusive, and diffusive motion is μ and ϕ dependent as one would expect based on the mechanical characteristics of the packing. The local neighborhood of particles shows on-average anticorrelated motion that reveals that two distinct mechanisms affect the mechanics of individual grains. Rotational motion fluctuations indicate the state of the system early in the deformation regime after a few percent shear strain, even though the average particle microrotation is zero. Critically, by controlling the rotational degrees-of-freedom, the mesoscopic spatial anticorrelations in the microrotation field can be suppressed leading to packing stiffening and the concomitant increase in system pressure.Our results suggest that rotational motion is a highly relevant field in the study of amorphous particulate materials, ranging from sands to frictional emulsions, colloids and even molecular glasses. Beyond materials analyses, the results have a broader relevance to spatial data science, particularly in reference to the “first law of Geography”62 stating that nearby things are similar. The value of the widely used geographical spatial autocorrelation measure Moran's I is negative for granular materials systems with a clear physical interpretation related to particle friction. Intriguingly, the role of absolute interparticle orientations has long been recognized for system mechanics: the role of the bond angle is recognized as essential in constraint counting approaches for glassy polymeric systems60 and is also relevant for protein folding dynamics.63 Not surprisingly rotational dynamics has been measured indirectly on a system scale via dielectric spectroscopy,64 for example to probe glassy dynamics in rotational degrees of freedom in nonspherically symmetric glassforming molecules. Note that friction is not the only parameter that can make the rotational degree of freedom relevant for the packing dynamics. Rotations also play a significant role for particle packings that are composed of aspherical, adhesive or deformable particles, which covers many types of particulate materials, ranging from granular materials to colloids, proteins,65 emulsions and even metamaterials in which the node hinges are not ideal.30 In particular, it is of interest to explore how energy is stored in sheared granular packings and how rotations and friction in contacts play a role in this. Our work in the context of prior work on rotational particle dynamics in other materials thus suggests that rotational particle dynamics is a broadly relevant characteristic that can aid a deeper understanding of the often suggested similarity among amorphous materials.
Author contributions
DW and JD performed the experiments. DW and NN and AM analyzed the microrotations. YL and SS analyzed the spatial correlations. All authors made substantial contributions to interpretation of the data and writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the organizers and participants of the Lorentz Center workshop “Granular Matter Across Scales” for fostering an environment where the seeds for this work were planted. We are grateful to the late Robert Behringer for inventing an experimental setup that suppresses shear localization. We thank Jie Ren for collecting some of the data used. AM and NN are supported in part by the United States National Science Foundation grant CMMI-1727433 and EEC-1840432 (which also involves SS). YL is supported by a University of Minnesota Doctoral Dissertation Fellowship.Notes and references
- P. V. Lade, Int. J. Solids Struct., 1977, 13, 1019–1035 CrossRef.
- V. Viasnoff and F. Lequeux, Phys. Rev. Lett., 2002, 89, 065701 CrossRef.
- H.-N. Lee, K. Paeng, S. F. Swallen and M. D. Ediger, Science, 2009, 323, 231–234 CrossRef CAS PubMed.
- B. P. Tighe, Granular Matter, 2014, 16, 203–208 CrossRef CAS.
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Rev. Mod. Phys., 1996, 68, 1259 CrossRef.
- C. Scholz, M. Engel and T. Pöschel, Nat. Commun., 2018, 9, 931 CrossRef PubMed.
- L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti and W. van Saarloos, Dynamical heterogeneities in glasses, colloids, and granular media, OUP, Oxford, 2011, vol. 150 Search PubMed.
- A. Tordesillas, S. Pucilowski, Q. Lin, J. F. Peters and R. P. Behringer, J. Mech. Phys. Solids, 2016, 90, 215–241 CrossRef.
- J. F. Peters and L. E. Walizer, J. Eng. Mech., 2013, 139, 1479–1490 CrossRef.
- E. Cosserat and F. Cosserat, Theory of deformable bodies, ed. D. H. Delphenich, 1909 Search PubMed.
- L. M. Schwartz, D. L. Johnson and S. Feng, Phys. Rev. Lett., 1984, 52, 831–834 CrossRef.
- F. H. Stillinger and J. A. Hodgdon, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 2064–2068 CrossRef CAS.
- K. V. Edmond, M. T. Elsesser, G. L. Hunter, D. J. Pine and E. R. Weeks, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17891–17896 CrossRef CAS PubMed.
- N. V. Brilliantov, T. Pöschel, W. T. Kranz and A. Zippelius, Phys. Rev. Lett., 2007, 98, 128001 CrossRef CAS PubMed.
- S. H. E. Rahbari, M. Otsuki and T. Pöschel, Commun. Phys., 2021, 4, 1–9 CrossRef.
- T. Matsushima, H. Saomoto, Y. Tsubokawa and Y. Yamada, Soils Found., 2003, 43, 95–106 CrossRef.
- P. Poorsolhjouy and A. Misra, J. Mech. Phys. Solids, 2019, 129, 244–260 CrossRef.
- A. Misra and P. Poorsolhjouy, Mech. Res. Commun., 2017, 81, 1–6 CrossRef.
- N. Nejadsadeghi and A. Misra, Math. Mech. Solids, 2020, 25, 407–429 CrossRef.
- E. Dickinson, S. A. Allison and J. A. McCammon, J. Chem. Soc., Faraday Trans. 2, 1985, 81, 591–601 RSC.
- O. R. Walton and R. L. Braun, J. Rheol., 1986, 30, 949–980 CrossRef.
- J. Bardet, Mech. Mater., 1994, 18, 159–182 CrossRef.
- I. Agnolin and J.-N. Roux, Int. J. Solids Struct., 2008, 45, 1101–1123 CrossRef.
- N. Nejadsadeghi and A. Misra, Int. J. Mech. Sci., 2020, 185, 105867 CrossRef.
- L.-S. Wei, Y.-Z. Wang and Y.-S. Wang, Int. J. Mech. Sci., 2020, 173, 105433 CrossRef.
- O. Mouraille and S. Luding, Ultrasonics, 2008, 48, 498–505 CrossRef CAS PubMed.
- N. Boechler, J. Yang, G. Theocharis, P. G. Kevrekidis and C. Daraio, J. Appl. Phys., 2011, 109, 074906 CrossRef.
- F. Göncü, S. Luding and K. Bertoldi, J. Acoust. Soc. Am., 2012, 131, EL475–EL480 CrossRef.
- A. Misra and P. Poorsolhjouy, Continuum Mech. Thermodyn., 2016, 28, 215–234 CrossRef.
- A. Misra, N. Nejadsadeghi, M. De Angelo and L. Placidi, Continuum Mech. Thermodyn., 2020, 32, 1497–1513 CrossRef CAS.
- A. Merkel, V. Tournat and V. Gusev, Phys. Rev. Lett., 2011, 107, 225502 CrossRef CAS PubMed.
- C. Zhai, E. Herbold, S. Hall and R. Hurley, J. Mech. Phys. Solids, 2019, 129, 19–38 CrossRef.
- J. Ren, J. A. Dijksman and R. P. Behringer, Phys. Rev. Lett., 2013, 110, 018302 CrossRef PubMed.
- D. Wang, J. Ren, J. A. Dijksman, H. Zheng and R. P. Behringer, Phys. Rev. Lett., 2018, 120, 208004 CrossRef CAS PubMed.
- D. Wang, J. A. Dijksman, J. Barés, J. Ren and H. Zheng, Phys. Rev. Lett., 2020, 125, 138001 CrossRef CAS PubMed.
- P. A. Moran, Biometrika, 1950, 37, 17–23 CrossRef CAS PubMed.
- P. Hébraud and F. Lequeux, Phys. Rev. Lett., 1998, 81, 2934–2937 CrossRef.
- L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001 CrossRef PubMed.
- D. L. Henann and K. Kamrin, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6730–6735 CrossRef CAS.
- A. Misra and H. Jiang, Comput. Geotech., 1997, 20, 267–285 CrossRef.
- M. R. Kuhn and K. Bagi, Int. J. Solids Struct., 2004, 41, 5793–5820 CrossRef.
- E. Andò, S. A. Hall, G. Viggiani, J. Desrues and P. Bésuelle, Acta Geotechnica, 2012, 7, 1–13 CrossRef.
- A. Peshkov, M. Girvan, D. C. Richardson and W. Losert, Phys. Rev. E, 2019, 100, 042905 CrossRef CAS PubMed.
- R. Seto, R. Mari, J. F. Morris and M. M. Denn, Phys. Rev. Lett., 2013, 111, 218301 CrossRef PubMed.
- N. Y. Lin, B. M. Guy, M. Hermes, C. Ness, J. Sun, W. C. Poon and I. Cohen, Phys. Rev. Lett., 2015, 115, 228304 CrossRef PubMed.
- A. Singh, C. Ness, R. Seto, J. J. de Pablo and H. M. Jaeger, Phys. Rev. Lett., 2020, 124, 248005 CrossRef CAS PubMed.
- M. P. Ciamarra, P. Richard, M. Schröter and B. P. Tighe, Soft Matter, 2012, 8, 9731–9737 RSC.
- X. Sun, W. Kob, R. Blumenfeld, H. Tong, Y. Wang and J. Zhang, Friction-controlled entropy-stability competition in granular systems, 2020 Search PubMed.
- Z. Cheng and J. Wang, Powder Technol., 2019, 344, 314–334 CrossRef CAS.
- S. A. Hall, M. Bornert, J. Desrues, Y. Pannier, N. Lenoir, G. Viggiani and P. Bésuelle, Géotechnique, 2010, 60, 315–322 CrossRef.
- K. A. Alshibli and B. A. Alramahi, J. Geotech. Geoenviron. Eng., 2006, 132, 80–91 CrossRef.
- M. Muthuswamy and A. Tordesillas, J. Stat. Mech.: Theory Exp., 2006, P09003 Search PubMed.
- D.-H. Nguyen, É. Azéma, F. Radjai and P. Sornay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012202 CrossRef.
- K. W. Desmond and E. R. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022204 CrossRef PubMed.
- K. Bagi, Stress and strain in granular assemblies, Mechanics of Materials, 1996, 22, 165–177 CrossRef.
- E. Aharonov and D. Sparks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 051302 CrossRef PubMed.
- F. Calvetti, G. Combe and J. Lanier, Mech. Cohesive-Frict. Mater., 1997, 2, 121–163 CrossRef.
- M. Kim, S. M. Anthony, S. C. Bae and S. Granick, J. Chem. Phys., 2011, 135, 054905 CrossRef PubMed.
- S. Vivek and E. R. Weeks, J. Chem. Phys., 2017, 147, 134502 CrossRef PubMed.
- M. Thorpe, J. Non-Cryst. Solids, 1995, 182, 135–142 CrossRef CAS.
- D. Wang, J. A. Dijksman, J. Barés, J. Ren and H. Zheng, Phys. Rev. Lett., 2020, 125, 138001 CrossRef CAS PubMed.
- W. R. Tobler, Econ. Geogr., 1970, 46, 234–240 CrossRef.
- D. J. Jacobs, L. A. Kuhn and M. F. Thorpe, in Flexible and Rigid Regions in Proteins, ed. M. F. Thorpe and P. M. Duxbury, Springer US, Boston, MA, 2002, pp. 357–384 Search PubMed.
- P. Madden and D. Kivelson, Adv. Chem. Phys., 1984, 56, 467–566 CAS.
- N. Haridasan, S. K. Kannam, S. Mogurampelly and S. P. Sathian, J. Phys. Chem. B, 2019, 123, 4825–4832 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Extra data and a description of videos of Moran's I for several μ, ϕ. See DOI: 10.1039/d1sm00525a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |