DOI:
10.1039/D1SM00466B
(Paper)
Soft Matter, 2021,
17, 6627-6636
Liquid–liquid crystalline phase separation in biological filamentous colloids: nucleation, growth and order–order transitions of cholesteric tactoids†
Received
27th March 2021
, Accepted 28th May 2021
First published on 31st May 2021
Abstract
The process of liquid–liquid crystalline phase separation (LLCPS) in filamentous colloids is at the very core of multiple biological, physical and technological processes of broad significance. However, the complete theoretical understanding of the process is still missing. LLCPS involves the nucleation, growth and up-concentration of anisotropic droplets from a continuous isotropic phase, until a state of equilibrium is reached. Herein, by combining the thermodynamic extremum principle with the Onsager theory, we describe the nucleation and growth of liquid crystalline droplets, and the evolution of their size and concentration during phase separation, eventually leading to a multitude of order–order phase transitions. Furthermore, a decreasing pitch behaviour can be predicted using this combined theory during tactoid growth, already observed experimentally but not yet explained by present theories. The results of this study are compared with the experimental data of cholesteric pitch, observed in three different systems of biological chiral liquid crystals. These findings give an important framework for predicting the formation, growth and phase behaviour of biological filamentous colloids undergoing LLCPS, advancing our understanding of liquid–liquid phase separation and self-assembly mechanisms in biological systems, and provide a valuable rationale for developing nanomaterials and applications in nanotechnology.
1 Introduction
Phase separation is a fundamental phenomenon observed in various branches of materials science, from superconductors to soft matter.1 Polymeric fluids or colloidal dispersions are just an example of systems undergoing a phase separation,2 where a single phase in a supersaturated state evolves into two different thermodynamically stable phases.3 These liquid states display distinct physical properties and different structures, even though their components are chemically identical.4 This phenomenon is called liquid–liquid phase separation (LLPS),5 which can be achieved by changing the pressure, temperature or concentration.6 Liquid–liquid phase separation in biology is associated with a multitude of cellular functions and structures,7 such as in membrane-less organelles,8 and understanding this process has important implications in the elucidation of several mechanisms of life functioning. The most common form of liquid–liquid phase separation involves two biopolymers (e.g. a protein and RNA)9 and is primarily regulated by enthalpic interactions.7 The classical system is therefore a two-component system in nature (in addition to the background solvent). In stark contrast, phase separation involving only one hydrocolloid component can occur on a purely entropic basis when the colloid is of filamentous type and has a large associated excluded volume. We refer to this type of 1-component (plus solvent) liquid–liquid phase separation as liquid–liquid crystalline phase separation (LLCPS) to fundamentally distinguish it from the LLPS introduced above. The thermodynamic description of the underlying physics is deeply rooted into the seminal formalism proposed by Onsager.10 More precisely, when the two liquids are distinguished by a different orientational distribution of the constituents, as in the case of liquid crystals,11 the two phases are called nematic and isotropic, for the ordered and unordered phase, respectively. In this case, the onset of phase separation is characterized by the formation of microdroplets of the nematic phase, from a supersaturated isotropic bulk phase.12 These nematic droplets are known as tactoids, and during phase separation, their shape and nematic director field configuration can change spontaneously, with increasing volumes.13–15 This becomes particularly significant when the filamentous colloid building blocks are chiral, with macroscopic chirality of the droplets also emerging during growth and leading to the formation of chiral nematic (or cholesteric) tactoidal droplets.16–18 The shape of these classes of tactoids has already been rationalized by the interaction between confinement, anisotropic surface energy, and Frank–Oseen elastic energy.19,20 To date, however, several thermodynamic, structural and kinetic aspects of this LLCPS process remain still unclear, such as the nature of the transitions between the different configurations, the dynamics of the growth process, and the change in cholesteric periodicity (pitch) observed with increasing volumes of the droplets. This latter effect has been observed experimentally in different chiral systems,18,21 and requires a more refined analysis to be explained, since the confinement effects are not sufficient to elucidate this phenomenon.
Here, we propose a theoretical description of the nucleation and growth phases of the tactoids during the LLCPS process, following the evolution of the composition of binodal lines describing the phase transition. In particular, we show that such phase separation leads to a change in the concentration, eventually leading to a change in the pitch of the cholesteric phase, i.e. during their growth, therefore having a pitch that decreases with an increase in the volume. To support these theoretical findings, we benchmark the theory with experimental data and successfully describe the evolution of pitch in cholesteric tactoids, obtained from three different systems of biological colloids: β-lactoglobulin (BLG) amyloid fibrils,20 carboxylated cellulose nanocrystals (C-CNCs)18 and sulfurated cellulose nanocrystals (S-CNCs).22
2 Phase behaviour: Onsager theory
There are various theories describing the phase behaviour in liquid crystals from Flory23 and Straley.24 A review of different approaches can be seen in ref. 25 The Onsager theory10 predicts accurately the phase boundaries of nematic and isotropic phases for the three systems under analysis, even though they are composed of charged polydisperse rods.21,26 The rods considered have a contour length well below the persistence length and deflection length, and therefore they can be considered effectively rigid rods.26 Moreover, the theory allows computing pressure and chemical potential at each concentration.
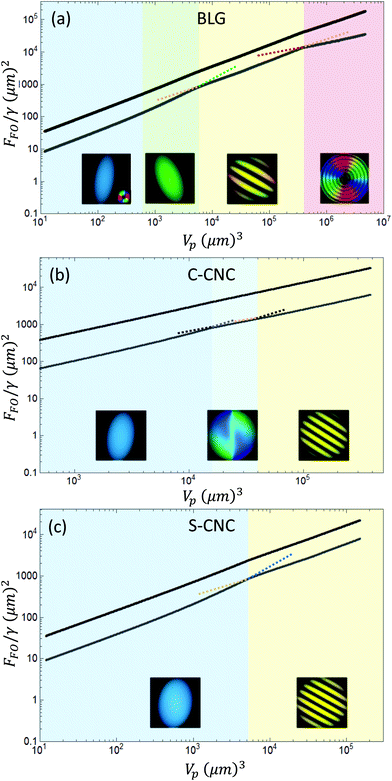
As a base for the discussion we briefly recapitulate the Onsager theory following his groundbreaking work.10 We define the excess free energy F of a volume V, containing N hard rods of diameter D and length L as
| | 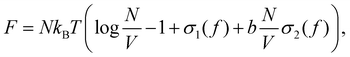 | (1) |
where

is half the excluded volume between two randomly oriented rods and
σ1 and
σ2 are functions of the distribution function
f of the angle
Θ between the rods and the director field; for a detailed description see
ref. 27. The derivatives of
F with respect to
V and
N are called respectively osmotic pressure (
Π) and chemical potential (
μ):
| |  | (2) |
| |  | (3) |
The isotropic distribution, where all directions are equally probable,  , results in σ1(fi) = 0 and σ2(fi) = 1, see ESI† for details. In the case of an anisotropic distribution, where f is not a constant, Onsager's trial function
, results in σ1(fi) = 0 and σ2(fi) = 1, see ESI† for details. In the case of an anisotropic distribution, where f is not a constant, Onsager's trial function  can be used. In case of large α, σ1(fα) and σ2(fα) can be substituted by their asymptotic series (ESI†). This parametrization allows F to be minimized at each rescaled concentration
can be used. In case of large α, σ1(fα) and σ2(fα) can be substituted by their asymptotic series (ESI†). This parametrization allows F to be minimized at each rescaled concentration  , where φ is the volume fraction of the rods. Fig. 1(a) (purple line) shows the order parameter S for increasing concentration ϕ. The order parameter remains zero up to a concentration of ϕ ≈ 3.68, where it jumps discontinuously to 0.6. As shown in Fig. 1(a), this is a first order transition from an isotropic phase, with S = 0 for ϕ < 3.68, to a nematic phase S ≠ 0 for ϕ > 3.68.27 Minimizing F and using asymptotic expansions, eqn (2) and (3) become
, where φ is the volume fraction of the rods. Fig. 1(a) (purple line) shows the order parameter S for increasing concentration ϕ. The order parameter remains zero up to a concentration of ϕ ≈ 3.68, where it jumps discontinuously to 0.6. As shown in Fig. 1(a), this is a first order transition from an isotropic phase, with S = 0 for ϕ < 3.68, to a nematic phase S ≠ 0 for ϕ > 3.68.27 Minimizing F and using asymptotic expansions, eqn (2) and (3) become
| |  | (4) |
and
| |  | (5) |
 |
| | Fig. 1 (a) Scaled free energy of the Onsager theory as a function of the scaled concentration ϕ for the equilibrium state (solid red) and isotropic phase (dashed red). Order parameter S in purple. (b) Osmotic pressure (blue) and chemical potential (green) for isotropic and nematic phases at given concentration ϕ. The coexistence boundaries are highlighted with a dashed line. | |
Fig. 1(b) shows how Π and μ change as a function of the concentration ϕ.
Simultaneously equating the pressure and chemical potential of the two phases gives the value of phase coexistence ϕI = 3.36 and ϕN = 4.68. These boundary concentrations are slightly different from the values of 3.34 and 4.48 obtained by Onsager,10 since they are derived from a first order expansion of the quantities described above. This approximation allows writing Π and μ as functions of ϕ. A more detailed discussion is included in the ESI.† In a system where ϕ < ϕI, the order parameter is S = 0, and therefore it is in an isotropic state. Conversely, for ϕ > ϕN the system is in a completely nematic state, with S > 0.8. For concentrations in between the two values, the system is said to be in a supersaturated state and it will undergo phase separation into two distinct phases, equilibrating at a concentration between the two boundary concentrations. The isotropic state becomes metastable for 3.68 < ϕ < 4,28 as shown by the dotted red line in Fig. 1(a), therefore nucleation and growth will only occur if the supersaturated solution concentration is in between these values, and for concentration beyond ϕ > 4 the system will phase separate following spinodal decomposition.29
3 Nucleation
The process of phase separation under the present analysis, in the context of LLCPS, starts with the nucleation of tactoids; more generally, both nucleation and growth and spinodal decomposition are possible. The mechanism of formation of colloidal droplets has been extensively studied thermodynamically.30 In the context of anisotropic, homogeneous liquid crystalline droplets of volume Vp, the free energy FW has been calculated by Wulff31 and reported by Prinsen and van der Schoot14 as| |  | (6) |
where γ is the isotropic surface tension and ω is the adimensional anchoring strength.19
Let Vp be a fixed volume at concentration ϕ ≥ 3.68, initially in a supersaturated isotropic state. From eqn (1) the change in free energy ΔFV, that occurs when the rods align into a nematic phase, can be expressed as
| |  | (7) |
where
g is a number depending only on
ϕ. It is the difference from the dashed and solid red line in
Fig. 1(a). The total change in free energy becomes
| | | ΔF = ΔFV + FW = −AVp + BVp2/3. | (8) |
where
A and
B are the other factors in
eqn (6) and (7), which do not depend on
V. Since Δ
FV is always negative, while
FW is always positive, there exists a minimum volume beyond which the tactoid will become stable.
32 This volume
Vmin corresponds to the value that nullifies the derivative,
i.e.
. With the previous symbolism it can be written as

. For volumes lower than
Vmin, the free energy increases with an increase in the size, thus the droplet shrinks redissolving in the solution, while for volumes larger than
Vmin,
ΔF decreases, leading to a growth behavior. A more detailed discussion on nucleation of hard rod systems can be found in
ref. 33 The surface tension
γ can be linked to the geometry of the rods as

, from Van der Shoot's previous work.
34 The minimum volume for nucleation scales as
For BLG,20 where L = 550 nm and ω = 1.3, we can compute the above mentioned quantities and obtain a minimal volume of Vmin = 19.6 μm3, for a nucleating concentration of ϕ = 3.8. For C-CNC,21 where L = 450 nm and ω = 0.8, the minimal volume is Vmin = 8.9 μm3, while for S-CNC,21 where L = 330 nm with ω = 0.5, we obtain Vmin = 3.0 μm3. The resulting shape of the curve is represented in Fig. 2(a). This quantity corresponds to the minimal volume needed by a homogeneous nematic tactoid to form a surface and initiate phase separation without redissolving into the isotropic solution. From the available experimental data, as shown in Fig. S3 (ESI†), the smallest volume measured for BLG tactoids was 80 μm3, while it was 20 μm3 for C-CNC, in line with the theoretical predictions. In the case of S-CNC, we cannot make a reasonable comparison, since the smallest tactoids are extremely elusive to experimental characterization, due to the faster equilibration of this system.35
 |
| | Fig. 2 (a) Difference in the free energy for a nucleated nematic domain from the isotropic background as a function of the volume Vp, for the BLG system (blue), C-CNC (red) and S-CNC (yellow). (b) Time evolution of the scaled volume ρ3 over the initial condition ρ(0)3; (c) Time evolution of the concentration ϕ for the nematic phase (blue) and the isotropic phase (orange). For both graphs, have been used the scaled variables ρ (eqn (12)) and τ as defined in the Appendix. | |
4 Growth phase
The nematic tactoids, nucleated from the supersaturated solution, undergo a growth process which increases their size and concentration, until an equilibrium between the chemical potential and pressure is reached, and therefore the boundaries of phase coexistence predicted using the Onsager theory. The growth phenomenon has been studied extensively and many models have been formulated to describe the increase in size in crystalline domains;32,36 a review of single-phase growth theories has been presented by Atkinson.37 To model the kinetics of this binary system, composed of a solvent and a solute, we resort to the thermodynamic extremum principle38 to derive the dynamics of change in volume and concentration of the droplets. This approach is based on the work of Onsager39 and has been implemented to describe growth in multi-component multi-phase systems,40 albeit not in liquid–liquid or in liquid–liquid crystalline phase separation. The full derivation is reported in the Appendix, and here, we summarize the most important steps.
In this section, we will assume that the tactoids are spherical in shape, thus only with isotropic surface tension  . The real shape of the droplets may be taken into account by adjusting the coefficients when the surface is involved. However, this correction will depend on the volume and the particular system under study,21 therefore overly complicating the analysis. The growth is influenced by three quantities: the difference in osmotic pressure ΔΠ, the chemical potential Δμ between the nematic and isotropic phase, and the external pressure, in this case, it is the Laplace pressure generated by the isotropic surface tension.41
. The real shape of the droplets may be taken into account by adjusting the coefficients when the surface is involved. However, this correction will depend on the volume and the particular system under study,21 therefore overly complicating the analysis. The growth is influenced by three quantities: the difference in osmotic pressure ΔΠ, the chemical potential Δμ between the nematic and isotropic phase, and the external pressure, in this case, it is the Laplace pressure generated by the isotropic surface tension.41
We consider a model system of a single nematic droplet n, of a size V larger than the critical nucleus size, growing in a continuous supersaturated isotropic phase i. The free energy can be written as the sum of three components: the free energy of the two phases and the free energy of the interaction Fγ, given by the surface energy Fγ = 4πR2γ. The total free energy FT of this system can be written as
The total volume and number of solute molecules are fixed, therefore FT becomes
| |  | (11) |
where the terms not depending on
R and
ϕ have been omitted. We define
R* as
| |  | (12) |
which scales as a length
R* ∼
L with the previously used scaling argument. With a change of variables
R =
R*
ρ, we can write
| |  | (13) |
where

and

. In this representation, for
ρ ≪ 1 the surface tension is the dominant term, while for larger sizes
ρ ≫ 1, the change in potentials becomes leading. The length
R* represents the characteristic length of the system and as shown in the previous section, the results of both classical nucleation theory and the following approach are based on this same length scale, since
R* ∼
L ∼
Vmin1/3.
The total free energy, in this formulation, depends only on ρ and ϕ. We can obtain the evolution equations of these two quantities using the modelling proposed by Svoboda et al.40 where the dynamical system can be written from the derivatives of a dissipation function Q depending on the flow of the solute and solvent.
In Fig. 2(b and c) are plotted the curves of (ρ/ρ(0))3(t) and ϕ(t) representing the numerical solutions of the presented differential equations. The initial conditions chosen are ρ(0) = 10, ϕ(0) = 4 and ϕi(0) = 3.6. Panel A represents the time evolution of the scaled volume ρ3 from the initial condition of ρ3(0), and the volumes increase by 4 orders of magnitudes before reaching a horizontal asymptote. The choice of initial conditions depends on the free energy of eqn (13). For small volumes, i.e. smaller than the critical nucleus size, the surface tension will be strong enough, leading to a dissolution of the droplet.36,42 In Fig. 2(c) are plotted the concentrations of the nematic droplet (in blue) and isotropic background (in orange). The concentration follows the same pattern as that of the volume, where it reaches an asymptote around 4.3. This is slightly lower than the boundaries presented in the previous paragraph, since the Laplace pressure caused by the surface tension has to be balanced by an additional difference in the osmotic pressure.43
From the estimates obtained from the nucleation theory, we can calculate the physical volume Vp, by setting  , and thus obtain the change in concentration with the volume of the droplet Vp. The results are shown in Fig. 3, where the concentrations of nematic and isotropic phases are plotted with the volume of the nematic phase. These two lines represent the binodal curve of the system undergoing the growth process, where with an increase in the volumes the concentration in the nematic phase increases, while the concentration in the isotropic phase slowing decreases. The real dynamics of phase separation depends on many different quantities: the diffusion coefficients, the total volume of solution and the initial conditions, which are different in every system. Also, in a real system, a population of tactoids with different volumes would nucleate and grow, possibly colliding and forming new tactoids. In this analysis, we considered the growth of a single droplet of a given concentration and volume immersed in a supersaturated isotropic solution, therefore the effects of having a population of droplets interacting have not been considered and it is outside the scope of this analysis.
, and thus obtain the change in concentration with the volume of the droplet Vp. The results are shown in Fig. 3, where the concentrations of nematic and isotropic phases are plotted with the volume of the nematic phase. These two lines represent the binodal curve of the system undergoing the growth process, where with an increase in the volumes the concentration in the nematic phase increases, while the concentration in the isotropic phase slowing decreases. The real dynamics of phase separation depends on many different quantities: the diffusion coefficients, the total volume of solution and the initial conditions, which are different in every system. Also, in a real system, a population of tactoids with different volumes would nucleate and grow, possibly colliding and forming new tactoids. In this analysis, we considered the growth of a single droplet of a given concentration and volume immersed in a supersaturated isotropic solution, therefore the effects of having a population of droplets interacting have not been considered and it is outside the scope of this analysis.
 |
| | Fig. 3 Change in concentration ϕ with the volume Vp for the analyzed systems: BLG (a), C-CNC (b) and S-CNC (c). The blue line represents the nematic phase, while the orange the isotropic phase. Additionally, the morphology of the droplet at the given volume is represented with a simulated PolScope image and a colored background, as in Fig. 1. The dashed lines represent the boundaries of the coexistence phase, as described by the theory ϕI = 3.36 and ϕN = 4.68. The dotted line represents the experimental boundaries measured by Bagnani et al.21 | |
5 Discussion
LLCPS behaviour has been observed in multiple biological colloids, such as viruses,44 DNA,45 cellulose nanocrystals (CNC)21,46 and amyloid fibrils.18,26 Understanding the underlining mechanisms in the formation of nematic and cholesteric tactoids is extremely important for functionalizing these materials, especially protein-based biocolloids, which have become increasingly significant in food,47 medicine48 and biological industries.49
In what follows, we show the prediction on the total free energy of the system during evolution of the volume of the three colloids considered, which is now obtained based on the theoretical approach described in the earlier sections, by taking into account liquid crystalline interactions within the growing droplets. The evaluation of the free energy follows the same approach used in the work of Bagnani et al.,20,21 where an extensive analysis has been performed to understand the change in shape and in the configuration of the nematic director field and how these different phases appear.
The free energy functional used is the Frank–Oseen bulk energy, composed of three independent terms proportional to the elastic constants K1, K2 and K3,19 coupled with an anisotropic surface energy.50
| |  | (14) |
where

is the nematic director field and
q∞ is the pitch wave number. Additional details can be found in the ESI
† of
ref. 20 This functional correctly predicts the shape and nematic field configuration for all the classes of nematic and cholesteric tactoids found experimentally.
20 The values of the constants used can be found in
ref. 21, for the three systems under study and are reported in
Table 1.
Table 1 Elastic constants and surface tension parameters for BLG, C-CNC and S-CNC, used in eqn (14), obtained from ref. 21
|
|
BLG |
C-CNC |
S-CNC |
|
K
1 (pN) |
2.0 |
0.6 |
2.6 |
|
K
2 (pN) |
2.7 |
0.1 |
0.02 |
|
K
3 (pN) |
1.5 |
1.0 |
2.3 |
|
γ (μN m−1) |
0.34 |
0.24 |
0.13 |
|
ω
|
1.3 |
0.8 |
0.5 |
The total free energy FFO at each volume has been plotted for each system in Fig. 4 (black line). However, it can be noted that elastic distortions and the anisotropy of the surface account for about one tenth of the total energy, even for homogeneous tactoids as shown in Fig. S2 (ESI†). Therefore, the approximation used in the previous paragraph, that is including only the surface energy of the tactoid, is appropriate for our case. To better visualize the transitions, the total free energy FFO has been reduced by the isotropic surface free energy of a sphere of equivalent volume and is plotted with a grey line. This line represents the energy contributions of elastic distortions and anisotropic surface tension. The various classes of tactoids are highlighted with a PolScope simulation,20 while their aspect ratios are included in Fig. S3 (ESI†).
 |
| | Fig. 4 The total free energy FFO/γ for different volumes (Vp) is marked in black and the sum of elastic distortions and anisotropic surface energy is marked in grey, for BLG (a), carboxylated (b) and sulfurated (c) CNC. The colored background represents the range of volumes over which a particular morphology of the tactoid is observed,21 integrated with a PolScope simulation of the particular configuration.20 | |
BLG amyloid fibrils form nematic tactoids with a rich palette of morphologies, including a variety of cholesteric phase configurations.20 These four different classes of tactoids are called homogeneous, bipolar, uniaxial and radial cholesteric. These four classes of tactoids, see Fig. S3(a) (ESI†), appear at increasing volumes with decreasing aspect ratios. It is interesting to note the two kinks in the grey line, corresponding to the phase transitions into uniaxial cholesteric and radial cholesteric morphologies. According to the Ehrenfest classification of phase transitions,51 the morphology transitions from bipolar to uniaxial cholesteric and from uniaxial to radial cholesteric are first order phase transitions, with a discontinuous jump in the first derivative of the free energy, which is reflected in a discontinuous jump in the observed aspect ratios, see Fig. S3(a) (ESI†). In the span of volumes where homogeneous turn into bipolar the derivative changes smoothly, implying that the phase transition is of an higher order, as already intuited by Prinsen and van der Schoot.14
A similar rich palette of structure has been observed in cholesteric phases formed by carboxylated and sulfurated cellulose nanoscrystals.21 The tactoid morphologies of C-CNCs are named homogeneous, radial nematic and uniaxial cholesteric,21 see Fig. S3(b) (ESI†). A similar energy landscape is shown in Fig. 4(b). Here, we observe a discontinuous derivative in the transition into radial nematic and another transition into the uniaxial cholesteric. Lastly, in the S-CNCs only two configurations appear, homogeneous and uniaxial cholesteric, see Fig. S3(c) (ESI†), where a first order transition is observed from one morphology to the other, as shown in Fig. 4(c).
Experimentally, liquid crystalline droplets have been observed under a cross-polarized microscope and for cholesteric configurations, the pitch has been measured from the generated images, as twice as the distance from band to band, and are plotted in Fig. 5 with their respective volumes. The additional details and methods regarding the experimental systems are given in ref. 21.
 |
| | Fig. 5 Periodicity of the cholesteric tactoids p as a function of the volume Vp for BLG (a), C-CNC (b), and S-CNC (c) with the fitted lines obtained by the theory. The fitting parameters are reported in the ESI.† The orange boxes ( ) symbolize the uniaxial cholesteric droplets, while the red stars ( ) symbolize the uniaxial cholesteric droplets, while the red stars ( ) symbolize the radial cholesteric droplets.21 ) symbolize the radial cholesteric droplets.21 | |
The tactoids obtained from BLG amyloid fibrils and carboxylated CNCs show a decreasing behavior of the pitch for increasing volumes. The BLG system reaches eventually the radial cholesteric configuration where the pitch does not decrease further. In contrast, the sulfurated cellulose shows a constant pitch, over two orders of magnitude in volumes. Previous attempts to connect this feature of cholesteric droplets with the constraint imposed by the confined geometry failed.18,20 Based on the theoretical framework introduced here, we now show that it becomes possible to link the change in pitch observed with the change in concentration during growth. From the work of Nystrom et al.52 we assume a pitch dependence of the concentration of the form p ∼ ϕ−1, even though there is much debate around the correct exponent.44,53,54 As a general formula, we adopt
| |  | (15) |
The expression for ϕ(Vp) is obtained from the blue line of Fig. 5. The results are plotted in Fig. 3 with the experimental data of the pitch of cholesteric tactoids of the systems analyzed. The quantities K, q, v are the fitted variables, which are included in Table S1 of the ESI.† For the case of BLG, the modeled growth stops at a volume of 106 μm3, with a pitch of p = 15 μm. In the fit obtained, the blue line is stopped at that maximum value, reached by the size of the droplet when the process halts. In this frame, the radial cholesteric morphology represents the last stage of growth, where the equilibrium concentrations are reached, therefore from this volume there are no further changes in the pitch. A similar behavior is observed in C-CNCs, although no radial configuration has been observed. Lastly, the S-CNC system results in a straight horizontal line from the theory. In this system the pitch remains constant for two possible reasons: as reported in ref. 21, the experimental coexistence boundaries are 3.16 and 3.70, for the isotropic and nematic phases, much closer than the predicted values from the Onsager theory and hence, much closer to the final asymptotic equilibrium conditions. This fact implies a possible change in the concentration in the nematic phase of maximum 20%, which would generate a shrinking of the pitch of the same magnitude, well within the standard deviation of the experimental data. The difference between the theoretical boundaries, obtained using the Onsager theory, and the experimentally measured ones can explain the different growth regimes between different systems. BLG, as shown in Fig. S3(a) (ESI†), grows in volume over six orders of magnitude, while the growth in cellulose systems is much more constrained. In fact, the evolution of sulfurated cellulose is more rapid than that of β-lactoglobulin, resulting in a faster equilibration of the cholesteric configurations.35
6 Conclusions
We formulated a general model to describe the nucleation, growth, order–order transitions and change in concentration of nematic tactoids immersed in an isotropic phase in the coexistence regime by taking into account how the chemical potential, osmotic pressure and surface tension influence the diffusion of the solvent and solute inside the droplets. With the application of thermodynamic extremum principle38 and the Onsager theory of liquid crystals,10 we formulated the kinetic equations for the growth of tactoids. The growth behaviour is linked to an increase in the concentration in the nematic phase, accompanied by a consequent decrease in the concentration of the isotropic phase. The resulting effect is the change in periodicity of the cholesteric droplets with increasing volumes. This model was applied and validated by three different systems of biocolloidal liquid crystals, namely β-lactoglobulin amyloid fibrils and carboxylated and sulfurated cellulose nanocrystals. The first two systems displayed a decreasing behavior of the pitch with an increasing droplet size18,46 which until this work has remained unexplained. With the elucidation of how the tactoidal droplets grow, we then applied the previous results obtained by the variational theory of the Frank–Oseen to benchmark the experimentally observed order–order transitions and to elucidate the thermodynamic nature of these transitions. This work introduces for the first time a non-equilibrium status of the tactoids, providing new insight into the dynamics of phase separation and cholesteric pitch evolution, useful for understanding and expanding the capabilities of using cholesteric liquid crystals as a template for nanotechnology and for the synthesis of new, functional biomaterials.
Conflicts of interest
There is no conflict of interest to declare.
Appendix
Following the work of Svoboda et al.,40 we set the starting point for the equations for the growth by writing the total free energy of the system. We consider a biphasic system composed of a nematic phase n confined in a sphere of radius R of concentration c = N/V = ϕ/b and a isotropic phase i of volume Vi. The two phases are separated by a surface, whose energy is Fγ = 4πR2γ.
Additionally, the free energy F of the two phases can be rewritten as the sum of two terms F = Nμ − VpΠ (see the main text).
| |  | (17) |
Since the total volume VT and total number of solute molecules NT are fixed, the isotropic quantities can be rewritten as
| |  | (18) |
By regrouping the important quantities, we get
| |  | (19) |
The Δ implies the difference of the potentials between the nematic phase and the isotropic phase.
The total free energy depends only on R and c. We can obtain the evolution equations of these two quantities using the modelling proposed by Svoboda et al.,38 based on the Onsager extremum principle,39 where the time evolution of the system comes from a set of linear equations
| |  | (20) |
where the dot represents the time derivative and
Q the dissipation function.
From Svoboda et al. work,38 the dissipation function for diffusive flows can be written as
| |  | (21) |
where
l is the diffusion coefficient and
jl is the flow of the component indexed with
l. In our case it can be the solvent
w or solute
s. We can split the integral as the sum of an integral in the nematic phase and one in the isotropic phase:
Since the total amount of volume is occupied by the solvent or solute, we can write
with
νs,w being the volume occupied by a single molecule. This constraint leads to two relationships between
cs and
cw| |  | (24) |
In the nematic phase, the volume is a sphere and the flow can be simply rewritten as  . By rewriting eqn (21) in the nematic phase, we get
. By rewriting eqn (21) in the nematic phase, we get
| |  | (25) |
with
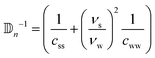
.
In the nematic phase, the total number of molecules of the compound l is  , thus the rate of change of Nl is
, thus the rate of change of Nl is
| |  | (26) |
This rate of change of number comes from the increase in volume and a diffusive flow through the surface40
| |  | (27) |
where
cl,i is the concentration of
l in the isotropic phase
i. The flow at the surface can be written as
| |  | (28) |
The flow at a distance r from the center of the sphere where r > R is  . This last expression can be used in eqn (21) to obtain the dissipation function in the isotropic phase Qi:
. This last expression can be used in eqn (21) to obtain the dissipation function in the isotropic phase Qi:
| | 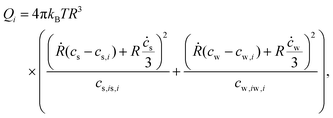 | (29) |
using

and
eqn (24), we obtain
| |  | (30) |
The derivatives of Q = Qi + Qn are
| |  | (31) |
| |  | (32) |
The derivatives of the free energy of eqn (19) are
| |  | (33) |
| |  | (34) |
Using eqn (20) we get
| |  | (35) |
| |  | (36) |
From the previous equations, it is possible to write the rate of change of concentration and radius
| |  | (37) |
| |  | (38) |
With a suitable change of variables, the equations can be rewritten in a more compact form
| |  | (39) |
| |  | (40) |
where
| |  | (41) |
| | 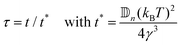 | (42) |
and
κ =
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) i
i/
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) n
n,

and

.
At each time, if the nematic phase has a volume  and concentration ϕ, the isotropic phase has a concentration of
and concentration ϕ, the isotropic phase has a concentration of
| | 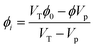 | (43) |
where
ϕ0 is the initial concentration of the supersaturated solution and
VT is the total volume available.
Even though ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) i,n depend on the concentration, we know from the Onsager theory that ϕ will range from 3.7 to 4.7 with a maximal increase of 27%. The isotropic phase ranges from 3.7 to 3.3 with a maximal decrease of 10%. From diffusion studies of hard rods we know that the diffusion coefficient remains constant at the coexistence and it is more than ten times larger compared to the nematic phase.55 Therefore, we can assume that
i,n depend on the concentration, we know from the Onsager theory that ϕ will range from 3.7 to 4.7 with a maximal increase of 27%. The isotropic phase ranges from 3.7 to 3.3 with a maximal decrease of 10%. From diffusion studies of hard rods we know that the diffusion coefficient remains constant at the coexistence and it is more than ten times larger compared to the nematic phase.55 Therefore, we can assume that ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) i,n will remain approximately constant during the process and the ratio κ will be much bigger than one.
i,n will remain approximately constant during the process and the ratio κ will be much bigger than one.
For the results presented, we set κ = 100 and a scaled total volume of  .
.
Acknowledgements
The authors acknowledge support with Grant No. CRSII5_189917 from the Swiss National Science Foundation.
Notes and references
- H. Tanaka, T. Araki, T. Koyama and Y. Nishikawa, J. Phys.: Condens. Matter, 2005, 17, S3195 Search PubMed
 .
.
- A. R. Hemsley and P. C. Griffiths, Philos. Trans. R. Soc., A, 2000, 358, 547–564 Search PubMed
 .
.
-
C. Domb, Phase transitions and critical phenomena, Elsevier, 2000 Search PubMed
 .
.
- P. H. Poole, T. Grande, C. A. Angell and P. F. McMillan, Science, 1997, 275, 322–323 Search PubMed
 .
.
- A. Mitus, A. Patashinskii and B. Shumilo, Phys. Lett. A, 1985, 113, 41–44 Search PubMed
 .
.
- Y. Katayama, T. Mizutani, W. Utsumi, O. Shimomura, M. Yamakata and K.-I. Funakoshi, Nature, 2000, 403, 170–173 Search PubMed
 .
.
- A. A. Hyman, C. A. Weber and F. Jülicher, Annu. Rev. Cell Dev. Biol., 2014, 30, 39–58 Search PubMed
 .
.
- H. Jing, Q. Bai, Y. Lin, H. Chang, D. Yin and D. Liang, Langmuir, 2020, 36, 8017–8026 Search PubMed
 .
.
- S. Watanabe, H. Inami, K. Oiwa, Y. Murata, S. Sakai, O. Komine, A. Sobue, Y. Iguchi, M. Katsuno and K. Yamanaka, Cell Death Dis., 2020, 11, 1–15 Search PubMed
 .
.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627–659 Search PubMed
 .
.
- T. Odijk, Macromolecules, 1986, 19, 2313–2329 Search PubMed
 .
.
- P. W. Oakes, J. Viamontes and J. X. Tang, Phys. Rev. E, 2007, 75, 061902 Search PubMed
 .
.
- V. Jamali, N. Behabtu, B. Senyuk, J. A. Lee, I. I. Smalyukh, P. van der Schoot and M. Pasquali, Phys. Rev. E, 2015, 91, 042507 Search PubMed
 .
.
- P. Prinsen and P. van der Schoot, Phys. Rev. E, 2003, 68, 021701 Search PubMed
 .
.
- A. Kaznacheev, M. Bogdanov and S. Taraskin, J. Exp. Theor. Phys., 2002, 95, 57–63 Search PubMed
 .
.
- L. Rossi, S. Sacanna and K. P. Velikov, Soft Matter, 2011, 7, 64–67 Search PubMed
 .
.
- L. Tortora and O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5163–5168 Search PubMed
 .
.
- G. Nyström, M. Arcari and R. Mezzenga, Nat. Nanotechnol., 2018, 13, 330–336 Search PubMed
 .
.
- F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19–28 Search PubMed
 .
.
- M. Bagnani, P. Azzari, S. Assenza and R. Mezzenga, Sci. Rep., 2019, 9, 1–9 Search PubMed
 .
.
- M. Bagnani, P. Azzari, C. De Michele, M. Arcari and R. Mezzenga, Soft Matter, 2021, 17, 2158–2169 Search PubMed
 .
.
- P.-X. Wang, W. Y. Hamad and M. J. MacLachlan, Nat. Commun., 2016, 7, 1–8 Search PubMed
 .
.
- P. J. Flory and G. Ronca, Mol. Cryst. Liq. Cryst., 1979, 54, 289–309 Search PubMed
 .
.
- J. Straley, Mol. Cryst. Liq. Cryst., 1973, 22, 333–357 Search PubMed
 .
.
-
A. N. Chester and S. Martellucci, Phase transitions in liquid crystals, Springer Science & Business Media, 2013, vol. 290 Search PubMed
 .
.
- M. Bagnani, G. Nystrom, C. De Michele and R. Mezzenga, ACS Nano, 2018, 13, 591–600 Search PubMed
 .
.
- P. Palffy-Muhoray, E. G. Virga and X. Zheng, J. Phys.: Condens. Matter, 2017, 29, 475102 Search PubMed
 .
.
- R. F. Kayser Jr and H. J. Raveché, Phys. Rev. A: At., Mol., Opt. Phys., 1978, 17, 2067 Search PubMed
 .
.
- M. P. Lettinga, K. Kang, A. Imhof, D. Derks and J. K. Dhont, J. Phys.: Condens. Matter, 2005, 17, S3609 Search PubMed
 .
.
-
J. W. Mullin, Crystallization, Elsevier, 2001 Search PubMed
 .
.
- G. Wulff, Z. Krystallog., 1901, 34, 449–530 Search PubMed
 .
.
- N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 Search PubMed
 .
.
- A. Cuetos, R. van Roij and M. Dijkstra, Soft Matter, 2008, 4, 757–767 Search PubMed
 .
.
- P. van der Schoot, J. Phys. Chem. B, 1999, 103, 8804–8808 Search PubMed
 .
.
- S. A. Khadem, M. Bagnani, R. Mezzenga and A. D. Rey, Nat. Commun., 2020, 11, 1–10 Search PubMed
 .
.
- I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 Search PubMed
 .
.
- H. Atkinson, Acta Metall., 1988, 36, 469–491 Search PubMed
 .
.
- J. Svoboda and I. Turek, Philos. Mag. B, 1991, 64, 749–759 Search PubMed
 .
.
- L. Onsager, Phys. Rev., 1931, 37, 405 Search PubMed
 .
.
- J. Svoboda, F. Fischer, P. Fratzl and E. Kozeschnik, J. Mater. Sci. Eng. A, 2004, 385, 166–174 Search PubMed
 .
.
-
A. Katchalsky and P. F. Curran, Nonequilibrium thermodynamics in biophysics, Harvard University Press, 2013 Search PubMed
 .
.
- A. Modlińska, A. M. Alsayed and T. Gibaud, Sci. Rep., 2015, 5, 1–10 Search PubMed
 .
.
- R. Mezzenga, B. M. Folmer and E. Hughes, Langmuir, 2004, 20, 3574–3582 Search PubMed
 .
.
- Z. Dogic and S. Fraden, Langmuir, 2000, 16, 7820–7824 Search PubMed
 .
.
- A. Goldar, H. Thomson and J. M. Seddon, J. Phys.: Condens. Matter, 2007, 20, 035102 Search PubMed
 .
.
- G. Nyström, M. Arcari, J. Adamcik, I. Usov and R. Mezzenga, ACS Nano, 2018, 12, 5141–5148 Search PubMed
 .
.
- Y. Cao and R. Mezzenga, Adv. Colloid Interface Sci., 2019, 269, 334–356 Search PubMed
 .
.
- G. G. Glenner, N. Engl. J. Med., 1980, 302, 1283–1292 Search PubMed
 .
.
- C. M. Dobson, Nature, 2003, 426, 884–890 Search PubMed
 .
.
-
E. G. Virga, Variational theories for liquid crystals, CRC Press, 1995, vol. 8 Search PubMed
 .
.
- P. Ehrenfest, Proc. R. Acad. Sci. Amsterdam, 1933, 36, 153–157 Search PubMed
 .
.
- G. Nyström and R. Mezzenga, Curr. Opin. Colloid Interface Sci., 2018, 38, 30–44 Search PubMed
 .
.
-
C. Honorato-Rios, J. Bruckner, C. Schütz, S. Wagner, Z. Tosheva, L. Bergström and J. P. Lagerwall, Liquid Crystals with Nano and Microparticles, World Scientific, 2017, pp. 871–897 Search PubMed
 .
.
- G. Chilaya, Z. Elashvili, L. Lisetski, T. Piliashvili and K. Vinokur, Mol. Cryst. Liq. Cryst., 1981, 74, 261–273 Search PubMed
 .
.
- M. P. B. van Bruggen, H. N. W. Lekkerkerker, G. Maret and J. K. G. Dhont, Phys. Rev. E, 1998, 58, 7668–7677 Search PubMed
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00466b |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Massimo
Bagnani
a,
Massimo
Bagnani
 a and
Raffaele
Mezzenga
a and
Raffaele
Mezzenga
 *ab
*ab
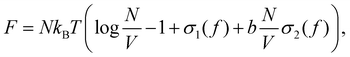
 is half the excluded volume between two randomly oriented rods and σ1 and σ2 are functions of the distribution function f of the angle Θ between the rods and the director field; for a detailed description see ref. 27. The derivatives of F with respect to V and N are called respectively osmotic pressure (Π) and chemical potential (μ):
is half the excluded volume between two randomly oriented rods and σ1 and σ2 are functions of the distribution function f of the angle Θ between the rods and the director field; for a detailed description see ref. 27. The derivatives of F with respect to V and N are called respectively osmotic pressure (Π) and chemical potential (μ):

 , results in σ1(fi) = 0 and σ2(fi) = 1, see ESI† for details. In the case of an anisotropic distribution, where f is not a constant, Onsager's trial function
, results in σ1(fi) = 0 and σ2(fi) = 1, see ESI† for details. In the case of an anisotropic distribution, where f is not a constant, Onsager's trial function  can be used. In case of large α, σ1(fα) and σ2(fα) can be substituted by their asymptotic series (ESI†). This parametrization allows F to be minimized at each rescaled concentration
can be used. In case of large α, σ1(fα) and σ2(fα) can be substituted by their asymptotic series (ESI†). This parametrization allows F to be minimized at each rescaled concentration  , where φ is the volume fraction of the rods. Fig. 1(a) (purple line) shows the order parameter S for increasing concentration ϕ. The order parameter remains zero up to a concentration of ϕ ≈ 3.68, where it jumps discontinuously to 0.6. As shown in Fig. 1(a), this is a first order transition from an isotropic phase, with S = 0 for ϕ < 3.68, to a nematic phase S ≠ 0 for ϕ > 3.68.27 Minimizing F and using asymptotic expansions, eqn (2) and (3) become
, where φ is the volume fraction of the rods. Fig. 1(a) (purple line) shows the order parameter S for increasing concentration ϕ. The order parameter remains zero up to a concentration of ϕ ≈ 3.68, where it jumps discontinuously to 0.6. As shown in Fig. 1(a), this is a first order transition from an isotropic phase, with S = 0 for ϕ < 3.68, to a nematic phase S ≠ 0 for ϕ > 3.68.27 Minimizing F and using asymptotic expansions, eqn (2) and (3) become



 . With the previous symbolism it can be written as
. With the previous symbolism it can be written as  . For volumes lower than Vmin, the free energy increases with an increase in the size, thus the droplet shrinks redissolving in the solution, while for volumes larger than Vmin, ΔF decreases, leading to a growth behavior. A more detailed discussion on nucleation of hard rod systems can be found in ref. 33 The surface tension γ can be linked to the geometry of the rods as
. For volumes lower than Vmin, the free energy increases with an increase in the size, thus the droplet shrinks redissolving in the solution, while for volumes larger than Vmin, ΔF decreases, leading to a growth behavior. A more detailed discussion on nucleation of hard rod systems can be found in ref. 33 The surface tension γ can be linked to the geometry of the rods as  , from Van der Shoot's previous work.34 The minimum volume for nucleation scales as
, from Van der Shoot's previous work.34 The minimum volume for nucleation scales as
 . The real shape of the droplets may be taken into account by adjusting the coefficients when the surface is involved. However, this correction will depend on the volume and the particular system under study,21 therefore overly complicating the analysis. The growth is influenced by three quantities: the difference in osmotic pressure ΔΠ, the chemical potential Δμ between the nematic and isotropic phase, and the external pressure, in this case, it is the Laplace pressure generated by the isotropic surface tension.41
. The real shape of the droplets may be taken into account by adjusting the coefficients when the surface is involved. However, this correction will depend on the volume and the particular system under study,21 therefore overly complicating the analysis. The growth is influenced by three quantities: the difference in osmotic pressure ΔΠ, the chemical potential Δμ between the nematic and isotropic phase, and the external pressure, in this case, it is the Laplace pressure generated by the isotropic surface tension.41


 and
and  . In this representation, for ρ ≪ 1 the surface tension is the dominant term, while for larger sizes ρ ≫ 1, the change in potentials becomes leading. The length R* represents the characteristic length of the system and as shown in the previous section, the results of both classical nucleation theory and the following approach are based on this same length scale, since R* ∼ L ∼ Vmin1/3.
. In this representation, for ρ ≪ 1 the surface tension is the dominant term, while for larger sizes ρ ≫ 1, the change in potentials becomes leading. The length R* represents the characteristic length of the system and as shown in the previous section, the results of both classical nucleation theory and the following approach are based on this same length scale, since R* ∼ L ∼ Vmin1/3.
 , and thus obtain the change in concentration with the volume of the droplet Vp. The results are shown in Fig. 3, where the concentrations of nematic and isotropic phases are plotted with the volume of the nematic phase. These two lines represent the binodal curve of the system undergoing the growth process, where with an increase in the volumes the concentration in the nematic phase increases, while the concentration in the isotropic phase slowing decreases. The real dynamics of phase separation depends on many different quantities: the diffusion coefficients, the total volume of solution and the initial conditions, which are different in every system. Also, in a real system, a population of tactoids with different volumes would nucleate and grow, possibly colliding and forming new tactoids. In this analysis, we considered the growth of a single droplet of a given concentration and volume immersed in a supersaturated isotropic solution, therefore the effects of having a population of droplets interacting have not been considered and it is outside the scope of this analysis.
, and thus obtain the change in concentration with the volume of the droplet Vp. The results are shown in Fig. 3, where the concentrations of nematic and isotropic phases are plotted with the volume of the nematic phase. These two lines represent the binodal curve of the system undergoing the growth process, where with an increase in the volumes the concentration in the nematic phase increases, while the concentration in the isotropic phase slowing decreases. The real dynamics of phase separation depends on many different quantities: the diffusion coefficients, the total volume of solution and the initial conditions, which are different in every system. Also, in a real system, a population of tactoids with different volumes would nucleate and grow, possibly colliding and forming new tactoids. In this analysis, we considered the growth of a single droplet of a given concentration and volume immersed in a supersaturated isotropic solution, therefore the effects of having a population of droplets interacting have not been considered and it is outside the scope of this analysis.

 is the nematic director field and q∞ is the pitch wave number. Additional details can be found in the ESI† of ref. 20 This functional correctly predicts the shape and nematic field configuration for all the classes of nematic and cholesteric tactoids found experimentally.20 The values of the constants used can be found in ref. 21, for the three systems under study and are reported in Table 1.
is the nematic director field and q∞ is the pitch wave number. Additional details can be found in the ESI† of ref. 20 This functional correctly predicts the shape and nematic field configuration for all the classes of nematic and cholesteric tactoids found experimentally.20 The values of the constants used can be found in ref. 21, for the three systems under study and are reported in Table 1.


 ) symbolize the uniaxial cholesteric droplets, while the red stars (
) symbolize the uniaxial cholesteric droplets, while the red stars ( ) symbolize the radial cholesteric droplets.21
) symbolize the radial cholesteric droplets.21






 . By rewriting eqn (21) in the nematic phase, we get
. By rewriting eqn (21) in the nematic phase, we get
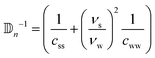 .
.
 , thus the rate of change of Nl is
, thus the rate of change of Nl is


 . This last expression can be used in eqn (21) to obtain the dissipation function in the isotropic phase Qi:
. This last expression can be used in eqn (21) to obtain the dissipation function in the isotropic phase Qi: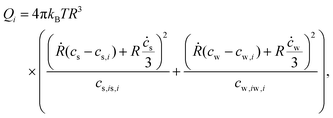
 and eqn (24), we obtain
and eqn (24), we obtain











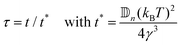
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) i/
i/![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) n,
n,  and
and  .
.
 and concentration ϕ, the isotropic phase has a concentration of
and concentration ϕ, the isotropic phase has a concentration of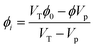
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) i,n depend on the concentration, we know from the Onsager theory that ϕ will range from 3.7 to 4.7 with a maximal increase of 27%. The isotropic phase ranges from 3.7 to 3.3 with a maximal decrease of 10%. From diffusion studies of hard rods we know that the diffusion coefficient remains constant at the coexistence and it is more than ten times larger compared to the nematic phase.55 Therefore, we can assume that
i,n depend on the concentration, we know from the Onsager theory that ϕ will range from 3.7 to 4.7 with a maximal increase of 27%. The isotropic phase ranges from 3.7 to 3.3 with a maximal decrease of 10%. From diffusion studies of hard rods we know that the diffusion coefficient remains constant at the coexistence and it is more than ten times larger compared to the nematic phase.55 Therefore, we can assume that ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) i,n will remain approximately constant during the process and the ratio κ will be much bigger than one.
i,n will remain approximately constant during the process and the ratio κ will be much bigger than one. .
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

