Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Data-driven approximations to the bridge function yield improved closures for the Ornstein–Zernike equation†
Rhys E. A.
Goodall
 and
Alpha A.
Lee
and
Alpha A.
Lee
 *
*
Cavendish Laboratory, University of Cambridge, Cambridge, UK. E-mail: aal44@cam.ac.uk
First published on 10th May 2021
Abstract
A key challenge for soft materials design and coarse-graining simulations is determining interaction potentials between components that give rise to desired condensed-phase structures. In theory, the Ornstein–Zernike equation provides an elegant framework for solving this inverse problem. Pioneering work in liquid state theory derived analytical closures for the framework. However, these analytical closures are approximations, valid only for specific classes of interaction potentials. In this work, we combine the physics of liquid state theory with machine learning to infer a closure directly from simulation data. The resulting closure is more accurate than commonly used closures across a broad range of interaction potentials.
1 Introduction
A central question in soft matter pertains to the inverse problem of determining the interaction potentials between building blocks, e.g. colloids or molecules, that give rise to desired structures through self-assembly.1,2 Applications of this inverse problem abound in disparate fields. For instance, molecular interactions can be optimised to yield porous structures in liquids3 which in turn are crucial for chemical processes such as gas separation and storage.4,5 Studying the inverse problem for these porous structures, both on computationally designed systems6 and by back-tracking potentials from experimental data, allows for greater understanding of their physics. This knowledge can then be leveraged to further optimise these systems and improve their properties. Similarly, bottom-up coarse-graining,7–9 an approach for accelerating soft matter simulations, can be viewed as an inverse problem. Coarse-graining involves finding effective inter-particle interactions between coarse-grained “beads” that reproduce the structure of the full system. A related but important class of inverse problems looks at how external fields can be applied to induce desired changes in the structures of fluids for example controlling the density profile at wall-fluid interfaces.10The inverse problem we consider in this work is: given the pair distribution function g(r) of an isotropic collection of particles with density ρ, can we determine a pairwise interaction potential ϕ(r) that would result in the original pair distribution g(r) being recovered from a forward simulation of particles with the same density. Although the forward problem of predicting condensed phase structure given a set of interactions can be tackled with standard methods such as molecular dynamics or Monte Carlo simulation, solving the inverse problem remains challenging. Iterative Boltzmann Inversion (IBI)11 and its extensions12–14 are perhaps the most common approaches. These methods involve iterative optimisation loops where the trial potential is updated based on the differences between the target g(r) and that obtained from converged simulations of the trial potential. Model-free predictor-correction methods15 solve a similar iterative problem to IBI but do so using test-particle sampling to obtain estimates for the g(r) resulting from a given trial potential. This approach avoids the need for multiple sets of simulations to be carried out. Other approaches include direct inversion schemes such as the generalized Yvon–Born–Green method16,17 that approximates the potential of mean-force from structural correlation functions and methods based on applying the variational principle within the context of free-energy functional theory.18
In theory, a rigorous framework in statistical physics known as the Ornstein–Zernike equation19 provides a direct and computationally efficient framework to solve this inverse problem without iterative approaches. In an isotropic fluid with density ρ and pair distribution function g(r), the Ornstein–Zernike equation defines the direct correlation function c(r) in terms of total correlation function, h(r) = g(r) − 1, via
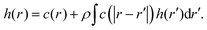 | (1) |
The key insight is that the total correlation function is a consequence of not only direct interactions between particles but also indirect correlations mediated through interactions with other particles.
Given a closure relationship coupling h(r) and c(r) with the interaction potential, ϕ(r), the Ornstein–Zernike equation provides a path to solve the inverse problem. The generally accepted form for the closure is
| h(r) + 1 = exp(−βϕ(r) + γ(r) + B(r)), | (2) |
Modern machine learning (ML) offers a suite of powerful tools for function approximation30–33 that have attracted attention in many areas within the physical sciences.34,35 In this work, we show that closures to the Ornstein–Zernike framework can be learnt directly from simulation data by approximating B(r) using an ML model. The results indicate that when used to solve the inverse problem such learnt closures yield better estimates of the bridge function and consequently better estimates of the interaction potential than either HNC or PY across a broad range of systems.
2 Methodology
2.1 Feature set design
Although the aim when solving the inverse problem is to determine an interaction potential ϕ(r) it is more convenient to consider approximating the bridge function B(r) in eqn (2) as opposed to the entire closure. Doing so allows our approach to be viewed as learning a correction to the successful HNC closure therefore building in a strong physical prior. This approach also presents a numerically easier learning problem because B(r) does not diverge in regions where ϕ(r) diverges (this can be seen for the Lennard-Jones 6-12 potential in36 and for the Soft-Sphere potential in ref. 37).In general, the performance of an ML model is circumscribed by whether the information captured in the model's inputs is sufficient to determine the system. Therefore, physically motivated input features are necessary to learn B(r) effectively. B(r) can be expanded as an infinite series in γ(r),38
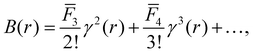 | (3) |
![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) n, are dependent on the density, ρ, and the temperature, T. By dimensional analysis, the bridge function can only be expressed in terms of dimensionless reduced quantities ρ* and T*. However, for complicated pairwise potentials, where multiple length and energy scales are required to define the system, comparable reduced quantities are ill-defined. This prevents the formulation of a truly general closure in terms of γ(r) only. However, this also suggests that there is scope to improve upon current closures by including additional input features that allow us to recover the degrees of freedom corresponding to ρ* and T*. This idea is apparent in how the modified Verlet closure39 achieves significant performance improvements over the standard Verlet closure (VM),40BVM(r) = −γ(r)2/2(1 + αγ(r)), in systems where ρ* and T* are well defined by expressing the α parameter of the Verlet closure as a function of ρ* and T* directly. If ρ* and T* are not well defined similar increases in accuracy can be achieved by introducing additional parameters into the closure that can be fitted for known systems to ensure the self-consistency of thermodynamic properties. Examples of such closures are the Rogers-Young and Zerah-Hansen closures41,42 which introduce switching functions parameterised with characteristic length-scales that must be fitted. However, for a closure to be generally applicable any additional input features or parameters must be determined without prior knowledge of the target system.
n, are dependent on the density, ρ, and the temperature, T. By dimensional analysis, the bridge function can only be expressed in terms of dimensionless reduced quantities ρ* and T*. However, for complicated pairwise potentials, where multiple length and energy scales are required to define the system, comparable reduced quantities are ill-defined. This prevents the formulation of a truly general closure in terms of γ(r) only. However, this also suggests that there is scope to improve upon current closures by including additional input features that allow us to recover the degrees of freedom corresponding to ρ* and T*. This idea is apparent in how the modified Verlet closure39 achieves significant performance improvements over the standard Verlet closure (VM),40BVM(r) = −γ(r)2/2(1 + αγ(r)), in systems where ρ* and T* are well defined by expressing the α parameter of the Verlet closure as a function of ρ* and T* directly. If ρ* and T* are not well defined similar increases in accuracy can be achieved by introducing additional parameters into the closure that can be fitted for known systems to ensure the self-consistency of thermodynamic properties. Examples of such closures are the Rogers-Young and Zerah-Hansen closures41,42 which introduce switching functions parameterised with characteristic length-scales that must be fitted. However, for a closure to be generally applicable any additional input features or parameters must be determined without prior knowledge of the target system.
From eqn (1), we see that the density of the system can be extracted if both h(r) and c(r) are given. This suggests that taking h(r) and c(r) together as input features should be more informative than γ(r) alone.43 An additional feature χ(r) can be constructed from the fluctuations of the pair distribution,
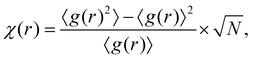 | (4) |
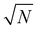 to remove the dependence on the number of particles under observation, N.
to remove the dependence on the number of particles under observation, N.
The final extension to the feature set considered was to include gradient information. This is done via γ′(r) rather than h′(r) and c′(r) as the latter contain sharp jumps around the first co-ordination shell that cancel in h′(r). Such behaviour is undesirable as it would provide artefacts to which the model could over-fit on in the training data, leading to poor generalisation performance in downstream applications. In general, a desirable closure should be scale-invariant, however, the definition of a gradient requires a length-scale. To deal with this, the radius of the first co-ordination shell is used as the reference length-scale in all systems. This allows gradient features to be defined in a consistent manner across systems.
2.2 Reliable calculation of the direct correlation function
Following from the Fourier transform of the Ornstein–Zernike equation the direct correlation function, c(r), can be evaluated from measurements of the static structure factor, S(q), based on the relationship that: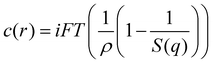 | (5) |
In simulation studies, the most common approach for calculating the S(q) is taking the Fourier transform of the total correlation function.
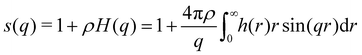 | (6) |
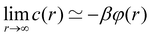 .20
.20
In previous work approximate extension schemes45 have been used to extend h(r) to infinity to avoid such issues. However, such extension schemes rely on the use of a pre-determined closure. The other approach is to calculate S(q) directly from the Fourier transform of the density. However, this approach is computationally much more expensive and is subject to significant noise in the expected value of S(q) for high wave vectors resulting in short-wavelength fluctuations in c(r).
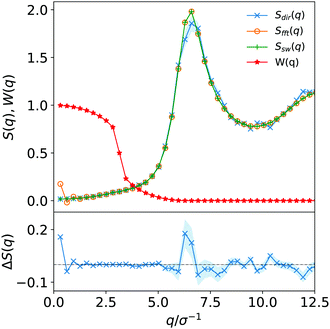
In this work to avoid both of these limitations, we opt for a Poisson re-summation inspired approach where we evaluate S(q) directly for small wave vectors and from the Fourier transform of h(r) for large wave vectors. A smooth cosine switching function is used to blend between the two regimes.
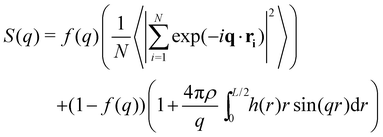 | (7) |
This approach ensures we get the correct behaviour in the q → 0 limit for high-density systems suppressing the non-physical artefacts that would otherwise observed in c(r). However, for a small number of systems we observed deviations between the direct and Fourier transform results around the principal peak (see Fig. 1) which in turn can lead to comparatively small but still undesirable intermediate wavelength fluctuations in c(r).
2.3 Model fitting and data generation
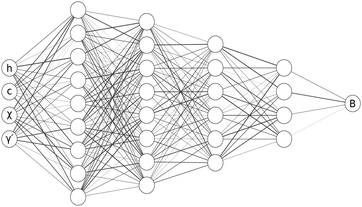
In this problem, data can be readily generated by solving the forward problem for specified potentials. When ϕ(r) is specified eqn (2) can be inverted to calculate B(r) if h(r) and S(q) are measured from a converged forward simulation such that we can calculate γ(r) leaving B(r) as the only unknown term in eqn (2).Having obtained numerical estimates for B(r) when ϕ(r) is known our aim is to train a model using this data to approximate B(r) in cases where ϕ(r) is unknown but where the structural correlation functions can be measured directly. An accurate model for B(r) would then allow ϕ(r) to be determined viaeqn (2). Using the physically motivated feature set described previously we employ neural networks to learn approximations for B(r) as a functional of the identified input features h(r), c(r), χ(r), γ′(r). To do this we make use of a class of neural networks called multi-layer perceptrons (MLP). A l-layer MLP approximates functions f(x) by l successive non-linear compositions, i.e. f(x) ≃ Wlσ(Wl−1…σ(W1x))), where x is a vector of input features, Wi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Mi×Mi−1 is a weight matrix inferred from data, Mi is the number of units in layer i, and σ(x) is a non-linear activation function - here we use rectified linear unit (ReLU) activations of the form ReLU(x) = max(x, 0). We use a 5-layer MLP with M = [256, 128, 64, 32] units in the 4 hidden layers and a single unit in the output layer (schematic shown in Fig. 2). In neural networks the gradients of the loss with respect to the model parameters W can be efficiently inferred via back-propagation.33,46 In this work the first-order stochastic optimiser Adam47 was used to train the model by adjusting its parameters W to minimise a squared error loss function between the model's predictions and training labels for B(r) obtained from the simulation data. The models were trained for 100 epochs (cycles through the training data) in mini-batches of 128 samples at a time. The Adam optimiser was configured with a learning rate of 0.001, β1 of 0.9, β2 of 0.999, and ε of 10−7.
Mi×Mi−1 is a weight matrix inferred from data, Mi is the number of units in layer i, and σ(x) is a non-linear activation function - here we use rectified linear unit (ReLU) activations of the form ReLU(x) = max(x, 0). We use a 5-layer MLP with M = [256, 128, 64, 32] units in the 4 hidden layers and a single unit in the output layer (schematic shown in Fig. 2). In neural networks the gradients of the loss with respect to the model parameters W can be efficiently inferred via back-propagation.33,46 In this work the first-order stochastic optimiser Adam47 was used to train the model by adjusting its parameters W to minimise a squared error loss function between the model's predictions and training labels for B(r) obtained from the simulation data. The models were trained for 100 epochs (cycles through the training data) in mini-batches of 128 samples at a time. The Adam optimiser was configured with a learning rate of 0.001, β1 of 0.9, β2 of 0.999, and ε of 10−7.
We use an MLP in this work as they are a numerically tractable way of representing complex functions that scale well to large data sets. However, there are no specific inductive biases built into the MLP. Thus alternative regression models30–32 would likely achieve similar performance. An example of a useful inductive bias is that the translational invariance of features/objects within images is automatically achieved in computer vision applications when using a convolutional neural network.
Despite remarkable successes, neural networks are essentially powerful interpolation frameworks. Therefore, to learn a generally applicable closure, a wide variety of possible interaction potentials need to be explored when fitting the model. We investigate 13 different interaction potentials that we group into four classes:
1. Fast-diverging – potentials containing strong divergences that prevent particles from overlapping,
2. Step-diverging – fast-diverging models where a repulsive plateau is added before the divergence to introduce complex multi-lengthscale structure,
3. Slow-diverging – weakly divergent systems analogous to fast-diverging systems, and
4. Core-overlapping – potentials that do not diverge and allow particles to overlap.
We will refer to Fast-Diverging and Step-Diverging potentials as hard potentials and Slow-Diverging and Core-Overlapping potentials as soft potentials. In total, we consider 96 different parameterisations of these 13 potentials by adjusting the length and energy scales. For each of these parameterisations the molecular dynamics package ESPResSo48,49 was used to determine h(r) and S(q) for systems of particles. We use a cubic simulation box with a side length of 20σ where numerically the length scale Sigma is set to 1. For each potential we look at reduced densities between 0.4 and 0.8 at increments of 0.1 giving a total of 480 systems. A cut-off length of rcut = 3σ was used for all potentials. The temperature of the Langevin thermostat used was set to 1/kb. Full details of the functional forms for the potentials investigated and simulation setup are available in the ESI.†
The Ornstein–Zernike formalism is only valid for fluid systems. Given that the high-throughput approach used to generate training data can result in simulations of non-fluid systems being carried out accidentally, it is necessary to identify and exclude solid and two-phase samples that arise before the data can be used. This is done using several physically motivated heuristics. The Hansen–Verlet criterion,50S(qpeak) > 2.8, is used to identify solid and two-phase solid–liquid samples. Two-phase liquid–gas systems are identified using the heuristic criteria that S(0) > 1. This criterion is derived by noting that the compressibility of a system is given by:
| S(q → 0) = ρkbTκT | (8) |
As gases are typically characterised by their highly compressible nature and noting that for an uncorrelated fluid S(0) ≃ 1, we propose that divergence of S(q) in the limit q → 0 is indicative of two-phase liquid–gas behaviour. We also check the consistency of the kinetic temperature across the simulation. In total 450 out of 480 systems investigated passed these heuristic criteria. There is potential that some examples outside the region of stability of the fluid phase may escape these heuristic criteria and consequently bias the training of our learnt closures. For the potentials studied in this work, this did not appear to be a problem. However, for other potential systems additional heuristics, for example looking at the residual multi-particle entropy,51,52 may be required to reliably exclude undesired phases.
3 Results
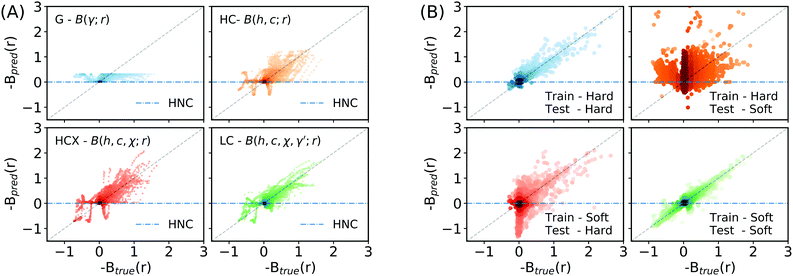
To examine the performance of learnt closures, we consider and fit MLP models for the following combinations of the feature set: (1) G = B(γ; r) – a closure just in terms of γ(r) as common for analytical closures in the field, (2) HC = B(h, c; r) – a closure in terms of h(r) and c(r), (3) HCX =B(h, c, χ; r) – a closure including h(r), c(r), and χ(r), and (4) LC = B(h, c, χ, γ′; r) – a learnt closure taking the full feature set as input. To compare these learnt closures to HNC, VM, and PY we look at how they perform on a randomly sampled test set comprising 90/450 (20%) of the simulation systems that were withheld when training the closures.Table 1 shows that the learnt closure based on just the indirect correlation function, G, has a negative coefficient of determination, R2, implying that it is worse than predicting a constant value (i.e. HNC). However, as the feature set is extended to include additional physically motivated features (Fig. 3A), the learnt closures offer rapidly improving performance compared to HNC, PY, and VM. Using the full feature set, LC, leads to a very strong correlation between the learnt closure's predictions and the ground truth with a R2 value of 0.693. Physically, this improved performance is due to the learnt closures capacity to capture more of the strongly correlated physics in the region around the first co-ordination shell across a broad range of interactions.
| Closure | R 2 | RMSE | MAE |
|---|---|---|---|
| HNC | 0.000 | 0.097 | 0.028 |
| PY | 0.060 | 0.541 | 0.113 |
| VM (α = 0.8) | 0.081 | 0.415 | 0.090 |
| G = B(γ; r) | −1.699 | 0.088 | 0.023 |
| HC = B(h, c; r) | 0.374 | 0.071 | 0.019 |
| HCX = B(h,c,χ;r) | 0.556 | 0.067 | 0.020 |
| LC = B(h, c, χ, γ′; r) | 0.693 | 0.052 | 0.017 |
3.1 Generalisation performance and universality
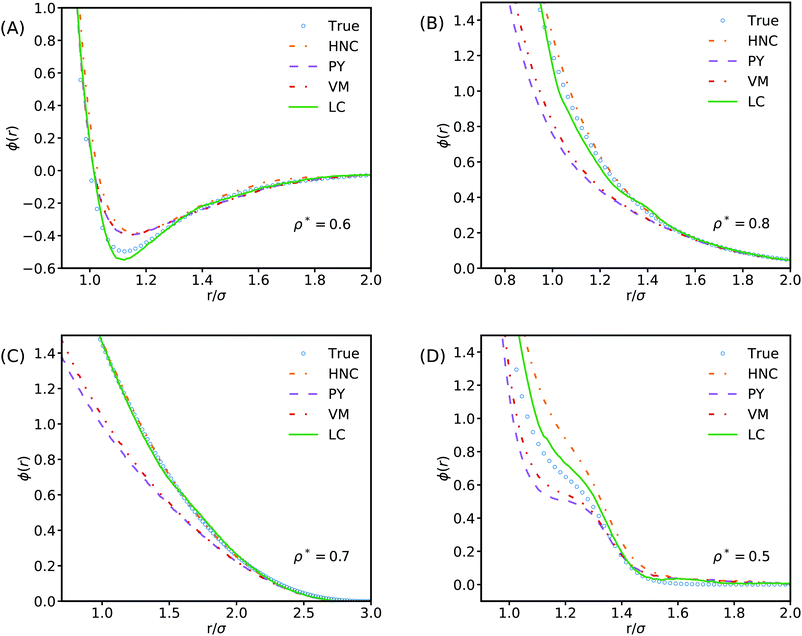
Our results show that learnt closures can exhibit greater universality than common analytical closures such as HNC, PY or VM when trained and tested on a diverse selection of potential systems. However, an interesting question is whether this is true generalisation performance that would extend to out-of-training-distribution regimes. This can be probed by examining the generalisation performance of learnt closures trained on restricted classes of potential. Two LC closure models were trained using the full feature set for this purpose, one on only hard potentials and a second on only soft potentials (Fig. 3B). When tested in this manner, the learnt closures are seen to be less accurate in their out-of-training-distribution regimes. The learnt closures can only generalise across a wider range of systems than typical analytical closures when they have been exposed to systems exhibiting similar physics during training. Consequently we suggest that it would not be reasonable to apply learnt closures in applications involving qualitatively different potentials (e.g. charged liquids, where the correlation length-scales are much longer) without first extending the training data to also include such systems. Accordingly, to allow the learnt closures to be used with greater confidence, it may be beneficial to investigate the use of a Bayesian neural network where the weights of the MLP are given as distributions rather than point estimates.53 In contrast to the standard MLP used here the Bayesian equivalent provides uncertainty estimates that could be used to highlight when the model may not behave as expected.We can also look at how well the model performs on individual systems. For an LC model trained on all the training data Fig. 4 shows the true potential function and potential functions derived from common approximations for the bridge function plotted alongside a potential using the LC model's predictions for example Lennard-Jones, Yukawa, Hertzian, and RSSAW systems across a range of reduced densities. The LC model matches or offers qualitatively improved performance for all of these different interactions, despite not having been exposed to training data at the state points being examined. For the Yukawa and Hertzian potentials, our results show that HNC performs remarkably well, in agreement with previous literature.54,55 Looking closely we observe small spurious fluctuations in the potential inferred by machine learning at radii corresponding to the principal peak in g(r). The presence of these fluctuations suggests that the feature set proposed in this work is insufficient to build a truly universal closure that can completely capture all the possible behaviour seen in this region. Development of additional meta-features is therefore a promising area of exploration for improving the predictability of learnt closures in this strongly correlated region. One potential class of meta-feature are features based on cumulative integrals of correlation functions i.e. the Kirkwood–Buff integral.56
4 Conclusions
In this work, we demonstrate that machine learning is an effective tool for tackling inverse problems in soft matter. We use the physics-derived framework of Ornstein–Zernike theory but employ machine learning to parameterise its closure relationship using physically relevant correlation functions. Our approach can be used to construct closures that are accurate in regions where traditional analytical approximations tend to fail. We observe that when trained on restricted classes of potentials learnt closures have restricted domains of applicability. However, extending the training set to include more diverse interaction potentials extends the domain of applicability without harming model performance for the initial classes of potential. This suggests that it should be feasible to construct a generally applicable data-driven closure. We envisage that future work will be able to generalise and extend upon the approach adopted here to obtain increased efficacy closures in a wide variety of systems to which the Ornstein–Zernike framework has been applied such as the RISM and Molecular Ornstein-Zernike approaches57–59 where HNC is often still the closure relationship of choice.60More broadly, whilst many theoretical frameworks in physical sciences are elegant and exact, the implementation of those frameworks typically requires approximations and fitted functions. This is particularly true in soft matter where timescale and lengthscale challenges necessitate the use of creative approximations. We believe advances abound in approaches that leverage the overall physics framework but employ machine learning to determine those fitting functions directly from data.
Author contributions
AAL was responsible for conceptualization of the idea, REAG implemented the methodology and conducted the investigation, REAG and AAL analysed the results and prepared the manuscript.Data availability
All the cleaned data produced in this work are shared on https://github.com/CompRhys/ornstein-zernike. The raw data is available from the corresponding author upon reasonable request.Code availability
All the simulation code and fitting code needed to reproduce this work are available from https://github.com/CompRhys/ornstein-zernike. The modified structure factor code added to the ESPResSo48,49 molecular dynamics package for this work is available from https://github.com/CompRhys/espresso.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
REAG and AAL acknowledge the Winton Programme for the Physics of Sustainability for funding. AAL acknowledges support from the Royal Society. Part of this research was performed while REAG was visiting the Institute for Pure and Applied Mathematics (IPAM), which is supported by the National Science Foundation (Grant No. DMS-1440415).References
- R. B. Jadrich, B. A. Lindquist and T. M. Truskett, J. Chem. Phys., 2017, 146(18), 184103 CrossRef.
- Z. M. Sherman, M. P. Howard, B. A. Lindquist, R. B. Jadrich and T. M. Truskett, J. Chem. Phys., 2020, 152(14), 140902 CrossRef CAS PubMed.
- N. Giri, M. G. D. Pópolo, G. Melaugh, R. L. Greenaway, K. Rätzke, T. Koschine, L. Pison, M. F. C. Gomes, A. I. Cooper and S. L. James, Nature, 2015, 527(7577), 216–220 CrossRef CAS PubMed.
- J. Zhang, S.-H. Chai, Z.-A. Qiao, S. M. Mahurin, J. Chen, Y. Fang, S. Wan, K. Nelson, P. Zhang and S. Dai, Angew. Chem., Int. Ed., 2015, 54(3), 932–936 CrossRef CAS PubMed.
- F. Zhang, F. Yang, J. Huang, B. G. Sumpter and R. Qiao, J. Phys. Chem. B, 2016, 120(29), 7195–7200 CrossRef CAS PubMed.
- B. A. Lindquist, R. B. Jadrich and T. M. Truskett, Soft Matter, 2016, 12(10), 2663–2667 RSC.
- S. Kmiecik, D. Gront, M. Kolinski, L. Wieteska, A. E. Dawid and A. Kolinski, Chem. Rev., 2016, 116(14), 7898–7936 CrossRef CAS PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. D. Vries, J. Phys. Chem. B, 2007, 111(27), 7812–7824 CrossRef CAS PubMed.
- E. Brini, E. A. Algaer, P. Ganguly, C. Li, F. Rodriguez-Ropero and N. F. A. van der Vegt, Soft Matter, 2013, 9(7), 2108–2119 RSC.
- J. R. Henderson, Mol. Phys., 1991, 74(5), 1125–1131 CrossRef CAS.
- W. Schommers, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 28(6), 3599 CrossRef CAS.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24(13), 1624–1636 CrossRef CAS PubMed.
- T. C. Moore, C. R. Iacovella and C. McCabe, J. Chem. Phys., 2014, 140(22), 06B606_1 CrossRef PubMed.
- M. Heinen, J. Comput. Chem., 2018, 39(20), 1531–1543 CrossRef CAS PubMed.
- A. E. Stones, R. P. A. Dullens and D. G. A. L. Aarts, Phys. Rev. Lett., 2019, 123(9), 098002 CrossRef CAS PubMed.
- J. W. Mullinax and W. G. Noid, Phys. Rev. Lett., 2009, 103(19), 198104 CrossRef CAS PubMed.
- J. F. Rudzinski and W. G. Noid, Eur. Phys. J.: Spec. Top., 2015, 224(12), 2193–2216 CAS.
- M. Torikai, J. Chem. Phys., 2015, 142(14), 144102 CrossRef PubMed.
- L. S. Ornstein and F. Zernike, Proc. Natl. Acad. Sci. U. S. A., 1914, 17, 793 Search PubMed.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier Science, 2006 Search PubMed.
- T. Morita, Prog. Theor. Phys., 1958, 20(6), 920–938 CrossRef.
- J. K. Percus and G. J. Yevick, Phys. Rev., 1958, 110, 1–13 CrossRef CAS.
- M. S. Wertheim, Phys. Rev. Lett., 1963, 10, 321–323 CrossRef.
- T. Morita and K. Hiroike, Prog. Theor. Phys., 1960, 23(6), 1003–1027 CrossRef.
- G. A. Martynov and G. N. Sarkisov, Mol. Phys., 1983, 49(6), 1495–1504 CrossRef CAS.
- D.-M. Duh and D. Henderson, J. Chem. Phys., 1996, 104(17), 6742–6754 CrossRef CAS.
- M. Kinoshita, Chem. Phys. Lett., 2002, 353(3–4), 259–269 CrossRef CAS.
- M. Kinoshita, J. Chem. Phys., 2003, 118(19), 8969–8981 CrossRef CAS.
- Y. Nakamura, S. Arai, M. Kinoshita, A. Yoshimori and R. Akiyama, J. Chem. Phys., 2019, 151(4), 044506 CrossRef PubMed.
- L. Breiman, Mach. Learn., 2001, 45(1), 5–32 CrossRef.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT press, Cambridge, MA, 2006, vol. 2 Search PubMed.
- M. Schmidt and H. Lipson, Science, 2009, 324(5923), 81–85 CrossRef CAS PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep Learning, The MIT Press, 2016 Search PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559(7715), 547–555 CrossRef CAS PubMed.
- G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto and L. Zdeborová, Rev. Mod. Phys., 2019, 91, 045002 CrossRef CAS.
- M. Llano-Restrepo and W. G. Chapman, J. Chem. Phys., 1992, 97(3), 2046–2054 CrossRef CAS.
- M. Llano-Restrepo and W. G. Chapman, J. Chem. Phys., 1994, 100(7), 5139–5148 CrossRef CAS.
- L. L. Lee. Molecular Thermodynamics of Electrolyte Solutions, World Scientific Publishing Company, 2008 Search PubMed.
- N. Choudhury and S. K. Ghosh, J. Chem. Phys., 2003, 119(9), 4827–4832 CrossRef CAS.
- L. Verlet, Mol. Phys., 1980, 41(1), 183–190 CrossRef CAS.
- F. J. Rogers and D. A. Young, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 999–1007 CrossRef CAS.
- G. Zerah and J. P. Hansen, J. Chem. Phys., 1986, 84(4), 2336–2343 CrossRef CAS.
- T. Tsednee and T. Luchko, Phys. Rev. E, 2019, 99(3), 032130 CrossRef CAS PubMed.
- D. Frenkel, Eur. Phys. J. Plus, 2013, 128(1), 10 CrossRef.
- D. L. Jolly, B. C. Freasier and R. J. Bearman, Chem. Phys., 1976, 15(2), 237–242 CrossRef CAS.
- C. M. Bishop, et al., Neural networks for pattern recognition, Oxford university press, 1995 Search PubMed.
- D. P. Kingma and J. Ba, Adam: A method for stochastic optimization, arXiv preprint arXiv:1412.6980, 2014.
- H. J. Limbach, A. Arnold, B. A. Mann and C. Holm, Comput. Phys. Commun., 2006, 174(9), 704–727 CrossRef CAS.
- A. Arnold, O. Lenz, S. Kesselheim, R. Weeber, F. Fahrenberger, D. Roehm, P. Košovan and C. Holm, ESPResSo 3.1 – Molecular Dynamics Software for Coarse-Grained Models, in Meshfree Methods for Partial Differential Equations VI, volume 89 of Lecture Notes in Computational Science and Engineering, ed. M. Griebel and M. A. Schweitzer, Springer, 2013, pp. 1–23 Search PubMed.
- N. H. March and M. P. Tosi, Introduction to Liquid State Physics, World Scientific, 2002 Search PubMed.
- P. V. Giaquinta and G. Giunta, Phys. A, 1992, 187(1), 145–158 CrossRef CAS.
- P. V. Giaquinta, J. Chem. Phys., 2009, 130, 037101 CrossRef PubMed.
- R. M. Neal, Bayesian learning for neural networks, Springer Science & Business Media, 2012, vol. 118 Search PubMed.
- G. Pellicane and M. Cavero, J. Chem. Phys., 2013, 138(11), 03B608 CrossRef.
- G. Munaò and F. Saija, J. Chem. Phys., 2019, 151(13), 134901 CrossRef PubMed.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19(6), 774–777 CrossRef CAS.
- L. Blum and A. J. Torruella, J. Chem. Phys., 1972, 56(1), 303–310 CrossRef CAS.
- D. Chandler and H. C. Andersen, J. Chem. Phys., 1972, 57(5), 1930–1937 CrossRef CAS.
- E. L. Ratkova, D. S. Palmer and M. V. Fedorov, Chem. Rev., 2015, 115(13), 6312–6356 CrossRef CAS.
- L. Ding, M. Levesque, D. Borgis and L. Belloni, J. Chem. Phys., 2017, 147(9), 094107 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The Supplementary Online Material contains the functional forms of the interaction potentials used, details of the general simulation setup using ESPResSo, and details about the calculation of the direct correlation function. See DOI: 10.1039/d1sm00402f |
| This journal is © The Royal Society of Chemistry 2021 |