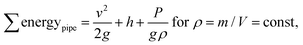Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fluid mechanics and rheology of the jumping spider body fluid†
Chantal
Göttler
ab,
Guillermo
Amador
 c,
Thomas
van de Kamp
c,
Thomas
van de Kamp
 de,
Marcus
Zuber
de,
Lisa
Böhler
a,
Roland
Siegwart
b and
Metin
Sitti
de,
Marcus
Zuber
de,
Lisa
Böhler
a,
Roland
Siegwart
b and
Metin
Sitti
 *af
*af
aPhysical Intelligence Department, Max Planck Institute for Intelligent Systems, 70569 Stuttgart, Germany. E-mail: sitti@is.mpg.de
bAutonomous Systems Laboratory, ETH Zurich, 8092 Zürich, Switzerland
cExperimental Zoology Group, Wageningen University & Research, 6708 WD Wageningen, The Netherlands
dInstitute for Photon Science and Synchrotron Radiation (IPS), Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
eLaboratory for Applications of Synchrotron Radiation (LAS), Karlsruhe Institute of Technology (KIT), Kaiserstr. 12, 76131 Karlsruhe, Germany
fInstitute for Biomedical Engineering, ETH Zurich, 8092 Zürich, Switzerland
First published on 3rd May 2021
Abstract
Spiders use their inner body fluid (“blood” or hemolymph) to drive hydraulic extension of their legs. In hydraulic systems, performance is highly dependent on the working fluid, which needs to be chosen according to the required operating speed and pressure. Here, we provide new insights into the fluid mechanics of spider locomotion. We present the three-dimensional structure of one of the crucial joints in spider hydraulic actuation, elucidate the fluid flow inside the spider leg, and quantify the rheological properties of hemolymph under physiological conditions. We observe that hemolymph behaves as a shear-thinning non-Newtonian fluid with a fluid behavior index n = 0.5, unlike water (n = 1.0).
Introduction
The “blood” of spiders, hemolymph, is not only important for circulatory purposes but enables locomotion in these eight-legged arthropods. Spider legs lack extensor muscles and employ hydraulics to generate the main driving force for extension.1–3 During activity, pressure of the hydraulic fluid, hemolymph, is increased inside the legs to achieve extension, while flexor muscles counteract.Arthropods have an open-circulatory system with no difference in blood and interstitial fluid. Their body fluid is pumped by a tubular heart in the abdomen through a delicate network of arteries into the cavities of the body.4 A large aorta supplies the front body-part, or prosoma, where it splits into the leg arteries.5,6 When the heart relaxes, oxygen-poor hemolymph travels through book lungs, to gain oxygen, before it enters back into the heart.5
Different to human blood, hemolymph is not red, but shows a light blue color, as it does not contain the iron-based protein, hemoglobin, but a copper-based hemocyanin to bind oxygen. Hemolymph consists of many nutrients, such as sugars, salts, amino acids, and proteins. Instead of white blood cells, spiders have different types of hemocytes as part of their immune system.7,8 When spider legs are injured, hemocytes induce coagulation, thus clogging the wound. To prevent stronger bleeding, spiders could amputate their legs near the body in a controlled way, also known as autotomy.9 Furthermore, juvenile spiders are capable of regrowing a complete leg inside the leg stump.10 Coagulation is a critical function of the hemolymph as leakages are fatal to hydraulic systems when operating at high pressures.
In hydraulic extension, the speed of leg extension depends directly on the transport velocity of hemolymph into the hydraulic joints of the leg (Fig. 1).11 Assuming a Poiseuille flow, the velocity of the fluid is directly proportional to the driving pressure. Therefore, fluid pressure determines the speed of reaction that can be achieved by the spider. During normal walking, spiders pressurize the hemolymph in their legs to 4–8 kPa, but pressures of 60 kPa and even up to 130 kPa have been reported during intense activity (e.g., jumping and running).11,12
 | ||
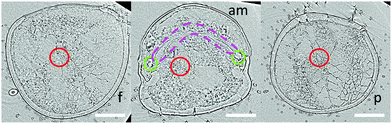
| Fig. 1 Hydraulic joint of jumping spider Phidippus regius. The femur-patella joint of jumping spiders is highly involved in running and jumping activities.13 During extension, the body fluid (hemolymph) leads to the unfolding of the articular membrane on the ventral side of the joint. Scale bar left: 5 mm; right: 0.4 mm. | ||
Various studies11,12,14,15 have investigated the pressure and velocity of hemolymph inside the body, in attempts to understand the hydraulic mechanism and how spiders are able to control the dynamics and kinematics of their multi-legged and multi-jointed body with hydraulics. However, due to the lack of information about flow geometry and rheological properties of the hemolymph, any kinematic and dynamic analysis of spider locomotion typically neglects flow through the gaps between muscles, nerves, and arteries, or lacunae, and assumes the fluid is Newtonian, like water.14–16 In this study, we present the first measurements of spider hemolymph viscosity and its non-Newtonian behaviour under physiological conditions. We reconstruct, in three-dimensions (3D), the fluid channels through the femur-patella joint, which plays an essential role during locomotion, and report the fluid flow inside this joint. Our results shed further light on the hemolymph-based hydraulic system of spiders. While being an exception in animal locomotion,17–19 fluidic actuation is, in contrast, an extremely useful and common tool in today's technology, especially in soft robotics,20 where fluid-driven locomotion has become essential.
Materials and methods
X-ray microtomography
Adult jumping spiders Phidippus regius were narcotized and transferred into a solution of 10% ethyl acetate, 20% ethanol and 70% water. Spiders were left in that solution overnight before being transferred into a container filled with 60% ethanol and 40% water. To increase contrast, 3–4 droplets of iodide were added. Extended legs were cut off and placed inside an Eppendorf tube filled with 70% ethanol and 30% water for scanning purposes. Synchrotron microtomography of the femur-patella leg segment was performed at the imaging cluster of the Karlsruhe Institute of Technology (KIT) light source. A parallel polychromatic X-ray beam produced by a 1.5 T bending magnet was spectrally filtered by 0.2 mm aluminum with a spectrum peak at about 15 keV and a full-width at half maximum bandwidth of about 10 keV. The fast indirect detector system consisting of an 18 μm LSO:Tb scintillator,21 diffraction limited optical microscope (Optique Peter) and a 12bit pco.dimax high speed camera with 2016 × 2016 pixels was employed. The sample was placed centrally and 3000 projections at 200 frames per second with an optical magnification of 10× were taken. The resulting effective pixel size was 1.22 μm. We used the control system concert22 for automated data acquisition. Tomographic reconstruction was done using the UFO framework.23 The individual segments were manually predefined with Amira (version 5.5) (Fig. 2) and segmentation was subsequently refined by Biomedisa.24OCT scanning
The fluid flow inside the spider leg joint was observed via optical coherent tomography (OCT) (TEL320C1 – Spectral Domain OCT System, Thorlabs). Adult spiders Phidippus regius usually have legs with diameters exceeding the penetration depth of the OCT. Therefore juvenile spiders (N4–5) were narcotized with Carbon dioxide (CO2) for 1 min and fixed with the ventral side up on a Petri dish. Dental polymer (Flexitime, Correct Flow) was used as glue, so that the living spider could be carefully detached after the experiments. Screenshots of the scanning positions were taken. The motion inside the leg was recorded with an image speed at a medium sensitivity (76 kHz). The refractive index was set to 1 and the Hann filter was used for the apodization window. The A-scan averaging was set to 3 and the B-scan averaging to 1 with a pixel size of 6.5 μm. Recorded images were used to manually track cell motion with the Tracker tool (http://physlets.org/tracker/). In total 36 cells were tracked inside the main artery. As the cells were randomly traveling through the artery at various radial locations, the average of the measured velocities is reported as mean flow velocity of the hemolymph.Hemolymph collection
Adult Phidippus regius were narcotized with CO2 and attached to a Petri dish. Hemolymph was collected on the ventral side between the sternum and the beginning of the petiole, before it flows through the book lungs back to the heart (Fig. 3). This method allowed collection of up to 50 μL of light-blue colored body fluid. Hemolymph collection by centrifuge as it is commonly done with Drosophila flies25 was not possible as the collected hemolymph would be contaminated with gut content leaking from the abdomen. Anti-coagulants were not used as they could affect the physical properties.26 The hemolymph was kept cool to slow down any biochemical reactions. Before experiments, it was warmed up to room temperature by hand.Hemolymph is a biological fluid, which could change its property under different conditions. Similar to blood, clotting could appear at wounds27 and coagulation could happen after 20–30 min. Additionally, a decrease in temperature could cause reduced deformability of the hemolymph cells.26 All of these could have an effect on the viscosity. Clotting and coagulation start to form after a specific time and can be identified by a drastic change in property (thickening into honey-like consistency and changing color to dark black).26 Therefore, only freshly collected samples were used. Influences as due to e.g. carbon dioxide were avoided by exposing the spider to CO2 for only 1–2 min and waiting 5 minutes before sample collection. Any temperature effects caused by e.g. anti-freezing agents28 were avoided as the animals were kept at 25–30 °C. Temperature effects during the experiment were excluded by keeping the temperature at the same level (room temperature) throughout the experiments. However, small variations could still appear. For this reason, we measured three samples at the same applied pressure (±3 kPa) and avoided to measure in only a specific direction (e.g., varying pressure from low to high) to avoid any time-correlated effects. As particles inside the fluid are usually the cause of shear-dependent behavior, we tried to use a homogenous sample, by carefully mixing (turning Eppendorf tube up and down) the collected hemolymph before the experiment, as hemolymph cells could slowly settle at the bottom of the container due to gravity.
Fabrication of the microchannel for rheological measurements
The desired microchannel was designed (length: 30 mm, width: 1 mm) and fabricated on a sodalime glass mask (Compugraphics Jena GmbH, Jena, Germany) for photolithography. Negative molds with 70 μm height were fabricated on a 3-inch circular silicon wafer using SU-8 photoresist (micro resist technology GmbH, Berlin, Germany) following standard protocol. The photoresist was spin-coated (WS-650MZ-8NPPB, Laurell Technologies, North Wales, PA, USA) to achieve a uniform thickness and etched using UV irradiation (MJB 4 mask alighner, SUSS MicroTex, Garching, Germany).The ingredients for PDMS (polydimethylsiloxane, Sylgard 184, Dow Corning, Inc., Midland, MI, USA) were mixed (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, elastomer
1, elastomer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hardener) with a spatula for 1 min in a beaker. Trapped air was removed by vacuum pumping the PDMS inside a desiccator for 15–20 min. A plastic ring was fixed around the silicon wafer with dental polymer (Flexitime, Correct Flow) to provide a border for the PDMS infill (0.5 cm PDMS thickness) and PDMS was poured over the silicon wafer. Trapped air inside the mold was removed by vacuum pumping. Surface air bubbles were carefully removed with a thin needle. The PDMS was then baked for 1 h at 90 °C and carefully removed from the silicon wafer afterwards. Excess material was cut off to produce a rectangular PDMS block with the microchannel. To enhance the stickiness of PDMS on the glass cover slide, it was treated with oxygen plasma (Diener Electronic Zepto, Ebhausen, Germany) with 1 min exposure. Treated PDMS was carefully pressed onto the glass slide and baked for 30 min at 60 °C. The glass slide served as base of the microchannel and sealed it. The circular endings of the microchannels were punctured with a needle and thin metal straws (1 mm diameter) were inserted for connection purposes. One side was connected to the aspirator, with a pressure sensor and the other side was used to pipette a 2 μL droplet of spider hemolymph.
hardener) with a spatula for 1 min in a beaker. Trapped air was removed by vacuum pumping the PDMS inside a desiccator for 15–20 min. A plastic ring was fixed around the silicon wafer with dental polymer (Flexitime, Correct Flow) to provide a border for the PDMS infill (0.5 cm PDMS thickness) and PDMS was poured over the silicon wafer. Trapped air inside the mold was removed by vacuum pumping. Surface air bubbles were carefully removed with a thin needle. The PDMS was then baked for 1 h at 90 °C and carefully removed from the silicon wafer afterwards. Excess material was cut off to produce a rectangular PDMS block with the microchannel. To enhance the stickiness of PDMS on the glass cover slide, it was treated with oxygen plasma (Diener Electronic Zepto, Ebhausen, Germany) with 1 min exposure. Treated PDMS was carefully pressed onto the glass slide and baked for 30 min at 60 °C. The glass slide served as base of the microchannel and sealed it. The circular endings of the microchannels were punctured with a needle and thin metal straws (1 mm diameter) were inserted for connection purposes. One side was connected to the aspirator, with a pressure sensor and the other side was used to pipette a 2 μL droplet of spider hemolymph.
Aspiration experiment
Tubes connected one side of the microchannel to an aspirator (Integra Bioscience 158300 Vacusafe Comfort Plus), commonly used in cell biology to create suction. A 2 μL sample droplet was carefully pipetted to the other end of the microchannel before opening the valve of the aspirator to suck the sample through the microchannel into the collection chamber at a given pressure. Pressure was recorded by a pressure sensor (RS Store, Panasonic DP102AEP). The aspirator suction pressure was varied from 25 kPa to 60 kPa. Water was used as control. Coagulated hemolymph was avoided for the experiments. After each experimental run with spider hemolymph, the channel was rinsed with water and dried.Mathematical model
The total sum of energy along a streamline of a flowing incompressible fluid is constant and consists of kinetic energy Ekin, potential energy Epot and enthalpy H. The enthalpy H consists of internal energy U (heat-dependent) and the work to move a volume V at pressure P.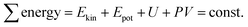 | (1) |
Neglecting thermal energy loss and the resulting internal energy (U = 0), the Bernoulli principle for pipe flow can be expressed as
For any two points along a pipe the energy remains the same and the Bernoulli equation follows as:
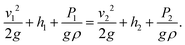 | (2) |
This equation, however, does not consider viscous dissipation, which results in a loss of energy between the two points, or head loss HL, described by the Darcy–Weisbach equation:
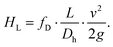 | (3) |
The head loss HL is influenced by the distance L between the two points, pipe hydraulic diameter Dh, and average fluid velocity v, as well as the friction of the pipe walls, represented by the empirical Darcy friction factor fD.
The extended Bernoulli equation can be now formulated as:
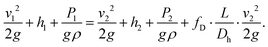 | (4) |
In horizontal pipes, as is the case for our microchannel, the elevation does not change along the pipe (h1 = h2). However, due to a high pressure gradient and elastic, polymeric material, the height differs along the channel (cf. Channel height deformation) leading to a difference in velocity (v1 ≠ v2). Following mass conservation, the average velocities are related, or:
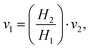 | (5) |
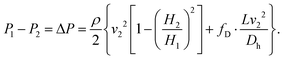 | (6) |
The Darcy friction factor fD depends on pipe geometry and material, represented by β, and the fluid flow Reynolds number Re, which is affected by the fluid viscosity μ29 so that
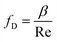 | (7) |
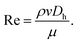 | (8) |
The hydraulic diameter Dh is given by the cross-sectional area A and the perimeter Pe of the cross-section:
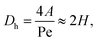 | (9) |
| ΔP·Across = τw·Awall | (10) |
| ΔP·W·H = τw·2·(WL + HL) | (11) |
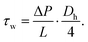 | (12) |
By integrating eqn (6) together with (7) and (8), and substituting for ΔP into (12), the following relationships can be expressed:
τw = μ·![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) a + τ0. a + τ0. | (13) |
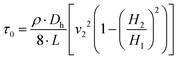 | (14) |
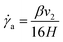 | (15) |
In our experiments, we calibrated β using water, given its known properties. This parameter has been previously observed to vary across a wide range for channels with low aspect ratios like those used in this study, or β = 56–320.30 This factor has been observed to be largely influenced by uncertainties in channel geometry and losses from inlets and outlets and developing flow regions. Our calibration with water resulted in β = 40, which should account for such uncertainties and minor losses.
For Newtonian fluids, the apparent shear rate and viscosity determine the wall shear stress as it is normally described by the Hagen–Poiseuille relation. In our case, the Ostwald–de Waele equation is a better choice as it also covers power law (or non-Newtonian) fluids:
τw = K·![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) nw + τ0 nw + τ0 | (16) |
μa = K·![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n−1w. n−1w. | (17) |
The wall shear stress and the apparent dynamic viscosity thereby depend directly on the wall shear rate, the dimensionless flow behavior index n and the flow consistency index K. For n = 1, the apparent viscosity does not depend on the shear rate, corresponding to Newtonian fluids. For values not equal to 1, the fluid exhibits shear-thickening or shear-thinning behavior.
To calculate the relation between the apparent and wall shear rate, the Weissenberg–Rabinowitsch correction for slit shaped channels can be used:
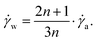 | (18) |
This relation can directly be integrated into the Ostwald–de Waele relation (16) and a linear fit through a log–log plot of the experimental data can be created.
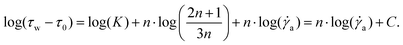 | (19) |
The apparent shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) a is directly proportional to the measured velocity v2 = v with experimental variance. The wall shear stress τw is only dependent on the pressure gradient, which is set and shows only minimal sensor errors. This means that for ordinary least square fitting methods the more accurate value needs to be on the x-axis to avoid fitting mistakes, or:
a is directly proportional to the measured velocity v2 = v with experimental variance. The wall shear stress τw is only dependent on the pressure gradient, which is set and shows only minimal sensor errors. This means that for ordinary least square fitting methods the more accurate value needs to be on the x-axis to avoid fitting mistakes, or:
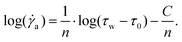 | (20) |
By using formula (16), the wall shear rate can then be fitted to calculate the flow consistency index and finally the dynamic viscosity (eqn (17)), or:
log(τw − τ0) = log(K) + n·log(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w) w) | (21) |
| K = 10intercept·(−n). | (22) |
Channel height deformation
Since the microfluidic channels used in the aspiration experiments were fabricated using an elastic polymer, i.e., polydimethylsiloxane (PDMS), the high pressures applied may deform the channels and affect their geometry during measurements. To determine how channel geometry could be affected by the suction pressures, numerical simulations using COMSOL Multiphysics (version 5.4) were conducted. The Structural Mechanics module with Solid Mechanics physics interface was used to determine the possible deflection of the inner walls of the channel when pressures ranging from 25–60 kPa were applied.The geometry consisted of a PDMS block 10 mm wide, 35 mm long, and 6 mm thick. The channel with width W, length L, and height H was subtracted from the bottom of the PDMS block, following the depiction in Fig. 7A. Since the PDMS block was bonded to a glass surface, the outer wall at the bottom of the block was prescribed a fixed constraint boundary condition, which fixed the deflections to zero. The other outer walls were prescribed as Free, where no loads or deflections are prescribed. For the inner walls of the channel, the Boundary Load boundary condition was prescribed with a linearly varying load to represent the pressure gradient ΔP applied during experiments. Here, the pressures applied at the outlet ranged from 25–60 kPa with 5 kPa increments, while the pressure at the inlet was fixed at zero (or atmospheric).
The built-in PDMS material was used with the Young's modulus specified at 1.35 MPa, following previous measurements with the same preparation protocol.31 The average deflection of the top wall of the channel where the observations were made, or halfway along the channel, was found to vary between 3–7 μm for the applied pressures. Therefore, the height of the channel at the inlet H1 = H = 70 μm, while the height where the velocity is measured H2 = 65 μm, to account for the deformation.
Results and discussion
Three-dimensional reconstruction of femur-patella joint
The hydraulic mechanism of spiders has been investigated since the early 1940s.1 Still, state-of-the art technologies can reveal new insights of its functioning. The femur-patella joint plays an important role in the jumping process of the studied jumping spiders Phidippus regius (Fig. 1). Although computerized tomography (CT) scans of spiders and spider legs have been conducted in the past,3,16,32 the resolution was either too low to capture detailed information about the inner construct or the femur-patella leg was often not scanned in an extended position, as spiders usually flex their legs after death. Using our preparation method13 and enhancing the contrast with iodine, these issues have been resolved. Detailed scans of a small, focused window of the sample (femur-patella joint) were obtained using high-resolution X-ray scanning at the synchrotron in Karlsruhe, Germany. We present such detailed scans of the inner and outer tomography in Fig. 4 and Movie S1 (ESI†).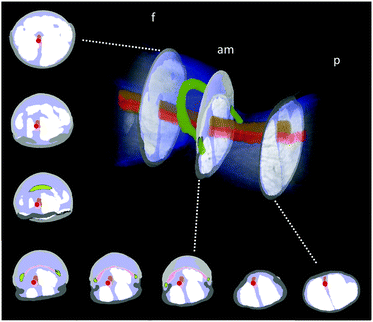 | ||
| Fig. 4 X-Ray reconstruction of the femur-patella joint. The leg segments are filled with flexor muscles (white) that pull on the arcuate sclerite (green). The articular membrane am, spanned between the two leg segments (femur f and patella p), forms a chamber that is filled with hemolymph during extension. The main artery (red) does not feed into this chamber, but is defined by a clear, separating wall (ESI† and Fig. 2) and runs along the nerve chords (brown). Empty spaces (lacunae, blue) are filled with oxygen-poor hemolymph that is transported back towards the body. | ||
These scans form a detailed, non-invasive addendum to the drawings of histological cross sections done in the past and used for simulation purposes. The arcuate sclerite (Fig. 4, green) seems to play an essential role as it connects the articular membrane to the patella segment (pink), partially forms the extension pocket and works as an attachment point for the flexing muscles (white). The femur segment is filled with muscles and at least two nerve cords (brown) run down the leg33 (Fig. 4).
While the 3D scan of deceased animals provides high-resolution information about the joint and the volume distribution of muscles and nerves, the fluid flow path and the flow direction can only be estimated, supplementing the previous literature.2,18 The main artery (Fig. 4, red) is formed by a thin wall, which is partially collapsed in the 3D scan (cf. Materials and methods: X-ray microtomography and Fig. 2) and needed to be manually reconstructed. Therefore, the size of arteries can only be approximated in these types of scans. Recently, Liu et al. used 3D CT-scan data to simulate fluid velocity inside the joint using computational fluid dynamics (CFD).16 However, the simulation was based on several assumptions, which were lacking in the literature, such as the flow direction and viscosity of the hemolymph.
Visualization and analysis of fluid flow inside the femur-patella joint
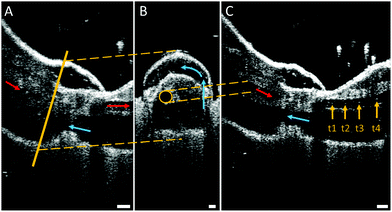
While the flow into the heart of tarantulas has been studied using magnetic resonance imaging (MRI) with a contrast medium, observations inside their legs and joints are lacking. For this reason, high-resolution optical coherent tomography (OCT) has been conducted to look inside the spider leg. This method has been used to observe the heart beat of Drosophila flies34 and air bubbles floating inside locust hearts,35 and does not require any contrast medium. However, limitations in penetration depth of OCT limit the field of view due to the thickness of the exoskeleton. For this reason, we used juvenile spiders with smaller leg diameters. The live and conscious spider was affixed onto a Petri dish to observe the speed and direction of hemolymph flow inside the femur-patella joint (Fig. 5 and Movie S2, ESI†).As the articular membrane is only a few tens of micrometres thick (30–60 μm),13 the penetration depth of the OCT was enough to observe inside of the joint. Although hemolymph consists mostly of water, which cannot be detected by the OCT, small particles flowing inside the arteries could be observed. The size of these particles correspond to the size (10–50 μm) of the free floating cells (hemocytes) inside the hemolymph.8 By tracking these particles, the average fluid velocity could be estimated, similar to particle image velocimetry (PIV) techniques. While previous fluid flow measurements were limited in the temporal resolution of their recording devices,35 the OCT recorded at 76 kHz, and revealed an average cell speed of 3.37 m s−1 (median: 2.67, std: 2.29, N = 36). With a leg artery diameter of 70–100 μm, this speed corresponds to a shear rate of approximately (25–40) × 103 s−1, which is 100 times higher than previous estimates.26
Fluid flow was observed in the chamber formed between the femur-patella joint by the articular membrane. The flow exhibited a circular motion (Fig. 5B and Movie S2, ESI†) and sometimes even stopped. Furthermore, the chamber seemed to be filled by fluid travelling back from distal segments (Fig. 6). Observations on the muscles pulling on the arcuate sclerite (cf.Fig. 4, green) lead us to believe that it may function as a valve that allows continuous fluid flow when the joint is extended. However, this observation needs to be carefully investigated in future studies.
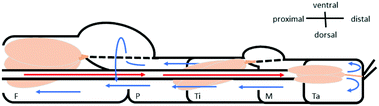 | ||
| Fig. 6 Schematic of the fluid flow inside the spider leg. The main artery transports the oxygen-rich hemolymph from the body into the distal part of the leg (red arrows). Hemolymph then flows back towards the body (blue arrows) along non-defined spaces (lacunae) between the muscles (beige) and nerves. The hemolymph travels mostly along the outer sides of the leg, however a circular flow filling up the femur F–patella P–joint chamber could be observed (see Fig. 5B). | ||
Rheological analysis of spider hemolymph by aspiration measurements
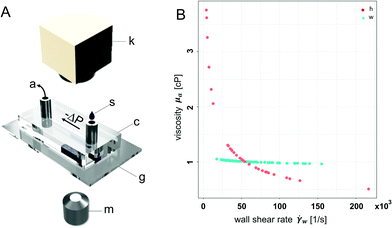
To analyze the physical properties of spider hemolymph under physiological conditions, we modified the experimental set-up used by Trejo-Soto et al.36 in order to allow measurements of small samples (2 μL) at much higher pressures and shear rates (Fig. 7).The samples were transported through a microchannel (height H = 70 μm, width W = 1 mm, length L = 30 mm, hydraulic diameter Dh = 2H = 140 μm) using different pressure differences −ΔP = 25–60 kPa created by an aspirator. Using high-speed videography at 5000 fps, the flow velocities v of hemolymph and water (as a control) within the micro channel were observed. The measured mean velocities v averaged over the cross-sectional area of the channel variate between 0.8–4.6 m s−1 depending on the applied pressure. As biological fluids are typically non-Newtonian, we could not use the standard Hagen–Poiseuille relation. Therefore, the following relations were used to calculate the wall shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w and wall shear stress τw given flow velocity v and pressure difference ΔP (cf. Materials and methods: Mathematical model with v2 = v):
w and wall shear stress τw given flow velocity v and pressure difference ΔP (cf. Materials and methods: Mathematical model with v2 = v):
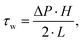 | (23) |
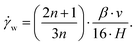 | (24) |
Following the Ostwald–de Waele relation and Weissenberg–Rabinowitsch correction,29,37 the flow behaviour index n and consistency index K can be derived through:
τw = K·(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w)n + τ0, w)n + τ0, | (25) |
μa = K·(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w)n−1. w)n−1. | (26) |
The experimental data of the spider hemolymph show a behaviour index n = 0.51, which coincides with shear-thinning behaviour. This means that with higher shear rates, the viscosity decreases. For our control fluid, water, we show a behaviour index n = 0.96, which is close to unity and corresponds to its Newtonian nature. While we used water to calibrate the friction losses for the microfluidic channel (cf. Materials and methods: Mathematical model), this calibration does not influence the behaviour index n. Therefore, the general fluid behaviour can be reflected by this experimental set-up.
For spider hemolymph, the measured viscosity values vary from μa = 2.7–3.7 cP at shear rates close to zero down to μa = 0.6–0.8 cP at wall shear rates of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) w = 105 s−1. This fluid behaviour corresponds to measurements of the caterpillar Manduca sexta, which shows a viscosity between 3.5 to 2.5 cP for shear rates between 100 to 900 s−1.26 While Kenny et al. studied the physical properties of a large amount of collected caterpillar hemolymph at different temperatures and low shear rates, the effects of physiologically-relevant pressures gradients have not been previously investigated. Our measurements were able to cover the high shear rates of the flows observed in live spiders. In spider locomotion, hemolymph pressure increases during activity.
w = 105 s−1. This fluid behaviour corresponds to measurements of the caterpillar Manduca sexta, which shows a viscosity between 3.5 to 2.5 cP for shear rates between 100 to 900 s−1.26 While Kenny et al. studied the physical properties of a large amount of collected caterpillar hemolymph at different temperatures and low shear rates, the effects of physiologically-relevant pressures gradients have not been previously investigated. Our measurements were able to cover the high shear rates of the flows observed in live spiders. In spider locomotion, hemolymph pressure increases during activity.
The actuation principle of spiders has become very interesting for bio-inspired robotic research over the last decades.3,13 While the viscosity and fluid behaviour has been assumed to be Newtonian and similar to water,12,16 our results may shed light onto the advantage of the non-Newtonian behaviour of hemolymph for multi-functional purposes in spiders. In spiders, the dual function of hemolymph as oxygen-supply for organs, but also as medium for hydraulic extension has led to many questions regarding the efficiency of the hydraulic system.38 The shear-thinning behaviour could allow a uniform and effective oxygen transport during resting as high viscosity at low pressures would achieve high volumetric efficiency.39,40 However, during activity, when the pressure is increased, high viscosity could lead to high shear dissipation and even cavitation. A lower viscosity could help avoid these undesired consequences and increase the hydro mechanical efficiency.39 While the viscosity of hydraulic fluids is usually chosen for a specific operating pressure and temperature, the advantage of non-Newtonian fluids for hydraulic actuators has not been tested in detail.41 The increase in interest for soft fluidic actuators42 could benefit from a deeper understanding of hemolymph and other complex biological fluids.
Conclusions
In this work we investigated the hydraulic fluid (hemolymph) of jumping spiders. We presented the 3D reconstruction of the femur-patella leg joint, which is hydraulically extended during jumping, and studied the internal flow of hemolymph within the joint and leg, as well as its rheological properties. Our results showed that the cells inside the fluid travel with speeds of 2–4 m s−1, which correspond to very high fluid shear rates ∼O(104–105) s−1. Our experimental analysis revealed that the fluid exhibits shear-thinning behaviour. This observation could be interesting for hydraulic systems that operate at wide ranges of pressures and flow speeds.Author contributions
C. Göttler: conceptualization, methodology, validation, formal analysis, investigation, resources, data curation, writing – original draft and visualization; G. Amador: conceptualization, methodology, validation, formal analysis, writing – review & editing, supervision for hemolymph experiments; T. v. d. Kamp and M. Zuber: methodology, validation, supervision for tomography scan; L. Böhler: data acquisition of OCT experiments (support); R. Siegwart: project administration, resources and supervision; M. Sitti: project administration, writing – review & editing, resources and supervision.Conflicts of interest
Authors declare no competing interest competing interests.Acknowledgements
We would like to thank Nagaraj Krishna-Subbaiah, Anitha Shiva and Joshua Giltinan for fabrication support of PDMS micro channels, Janes Odar and Philipp Lösel for advice in usage of 3D reconstruction tools, Karin Elflein for support in testing hemolymph extraction methods, and Thorsten Göttler for assisting in aspiration experiments. We further acknowledge the KIT light source for provision of instruments at their beamlines and we would like to thank the Institute for Beam Physics and Technology (IBPT) for the operation of the storage ring, the Karlsruhe Research Accelerator (KARA). This work was funded by the Max Planck Society (C. G., G. A., L. B., M. S.), ETH Zurich (C. G., R. S.), the Max Planck ETH Zurich Center for Learning Systems (C. G.), and the 4TU.Federation (G. A.). Open Access funding provided by the Max Planck Society.Notes and references
- C. H. Ellis, Biol. Bull., 1944, 86, 41–50 CrossRef.
- R. Blickhan, J. Biomech., 1986, 19, 375–384 CrossRef CAS.
- S. Landkammer, F. Winter, D. Schneider and R. Hornfeck, Robotics, 2016, 5, 15 CrossRef.
- C. S. Wirkner and K. Huckstorf, Spider Ecophysiology, Springer, 2013, pp. 15–27 Search PubMed.
- K. Huckstorf, G. Kosok, E.-A. Seyfarth and C. S. Wirkner, Zoologischer Anzeiger-A Journal of Comparative Zoology, 2013, 252, 76–87 CrossRef.
- J. Runge and C. S. Wirkner, Zool. J. Linn. Soc., 2019, 186, 353–384 CrossRef.
- L. Kuhn-Nentwig and W. Nentwig, Spider Ecophysiology, Springer, 2013, pp. 81–91 Search PubMed.
- L. Kuhn-Nentwig, L. S. Kopp, W. Nentwig, B. Haenni, K. Streitberger, S. Schürch and J. Schaller, Dev. Comp. Immunol., 2014, 43, 59–67 CrossRef CAS PubMed.
- D. A. Parry, Q. J. Microsc. Sci., 1957, 3, 331–340 Search PubMed.
- D. Maruzzo and F. Bortolin, Arthropod Biology and Evolution, Springer, 2013, pp. 149–169 Search PubMed.
- J. Anderson and K. Prestwich, Z. Morphol. Tiere, 1975, 81, 257–277 CrossRef.
- D. Parry and R. Brown, J. Exp. Biol., 1959, 36, 423–433 CrossRef.
- C. Göttler, K. Elflein, R. Siegwart and M. Sitti, Adv. Sci., 2021, 2003890 CrossRef PubMed.
- D. Parry and R. Brown, J. Exp. Biol., 1959, 36, 654–664 CrossRef.
- L. Zentner, Spider Ecophysiology, Springer, 2013, pp. 451–462 Search PubMed.
- C. Liu, S. Chen, C. Sheng, P. Ding, Z. Qian and L. Ren, J. Comp. Physiol., A, 2019, 205, 491–504 CrossRef PubMed.
- V. Pavlov, B. Rosental, N. F. Hansen, J. M. Beers, G. Parish, I. Rowbotham and B. A. Block, Science, 2017, 357, 310–314 CrossRef CAS PubMed.
- C. Kropf, Spider Ecophysiology, Springer, 2013, pp. 43–56 Search PubMed.
- G. Farley, M. Wise, J. Harrison, G. Sutton, C. Kuo and S. Patek, J. Exp. Biol., 2019, 222(15) DOI:10.1242/jeb.201129.
- T. Wallin, J. Pikul and R. Shepherd, Nat. Rev. Mater., 2018, 3, 84–100 CrossRef.
- A. Cecilia, A. Rack, P.-A. Douissard, T. Martin, T. dos Santos Rolo, P. Vagovič, E. Hamann, T. van de Kamp, A. Riedel and M. Fiederle, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2011, 648, S321–S323 CrossRef CAS.
- M. Vogelgesang, T. Farago, T. F. Morgeneyer, L. Helfen, T. dos Santos Rolo, A. Myagotin and T. Baumbach, J. Synchrotron Radiat., 2016, 23, 1254–1263 CrossRef PubMed.
- M. Vogelgesang, S. Chilingaryan, T. dos Santos Rolo and A. Kopmann, 2012 IEEE 14th International Conference on High Performance Computing and Communication & 2012 IEEE 9th International Conference on Embedded Software and Systems, 2012, pp. 824-829.
- P. D. Lösel, T. van de Kamp, A. Jayme, A. Ershov, T. Faragó, O. Pichler, N. T. Jerome, N. Aadepu, S. Bremer and S. A. Chilingaryan, et al. , Nat. Commun., 2020, 11, 1–14 Search PubMed.
- C. Damrau, N. Toshima, T. Tanimura, B. Brembs and J. Colomb, Front. Syst. Neurosci., 2018, 11, 100 CrossRef PubMed.
- M. C. Kenny, M. N. Giarra, E. Granata and J. J. Socha, J. Exp. Biol., 2018, 221, 1–17 Search PubMed.
- U. Theopold, O. Schmidt, K. Söderhäll and M. S. Dushay, Trends Immunol., 2004, 25, 289–294 CrossRef CAS.
- S. Vanin, L. Bubacco and M. Beltramini, CryoLetters, 2008, 29, 485–491 CAS.
- Y. Son, Polymer, 2007, 48, 632–637 CrossRef CAS.
- M. E. Steinke and S. G. Kandlikar, Int. J. Therm. Sci., 2006, 45, 1073–1083 CrossRef CAS.
- Z. Ye, G. Z. Lum, S. Song, S. Rich and M. Sitti, Adv. Mater., 2016, 28, 5088–5092 CrossRef CAS PubMed.
- M. R. A. Nabawy, G. Sivalingam, R. J. Garwood, W. J. Crowther and W. I. Sellers, Sci. Rep., 2018, 8, 1–15 CAS.
- R. Foelix, Biology of Spiders, OUP, USA, 2011 Search PubMed.
- M. A. Choma, S. D. Izatt, R. J. Wessells, R. Bodmer and J. A. Izatt, Circulation, 2006, 114, e35–e36 CrossRef PubMed.
- W.-K. Lee and J. J. Socha, BMC Physiol., 2009, 9, 1–11 CrossRef PubMed.
- C. Trejo-Soto, E. Costa-Miracle, I. Rodriguez-Villarreal, J. Cid, M. Castro, T. Alarcon and A. Hernandez-Machado, Soft Matter, 2017, 13, 3042–3047 RSC.
- S. K. Tiwari, S. Bhat and K. K. Mahato, Sci. Rep., 2020, 10, 1–14 CrossRef PubMed.
- R. S. Wilson, Z. Morphol. Oekol. Tiere, 1970, 68, 308–322 CrossRef.
- B. Vanwalleghem, C. Dousy, G. Pinte and B. Vanseveren, Optimization of the efficiency of hydrostatic drives, 8th International Fluid Power Conference, Dresden, 2012 Search PubMed.
- S. R. Singireddy and S. Javalagi, Hydraulic fluid properties and its influence on system performance, Linköping University, Fluid and Mechatronic Systems, 2012,(MSc Thesis) Search PubMed.
- M. F. Ahamed and S. Chauhan, Bonfring International Journal of Industrial Engineering and Management Science, 2016, 6, 135–139 CrossRef.
- G. M. Whitesides, Angew. Chem., Int. Ed., 2018, 57, 4258–4273 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: See pages following main text and attached movies. See DOI: 10.1039/d1sm00338k |
| This journal is © The Royal Society of Chemistry 2021 |