Open Access Article
Open Access ArticleLong-range order in quadrupolar systems on spherical surfaces†
Andraž
Gnidovec
 * and
Simon
Čopar
* and
Simon
Čopar

University of Ljubljana, Faculty of Mathematics and Physics, SI-1000 Ljubljana, Slovenia. E-mail: andraz.gnidovec@fmf.uni-lj.si
First published on 23rd April 2021
Abstract
The interplay between curvature, confinement and ordering on curved manifolds, with anisotropic interactions between building blocks, takes a central role in many fields of physics. In this paper, we investigate the effects of lattice symmetry and local positional order on orientational ordering in systems of long-range interacting point quadrupoles on a sphere in the zero temperature limit. Locally triangular spherical lattices show long-range ordered quadrupolar configurations only for specific symmetric lattices as strong geometric frustration prevents general global ordering. Conversely, the ground states on Caspar–Klug lattices are more diverse, with many different symmetries depending on the position of quadrupoles within the fundamental domain. We also show that by constraining the quadrupole tilts with respect to the surface normal, which models interactions with the substrate, and by considering general quadrupole tensors, we can manipulate the ground state configuration symmetry.
1 Introduction
One of the central concepts in studying the electrostatic interactions between building blocks of matter is the multipolar expansion of electric and magnetic potentials. The significant terms in this expansion depend on the charge or polarization distribution, as well as the shape of interacting particles.1 Objects with high symmetry only have a small number of nonvanishing multipolar moments and the expansion can be truncated after the first significant term as subsequent contributions are often small in comparison. In many cases, however, higher multipole contributions can have a determining effect on system behavior. They play an important role in nonlinear optical phenomena,2 interactions between molecules3,4 and can significantly alter orientational configurations in 2D magnetic systems.5–7 Furthermore, multipolar interactions are highly relevant in many systems of colloidal nanoparticles where they influence their self-assembly.8–12 While interactions in these systems are most commonly dipolar, particles with induced higher order interactions, such as the quadrupolar interaction, expand the assembly possibilities beyond the head-to-tail configurations typical for dipoles.13–15 At larger scales, quadrupolar assemblies were also recently shown to enable programmable actuation in magnetic metamaterials.16An important class of systems interacting predominantly via multipole interactions are molecular adsorbates of H2, N2, O2 or CO,17–27 molecular crystals,28,29 and adsorbates of some organic molecules,30 where quadrupole moments of positionally fixed building blocks dictate the orientational ordering in the system. The energetically preferred configuration of two quadrupoles is the mutually orthogonal T-configuration. This leads to high geometrical frustration in systems where the symmetries of interaction and lattice are not compatible, e.g. quadrupolar glasses31–33 and systems of quadrupoles on 2D triangular lattices. Such systems consequently show complex orientational ordering in low temperature states, as well as rich phase behavior. As found from theoretical considerations17,24,34 and corroborated by simulations,18,35,36 the ground state of a quadrupolar system on a triangular lattice is a long-range ordered pinwheel structure. If additional interaction with the substrate is present that favors in-plane ordering of quadrupoles, the ground state assumes the herringbone structure instead.17,36–38
Whereas the behavior of systems with multipolar interparticle interactions is well understood in Euclidean geometries, in recent years there has been a general surge of interest in systems on curved surfaces governed by different anisotropic interactions. Curved interfaces and anisotropy are in the forefront of colloidal systems aiming for self-assembly and drug delivery.39–42 The sphere in particular is one of the prototype systems to study the effects of curvature on system behavior due to its constant positive curvature.43 Many artificial or biological agents are generally spherical in shape, and often possess high rotational symmetry.44–47 Symmetry breaking in otherwise symmetric structures can also aid in self-assembly.48 Intriguing structural order supported by curvature and interaction anisotropy emerges in liquid crystals,49,50 dynamical systems51,52 and thin magnetic spherical shells.53–55 Furthermore, orientational ordering in systems with pure multipolar interaction, specifically the dipole–dipole interaction, has also recently been studied on spherical lattices.56,57 It was shown that the local positional order and the symmetry of the lattice play a fundamental role in determining the symmetries of the ground state and excited state configurations.
The absence of translational symmetry was previously shown to break long-range ordering in some 2D systems of quadrupoles.58 As spherical lattices lack any translational symmetries and also require the presence of structural defects due to its nonzero Euler characteristic, the pinwheel and herringbone quadrupole global ordering are in general not possible on a sphere even in cases where the lattice locally resembles the triangular lattice. Instead, spherical lattices may possess rotational symmetries, to which the orientational order may conform, or assume a state of lower symmetry. Theoretical studies of systems on spherical lattices are therefore needed to provide further insight on the effects of compactness, curvature and local lattice type on long-range quadrupole ordering.
In this work, we use numerical modeling to examine stable orientational configurations of point quadrupoles, positionally fixed to different spherical lattices. We first define the interaction potential and describe the general parametrization of quadrupole tensors along with simulation methods used to acquire stable configurations. We consider two classes of positional order. As a representative of closely packed, locally triangular lattices, we consider the Thomson lattice, defined as the minimum elecrostatic energy arrangement of equally charged particles. Most particle systems under the effect of isotropic repulsive interactions will result in a qualitatively comparable arrangement. The other considered case are Caspar–Klug (CK) lattices, which have hexagonal local order, and represent order in systems that are either assembled under directional bonds, such as the fullerenes, or under sterically-constrained self-assembly, such as viral capsids and other spherical protein assemblies. CK lattices exhibit icosahedral symmetry, and the Thomson lattices at different particle numbers have different rotational symmetries. We investigate in what way the added quadrupolar order impacts the symmetry, as the symmetric arrangements do not necessarily correspond to the minimum of the interaction energy. Finally, a variant of the problem with constrained tilt between the quadrupoles and the surface normal is considered as it more closely resembles some of the possible experimental realizations.
2 Simulation methods
We consider a system of N point quadrupoles, described by Cartesian tensors {QA} and positionally fixed to lattice points {rA}. The interaction energy functional of the system in units of 1/4πε0 can be written as a quadratic form, | (1) |
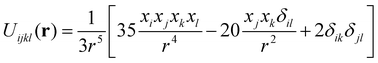 | (2) |
Most commonly, quadrupole moments found in nature are of the rotationally symmetric linear (uniaxial) type with eigenvalues e1= −2e2 = −2e3 = 1. Unless specifically mentioned, this is the type we focus on throughout this paper. For a complete description, we later also consider a continuous parametrization of all possible quadrupole eigentensors, with eigenvalues e1 = 2 + a, e2 = −1 − 2a and e3 = −1 + a where a ∈ [0, 1]. The case of a = 0 corresponds to the linear type whereas a = 1 describes planar quadrupoles with eigenvalues e1 = −e2 = 1 and e3 = 0 which are not extensively studied in literature. In energy calculations, we additionally rescale the parameterized eigenvalues so that Tr(Q2) = 1 which can be formally done by introducing a constraint to minimization of eqn (1).
We parameterize the orientations of uniaxial quadrupoles in their respective local coordinate frames by two angles, azimuthal angle ϕA and polar angle θA. However, this parametrization is not sufficient to describe orientations of biaxial quadrupoles where the description with Euler angles is used instead. We use numerical minimization of energy with respect to the parametrization angles to find the ground state configurations of the system. Our algorithm of choice is the Broyden–Fletcher–Goldfarb–Shanno algorithm which proved effective as well as time efficient in finding the ground state and excited state configurations for smaller system sizes (N < 150). Although previous studies of quadrupolar ordering mostly relied on the simulated annealing Monte Carlo simulations to find the ground state structure of the system,1,58 the use of a deterministic minimization method allows us to more systematically examine some excited state configurations. We performed 1000 minimizations at each N, starting from different random initial conditions to ensure finding the global minimum as well as to find excited states with distinct symmetries. Nevertheless, finding the ground state in this way becomes increasingly difficult with the increase in system size as the number of metastable states grows exponentially with N. The limit N = 150 represents the approximate size above which the deterministic minimization becomes sub-optimal. Difficulties in finding a global minimum numerically arise due to the rough energy landscape. This would also reflect in a physical system where we would most likely find a glassy, disordered state instead of the true ground state.
Finding the true ground state from random initial orientations of quadrupoles can be inconsistent on some non-uniform lattices that deviate strongly from equilateral positional order, due to the fast decay of the interaction strength with the distance that promotes metastable states on such lattices. In particular, this problem emerges for many CK lattices. To circumvent it, we additionally performed minimization simulations with constrained orientational order symmetry, considering all symmetry subgroups of the icosahedral group of the underlying lattice which drastically improves the quality and consistency of the results. Such constrained minimization is also computationally more efficient as imposing symmetries on the resulting orientational order decreases the number of degrees of freedom in the system.
Due to the complex ordering of quadrupolar systems on the sphere, no single order parameter can itself sufficiently quantify the long range order. As we will demonstrate in the following sections, some properties of the quadrupolar systems can be deduced based on the out-of-plane parameter
 | (3) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006b_0302.gif) is the direction of the main quadrupolar axis, evaluating the average of the deviation ξi of quadrupole orientations from tangential ordering. A more comprehensive quantitative approach to differentiate between quadrupolar states with different degrees of ordering is the expansion of their orientations over tensor spherical harmonics.60 This expansion can be defined analogously to the definitions of scalar and vector spherical structure factors used for investigating scalar and vector order on the surface of the sphere.57,61,62 However, comparison between configurations at different N still proves to be challenging because of relatively small system sizes that strongly influence expansion coefficients, especially at higher orders in the expansion. As will be shown in the following sections, long-range order in quadrupolar systems is adequately described by state symmetries and, therefore, tensor spherical harmonic analysis remains beyond the scope of this article.
is the direction of the main quadrupolar axis, evaluating the average of the deviation ξi of quadrupole orientations from tangential ordering. A more comprehensive quantitative approach to differentiate between quadrupolar states with different degrees of ordering is the expansion of their orientations over tensor spherical harmonics.60 This expansion can be defined analogously to the definitions of scalar and vector spherical structure factors used for investigating scalar and vector order on the surface of the sphere.57,61,62 However, comparison between configurations at different N still proves to be challenging because of relatively small system sizes that strongly influence expansion coefficients, especially at higher orders in the expansion. As will be shown in the following sections, long-range order in quadrupolar systems is adequately described by state symmetries and, therefore, tensor spherical harmonic analysis remains beyond the scope of this article.
3 Results
We study the orientational ordering of quadrupoles, positionally fixed to different spherical lattices, and explore the general properties and possible symmetries of the ground state and excited state configurations. First, we focus on closely packed lattices, in particular the Thomson lattice, which is a common reference for a spherical lattice. Its vertex positions and rotational symmetry groups are readily available for most sufficiently low numbers of particles.63 While the Thomson problem refers to finding the lowest energy state of a system of mutually repelling equal electrostatic monopoles, the obtained lattice can be taken as a representative for other locally triangular lattices that have a very similar structure. In ESI,† we additionally show a comparison with the results on the Tammes lattice, constructed by maximizing the minimal distance between points on the sphere, and the Fibonacci lattice. Both the Thomson and Tammes lattices have many distinct symmetries at different system sizes, which is relevant for high symmetry quadrupolar ordering.Fig. 1 shows the dependence of the ground state energies on the size of the underlying Thomson lattice N that determines the positional order in the system. Fitting the power law curve shows scaling as E0 ∝ N3.48, closely matching the exponent estimate of 7/2 calculated from the neighbor distance and energy scalings r ∝ N−1/2 and E ∝ N/r5, respectively. Another quantity showing a distinct trend with increasing system size is the out-of-plane parameter ξ (eqn (3)). Whereas the ground state values, marked by red dots, vary significantly with N, the average values of ξ over all configurations at each N are smaller for bigger systems. Note that in the 2D pinwheel configuration ξ = 1/4 which already shows that the ordering in spherical case is more complex. Additionally, the decrease in ξ with N is consistent with the assumption that in the limit of large system sizes, the role of curvature on ordering is small and the pinwheel structure again becomes the ground state of the system, at least in regions away from disclinations and dislocations.
Large deviations in ground state values of the out-of-plane parameter ξ indicate that there is no general structural order in quadrupolar systems on the Thomson lattice which can be quickly confirmed by examining individual ground state configurations. This is in stark contrast to the dipolar case where a macrovortex configuration was found to be a universal ground state (cf.ref. 56), but it is expected as dipolar configurations are not geometrically frustrated on locally triangular lattices. Nevertheless, we find that many individual configurations with symmetric quadrupolar order are possible on certain lattices with high positional order symmetry, not only in the ground state but also in the excited state configurations.
Some of these structures are presented in Fig. 2 where quadrupoles are colored depending on the inclinations with their respective tangent planes, ξi. More information on ordering at different system sizes is available in ESI.† We first take a look at the ground state configuration for N = 12 with icosahedral positional order. Quadrupoles order in a quasi-vortex configuration with three-fold rotational and inversion symmetries (S6 point group), with all quadrupoles showing considerable out-of-plane ordering. This results in the highest value of ξ among all ground state configurations found, at ξ = 0.520. Similar vortex ordering is possible for N = 14 with D6d positional symmetry, where it actually resembles the pinwheel structure as quadrupoles on the symmetry axis orient radially to the surface. However, this six-fold rotationally symmetric (C6 point group) configuration is not the ground state. In fact, all 8 other configurations found have lower energies and are less symmetric; the ground state has no symmetries and three other excited states show C2 symmetry (the symmetry axis is the same as for the C6 case, but is only two-fold).
Increasing the system size, we find many other cases of axial symmetries both for the ground state and excited state configurations. To illustrate this, we show the ground state configurations belonging to C4 point group found on the octahedral N = 48 lattice and S10 point group on the icosahedral N = 32 lattice. The latter includes two pinwheels centered at the poles of the sphere. Note that some excited states for the N = 48 lattice show other symmetries as well, i.e. D4, C2 and C3. We can find intriguing configurations also for the case of N = 78 with tetrahedral positional symmetry. The quadrupolar ground state is not shown here as it is less interesting with only C2 symmetry and excited states showing higher degrees of orientational ordering. In particular, the S6 configuration is structurally similar to the ground state of N = 12 with quasi-vortex ordering and the highest value of the out-of-plane parameter at this system size, ξ = 0.438. In contrast, we also find a configuration where ordering gravitates towards a pure pinwheel structure, though some quadrupoles still deviate from in-plane or radial orientations. This provides another demonstration that the long-range nature of quadrupolar interaction influences local ordering on curved surfaces. The configuration belongs to the D2 point group, with three distinct 2-fold rotation axes that are perpendicular to one another, inherited from the tetrahedral group of the positional order.
The last presented configuration in Fig. 2 indicates that pure pinwheel structures could be possible on certain Thomson lattices. This is indeed the case, in Fig. 3 we present three such structures at different system sizes, N = 16 (not the ground state), N = 44 and N = 122. What is more, these quadrupolar configurations preserve the symmetries of their positional order, tetrahedral, octahedral and icosahedral, respectively. It is clear from these configurations that pure pinwheel ordering is not compatible with every Thomson lattice and emerges only for specific arrangements of lattice defects. The perpendicular quadrupoles should be centered at all lattice disclinations (as for N = 122) or completely avoid them (e.g. for N = 16 and N = 44). The arrangement of defects determines if constructing a complete pinwheel lattice is possible with these conditions. It should be pointed out that quadrupoles in these pinwheels deviate slightly from the tangential orientations. Nevertheless, the out-of-plane parameter ξ is significantly smaller for these configurations than the others at the same system size which is also reflected in Fig. 1.
We can relate our results to ordering in molecular adsorbates of nonpolar molecules on fullerene C60. These systems are still actively researched to this date64–67 and represent a spherical analogue of the 2D adsorption cases where quadrupolar interaction between molecules was shown to dictate the orientational order. If quadrupolar moments of adsorbed molecules are high enough (as is the case for H2, N2 and ethylene), the positional order of quadrupoles can become commensurate with the underlying lattice.68,69 For fullerene C60 adsorbates, we get a 1 × 1 commensurate state where all pentagons and hexagons are occupied by exactly one molecule of the adsorbate and the first adsorption shell is considered full.65,69–71 These 32 polygonal centers form exactly the same icosahedral positional configuration as the N = 32 Thomson solution which leads to geometric frustration of their orientations and enables a direct comparison with our results. Orientational order of adsorbed ethylene molecules in such 1 × 1 commensurate configuration was investigated in a molecular dynamics (MD) simulation in ref. 71. Note that while quadrupolar interactions represent only a contribution to interparticle interactions between ethylene molecules, they still significantly influence their orientational ordering.68,72 It was found that at low temperature (1 K), two ethylene molecules orient perpendicular to the surface of the fullerene whereas other 30 lie almost tangentially. This result resembles the quadrupolar ground state configuration presented in Fig. 2, however, our result shows deviations from tangential ordering for quadrupoles around the equator. This discrepancy can be attributed mainly to interactions with the substrate that promote tangential ordering. More precise calculations should also take into account that the ethylene molecule is not rotationally symmetric and modeling with linear quadrupoles is just an approximation. We will further comment on the solutions for constrained particle inclinations and different quadrupole tensors in Section 3.2. Moving away from the specific case of ethylene adsorbates, it was shown that in multilayered systems, molecules in outer layers can have higher degrees of rotational freedom compared to those in the first layer that prefer in-plane ordering.73 Orientational order in full and closely packed higher shells, adsorbed on fullerene C60, could therefore more closely match our simulation results (at some N > 32).
We showed that certain symmetric Thomson lattices support long-range ordered symmetric quadrupolar configurations, however, these should be searched for on per lattice basis. Examining stable configurations on the Tammes and Fibonacci lattices, we further confirm this observation (see ESI†). The Tammes lattice is similar to the Thomson lattice, i.e. it is locally composed of close-to-equilateral triangles. This characteristic was found to be central in determining the orientational order in discrete dipolar systems (cf.ref. 56). In quadrupolar systems on a sphere, it leads to strong geometric frustration, especially considering the topological requirement for lattice defects which act as local points of frustration. The ordering on the Tammes lattice is expectedly similar to the results presented above, with long-range ordered quadrupolar configurations only at specific system sizes, confirming that the exact positional order is less important than its global properties such as the symmetry. On the other hand, quadrupolar ordering changes if the lattice deviates systematically from local triangular order. An example is the Fibonacci lattice, where for high enough system sizes, it locally resembles the square lattice around the equator and, consequently, for N ≳ 70 the quadrupoles order in the local windmill configuration. The same ordering was found in the mean-field calculations for the 2D square lattice.37 On the poles of the Fibonacci lattices where positional order is highly irregular, long-range quadrupolar order is again absent.
3.1 Icosahedral Caspar–Klug lattices
The symmetry of the quadrupolar order is limited by the symmetry of the underlying lattice. Investigation of stable states on the Thomson lattices showed some symmetries in both the ground states and excited states. We further explore the role of local order and global positional arrangement on quadrupolar configurations by examining ordering on the CK lattices74–76 where we can manipulate local positional order while retaining the icosahedral lattice symmetry. We focus on CK lattices with the triangulation parameters (n, m) = (1, 0), resulting in system size N = 60, at different values of parameters (u,v) that determine the positions of quadrupoles inside the fundamental domain (see ref. 57 for more information on the parameterization). These lattices are intrinsically non-uniform, with vacancies in the positional order even in the equidistant cases (constant nearest neighbor distances) which leads to ordering that is markedly different than in the Thomson case studied above.Quadrupolar ground states on some equidistant CK lattices are presented in Fig. 4, marked as A (truncated icosahedron), B (small rhombicosidodecahedron) and C (snub dodecahedron). The lattice A supports an icosahedral quasi-pinwheel structure around each vertex (five-fold axis) of the icosahedron, with a missing perpendicular central quadrupole. Quadrupoles are oriented close to their tangential planes which results in ξ ≈ 0.1, a value much lower than for any configuration on Thomson lattices. The configuration on the lattice B is similar to the lattice A, with only the arrangement of the quasi-pinwheels being different. The lattice C, however, does not support any symmetries in the ground state despite equal distances between quadrupoles. It consists of pentagons and equilateral triangles between them which leads to geometric frustration of quadrupole orientations and results in a non-symmetric ground state.
We conducted symmetry analysis of the ground state configurations in dependence to the position of quadrupoles in the fundamental domain as determined by the parameters u and v. To ensure finding the true ground state of the system, we additionally performed energy minimizations with constrained orientational order symmetries. The results are presented in Fig. 4. In the left part of the diagram, quadrupoles are positionally arranged in pentagonal quasi-pinwheel structures around icosahedral vertices, with the spacing between the nearest neighbors increasing as we move towards the right. Fast decay of the quadrupolar interaction strength with the distance makes rotational directions for these pinwheels nearly independent of one-another which leads to configurations with lower symmetries (i.e. different directions of pinwheel rotations) having very similar energies to the icosahedral case.
As we move towards the right side of the diagram and the quasi-pinwheels become closer to one another, their mutual interactions become significant and configurations with uniaxial rotation symmetries, C2, C3 or C5, show lower energies compared to the icosahedral structures. Nevertheless, these still prevail along the top edge of the fundamental domain as we transition towards locally triangular arrangement of particles in the top right part of the diagram. This positional order also supports tetrahedral ground state configurations that occupy part of the top right corner of the fundamental domain. Conversely, ground state configurations in the center and lower right parts of the fundamental domain only show axial symmetries. In the bottom right corner, each quadrupole only has one nearest neighbor, leading to a strong preference for the local orthogonal T-configuration. This effectively precludes tetrahedral and icosahedral configuration symmetry as it is not compatible with two-fold (C2 axis) rotations of the lattice. In the center of the diagram, many ground state configurations show no symmetries. This is attributed to strong geometric frustration as argued already for the case of the lattice C.
In general, the symmetry diagram of quadrupolar ground states on CK lattices qualitatively strongly resembles the one for the dipolar case studied in ref. 57. Icosahedral and tetrahedral configurations are found in the same parts of the fundamental domain (even though they cover slightly larger regions in the quadrupolar case) and there are almost no configurations with dihedral symmetries in the ground state. Nevertheless, the locations of no symmetry regions are different between the dipolar and quadrupolar case, and in the bottom right corner, the C5 and C3 regions are exchanged which is a direct consequence of different preferential orientational configurations for pairs of dipoles and quadrupoles.
Returning back to the quadrupolar case, we plot the values of the out-of-plane parameter ξ (eqn (3)) for ground state configurations in the whole fundamental domain (Fig. 5a). The results in all three corners are as expected, approaching zero in the bottom left and top right corners, for configurations with pentagonal and triangular local arrangements of quadrupoles, respectively, and assuming higher values in the bottom right corner for configurations with pair T-ordering. Approaching the center of the fundamental domain from ξ = 0 in the corners, we observe a gradual increase in ξ, with a more noticeable change towards higher values in the region with no ground state orientational order symmetry. Conversely, some configurations on the edges of the fundamental domain, where the positional order of the lattice is (nearly) equidistant (i.e. around lattices A and B as well as in the middle of the right edge), show close to tangential ordering.
Furthermore, we compare the energies of ground state configurations with the lowest energy icosahedral state on the same lattice. Note that the icosahedral configuration is not stable in general and may decay after the symmetry constraint is lifted, especially in the part of the diagram with non-symmetric ground states. The ratio −Δ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) /
/![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) of the energy difference to the icosahedral state and the energy of the ground state configuration is shown in Fig. 5b. It is small in the bottom left and top right parts of the fundamental domain which shows that reducing the symmetry to tetrahedral or axial does not lead to a substantial decrease in the configuration energy for locally pentagonal and triangular lattices. As expected, the energy difference is proportionally higher in the bottom right corner where quadrupoles order in local T-configurations, as well as in the center of the diagram with no symmetric ground states. There are two distinct peaks of the energy ratio; some configurations between the two also exhibiting symmetries in the ground state as shown in Fig. 4.
of the energy difference to the icosahedral state and the energy of the ground state configuration is shown in Fig. 5b. It is small in the bottom left and top right parts of the fundamental domain which shows that reducing the symmetry to tetrahedral or axial does not lead to a substantial decrease in the configuration energy for locally pentagonal and triangular lattices. As expected, the energy difference is proportionally higher in the bottom right corner where quadrupoles order in local T-configurations, as well as in the center of the diagram with no symmetric ground states. There are two distinct peaks of the energy ratio; some configurations between the two also exhibiting symmetries in the ground state as shown in Fig. 4.
3.2 Constrained solutions and different quadrupole tensors
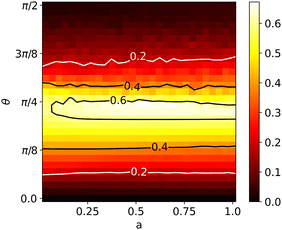
In many real systems, quadrupoles are not free to rotate but are rather constrained around some preferred tilt, dictated by the interaction with the substrate as well as temperature.66,71 Additionally, quadrupole eigentensors can differ from the rotationally symmetric linear type. We examine the dependence of the ground state configuration on the parameter a that determines the quadrupolar eigenvalues, at different fixed inclinations θ between the surface normal and the eigenvector corresponding to the highest eigenvalue e1 = 2 +a. To do so, minimization over two Euler angles for each quadrupole is still required (only the third is constant and fixes the value of θ).Fig. 6 shows a heatmap of the optimal configuration energies in the (a,θ) plane for a quadrupolar system on the N = 72 icosahedral Thomson lattice. Configurations at higher θ on the top of the diagram always show lower energies compared to lower θ configurations. Similarly, we observe a general decrease in energy as quadrupoles transition from the linear (left edge) to the planar (right edge) quadrupole type. Calculating energy heatmaps for quadrupolar systems on lattices of different sizes and types (including the CK lattices), we note that the dependence of energy on parameters a and θ is qualitatively the same. We also visualize the limiting configurations in all four edges of the diagram. The configuration at (0,0) is trivially radial whereas at (0,π/2), quadrupoles form regions with the herringbone orientational order as is also typical on 2D triangular lattices with forced tangential order. At the pentagonal lattice defects, the herringbones change orientational direction. Ordering at (1,0) is similar, as constraining one axis of planar quadrupoles to the radial direction results in the other axis lying tangent to the surface. The solution at (1,π/2) is completely planar with neighboring quadrupoles trying to align perpendicular to one another. Considering only the main (red) axes, we again notice the local herringbone structures.
While Fig. 6 only shows ground state configurations for the limiting cases of the parametrization, the way in which configurations transition from perpendicular to tangential main axis orientation (θ = 0 → θ = π/2) warrants an additional comment. If we consider only the orientations of the tangential components of main axis orientations at increasing inclinations (θ = 0 towards θ = π/2), we notice that for small values of θ, the main axes projections form a quasi-macrovortex. Around θ = π/4, the projected orientations transition towards the herringbone order that then consistently emerges for θ ≳ π/3. This behavior does not depend on the eigenvalues of the quadrupoles (parameter a). Additionally, such orientational order for all configurations of constrained quadrupoles also breaks any rotational symmetry that might emerge for a system of unconstrained linear quadrupoles on the same lattice.
It should be noted that while we constrained the tilt of the main quadrupole axes (red double arrows in Fig. 6) with respect to the surface normal, the orientations of the secondary axes (blue double arrows) are determined by energy minimization and can therefore be tilted out of the tangent plane. We plot the average inclination of the secondary axes ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) i to the surface normal
i to the surface normal  in Fig. 7. The result ν = 0 along the bottom edge of the diagram is trivial, as the secondary axis must be perpendicular to the main axis at a > 0. Along the top edge, there is no constraint for the orientations of the secondary axes, therefore, values of ν close to 0 show that planar ordering is energetically favorable. Conversely, values of ν increase as we approach θ = π/4 in the middle of the diagram. These configurations have both the main and secondary axis strongly tilted from the planar configuration with virtually no dependence on the eigenvalue parameter a (for a > 0). The results for other lattices (including CK lattices) are similar.
in Fig. 7. The result ν = 0 along the bottom edge of the diagram is trivial, as the secondary axis must be perpendicular to the main axis at a > 0. Along the top edge, there is no constraint for the orientations of the secondary axes, therefore, values of ν close to 0 show that planar ordering is energetically favorable. Conversely, values of ν increase as we approach θ = π/4 in the middle of the diagram. These configurations have both the main and secondary axis strongly tilted from the planar configuration with virtually no dependence on the eigenvalue parameter a (for a > 0). The results for other lattices (including CK lattices) are similar.
We argue that locally triangular lattices do not support symmetric configurations of quadrupoles if we constrain their inclinations to θ > 0 or if we consider quadrupoles that deviate from the linear type (a > 0). Geometric frustration that emerges on these lattices, especially as a consequence of lattice disclinations, cannot be offset by different quadrupole tilts as is the case for the symmetric ground states in Fig. 3, leading to a lack of long-range orientational order. In comparison, quadrupoles in many ground state configurations on CK lattices already have the same inclinations and, due to vacancies in the positional order, local herringbone structures do not form on these lattices. This opens up the possibility that long-range ordered symmetric quadrupolar configurations exist on CK lattices also if the orientations are constrained to a specific inclination θ. More specifically, this inclination, as well as the type of the quadrupole given by parameter a, can influence the symmetry of the configuration as shown in Fig. 8 for the equidistant CK lattices A, B and C.
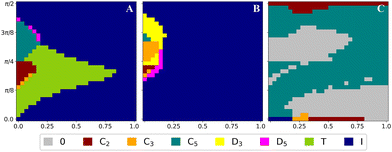 | ||
| Fig. 8 Ground state configuration symmetries for CK lattices A, B and C in dependence to the main axis inclination θ and eigenvalue parameter a (axes are the same as in Fig. 6 and 7). On the lattices A and B, the most common symmetry is the icosahedral symmetry as in the case of freely rotating linear quadrupoles. The lattice A also shows a large tetrahedral region as well as smaller C3 and C5 regions. The C2 and D5 configurations appear to be only transitional. The results on the lattice B are even more diverse in the non-icosahedral part of the diagram, indicating possible minimization imperfections. The lattice C which does not support a symmetric ground state without the constraint to the main quadrupole axes inclinations, assumes the C5 symmetry in a large portion of the parameter space when constrained. | ||
Systems on lattices A and B show icosahedral ground state structures in the majority of the diagram. In both cases, this symmetry breaks along the left edge, i.e. as we increase the tilts of the quadrupoles with respect to the surface normal. For the lattice A, the ground state first transforms into the tetrahedral configuration that also prevails towards the center of the diagram (with increasing a) and, increasing θ even further, we encounter regions with C3 and C5 symmetries. Notice also the narrow C2 and D5 transitional regions. For the lattice B, the part of the diagram without the icosahedral symmetry is subdivided into many smaller regions, possibly indicating that we failed to find the true ground state in all points. Similarly, some imperfections in the simulations are present in the diagram of the lattice C. Despite the lack of symmetry in the ground state of freely rotating linear quadrupoles (Fig. 4) on this lattice, a large part of the diagram for the constrained case shows C5 symmetric ordering. Both inclination extremes, i.e. the radial (θ = 0) and tangential cases (θ = π/2), assume configurations with different symmetries.
4 Conclusions
We investigated the role of local positional order, lattice symmetry, and inclination constraints on the orientational ordering in quadrupolar systems on the surface of the sphere. Triangular local positional order in particular leads to geometric frustration and in general does not support global (long-range) orientational order, as indicated by the solutions on many Thomson and Tammes lattices. However, we have shown that lattice symmetry can stabilize long range order for certain lattices, resulting in quadrupolar configurations with different axial symmetries as well as pure pinwheel configurations with higher symmetry, i.e. tetrahedral, octahedral and icosahedral. Orientational order supported by positional symmetry emerges also in many ground state configurations on CK lattices. The symmetry diagram shows rich behavior that can be directly attributed to the competition between the local geometric frustration and icosahedral lattice symmetry. We further expended the discussion by examining ordering of general quadrupole tensors. Additionally, we constrained the inclinations of the main quadrupole axis to model possible effects of interactions with the substrate. We find that both the inclination and the type of quadrupoles influence the ground state ordering, in particular its symmetry.In real physical systems, interactions are rarely as ideal as presented in this work. Nevertheless, by keeping our discussion as general as possible, the role of quadrupolar interaction on orientational ordering can be analyzed and evaluated in a diverse range of physical systems. In adsorbates of nonpolar molecules on spherical fullerenes, orientational ordering is usually influenced by other interactions besides the quadrupole–quadrupole interaction.64 Most notably, interactions with the substrate can impose preferential tilt of the quadrupoles, leading to some discrepancies with our results. Similar reasoning would apply to adsorbates or flexible chains attached to nanocages or faceted nanoparticles. With complex molecules, such as proteins, the main interactions that govern their positioning and orientations are sterical and local interactions between chemical groups, which are far from quadrupolar. However, in addition to these interactions, electrostatic interactions due to inhomogeneous charge distribution can be expanded and contribute a perturbative term to the free energy. As charge distribution depends on the pH of the solution, these additional interactions can change, and affect the stability and self-assembly of the structure.47 If the building blocks have a head–tail symmetry, such as capsid dimers (e.g. in Flavivirus genus77), the lowest anisotropic contribution will be quadrupolar. In colloidal systems of hard spheres, positional order is also expected to be closely packed and mostly fixed,78 while any additional interactions, such as quadrupolar, can affect orientational order and local structure.79
Our results show the possibility for the construction of systems with the desired orientational order by choosing the appropriate positional lattice and manipulating the inclinations of the quadrupoles. This can be a starting point for self-assembly of spherical structures. On the other hand, modeling of quadrupolar systems at finite temperature, under influence of external fields, or in fluid-like motion, requires a different modeling approach and ultimately focuses not on structure and symmetry, but on dynamical phenomena, which is left as an open question for future investigation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank A. Božič for helpful discussions and suggestions during our research. We acknowledge support by Slovenian Research Agency (ARRS) under contracts P1-0099 and J1-9149. The work is associated with the COST action CA17139.Notes and references
- E. Y. Vedmedenko and N. Mikuszeit, ChemPhysChem, 2008, 9, 1222–1240 CrossRef CAS PubMed.
- Y. R. Shen, Principles of nonlinear optics, Wiley, 2003 Search PubMed.
- A. D. Buckingham, Advances in Chemical Physics, John Wiley & Sons, Inc., 1967, pp. 107–142 Search PubMed.
- G. Birnbaum, Phenomena induced by intermolecular interactions, Plenum Press, 1985 Search PubMed.
- E. Y. Vedmedenko, N. Mikuszeit, H. P. Oepen and R. Wiesendanger, Phys. Rev. Lett., 2005, 95, 207202 CrossRef CAS PubMed.
- M. Ewerlin, D. Demirbas, F. Brüssing, O. Petracic, A. A. Ünal, S. Valencia, F. Kronast and H. Zabel, Phys. Rev. Lett., 2013, 110, 177209 CrossRef PubMed.
- N. Mikuszeit, L. Baraban, E. Y. Vedmedenko, A. Erbe, P. Leiderer and R. Wiesendanger, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014402 CrossRef.
- A. V. Titov and P. Král, Nano Lett., 2008, 8, 3605 CrossRef CAS PubMed.
- D. V. Talapin, E. V. Shevchenko, C. B. Murray, A. V. Titov and P. Král, Nano Lett., 2007, 7, 1213 CrossRef CAS PubMed.
- M. A. Gharbi, M. Cavallaro, G. Wu, D. A. Beller, R. D. Kamien, S. Yang and K. J. Stebe, Liq. Cryst., 2013, 40, 1619–1627 CrossRef CAS.
- A. Baskin, W.-Y. Lo and P. Král, ACS Nano, 2012, 6, 6083 CrossRef CAS PubMed.
- J. Hernández-Rojas, D. Chakrabarti and D. J. Wales, Phys. Chem. Chem. Phys., 2016, 18, 26579–26585 RSC.
- S. Gangwal, A. Pawar, I. Kretzschmar and O. D. Velev, Soft Matter, 2010, 6, 1413 RSC.
- H. Schmidle, S. Jäger, C. K. Hall, O. D. Velev and S. H. L. Klapp, Soft Matter, 2013, 9, 2518 RSC.
- B. Bharti and O. D. Velev, Langmuir, 2015, 31, 7897 CrossRef CAS PubMed.
- H. Gu, Q. Boehler, D. Ahmed and B. J. Nelson, Sci. Robot., 2019, 4, eaax8977 CrossRef PubMed.
- A. J. Berlinsky and A. B. Harris, Phys. Rev. Lett., 1978, 40, 1579–1582 CrossRef CAS.
- S. F. O'Shea and M. L. Klein, Chem. Phys. Lett., 1979, 66, 381–383 CrossRef.
- S. F. O'Shea and M. L. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25, 5882–5888 CrossRef.
- O. G. Mouritsen and A. J. Berlinsky, Phys. Rev. Lett., 1982, 48, 181–184 CrossRef CAS.
- R. P. Pan, R. D. Etters, K. Kobashi and V. Chandrasekharan, J. Chem. Phys., 1982, 77, 1035–1047 CrossRef CAS.
- C. Peters and M. L. Klein, Mol. Phys., 1985, 54, 895–909 CrossRef CAS.
- K. Kim and N. S. Sullivan, J. Low Temp. Phys., 1999, 114, 173–201 CrossRef CAS.
- N. S. Sullivan and K. Kim, J. Low Temp. Phys., 2000, 120, 89–106 CrossRef CAS.
- D. Boyd, F. Hess and G. Hess, Surf. Sci., 2002, 519, 125–138 CrossRef CAS.
- E. A. Ustinov, Carbon, 2016, 100, 52–63 CrossRef CAS.
- E. Ustinov, V. Gorbunov and S. Akimenko, J. Phys. Chem. C, 2018, 122, 2897–2908 CrossRef CAS.
- J. A. Hamida, N. S. Sullivan and M. D. Evans, Phys. Rev. Lett., 1994, 73, 2720–2723 CrossRef CAS PubMed.
- S. Raugei, G. Cardini, V. Schettino and H. Jodl, Chem. Phys., 1997, 106, 8196–8203 CAS.
- N. Kleppmann and S. H. L. Klapp, J. Chem. Phys., 2015, 142, 064701 CrossRef PubMed.
- N. S. Sullivan, M. Devoret, B. P. Cowan and C. Urbina, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17, 5016–5024 CrossRef CAS.
- N. S. Sullivan, Can. J. Chem., 1988, 66, 908–914 CrossRef CAS.
- K. Kim and N. S. Sullivan, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, R664–R667 CrossRef CAS.
- A. B. Harris, O. G. Mouritsen and A. J. Berlinsky, Can. J. Phys., 1984, 62, 915–934 CrossRef CAS.
- M. A. Klenin and S. F. Pate, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 3969–3972 CrossRef CAS.
- L. Mederos, E. Chacón and P. Tarazona, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 8571–8576 CrossRef PubMed.
- V. Massidda and J. Hernando, Phys. A, 1984, 128, 318–333 CrossRef.
- D. Marx, O. Opitz, P. Nielaba and K. Binder, Phys. Rev. Lett., 1993, 70, 2908–2911 CrossRef CAS PubMed.
- K. J. Lee, J. Yoon and J. Lahann, Curr. Opin. Colloid Interface Sci., 2011, 16, 195 CrossRef CAS.
- S. N. Fejer, D. Chakrabarti and D. J. Wales, Soft Matter, 2011, 7, 3553 RSC.
- T. Beck, S. Tetter, M. Künzle and D. Hilvert, Angew. Chem., 2015, 127, 951 CrossRef.
- C. H. J. Evers, J. A. Luiken, P. G. Bolhuis and W. K. Kegel, Nature, 2016, 534, 364 CrossRef PubMed.
- M. J. Bowick and L. Giomi, Adv. Phys., 2009, 58, 449–563 CrossRef CAS.
- D. Bhatia, S. Mehtab, R. Krishnan, S. Indi, A. Basu and Y. Krishnan, Angew. Chem., Int. Ed., 2009, 48, 4134 CrossRef CAS PubMed.
- S.-H. Kim, S.-J. Jeon and S.-M. Yang, J. Am. Chem. Soc., 2008, 130, 6040 CrossRef CAS PubMed.
- M. Engel, P. F. Damasceno, C. L. Phillips and S. C. Glotzer, Nat. Mater., 2015, 14, 109 CrossRef CAS PubMed.
- R. F. Bruinsma and W. S. Klug, Annu. Rev. Condens. Matter Phys., 2015, 6, 245 CrossRef CAS.
- L. E. Perotti, J. Rudnick, R. F. Bruinsma and W. S. Klug, Phys. Rev. Lett., 2015, 115, 862 CrossRef PubMed.
- V. Vitelli and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021711 CrossRef CAS PubMed.
- Y. Li, H. Miao, H. Ma and J. Z. Y. Chen, Soft Matter, 2013, 9, 11461 RSC.
- R. Sknepnek and S. Henkes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022306 CrossRef.
- S. Praetorius, A. Voigt, R. Wittkowski and H. Löwen, Phys. Rev. E, 2018, 97, 70 CrossRef PubMed.
- V. P. Kravchuk, U. K. Rößler, O. M. Volkov, D. D. Sheka, J. van den Brink, D. Makarov, H. Fuchs, H. Fangohr and Y. Gaididei, Phys. Rev. B, 2016, 94, 144402 CrossRef.
- G. Milagre and W. A. Moura-Melo, Phys. Lett. A, 2007, 368, 155–163 CrossRef CAS.
- M. I. Sloika, D. D. Sheka, V. P. Kravchuk, O. V. Pylypovskyi and Y. Gaididei, J. Magn. Magn. Mater., 2017, 443, 404–412 CrossRef CAS.
- A. Gnidovec and S. Čopar, Phys. Rev. B, 2020, 102, 075416 CrossRef CAS.
- S. Čopar and A. Božič, Phys. Rev. Res., 2020, 2, 043199 CrossRef.
- E. Vedmedenko, S. E.-D. Mandel and R. Lifshitz, Philos. Mag., 2008, 88, 2197–2207 CrossRef CAS.
- E. Y. Vedmedenko, Competing interactions and patterns in nanoworld, Wiley-VCH, 2007 Search PubMed.
- K. S. Thorne, Rev. Mod. Phys., 1980, 52, 299–339 CrossRef.
- S. Franzini, L. Reatto and D. Pini, Soft Matter, 2018, 14, 8724–8739 RSC.
- A. Lošdorfer Božič and S. Čopar, Phys. Rev. E, 2019, 99, 032601 CrossRef PubMed.
- D. J. Wales, J. P. K. Doye, A. Dullweber, M. P. Hodges, F. Y. Naumkin, F. Calvo, J. Hernández-Rojas and T. F. Middleton, Cambridge Cluster Database, http://www-wales.ch.cam.ac.uk/CCD.html, accessed: 2021-01-21.
- A. Martínez-Alonso, J. M. D. Tascón and E. J. Bottani, Langmuir, 2000, 16, 1343–1348 CrossRef.
- A. Kaiser, C. Leidlmair, P. Bartl, S. Zöttl, S. Denifl, A. Mauracher, M. Probst, P. Scheier and O. Echt, J. Chem. Phys., 2013, 138, 074311 CrossRef CAS PubMed.
- S. Ralser, A. Kaiser, M. Probst, J. Postler, M. Renzler, D. K. Bohme and P. Scheier, Phys. Chem., 2016, 18, 3048–3055 CAS.
- F. Calvo, E. Yurtsever and A. Tekin, J. Phys. Chem. A, 2018, 122, 2792–2800 CrossRef CAS.
- W. A. Steele, Langmuir, 1996, 12, 145–153 CrossRef CAS.
- O. Echt, A. Kaiser, S. Zöttl, A. Mauracher, S. Denifl and P. Scheier, ChemPlusChem, 2013, 78, 910–920 CrossRef CAS PubMed.
- F. Calvo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 060502 CrossRef.
- S. Zöttl, A. Kaiser, M. Daxner, M. Goulart, A. Mauracher, M. Probst, F. Hagelberg, S. Denifl, P. Scheier and O. Echt, Carbon, 2014, 69, 206–220 CrossRef.
- A. Cheng and M. L. Klein, Langmuir, 1992, 8, 2798–2803 CrossRef CAS.
- M. Golebiowska, L. Firlej, B. Kuchta and R. Fabianski, J. Chem. Phys., 2009, 130, 204703 CrossRef CAS PubMed.
- D. L. D. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1 CrossRef CAS PubMed.
- R. F. Bruinsma and W. S. Klug, Annu. Rev. Condens. Matter Phys., 2015, 6, 245–268 CrossRef CAS.
- S. B. Rochal, O. V. Konevtsova and V. L. Lorman, Nanoscale, 2017, 9, 12449–12460 RSC.
- E. R. Oliveira, R. Mohana-Borges, R. B. de Alencastro and B. A. Horta, Virus Res., 2017, 227, 115 CrossRef CAS PubMed.
- A. B. Subramaniam, M. Abkarian and H. A. Stone, Nat. Mater., 2005, 4, 553 CrossRef CAS PubMed.
- M. Miller, J. Shepherd and D. Wales, Mol. Phys., 2008, 106, 1655 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: More details on quadrupolar configurations at different system sizes, including on the Tammes and Fibonacci lattices. See DOI: 10.1039/d1sm00228g |
| This journal is © The Royal Society of Chemistry 2021 |