 Open Access Article
Open Access ArticleRebound and scattering of motile Chlamydomonas algae in confined chambers†
Albane
Théry
 *a,
Yuxuan
Wang
b,
Mariia
Dvoriashyna
*a,
Yuxuan
Wang
b,
Mariia
Dvoriashyna
 a,
Christophe
Eloy
a,
Christophe
Eloy
 c,
Florence
Elias
c,
Florence
Elias
 b and
Eric
Lauga
b and
Eric
Lauga
 *a
*a
aDepartment of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK. E-mail: at830@cam.ac.uk; e.lauga@damtp.cam.ac.uk
bUniversité de Paris, CNRS UMR 7057, Laboratoire Matière et Systèmes Complexes MSC, F-75006 Paris, France
cAix Marseille Univ., CNRS, Centrale Marseille, IRPHE, 13013 Marseille, France
First published on 16th April 2021
Abstract
Motivated by recent experiments demonstrating that motile algae get trapped in draining foams, we study the trajectories of microorganisms confined in model foam channels (section of a Plateau border). We track single Chlamydomonas reinhardtii cells confined in a thin three-circle microfluidic chamber and show that their spatial distribution exhibits strong corner accumulation. Using empirical scattering laws observed in previous experiments (scattering with a constant scattering angle), we next develop a two-dimension geometrical model and compute the phase space of trapped and periodic trajectories of swimmers inside a three-circles billiard. We find that the majority of cell trajectories end up in a corner, providing a geometrical mechanism for corner accumulation. Incorporating the distribution of scattering angles observed in our experiments and including hydrodynamic interactions between the cells and the surfaces into the geometrical model enables us to reproduce the experimental probability density function of micro-swimmers in microfluidic chambers. Both our experiments and models demonstrate therefore that motility leads generically to trapping in complex geometries.
1 Introduction
Microorganisms display a wide range of mechanisms in order to swim in fluids on small scales.1–3 Although the flagellar structure is a highly conserved trait in both prokaryotic and eukaryotic motile cells, the detailed mechanisms for self-propulsion differ.4 Most bacteria use the passive rotation of helical flagellar filaments by a basal rotary motor.5,6 In contrast, eukaryotic cells swim using active flexible flagella that bend in periodic waves through the coordinated contraction of distributed motor proteins.7,8 Mammalian spermatozoa are propelled by a single flagellum,9 while the model green algal genus Chlamydomonas has two flagella10 and ciliates, such as the model genus Paramecium, are actuated by an array of small synchronised flagella termed cilia.11These diverse swimming mechanisms have been extensively studied, in particular those of model microorganisms with well-established experimental protocols, such as the bacterium Escherichia coli (E. coli)12 or the alga Chlamydomonas reinhardtii (CR).13,14 Along with experimental work, significant theoretical modelling has been developed to quantify and predict the motion of swimming cells.1–3,15 In particular, the flow generated by the breaststroke motion of free-swimming CR cells used in this paper has been quantified experimentally and modelled in the far field using three point forces for the body and two flagella.16–20
The habitat of microorganisms is often far from the idealised bulk fluids considered in model biophysical experiments and theoretical modelling. Cells interact with their surroundings through complex hydrodynamic and steric interactions.21,22 Rigid boundaries, free surfaces and other obstacles in suspensions are known to strongly affect swimming behaviour.23,24 Relevant complex media include thin films,19 porous media such as soil,25 the ovary tract in the case of mammalian spermatozoa,26 or tissues within higher organisms, including the bloodstream27 and gastrointestinal mucus for pathogens.28 Complex environments are therefore ubiquitous in the life of self-propelled microswimmers, and as a result their swimming patterns have been studied both theoretically and experimentally in a wide range of geometries, including near rigid surfaces,29,30 corners,31,32 in strong confinement,33 in the interstices between inclined plates,34 in channels,35 as well as in droplets and crowded environments.36–38
Long-range hydrodynamic interactions between microswimmers and any obstacles surrounding them are governed by the flow created by the beating flagella and the motion of the cell body.39 Swimming organisms are typically divided into two categories, depending on the type of long-ranged flow they create in the surrounding fluid: pushers, a group that includes spermatozoa and E. coli bacteria,30 are pushed from the back by their flagella; in contrast, pullers, such as CR cells,18 swim flagella first. This distinction originates from the symmetries in the flow field created by the swimmers, with a puller being equivalent to a pusher seen under a time-reversal symmetry, and as a result these two categories lead to very different dynamic behaviours close to boundaries and obstacles. Noise40 and steric interactions37,41 also affect the trapping and scattering of swimmers of surfaces, including CR in microfluidic chambers.42
An important instance of swimming in a complex environment is the propagation of microorganisms in porous media such as soils43 and foams.44 The formation of aquatic foams on certain rivers, lakes and coastlines has been reported to be associated with a loss of phytoplanktonic biomass in the water column.45,46 The role of aquatic foams on microorganism populations has, however, yet to be understood. The trapping of algae brings them out of their aquatic environment, thus leading to depletion, but this could also favour dissemination to new environments. Exploring the physical mechanisms at play in the interactions of motile organisms with foams would strengthen our understanding of the influence of foam formation on local ecosystems.
Recent work in this direction investigated the fate of planktonic biomass trapped in foams, showing experimentally that flagellated CR cells remain actively trapped over long periods of time in a draining foam, while passive bodies of the same size and density (including dead cells) escape the foam with the gravity-driven flow.44 The liquid part of a foam consists of interconnected micro-channels formed by the edges of contacting bubbles, in which the liquid flows as in a pipe. These microchannels, called Plateau borders, have a well-defined structure imposed by interfacial minimisation and are classically described by Plateau's rules47 wherein bubbles always meet by three. The cross-section of the Plateau border is therefore triangular with concave curved sides (see illustration in Fig. 1). Microscopic observations of CR cells swimming in a chamber mimicking the cross-section of foam Plateau border further revealed that cells accumulate near the corners of the Plateau border.44 We note that the presence of surfactants rigidifies the foam boundaries in the experiments, thus allowing comparison with no-slip walls.44
In this article, we present a combined experimental and theoretical analysis of the swimming behaviour of CR cells in two-dimensional (2D) microscopic chambers imitating the cross-section of a single foam Plateau border. We first use tracking data on the swimming dynamics of the cells in three different chambers to derive the full steady-state probability distribution function (pdf) of swimming CR cells. This distribution is seen to be strongly peaked in the corners of the chambers. Next, we use empirical scattering laws observed in previous experiments (scattering with a constant scattering angle) to analyse theoretically the phase space of trapped and escaping trajectories inside a three-circles billiard. We show that the experimentally-observed accumulation of swimmers in the corners has a geometrical origin. We then develop a more detailed theoretical model based on experimental data to reproduce quantitatively the probability density function of swimmers in the chambers. We show that the trapping of CR is controlled by the shape of the concave microchambers, the finite size of the CR cells, and the angle distribution of the cells scattering off the walls. We also observe that the microswimmers are significantly slowed down in the vicinity of walls at distances much larger than those of contact interactions, an effect which, as we quantify using numerical simulations, is of purely hydrodynamic origin.
2 Probability density function of cells in a quasi-two-dimensional chamber
2.1 Experimental set-up
Individual microswimmers cells were incorporated in microscopic chambers mimicking the cross-section of a foam channel, as shown on Fig. 2a. The chambers consists in a triangular shape with concave curved sides with identical radius of curvature R. The thickness of the chambers is 20 μm. The experimental procedure described below has been presented in a previous publication.44 Here, we use the raw experimental data and develop a new tracking algorithm which follows the position of an individual cell and its interactions with the chamber walls.The microswimmer used is the model alga Chlamydomonas reinhardtii (CR), which is a single-cell green alga about 10 μm in diameter that swims with two flagella at the front of the organism. We used the wild type strain CC124- obtained from the Chlamydomonas Resource Center. The algae were inoculated into High Salt Acetate (HSA) culture medium48 and maintained at 25 degrees under constant gentle agitation and a day/night illumination conditions of 12 h/12 h. The experiments were carried out between 48 and 72 hours after inoculation. This preparation ensures the synchronisation of the algae and thus the reproducibility of their behaviour.
The micro-chambers were designed using soft lithography techniques. Polydimethylsiloxane (PDMS) chips were obtained from a mould consisting in an array of identical micro-chambers. Three different sizes of PDMS microchambers were used, with R = 260 μm, 520 μm and 1040 μm. Just before any experiment, the PDMS device was made hydrophilic by oxidation using air plasma device over 2 minutes.
Immediately after oxidation, a ∼ 3 μL drop of suspension of CR algae in their culture medium was deposited on the PDMS device and a microscope slide was placed gently on the top. The chambers were placed under an inverted phase contrast microscope (Olympus IX73, fitted with the contrast module PH1U and two objectives: UPLFLN4X and UCPLFLN20X). The position of each CR cell was recorded during 5 min at a rate of 10 fps, using a red illumination (wavelength >630 nm) to avoid any phototactic effect (see Fig. 2b). Each experiment was repeated 15 to 17 times. Since we are interested in trapping in foams, which occurs at very low density and in order to avoid algae interactions interfering with the single particle tracking, chambers containing one cell were used for the experiments. We thus excluded the data from 14 experiments for which two cells or more were present in the chamber. Having multiple cells in a given experiment happened more frequently in the larger chambers, as the filling solution had constant algae concentration. In total, we analysed 33 trajectories, 17 for the R = 260 μm chamber, 9 for R = 520 μm and 7 for R = 1040 μm. We show videos of experiments in each of the three chambers in the ESI,† movies SM2.mp4, SM3.mp4 and SM4.mp4.
We track the position of each CR cell in the chamber by subtracting the first image of the sequence and finding the local intensity maximum, which corresponds to the algae body. We check for errors in the points by defining a maximum speed of 260 μm s−1. If a single point is out of this speed scope, we replace it by the average of the previous and subsequent points. If more than one point is wrong, we move to manual tracking for this set of images. Obtained trajectories lasting 30 s and 250 s, respectively, are depicted in Fig. 2c and d, with the colormap indicating the direction of time, from dark blue to yellow. For clarity, the z-direction of Fig. 2d also represents time. ESI,† video SM1.mp4 also shows tracking in a R = 520 μm chamber.
2.2 Probability density function
The positions of each cell were statistically averaged over all experiments in a given chamber and converted into relative probability density maps for the algae position. Additional averages were performed using rotation of the entire map by angles 2π/3 and 4π/3, thereby exploiting the angular symmetry of the Plateau border cross-section. These pdfs are presented in Fig. 3 for the three different chambers, with both colour and height (bottom panel: side view) representing the magnitude of the probability density function for the swimmer position. Lengths are nondimensionalised using the radius R of the three walls as unit.The most striking feature of the pdfs is a sharp accumulation of the swimmers in the corners of the Plateau borders. The models developed in the following sections of the paper will explain this phenomenon of corner accumulation, a key element to understanding the trapping of motile cells in complex geometries such as foams.
We measure that cells spend about a third of their time in corners, with details varying with the chamber (and therefore the sharpness of the corners); the exact fraction of time spent in the corners is shown in Fig. 3 (top). Inspecting individual trajectories where algae swim into a corner, we see that after some time the trapped cells turn back and escape. These cells then follow a new trajectory and eventually end up stuck in another corner, and the process repeats. Those half-turn motions of the trapped cells will be explicitly taken into account in Section 4.
A second feature of the algae trajectories is that the cells spend more time swimming near boundaries than in the centre of the chamber. Contact interaction of CR with walls has been previously studied,41 and the authors showed that cells have a tendency to swim along the boundary before scattering away. Wall accumulation of CR has also been reported in spherical and elliptical channels, which has been rationalised using an active Brownian model.42 By measuring the range of the interaction, we show below that, while contact interactions dominate surface interactions,41 far-field hydrodynamic effects must also be taken into account in order to reproduce quantitatively the distribution of swimming cells in chambers. We will also show that corner accumulation is not due to boundary-following swimming but that instead it has a geometrical origin.
In Fig. 3, we further observe some smaller peaks in the pdf close to some walls, especially in the 1040 μm chamber (light colours). These correspond to experimental irregularities or dust particles close to the chamber walls, which then decrease the time spent in corners by the cells; they are not relevant for our analysis in the context of foams and wall interactions and can thus be ignored in our modelling approach.
3 A geometrical approach to trapping in corners
3.1 Two-dimensional model for algae scattering with constant scattering angle
In this section, we develop a simple geometrical model to explain the most striking aspect of the algae spatial distribution, i.e. the accumulation of the swimming cells in the chamber corners. We take a two-dimensional geometrical approach to the problem and consider a cell swimming in a domain obtained as the outside of the three tangent circles (Fig. 4). We study mathematically all possible trajectories of the cell and show that most of them end in a corner.We assume that the cells swim along straight lines before scattering off walls. Experimentally, the swimming behaviour of CR cells is ballistic at short times and diffusive at long times41 with a transition time of several seconds. When the cells are confined in a plane, however, the trajectories become predominantly ballistic,42 justifying this modelling assumption.
A key element is the modelling of individual scattering events when the swimmer encounters a wall. We assume each scattering event to be punctual, and neglect here any sliding of the algae along the chamber wall (which will be incorporated in the detail model of Section 4). Motivated by past experimental data,41 we assume here that the orientation of the swimmer after the wall-bounce is independent of its initial orientation. Specifically, if we denote, for a given scattering event, the incident angle of a CR cell θin and the scattering angle θout (see notation Fig. 4a), we assume θout to be independent of θin.
Additionally, we take in this section the scattering angle θout to be fixed and constant for a given swimmer. This choice for θout is an important difference with well-studied classical billiards,49 including three-disks ones,50,51 where the particle reflection is specular, meaning that θin = θout. Microorganisms billiards with constant scattering angle θout, also motivated by experimental work,41 have been previously studied in polygonal geometries36 as well as ellipses and more complex closed curves.52 We extend here these analysis to the particular geometry of the Plateau border section, thus providing a link between past work on microorganisms billiards and our new experiments.
Because of the existence of cusps in our billiard geometry (corner points with zero interior angles), ‘trapping’ events in which the swimmer never exits a corner can occur. Note that this would also be true in geometries with acute angles, such as triangles. In this paper we denote ‘escaping’ the opposite of trapping, keeping in mind our initial motivation of understanding the fate of algae in foams. We are interested in what follows in characterising the possibility of trapping events, and in quantifying how likely they are to occur as a function of the value of θout. We demonstrate that the concavity of the walls makes the future of a given trajectory (trapped vs. escape) dependent on the initial position of the swimmer, which is not the case for polygons. Consequently, in this section, we aim to determine the phase space of trapped trajectories as a function of the initial conditions of the cell and on the (constant) scattering angle.
3.2 System geometry
In order to list all the possible trajectories, we parametrise our system as shown in Fig. 4. A trajectory is characterised by the value of θout and the initial position and swimming direction of the cell. Instead of listing all possible starting points and orientations in the chamber, we may only consider the first contact point with the walls and the side of the normal from which the swimmer arrived. Taking into account the angular symmetry of the three circles for rotations of 2π/3 and 4π/3, we can limit our analysis to trajectories starting from the bottom circle. The first contact point is defined by the angle θ0 measured from the centre of the bottom circle and taking its value between −π/6 (left corner) and π/6 (right corner) (see illustration in Fig. 4a). In what follows, all angles defining the position of the swimmer on the circles are oriented counter-clockwise. Further, for a given contact point, the swimmer comes from either left or right side of the normal. Recalling the mirror symmetry between θ0 and −θ0, we only consider trajectories coming from the left at the first contact point. For consistency with past experiments41 and previous analysis of microswimmers billiards,53 the model swimmer is assumed to always leave from the opposite side of the normal, which means that θout ∈ [0; π/2]. Possible reversals of the swimming direction upon scattering off a wall will be included in the following section where non-constant values of θout are discussed.With the appropriate symmetries, each possible swimmer trajectory in the geometrical approach is therefore indexed by a single (θ0, θout) pair, with θ0 ∈ [−π/6; π/6] and θout ∈ [0; π/2], and the trajectory of the swimmer is fully deterministic. The consecutive contact points with the walls are characterised by a position measured by the angle θ ∈ [ −π/6; π/6] on one of the three circles (see Fig. 4a), and by the direction of arrival of the swimmer with respect to the normal at the contact point. We investigate the outcome of all the possible trajectories, either trapped in a corner or escaped, for each pair of angles (θ0, θout).
3.3 Phase map of the trajectories
By integrating the model numerically, we can obtain the outcome of all possible trajectories indexed by the (θ0, θout) pairs and look at whether they end up in a corner. To do so, we run simulations for 250 evenly spaced values for both θ0 ∈ [−π/6 + 0.05; π/6 − 0.05] and θout ∈ [0; π/2]. We stop each simulation after 200 bounces and report on the position of the swimmer in the chamber. We plot the results for all trajectories in the phase map of Fig. 5. There are four different possible outcomes for each (θ0, θout), as illustrated using four colours: no trapping after 200 reflections (black) trapping in right (blue), top (yellow) and left (red) corners. Illustrative trajectories are also shown on the figure, with trapped trajectories on the left and escaping ones on the right.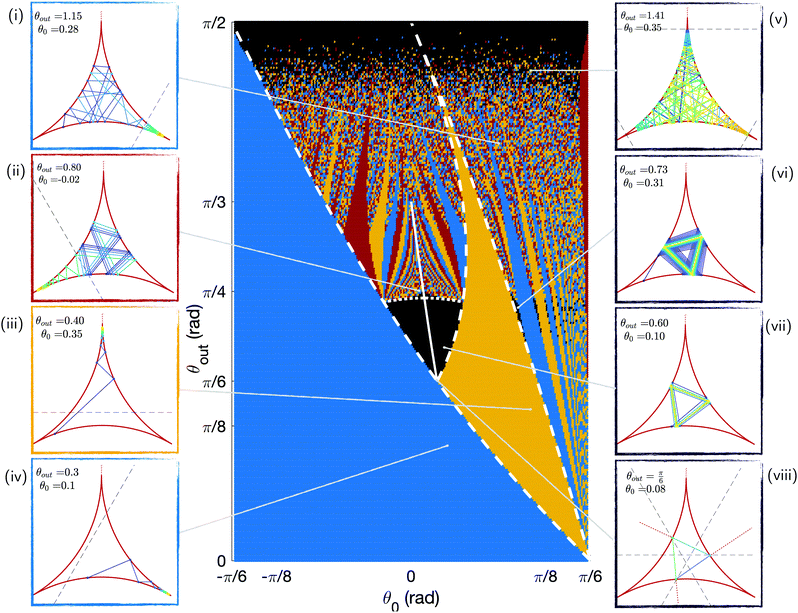 | ||
| Fig. 5 Phase map of the trapping vs. escaping outcome for swimmers undergoing 200 bounces with different initial positions θ0 and scattering angles θout. These results are obtained numerically. The escaping trajectories are shown in black and are illustrated on the right panels (v to viii). The trapping trajectories are shown in colours, with illustrations on the left panels: blue for the right corner of Fig. 4i and iv, yellow for the top corner (iii), and red for the left one (ii). The white lines correspond to analytical limits for some of the regions of the phase map: the plain line depicts periodic triangular orbits, the dotted line six-points periods, and the dashed lines some coloured regions areas. In the panels, the colour of the trajectory indicates the swimming direction (increasing time from blue to yellow), and the dashed black line shows the attraction range of the corner region, as detailed in Section 3.4.1. | ||
The most striking feature of this phase map is that a large majority of the trajectories, over 80%, end in one of the three corners. For small values of θout or θ0, all trajectories end up in the right corner from the first bounce (blue colour in Fig. 5), a result true for nearly half of all swimmers. This is due to the existence of regions of the chamber around the corners from which the swimmer cannot escape. We show later that the size of these trapping regions decreases with θout, leading to the appearance of more intricate trajectories before trapping and even escaping ones at high scattering angles. Indeed, for large values of θout, the structure of the phase space becomes more complex. We further note that there are two regions where some trajectories escape the corners (these are the black areas on the phase map): some orbits with intermediate values of θout are perfectly periodic, and some trajectories come close to the corners but escape them as θout → π/2. In the rest of this section, we interpret the main areas of the phase space and obtain some analytical expressions for their boundaries; these analytical limits are depicted as white lines in Fig. 5.
3.4 Understanding the phase map
 | (1) |
A swimmer coming from outside this region is therefore sure to be trapped in the corner when it touches a wall with |θ| > θc, with
 | (2) |
We note that a trajectory might leave this region if it starts inside it but is oriented outwards. We also compute the extension of the trapping region Hc defined as the distance between the corner and the boundary of the trapping region, as shown on Fig. 6a. Hc is the height of the previously used triangle, with
 | (3) |
 | (4) |
The dependence of the size of the trapping region on θout is plotted Fig. 6b and we see a systematic decrease, with θout, from 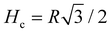 at zero scattering angle to 0 when θout = π/2.
at zero scattering angle to 0 when θout = π/2.
When the sizes of the three trapping regions are made to increase (by lowering the value of θout), we can reach a point where all three cover the whole chamber; this occurs for  and θout ≈ 0.35. We therefore know that there exists a limit value for θout, equal to or larger than 0.35, below which all swimmers end up trapped, as seen on the phase map in Fig. 5. The limiting case corresponds to the lowest value of θout for which the swimmer can successfully escape all three corners. In this trajectory, the swimmer reaches all three circles precisely at the border of the trapping regions, as presented on Fig. 5viii. This occurs for θout = π/6, which is the desired limit. In that case, all trajectories arrive normally and are therefore aligned with the three centres of the circles.
and θout ≈ 0.35. We therefore know that there exists a limit value for θout, equal to or larger than 0.35, below which all swimmers end up trapped, as seen on the phase map in Fig. 5. The limiting case corresponds to the lowest value of θout for which the swimmer can successfully escape all three corners. In this trajectory, the swimmer reaches all three circles precisely at the border of the trapping regions, as presented on Fig. 5viii. This occurs for θout = π/6, which is the desired limit. In that case, all trajectories arrive normally and are therefore aligned with the three centres of the circles.
We note that experimental work on the scattering angles41 found that the distribution of θout exhibits a peak at θout ≈ 0.28 rad. Using this value in our model results in prediction of trapping for all swimmers with any initial position.
The existence of a trapping region due to the cusps in the geometry considered in our paper is an important difference with the case of a polygonal chamber, and in particular a triangular one. It means that attractive periodic orbits, if they exist, only have a limited attraction range, making trapping more likely.
We therefore look for periodic values  as well as neighbouring trajectories
as well as neighbouring trajectories 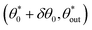 tending to the periodic trajectory (as in Fig. 5vi and vii). Since periodic orbits are, by definition, trajectories that reach the same point after a number of bounces, we look for a mathematical relationship between the position of consecutive contact points. A swimmer starting from a circle can reach either of the two remaining walls, and its scattering orientation depends on the side of the normal from which it arrives at the wall; there is unfortunately no general analytical expression for the position successive contact points of a trajectory. However, we can find expressions relating consecutive scattering angles in some specific cases. This enables us to express the position of some of the regions on the phase map, in particular some positions for periodic
tending to the periodic trajectory (as in Fig. 5vi and vii). Since periodic orbits are, by definition, trajectories that reach the same point after a number of bounces, we look for a mathematical relationship between the position of consecutive contact points. A swimmer starting from a circle can reach either of the two remaining walls, and its scattering orientation depends on the side of the normal from which it arrives at the wall; there is unfortunately no general analytical expression for the position successive contact points of a trajectory. However, we can find expressions relating consecutive scattering angles in some specific cases. This enables us to express the position of some of the regions on the phase map, in particular some positions for periodic  and attraction range.
and attraction range.
To do so, we use the relationship between the Cartesian coordinates of contact points and the orientation of the swimming segment between them. From Fig. 7a, for a swimmer leaving the bottom circle at θ1 towards the right one at θ2, this gives
 | (5) |
 | ||
| Fig. 7 (a) Position of successive contact points on the circles, which we use to derive eqns (5) and (6). (b) Periodic triangular orbits. (i) Position of the triangle edges as in eqn (7). (ii) Complete range of periodic triangular orbits, with two stable orbits (θout = π/6, 0.7) and two unstable orbits (θout = 0.9, π/3). (c) Trajectories for constant value θ0 = 0.08 and decreasing values of θout showing dynamics ranging from (i) trapping, (ii) six-points periodic orbit, and (iii) asymptotic motion towards the stable triangular periodic orbit. | ||
Similarly, for a trajectory starting on the bottom circle at θ1 and reaching the left one at θ2, we get
 | (6) |
There are no two-point periodic orbits for this system, as a swimmer scattering between two circles with constant θout goes monotonously towards or away from the corner. The simplest periodic orbits are therefore triangular ones with a swimmer scattering successively on the three circles. These triangular periodic trajectories exist when the point reached after one reflection has the same value of θ (this corresponds to a 2π/3 rotation), and is reached from the same side of the normal. The first condition can be met only when θout < π/3 (see Fig. 7b). Besides, the condition for the two sides of the triangle to be on different sides of the normal yields θout > π/6 (see Fig. 5viii).
We thus find that for θout ∈ [π/6; π/3], periodic triangular orbits do exist. We illustrate some of these periodic triangular orbits in Fig. 7b, including the limit ones. Using θ1 = θ2 in eqn (5), some trigonometric manipulation leads to the position of the triangle vertices at
 | (7) |
The values of the pairs  corresponding to periodic triangular orbits of the system are plotted as a solid white line on Fig. 5. Numerically, we observe that the only stable periodic trajectories are some of these periodic triangular orbits, as illustrated in Fig. 5vii.
corresponding to periodic triangular orbits of the system are plotted as a solid white line on Fig. 5. Numerically, we observe that the only stable periodic trajectories are some of these periodic triangular orbits, as illustrated in Fig. 5vii.
We now consider their attraction range, and focus on those of the trajectories that tend to periodic triangular orbits. These are included within the central black area in Fig. 5, and the smaller black areas for higher values of θ0. The smaller black zones are trajectories that reach the same value of θ as the central one after a few reflections (thus leaving the left corner).
We therefore focus only on the central black area of the phase map. It is delimited, on the left, for decreasing values of θ0, by the line for which the swimmer enters the right trapping region (blue) after one bounce. From the previous section, we know this occurs for θ0 = θc as in eqn (2). The right boundary, for increasing values of θ0, is the line for which the swimmer enters the top trapping region (yellow) after two bounces. This corresponds to taking θ2 = θc in eqn (5) which leads to
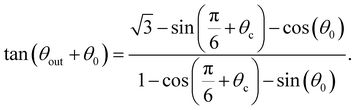 | (8) |
Finally, when increasing the value of θ0, the limit of the yellow region corresponds to trajectories reaching the left circle first. In the limiting case, the left circle will be reached tangentially, giving rise to θ1 + θout = π/3 + θ2. Incorporating this to eqn (6), we obtain
 | (9) |
These mathematical boundaries to the blue and yellow areas of the phase map are plotted as dashed white lines in Fig. 5 and match exactly the numerical simulations.
We obtain that the limit of the attraction region of periodic triangular orbits for increasing values of θout is given by six-point periodic orbits. This can be intuitively understood by inspecting trajectories for a given value of θ0, such as the three trajectories shown in Fig. 7c. We take a swimmer starting close to the triangular periodic orbit vertex, at θ0 = θ* + δθ0 (δθ0 is small), and scattering successively on the three circles. We then look for the condition for the swimmer to go towards, or away from, the triangular orbit. Its position after two bounces is given by θ3 = θ* + δθ3 (see Fig. 7a for notations). If δθ3 < δθ0, then the trajectory is going towards the triangular periodic orbit, and will thus escape the corner; this is shown in Fig. 7iii. In contrast, if δθ3 > δθ0, the swimmer goes away from the periodic orbit and ends up reaching the limit for a trapping region, as in Fig. 7i. The limit case is for the exact equality θ0 = θ3, which is a periodic trajectory with period 6, as in Fig. 7ii. The location of these six-point periodic orbits on the phase map can be found using the θ3 = θ1 relationship, after an intermediate bounce at θ2. This leads to a system of two equations, namely eqn (5) together with the same equation inverting the 1 and 2 indices. We can numerically solve for this system and we obtain the dotted line shown on Fig. 5. This theoretical prediction is seen to be in excellent agreement with the numerical simulations.
We finally note the existence of some escaping (black) trajectories on the phase map with θout higher than the six-point periodic orbits. This corresponds to trajectories that will end up in a corner at larger times but go slowly away from the six-point periodic orbits. From the previous notations, this means that δθn is slowly increasing but the swimmer is not yet trapped after 200 bounces.
The model could also be extended to consider a swimmer that consistently leaves the wall in the same direction that it arrived from, leading to a constant scattering angle θout > π/2. This case would of course not be directly relevant to CR, which is more likely to maintain its swimming direction.41,42 In that case, the attraction region we studied for π − θout would now repel the swimmer away from the corner it entered. New orbits of periodicity two, three, four or higher, including stable ones, would occur, and they could be analytically studied using eqns (5) and (6). However, periodic trajectories in this case would not alter the future of the swimmer, which would have a probability 1 of escaping regardless of the details of its trajectory.
3.5 Suppressed escapes: noise and finite algae size
With the 2D geometrical approach, we have observed the tendency of swimmers to accumulate in corners. However, we have also identified two situations in which some trajectories do not reach the chamber corners: periodic trajectories for intermediate values of the scattering angle and trajectories with a trapping region size going to 0 in the limit θout → π/2. We now show that incorporating simple additional physical elements, namely noise and the finite size of the swimmer, leads to the suppression of both these escaping regions.Firstly, we include noise in the scattering angle. Since we want to keep a simple geometrical model, we consider small deviation around a constant θout rather than a more realistic distribution of scattering angle as in the next section. We choose a scattering angle of the form θout = θ0out + θnoise; we take θnoise to be normally distributed with a noise strength α = 0.2, so that θnoise ∼ α![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) (0, σnoise), and vary the value of the noise standard deviation σnoise. For the swimmer to remain in the chamber, we check that it does stay in the interior side of the tangent to the circle after a bounce, and otherwise we redraw θnoise.
(0, σnoise), and vary the value of the noise standard deviation σnoise. For the swimmer to remain in the chamber, we check that it does stay in the interior side of the tangent to the circle after a bounce, and otherwise we redraw θnoise.
We plot the resulting probability for a swimmer to escape as a function of θout in Fig. 8a. This corresponds to integrating the phase map over all values of the initial position θ0. Without noise, we observe escaping trajectories for both periodic orbits and large scattering angle. Adding even a small amount noise (as shown in the inset histogram of Fig. 8a) leads to a rapid decrease in the number of trajectories going to periodic orbits. When σnoise is above 0.28 approximately, the periodic trajectories are entirely suppressed. We note that this corresponds to variation in the scattering angle that are much weaker than the ones measured experimentally.41 This suppression of periodic trajectories for noisy values of θout is not unexpected, since noise makes the swimmer more likely to go out of the basin of attraction of a periodic orbit. On the contrary, escapes at values of large θout appear to become more likely in the case of noisy scattering angles.
A closer look at the escaping trajectories at high values of θout reveals that the cells are likely to approach the corners closely before leaving (see Fig. 5v). However, in practice, we expect this to be impossible experimentally, as the swimmer has a finite size. Taking into account its body size s, we may then declare a swimmer to be trapped when it reaches a point where the distance between two walls is smaller than s. This occurs when the swimmer approaches a corner closer than the critical distance dc. From the inset in Fig. 8b,
dc = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(α) and s = 2R(1 − cos sin(α) and s = 2R(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α) α) | (10) |
and therefore
 | (11) |
With this, we can then plot the escape probability as a function of the value of θout for different ratios between the swimmer size s and the surface radius R in Fig. 8b. Including the finite size of the swimmer in our simulations leads clearly to a decrease in the number of escaping trajectories for high values of θout. The relevant experimental parameters for CR in foams and our chambers are s ≈ 10 μm for swimmers and R ≈ 1 mm for bubbles. The relevant size ratios s/R are 0.01 to 0.03, which correspond to sharp decreases in escaping trajectories (![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) escape < 0.2), though without completely suppressing them. As expected, however, the periodic trajectories are unaffected by finite swimmer size in the absence of noise.
escape < 0.2), though without completely suppressing them. As expected, however, the periodic trajectories are unaffected by finite swimmer size in the absence of noise.
These simple considerations show that noise tends to suppress periodic orbits while including the finite size of the swimmers reduces the number of escaping trajectories at high values θout. By choosing parameters for our model that match experimental conditions (average value of θout, noise level and algae size), trapping would in fact be predicted to occur for all trajectories. Our purely 2D geometrical model is thus able to explain the main features of the spatial distribution of CR cells in the experiments, namely their tendency to swim in the corners.
While the geometrical model is able to rationalise corner accumulation, it cannot reproduce quantitatively the distribution of swimmers in the chamber. There are two main reasons for this: the trapped swimmers in our model never escape the corners, and in addition, the geometrical model is very sensitive to the chosen value of scattering angle, θout, which is nor constant nor normally distributed around a central value in the experiments. A full understanding of the probability density functions shown in Fig. 3 requires therefore to incorporate additional elements to our model. In the next section we present a quantitative analysis of the swimming behaviour of the confined algae, and find appropriate laws for our simulations to match the experimental distribution.
4 Detailed modelling of the probability density function
In this section, we build on the geometrical model above to reproduce quantitatively the distribution of CR cells in the microfluidic chamber measured experimentally. To do so, we examine the experimental values of parameters that control the spatial distribution of algae in the chambers. We know from our geometrical model that contact interactions with the walls, including the values of scattering angle, are crucial to understanding the corner accumulation of CR cells. We therefore start by analysing the experimental distribution of scattering angles and reproduce it in our simulations. We next show that sliding along surfaces also affects the probability of cell presence in the corners. As opposed to the simple approach above, we will now also allow swimmers to escape the corners once they have been trapped. Finally, we go beyond corner trapping and investigate the accumulation along curved boundaries observed in our experiments (which was absent from the geometrical model).4.1 Scattering angle
We first focus on the individual contact events with the walls, and in particular on the orientation of the CR cells before and after encountering a wall. We measure experimentally the incident and scattering angles, θin and θout respectively, of Chlamydomonas in our quasi two-dimensional chambers. A contact event occurs when the swimmer is on, or very close to, the surface. We define the surface to be a region of thickness 20 μm near the three theoretical circular walls. This region is shown as a dashed line in Fig. 9 and in green Fig. 11a. We then measure the distribution of residence times in the experiments, with results shown in Fig. 11b.Contact events begin when the cell first enters the wall region of the chamber and end when it leaves it for more than a second. We check that histograms for the distribution of angles do not change significantly when the minimal take-off time exceeds a threshold of 0.5 s. This definition enables us to ignore imperfections in the chambers and details of the steric interaction between the cell and the wall. Short consecutive contact events, where the cell bounces on and off the surface while swimming along it, are therefore excluded, and instead considered as continuous sliding along the wall. When comparing our data to past scattering angle measurements,41,42 this takes out some small values of θout and skews our data towards higher scattering angles. Unfortunately, we do not have sufficient precision in our measurement to describe further the sliding events in our description. This does not affect our results, which focus on the probability density function of the algae in the chamber as opposed to details of the contact interactions.
We also only consider contacts that occur outside the corner region, where steric interactions could instead involve more than one wall at a time so that the measure angles are independent of the local corner geometry and can be readily extended to other microfluidic chambers geometries.
We define the incident and scattering angles, θin and θout, as the angles relative to the tangent at the incidence and departure points, xin and xout, measured using a linear fit to the 0.5 s-long trajectories before and after the contact event (see Fig. 9a). We allow the values of θin and θout to be more than π/2 when the cell crosses the normal to the incidence or leaving point, respectively. An incidence angle above π/2 coincides with the algae sliding along the wall in the direction opposite to its arrival at the wall. We show in Fig. 9b examples illustrating all possible contact configurations in the R = 520 μm chamber, along with the fitted angles.
We plot the histogram of θin in the three chambers in Fig. 10b. We note that there are only small qualitative differences between them. We next use our results to plot the histogram of θout in Fig. 10a. As mentioned above, our definition of contact events leads to a distribution of scattering angles shifted towards larger values of θout (Fig. 10a) compared to past work.41
We further note that the contact angles are not significantly affected by the curvature of the chamber walls. This can be understood by recalling that the contact interaction dominates the interaction of swimmers with the walls and thus the scattering angle. Since the radii of the chambers (R ∼ 260 − 1040 μm) are large relative to the size of a CR (body radius, s ∼ 5 μm with flagella ∼10 μm), there is a clear separation of length scales.
The distribution of incidence angles is maximal around π/2 and decreases continuously towards 0 and π (Fig. 10b). Is it predominantly set by local cell-wall interactions or by the global chamber geometry? To understand the origin of the distribution triangular shape, we compare it with the same histogram obtained from the geometrical model from Section 3. We note that in that case, we always had that θin < π/2 since we did not include the displacement of the cell along the surface. We find that the distribution of θin obtained using a constant value of θout does depend on the value of θout. However, if we draw the value of the scattering angle from the experimental distribution shown in Fig. 10a, we obtain a histogram qualitatively identical to experiments, as shown in the inset of (b). Using other physical distribution of scattering angle41 produces the same result. We have thus shown that the distribution of incident angles is dominated by the geometry of the system described in the previous section rather than by hydrodynamic interactions of the swimmers with the wall.
As a difference with the incident angle, the distribution of θout in Fig. 10b shows two distinct regions, pθout<π/2 and pθout<π/2, with a peak for θout < π/2. Overall, the probabilities for θout to be below or above π/2 are approximately 66% and 34%. We then consider the conditional scattering probability distribution for θout given the incident angle, i.e. p(θout|θin), which has been investigated close to straight walls41 and to pillars.37 In order to use our results for simulations and for comparison with existing literature, we assume θin ∈ [0, π/2] and if θin > π/2, we redefine θin to be its complement to π. The resulting plot for the 2094 contact events in all chambers is shown on Fig. 10c. It appears that the values of θin and θout are not independent; for a given value of θin we mostly observe two peaks for θout, the highest below π/2 and the second one above it. From this point on, we will use this measured angle distribution in the chambers in order to obtain an accurate spatial distribution of swimmers in our simulations.
4.2 Time at the wall
The second important feature of the experimental distribution of CR in the microfluidic chambers is the increased concentration of swimmers close to the boundaries. This concentration has been described in past work in the case of a curved surface based on purely steric interactions and noise42 and it has been experimentally measured,41 but both studies considered only steric (not hydrodynamic) interactions. We will first consider algae in contact with the wall and measure the time they spend swimming along it.A contact event occurs when the swimmer is on, or very close to, the surface. As when measuring scattering angles, we define the surface to be a region of thickness 20 μm near the three theoretical circular walls (Fig. 11a) and measure the distribution of residence times in the experiments, with results shown in Fig. 11b. The average duration of residence near the wall is 1 s. We observe no significant change for the duration of contact between chambers, except some longer contacts for the 1040 μm one (up to 35 s) due to dust near the boundary that locally trapped cells for long periods. During this contact, the cells move along the surface for an average of 31 μm (21 μm in the 260 μm chamber, 38 μm in the 520 μm chamber and 45 μm in the 1040 μm one). Interestingly, the contact with a wall is not a memory-less event, as steric interactions do take time to cause reorientation of the algae.41 Nevertheless, the exponential fit shown in Fig. 11b is able to capture the experimental distribution. Any further study of contact interactions with surfaces would require including the detailed shape of the swimmer54 and the interactions between the walls and the flagella,41 both of which are beyond the precision of our experiments.
4.3 Slowing down when approaching the wall
We next address long-range interactions between the microorganisms and the walls (i.e. that don't have a steric origin). We measure the velocity of the CR cells as a function of their distance to the nearest wall. To do so, we approximate the channel surface by three mathematical circles of radius R, and measure the distance of the swimmer to the closest circle centre (Fig. 11a). Note that this method introduces some uncertainty in the distance measured since the channel walls in the experiments are not perfectly regular, leading to an error of order ±5 μm; depending on the local shape of the surface, we can thus occasionally find some cells swimming as close as 1 μm from the theoretical boundary. We include only algae that interact strongly with a single boundary at a time, outside the corner regions. Furthermore, we only take into account trajectories for which the speed in the middle of the chamber, denoted by vcenter, is at least 2/3 of the average speed in the middle for all trajectories in a given chamber (keeping 25 out of 30 trajectories). This method eliminates CR cells that could have deficient swimming. The average swimming speed close to the centre of our chambers is found to be 111 ± 33 μm s−1 for the 260 μm chamber, 114 ± 31 μm s−1 for the 520 μm chamber and 123 ± 27 μm s−1 for the 1040 μm one.With this methodology, we plot in Fig. 12 the swimming speed of the cells normalised by their speed far from the walls, vcenter. We observe an almost perfect collapse of the plots not only for individual experiments but also for all three chambers. It is notable that the swimming speed undergoes a sharp decrease when the cells approach walls. The decrease starts approximately 40 μm away from the closest surface and is therefore not caused by steric interaction.
In order to understand the decrease in speed of the swimmer when approaching the wall, we perform numerical simulations using COMSOL Multiphysics®, with notation shown in Fig. 13a. We consider a sphere of diameter D in a confined domain of thickness H (so no-slip surfaces are located at z = ±H/2) in the presence of a third no-slip wall at x = 0. The centre of the sphere is located at a distance x = d from the left wall. The computational domain is closed with three rigid surfaces located far from the sphere at x = 25D and y = ±25D that do not affect the flow. We non-dimensionalise the geometry with the radius of the sphere, D/2.
We consider two setups; in the first one the sphere is moving towards the wall at x = 0 and in the second one parallel to it. In both cases the sphere has a unit velocity. The problem is solved using the fluid module of COMSOL, with tetrahedral mesh of about 966k elements. An example of a velocity magnitude profile for a sphere swimming towards the wall is illustrated in Fig. 13b. We use the simulations to compute the drag force on a sphere, denoted by Fi, with the notation i = ⊥, ‖ used to denote motion orthogonal and parallel to the surface at x = 0, respectively. To simulate the effect of an organism pushing with constant force, rather than having constant velocity, we may invoke the linearity of Stokes flows and rescale at each point the force on the sphere to be that in the centre of the domain, Fcenter, so that the speed of the sphere is given by Ui = Fcenter/Fi with i = ⊥, ‖ (see Fig. 13).
Modelling a CR as a sphere dragged by a constant force turns out to lead to a good agreement with our measurements of swimming speed vs. distance to wall, as demonstrated in Fig. 12 showing both the correct range of hydrodynamic interactions between the surface and the swimmer and the magnitude of the decrease. We note that the velocity drop in the simulations is smaller when the sphere is moving parallel to the walls; this is also in good agreement with our experiments with the confined algae, as we show in Fig. 13c by plotting the swimming speed only for a range of orientations α relative to the nearest surface (see details in figure caption).
A real swimming cell is, of course, not subject to a constant force, but is instead free-swimming. Our modelling approach focuses therefore only on the hydrodynamic interaction between the confined cell body and the walls, ignoring any effects arising from the smaller flagella. The good agreement between numerics and experiments allows us to confirm, as posterori, that these wall-body interactions govern the long–range interactions in the experiments.
Experimentally, we note an asymmetry between the speed of algae swimming away from the wall and towards the wall, the latter being smaller. This feature cannot be reproduced from the sphere model, in which the two cases are identical (a consequence of reversibility of Stokes flows). Recent experiments33,55 have shown that the flow field around a confined Chlamydomonas is dipolar (two-dimensional source dipole). Furthermore, the impact of the dipolar flow field created by the algae body increases with confinement relative respect to the propulsive forces from the flagella.55 It was noted in past work that when fitting the experimental flow of a confined Chlamydomonas to a dipolar model, the source dipole should be positioned in front of the algae rather than in the middle of the cell body.55 This additional parameter leads to a shift in the distance from the wall at which the velocity decay occurs for forward and leaving algae. We measure this shift to be ∼ 5 μm in our experiments, consistently with a characteristic CR size.
4.4 Trapping in a corner
When a Chlamydomonas cell reaches a corner of the chamber, we observe experimentally that it stays trapped there longer than at a single wall. This is expected due to the geometry of the chamber and the results from our geometrical model. We plot the distribution of trapping times for the cells in Fig. 11c. Since the corners of the PDMS chamber are truncated rather than acute, they are not really biologically relevant to the case of foam structures and there is need to focus on the details of the cell behaviour in a corner.Assuming that escaping the corner are events that occur continuously and independently from one another at a fixed rate, we expect the probability density function of the residency time in a corner to be an exponential law. We find a good fit, shown in Fig. 11c, for this exponential distribution with characteristic times in the three chambers given by τ260 = 1.5 s, τ520 = 2.5 s, and τ1040 = 3.5 s. The longer residency times in larger chambers is due to the local corner geometry and in particular the increasing sharpness of the corner. The corner size Lc is approximately 22G μm for the chamber with R = 260 μm, 17 μm for R = 520 μm and 16 μm for R = 1040 μm.
4.5 Final model for the cell probability density function
Using our analysis of the different aspects of the swimming behaviour of CR in a microfluidic chamber, we can modify the model to reproduce the probability density function for the position of swimming algae in a microfluidic chamber. We use methods similar to the ones described in the geometrical model of Section 3 but we fit the model parameters with the measured quantities from the experiments, thereby incorporating the parameter distributions directly from the data. Instead of a binary trapped vs. escaped fate for the swimming trajectories, our modified simulations lead now to a spatial probability density function for the swimmers in the chamber.In the simulations, the swimmers end up spending 29% of their time trapped, which matches well with the 32% measured experimentally (see Fig. 3, top left). Carrying out the same simulations with parameters from the other two chambers, we obtain trapping 22% and 14% of the time in the 520 μm and 1040 μm chambers, respectively, both of which compare well with the figures of 29% and 14% from our experiments. Remarkably, although the model does not of course reproduce exactly the trajectories for cells swimming in the microfluidic chamber, which would be noisy,42,56 the modelling illustrated in Fig. 14 successfully identifies the main ingredients governing the spatial distribution of the microswimmers in the chamber.
In our model, the interactions between a single wall and a swimmer are all encoded in the distribution of scattering angles, sliding along the wall, and long–range hydrodynamics. These are local properties of a confined system and are thus independent of the chamber geometry and in particular of chamber size. Their distribution could therefore be used directly in different chamber geometries with the same swimming cells. In contrast, trapping in corners is exponentially distributed with a characteristic time that depends on the cusp steepness. Extending our model quantitatively to different geometries would therefore require a new calibration of the corner trapping time, or at least an extrapolation of our measurements. Other microswimmers, such as different strains of Chlamydomonas or swimming bacteria, are expected to have different steric interactions with boundaries.41 This would result in different behaviours when bouncing and swimming along walls. Adapting our model to those would then require measuring the distributions of the elements that we have shown dominate the spatial distribution of swimmers and incorporating them in our analysis.
5 Conclusions
In this paper, motivated by the fate of algal cells in foams, we investigate the spatial distribution of motile CR cells in microfluidic chambers shaped as cross-sections of Plateau borders. We observe that the cells are more likely to be found in the corners of the channel, where they spend about a third of their time. To explain this tendency to swim in the chamber corners, we first develop a geometrical (billiard) model with reflection laws adapted to the case of swimming microorganisms. Namely, we consider trajectories of model cells bouncing on walls with constant scattering angles to mimic steric interactions with a boundary. The cells swim otherwise in straight lines inside a domain bounded by three disks, to represent the cross-section of foam Plateau borders. We find that most trajectories end up converging towards a cusp of the domain. We quantify corner accumulation by analysing the phase space diagram of all possible trajectories, which are fully characterised by their initial position and constant scattering angle. In particular, we show that small scattering angles lead to corner accumulation, while the trapping time increases at large scattering angles. We also discover some periodic trajectories, which are suppressed when including noise in the choice of the scattering angle. Our model shows therefore that corner accumulation has a geometrical origin. In particular, cusps create attracting trapping regions for swimmers bouncing on the walls of closed system with acute angles. This is a generic result relevant to many different geometries, which is therefore likely to be significant in a wide variety of complex environments beyond the microfluidic chambers presented here. Corner angles and cusps are thus likely to cause an accumulation of microswimmers regardless of the details of hydrodynamic or steric interactions with their environment.We next develop a more detailed model based on data from experiments to explain and reproduce quantitatively the location of the CR cells in the chambers. From our geometrical model, we know that the value of the scattering angle, and more generally wall interactions, control the location of the swimmers. We define and measure experimentally three main elements in a contact event: the incident angle θin, the scattering angle θout, and the distance during which CR swims along the wall without leaving it for more than 1 s. While the value of θin stems from the geometry of the system, θout is found to have a complex distribution, which we use as an empirical law for our simulations. We observe that θin and θout are slightly correlated but the scattering distribution is very noisy and this correlation does not affect the result of our simulations. The time spent by the cell swimming along the wall does explain the boundary accumulation that we observe experimentally, and enhances corner accumulation. Geometrically, sliding along the walls is equivalent to a shift of the scattering angle distribution towards lower θout. We also observe that walls exert a long–range hydrodynamic influence on the CR cells, which slow down when swimming close to a wall. This can be reproduced accurately by taking into account the hydrodynamic drag acting on the body of the confined algal cells in the 2D chambers. The swimming elements we incorporate in our model, notably the scattering angles and sliding distribution that describe cell–wall interactions, are local and robust to change in the geometry of the confined chamber. Including finally the distribution of time the swimmers spend trapped in the corners allows us to obtain a complete model that quantitatively reproduces the probability density function of CR cells in the microfluidic chambers. This is the only quantitative element of our model that is geometry-dependent: steeper corners lead to longer trapping times, and a new calibration or fitting from our own measurements is needed to extend the model quantitative predictions.
We describe the swimming behaviour of Chlamydomonas algae through local swimming properties, and thus expect our full quantitative model to be valid for other confined geometries. However, the interaction between a microorganism and a boundary is organism-dependent,41 and when using different strains of Chlamydomonas or other swimmers, scattering angle and sliding distributions should be experimentally determined.
This work was initially motivated by an experimental study of motile Chlamydomonas algae remaining trapped in a foam draining under gravity.44 We have shown here that the local geometry of the channels in the foam is likely to play a decisive role in the spatial distribution of motile CR and therefore in their trapping. Indeed, if the motile cells spend a large fraction of their time stuck in the cusps of the Plateau Borders, this will slow down their escape and effectively retain them in the foam.
To address fully the problem of trapping of planktonic microorganisms in foams, the third dimension of the Plateau borders should of course be taken into account. The first natural extension of our geometric approach to an elongated channel would be to incorporate a new swimming component in the third direction. The 2D model would then be a projection of the 3D one. Scattering angle distribution and wall sliding properties might be affected, and would need to be experimentally measured close to an unconfined wall. However, the results would be qualitatively identical and quantitatively similar to those presented above. Crucially, corner accumulation is a robust feature of the three-circle geometry regardless of the local details of swimmer-wall interactions. Additional 3D kinematics, including rebounds on the top and bottom walls, would need to be included to describe algae swimming in thicker chambers.
However, we expect new features that are absent in 2D to play a substantial role in a 3D Plateau borders, predominantly flow and gravity. Gravity is known to bias the movement of Chlamydomonas algae through gyrotaxis, encouraging cells to swim upwards. Gravity also leads to a slow sedimentation of the algae, which are slightly heavier than water. In this case, the orientation of the channel relative to the vertical direction would have an additional influence on the accumulation of swimmers, and would introduce differences in accumulation between horizontal and vertical borders, as well as an asymmetry between the corners. A similar effect could be induced by the responses of the cells to other cues, including phototaxis (light).
Furthermore, for a foam draining under gravity, motile swimmers will interact with the bulk flow through both advection and reorientation due to shear. The effect of the flow will vary in the different regions of the foam channels. In the central area, shear coupled to gyrotaxis could concentrate swimmers in the centre. However, the liquid speeds and hence shear rates in the Plateau borders will be small in the corners compared to the central region. This could then contribute to corner accumulation: advection is slower there, and algae already retained in the corners have less chances to escape by shearing. We expect a competition between the geometric effects of swimming highlighted in our paper and the interactions with the flow. In contrast, for non-motile cells or non-Brownian tracers, the dominant effect will be passive advection with the draining flow, as seen experimentally.44
Our present study could be extended to incorporate these elements and investigate which increase the retention of algae in the draining foam.
The method we develop in our paper, combining a purely geometrical billiard model with non-elastic bouncing with experimental data to reproduce accurately scattering and wall motion, could be applicable to other geometries and organisms. Since microswimmers often inhabit complex environments, e.g. soil or porous media and biological tissues, the local features of their habitats are expected to influence their ability to move, escape local asperities and access resources. Singular features such as corners are expected to be important for cell motility. In particular, cusps create local traps for swimming cells and are likely to retain them. We hope that our experimentally-driven approach to microorganism billiards will be used to complement existing models of swimmers in complex media, such as active Brownian particles and models with full hydrodynamic interactions, helping uncover the impact of local geometry on the dynamics of swimming cells.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement 682754 to EL). F. E. thanks the CNRS for support from MITI 2019 and 2020.Notes and references
- C. Brennen and H. Winet, Annu. Rev. Fluid Mech., 1977, 9, 339–398 CrossRef.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- J. Elgeti, R. G. Winkler and G. Gompper, Rep. Prog. Phys., 2015, 78, 056601 CrossRef CAS PubMed.
- D. Bray, Cell movements: from molecules to motility, Garland Science, 2000 Search PubMed.
- H. C. Berg and R. A. Anderson, Nature, 1973, 245, 380–382 CrossRef CAS PubMed.
- M. Silverman and M. Simon, Nature, 1974, 249, 73–74 CrossRef CAS PubMed.
- C. B. Lindemann, Cell Motil. Cytoskeleton, 1994, 29, 141–154 CrossRef CAS PubMed.
- D. Nicastro, C. Schwartz, J. Pierson, R. Gaudette, M. E. Porter and J. R. McIntosh, Science, 2006, 313, 944–948 CrossRef CAS PubMed.
- S. Ishijima, S. Oshio and H. Mohri, Gamete Res., 1986, 13, 185–197 CrossRef.
- E. H. Harris, Annu. Rev. Plant Biol., 2001, 52, 363–406 CrossRef CAS PubMed.
- J. R. Blake and M. A. Sleigh, Biol. Rev. Cambridge Philos. Soc., 1974, 49, 85–125 CrossRef CAS PubMed.
- H. C. Berg, E. coli in Motion, Springer Science & Business Media, 2008 Search PubMed.
- E. H. Harris, D. B. Stern and G. B. Witman, The chlamydomonas sourcebook, Academic Press, San Diego, 1989, vol. 2 Search PubMed.
- R. E. Goldstein, Annu. Rev. Fluid Mech., 2015, 47, 343–375 CrossRef PubMed.
- E. Lauga, The Fluid Dynamics of Cell Motility, Cambridge University Press, 2020 Search PubMed.
- U. Rüffer and W. Nultsch, Cell Motil., 1985, 5, 251–263 CrossRef.
- M. Polin, I. Tuval, K. Drescher, J. P. Gollub and R. E. Goldstein, Science, 2009, 325, 487–490 CrossRef CAS PubMed.
- K. Drescher, R. E. Goldstein, N. Michel, M. Polin and I. Tuval, Phys. Rev. Lett., 2010, 105, 168101 CrossRef PubMed.
- J. S. Guasto, K. A. Johnson and J. P. Gollub, Phys. Rev. Lett., 2010, 105, 168102 CrossRef PubMed.
- D. Tam and A. Hosoi, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1001–1006 CrossRef CAS PubMed.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- T. Jakuszeit, O. A. Croze and S. Bell, Phys. Rev. E, 2019, 99, 012610 CrossRef CAS PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- D. Takagi, J. Palacci, A. B. Braunschweig, M. J. Shelley and J. Zhang, Soft Matter, 2014, 10, 1784–1789 RSC.
- M. Theves, J. Taktikos, V. Zaburdaev, H. Stark and C. Beta, EPL, 2015, 109, 28007 CrossRef.
- P. Denissenko, V. Kantsler, D. J. Smith and J. Kirkman-Brown, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8007–8010 CrossRef CAS PubMed.
- N. Heddergott, T. Krüger, S. B. Babu, A. Wei, E. Stellamanns, S. Uppaluri, T. Pfohl, H. Stark and M. Engstler, PLoS Pathog., 2012, 8, e1003023 CrossRef CAS PubMed.
- K. M. Ottemann and J. F. Miller, Mol. Microbiol., 1997, 24, 1109–1117 CrossRef CAS PubMed.
- A. Maude, Nature, 1963, 200, 381 CrossRef CAS PubMed.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- H. Shum and E. A. Gaffney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 063016 CrossRef PubMed.
- R. Nosrati, P. J. Graham, Q. Liu and D. Sinton, Sci. Rep., 2016, 6, 1–9 CrossRef PubMed.
- D. Mondal, A. G. Prabhune, S. Ramaswamy and P. Sharma, arXiv preprint arXiv:2003.02040, 2020.
- T. Ishikawa, J. Appl. Phys., 2019, 125, 200901 CrossRef.
- A. Zöttl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 1–10 CrossRef PubMed.
- S. E. Spagnolie, G. R. Moreno-Flores, D. Bartolo and E. Lauga, Soft Matter, 2015, 11, 3396–3411 RSC.
- M. Contino, E. Lushi, I. Tuval, V. Kantsler and M. Polin, Phys. Rev. Lett., 2015, 115, 258102 CrossRef PubMed.
- O. Chepizhko and T. Franosch, Soft Matter, 2019, 15, 452–461 RSC.
- T. J. Böddeker, S. Karpitschka, C. T. Kreis, Q. Magdelaine and O. Bäumchen, J. R. Soc., Interface, 2020, 17, 20190580 CrossRef PubMed.
- K. Schaar, A. Zöttl and H. Stark, Phys. Rev. Lett., 2015, 115, 038101 CrossRef PubMed.
- V. Kantsler, J. Dunkel, M. Polin and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 1187–1192 CrossRef CAS PubMed.
- T. Ostapenko, F. J. Schwarzendahl, T. J. Böddeker, C. T. Kreis, J. Cammann, M. G. Mazza and O. Bäumchen, Phys. Rev. Lett., 2018, 120, 068002 CrossRef CAS PubMed.
- L. Ranjard and A. Richaume, Res. Microbiol., 2001, 152, 707–716 CrossRef CAS PubMed.
- Q. Roveillo, J. Dervaux, Y. Wang, F. Rouyer, D. Zanchi, L. Seuront and F. Elias, J. R. Soc., Interface, 2020, 17, 20200077 CrossRef CAS PubMed.
- L. Seuront, D. Vincent and J. G. Mitchell, J. Mar. Syst., 2006, 61, 118–133 CrossRef.
- K. Schilling and M. Zessner, Water Res., 2011, 45, 4355–4366 CrossRef CAS PubMed.
- I. Cantat, S. Cohen-Addad, F. Elias, F. Graner, R. Höhler, O. Pitois, F. Rouyer and A. Saint-Jalmes, Foams: structure and dynamics, OUP, Oxford, 2013 Search PubMed.
- N. Sueoka, Proc. Natl. Acad. Sci. U. S. A., 1960, 46, 83 CrossRef CAS PubMed.
- N. Chernov and R. Markarian, Chaotic billiards, American Mathematical Soc., 2006 Search PubMed.
- M. M. Sano, J. Phys. A: Math. Gen., 1994, 27, 4791 CrossRef.
- K. Weibert, J. Main and G. Wunner, Phys. Lett. A, 2002, 297, 87–91 CrossRef CAS.
- M. S. Krieger, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 122 CrossRef PubMed.
- S. E. Spagnolie, C. Wahl, J. Lukasik and J.-L. Thiffeault, Phys. D, 2017, 341, 33–44 CrossRef.
- H. Chen and J.-L. Thiffeault, arXiv preprint arXiv:2006.07714, 2020.
- R. Jeanneret, D. O. Pushkin and M. Polin, Phys. Rev. Lett., 2019, 123, 248102 CrossRef CAS PubMed.
- K. Y. Wan, K. C. Leptos and R. E. Goldstein, J. R. Soc., Interface, 2014, 11, 20131160 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02207a |
| This journal is © The Royal Society of Chemistry 2021 |












