Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure and thermodynamics of grafted silica/polystyrene dilute nanocomposites investigated through self-consistent field theory†
Apostolos T.
Lakkas‡
 ,
Aristotelis P.
Sgouros‡
,
Aristotelis P.
Sgouros‡
 ,
Constantinos J.
Revelas‡
,
Constantinos J.
Revelas‡
 and
Doros N.
Theodorou
and
Doros N.
Theodorou
 *
*
School of Chemical Engineering, National Technical University of Athens (NTUA), GR-15780 Athens, Greece. E-mail: doros@central.ntua.gr; Fax: +30 210 772 3112; Tel: +30 210 772 3157
First published on 1st March 2021
Abstract
Polymer/matrix nanocomposites (PNCs) are materials with exceptional properties. They offer a plethora of promising applications in key industrial sectors. In most cases, it is preferable to disperse the nanoparticles (NPs) homogeneously across the matrix phase. However, under certain conditions NPs might lump together and lead to a composite material with undesirable properties. A common strategy to stabilize the NPs is to graft on their surface polymer chains of the same chemical constitution as the matrix chains. There are several unresolved issues concerning the optimal molar mass and areal density of grafted chains that would ensure best dispersion, given the nanoparticles and the polymer matrix. We propose a model for the prediction of key structural and thermodynamic properties of PNC and apply it to a single spherical silica (SiO2) nanoparticle or planar surface grafted with polystyrene chains embedded at low concentration in a matrix phase of the same chemical constitution. Our model is based on self-consistent field theory, formulated in terms of the Edwards diffusion equation. The properties of the PNC are explored across a broad parameter space, spanning the mushroom regime (low grafting densities, small NPs and chain lengths), the dense brush regime, and the crowding regime (large grafting densities, NP diameters, and chain lengths). We extract several key quantities regarding the distributions and the configurations of the polymer chains, such as the radial density profiles and their decomposition into contributions of adsorbed and free chains, the chains/area profiles, and the tendency of end segments to segregate at the interfaces. Based on our predictions concerning the brush thickness, we revisit the scaling behaviors proposed in the literature and we compare our findings with experiment, relevant simulations, and analytic models, such as Alexander's model for incompressible brushes.
1. Introduction
Solid particles with polymer chains anchored on their surface hold a central place in nanocomposite materials research,1,2 since they are widely used in a variety of scientific and industrial applications such as sensing and therapy in biotechnology and biomedicine, wettability of membranes, surface activation, and interfacial electronic modulation.3 Usually, grafted polymer chains are used to stabilize inorganic nanoparticles (NPs) inside a host polymer matrix. When NPs are properly dispersed inside the polymeric material, they lead to mechanical reinforcement and improvement of viscoelastic properties in comparison to the pure material.The state of dispersion of NPs inside a polymer matrix depends on solid–solid and solid–polymer interactions as well as on entropic effects. In most cases, the embedded NPs tend to stick to each other due to attractive forces between them.4 Addressing this behavior, a widely used methodology is to graft homopolymer chains on the NP surface. Under certain conditions, the entropic cost related to the configurational restriction of grafted chains when the particles get closer to each other is able to keep the particles separated.
The key factors influencing NP separation are their size, the molecular weight of grafted chains, and the surface grafting density. Trombly et al.5 studied the effect of curvature of the solid surface on polymer mediated interactions among grafted NPs and demonstrated that the dependence of their separation on the grafting density becomes weaker with increasing particle curvature.
We say that matrix chains wet the grafted polymer brush when they are able to interpenetrate with grafted chains and therefore diffuse inside the space occupied by the polymer brush. Such a situation leads to a well-dispersed set of NPs. It has been seen that, in most cases, matrix chains are able to wet the polymer brush when their molecular weight is less than that of the grafted chains.3 Depending on the grafting density, when matrix chains are longer than the grafted chains, it is harder for them to penetrate into the interfacial region due to the higher entropy loss they experience. This is known as “autophobic dewetting”. One way to reduce the possibility for autophobic dewetting is to disperse smaller NPs.6 When grafted chains are attached to smaller particles, they have more available space, thus the penetration of matrix chains is facilitated and the corresponding conformational entropy cost becomes smaller.
As mentioned before, another important parameter for nanoparticle dispersion is the solid surface grafting density. When grafting density is lower than a threshold value, the particle cores are no longer screened by the grafted chains surrounding them, so they attract each other, leading to aggregation. This is known as “allophobic dewetting”. Sunday et al.3 derived experimentally a phase diagram demonstrating the regions where autophobic, allophobic dewetting, and complete wetting occurs.
Major experimental work has been conducted to understand the behavior of polymer grafted NPs and their influence on the properties of the composite material.7–17 Experimentalists are also interested in studying the interactions among grafted inorganic NPs in the absence of a host polymer matrix (particle-solids).18–20 Most of the experimental work up to now has been concentrated on medium grafting densities (<0.2 nm−2).15 However, silica particles with higher grafting densities (around 1.0 nm−2) coated with asymmetric block copolymers have also been synthesized.7
Atomistic molecular dynamics simulations have been performed by Ndoro et al.,21 while Meng et al.22 and Kalb et al.23 have performed coarse-grained molecular dynamics simulations representing the polymer chains by the Kremer-Grest bead-spring model. Using the same coarse-grained model, Ethier and Hall24 studied the structure and entanglements of grafted chains on an isolated polymer-grafted NP. Various additional studies employing particle-based simulation methods exist in the literature addressing nanoparticles in a polymer melt or solution,25–27 as well as isolated nanoparticles.28–31 Dissipative particle dynamics (DPD)32 and density functional theory (DFT)33 simulations addressing systems of polymer brushes are also reported. Vogiatzis et al.34 devised a hybrid particle-field approach called FOMC (Fast Off-lattice Monte Carlo) which is a coarse-grained class of Monte Carlo simulations, where the nonbonded interactions are described by a mean-field inspired Hamiltonian.
Another popular approach for investigating the structure and thermodynamics of polymer grafted NPs and brushes is self-consistent field theory (SCFT).35–45 It invokes a mathematical transformation from a system of interacting chains to an equivalent system of independent chains, where each chain interacts with a chemical potential field, w, created by the rest of the chains.46 SCFT is a strong modeling tool for describing equilibrium properties of interfacial systems involving polymer melts or solutions. Besides the fact that it is accurate in high density and large molar mass systems, it is able to derive directly the free energy of the investigated system. For a detailed explanation of SCFT and the transition from particle-based to field-theoretic formulations, the reader is referred to the relevant monograph by Fredrickson.47
In the present article, we employ SCFT to investigate the structure and thermodynamics of systems comprising atactic polystyrene (PS) chains grafted on a single spherical nanoparticle or planar surface made of silica (SiO2), immersed in a PS melt. The chemical constitution of the system under study is identical to the one investigated with FOMC by Vogiatzis et al.34 The range of molecular parameters (nanoparticle size, surface grafting density, molar masses of grafted and matrix chains) has been chosen so as to encompass that of experimental investigations of SiO2/PS nanocomposite systems.48 It is mentioned here, that no adjustment of parameters has been undertaken to fit with experiment or FOMC; rather, the actual physical parameters of silica and polystyrene have been used. The main virtue of FOMC is that it can directly sample chain conformations. On the other hand, the main advantage of SCFT in relation to FOMC is that it can directly calculate the free energy, enthalpy and entropy of mixing between the NP and the polymer matrix and the potential of mean force between two nanoparticles immersed in a host polymer matrix.39,49,50
The calculations were performed by employing the SCFT in one dimension (radial distance or normal distance coordinates) by taking advantage of the symmetry of the nanoparticle/planar surface. This one-dimensional treatment is expected to perform fairly well at moderate to large grafting densities and molecular weights of grafted chains. As in previous work,51 our SCFT model has finite compressibility. We apply the Gaussian string model to describe chain conformations, which punishes stretching of chain contours, since stretched contours have less available conformations, thus reducing the entropy. Nonbonded interactions in the polymer are calculated from an expression giving the free energy density as a function of the polymer local segment density. Polymer/solid interactions are accounted for by Hamaker integration.
That SCFT calculations are computationally inexpensive in one dimension allowed us to perform an extensive and dense grid search over a broad parameter space spanning: (i) the radii of the NP, RNP = 20 nm to 214 nm, as well as RNP → ∞ (planar surfaces); (ii) the molar mass of the grafted chains, Mg = 1.25 kg mol−1 to 100 kg mol−1; (iii) the grafting densities σg = 0.1 nm−2 to 1.6 nm−2. These calculations provide useful quantitative understanding of the limiting cases of sparse/dense grafting of short/long chains, on surfaces with low/high curvature, as well as of the intermediate transition regimes.
In particular, throughout our calculations, we extracted the density profiles of the grafted and matrix chains, which provide a direct picture of their conformations across the parameter space. The density profiles of the matrix chains are decomposed into contributions from “adsorbed” and “free” chains, the categorization of which is based on distance-based criteria; these results unveil the tendency of the matrix chains to penetrate the brush emanating from the nanoparticle/flat surface. The shape of polymer chains is investigated in terms of the number of chains passing through a unit surface51–53 and provides a measure of “crowding” phenomena and of the tendency of the chain ends to segregate at the matrix-grafted interface. Subsequently, the distributions of the grafted chains are analyzed in terms of their corresponding brush thickness, wherein we compare our findings to correlations that are reported in the literature.54,55 The brush thickness exhibits a rather complicated behavior across the transition regime from spherical nanoparticle to flat surface, which we try to describe through a scaling equation. Finally, the thermodynamics of these systems is examined in terms of the grand potential across the parameter space and a direct comparison with the Alexander model at fixed density56,57 (which is similar to the dry part of the two-layer model)58,59 is performed regarding the stretching free energy of grafted chains.
Before presenting the main results, we first validate our model and implementation by comparing our density profiles against FOMC34 across the same regime of grafting densities and chain molar masses that was investigated by Vogiatzis et al.34 This comparison is made for profiles obtained via both the Sanchez-Lacombe (SL) equation of state coupled with square-gradient theory (SGT) for nonbonded interactions, that we have adopted herein, and the Helfand (HLF) free energy density using the same compressibility employed by Vogiatzis et al.;34 the latter model is typically used in most field theory-inspired simulations.
The article is structured as follows: Section 2 outlines the overall mathematical formulation of the problem under study. Section 3 discusses specific details of the calculations performed herein. Section 4 presents the main results concerning the density profiles of matrix and grafted chains, the structure of polymer chains adsorbed on the NP surface, the number of chains per unit area profiles, the profiles of chain-ends, the scaling of grafted polymer layers, the free energy of the system, and the stretching free energy of grafted chains which is compared with the one obtained from the Alexander model. Finally, Section 5 concludes the article by summarizing the main findings of this work. The ESI† section includes the full formulation of our model in three dimensions, the extension of Alexander's model for a polymer-grafted NP, and technical details regarding the numerical evaluations of SCFT.
2. Model and theoretical formulation
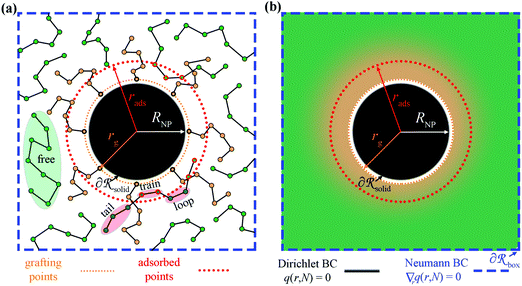
In Fig. 1a we depict the geometry of the three-dimensional region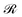 of the system that we wish to model. Grafted polymer chains (circles with orange fill) are chemically anchored at the grafting points, rg (orange arrow), which are located at a small distance (circle of small orange dots) from the surface of the NP (black) of radius RNP (white arrow). On the surface of the NP,
of the system that we wish to model. Grafted polymer chains (circles with orange fill) are chemically anchored at the grafting points, rg (orange arrow), which are located at a small distance (circle of small orange dots) from the surface of the NP (black) of radius RNP (white arrow). On the surface of the NP, 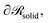 Dirichlet boundary conditions are imposed. The red dotted circle of radius rads (red arrow) defines the region where the segments of matrix chains (green circles connected by black line) are considered to be “adsorbed” (red circles with a green fill). These can be additionally subdivided into tails, loops and trains.60,61 Those matrix chains whose segments lie exclusively at a distance larger than rads from the NP center are called “free” (black circles with a green fill). Across the edges of the simulation box,
Dirichlet boundary conditions are imposed. The red dotted circle of radius rads (red arrow) defines the region where the segments of matrix chains (green circles connected by black line) are considered to be “adsorbed” (red circles with a green fill). These can be additionally subdivided into tails, loops and trains.60,61 Those matrix chains whose segments lie exclusively at a distance larger than rads from the NP center are called “free” (black circles with a green fill). Across the edges of the simulation box, 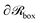 (dashed blue lines), Neumann boundary conditions with zero flux are applied.
(dashed blue lines), Neumann boundary conditions with zero flux are applied.
In SCFT, the degrees of freedom associated with the positions of chain segments are replaced by a spatially varying chemical potential field, as illustrated in Fig. 1b. This field governs the chain conformations and thus the segment density. At the same time, the field is dictated by the polymer segment density, so the field must be self-consistent and correctly describe the thermodynamic properties of the polymer. Furthermore, Fig. 1b depicts the smearing of grafting points normal to the radial direction.
2.1 Iterative procedure for obtaining the self-consistent field
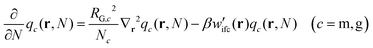 | (1) |
The iterative convergence procedure can be summarized as follows:
(1) Eqn (1) is solved for the matrix chains 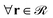 for 0 < N < max(Nm,Ng) with Nm and Ng being the length of the matrix and grafted chains, respectively. The initial condition is set to qm(r,0) = 1 across the polymer domain, whilst Dirichlet, qm(r,N) = 0 and Neumann (∇rqm(r,N) = 0) boundary conditions are imposed at the solid surface and system box boundaries, respectively (see Fig. 1).
for 0 < N < max(Nm,Ng) with Nm and Ng being the length of the matrix and grafted chains, respectively. The initial condition is set to qm(r,0) = 1 across the polymer domain, whilst Dirichlet, qm(r,N) = 0 and Neumann (∇rqm(r,N) = 0) boundary conditions are imposed at the solid surface and system box boundaries, respectively (see Fig. 1).
(2) Subsequently, eqn (1) is solved for the grafted chains for 0 < N < Ng, 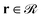 and r ≠ rg,ig where rg,ig is the grafting point of the igth grafted chain, 0 ≤ ig ≤ ng. The boundary conditions are the same as those for the matrix chains. In contrast, the initial condition is given by the following equation:36
and r ≠ rg,ig where rg,ig is the grafting point of the igth grafted chain, 0 ≤ ig ≤ ng. The boundary conditions are the same as those for the matrix chains. In contrast, the initial condition is given by the following equation:36
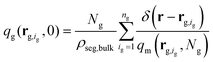 | (2) |
(3) With qc(r,N) known, the reduced densities, φc = ρc/ρseg,bulk, can be calculated by the following convolution integral:
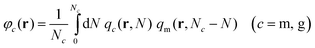 | (3) |
Note that in both m and g chains the second term of the convolution integral is qm (for details see Section S1.4, ESI†).
(4) Having calculated the density profiles of matrix and grafted chains, an EoS must be used to determine the free energy density functional and the corresponding chemical potential field:
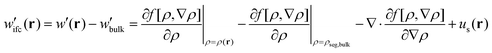 | (4) |
(5) To inspect the convergence, the maximum difference between the fields of the previous and the current iteration, 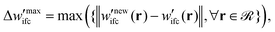 is estimated, therefore:
is estimated, therefore:
(a) If 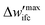 is smaller than a tolerance value,
is smaller than a tolerance value, 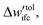 the simulations are considered converged and the procedure ends.
the simulations are considered converged and the procedure ends.
(b) If not, the algorithm cycles back to step (1) wherein the Edwards equation is reevaluated in the presence of the mixed field for numerical stability purposes:
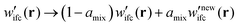 | (5) |
The above algorithm is generic and applicable to arbitrary system geometries.
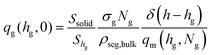 | (6) |
For planar surfaces with area Ssolid, the Edwards diffusion equation is evaluated across the normal direction with respect to the surface, and the differential dr of the spatial integration equals the volume of the layer, dr → Ssoliddh. The delta function in eqn (6) is set to the inverse discretization step in the h direction; i.e., δ(h − hg) ≃ 1/Δh, with Δh being the width of the intervals in which h is subdivided in the numerical solution.
For spherical nanoparticles, with area equal to Ssolid = 4πRNP2, the Edwards equation can be evaluated across a radial direction (normal to the surface) as shown in the Section S2 (ESI†). The differential dr for spatial integration is equal to the volume of the spherical cell, dr → 4π(RNP + h)2dh. The delta function in eqn (6) is again set to the inverse width of the intervals in which length is subdivided in the radial direction; i.e., δ(h − hg) ≃ 1/Δh.
Throughout the manuscript we present the overall mathematical formulation in three dimensions; one can derive the corresponding expressions in spherical and planar geometries by employing the aforementioned relations.
2.2 Thermodynamics
| ΔΩ = Ω − Ωbulk − Abulk = ΔΩcoh + ΔΩfield + ΔΩm + ΔAg + Us | (7) |
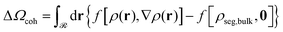 | (8) |
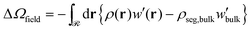 | (9) |
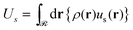 | (10) |
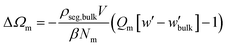 | (11) |
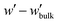 ,
,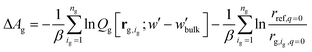 | (12) |
The partition function, 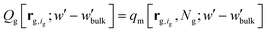 , appearing in the first term of eqn (12) depends on the position of the grafting point, and therefore on the discretization of space. In order to overcome this technical issue and normalize ΔAg with respect to the distance of the grafting point from the surface where Dirichlet boundary conditions, qc(r,N) = 0, are imposed, we have introduced the second term in eqn (12). Based on the observation that the chain propagator, qm, decreases linearly close to the Dirichlet boundary, adding the second term ensures that ΔAg is discretization independent; i.e., for a set rref,q=0, ΔAg is independent of the position of the grafting point, while, if rg,ig,q=0 = rref,q=0, the contribution of this term vanishes. This allows for comparisons for different spatial discretization and slightly altered grafting positions.
, appearing in the first term of eqn (12) depends on the position of the grafting point, and therefore on the discretization of space. In order to overcome this technical issue and normalize ΔAg with respect to the distance of the grafting point from the surface where Dirichlet boundary conditions, qc(r,N) = 0, are imposed, we have introduced the second term in eqn (12). Based on the observation that the chain propagator, qm, decreases linearly close to the Dirichlet boundary, adding the second term ensures that ΔAg is discretization independent; i.e., for a set rref,q=0, ΔAg is independent of the position of the grafting point, while, if rg,ig,q=0 = rref,q=0, the contribution of this term vanishes. This allows for comparisons for different spatial discretization and slightly altered grafting positions.
Our formalism is based on the works by Daoulas et al.51 and Schmid et al.,64 which have been extended in systems of arbitrary geometry comprising polymer chains grafted on solid surfaces. Furthermore, it was generalized so that any suitable equation of state can be applied to describe the non-bonded interactions among chain polymer segments. In-depth information regarding our mathematical formulation can be found in the Sections S1.1–S1.3 (ESI†).
2.2.2/a Helfand's free energy density. The Helfand free energy density and its first derivative with respect to the density are the following:
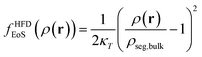 | (13) |
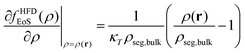 | (14) |
2.2.2/b Sanchez-Lacombe free energy density. The SL-EoS is the following:
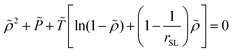 | (15) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) = ρmass/ρ*,
= ρmass/ρ*, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) = T/T* and
= T/T* and ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) = P/P* are the reduced density, temperature and pressure; ρ*, T* and P* are the corresponding characteristic SL parameters; rSL is the number of SL segments constituting a molecule. The mass density ρmass,bulk for each chain length across the bulk liquid phase is derived from the vapor–liquid equilibrium of a Sanchez-Lacombe fluid using eqn (15) (see Section S1 in ref. 61, ESI). The compressibility of the SL-EoS as a function of chain length and temperature is given by the following equation:
= P/P* are the reduced density, temperature and pressure; ρ*, T* and P* are the corresponding characteristic SL parameters; rSL is the number of SL segments constituting a molecule. The mass density ρmass,bulk for each chain length across the bulk liquid phase is derived from the vapor–liquid equilibrium of a Sanchez-Lacombe fluid using eqn (15) (see Section S1 in ref. 61, ESI). The compressibility of the SL-EoS as a function of chain length and temperature is given by the following equation: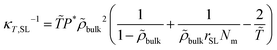 | (16) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) bulk = ρmass,bulk/ρ*.
bulk = ρmass,bulk/ρ*.
The corresponding free energy density and its first derivative with respect to the density are the following:
fSLEoS(ρ(r)) = P*[![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) − − ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) 2 + 2 + ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (1 − (1 − ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) )ln(1 − )ln(1 − ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) )] )] | (17) |
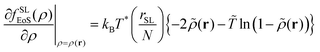 | (18) |
Section S3 (ESI†) includes evaluations of the free energy density and the field terms from the SL-EoS. The reader is reminded that the Sanchez-Lacombe model has a firm theoretical basis in a mean field statistical mechanical analysis of a lattice fluid composed of chains and voids, reminiscent of Flory–Huggins theory with voids playing the role of solvent molecules.65,66
2.2.2/c Square gradient term. A more realistic treatment of inhomogeneous systems is achieved by including nonlocal contributions to the Helmholtz energy density. A common form assumed for f[ρ(r),∇ρ(r)] is the one presented in eqn (19):61,67–70
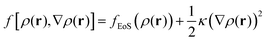 | (19) |
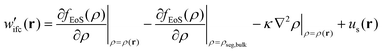 | (20) |
Section S4 (ESI†) includes details regarding the estimation of the square gradient contribution to the free energy in Cartesian and spherical coordinates.
3. Calculation details
The system considered in the present study consists of polystyrene (PS) chains grafted on a silica (SiO2) NP or planar surfaces, in contact with a polymer melt of the same chemical constitution as the grafted chains. All calculations were carried out in the grand canonical ensemble at a temperature equal to T = 500 K.The PS–SiO2 interactions are described with the Hamaker potential71 using the interaction parameters, APS and ASiO2, and the effective radii, σPS and σSiO2, presented in Table 1. Given that the repulsive term of the Hamaker potential increases steeply at short distances, we opted to replace the Hamaker potential below a segment-surface distance, hHS ∼ 0.4 nm, where us(hHS) = 5kBT, with a hard sphere wall. To impose the hard sphere wall, the coordinate of the first node of the simulation domain was set at a distance hHS from the surface. As a result, the region below hHS becomes inaccessible to the polymer chains; for more details, see Section S5 (ESI†).
| Parameter | Value | Ref. | |
|---|---|---|---|
| System | T | 500 K | 54 |
| r ref,q=0 | 0.05 nm | — | |
| r g,ig,q=0 | 0.05 nm | — | |
| Chain stiffness | b k | 1.83 nm | 54 |
| l c–c | 0.154 nm | — | |
| γ | 0.829 | 63 | |
| m monomer | 52.08 g mol−1 | — | |
| Hamaker | h HS | ∼0.4 nm | — |
| σ PS | 0.37 nm | 54 | |
| σ SiO2 | 0.30 nm | 54 | |
| A PS | 5.84 × 10−20 J | 54 | |
| ASiO2 | 6.43 × 10−20 J | 54 | |
| SL | T* | 735 K | 66 |
| P* | 357 MPa | 66 | |
| ρ* | 1105 kg m−3 | 66 | |
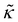
|
0.55 | 61 | |
| Helfand | κ T=500K | 1.07 (GPa)−1 | 54 |
| ρ mass,bulk | 953 kg m−3 | 54 | |
| Edwards diffusion | Δh | 0.05 nm | [Section S7.1 (ESI)] |
| ΔN | 0.25 segs | [Section S7.1 (ESI)] | |
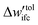
|
10−5kBT | — | |
As Chantawansri et al.35 observed, in the context of SCFT there is a special difficulty in the case of polymer chains whose one end is grafted to the solid surface. The grafted chains propagator is subject to a Dirac delta function initial condition as shown in eqn (6). In addition to that, the denominator on the right-hand side of eqn (6) is problematic, since the chain propagator of matrix chains goes to zero close to the solid surface. A usual approach to bypass these issues is to reposition the grafting points to a surface close to the solid instead of right on top of it.72–74 Regarding the numerical implementation of the delta function, smearing of the grafting points in the direction normal to the surface is often introduced by treating the grafting point density as a Gaussian distribution35 or as a rectangular function. In the three-dimensional analog of our in-house code named RuSseL, where we employ a Finite Element Method numerical scheme, the initial condition of the grafting points is evaluated exactly upon the desired points of the domain and the delta function is again evaluated as the inverse volume assigned to the node.74 Guided by these studies, in the present work we set the location of the grafting points at the discretization nodal point which is nearest to the hard-sphere wall. Furthermore, a smearing of the grafting points was introduced, so that they degenerate into a grafting “spherical shell” with radius slightly larger than that of the NP itself (Fig. 1, orange arrow) and thickness Δh.
Unless otherwise stated, the nonbonded interactions are described by the SL EoS in conjunction with square gradient theory (eqn (17) and (19)). We employed the characteristic SL parameters for PS66 and the influence parameter from the relation: κ = 2(rSL/N)2P*(ν*)8/3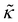 , with the reduced influence parameter being set to
, with the reduced influence parameter being set to 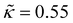 , same as in ref. 61.
, same as in ref. 61.
The Edwards diffusion equation was solved with a finite difference scheme (see Section S6, ESI†) with spatial discretization, Δh = 0.05 nm, and contour length discretization, ΔN = 0.25 segments; details regarding the choice of these parameters can be found in Section S7.1 (ESI†). The rectangle integration method has been employed to evaluate the convolution integrals, since other higher-order methods such as Simpson integration can produce artifacts in the presence of grafting points (see Section S7.1, ESI†). The field mixing fraction, amix, for the iterative convergence of the field in eqn (5) was optimized for each chain length so as to enhance the efficiency of our evaluations (see Section S7.2, ESI†). The tolerance value for the convergence was set to 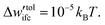 In all cases, the system dimensions were at least 10 nm larger than the edge of the brush of the grafted chains in order to avoid finite size effects.
In all cases, the system dimensions were at least 10 nm larger than the edge of the brush of the grafted chains in order to avoid finite size effects.
The simulations were realized with RuSseL; an in-house developed code which is designed to run calculations based on SCFT in both one and three dimensional systems, using the finite differences and finite element method, respectively.74 The evaluations were performed across a broad parameter space concerning RNP, σg and Mg: RNP = {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384} nm, σg = {0.1, 0.4, 0.8, 1.2, 1.6} nm−2 and, Mg = {1.25, 2.5, 5, 10, 20, 40, 80} kg mol−1. According to ref. 34, as long as the matrix chains are longer than the grafted ones, the latter are not perturbed considerably; thus, unless otherwise stated, Mg = Mm. The diagrams were designed using relevant software.75
4. Results
4.1 Radial density profiles
The radial segment density profile distributions of matrix and grafted chains can be employed as a measure of the particle–polymer interactions and reveal how these interactions are affected by the grafting density and the molecular weight of matrix and grafted chains.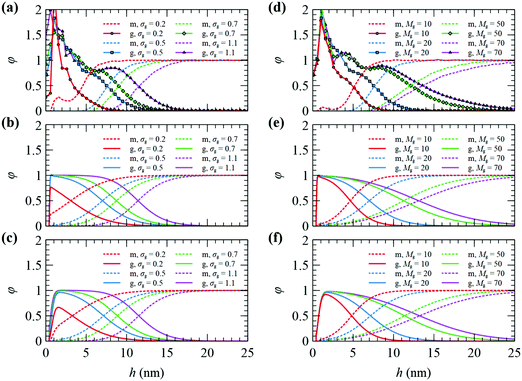 | ||
| Fig. 2 Radial density distribution for matrix (m) and grafted (g) chains on a NP with RNP = 8 nm, from FOMC34 (top), SCFT with Helfand (middle), and SCFT with SL + SGT (bottom). In (a–c) Mg = 20 kg mol−1, Mm = 100 kg mol−1, and σg varies from 0.2 to 1.1 nm−2. In (d–f) σg = 0.5 nm−2, Mm = 100 kg mol−1 and Mg varies from 10 to 70 kg mol−1. | ||
Nevertheless, there is a discrepancy near the surface of the NP, which could be related to the fact that SCFT cannot describe in detail the packing of chain segments or the anchoring of grafted segments at discrete points close to the surface, while FOMC invokes not an atomistic, but rather a coarse-grained model. Another observation is that the SCFT/SL + SGT model provides smoother radial density profiles for grafted chain segments in comparison to FOMC or SCFT/HFD. This mainly has to do with the incorporation of the square gradient term in the description of nonbonded interactions, which does not affect the long-ranged segment interactions, but rather the smoothness of the density profiles in the region near the solid surface. In addition, SCFT features a depletion region ranging from the solid surface up to a distance equal to hHS = 4 Å (the position of the aforementioned hard-sphere wall), wherein the repulsive interactions from the Hamaker potential are very strong.
It is stressed at this point that the density profiles obtained from our SCFT/SL + SGT model are closer to the corresponding ones obtained from atomistic molecular dynamics simulations21,76–78 than FOMC. If one averages out the oscillations of the atomistic density profiles, then their smeared analogues come out very close to the density profiles of SCFT/SL + SGT (and especially close to HFD) in terms of the position of the peak and the width of the depletion zone near the solid surface.21,76–78 Interestingly, the peak of the density profiles appears to become less pronounced in atomistic simulations with increasing grafting density, presumably due to excluded volume effects.21,78 Hereafter, all presented results are obtained with the SL + SGT model, since it is more realistic and reproduces the experimentally measured surface tension of PS.61 It is also mentioned that no fitting of parameters with respect to experiment or FOMC has been performed to describe this silica-polystyrene interfacial system, but the actual physical parameters of silica and polystyrene have been used.
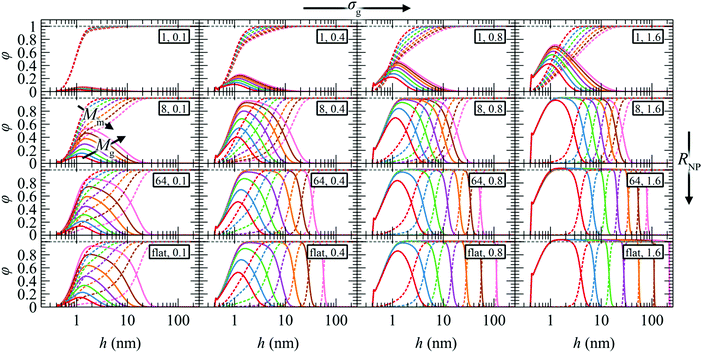
The radial density profiles exhibit a rather rich behavior which could be classified into three distinct regimes:
(i) Mushroom regime. In the region of low σg, Mg and RNP, the radial density profiles of the grafted chains become very suppressed and their density peaks are much lower than the bulk density. That the grafted chains are short and the distance between them is relatively large implies that they cannot experience the presence of each other. In other words, the density distributions of individual chains do not overlap and therefore chains tend to form mushroom-like structures;79 this effect is expected to be more pronounced at small RNP, since the chains would have more available space thanks to the increased curvature. Matrix chains, on the other hand, can penetrate the polymer brush readily and reach the surface of the NP. However, in the one-dimensional model employed herein, the inevitable smearing of grafting points may prevent us from accurately predicting the density profiles of grafted chain segments in this regime. Our subsequent work with the three-dimensional analog of RuSseL will investigate the mushroom regime more realistically, transcending the limitations of the one-dimensional approximation.74
(ii) Dense brush regime. With increasing σg, Mg and RNP the radial density profiles become more pronounced and feature extended regions with bulk densities; e.g., see Fig. 3 for σg ≥ 0.8 nm−2 and RNP ≥ 64 nm. Towards the matrix phase, the radial density profiles feature a characteristic sigmoid shape61 suggesting stretched brushes. The profiles of grafted and matrix chains intercept at reduced densities φm = φg ≃ 0.5. The presence of chemically grafted chains on the particle surface inhibits the penetration of matrix chains into the solid–polymer interfacial region and the strength of this exclusion of matrix chains increases with increasing σg, RNP, and Mg.
(iii) Crowding regime. In the extreme case of high grafting densities (σg ≥ 1.6 nm−2) and low curvatures (e.g., RNP ≥ 64 nm), the crowding experienced by the grafted chain segments reaches a level where their densities exceed the bulk densities somewhat (see dashed grey line in the plots of Fig. 3). In other words, the compressing forces imposed by the stretching of grafted chains overcome the tendency of the equation of state to maintain bulk reduced densities at unity; hence, the densities exceed this level. In this regime matrix chains are unable to reach the surface of the NP, even for the shortest grafted chains (Mg = 1.25 kg mol−1) studied herein.
In Fig. 3, for given σg and RNP, the radial density profiles are shifted by about a constant amount along the abscissa whenever the Mg is doubled; this effect becomes more pronounced with increasing RNP. Given that the radial density profiles are presented in semi-log plots, this observation leads to the conclusion that the edges of the profiles follow a ∼Mng power-law for constant σg and RNP. This scaling exponent exhibits a complicated dependence on σg and RNP, which is explored below (see Section 4.5).
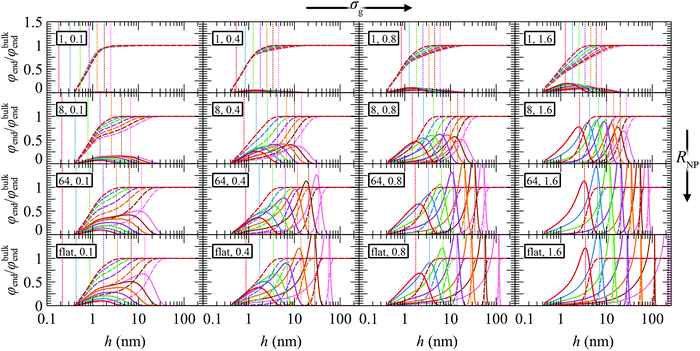
Regarding the total reduced density profiles (see Fig. S8 in the Section S8, ESI†), even though they are practically insensitive to Mg (except under very crowded conditions), they are somewhat enhanced near the surface with increasing σg and deviate from unity across the brush region under conditions of intense chain crowding.
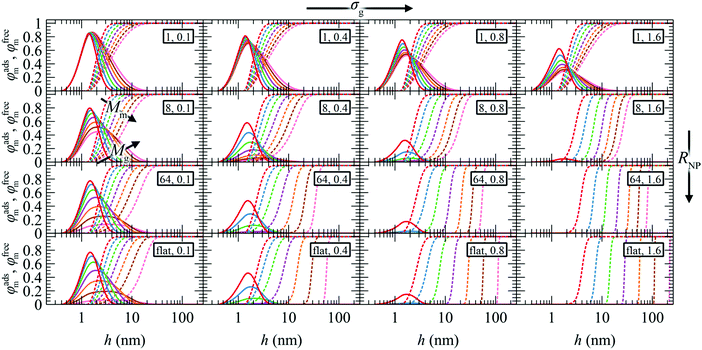
4.2 Structure of adsorbed polymer layer
The chains cannot propagate against the solid surface; as a consequence, their conformation is dictated by configurational entropy effects different from those prevailing in the bulk melt. Furthermore, the presence of the NP or the planar surface brings about an attraction of the polymer segments—which belong either to grafted or matrix chains—towards the solid surface. The strength of this attraction, in relation to the cohesive interactions of the polymer, determines the wetting behavior of the melt on the solid surface. Low, moderate, and high energy surfaces lead to low, high (e.g., treated silica80) and perfect (e.g., untreated silica80) wetting conditions which may alter the local configurations of the grafted and matrix chains relative to what is dictated by entropic phenomena.In order to investigate these effects, a distinction is made between “adsorbed” and “free” chains. By definition, grafted chains are adsorbed, therefore the aforementioned distinction concerns primarily the matrix chains. The value of the characteristic distance of closest approach to the NP surface, below which a matrix chain is characterized as adsorbed, is set at hads = 1.28 nm. This is where the tail of the Hamaker potential emanating from the solid starts, i.e., where the Hamaker potential assumes a value equal to ∼−0.005kBT. It should be emphasized at this point that the distinction between “adsorbed” and “free” chains is not based on chain dynamics, but rather on a geometric criterion revealing the tendency/ability of matrix chains to penetrate the brush and experience the potential exerted by the solid surface.
The reduced density of free matrix chains can be derived from the convolution integral of eqn (21).
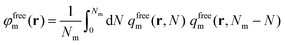 | (21) |
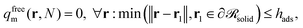 whilst the other boundary conditions remain the same. Subsequently, the reduced density of the segments of adsorbed matrix chains is obtained as φadsm(r) = φm(r) − φfreem(r).
whilst the other boundary conditions remain the same. Subsequently, the reduced density of the segments of adsorbed matrix chains is obtained as φadsm(r) = φm(r) − φfreem(r).
Fig. 4 presents the reduced radial density profiles of free (φfreem) and adsorbed (φadsm) matrix chains across the (RNP, σg, Mg) parameter space. The reduced radial density profiles of segments belonging to free chains assume a value equal to unity in the bulk, while going by definition to zero when approaching hads. According to Fig. 4, the matrix chains can easily penetrate the brush of grafted chains in the mushroom regime. With increasing σg and RNP, the matrix chains experience noticeable resistance in penetrating the brush, while φadsm → 0 upon transitioning to the crowding regime.
4.3 Chains/area profiles
In three dimensions, the chains/area can be defined as the number of chain segments which cross at least once a surface and it is a measure of chain orientation introduced in ref. 51, 61 and 81. A meaningful choice for
and it is a measure of chain orientation introduced in ref. 51, 61 and 81. A meaningful choice for  would be a surface which is parallel to the surface of the solid
would be a surface which is parallel to the surface of the solid 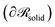 at distance h0;
at distance h0; 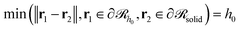 . Ref. 51, 61 and 81 include a detailed explanation of the chains/area calculation in one dimension; in this work we present a more general formalism in three dimensions which is compatible with smooth surfaces of arbitrary shape. To compute the chains/area we use the following eqn (22).
. Ref. 51, 61 and 81 include a detailed explanation of the chains/area calculation in one dimension; in this work we present a more general formalism in three dimensions which is compatible with smooth surfaces of arbitrary shape. To compute the chains/area we use the following eqn (22).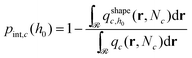 | (22) |
Initially, we estimate the probability pint,c that a chain will intersect 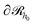 at least once (regardless of where in
at least once (regardless of where in 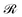 it may have started) using eqn (22), with
it may have started) using eqn (22), with 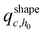 being the propagator of a type “c” chain arising from solving the Edwards diffusion equation (eqn 1) with an additional constraint that the chains cannot propagate past the surface,
being the propagator of a type “c” chain arising from solving the Edwards diffusion equation (eqn 1) with an additional constraint that the chains cannot propagate past the surface, 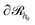 . To impose this constraint, we apply the Dirichlet boundary condition to all of the nodes that belong to this surface;
. To impose this constraint, we apply the Dirichlet boundary condition to all of the nodes that belong to this surface; 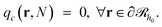 Subsequently, the number of chains (nch,c) of type c that pass at least once through
Subsequently, the number of chains (nch,c) of type c that pass at least once through 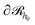 per unit area of the surface is calculated as follows:
per unit area of the surface is calculated as follows:
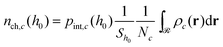 | (23) |
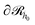 , and
, and 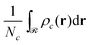 is the total number of type-c chains.
is the total number of type-c chains.
At this point, for the sake of comparison, we define a reference chain which obeys the Gaussian model and has infinite length. Given this definition, the reference chain will cross any shell-surface at least one time. Therefore, since the number of grafted chains equals ng = σg4πRNP2, the number of these reference chains passing through a surface separated by h from the surface of the solid per unit area of that surface is given by the following eqn (24).
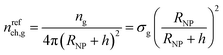 | (24) |
In Fig. 5a, we present nch for the matrix and the grafted chains, while Fig. 5b illustrates nch,g/σg for the grafted chains across the considered parameter space (RNP, σg, Mg). In both panels, the corresponding nrefch,g are represented by dotted lines. In the flat geometry nrefch,g = σg throughout the domain, while for finite curvatures, nrefch,g decreases with distance from the surface according to eqn (24), since the polymer chains have more available space to diffuse.
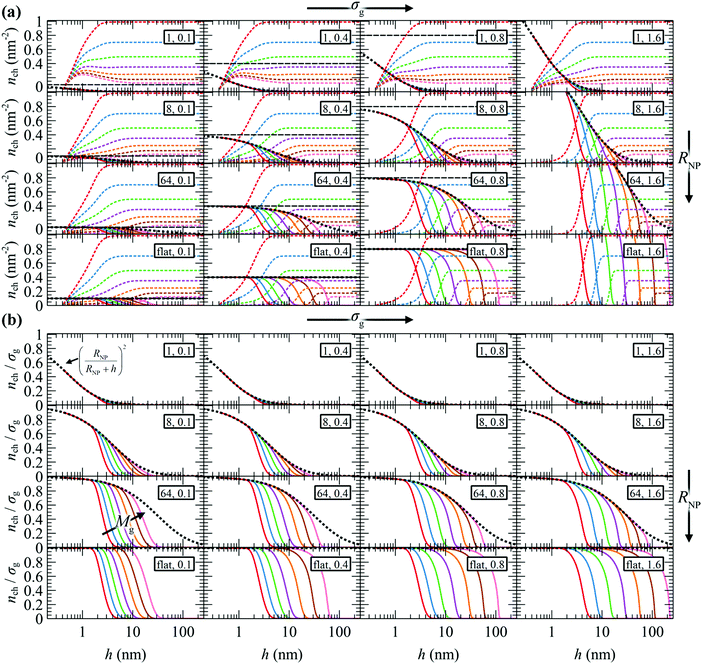 | ||
| Fig. 5 Profiles of (a) nch of m (dashed lines) and g (solid lines) chains, (b) nch/σg of g chains. Mg equals 1.25 (red), 2.5 (blue), 5 (green), 10 (violet), 20 (orange), 40 (brown) and 80 (pink) kg mol−1. In all cases, Mg = Mm. Legend in rectangles: RNP (nm), σg (nm−2). The dotted lines depict nrefch,g/σg for the reference chain from eqn (24). The horizontal dashed lines denote the grafting density. | ||
The behavior of the chains per area profiles with increasing grafting density or molar mass is consistent with the reduced radial density profiles of Fig. 3. For low nanoparticle radius, the chains per area profiles are insensitive to the grafting density, a picture that is consistent with the mushroom regime. Higher grafting density or molar mass leads to a gradual extension of grafted chains towards the bulk region and a simultaneous exclusion of matrix chains from the solid–melt interface. For larger NPs and grafting densities, the crowding phenomena inside the interfacial region intensify and push the grafted chain segments further towards the bulk region.
As expected, in the planar geometry case the number of grafted chains per area on the surface of the solid equals the grafting density throughout a broad region of the profile and starts to deviate upon approaching the region where ends terminate, where the number of grafted chains per area decreases. It is also noted that, since the hard sphere wall is located at ∼0.4 nm from the solid surface, the maximum nch,g assumed by the chains is nch = σgRNP2/(RNP + hHS)2, albeit nch = σg upon extrapolation towards h → 0.
4.4 Chain end segregation at the interface
The reduced density of the Nth segment, φc,N, of a chain of kind c located at r can be retrieved by the following expression: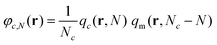 | (25) |
Normalizing this quantity with the corresponding density in the bulk phase (φbulkc,N = 1/Nc; since q = 1 in the bulk), we obtain a quantity of particular interest, which denotes the tendency of a region to attract or repel these segments.
Fig. 6 depicts the reduced radial density profiles of the end segments of grafted and matrix chains across the investigated parameter space. As expected, the density of free ends of grafted chains increases with increasing σg as well as with increasing RNP, since there is less space for the grafted chains to develop their conformations. With increasing grafting density the radial density profiles of the chain ends are shifted towards the bulk region. In the crowding regime where σg and RNP are high, the chain ends are segregated far from the surface, suggesting that the grafted chains are stretched. These profiles resemble those obtained for incompressible brushes, such as those in ref. 82, and with the more extreme case of Alexander's model,56,57 in which all chain ends are by definition concentrated at the edge of the brush, hedge, the position of which is denoted by the vertical dotted lines in Fig. 6 (for more details see Section S9, ESI†). In the mushroom regime, the chain ends from Alexander's model are segregated much closer to the solid wall as compared to our model and this is attributed to the following factors: (i) Alexander's model requires constant segment density of the grafted polymer, equal to that of the bulk melt; therefore, in the mushroom regime—where interpenetration between the matrix and grafted chains becomes significant—it needs to squeeze the profiles of grafted chain segments in order to maintain this bulk density and conserve the amount of material at the same time, (ii) the segments in our model experience an additional repulsive interaction which is modeled by a hard sphere wall located at hHS ∼ 0.4 nm. Clearly, Alexander's model with fixed density is not appropriate for the mushroom regime and generally in regimes where the matrix chains can penetrate the brush. Nevertheless, Alexander's model is expected to perform very well under bad solvent conditions (e.g., polymer/vacuum interphases) which lead to collapsed brushes across the solid surface.
4.5 Scaling of grafted polymer layers
As was mentioned in Section 4.1.2, the expansion of the grafted polymer brushes features a complicated dependence on σg, RNP and Mg. In the present section, an attempt will be made to analyze this dependence in terms of the mean brush thickness, 〈hg2〉1/2, which is directly related to the radial density profiles.83 In particular, the mean brush thickness is a functional of the density profile illustrating the mean distance of the segments of grafted chains from the solid surface. It can be estimated from the following expression: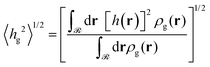 | (26) |
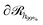 , which is parallel to the surface of the nanoparticle and encloses 99% of grafted chain segments:
, which is parallel to the surface of the nanoparticle and encloses 99% of grafted chain segments: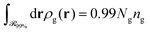 | (27) |
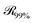 being the three-dimensional domain between
being the three-dimensional domain between  and
and 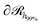 .
.
The scaling behavior of the polymer brushes shows quite a similar behavior to star polymers. According to Daoud and Cotton,55 the radius of a star polymer (Rstar) in a solvent exhibits a power-law dependence of the form: Rstar ∼ Nnstarfmstarνk, where Nstar is the number of segments constituting a branch, fstar is the number of branches, ν = 0.5 − χ is the monomer excluded volume parameter, χ is the Flory–Huggins parameter and n, m and k are the corresponding scaling exponents.84–86 They55 classified the behavior of the stars into three distinct regimes: (i) Nstar ≫ fstar1/2ν−2, Rstar ∼ Nstar3/5fstar1/5ν1/5bk; (ii) fstar1/2ν−2 ≫ Nstar ≫ f1/2, Rstar ∼ Nstar1/2fstar1/4bk; (iii) fstar1/2 ≫ Nstar, Rstar ∼ Nstar1/3fstar1/3bk, with bk being the Kuhn length. By substituting fstar → σg and Nstar → Mg, and by ignoring the contribution of the core of the NP to the brush, the model by Daoud and Cotton55 could be applied to describe the scaling of the polymer brushes via the following eqn (28),
| 〈hg2〉1/2 = Mngσmglg | (28) |
It should be noted here that the first regime of Daoud and Cotton's model, Nstar ≫ fstar1/2ν−2, cannot be addressed through our calculations, since they were performed in melt conditions (analogous to a theta-solvent), where χ = 0.5 and therefore ν−2 becomes infinite. Another key difference with Daoud and Cotton's model is that in NPs, the chains emanate from different grafting points, whereas in star polymers the chains emanate from the same point. Therefore, under theta or better solvent conditions and for large curvatures the chains will not interact with each other and the dependence on grafting density will be weak. The situation might be different under worse solvent conditions, where the brushes collapse partially (or fully for very large χ).
Fig. 7 illustrates evaluations for NPs with RNP = 8 nm, from RuSseL, from FOMC34 (blue “+”) and from small angle neutron scattering (SANS)48 measurements (red “×”). Overall, eqn (28) can describe accurately the scaling of the PS brushes on SiO2 nanoparticles with RNP = 8 nm, since both 〈hg2〉1/2 and 〈h99%〉 appear to be proportional to ∼M0.5gσ0.25g. Note that the evaluations from RuSseL appear shifted with respect to FOMC. This is attributed to the fact that, in FOMC, the increased density near the solid increases the weight of smaller hg in the integration of eqn (26); thus, it leads to decreased overall 〈hg2〉1/2. In addition, 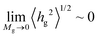 in RuSseL, since the length of grafted chains goes to zero. For the same reasons, the h99% points obtained with RuSseL lie slightly higher than FOMC and SANS values, while the minimum value of h99% is equal to the radius of the nanoparticle. In the mushroom regime (square points in Fig. 7), the evaluations from RuSseL deviate from the linear behavior and this could be a consequence of the fact that the one-dimensional model employed herein cannot capture accurately the behavior of chain segments for low grafting densities, i.e., the smearing of grafting points might be a poor approximation in this region. In our subsequent work, the mushroom regime will be thoroughly examined with the three-dimensional version of RuSseL.
in RuSseL, since the length of grafted chains goes to zero. For the same reasons, the h99% points obtained with RuSseL lie slightly higher than FOMC and SANS values, while the minimum value of h99% is equal to the radius of the nanoparticle. In the mushroom regime (square points in Fig. 7), the evaluations from RuSseL deviate from the linear behavior and this could be a consequence of the fact that the one-dimensional model employed herein cannot capture accurately the behavior of chain segments for low grafting densities, i.e., the smearing of grafting points might be a poor approximation in this region. In our subsequent work, the mushroom regime will be thoroughly examined with the three-dimensional version of RuSseL.
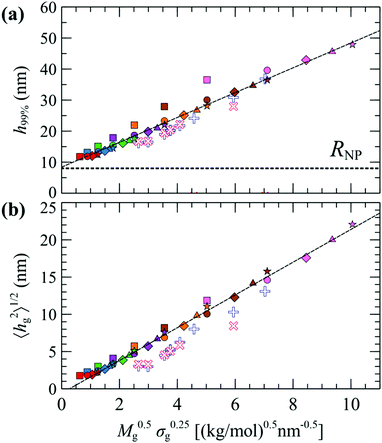 | ||
| Fig. 7 Evaluations of (a) h99% and (b) 〈hg2〉1/2 as a function of M0.5gσ0.25g for RNP = 8 nm, from FOMC (+),34 SANS measurements (×),48 and RuSseL; in the latter, colors denote chains with Mg = 1.25 (red), 2.5 (blue), 5 (green), 10 (violet), 20 (orange), 40 (brown) and 80 (pink) kg mol−1, and shapes denote grafting densities, σg = 0.1 (□), 0.4 (O), 0.8 (◇), 1.2 (△) and 1.6 (☆) nm−2. The dashed lines are guides to the eye. | ||
In the following we test these scaling laws across the full parameter space explored herein. Fig. 8a–e displays evaluations of 〈hg2〉1/2 plotted versus M0.5gσ0.25g for NP with radius 1, 4, 16 and 64 nm as well as for flat surfaces, for various Mg and σg. An interesting behavior is manifested in these plots, which reveals three distinct regimes: (i) for NP with small RNP (e.g., Fig. 8a) the curves for specific Mg (same colors) are disconnected and feature a very weak slope; (ii) for NP with intermediate sizes RNP = 4–8 nm (e.g., Fig. 8b) the curves for specific Mg connect with each other, suggesting that the ∼M0.5gσ0.25g correlation is fairly accurate in the description of this regime;34 (iii) for NP with larger sizes RNP > 8 nm (e.g., Fig. 8c–e) the curves appear disconnected as in the case of small NPs, the difference now being that the slope for each individual Mg curve appears to be stronger. The aforementioned analysis suggests that even though the ∼M0.5gσ0.25g correlation appears to describe the brush scaling with reasonable accuracy for RNP ∼ 4–8 nm, it becomes inaccurate for NP with relatively large or small radius.
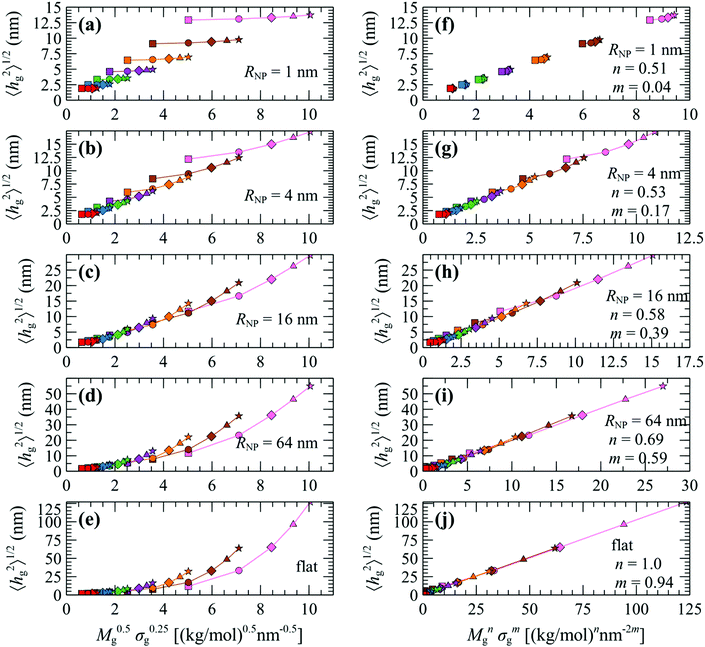 | ||
| Fig. 8 Evaluations of the mean brush thickness 〈hg2〉1/2 as a function of (a–e) M0.5gσ0.25g and (f–j) Mngσmg, where n, m are the optimized exponents from Fig. 10a. Colors denote chains with Mg = 1.25 (red), 2.5 (blue), 5 (green), 10 (violet), 20 (orange), 40 (brown) and 80 (pink) kg mol−1. Shapes denote grafting densities, σg = 0.1 (□), 0.4 (O), 0.8 (◇), 1.2 (△) and 1.6 (☆) nm−2. In all cases, Mg = Mm. | ||
In view of these observations, one can optimize the n and m exponents for each RNP to retrieve the power-law in eqn (28). According to Fig. 3, for constant RNP and σg, the radial density profiles expand by a roughly constant factor when doubling Mg; thus, it is reasonable to assume that 〈hg2〉1/2 ∼ Mng with n being a function of (RNP, σg). Fig. 9 presents the optimized n exponent from fitting RuSseL results to a power law 〈hg2〉1/2 ∼ Mng over all RNP and σg. The reader is reminded that the 1D model employed here might not be able to describe accurately the chain configuration at low grafting densities or molecular weights of grafted chains due to the inevitable smearing of grafting points. For this reason we decided to not take into account the cases corresponding to values of σgRg2 < 3, and σg = 0.1 nm−2 (which excluded the larger part of cases corresponding to the mushroom regime) when fitting the scaling exponents for the master equation, eqn (28).
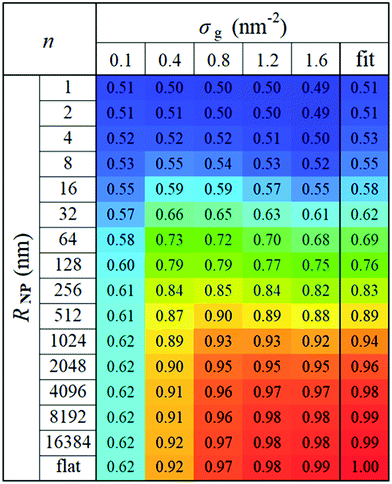 | ||
| Fig. 9 Optimized n exponents of the power-law in eqn (28) for set σg and RNP. The rightmost column depicts the fit with eqn (29). | ||
For large σg, the exponent n presents a stronger dependence on RNP than σg; thus, for simplicity, one could treat n as being independent of σg and instead being function of only RNP. Consequently, the data for σg > 0.1 nm−2 were fitted to a sigmoid function of the form:
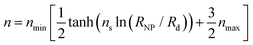 | (29) |
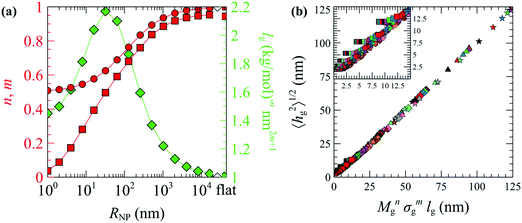 | ||
| Fig. 10 (a) The optimized n (circles) and m (squares) exponents of eqn (28) and lg (diamonds) as functions of RNP. The rightmost data points correspond to flat surfaces. (b) Evaluations of eqn (28) using the n, m and lg parameters in (a). Colors denote chains with Mg = 1.25 (red), 2.5 (blue), 5 (green), 10 (violet), 20 (orange), 40 (brown) and 80 (pink) kg mol−1. Shapes denote grafting densities, σg = 0.1 (□), 0.4 (O), 0.8 (◇), 1.2 (△) and 1.6 (☆) nm−2. The size of the symbols increases slightly with RNP. The inset in (b) depicts a zoomed region of the master curve. In all cases, Mg = Mm. | ||
Several key points can be retrieved by analyzing the scaling behavior of the brushes. Across the mushroom regime (small RNP or small σgNg), 〈hg2〉1/2 is practically independent of σg and scales as M0.5g. This is a characteristic property of the mushroom regime, in which the grafted chains do not interact with each other and behave as (reflected) ideal/unperturbed chains. The insensitivity of the brush thickness on the grafting density across the mushroom regime, hg ∼ σ0, is to be expected for small nanoparticles embedded in theta solvents or better. With increasing RNP and increasing σg the n and m exponents increase, while in the limit of large RNP and σg (crowding regime) the exponents reach unity indicating linear scaling, 〈hg2〉1/2 ∼ Mg1σg1; this kind of scaling is characteristic of the incompressible Alexander brushes;56,57 for more details see Section S9 (ESI†).
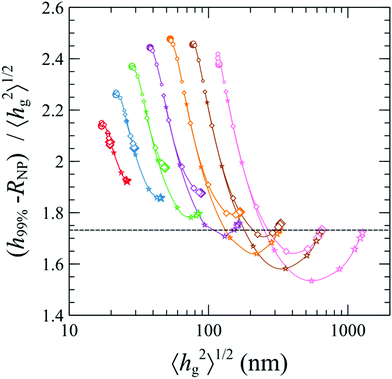
In Fig. 11, we demonstrate the (h99% – RNP) to mean brush thickness ratio against the mean brush thickness. In the Alexander model, this ratio is constant and equal to 31/2 and corresponds to the horizontal dashed line. Regarding our SCFT results, for small grafted chain lengths, the ratio is higher than the one of Alexander for all grafting densities and nanoparticle radii. For higher chain lengths, a minimum is manifested, while in the dense brush regime the ratio reaches the Alexander value as a limiting case. Overall, for small grafting density (0.1 nm−2) the dependence on the nanoparticle radius (ratio increasing with increasing RNP) features opposite trends as compared to the one for larger grafting densities (ratio decreasing with increasing RNP).
4.6 Thermodynamics
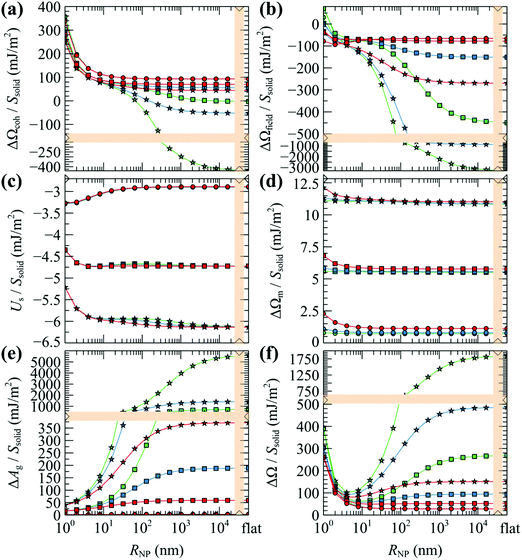 | ||
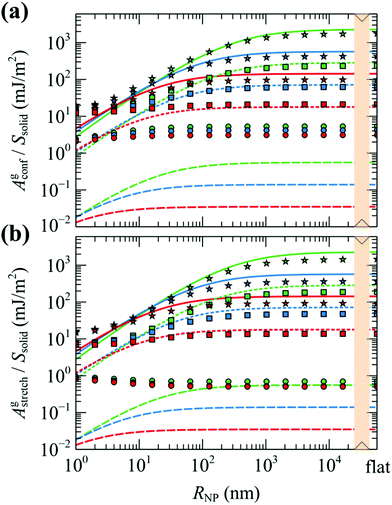
| Fig. 12 (a–e) Partial contributions to the grand potential per unit area from eqn (8)–(12). (f) Total grand potential per unit area. Colors denote chains with Mg = 5 (red), 20 (blue) and 80 (green) kg mol−1. Shapes denote grafting densities, σg = 0.1 (O), 0.8 (□) and 1.6 (☆) nm−2. In all cases, Mg = Mm. The rightmost data points correspond to flat surfaces. Bands denote scale changes along the axes. | ||
Similarly, the field term (ΔΩfield/Ssolid in Fig. 12b) presents the same qualitative behavior as ΔΩcoh/Ssolid for the exact same reasons: (i) steep initial decline due to high curvature; (ii) accumulation of negative values (see −ρdf/dρ| + [ρdf/dρ]|ρ=ρseg,bulk in Fig. S7b (ESI†) for φ > 1) by integrating over gradually larger brushes.
Considering the solid–polymer interaction term (Us/Ssolid), it is practically insensitive to chain molar mass; i.e., in Fig. 12c the energies for different chain molar masses do not exhibit noticeable variations with each other, irrespectively of NP size. With increasing grafting density it is obvious that the cohesion between the solid and the polymer is enhanced because of the increased density of polymer segments close to the surface as it is depicted in the total density profiles presented in Fig. S8 (ESI†).
In all cases, the entropy term associated with the partition function of matrix chains (ΔΩm/Ssolid in Fig. 12d) appears to be rather weak. It shifts upwards by a constant amount with increasing grafting density, because grafted chains claim more space in the interfacial region, leaving the matrix chains with fewer available conformations.
Concerning the entropy term associated with the grafted chains (ΔAg/Ssolid in Fig. 12e), it exhibits a rather interesting behavior: in the mushroom regime (σg = 0.1 nm−2, circles in Fig. 12e), ΔAg/Ssolid appears to be flat and roughly equal to zero, indicating that for low grafting densities there is no entropic penalty with increasing RNP associated with chain conformations. On the contrary, for larger σg (squares and stars), ΔAg/Ssolid increases with RNP for RNP up to ∼100 nm and plateaus to finite values in the limit of flat surfaces. This response is attributed to the stretching of the grafted chains due to crowding phenomena. A direct manifestation of this effect is presented in Fig. 6 that depicts the segregation of the grafted chain ends towards the matrix phase in crowded conditions.
The total grand potential from eqn (7) is illustrated in Fig. 12f. Across the mushroom regime (σg = 0.1 nm−2, circles) ΔΩ/Ssolid exhibits a monotonic decrease and plateaus to a value commensurate to the surface tension of PS for RNP ≥ 100 nm which is about γPS ∼ 25.9 mN m−1 at T = 500 K;61 note that, in the limiting case σg → 0 and RNP → ∞, and in the absence of the Hamaker potential, γPS ≡ ΔΩ/Ssolid. With increasing σg, the grand potential features a minimum at RNP ∼ 10 nm, after which it increases in a way suggesting the domination of the stretching term in Fig. 12e.
| Agconf = ΔAg + ΔAgfield | (30) |
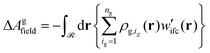 | (31) |
At this point, it is worth analyzing and comparing the conformational free energy of grafted chains with a rough estimate of the stretching free energy obtained by the density profiles of the grafted chain ends. In the one-dimensional model employed herein, the grafted chain conformations are reflected random walks starting at hg. Assuming that the system finds itself in the dense brush, rather than in the mushroom regime, the number of conformations of a chain such that the end-to-end vector projection normal to the solid surface is between h and h + Δh, can be estimated through the corresponding number in the unperturbed melt. It will be proportional to fend(h)dh, where the probability density fend(h) is given by eqn (32) in the context of the Gaussian chain model.
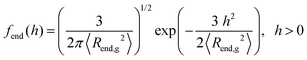 | (32) |
Note that this is based on the approximation that a grafted chain will access all conformations accessible to it at given value of the end-to-end distance. In reality, as is obvious from the profiles in Fig. 5 and 6, grafted chains are more stretched near their grafted end and less stretched near their free end. Based on eqn (32), the Helmholtz energy contribution, Achain, of a Gaussian chain grafted at rig whose end lies at point r, is given by eqn (33) within an additive constant. In eqn (32) and (33) 〈Rend,g2〉 is the mean squared end-to-end distance of an unperturbed chain of length Ng.
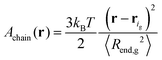 | (33) |
Let ρg,end = φg,endρseg,bulk be the local number density (segments per unit volume) of free ends of grafted chains; note that each grafted chain contributes one free end. Consecutively, integrating ρg,end across the domain results the total number of chains; 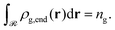 The total stretching free energy of grafted chains in our system within an additive constant equals
The total stretching free energy of grafted chains in our system within an additive constant equals 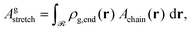 and it can be approximated across the dense brush regime as
and it can be approximated across the dense brush regime as
 | (34) |
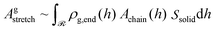 | (35) |
In the special case of Alexander's model in which all chain ends are segregated at the edge of the film, ρg,end = σgδ(h − hedge), thus eqn (34) becomes:
| Agstretch ∼ SsolidσgAchain(hedge) | (36) |
We can see that for larger grafting densities, our SCFT results and Alexander's model are in good agreement for all chain lengths in describing the conformational entropy of grafted chains as a function of the nanoparticle radius. A large discrepancy between the two models occurs for low grafting density; there, the totally stretched chains assumption of the Alexander model and the requirement to maintain bulk density everywhere result in suppressed grafted chains and thus lower Agstretch (compare the evaluations of Alexander's model in low grafting densities in Fig. 6). On the contrary, in the mushroom regime the profiles of grafted chains obtained with our model appear broader and this is reflected in the increased contribution to the conformational component of the free energy. Agstretch is consistently lower than Agconf—especially at low σg—and this is attributed to approximations in eqn (34) and (35) not sufficing in the regime; this effect will be investigated in detail in our subsequent work with RuSseL in three dimensions.
5. Concluding remarks
The conformation and shape of chains grafted on a solid surface immersed in a homopolymer melt of the same chemical constitution as the grafted chains are complex and depend on a number of molecular parameters. In this work, we have explored a broad parameter space for a system of a single grafted nanoparticle immersed in a homopolymer matrix. Adopting a self-consistent field theory modeling approach, the Edwards diffusion equation is solved by means of an implicit finite-difference algorithm in one dimension, introducing a smearing approximation for grafting points and taking advantage of the spherical symmetry of the problem. The parameterization is chosen so as to correspond to a particular chemical constitution (silica/polystyrene), which is readily accessible experimentally.48The spatial distributions and the conformations of grafted and matrix chain segments have been derived for different surface grafting densities, nanoparticle radii and chain lengths of grafted chains, taken equal to those of matrix chains. In order to better describe the results of our work, we define three different regimes: the mushroom regime, the dense brush regime, and the crowding regime. The behavior of the system in each of these regimes is well described and quantified in multiple ways, namely through the chains/area profiles, the distribution of matrix and grafted chain ends, as well as the segment density profiles of adsorbed and free matrix chains. It is clear that with increasing grafting density and chain molar mass, the grafted chains need to stretch towards the bulk in order to adjust to their conformational restriction.34,48,55 As a result, it is more difficult for the matrix chains to penetrate into the interfacial region.
The dependence of the brush thickness is examined with respect to all the aforementioned parameters in order to thoroughly investigate and clarify the behavior reported in the literature. The scaling law, ∼Nstar1/2fstar1/4, proposed by Daoud and Cotton for star polymers in the intermediate regime, fstar1/2ν−2 ≫ Nstar ≫ f1/2, is accurate over a specific range of nanoparticle radii, specifically from 4 nm to 8 nm. For larger nanoparticles, the scaling exponents exhibit a complicated behavior and thus a more general equation must be implemented, which treats the exponents of the molecular weight and grafting density as functions of nanoparticle radius. Adjusting also the pre-exponential factor of the scaling law, a master curve can be obtained, which provides a faithful description of SCFT predictions for the brush height given the molecular weight of grafted chains, the grafting density and the radius of the nanoparticle. This master curve seems to be quite accurate, especially in the region of high molecular weight and grafting density. In the mushroom regime, the brush height exhibits a weak dependence on the grafting density and nanoparticle radius and is proportional to the square root of the molecular weight. In the crowding regime the brush scales linearly with grafting density and molecular weight, while the density profiles of grafted chains, and in general the overall behavior of the brushes, compares well with Alexander's model for incompressible brushes.
In calculating the free energy of the system, the term associated with the conformational entropy of grafted chains does not depend on nanoparticle radius for low grafting densities and molar masses (Fig. 12e). The same plot reflects that with increasing grafting density or molar mass the chains need to stretch and therefore the free energy penalty associated with chain stretching increases. This entropy contribution of the grafted chains becomes dominant for high grafting densities and molar masses. The stretching free energy of grafted chains has been estimated in two different ways (1: from the configurational partition function of grafted chains and 2: approximately from the density profiles of the grafted chain ends) and a good agreement with the Alexander model was observed in the limit of large grafting densities. The corresponding entropic term of matrix chains has a minor contribution to the total free energy.
Future prospects of this study include the investigation of the structure and thermodynamics of an isolated NP and comparison against those of a NP embedded in polymer matrices; such comparisons allow for the prediction of meaningful thermodynamic quantities such as the solvation free energy of the nanoparticle. A more detailed investigation can be performed across the mushroom regime for low σg and RNPvia the three-dimensional finite element version of RuSseL developed in ref. 74, which treats the grafted chains as single entities, each one emanating from a single grafting point, avoiding the smearing approximation. A detailed comparison will be provided between the model employed herein and its 3D analogue in a forthcoming work, in terms of both thermodynamic and structural properties. The role of the distribution of the grafting points on the surface of the NP will also be explored. Finally, through the same three-dimensional finite element scheme, the potential of mean force between grafted NPs immersed in the melt can be predicted as a function of their center-to-center distance.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The valuable contribution of Dr Georgios G. Vogiatzis is deeply appreciated. Financial support by the Hellenic Foundation for Research and Innovation (H.F.R.I), project number 1263, under the “First Call for H.F.R.I. Research Projects to support Faculty members and Researchers and the procurement of high-cost research equipment grant,” is gratefully acknowledged. A. P. Sgouros thanks SOLVAY, Paris, France, for financial support through the project “Multiscale Modeling for the Design of Antifouling Copolymers”. C. J. Revelas gratefully acknowledges financial support through a doctoral fellowship from the “Special Account for Research Funding” of the National Technical University of Athens and also through the project MuSiComPS, Grant Agreement 10062/19, sponsored by the Limmat foundation. Part of this work was supported by computational time granted from the Greek Research and Technology Network (GRNET) in the National HPC facility—ARIS—under project ID pa201203 (MuSiPolI).References
- S. K. Kumar, V. Ganesan and R. A. Riggleman, Perspective: Outstanding theoretical questions in polymer-nanoparticle hybrids, J. Chem. Phys., 2017, 147, 020901 CrossRef PubMed.
- M. W. Matsen and J. M. Gardiner, Autophobic dewetting of homopolymer on a brush and entropic attraction between opposing brushes in a homopolymer matrix, J. Chem. Phys., 2001, 115, 2794–2804 CrossRef CAS.
- D. Sunday, J. Ilavsky and D. L. Green, A phase diagram for polymer-grafted nanoparticles in homopolymer matrices, Macromolecules, 2012, 45, 4007–4011 CrossRef CAS.
- R. Everaers and M. R. Ejtehadi, Interaction potentials for soft and hard ellipsoids, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2003, 67, 8 CrossRef.
- D. M. Trombly and V. Ganesan, Curvature effects upon interactions of polymer-grafted nanoparticles in chemically identical polymer matrices, J. Chem. Phys., 2010, 133, 154904 CrossRef PubMed.
- P. F. Green, The structure of chain end-grafted nanoparticle/homopolymer nanocomposites, Soft Matter, 2011, 7, 7914–7926 RSC.
- X. Jiang, B. Zhao, G. Zhong, N. Jin, J. M. Horton, L. Zhu, R. S. Hafner and T. P. Lodge, Microphase separation of high grafting density asymmetric mixed homopolymer brushes on silica particles, Macromolecules, 2010, 43, 8209–8217 CrossRef CAS.
- C. Chevigny, F. Dalmas, E. Di Cola, D. Gigmes, D. Bertin, F. Boué and J. Jestin, Polymer-grafted-nanoparticles nanocomposites: Dispersion, grafted chain conformation, and rheological behavior, Macromolecules, 2011, 44, 122–133 CrossRef CAS.
- J. F. Moll, P. Akcora, A. Rungta, S. Gong, R. H. Colby, B. C. Benicewicz and S. K. Kumar, Mechanical reinforcement in polymer melts filled with polymer grafted nanoparticles, Macromolecules, 2011, 44, 7473–7477 CrossRef CAS.
- D. A. Savin, J. Pyun, G. D. Patterson, T. Kowalewski and K. Matyjaszewski, Synthesis and characterization of silica-graft-polystyrene hybrid nanoparticles: effect of constraint on the glass-transition temperature of spherical polymer brushes, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 2667–2676 CrossRef CAS.
- M. Giovino, E. Buenning, A. Jimenez, S. K. Kumar and L. Schadler, Polymer Grafted Nanoparticle Viscosity Modifiers, Macromol. Chem. Phys., 2019, 220, 1–7 CrossRef.
- D. Zhao, S. Ge, E. Senses, P. Akcora, J. Jestin and S. K. Kumar, Role of Filler Shape and Connectivity on the Viscoelastic Behavior in Polymer Nanocomposites, Macromolecules, 2015, 48, 5433–5438 CrossRef CAS.
- S. Kim, K. Hyun, B. Struth, K. H. Ahn and C. Clasen, Structural Development of Nanoparticle Dispersion during Drying in Polymer Nanocomposite Films, Macromolecules, 2016, 49, 9068–9079 CrossRef CAS.
- S. Askar, L. Li and J. M. Torkelson, Polystyrene-Grafted Silica Nanoparticles: Investigating the Molecular Weight Dependence of Glass Transition and Fragility Behavior, Macromolecules, 2017, 50, 1589–1598 CrossRef CAS.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos, V. Pryamitsyn, V. Ganesan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Anisotropic self-assembly of spherical polymer-grafted nanoparticles, Nat. Mater., 2009, 8, 354–359 CrossRef CAS PubMed.
- M. Giovino, J. Pribyl, B. Benicewicz, S. Kumar and L. Schadler, Linear rheology of polymer nanocomposites with polymer-grafted nanoparticles, Polymer, 2017, 131, 104–110 CrossRef CAS.
- Z. M. Abbas, M. Tawfilas, M. M. Khani, K. Golian, Z. M. Marsh, M. Jhalaria, R. Simonutti, M. Stefik, S. K. Kumar and B. C. Benicewicz, Reinforcement of polychloroprene by grafted silica nanoparticles, Polymer, 2019, 171, 96–105 CrossRef CAS.
- Y. Jiao, M.-S. Hsiao, R. A. Vaia, A. Tibbits, L. F. Drummy, A. Gillman and P. Buskohl, Deformation Behavior of Polystyrene-Grafted Nanoparticle Assemblies with Low Grafting Density, Macromolecules, 2018, 51, 7257–7265 CrossRef CAS.
- Y. Wei, Y. Xu, A. Faraone and M. J. A. Hore, Local Structure and Relaxation Dynamics in the Brush of Polymer-Grafted Silica Nanoparticles, ACS Macro Lett., 2018, 7, 699–704 CrossRef CAS.
- M. Jhalaria, E. Buenning, Y. Huang, M. Tyagi, R. Zorn, M. Zamponi, V. García-Sakai, J. Jestin, B. C. Benicewicz and S. K. Kumar, Accelerated Local Dynamics in Matrix-Free Polymer Grafted Nanoparticles, Phys. Rev. Lett., 2019, 123, 158003 CrossRef CAS PubMed.
- T. V. M. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C. Böhm and F. Müller-Plathe, Interface of grafted and ungrafted silica nanoparticles with a polystyrene matrix: atomistic molecular dynamics simulations, Macromolecules, 2011, 44, 2316–2327 CrossRef CAS.
- D. Meng, S. K. Kumar, J. M. D. Lane and G. S. Grest, Effective interactions between grafted nanoparticles in a polymer matrix, Soft Matter, 2012, 8, 5002–5010 RSC.
- J. Kalb, D. Dukes, S. K. Kumar, R. S. Hoy and G. S. Grest, End grafted polymer nanoparticles in a polymeric matrix: effect of coverage and curvature, Soft Matter, 2011, 7, 1418–1425 RSC.
- J. G. Ethier and L. M. Hall, Modeling individual and pairs of adsorbed polymer-grafted nanoparticles: structure and entanglements, Soft Matter, 2018, 14, 643–652 RSC.
- G. D. Smith and D. Bedrov, Dispersing nanoparticles in a polymer matrix: are long, dense polymer tethers really necessary?, Langmuir, 2009, 25, 11239–11243 CrossRef CAS PubMed.
- T. B. Martin, P. M. Dodd and A. Jayaraman, Polydispersity for tuning the potential of mean force between polymer grafted nanoparticles in a polymer matrix, Phys. Rev. Lett., 2013, 110, 018301 CrossRef PubMed.
- A. Jayaraman and N. Nair, Integrating PRISM theory and Monte Carlo simulation to study polymer-functionalised particles and polymer nanocomposites, Mol. Simul., 2012, 38, 751–761 CrossRef CAS.
- J. W. Barnett and S. K. Kumar, Modeling gas transport in polymer-grafted nanoparticle membranes, Soft Matter, 2019, 15, 424–432 RSC.
- A. Chakrabarti, P. Nelson and R. Toral, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 4930–4934 CrossRef CAS PubMed.
- T. Lafitte, S. K. Kumar and A. Z. Panagiotopoulos, Self-assembly of polymer-grafted nanoparticles in thin films, Soft Matter, 2014, 10, 786–794 RSC.
- C. R. Bilchak, E. Buenning, M. Asai, K. Zhang, C. J. Durning, S. K. Kumar, Y. Huang, B. C. Benicewicz, D. W. Gidley, S. Cheng, A. P. Sokolov, M. Minelli and F. Doghieri, Polymer-Grafted Nanoparticle Membranes with Controllable Free Volume, Macromolecules, 2017, 50, 7111–7120 CrossRef CAS.
- C. Ibergay, P. Malfreyt and D. J. Tildesley, Electrostatic interactions in dissipative particle dynamics: toward a mesoscale modeling of the polyelectrolyte brushes, J. Chem. Theory Comput., 2009, 5, 3245–3259 CrossRef CAS PubMed.
- F. Lo Verso, S. A. Egorov, A. Milchev and K. Binder, Spherical polymer brushes under good solvent conditions: molecular dynamics results compared to density functional theory, J. Chem. Phys., 2010, 133, 184901 CrossRef PubMed.
- G. G. Vogiatzis and D. N. Theodorou, Structure of polymer layers grafted to nanoparticles in silica–polystyrene nanocomposites, Macromolecules, 2013, 46, 4670–4683 CrossRef CAS.
- T. L. Chantawansri, S. M. Hur, C. J. Garca-Cervera, H. D. Ceniceros and G. H. Fredrickson, Spectral collocation methods for polymer brushes, J. Chem. Phys., 2011, 134, 244905 CrossRef PubMed.
- M. Müller, Phase diagram of a mixed polymer brush, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2002, 65, 1–4 Search PubMed.
- D. J. Irvine, A. M. Mayes and L. Griffith-Cima, Self-consistent field analysis of grafted star polymers, Macromolecules, 1996, 29, 6037–6043 CrossRef CAS.
- S. Deng, L. Zhang, X. Zhou, C. Fan, Q. Lin and J. Lin, Exploring Microstructures and Interphase Properties of Surface- Grafted Diblock Copolymers in a Homopolymer Melt by Self-Consistent Field Theory Simulations, J. Macromol. Sci., Part B: Phys., 2015, 54, 348–364 CrossRef CAS.
- J. Xu, H. Zhang and Y. Yang, Morphology and Interactions of Polymer Brush-Coated Spheres, J. Polym. Sci., 2006, 44, 2811–2820 CrossRef CAS.
- S. E. Harton and S. K. Kumar, Mean-Field Theoretical Analysis of Brush-Coated Nanoparticle Dispersion in Polymer Matrices, J. Polym. Sci., 2008, 46, 351–358 CrossRef CAS.
- M. P. Pépin and M. D. Whitmore, Monte Carlo and numerical self-consistent field study of systems with end-grafted and free polymers in good solvent, J. Chem. Phys., 2001, 114, 8181–8195 CrossRef.
- J. R. Roan and T. Kawakatsu, Self-consistent-field theory for interacting polymeric assemblies. I. Formulation, implementation, and benchmark tests, J. Chem. Phys., 2002, 116, 7283–7294 CrossRef CAS.
- J. R. Roan and T. Kawakatsu, Self-consistent-field theory for interacting polymeric assemblies. II. Steric stabilization of colloidal particles, J. Chem. Phys., 2002, 116, 7295–7310 CrossRef CAS.
- C. Tong, Numerical self-consistent field theory study of the response of strong polyelectrolyte brushes to external electric fields, J. Chem. Phys., 2015, 143, 054903 CrossRef PubMed.
- E. B. Zhulina, O. V. Borisov, V. A. Pryamitsyn and T. M. Birshtein, Coil-Globule Type Transitions in Polymers. 1. Collapse of Layers of Grafted Polymer Chains, Macromolecules, 1991, 24, 140–149 CrossRef CAS.
- G. H. Fredrickson, V. Ganesan and F. Drolet, Field-theoretical computer simulation methods for polymer and complex fluids, Macromolecules, 2002, 35, 16–39 CrossRef CAS.
- G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, International Series of Monographs on Physics, Oxford University Press, Oxford, UK, 2006 Search PubMed.
- M. Mayer, Westfäalischen Wilhelms-Universitäat Müunster, Müunster, 2012 Search PubMed.
- G. Munaò, A. Pizzirusso, A. Kalogirou, A. De Nicola, T. Kawakatsu, F. Müller-Plathe and G. Milano, Molecular structure and multi-body potential of mean force in silica–polystyrene nanocomposites, Nanoscale, 2018, 10, 21656–21670 RSC.
- G. Munaò, A. Correa, A. Pizzirusso and G. Milano, On the calculation of the potential of mean force between atomistic nanoparticles, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 38 CrossRef.
- K. C. Daoulas, D. N. Theodorou, V. A. Harmandaris, N. C. Karayiannis and V. G. Mavrantzas, Self-consistent-field study of compressible semiflexible melts adsorbed on a solid substrate and comparison with atomistic simulations, Macromolecules, 2005, 38, 7134–7149 CrossRef CAS.
- D. N. Theodorou, Microscopic Structure and Thermodynamic Properties of Bulk Copolymers and Surface-Active Polymers at Interfaces. 1. Theory, Macromolecules, 1988, 21, 1411–1421 CrossRef CAS.
- D. N. Theodorou, Structure and Thermodynamics of Bulk Homopolymer/Solid Interfaces: A Site Lattice Model Approach, Macromolecules, 1988, 21, 1400–1410 CrossRef CAS.
- G. G. Vogiatzis and D. N. Theodorou, Structure of polymer layers grafted to nanoparticles in silica–polystyrene nanocomposites, Macromolecules, 2013, 46, 4670–4683 CrossRef CAS.
- M. Daoud and J. P. Cotton, Star Shaped Polymers: a Model for the Conformation and Its Concentration Dependence, J. Phys., 1982, 43, 531–538 CrossRef CAS.
- S. Alexander, Adsorption of Chain Molecules with a Polar Head – A Scaling Description, Le J. Phys., 1977, 38, 983–987 CrossRef CAS.
- P. G. de Gennes, Conformations of Polymers Attached to an Interface, Macromolecules, 1980, 13, 1069–1075 CrossRef CAS.
- J. Midya, M. Rubinstein, S. K. Kumar and A. Nikoubashman, Structure of polymer-grafted nanoparticle melts, ACS Nano, 2020, 14, 15505–15516 CrossRef PubMed.
- C. R. Bilchak, M. Jhalaria, Y. Huang, Z. Abbas, J. Midya, F. M. Benedetti, D. Parisi, W. Egger, M. Dickmann, M. Minelli, F. Doghieri, A. Nikoubashman, C. J. Durning, D. Vlassopoulos, J. Jestin, Z. P. Smith, B. C. Benicewicz, M. Rubinstein, L. Leibler and S. K. Kumar, Tuning Selectivities in Gas Separation Membranes Based on Polymer-Grafted Nanoparticles, ACS Nano, 2020, 14, 17174–17183 CrossRef CAS PubMed.
- A. P. Sgouros, G. G. Vogiatzis, G. Kritikos, A. Boziki, A. Nikolakopoulou, D. Liveris and D. N. Theodorou, Molecular Simulations of Free and Graphite Capped Polyethylene Films: Estimation of the Interfacial Free Energies, Macromolecules, 2017, 50, 8827–8844 CrossRef CAS.
- A. T. Lakkas, A. P. Sgouros and D. N. Theodorou, Self-Consistent Field Theory Coupled with Square Gradient Theory of Free Surfaces of Molten Polymers and Compared to Atomistic Simulations and Experiment, Macromolecules, 2019, 52, 5337–5356 CrossRef CAS.
- S. F. Doi and M. Edwards, The Theory of Polymer Dynamics, Clarendon Press, 1986 Search PubMed.
- D. N. Theodorou, Polymers at Surfaces and Interfaces, Comput. Simulations Surfaces Interfaces, 2003, 329–419 CAS.
- F. Schmid, Self-consistent-field theories for complex fluids, J. Phys.: Condens. Matter, 1998, 10, 8105–8138 CrossRef CAS.
- I. C. Sanchez and R. H. Lacombe, An elementary molecular theory of classical fluids. Pure fluids, J. Phys. Chem., 1976, 80, 2352–2362 CrossRef CAS.
- I. C. Sanchez and R. H. Lacombe, Statistical Thermodynamics of Polymer Solutions, Macromolecules, 1978, 11, 1145–1156 CrossRef CAS.
- J. S. Rowlinson, Translation of J. D. van der Waals’ ‘The thermodynamik theory of capillarity under the hypothesis of a continuous variation of density’, J. Stat. Phys., 1979, 20, 197–200 CrossRef.
- A. P. Sgouros, A. T. Lakkas, G. Megariotis and D. N. Theodorou, Mesoscopic Simulations of Free Surfaces of Molten Polyethylene: Brownian Dynamics/kinetic Monte Carlo Coupled with Square Gradient Theory and Compared to Atomistic Calculations and Experiment, Macromolecules, 2018, 51, 9798–9815 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, Free energy of a nonuniform system. I. Interfacial free energy, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- H. Lin, Y. Y. Duan and Q. Min, Gradient theory modeling of surface tension for pure fluids and binary mixtures, Fluid Phase Equilib., 2007, 254, 75–90 CrossRef CAS.
- H. C. Hamaker, The London—van der Waals attraction between spherical particles, Physica, 1937, 4, 1058–1072 CrossRef CAS.
- J. U. Kim and M. W. Matsen, Finite-stretching corrections to the Milner–Witten–Cates theory for polymer brushes, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 135–144 CrossRef CAS PubMed.
- M. W. Matsen and G. H. Griffiths, Melt brushes of diblock copolymer, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 219–227 CrossRef CAS PubMed.
- C. J. Revelas, A. P. Sgouros, A. T. Lakkas and D. N. Theodorou, A Three-Dimensional Finite Element Methodology for Addressing Heterogeneous Polymer Systems with Simulations Based on Self-Consistent Field Theory in International Conference of Computational Methods In Science and Engineering 2020 (ICCMSE 2020), 2020.
- J. Sanders, Veusz-3.2.1 Search PubMed.
- I. G. Mathioudakis, G. G. Vogiatzis, C. Tzoumanekas and D. N. Theodorou, Multiscale simulations of PS–SiO2 nanocomposites: from melt to glassy state, Soft Matter, 2016, 12, 7585–7605 RSC.
- P. Träskelin, T. L. Kuhl and R. Faller, Molecular dynamics simulations of polystyrene brushes in dry conditions and in toluene solution, Phys. Chem. Chem. Phys., 2009, 11, 11324–11332 RSC.
- M. R. Gharib-Zahedi, M. Tafazzoli, M. C. Böhm and M. Alaghemandi, Interfacial thermal transport and structural preferences in carbon nanotube-polyamide-6,6 nanocomposites: How important are chemical functionalization effects?, Phys. Chem. Chem. Phys., 2015, 17, 14502–14512 RSC.
- P. G. de Gennes, Polymers at an interface; a simplified view, Adv. Colloid Interface Sci., 1987, 27, 189–209 CrossRef CAS.
- M. Mortezaei, M. H. N. Famili and M. Kokabi, The role of interfacial interactions on the glass-transition and viscoelastic properties of silica/polystyrene nanocomposite, Compos. Sci. Technol., 2011, 71, 1039–1045 CrossRef CAS.
- D. N. Theodorou, Lattice Models for Bulk Polymers at Interfaces, Macromolecules, 1988, 21, 1391–1400 CrossRef CAS.
- S. T. Milner, T. A. Witten and M. E. Cates, Theory of the Grafted Polymer Brush, Macromolecules, 1988, 21, 2610–2619 CrossRef CAS.
- C. M. Wijmans and E. B. Zhulina, Polymer Brushes at Curved Surfaces, Macromolecules, 1993, 26, 7214–7224 CrossRef CAS.
- P. J. Flory, In Principles of polymer chemistry, Cornell University Press, Ithaca NY, 1953 Search PubMed.
- F. Candau, P. Rempp and H. Benoit, A New Theoretical Approach to the Problem of Solution Behavior of Branched Polymers, Macromolecules, 1972, 5, 627–635 CrossRef CAS.
- P. G. De Gennes, Scaling concepts in polymer physics, Cornell University Press, Ithaca NY, 1979 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm00078k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |