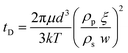Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stabilizing liquid drops in nonequilibrium shapes by the interfacial crosslinking of nanoparticles†
Mohd A.
Khan
and
Martin F.
Haase
 *
*
Van’t Hoff Laboratory of Physical and Colloid Chemistry, Department of Chemistry, Debye Institute of Nanomaterials Science, Utrecht University, Utrecht, CH 3583, The Netherlands. E-mail: m.f.haase@uu.nl
First published on 7th January 2021
Abstract
Droplets are spherical due to the principle of interfacial energy minimization. Here, we show that nonequilibrium droplet shapes can be stabilized via the interfacial self-assembly and crosslinking of nanoparticles. This principle allows for the stability of practically infinitely long liquid tubules and monodisperse cylindrical droplets. Droplets of oil-in-water are elongated via gravitational or hydrodynamic forces at a reduced interfacial tension. Silica nanoparticles self-assemble and cross-link on the interface triggered by the synergistic surface modification with hexyltrimethylammonium- and trivalent lanthanum-cations. The droplet length dependence is described by a scaling relationship and the rate of nanoparticle deposition on the droplets is estimated. Our approach potentially enables the 3D-printing of Newtonian Fluids, broadening the array of material options for additive manufacturing techniques.
1. Introduction
The dripping of water from a faucet is an everyday life example of interfacial phenomena. Gravity pulls the droplet down, but surface tension “glues” it to the faucet. When the inflowing water grows the pendant droplet to a critical size, surface tension cannot hold it anymore. The droplet breaks off via the Plateau–Rayleigh instability.1 Understanding the underlying physics of this process is essential for technologies such as ink-jet printing.Recent work by Liu et al. shows that the Plateau Rayleigh instability can be completely suppressed, and instead of droplets, stable liquid tubules are formed. This apparent violation of the surface energy minimization principle is possible because a rigid skin forms on the droplet. In their work, cellulose nanocrystals interact with polymer surfactants, causing them to attach to the droplets. The resulting cellulose nanocrystal surfactants adhere so strongly to the droplet interface that they mechanically jam.2 The shaping of liquids based on interfacial jamming was further explored by Forth et al. to print water into various tubular arrangements within a viscous oil phase.3
The possibility to 3D-print Newtonian fluids such as water into different shapes can complement the existing additive manufacturing techniques. Conventional 3D-printing requires yield stress fluids such as polymer melts, metals, or ceramic suspensions as printing materials. Printing yield-stress fluids layer-by-layer followed by solidification allows to fabricate complicated shapes or geometries that would be otherwise impossible to construct by hand. More research is needed to facilitate similar precision printing for Newtonian fluids, but the printing of liquids has already facilitated the construction of devices that are not possible with conventional additive manufacturing techniques. Examples are all-liquid fluidic devices4 and flow-through-coordinated reaction systems.5
Shaping liquids via interfacial jamming also enables the fabrication of droplets with anisotropic shapes with potential applications as reinforcements for structural materials,6 drug delivery vehicles7 or as photonic crystals.8 Rigid interfacial assemblies of solid particles have previously been used to stabilize droplets of anisotropic shapes by squeezing droplets through capillaries,9 compression of droplets between plates,10 partial droplet coalescence,11 droplet elongation by electric fields,12 controlled droplet shearing,13 droplet deformation via mechanical tools,14 and shaping of droplets in molds.15
Here, we introduce a new technique to generate liquid tubules and droplets of anisotropic shapes. We argue that the nonequilibrium droplet shapes are not stabilized by interfacial jamming,2,12,16 but instead by interfacial crosslinking of nanoparticles.
We distinguish these two terms as follows: an interfacially jammed film is composed of densely packed particles with the individual particles adhering so strongly to the interface that their removal is effectively impossible. Reducing the volume of a droplet covered by an interfacially jammed film results in the buckling of the interface, as the strong attachment of the particles conserves the overall surface area of the droplet. In an interfacially cross-linked film, the particles do not necessarily adhere strongly to the interface but are connected to each other laterally via chemical forces. Reduction of the droplet volume with an interfacially cross-linked film can result in partial detachment of the particles but the rigidity of the remaining film facilitates out-of-equilibrium droplet shapes.
To realize interfacial crosslinking, we previously used 3 valent lanthanum cations (La3+) to electrostatically bind interfacially attached particles to each other.17 Here, we show that interfacial crosslinking also enables the stabilization of virtually infinitely long liquid tubules. We demonstrate this by flowing a mixture of oil and ethanol through a small needle into an aqueous phase containing silica nanoparticles (SNP), hexyltrimethylammonium (HTA+) cations and La3+. Pendant drop tensiometry shows that HTA+ and La3+ act synergistically in generating a rigid interfacial assembly of the nanoparticles. We find that the formation of liquid tubules requires a lowering of the interfacial tension, which in our system is facilitated by mass transfer of ethanol from oil to water. Based on our experimental analysis, we demonstrate that liquid tubules can be generated via the action of gravitational forces and monodisperse droplets of anisotropic shape via controlled shear stresses in a microfluidic device. Finally, we describe the mechanics of anisotropic droplet formation with a previously introduced shear stress equation18 and approximate the interfacial nanoparticle deposition rate.
2. Materials and methods
Materials
Aqueous SNP suspensions (Ludox TM-50, pH 9), hexadecyl-trimethylammonium bromide (C16TAB) with purity >98%, hexyltrimethylammonium bromide (C6TAB, >98%), diethyl phthalate (DEP, 99.5%), lanthanum(III) chloride heptahydrate (LaCl3·7H2O), 1H,1H,2H,2H-perfluorooctyltriethoxysilane, 2-propanol (anhydrous, 99.5%) were purchased from Sigma-Aldrich and used as received. Deionized water and ethanol (>99.5%) were used for all the experiments.Foam stability
10 mL stock solutions of 50 wt% Ludox TM-50 (A), 100 mM HTA+ (B), and 10 mM La3+ (C) were prepared in deionized water. As shown in Fig. 2, different mixtures were prepared with final concentration of 5 wt% nanoparticles, 10 mM HTAB and 1 mM La3+. The pH values of all mixtures was determined to be 9 ± 0.2.Pendant drop tensiometry
Interfacial tension measurements were carried out using a pendant drop tensiometer (ThetaPhysics OCA) by fitting the droplet shape with the Young–Laplace equation. Please see ESI† for more details about the procedures.Dynamic light scattering
The size of Ludox TM-50 particles/aggregates was measured at varying La3+ concentration by dynamic light scattering (Malvern Zetasizer Ultra) at 633![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm wavelength of a He–Ne laser; the back scattered light was detected at 173°. The size of particle/aggregates was obtained from the intensity distribution by cumulant analysis.
nm wavelength of a He–Ne laser; the back scattered light was detected at 173°. The size of particle/aggregates was obtained from the intensity distribution by cumulant analysis.
Zeta potential measurement
Electrophoretic mobility measurements were carried out to measure the zeta potential of the SNP as a function of La3+ ion concentration. Zeta potential was calculated from the electrophoretic mobility with the Smoluchowski equation.Microfluidic device fabrication and experiments
Please see ESI† for experimental details about the procedures.3. Results and discussion
3.1 Interfacial attachment and crosslinking by HTA+ and La3+ modification of SNP
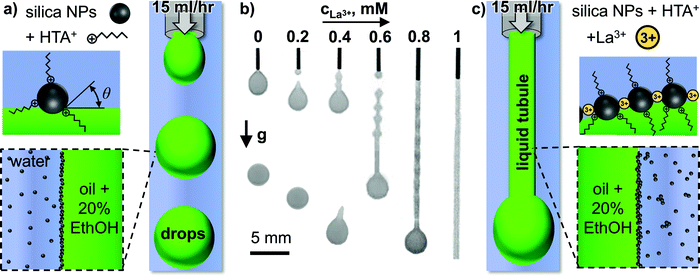
Fig. 1(a) schematically depicts the experimental setup employed to study liquid tubule formation. A mixture of diethyl phthalate (DEP) containing 20 vol% ethanol is flown through a small needle (260 μm inner diameter) into stagnant water containing 5 wt% SNP (Ludox TM, 20–30 nm particle diameter), 10 mM hexyltrimethylammonium cations (HTA+), and variable concentrations of trivalent lanthanum cations (La3+). Fig. 1(b) shows photographs of the resulting two-phase-flow at a constant flowrate of 15 mL h−1 for different La3+ concentrations in the aqueous phase.Increasing the La3+ concentration in the aqueous phase results in a gradual transition from spherical droplets forming below 0.2 mM La3+, to tadpole shaped droplets forming between 0.4–0.6 mM, to a liquid tubule forming above 0.8 mM La3+ (see Video S1, ESI†).
Why does the increase of the La3+ concentration result in this remarkably different two-phase flow behavior? In the following, we attempt to answer this question based on additional experiments. First, we demonstrate the interfacial behavior of the HTA+ and La3+ surface modification of the SNP qualitatively based on testing the foam stability. To this end, we prepare solutions and dispersions of the individual components, as well as their mixtures. These are shown as photographs in Fig. 2, taken immediately after vigorous shaking.
Neither the dispersion of 5 wt% SNP (A), nor the solution of 100 mM HTA+ (B) shows any stable foam phase, indicating that both components alone are not interfacially active. However, the mixture of both (5 wt% SNP, 10 mM HTA+) shows a foam layer that remains stable for several minutes (Fig. 2A + B). This can be explained as follows. Both, the negatively charged SNP and the HTA+ cations are hydrophilic and therefore remain in the water phase. However, in the mixture, HTA+ renders the SNP surface active, as it adsorbs electrostatically on silica, covering the surface partially with hexyl-chains in situ.19 This is confirmed by measurements of the contact angles of sessile water droplets on flat HTA+ modified silica surfaces, which show decreasing hydrophilicity of the surface.20 The HTA+ adsorption on the SNP increases their interfacial attachment energy, given by ΔGattach = −π·r2·γow(1 − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)2, with r the particle radius, γow the water/oil interfacial tension and θ the contact angle.21 For particles of 10 nm radius, ΔG can reach several hundred times the thermal energy of the particles (in kT), resulting in a densely packed self-assembled particle monolayer at the air/water interface, stabilizing the foam in Fig. 2(A + B).22,23
θ)2, with r the particle radius, γow the water/oil interfacial tension and θ the contact angle.21 For particles of 10 nm radius, ΔG can reach several hundred times the thermal energy of the particles (in kT), resulting in a densely packed self-assembled particle monolayer at the air/water interface, stabilizing the foam in Fig. 2(A + B).22,23
The second component influencing the interfacial assembly of the SNP in our experiments are La3+ cations. Fig. 2 shows that neither a solution of La3+ (C), nor a mixture of the SNP with 1 mM La3+ (A + C, 5 wt% silica, 1 mM La3+) allows for a stable foam formation. However, the mixture containing the SNP, 10 mM HTA+ and 1 mM La3+ (A + B + C) shows a stable foam, which even exceeds the height of the foam layer formed with SNP + 10 mM HTA+ (A + B). This indicates that HTA+ and La3+ act synergistically in enhancing the SNP surface activity.
The slightly cloudier appearance of the mixture SNP + HTA+ + La3+ (A + B + C) indicates that particle aggregation has occurred. We analyze the colloidal stability of the SNP next. Fig. 3 shows zeta potential and dynamic light scattering data for aqueous SNP dispersions at different La3+ concentrations.
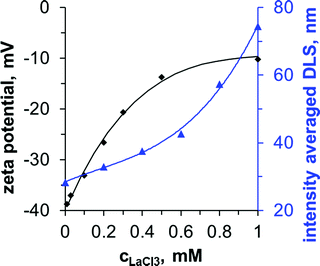 | ||
| Fig. 3 Colloidal stability of Ludox-TM in dependence of the La3+ concentration (pH 9). The corresponding DLS polydispersity index range from 0.18 (0 mM)–0.48 (1 mM), see ESI.† | ||
The zeta potential of the SNP in the absence of La3+ is −40 mV. As the La3+ concentration increases to 1 mM, the zeta potential increases to −10 mV. La3+ ions adsorb specifically on the negatively charged particles, reducing the zeta potential due to ion pairing with the deprotonated silanol groups. The decrease of the negative zeta potential results in partial aggregation of the particles as shown by the increase in the intensity averaged dynamic light scattering (DLS) signal from 30 nm to 75 nm (Fig. 3, secondary y-axis). Above 0.2 mM the particle size distributions become bimodal, with a second peak at around 100 nm (see ESI). The particles flocculate strongly above 1 mM La3+. In contrast, DLS measurements show that HTA+ causes only minor aggregation with an increase of the intensity averaged size to 40 nm at 10 mM HTA+ (see ESI†). Prior studies have found that the La3+ induced flocculation of SNP enhances emulsion stability and cryo-SEM images revealed the interfacial assembly of the particles.24,25 However, for liquid tubules to form in our experiments, the simultaneous adsorption of 1 mM La3+ and 10 mM HTA+ on the SNP is required (see Fig. 1 and ESI†).
Which properties of the HTA+ and La3+ induced interfacial SNP assembly to enable the droplet deformation away from spherical? We explore this in the following based on pendant drop tensiometry. Fig. 4(a) shows photographs of pure DEP droplets hanging on dispensing needles in different aqueous phases. We rapidly withdraw a DEP volume ΔV into the syringe to reduce the droplet area by 50%.
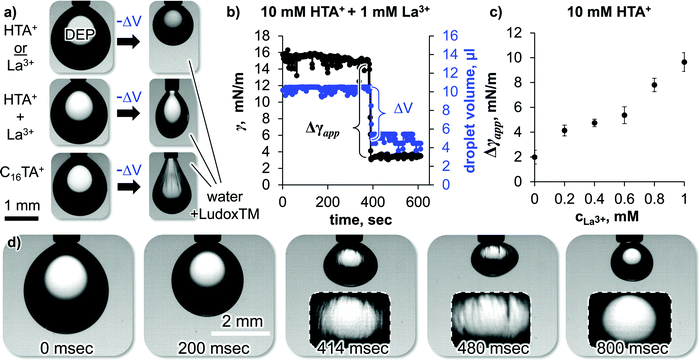 | ||
| Fig. 4 Effect of surface area reduction on droplet shape and apparent interfacial tension reduction (Δγapp). (a) Photographs of DEP droplets in different aqueous phases before and after droplet area reduction by 50%, (b) droplet volume and interfacial tension from pendant drop shape analysis against time before, before, during and after the droplet area reduction, (c) apparent interfacial tension reduction against La3+ concentration. (d) 90% volume reduction of a DEP droplet in a Ludox TM dispersion containing 10 mM HTA+ and 1 mM La3+ (see also Video S2, ESI†). | ||
Upon withdrawing DEP from a pendant droplet in a SNP dispersion containing 10 mM HTA+, the droplet becomes more spherical (Fig. 4(a), top row). This occurs since the gravitational force on the droplet decreases and the interfacial tension becomes more dominant in the force balance. The same happens when DEP is withdrawn from a droplet in a SNP dispersion with 1 mM La3+ (see ESI†).
In sharp contrast, when the droplet volume is reduced in a SNP dispersion containing 10 mM HTA+ and 1 mM La3+, the droplet shape becomes less spherical and rather ellipsoidal (Fig. 4(a), middle row). The counterintuitive shape change results from the rigid nature of the self-assembled nanoparticle coating on the droplet, as discussed in the following.
Fig. 4(b) plots the measurements of the droplet volume and interfacial tension γ during the shape change of the droplet shown in the middle row of Fig. 4(a). Before the shape change, γ is ∼15 mN m−1, slightly below the interfacial tension of pure water and DEP (∼16 mN m−1). Upon volume reduction, the software of the pendant drop tensiometer interprets the shape change as a reduction of the interfacial tension. To the software, the ellipsoidal shape indicates that gravity is strong enough to elongate the droplet against the surface tension. However, a lowering of the surface tension seems unlikely in our experiment, as there is no change in the chemical composition during the droplet volume reduction. Therefore, we will call the measured interfacial tension change here “apparent interfacial tension change”, or Δγapp.
Fig. 4(c) plots Δγapp for the DEP droplet volume reduction in a SNP dispersion containing 10 mM HTA+ as a function of the La3+ concentration. We find that Δγapp is independent of the droplet age, indicating that the interfacial assembly of the nanoparticles takes place on faster timescales than the timescales of the experiment (see ESI†). Δγapp increases with increasing La3+ concentration, or in other words the droplet shapes become more ellipsoidal.
To understand this further, we show in the bottom row of Fig. 4(a) the droplet shape change in a SNP dispersion containing 1 mM hexadecyltrimethylammonium cations (C16TA+). Upon volume reduction, the droplet also deforms in the C16TA+ system. However, this time permanent wrinkles can be observed on the surface of the droplet. Such wrinkles26–28 have been previously found for particle coated pendant droplets.10,12 Upon droplet area reduction, the particle monolayer buckles due to interfacial jamming of the particles, resulting in wrinkles.
Why does a volume reduction of the droplets in the SNP dispersion containing 1 mM C16TA+ result in wrinkles, but no wrinkles are observed for the same volume reduction in a SNP dispersion containing 10 mM HTA+ and 1 mM La3+? We believe that the different behaviors show that the C16TA+ modified particles are interfacially jammed, while the HTA+ + La3+ modified particles are interfacially cross-linked (and not jammed). We explain our interpretation in the following.
As mentioned in the introduction, particles jam on an interface because their high attachment energy does not allow them to escape to the bulk when they experience lateral forces. By using C16TA+ in the aqueous phase, long hydrocarbon chains adsorb on the particles. This results in a high contact angle θ. We do not have precise measurements for the contact angle as this requires advanced electron microscopy characterization.29 However, we estimate that C16TA+ modified Ludox TM particles have contact angles close to 90°, as they have previously been employed for the stabilization of bijels,30 which requires a θ of 90°. With the interfacial tension between DEP and water, the Ludox TM particle radius of 10 nm and θ = 90°, ΔGattach equals to −1220kT (with the Boltzmann constant k and the absolute temperature T). In other words, the particles are 1220 times stronger attached than their thermal energy allows them to escape. This high attachment energy forces the particles to stay at the interface when the droplet volume is reduced. Since the particles occupy a fixed area on the droplet, the interface must buckle to accommodate the interfacial particle coverage.
In contrast, the particles modified with 10 mM HTA+ and 1 mM La3+ have a lower contact angle, as the hexyl chain of the HTA+ and the lower HTA+ adsorption density does not impart much hydrophobicity to the particles. Macroscopic θ measurements of a sessile water droplet on a flat silica surface give a value of θ = 40° at a pH value of 9.20 It is unlikely that La3+ increases the contact angle significantly, as it does not introduce apolar chemical groups to the surface of the particles. For θ = 40°, ΔGattach calculates to −66.9kT. Based on this, the HTA+ + La3+ modified particles can detach more easily from the pendant droplet upon volume reduction. To test this hypothesis, we have reduced the volume of the droplet by ∼90% in Fig. 4d (see also Video S2, ESI†).
The experiment shows that wrinkles can be observed for a duration of 400 milliseconds during the droplet volume reduction in the presence of Ludox modified with 10 mM HTA+ and 1 mM La3+. Shortly after, the wrinkles disappear, demonstrating that the particles have detached from the interface. We therefore conclude, that HTA+ and La3+ modified particles are not interfacially jammed, as they can leave the interface (likely as aggregated clusters or sheets). However, the La3+ mediated crosslinking of the remaining particles at the interface provides rigidity, allowing the stabilization of out-of-equilibrium droplet shapes.
3.2 Interfacial tension reduction by ethanol addition to the droplet phase
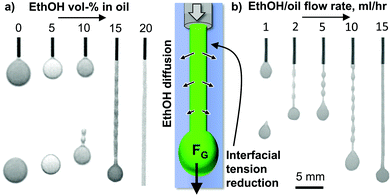
After analyzing the nanoparticle assembly on the oil/water interface, we next investigate the role of ethanol in the oil phase. Fig. 5(a) shows photographs of injecting DEP with variable ethanol volume fractions into a 5 wt% Ludox TM nanoparticle dispersion with 10 mM HTA+ and 1 mM La3+ (see also Video S3, ESI†).Injecting pure DEP or DEP containing 5 vol% ethanol results in dripping of spherical droplets. At 10 vol%, tadpole-like droplets pinch-off periodically from the dispensing needle. Once the ethanol content in DEP reaches 15 vol%, a liquid tubule with periodic bulges forms. Above 20 vol% ethanol in DEP the liquid tubule has a flat surface, indicating that the Plateau–Rayleigh instability has been completely suppressed.
The transition from dripping to liquid tubule formation is correlated with a reduction of the interfacial tension. We arrive at this conclusion based on the effect of the ethanol fraction in DEP on the size of the formed droplets. When increasing from 0 to 10 vol% ethanol in DEP the pinch off droplet size decreases gradually from 2 mm to 1.6 mm (see ESI†). This trend continues for the liquid tubules formed from 15 to 20 vol% ethanol in DEP, for which the diameter of the droplet at the tubule front decreases from 1.4 to 1.1 mm. This means, a lower gravitational force is required to pinch the droplet off, or for ethanol contents above 15 vol%, to pull the liquid tubule out of the needle (see ESI†).
During liquid tubule formation, ethanol diffuses from DEP to the surrounding water, lowering the interfacial tension locally. Increasing the ethanol content in water from 0–40 vol% reduces the interfacial tension between pure DEP and water from 16 to 2 mN m−1 (see ESI†). This finding is analogous to the observation of Liu et al.,2 where liquid tubule formation is made possible by a polymeric surfactant lowering the interfacial tension.
Fig. 5(b) shows liquid tubule formation in dependence of the flow rate of a mixture of 20% ethanol in DEP (see also Video S4, ESI†). At 1 mL h−1, dripping occurs. Between 2–10 mL h−1 a liquid tubule with a “beads on a string” like pattern forms. Above 15 mL h−1 a continuous cylindrical liquid tubule is generated. The origin of this transition has not been analyzed here and is subject to further work.
3.3 Microfluidic generation of elongated droplets
In the last part of this paper, the principles of droplet elongation by interfacial tension reduction and interfacial rigidification will be used to generate nonspherical droplets in a microfluidic device as depicted in Fig. 6(a).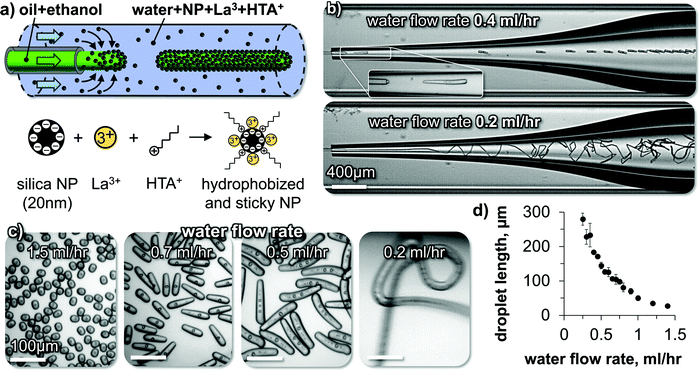 | ||
| Fig. 6 Liquid tubule formation and droplet elongation. (a) Schematics of droplet extrusion and nanoparticle surface modification. (b) Micrographs of elongated droplet and liquid tubule formation. The DEP droplets include internal water droplets which have been formed by phase separation of water, which was taken up by the droplet during the ethanol diffusion, as described in ref. 31. (c) Micrographs of collected droplets and fiber. (d) Droplet length dependence on water flow rate. | ||
A perfluorooctyltriethoxysilane coated glass capillary is centered inside a second larger glass capillary (see ESI). We flow a mixture of ethanol and DEP at a constant rate out of the first capillary into the second capillary. In the second capillary, an aqueous phase of 5 wt% SNP, 10 mM HTA+ and 1 mM La3+ flows at variable rates. Fig. 6(b) shows snapshots of high-speed video microscopy of the droplet elongation for two different flow rates of the aqueous phase.
At an aqueous phase flow rate of 0.4 mL h−1, short cylindrical droplets pinch off from the extrusion nozzle. Lowering the flow rate of the aqueous phase to 0.2 mL h−1 results in the extrusion of a continuous liquid tubule. The fiber undulates in the widening channel due to the reduced shear stress (see Video S5, ESI†).
Different shapes of droplets can be obtained by varying the water phase flow rate (Fig. 6(c) and Video S6, ESI†). The droplet length increases by lowering the water flow rate until a continuous liquid tubule is formed below 0.2 mL h−1(Fig. 6(d)).
The observed flow behavior is the opposite from what one would expect during a microfluidic dripping to jetting transition.32 Rather than obtaining a continuous jet of the DEP/ethanol mixture via increasing the water flow rate, here increasing the water flow rate results in a transition from a liquid tubule to shorter cylindrical droplets. We discuss in the following how this behavior originates from the rigid interfacial assembly of the SNP.
High-speed video microscopy shows the individual droplet pinch-off events (Fig. 7(a)). A single droplet elongates until a critical length and pinches off. The critical length depends on the water flow rate as shown in Fig. 6(c and d). At a constant water flow rate, the pinch-off events repeat themselves always at the same critical length, explaining the monodispersity of the elongated droplets.
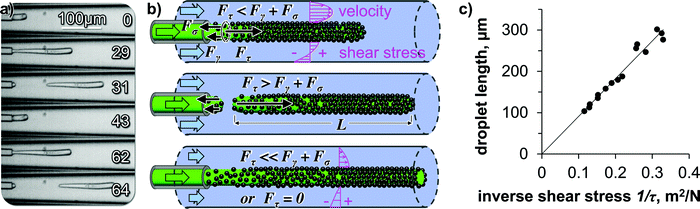 | ||
| Fig. 7 Mechanics of droplet pinch off. (a) High-speed video micrographs of droplet pinch-off with time in milliseconds, (b) Illustration of the force balance during droplet pinch off (not drawn to scale), illustration includes depiction of calculated velocity and shear stress profiles in water stream, (c) droplet lengths from Fig. 6(d) plotted against inverse shear stress. | ||
We hypothesize that the droplet elongation can be described by a simple force balance. While the oil/ethanol mixture flows out of the capillary as a droplet, it experiences a pull from the surrounding water flow. The droplet elongates as a cylinder from the capillary orifice facilitated by the ethanol transfer induced lowering of the interfacial tension. The cylindrical shape is then stabilized via the interfacial deposition and crosslinking of the SNP.
The pulling force on the droplet originates from the shear-force of the surrounding water stream. The resulting shear force can be written as Fτ = L·π·D·τ, with L the droplet length, D the diameter of the droplet, and τ the shear stress. While L increases, Fτ increases proportionally. Two forces are resisting the shear force: (i) the surface tension force calculates to Fγ = γow·π·D, with γow the oil/water interfacial tension, (ii) a tensile force builds up gradually in the deposited interfacial nanoparticle film on the droplet, equaling to Fσ = σ·π·D·s, with σ the tensile strength and s the nanoparticle film thickness. We hypothesize that instantaneously before droplet pinch off, the forces balance each other according to Fτ = Fγ + Fσ (see Fig. 7(b)).
Substituting and rearranging the force balance yields L = (γow + σs)·1/τ. If our hypothesis holds true, plotting L against the inverse shear stress 1/τ on the fiber surface will give a linear trend (for constant γow + σs). To obtain the shear stress on the fiber surface, we use the solution for the Navier–Stokes-equation for pressure driven flow in a cylindrical annulus, with the inner cylinder (the droplet) moving at the velocity U (see ESI†).18
Indeed, the data points for the droplet lengths fall on a linear line when plotted against the inverse shear stress (Fig. 7(c)), suggesting that our force balance model is a valid approximation of the droplet pinch-off physics here.
Last, we discuss the particle attachment rate to the oil/water interface. As the droplet flows out of the tip of the glass capillary, silica nanoparticles attach to the newly formed oil/water interface (Fig. 6(a)). The stabilization of the out-of-equilibrium droplet shapes suggests that the particle deposition rate exceeds the droplet area generation rate. We approximate the average particle deposition time tD to form a monolayer on the interface by combining the Stokes–Einstein equation, the formula for the 1-dimensional mean square displacement, and a formula estimating the diffusion distance (see ESI†).
Before we conclude, we briefly state the limitations of our model to estimate tD. Our calculation neglects that not all particles that diffuse to the interface attach successfully. There can be an electrostatic energy barrier to overcome. Moreover, the more particles attach, the harder it is to find a “free spot”. These two processes can increase tD. On the other hand, the initial stabilization of the out-of-equilibrium droplet shape may not require full coverage by the nanoparticles, as a partially covered surface can already provide sufficient rigidity based on the formation of a La3+ cross-linked silica particle gel like structure on the droplet surface. Another aspect favoring a more rapid stabilization is that the convective flow of water around the droplet replenishes the nanoparticles that have been deposited on the interface, thereby shortening the diffusion distance. Last, the diffusion of ethanol from oil to water during the experiments may induce Marangoni flows that additionally transport particles by convection to the interface.
4. Conclusion
In summary, we introduce a facile route to generate stable cylindrical droplets and tubules of oil in water. The anisotropic droplet shapes are stabilized by a rigid interfacial assembly of silica nanoparticles. The nanoparticles self-assemble on the oil/water interface due to their partial wettability by the oil phase, imparted by the adsorption of a small cationic organic molecule on the nanoparticles. The rigidity of the assembled nanoparticle film results from interfacial particle crosslinking, facilitated by their interaction with a three-valent cation. The droplet deformation to cylinders or tubules is realized either via gravitational or hydrodynamic forces. A deformation away from spherical is made possible due to a reduction of the interfacial tension, enabled by the mass transfer of a solvent. We introduce models to analyze the hydrodynamic forces and the nanoparticle deposition rates on the droplets. Our technique of forming anisotropic oil droplets and tubules can potentially be used for different types of oil. For instance, acrylic oils can allow for the formation of polymeric microparticles and fibers. Moreover, our approach can be further developed for the 3D-printing of Newtonian fluids, complementing the existing additive manufacturing techniques.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Grant agreement no. 802636). We thank Dr Jan Groenewold for insightful discussions.References
- L. Rayleigh, Proc. Lond. Math. Soc., 1878, S1–S10, 4–13 CrossRef.
- X. Liu, S. Shi, Y. Li, J. Forth, D. Wang and T. P. Russell, Angew. Chem., Int. Ed., 2017, 56, 12594–12598 CrossRef CAS.
- J. Forth, X. Liu, J. Hasnain, A. Toor, K. Miszta, S. Shi, P. L. Geissler, T. Emrick, B. A. Helms and T. P. Russell, Adv. Mater., 2018, 30(16), 1707603 CrossRef.
- W. Feng, Y. Chai, J. Forth, P. D. Ashby, T. P. Russell and B. A. Helms, Nat. Commun., 2019, 10, 1095 CrossRef.
- G. Xie, J. Forth, Y. Chai, P. D. Ashby, B. A. Helms and T. P. Russell, Chem, 2019, 5, 2678–2690 CAS.
- A. R. S. L. J. Bonderer and L. J. Gauckler, Science, 2008, 319, 1069–1073 CrossRef.
- D. Kohler, M. Schneider, M. Krüger, C.-M. Lehr, H. Möhwald and D. Wang, Adv. Mater., 2011, 23, 1376–1379 CrossRef CAS.
- Y. Lu, Y. Yin and Y. Xia, Adv. Mater., 2001, 13, 415–420 CrossRef CAS.
- S. A. F. Bon, S. D. Mookhoek, P. J. Colver, H. R. Fischer and S. van der Zwaag, Eur. Polym. J., 2007, 43, 4839–4842 CrossRef CAS.
- A. Bala Subramaniam, M. Abkarian, L. Mahadevan and H. A. Stone, Nature, 2005, 438, 930 CrossRef CAS.
- A. R. Studart, H. C. Shum and D. A. Weitz, J. Phys. Chem. B, 2009, 113, 3914–3919 CrossRef CAS.
- M. Cui, T. Emrick and T. P. Russell, Science, 2013, 342, 460–463 CrossRef CAS.
- T. Merkel, V. Gräf, E. Walz and H. P. Schuchmann, Chem. Eng. Technol., 2015, 38, 1490–1493 CrossRef CAS.
- X. Li, Y. Xue, P. Lv, H. Lin, F. Du, Y. Hu, J. Shen and H. Duan, Soft Matter, 2016, 12, 1655–1662 RSC.
- S. Shi, X. Liu, Y. Li, X. Wu, D. Wang, J. Forth and T. P. Russell, Adv. Mater., 2018, 30(9), 1705800 CrossRef.
- Y. Jiang, T. I. Löbling, C. Huang, Z. Sun, A. H. E. Müller and T. P. Russell, ACS Appl. Mater. Interfaces, 2017, 9, 33327–33332 CrossRef CAS.
- L. Tran, H.-N. Kim, N. Li, S. Yang, K. J. Stebe, R. D. Kamien and M. F. Haase, Sci. Adv., 2018, 4, eaat8597 CrossRef CAS.
- M. F. Haase, N. Sharifi-Mood, D. Lee and K. J. Stebe, ACS Nano, 2016, 10, 6338–6344 CrossRef CAS.
- L. Tran and M. F. Haase, Langmuir, 2019, 35, 8584–8602 CrossRef CAS.
- M. F. Haase, Modification of nanoparticle surfaces for emulsion stabilization and encapsulation of active molecules for anti-corrosive coatings, Universität Potsdam, 2011 Search PubMed.
- A. F. Koretsky and P. M. Kruglyakov, Izv. Sib. Otd. Akad. Nauk USSR, 1971, 2, 139 Search PubMed.
- B. P. Binks and T. S. Horozov, Colloidal particles at liquid interfaces, 2006 Search PubMed.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546 CrossRef CAS.
- W. J. Frith, R. Pichot, M. Kirkland and B. Wolf, Ind. Eng. Chem. Res., 2008, 47, 6434–6444 CrossRef CAS.
- B. P. Binks and S. O. Lumsdon, Phys. Chem. Chem. Phys., 1999, 1, 3007–3016 RSC.
- J. K. Ferri, C. Kotsmar and R. Miller, Adv. Colloid Interface Sci., 2010, 161, 29–47 CrossRef CAS.
- B. Noskov, G. Loglio and R. Miller, Adv. Colloid Interface Sci., 2011, 168, 179–197 CrossRef CAS.
- J. Hegemann, S. Knoche, S. Egger, M. Kott, S. Demand, A. Unverfehrt, H. Rehage and J. Kierfeld, J. Colloid Interface Sci., 2018, 513, 549–565 CrossRef CAS.
- B. P. Binks, L. Isa and A. T. Tyowua, Langmuir, 2013, 29, 4923–4927 CrossRef CAS.
- M. F. Haase, K. J. Stebe and D. Lee, Adv. Mater., 2015, 27, 7065–7071 CrossRef CAS.
- M. F. Haase and J. Brujic, Angew. Chem., 2014, 126, 11987–11991 CrossRef.
- A. S. Utada, Phys. Rev. Lett., 2007, 99, 094502 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02120b |
| This journal is © The Royal Society of Chemistry 2021 |