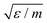Open Access Article
Open Access ArticleNano-pump based on exothermic surface reactions†
Shaltiel
Eloul
 and
Daan
Frenkel
and
Daan
Frenkel

Department of Chemistry, University of Cambridge, UK. E-mail: df246@cam.ac.uk
First published on 29th January 2021
Abstract
We present simulations indicating that it should be possible to construct a switchable nano-scale fluid pump, driven by exothermic surface reactions. Such a pump could, for instance, be controlled electro-chemically. In our simulations we explore a simple illustration of such a pump. We argue that the simplicity of the pump design could make it attractive for micro/nano-fluidics applications.
1 Introduction
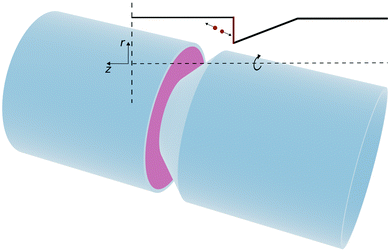
Inducing flow in a nano-channel requires a mechanism which can efficiently convert energy input into a sustained fluid flow. As pressure-driven flow becomes less efficient in sub-micron channels, there is much interest in pumps that use electro,1,2 diffusio3–5 or thermo6,7 osmosis transport mechanisms. Electro-chemical micro-pumps, which generate convective flow8 are also being explored, but require relatively large channels (order of 10–100 μm) that can sustain fully developed convective flows.Here, we propose that robust fluidic pumping, can be based on locally switchable electrochemical or catalytic reactions that release energy on a reactive surface. Our approach is based on our recent observation that exothermic energy released on a catalytic platinum surface can propel micro-sized Janus particles at a speed of a few microns per second.9 If, instead of considering an uncontrolled chemical reaction on a Janus particle, we consider a reaction on suitably oriented reactive surface (e.g. on fixed electrodes), then the surface reaction could generate flow by exploiting the large, directional momentum release into the fluid at the electrode surface (see Fig. 1). In the case of electrochemically driven flow, the exothermic energy release is driven by applying over-potential that converts an electro-active redox species in solution. A representative geometry of such a reaction-driven pump is shown in Fig. 1. In this pump geometry, we assume a cylindrical channel with an asymmetric conical constriction: the active surface is chosen perpendicular to the tube axis, while the conical surface is inert.
We use a general particle-based model (dissipative particle dynamics, DPD10,11) to describe the effect of a local kinetic energy release on the microscopic flow properties of a fluid. DPD provides a cheap, yet realistic description of micro-scale hydrodynamic flow in compressible fluids.12 In principle, the surface reaction might also drive thermo-osmotic and diffusio-osmotic flows (provided the surfaces are suitably functionalized). However, in this study we intentionally exclude possible osmotic effects. We use a DPD model, as it allows us to focus on the effect of direct momentum transfer: we can switch off thermal gradients to neglect thermo-osmosis, and by using a one-component fluid, we eliminate possible diffusio-osmosis. Note that interaction wall-fluid has been chosen to be repulsive such that there is negligible excess enthalpy near the surface and thermo-osmosis is expected to be negligible in the DPD model even with no thermostat.
In DPD, the interaction between fluid particles is described as a sum of pair forces:
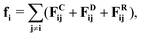 | (1) |
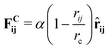 | (2) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = (ri − rj)/rij is the unit vector in the direction of |ri − rj|. rc is the cut-off radius and is set to 1. The constant α sets the strength of the repulsion: it is chosen to mimic the compressibility of water.12 The dissipative and random forces are related via the fluctuation–dissipation relation:11
ij = (ri − rj)/rij is the unit vector in the direction of |ri − rj|. rc is the cut-off radius and is set to 1. The constant α sets the strength of the repulsion: it is chosen to mimic the compressibility of water.12 The dissipative and random forces are related via the fluctuation–dissipation relation:11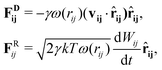 | (3) |
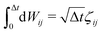 , where ζij is a standard Gaussian random number. The weight function ω(r) is assumed to be of the form
, where ζij is a standard Gaussian random number. The weight function ω(r) is assumed to be of the form 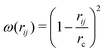 .
.
As we chose our DPD model parameters to correspond to water12 (see also Table 1), our results should be indicative of pumping rates in aqueous medium, once we correct for the difference between the viscosity of real water and that of the DPD model12 (ESI†). In what follows, we use the cut-off distance rc as our unit of length: for water, rc ∼ 6.46 Å. The DPD density is chosen to be ρrc3 = 3.0. To reproduce the compressibility of water at room temperature, we choose α = 25 and γ = 4.5 as proposed by Groot and Warren.12 We choose the thermal energy kBT as our unit of energy, and m, the dimensionless mass of a fluid particle is our mass unit. As a consequence, our unit of time is 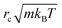 . The equations of motion were integrated using a modified velocity-Verlet algorithm12 with a time step of 10−3, corresponding to 3 ps in SI units, allowing us to simulate local transient momentum dissipation up to hydrodynamic timescales.
. The equations of motion were integrated using a modified velocity-Verlet algorithm12 with a time step of 10−3, corresponding to 3 ps in SI units, allowing us to simulate local transient momentum dissipation up to hydrodynamic timescales.
The inner surface of the tube geometry is modeled with ‘frozen’ particles and we consider here two different modifications to the surface (ESI†). The first modification allows us to change the hydrodynamic boundary conditions on the tube surface from slip to non-slip. In the slip case, the surface is formed using smooth high density of frozen particles to suppress hydrodynamic drag. In the non-slip case, we construct the boundary to be a non-smooth surface by corrugating the tube surface sufficiently to measure zero slip velocity of the fluid adjacent to the surface. The second modification is that we allow collisions of fluid with the pump surface to be either elastic or inelastic. When using only repulsive force (but no friction) in fluid-surface interaction, collisions are elastic and the wall does not act as an energy sink. Alternatively, we can use dissipative forces between the fluid and wall particles to define an energy absorbing (or, more precisely, thermalizing) boundary. The energy-absorbing surface is not an ideal inelastic wall, and some slip can still happen in smooth surfaces. However, high energy from reactions are sufficiently suppressed. Note that in reality, the chemical reaction is catalysed by the surface, but the heat released is unrelated to the physical heat of adsorption.
We assume that, during a surface reaction in a catalytic system, a significant fraction of the reaction enthalpy is taken up by the fluid. For example: the catalytic reaction 2H2O2 → O2 + 2H2O on a Pt surface has a standard enthalpy ΔH⦵ = 1.017 eV. In the case of reversible electrochemical reactions, heat release is associated with entropy changes. The heat is measured as the electrochemical Peltier heat (Π).13 Π is related to the apparent enthalpy of change in the reaction: Π − We = ΔH⦵, where We is the electric work due to electron transfer in the electrode reaction. For example, for the redox couple [Fe(CN)6]−3/−4, Π ∼ 0.5 eV and ΔH⦵ ∼ 1–1.5 eV.14 Therefore, in our model calculations, we consider energy releases in the range of 0–2 eV.
The energy E released by a surface reaction into the fluid, is assumed to increase the kinetic energy of relative motion of a reactive pair of neighboring DPD particles. The pair (a,b) is chosen by finding the closest fluid particle to the catalytic surface at the time of reaction. The effect of individual reactions is additive as discussed later. In our calculations, we therefore did not compute the reaction rate, but can linearly extrapolated our results to the experimentally available data. As we only change the relative motion of two DPD particles, the total momentum in the fluid is conserved and all species are unchanged. As a result of a reaction, the kinetic energy of the DPD particles involved is changed:
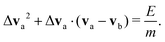 | (4) |
2 Results and discussion
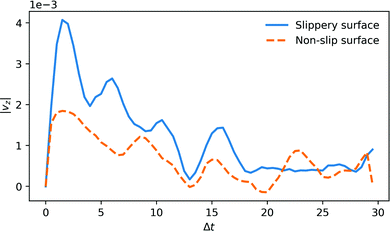
The average time-dependence of the fluid velocity profile from a 1 eV single reaction in a cylinder with radius of 4rc is plotted in Fig. 2. The profile is computed by averaging independent DPD configurations. To improve the statistics of the analysis of the surface effect on the momentum decay, the fluid thermostat was switched off in this specific simulation.We show the results of two limiting cases. One case (drawn curve) corresponds to slip and elastic boundary conditions. The other case corresponds to non-slip boundary conditions, and inelastic fluid-wall collisions (dashed curve). Interestingly, there is an appreciable flow response, even for the case of inelastic, non-slip boundaries. It is likely that experiments will be closer to the non-slip/inelastic case, although increasing the hydrophobicity of the walls of the channels may change this picture somewhat.15
The reaction also creates a damped sound wave in the tube (see Supporting Video, ESI†), which results in temporal oscillations of the fluid momentum, but this oscillatory flow field appears not to contribute to the net fluid flow. The fluid momentum imparted by a single reaction decays within 20–30 time units for the non-slip boundary, but for the slip boundary the initial momentum has not yet fully decayed on this time scale. Converting to SI units, transient fluid velocity in the channel peaks at ∼1 m s−1 and decays within 100 ps. Hence, a single reaction event leads to a DPD fluid volume displacement of order 1 Å. By scaling the viscosity to water (ESI†), we expect an order of magnitude smaller displacement from a single event, but multiple reaction events can generate significant pumping rates.
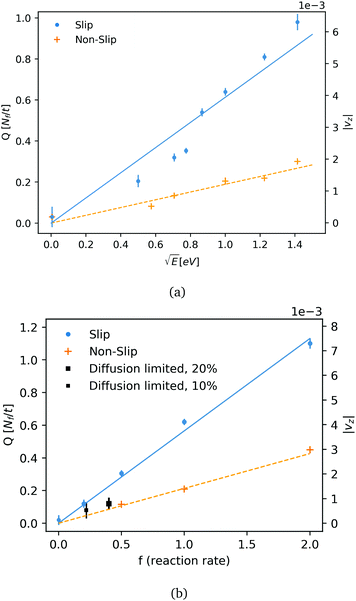
The particle flow rate (Q) is measured by calculating the total flux of fluid particles mass (m) per time through the channel surface at z = Lz/2. The flow rate is shown as function of the reaction energy and reaction rate (f) is shown in Fig. 3a and b. The flow rate is plotted for the two cases of a slip and non-slip boundary conditions (in what follows, we consider in both cases an inelastic surface and a thermostated fluid). Fig. 3a shows that the flow velocity varies as the square root of released energy, indicating that momentum is mainly a result of direct momentum transfer from reaction energy: in the scenario of thermo-osmosis the flow velocity would vary linearly with E. In our simulations, the reaction rates were low enough to ensure that the flow velocity was linear in the reaction rate. This linear relation (Fig. 2b) allows us to extrapolate our simulation results to realistic catalytic and electrochemical rates (which are few orders slower for water, as discussed below).
We also consider the case of a diffusion-limited rate of electro-active species in a short pump of a total length equals Lz. The short pump acts as a ‘gate’, releasing fluid from one side (−Lz/2) to another side of the nano-channel (Lz/2). The pump switches-on flow by applying a sufficient over-potential on the active surface, so the maximum reaction rate is limited by active-species entering and diffusing through the channel towards the electro-active surface (electrode). Close to the active surface and in a reaction zone, active particles would undergo exothermic reactions with energy of 1 eV. The reaction zone in the diffusion limited case is set to 1.5 rc, compatible with the typical range for electron-transfer in an aqueous electrochemical system (order of 1 nm). The density of the active particles at the edge (−Lz/2) is kept constant to satisfy a Dirichlet boundary condition. Average rates of the stochastic reaction at two concentrations and their observed flow rates are plotted in Fig. 3b. We note that in addition to reactant diffusion, there is also advection. However, we found this non-zero Peclet effect to be relatively small <10%. For water, with a 10% reactant concentration, a pump with a length of 10.3 nm and a radius of 2.6 nm produces a flow rate of ∼1.3 water molecules per nano-second. The high flow rate obtained for the diffusion limited case shows that direct momentum transfer rate would be significant for smaller concentrations and slower reactions rate. Table 2 summarises the computed flow rates for an aqueous solution, as a function of the key geometric control parameters (tube length, tube diameter), and the reactant concentration. All results in Table 2 were obtained for the non-slip, inelastic boundaries. The fluid flow velocity in water is predicted to be in the order of 1–10 μm s−1 for catalytic rates which are usually kinetic limited. The velocity could be increased by a few order of magnitudes by tuning the size of the pump, the surface of the active area, and by adjusting the electro-chemical reaction rate. We can also compare the force from a reaction at a unit rate (f = 1) to an effective force of a laminar flow in a cylinder, and roughly estimate the force in the pump of DPD fluid as function of size and rates. For Lz = 16, R = 4 (in DPD units): Favg ∼ 8LzνQ/R2 ∼ 0.5 where the kinematic viscosity of the fluid is ν ∼ 0.3. The effective force provides a crude but useful measure of how rates are influenced by the geometry. For instance, doubling the length Lz to 20.6 nm shows that rate is indeed reduced by around 50% (Table 2). As expected, the volumetric rate scales approximately as 1/R2. We did not attempt to optimize the flow rates by systematically varying the tube geometry or the surface topography.
| Physical estimates | Rate [ns−1], [s−1 nm−2] | L z ,R [nm] | Flow Q[H2O s−1], vz[mm s−1] |
|---|---|---|---|
| a Diffusion-limited rate of electro-active fuel at 10%. The reaction rate and the flux have been converted to values relevant for an aqueous solution, by scaling the diffusion coefficient and the viscosity of the DPD fluid to water. b A representative reaction-limited rate equal to 0.25% of the diffusion-limited rate. | |||
| f = 0.1 and 1 eV | 33, 3.6 × 109 | 10.3, 2.6 | 1.05 × 109, 4.5 |
| Double length | 33, 3.6 × 109 | 20.6, 2.6 | 6.3 × 108, 2.7 |
| Double radius & length | 72, 3.6 × 109 | 20.6, 5.2 | 1.87 × 109, 1.97 |
| 10% fuela | 4.0, 4.0 × 108 | 10.3, 2.6 | 1.27 × 108, 0.54 |
| 10% fuel, reaction-limited rateb | 0.017, 1.8 × 106 | 10.3, 2.6 | 3.2 × 105, 1.4 × 10−3 |
Other models of pumps based on temperature gradient show comparable velocities at a micro sized pump.6 High pumping rates (∼1 m s−1) theoretically can be obtained with high temperature gradients (∼20–100 K nm−1) at nano-sized pumps,7,16 but such extreme gradients may be difficult to achieve in experiments.
Experiments on diffusio-osmotic flow have found flow rates of ∼100 fl min−1 for a nano-channel with height of 163 nm and width of 5 μm. If we roughly compare the diffusio-osmosis data to the case presented here of a channel that is 3 orders of magnitude narrower, it would correspond to Q = 5 × 107 H2O s−1 which is of the same order as the rates predicted on the basis of direct reactive momentum transfer.
In summary, we have shown that heat release due to an exothermic surface reaction can drive fluid flow in a nano-channel. Energy from catalytic or electro-chemical reactions can generate momentum in the fluid which results in significant flow rates, provided that the active surface is placed in such a way that it favors uni-directional momentum transfer into the fluid. Fabrication of electrodes with such a directional preference could for instance be achieved using pulse electroplating or, possibly, nano-array printing techniques.17 The ease of design of the pump makes the momentum transfer mechanism attractive for applications and experimental studies. Further study of the momentum transfer mechanism is also required. In order to gain a better understanding of the factors that can affect the direct momentum transfer mechanism, more detailed, atomistic simulations would be needed. With such simulations, one could quantify the effect of thermalization at the wall and the influence of the topography of the active surface during heat release.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was funded by the EU Horizon 2020 program through 766972-FET-OPEN-NANOPHLOW.Notes and references
- Y. Takamura, H. Onoda, H. Inokuchi, S. Adachi, A. Oki and Y. Horiike, Electrophoresis, 2003, 24, 185–192 CrossRef CAS PubMed.
- C.-H. Chen and J. G. Santiago, J. Microelectromech. Syst., 2002, 11, 672–683 CrossRef CAS.
- A. Ajdari and L. Bocquet, Phys. Rev. Lett., 2006, 96, 186102 CrossRef PubMed.
- S. Michelin, T. D. Montenegro-Johnson, G. De Canio, N. Lobato-Dauzier and E. Lauga, Soft Matter, 2015, 11, 5804–5811 RSC.
- C. Lee, C. Cottin-Bizonne, A.-L. Biance, P. Joseph, L. Bocquet and C. Ybert, Phys. Rev. Lett., 2014, 112, 244501 CrossRef CAS PubMed.
- M. Yang and M. Ripoll, Soft Matter, 2016, 12, 8564–8573 RSC.
- C. Liu and Z. Li, Phys. Rev. Lett., 2010, 105, 174501 CrossRef PubMed.
- T. R. Kline, W. F. Paxton, Y. Wang, D. Velegol, T. E. Mallouk and A. Sen, J. Am. Chem. Soc., 2005, 127, 17150–17151 CrossRef CAS PubMed.
- S. Eloul, W. C. K. Poon, O. Farago and D. Frenkel, Phys. Rev. Lett., 2020, 124, 188001 CrossRef CAS PubMed.
- P. Hoogerbrugge and J. Koelman, EPL, 1992, 19, 155 CrossRef.
- P. Espanol and P. B. Warren, EPL, 1995, 30, 191 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- P. Boudeville and A. Tallec, Thermochim. Acta, 1988, 126, 221–234 CrossRef CAS.
- Z. Fang, S. Wang, Z. Zhang and G. Qiu, Thermochim. Acta, 2008, 473, 40–44 CrossRef CAS.
- D. M. Huang, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2008, 101, 064503 CrossRef PubMed.
- R. Rajegowda and S. P. Sathian, Phys. Chem. Chem. Phys., 2018, 20, 30321–30330 RSC.
- H.-S. Ko, Y. Lee, S.-Y. Min, S.-J. Kwon and T.-W. Lee, Nanoscale, 2017, 9, 15766–15772 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02079f |
| This journal is © The Royal Society of Chemistry 2021 |