Open Access Article
Open Access ArticleSelf-assembly in mixtures with competing interactions
Oksana
Patsahan
 a,
Marek
Litniewski
b and
Alina
Ciach
a,
Marek
Litniewski
b and
Alina
Ciach
 *b
*b
aInstitute for Condensed Matter Physics, National Academy of Sciences of Ukraine, Lviv, Ukraine
bInstitute of Physical Chemistry, Polish Academy of Sciences, 01-224 Warszawa, Poland. E-mail: aciach@ichf.edu.pl
First published on 1st February 2021
Abstract
A binary mixture of particles interacting with spherically-symmetrical potentials leading to microsegregation is studied by theory and molecular dynamics (MD) simulations. We consider spherical particles with equal diameters and volume fractions. Motivated by the mixture of oppositely charged particles with different adsorption preferences immersed in a near-critical binary solvent, we assume short-range attraction long-range repulsion for the interaction between like particles, and short-range repulsion long-range attraction for the interaction between different ones. In order to predict structural and thermodynamic properties of such complex mixtures, we develop a theory combining the density functional and field-theoretical methods. We show that concentration fluctuations in mesoscopic regions lead to a qualitative change of the phase diagram compared to mean-field predictions. Both theory and MD simulations show coexistence of a low-density disordered phase with a high-density phase with alternating layers rich in the first and second components. In these layers, crystalline structure is present in the solid, and absent in the liquid crystals. The density and the degree of order of the ordered phase decrease with increasing temperature, up to a temperature where the theory predicts a narrow two-phase region with increasing density of both phases for increasing temperature. MD simulations show that monocrystals of the solid and liquid crystals have a prolate shape with the axis parallel to the direction of concentration oscillations, and the deviation from the spherical shape increases with increasing periodic order.
1 Introduction
Competing interactions between particles in suspensions may lead to a variety of patterns formed either by individual particles, or by assemblies with well-defined size and shape. In particular, core–shell particles adsorbed at fluid interfaces form different highly ordered patterns for different thicknesses and structures of the polymeric shell, and different area fractions.1–3 In this case, effective repulsion induced by overlapping soft shells competes with effective attraction induced at larger distances by capillary forces. On the other hand, charged particles in solvents containing depletion agents attract or repel each other at short or at large distances, respectively.4–6 This short-range attraction long-range repulsion (SALR) interaction is known also as the ‘mermaid’ potential due to the attractive head and the repulsive tail.7 When the volume fraction of the particles increases, spherical or cylindrical clusters, or slabs are formed, and these assemblies can be periodically distributed in space at sufficiently low temperatures.8–14 When the volume fraction further increases, voids instead of the assemblies are formed in a reverse order.15 Notably, the sequence of the ordered phases in the SALR systems is universal, i.e. it is independent of the details of the interacting potential, and is the same as in the amphiphilic systems.10 Note that outside the hard cores, the interaction between the core–shell particles is a ‘negative’ of the SALR (or the mermaid) potential, and can be memorized as a ‘peacock potential’ because of the repulsive head and the attractive tail.The ordered phases in the SALR system were predicted theoretically8,13,14,16 and observed in simulations.11,12,15,17 The rich variety of long-lived metastable states, where small ordered domains are randomly connected, makes it difficult to reach the equilibrium. In simulations it was necessary to use intelligent tricks to obtain the stable phases.11,12 Similar difficulties are present in experiments, and the ordered phases have not been detected yet,7 although gels with novel structures and clusters of different morphologies have been observed.18–21 A very special methodology is necessary for obtaining the true equilibrium. For this reason, various systems and scenarios were suggested in order to overcome the problem of long-lived metastable states in experiments. In ref. 22 and 23 it was suggested to investigate colloid particles with surfaces preferentially adsorbing one component of a near-critical mixture, in which the particles were suspended. Critical concentration fluctuations in the mixture confined between selective surfaces induce the so-called thermodynamic Casimir potential between these surfaces. The potential is attractive for surfaces with like- and repulsive between surfaces with different adsorption preferences.24,25 Charged particles interact in addition with screened coulombic forces that are repulsive for like charges. The screened electrostatic interactions compete in this system with the thermodynamic Casimir potential induced by the critical fluctuations in the solvent. The sum of the Casimir and the electrostatic interactions between like particles has the SALR form when the charge is relatively small, and the screening length is larger than the decay length of the Casimir potential.26 The latter can be finely tuned by temperature. Because the repulsion can be easily turned on and off at a controlled speed, this system may be a good candidate for experimental detection of the ordered phases in the SALR systems.
A suspension of charged selective particles in a near-critical mixture offers many other opportunities for spontaneous formation of ordered patterns. Let us consider a binary mixture of colloid particles suspended in such a complex solvent. Let the particles of the first kind adsorb one component of the binary solvent, and the particles of the second kind adsorb the other component, and let the different particles be oppositely charged. When the charge and temperature are tuned so that the like particles interact with the mermaid potential, then the interaction between different particles has the form of the peacock potential, because the Casimir force dominating at shorter distances is repulsive, and the electrostatic force dominating at larger distances is attractive. As both types of interactions lead to formation of various patterns, one can expect interesting structural and thermodynamic properties in the system where both types of interactions are present. To memorize the complex interactions in such systems more easily, we may imagine ‘two mermaids and a peacock’ (2MP).
Motivated by the properties of the above binary mixture of particles in the binary critical solvent, in this work we focus on a general case of the mixture with the mermaid potential between like- and the peacock potential between different particles, since the 2MP potentials may be present in different soft-matter systems as well. We intend to determine these structural and thermodynamic features of such systems that are not limited to any specific shape of the interactions, but are common to all 2MP systems. As the SALR systems have a universal topology of the phase diagram, but the patterns in the core–shell particles depend sensitively on the shape of the interaction potential, the question to what extent the properties of the 2MP systems are universal or specific is open.
A mixture of the above kind was studied in ref. 27 for a particular choice of the interaction potentials by both theory and Monte Carlo simulations. Chains of alternating clusters composed of particles of the first kind followed by the clusters composed of the particles of the second kind were observed at relatively high temperature, where the long-range order was absent. Theoretical predictions for the correlation functions were obtained within the mesoscopic approach8,28 combining the density functional and the Brazovskii-type field theories.29,30 The theoretical results agreed with the Monte Carlo simulations on a semi-quantitative level. The phase diagram, however, has not been determined yet, but is a purpose of this work.
It is important to stress that in the case of systems with spontaneous inhomogeneities the predictions of the mean-field (MF) theories are not correct at high temperatures where fluctuations play an important role. Even the sequence of the phases in the SALR systems is not correctly predicted on the MF level, except at a low T. The continuous transition between the disordered and ordered phases predicted in MF turns out to be fluctuation-induced first order.30 For this reason it is necessary to take the fluctuations into account, by which the theory becomes more complex.31
In this work we further develop the mesoscopic theory for inhomogeneous mixtures.28 We make assumptions based on physical grounds that allow us to calculate the phase diagram for a symmetrical mixture of particles of identical size and of equal volume fractions with reasonable effort. We calculate the correlation functions, and determine the phase diagram for a particular choice of the interactions of the particles both in MF and beyond it. The theoretical predictions are compared with molecular dynamics (MD) simulations. The simulations, however, are performed for particles that are not composed of hard cores, but rather interact with the repulsive part of the Lenard-Jones potential. At large separations, the shapes of the interaction potentials in simulations and theory are very similar, but are not the same at short separations. On one hand, we choose the potentials convenient for the theoretical and the simulation studies. On the other hand, from our approximate theory it follows that the phase diagram should depend only on some gross features of the interactions, when appropriate units for temperature are used. By comparison with the MD simulations for a somewhat different shape of the potential, we will verify if the predictions of the theory with the Brazovskii-type approximation for the effects of fluctuations are valid.
The interaction potentials used in theoretical calculations and in simulations are presented and characterized in Section 2. The theoretical and simulation methods are presented in Sections 3 and 4, respectively. In Section 3.1, we present the general formalism of our theory. In Sections 3.2 and 3.3, we derive the equations for the correlation functions, the chemical potential and the grand thermodynamic potential in MF and in the Brazovskii-type approximation, respectively. Readers not interested in the formalism, may skip these sections. Section 5 contains our results, and in the last section our results are summarized and discussed.
2 The model
We consider a binary mixture of spherical particles with the particle diameter a, and assume that the interaction potential uij with i, j = 1, 2 consists of strong repulsion for the center-to-center distance r ≤ a, and of competing interactions for r > a. In the following, we consider dimensionless distance r* = r/a, and omit the asterisk for clarity. We assume the same interaction between like particles of both species, uii(r) = u(r) that for r > 1 has the form of the short-range attraction and long-range repulsion. For the interaction between different particles, we assume for r > 1 short-range repulsion and long-range attraction.In the theory, we assume hard cores of the particles and uij(r) = ∞ for r < 1. For r > 1, we assume u12(r) = −u(r), with
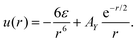 | (1) |
 | ||
| Fig. 1 (a) The interaction potentials uij, eqn (1), between like particles (solid line) and between different particles (dashed line) for AY = 1.8, chosen in our studies; (b) the interaction potentials ũ(k) in Fourier representation. From the bottom to the top line AY = 0, 0.36, 1.35, and 1.8, respectively. u, r and k are in units of ε, the particle diameter a and a−1, respectively. | ||
In the MD simulations, we assume
 | (2) |
 | (3) |
 | ||
| Fig. 2 The interaction potentials between like particles (solid line) and between different particles (dashed line) used in the MD simulations (see eqn (2) and (3) for AY = 1.8) in real space (a) and in Fourier representation (b). u, r and k are in units of ε, the particle diameter a, and a−1, respectively. | ||
The strength of the repulsion AY can be varied to model various charges of the particles. For AY = 0, the potential uij reduces to attractive interactions between like particles, and to a repulsion between different particles, leading to a macroscopic phase separation. On the other hand, for ε = 0 the potential u(r) (eqn (1)) reduces to the screened Coulomb potential between charged colloid particles.
The potential outside the hard core, u(r)θ(r − 1), in Fourier representation is denoted by ũ(k), and takes the form shown in Fig. 1b for a few values of AY ≤ 1.8. Note that in the absence of the repulsion, the potential takes the minimum for k = 0, whereas for sufficiently strong repulsion, the minimum occurs for k0 > 0 that increases with increasing AY.
ũ(k) describes the increase of the energy of the homogeneous system when the concentration wave with the wave number k is excited. The most probable concentration wave corresponds to the minimum of ũ(k); the most probable distance between like clusters or layers is 2π/k0, and the thickness of the aggregates is ∼π/k0. Moreover, ũ(k0) sets the energy scale connected with the process of self-assembly.
To compare the relevant energy units in the theory and simulations, we should know uMDij outside the particle core in Fourier representation. Unfortunately, the size of the core is not uniquely defined. To have some insight, we Fourier transform uMDij(r)θ(r − 1) for uMDij given in eqn (2) and (3). The results are shown in Fig. 2b. Different forms of uMDii(r) and −uMD12(r) at short distances lead to different positions and magnitudes of the minima of ũMDii(k) and −ũMD12(k) that are also somewhat different from the corresponding values in the theoretical model. Moreover, the form of ũMDij(k) depends strongly on the arbitrary choice of the particle diameter. Because of that, the energy scale for the process of self-assembly for softened particle cores is not uniquely defined. In addition, different forms of the potentials for r < 1.5 lead to about ten times larger thermal energy kT that is equal to the minimum of uii(r), compared to the thermal energy equal to the minimum of uMDii(r) (see Fig. 1a and 2a). To compare the theoretical and simulation results, we will consider kT/u(rmin) and kT/uMDii(rmin).
We choose for further calculations and simulations AY = 1.8 that leads to small aggregates, π/k0 ∼ 2. In this case, a relatively small number of particles gives a sufficiently large number of aggregates, and in turn leads to reliable results in simulations at a reasonable computational cost.
3 Theory
3.1 The formalism for symmetrical mixtures
In the mesoscopic approach developed for inhomogeneous mixtures in ref. 28, we consider mesoscopic regions and mesoscopic states. In a particular mesoscopic state, the volume fraction of particles of the i-th species around the point r, ζi(r), is the fraction of the volume of the mesoscopic region occupied by the particles. The mesoscopic regions are comparable with or larger than 1 (in a-units), and smaller than the scale of the inhomogeneities. If we assume that the dimensionless “mass” of the particle is homogeneously distributed over its volume π/6, then ζi(r) is a continuous function of r.31 The functions representing the local concentration and volume fraction, c(r) = ζ1(r) − ζ2(r) and ζ(r) = ζ1(r) + ζ2(r), respectively, can be considered as constraints imposed on the microscopic states. The concentration and the volume fraction averaged over the system volume V are denoted by![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) and
and ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) , respectively. We limit ourselves to a symmetrical case, with
, respectively. We limit ourselves to a symmetrical case, with ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) = 0, and consider a range of
= 0, and consider a range of ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) .
.
In theoretical considerations, it is convenient to consider an open system, with fixed chemical potentials μ1 and μ2. In the symmetrical case, μ1 = μ2 = μ. We assume that in the presence of the above constraints the grand potential can be written as
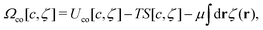 | (4) |
 , where fh(c,ζ) is the free-energy density of the hard-core reference system in the local-density approximation,
, where fh(c,ζ) is the free-energy density of the hard-core reference system in the local-density approximation,βfh(c,ζ) = ζ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ1 + ζ2 ζ1 + ζ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ2 + βfex(ζ). ζ2 + βfex(ζ). | (5) |
 | (6) |
 | (7) |
In Fourier representation,
 | (8) |
Importantly, Ṽ(k) = (6/π)2ũ(k) takes the minimum for k = k0 > 0 when AY > 0. Note that the ordering effect of the energy concerns only the concentration, and the largest energy gain is for the concentration wave with the wave number k0.
When the constraints imposed on the microscopic states by c(r) and ζ(r) are released, the microscopic states incompatible with c(r) and ζ(r) can appear, and the grand potential contains a fluctuation contribution and has the form28
 | (9) |
 | (10) |
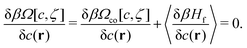 | (11) |
In the disordered fluid phase, both functions are position independent. For fixed T and μ, the two phases coexist when the grand potentials of these phases, Ω = −pV, where p is pressure, are equal.
The correlation functions Gij for ζi, and ζj are the matrix elements of G = C−1, where the elements Cij of the matrix C are the second functional derivatives of βΩ[c,ζ] with respect to ζi and ζj. Because of the symmetry of the interactions, the eigenvectors of the matrix C are the c and ζ fields. In this case, we consider Gcc(r) = 〈c(r1)c(r2) 〉 and Gζζ(r) = 〈ζ(r1)ζ(r2) 〉 − ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) 2. The above correlation functions in Fourier representation are simply given by
2. The above correlation functions in Fourier representation are simply given by ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) cc(k) = 1/
cc(k) = 1/![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k) and
cc(k) and ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) ζζ(k) = 1/
ζζ(k) = 1/![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ζζ(k).
ζζ(k).
3.2 Mean field approximation
In this subsection we limit ourselves to the MF approximation, where the last term in eqn (9) is disregarded. The correlation functions in the disordered phase are simply given by![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) MFcc(k)−1 = MFcc(k)−1 = ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) MFcc(k) = βṼ(k) + 1/ MFcc(k) = βṼ(k) + 1/![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) , , | (12) |
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) MFζζ(k)−1 = MFζζ(k)−1 = ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) MFζζ(k) = 1/ MFζζ(k) = 1/![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) + ∂2fex( + ∂2fex(![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) )/∂ )/∂![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) 2. 2. | (13) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) MFζζ(k) is independent of k. This means strictly local correlations.
MFζζ(k) is independent of k. This means strictly local correlations.
In MF, the disordered fluid loses stability with respect to a periodic c(r) with the wave number k0 along the so called λ-line given by ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) MFcc(k0) = 0, i.e.
MFcc(k0) = 0, i.e.
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) λ = −Ṽ(k0) λ = −Ṽ(k0)![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) , , | (14) |
Some comments are in order here. The λ-line for k0 ≠ 0 given by eqn (14) differs significantly from the λ-line for k0 = 0. For a binary symmetric mixture, the latter is a critical line of the mixing-demixing critical points related to long-length fluctuations of concentration.32,33 In this case, taking fluctuations into consideration does not change the qualitative picture of the phase diagram topology emerging from the MF theory33,34 that agrees with MC simulation results.32 For k0 ≠ 0, the λ-line marks the boundary of stability of the disordered phase with respect to mesoscopic fluctuations of concentration and separates the phase space into regions corresponding to the homogeneous and inhomogeneous (on the mesoscopic length scale) systems. It will be shown below that taking fluctuations into account leads to the change of the MF phase diagram. It is worth noting that the binary mixture considered here does not exhibit the macroscopic demixing phase separation.
Let us first consider the disordered phase, where c = 0, and ζ = ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) is determined by the minimum of Ωco[0,ζ]. Minimization of eqn (4) with respect to ζ gives
is determined by the minimum of Ωco[0,ζ]. Minimization of eqn (4) with respect to ζ gives
βΩg/V = βfex(![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) ) − A1( ) − A1(![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) ) )![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) − − ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) , , | (15) |
![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) is the solution of the equation
is the solution of the equation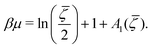 | (16) |
 | (17) |
In the case of the periodic phase, we postulate that in the symmetrical case, the concentration is a periodic function with oscillations in one direction, say z. We assume that
c(z) = Φgc(z), and ζ(z) = ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) + Ψgζ(z), + Ψgζ(z), | (18) |
 ,
, 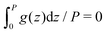 and
and  for g = gc, and gζ, and P denotes the period of oscillations of c. The period of gζ is P/2 because of the symmetry of the model. The oscillations of ζ appear because of the coupling between c and ζ in the entropy of mixing.
for g = gc, and gζ, and P denotes the period of oscillations of c. The period of gζ is P/2 because of the symmetry of the model. The oscillations of ζ appear because of the coupling between c and ζ in the entropy of mixing.
The problem simplifies greatly, if we restrict ourselves to relatively high T, where Φ is small, and we can make the assumptions 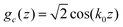 and
and  . Such sinusoidal shapes were indeed observed in the one-component SALR systems for not very low T.14 With the above assumption, we have to minimize a function of 3 variables, Φ,Ψ and
. Such sinusoidal shapes were indeed observed in the one-component SALR systems for not very low T.14 With the above assumption, we have to minimize a function of 3 variables, Φ,Ψ and ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) . We have:
. We have:
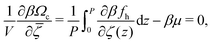 | (19) |
 | (20) |
 | (21) |
 | (22) |
 | (23) |
![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) < 0, i.e. in the region where the disordered fluid is unstable. From (19) we obtain, keeping terms up to O(Φ4),
< 0, i.e. in the region where the disordered fluid is unstable. From (19) we obtain, keeping terms up to O(Φ4), | (24) |
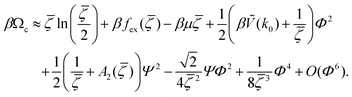 | (25) |
From the above equation it follows that the natural variables are βμ and βṼ(k0). Thus, we will consider βμ and T* = kT/|Ṽ(k0)|. Note that in this MF approximation, the grand potential depends on the interaction potential only through Ṽ(k0). This means universal phase diagrams with properly scaled temperature.
By inserting Ψ and Φ given by (22) and (23) in (24) and (25), and by eliminating ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) from (25) and (24), we obtain βΩc as a function of T* and βμ. The stable phase for the given T* and βμ is the one corresponding to the smaller value of the grand potential. We obtain the MF phase diagram by comparing βΩc with βΩg for fixed T* and βμ in Section 5.
from (25) and (24), we obtain βΩc as a function of T* and βμ. The stable phase for the given T* and βμ is the one corresponding to the smaller value of the grand potential. We obtain the MF phase diagram by comparing βΩc with βΩg for fixed T* and βμ in Section 5.
3.3 The Brazovskii-type theory for symmetrical mixtures
The MF is not expected to give correct results for high T, where the fluctuations play an important role and lead to formation of delocalized aggregates. Thus, the more accurate expression for Ω, eqn (9), should be considered. Because the energy gain concerns the local deviations of the concentration from![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) , and the deviations of ζ from
, and the deviations of ζ from ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) do not directly influence the energy, we expect that fluctuations of the former are much more probable and of larger magnitude than fluctuations of the latter. If the fluctuations of the local concentration are of a significantly larger magnitude than the fluctuations of the local volume fraction, we can consider a simplified theory, where the fluctuations of the local concentration are taken into account, but the fluctuations of the total volume fraction are disregarded.
do not directly influence the energy, we expect that fluctuations of the former are much more probable and of larger magnitude than fluctuations of the latter. If the fluctuations of the local concentration are of a significantly larger magnitude than the fluctuations of the local volume fraction, we can consider a simplified theory, where the fluctuations of the local concentration are taken into account, but the fluctuations of the total volume fraction are disregarded.
In the approximation with only the concentration fluctuations taken into account, the grand potential (9) takes the form
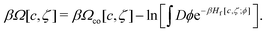 | (26) |
Following ref. 31, we make the approximation
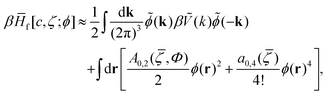 | (27) |
 | (28) |
 | (29) |
In order to calculate the fluctuation contribution to Ω, we make the approximation35
 | (30) |
 | (31) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k) contains the fluctuation contribution. Finally, we approximate 〈X〉 by averaging the quantity X with the probability ∝ exp(−βHG). In order to calculate the fluctuation contributions in (26), (10) and (11), we need to know
cc(k) contains the fluctuation contribution. Finally, we approximate 〈X〉 by averaging the quantity X with the probability ∝ exp(−βHG). In order to calculate the fluctuation contributions in (26), (10) and (11), we need to know ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k). In the Brazovskii-type approximation, it obeys the equation30,31,35
cc(k). In the Brazovskii-type approximation, it obeys the equation30,31,35 | (32) |
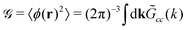 is well known for Ṽ(k) assuming the minimum for k = k0 > 0 from the previous studies,35
is well known for Ṽ(k) assuming the minimum for k = k0 > 0 from the previous studies,35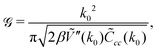 | (33) |
![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k0) is the solution of (33) and (32) with k = k0. The explicit expression for
cc(k0) is the solution of (33) and (32) with k = k0. The explicit expression for ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k0) is given in ref. 31 and 35. Note that in MF, the λ-line is given by
cc(k0) is given in ref. 31 and 35. Note that in MF, the λ-line is given by ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k0) = 0. When fluctuations are taken into account, however,
cc(k0) = 0. When fluctuations are taken into account, however, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k0) = 0 would lead to vanishing LHS of (32), and diverging RHS of (32), when
cc(k0) = 0 would lead to vanishing LHS of (32), and diverging RHS of (32), when ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) is given in (33). Thus,
is given in (33). Thus, ![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) cc(k0) > 0 and the continuous transition between the disordered and periodic phases cannot occur.
cc(k0) > 0 and the continuous transition between the disordered and periodic phases cannot occur.
Using (26), (30), (33) and (31) we obtain (see ref. 35 for more details)
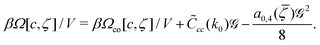 | (34) |
We make the same assumptions concerning c and ζ as in MF, and we need to minimize Ω with respect to ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) , Φ and Ψ. In this approximation, the fluctuation contribution is independent of Ψ and (22) holds, but the minimum with respect to Φ gives
, Φ and Ψ. In this approximation, the fluctuation contribution is independent of Ψ and (22) holds, but the minimum with respect to Φ gives
 | (35) |
![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) is a function of Φ (see (33), (32) and (28)). In this Gaussian approximation, we obtain from (10) and (27) the chemical potential
is a function of Φ (see (33), (32) and (28)). In this Gaussian approximation, we obtain from (10) and (27) the chemical potential | (36) |
Eqn (36), (34), (33) and (32) hold for both, the periodic and the disordered phases, with Φ = Ψ = 0 in the latter case. In contrast to the MF approximation, βμ depends on T* in the disordered phase (for Φ = Ψ = 0), because of the dependence on T* of ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) .
.
It is important to note that in contrast to the MF approximation, where the only dependence on the interaction potential is through Ṽ(k0), in this Brazovskii approximation, ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) and hence the phase diagram, depend in addition on Ṽ′′(k0). Still, just two parameters are sufficient to characterize the interactions in this theory. With Ṽ(k0) setting the energy scale (i.e. T* = kT/|Ṽ(k0)|), the same phase diagrams are expected for all interaction potentials with the same value of Ṽ′′(k0)/Ṽ(k0).
and hence the phase diagram, depend in addition on Ṽ′′(k0). Still, just two parameters are sufficient to characterize the interactions in this theory. With Ṽ(k0) setting the energy scale (i.e. T* = kT/|Ṽ(k0)|), the same phase diagrams are expected for all interaction potentials with the same value of Ṽ′′(k0)/Ṽ(k0).
In order to obtain the phase diagram, we first calculate Ψ and Φ from (22) and (35), respectively, and insert the results in (36) and (34). From the last pair of equations, we obtain Ω as a function of μ and compare the solution for Φ = Ψ = 0 with the solution with Φ ≠ 0. The results are presented in Section 5.
4 Simulations
The simulations were performed using classical molecular dynamics constant energy and volume method.36 We considered the systems of N = N1 + N2 particles with N1 = N2, enclosed in a rectangular box, where Lx, Ly, and Lz give the length of the edges. The temperature was always kept constant by scaling the particle velocities once for the time interval τ = 100–250a(m/ε)1/2, where m is the mass of the particle, and we assumed m = 1. As in the previous paper,37 the potentials (2) and (3) were truncated at r = rc = 6.75.The purpose of our simulations was to characterize the structure of the high-temperature disordered phase, and the structure of the ordered phase at coexistence with the low-density gas at low T. In addition, we estimated densities of the coexisting disordered and ordered phases in order to determine the shape and approximate positions of the coexistence lines.
The simulation shows that at sufficiently low temperature the fluid under consideration crystalizes. A monocrystal can be formed by condensation of rare gas on an attractive wall. In order to promote the nucleation of the monocrystal, we performed simulations (crystalization) in a system with periodic boundary conditions (BC) along the x and y directions, and the walls at z = 0 and z = Lz interacting with the particles. Attraction of component 1 and repulsion of component 2 from the left-hand side wall was assumed, with the potentials
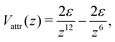 | (37) |
 | (38) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Lx = Ly = 200, and Lz = 800. Two crystals at
000, Lx = Ly = 200, and Lz = 800. Two crystals at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.16 obtained this way were subsequently used as an initial configuration in the simulations with the BC appropriate for determination of the properties of the dense phase at coexistence with the gas.
= kT/ε = 0.16 obtained this way were subsequently used as an initial configuration in the simulations with the BC appropriate for determination of the properties of the dense phase at coexistence with the gas.
The simulation results can be strongly influenced by the finite size effects and by the type of the BC. In order to control the above effects, we considered several systems, with different N, Lx, Ly and Lz, and different BC, and compared the results.
The computer simulation at constant N gives us the possibility of observing a monocrystal or a droplet of the dense phase surrounded by the coexisting low-density gas. The standard way for such a direct approach38,39 is to consider the system with the periodic boundary conditions (PBC). The problem is that the crystal considered here is a result of the balance between the attractive and the repulsive terms of potentials (2) and (3) and, as a consequence, PBC may strongly influence simulation results. This disadvantage can be eliminated by applying the reflecting boundary conditions (RBC) instead of PBC. An obvious condition for physically reasonable results is that the size of the simulation box for RBC is large enough so that the presence of the walls do not influence the crystal properties neither directly nor via the interaction with the gas particles. The necessary conditions that can be easily checked via simulations are that the crystal properties do not change with increasing size of the box, as well as the density profile around the center of the crystal is flat for a sufficiently large range. An advantage of the system with PBC is that it is better adopted to take into account the interaction between the dense phase and the gas as well as to measure the gas density. As a consequence, we decided to perform the simulations for both PBC and RBC and compare the results.
Based on the above discussion, we considered System 1 with all walls repulsing the particles with the potential (38), where z represents the distance from the wall for all 6 walls of the simulation box. The simulations were performed for N = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 and Lx = 45, Ly = 107, and Lz = 35, starting from a low temperature. As the initial configuration, the crystal obtained in the crystalization simulations, but placed in the center of the box was used. The crystal density was determined by counting the mean number of particles placed in the spheres, whose center coincides with the center of the crystal mass. Six spheres with radii Rμ = 5, 6, 7, 8, 9, and 10 were considered. Using this method, we can also check if the density profile in the vicinity of the mass center is flat, which is the necessary condition for neglecting the size effect. The densities calculated this way were independent of Rμ up to
566 and Lx = 45, Ly = 107, and Lz = 35, starting from a low temperature. As the initial configuration, the crystal obtained in the crystalization simulations, but placed in the center of the box was used. The crystal density was determined by counting the mean number of particles placed in the spheres, whose center coincides with the center of the crystal mass. Six spheres with radii Rμ = 5, 6, 7, 8, 9, and 10 were considered. Using this method, we can also check if the density profile in the vicinity of the mass center is flat, which is the necessary condition for neglecting the size effect. The densities calculated this way were independent of Rμ up to ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.32. A very low decrease in the calculated density with increasing Rμ appeared only for
= 0.32. A very low decrease in the calculated density with increasing Rμ appeared only for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.32; the effect, however, was very weak. The largest difference in the density for Rμ = 8 and 10 appeared for
> 0.32; the effect, however, was very weak. The largest difference in the density for Rμ = 8 and 10 appeared for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.35, but it did not exceed 1% of relative value. The method has been applied for all the state points and the results are shown in the Series 1 column in Table 1.
= 0.35, but it did not exceed 1% of relative value. The method has been applied for all the state points and the results are shown in the Series 1 column in Table 1.
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) for Series 1 and 2. All values of ζdens for Series 1 and that for
for Series 1 and 2. All values of ζdens for Series 1 and that for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) < 0.27 for Series 2 are obtained for Rμ = 10. The remaining values are obtained from density profiles. The bar means that the value is not measured.
< 0.27 for Series 2 are obtained for Rμ = 10. The remaining values are obtained from density profiles. The bar means that the value is not measured. ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε, ζ = πρ/6, and ρ = N/V
= kT/ε, ζ = πρ/6, and ρ = N/V
![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif)
|
Series 1 | Series 2 | Series 2a | ||
|---|---|---|---|---|---|
| ζ dens | ζ dens | ζ gas | ζ dens | ζ gas | |
| 0.140 | 0.383 | — | — | — | — |
| 0.180 | 0.379 | — | — | — | — |
| 0.220 | 0.374 | — | — | — | — |
| 0.250 | 0.370 | 0.370 | 0.0014 | — | — |
| 0.260 | 0.369 | 0.369 | 0.0023 | — | — |
| 0.270 | 0.281 | 0.278 | 0.0034 | — | — |
| 0.280 | 0.273 | 0.270 | 0.0048 | — | — |
| 0.290 | 0.263 | 0.259 | 0.0067 | — | — |
| 0.300 | 0.250 | 0.245 | 0.0091 | — | — |
| 0.310 | 0.233 | 0.208 | 0.0120 | — | — |
| 0.315 | 0.206 | 0.200 | 0.0136 | — | — |
| 0.320 | 0.197 | 0.192 | 0.0160 | — | — |
| 0.330 | 0.181 | 0.173 | 0.0212 | — | — |
| 0.340 | 0.165 | 0.152 | 0.0285 | 0.152 | 0.0288 |
| 0.350 | 0.152 | 0.128 | 0.0414 | 0.127 | 0.0429 |
The snapshots confirmed that the monocrystal surrounded by the dilute gas was placed in the center of the box for the low T. However, the density of the dense phase decreased with increasing T, and the swollen crystal became too large for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.32. We performed additional simulations (Test) with the box enlarged to Lx = 55, Ly = 112, and Lz = 45. For
> 0.32. We performed additional simulations (Test) with the box enlarged to Lx = 55, Ly = 112, and Lz = 45. For ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≤ 0.32, the increase of the system volume (by a factor of over 1.6) influenced neither the density nor the structure of the dense phase. Also the shape and the volume occupied by the dense phase remained nearly unchanged. For
≤ 0.32, the increase of the system volume (by a factor of over 1.6) influenced neither the density nor the structure of the dense phase. Also the shape and the volume occupied by the dense phase remained nearly unchanged. For ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.35, however, consequences of the increase of the system volume were very significant: the measured density decreased by around 0.1 relative value. This shows that for high
= 0.35, however, consequences of the increase of the system volume were very significant: the measured density decreased by around 0.1 relative value. This shows that for high ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) the volume of System 1 is too small, and the results are burdened with very high errors.
the volume of System 1 is too small, and the results are burdened with very high errors.
In order to verify the results of System 1 (Series 1 in Table 1), we considered System 2 with periodic BC in x, y, and z directions. In our study we considered N = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 812 particles enclosed in the box of Lx = 28, Ly = 44, and Lz = 200, i.e. the shape well adopted to measure the gas density. As before, the simulations started at low temperature, and the crystal obtained in the crystalization procedure was placed in the center of the box. The results are presented in the Series 2 column in Table 1.
812 particles enclosed in the box of Lx = 28, Ly = 44, and Lz = 200, i.e. the shape well adopted to measure the gas density. As before, the simulations started at low temperature, and the crystal obtained in the crystalization procedure was placed in the center of the box. The results are presented in the Series 2 column in Table 1.
With these BC, a slab of the gas and a slab of the dense phase, with two interfaces between them, are formed along the z axis. The density of both the gas and the dense phase could be easily determined directly from the density profile from Series 2. Unfortunately, the crystal may not adapt to the box shape and the method may not work correctly, in particular for highly ordered crystals at a low ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) . For this reason, the density was determined in the same way as in System 1 for
. For this reason, the density was determined in the same way as in System 1 for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) < 0.27. For the remaining state points, the densities were determined from the density profile from Series 2.
< 0.27. For the remaining state points, the densities were determined from the density profile from Series 2.
As shown in Table 1, the results obtained for System 1 (Series 1) and System 2 (Series 2) are in good agreement, except for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.31, 0.34, and 0.35. To verify the results for high
= 0.31, 0.34, and 0.35. To verify the results for high ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) , Series 2 was extended by two additional simulations (Series 2a) for larger systems: N = 110
, Series 2 was extended by two additional simulations (Series 2a) for larger systems: N = 110![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184, Lx = Ly = 65.73, and Lz = 173.44 at
184, Lx = Ly = 65.73, and Lz = 173.44 at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.34 and N = 116
= 0.34 and N = 116![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544, Lx = Ly = 65.73, and Lz = 172.11 at
544, Lx = Ly = 65.73, and Lz = 172.11 at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.35. The results of Series 2a are in good agreement with those from Series 2, which strongly validate the latter.
= 0.35. The results of Series 2a are in good agreement with those from Series 2, which strongly validate the latter.
The alternating layers of particles are no longer seen in the snapshots for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.31 in System 1 and
> 0.31 in System 1 and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.30 in System 2. The difference is also seen in Table 1: the rapid decrease of density for System 1 (0.31 <
> 0.30 in System 2. The difference is also seen in Table 1: the rapid decrease of density for System 1 (0.31 < ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) < 0.315) is shifted when compared to that for System 2 (0.30 <
< 0.315) is shifted when compared to that for System 2 (0.30 < ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) < 0.31). According to the test, the volume of System 1 is large enough and the repulsive walls should not influence the density and
< 0.31). According to the test, the volume of System 1 is large enough and the repulsive walls should not influence the density and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) at this structural change. A much more probable reason for the shift of the structural change is the periodic boundary conditions applied for System 2 that may have a disordering effect if the size of the box and the characteristic lengths in the ordered phase are not commensurate.
at this structural change. A much more probable reason for the shift of the structural change is the periodic boundary conditions applied for System 2 that may have a disordering effect if the size of the box and the characteristic lengths in the ordered phase are not commensurate.
To summarize, we can conclude that the most probable curve for the dense phase in equilibrium with the gas is that from Series 1 for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≤ 0.32, and Series 2 for
≤ 0.32, and Series 2 for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≥ 0.33. The simulations for the Lennard-Jones systems38–40 show that the size effect is very weak as long as we are not too close to the gas–liquid critical point. Taking into account the value of N applied for Series 2, we expect that the results may be significantly affected by the size effect for
≥ 0.33. The simulations for the Lennard-Jones systems38–40 show that the size effect is very weak as long as we are not too close to the gas–liquid critical point. Taking into account the value of N applied for Series 2, we expect that the results may be significantly affected by the size effect for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.35 for which the gas density is only 3 times lower than that for the dense phase (see the results of Watanabe et al.38). The comparison with Series 2a shows that even in this case the size effect is still reasonably weak. On the other hand, considering ref. 38, the systems considered here are too small for successful simulation for
= 0.35 for which the gas density is only 3 times lower than that for the dense phase (see the results of Watanabe et al.38). The comparison with Series 2a shows that even in this case the size effect is still reasonably weak. On the other hand, considering ref. 38, the systems considered here are too small for successful simulation for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.35. Of course, on the quantitative level the results for
> 0.35. Of course, on the quantitative level the results for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≤ 0.35 can still be affected by the finite size of the system, but our goal was to find approximate shapes and positions of the coexistence lines between the gas and the ordered phases.
≤ 0.35 can still be affected by the finite size of the system, but our goal was to find approximate shapes and positions of the coexistence lines between the gas and the ordered phases.
While for the low ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) the alternating layers rich in the first and the second components can be seen by inspection of the snapshots; for
the alternating layers rich in the first and the second components can be seen by inspection of the snapshots; for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.31 the individual snapshots are not sufficient to determine if a weak periodic order is present or not. In order to shed more light on the structure of the dense phase for
> 0.31 the individual snapshots are not sufficient to determine if a weak periodic order is present or not. In order to shed more light on the structure of the dense phase for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.31, one should determine the ensemble-averaged concentration. In order to eliminate the thermally induced translations of the crystal, we considered a simulation box with the wall at z = 0 attractive for the first, and repulsive for the second components, and all the remaining walls of the simulation box repulsive. For the attraction we assumed 2Vattr(z) with Vattr given in eqn (37), and for the repulsion eqn (38) was assumed. N = 85
> 0.31, one should determine the ensemble-averaged concentration. In order to eliminate the thermally induced translations of the crystal, we considered a simulation box with the wall at z = 0 attractive for the first, and repulsive for the second components, and all the remaining walls of the simulation box repulsive. For the attraction we assumed 2Vattr(z) with Vattr given in eqn (37), and for the repulsion eqn (38) was assumed. N = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 particles and Lx = Ly = 76.5, and Lz = 111.5 for
184 particles and Lx = Ly = 76.5, and Lz = 111.5 for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.33 were simulated with these BC. The wall at z = 0 induces exponentially damped oscillations of the concentration, and the range of the wall-induced periodic order should be significantly shorter than the size of the crystal in the z direction if we want to avoid the effect of the wall on the dense phase. We were interested in the concentration profile for z larger than the range of the wall-induced order, and smaller than the distance from the wall of the interface between the dense phase and the gas phase.
= kT/ε = 0.33 were simulated with these BC. The wall at z = 0 induces exponentially damped oscillations of the concentration, and the range of the wall-induced periodic order should be significantly shorter than the size of the crystal in the z direction if we want to avoid the effect of the wall on the dense phase. We were interested in the concentration profile for z larger than the range of the wall-induced order, and smaller than the distance from the wall of the interface between the dense phase and the gas phase.
Finally, to determine the structure of the high-temperature disordered phase, we computed correlation functions for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.40 and four densities, N/V = 0.1, 0.2, 0.3, and 0.4. The simulations were performed for N = 85
= 0.40 and four densities, N/V = 0.1, 0.2, 0.3, and 0.4. The simulations were performed for N = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184 with periodic BC.
184 with periodic BC.
5 Results
As already mentioned in Section 3.1, in the theory we consider the interaction potential V = u(6/π)2, with uii = u = −u12 defined in eqn (1), and in the simulations, uMDii and uMD12 are given in eqn (2) and (3). In both, theory and simulations, we assume AY = 1.8. The thermodynamic states are represented by the volume fraction, , and temperature. As discussed in Sections 3.2 and 3.3, in the case of hard cores we should choose T* = kT/|Ṽ(k0)|, because the coexistence lines for different microsegregating systems collapse on a universal line if the temperature is scaled in this way. Our potential in Fourier representation takes the minimum Ṽ(k0) ≈ −30.9ε at k0 ≈ 1.33. In the case of the softened core studied in the simulations, one typically considers
, and temperature. As discussed in Sections 3.2 and 3.3, in the case of hard cores we should choose T* = kT/|Ṽ(k0)|, because the coexistence lines for different microsegregating systems collapse on a universal line if the temperature is scaled in this way. Our potential in Fourier representation takes the minimum Ṽ(k0) ≈ −30.9ε at k0 ≈ 1.33. In the case of the softened core studied in the simulations, one typically considers ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε, as we did in Section 4. In order to compare the theoretical and simulation results, however, we choose consistent temperature scales, namely kT/u(rmin) ≈ 6.3T* and kT/uMDii(rmin) ≈ 1.7
= kT/ε, as we did in Section 4. In order to compare the theoretical and simulation results, however, we choose consistent temperature scales, namely kT/u(rmin) ≈ 6.3T* and kT/uMDii(rmin) ≈ 1.7![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) .
.
5.1 Theoretical results for the phase diagram
Let us first discuss the theoretical results, and focus on the MF approximation (Section 3.2). The chemical potential isotherms for the disordered and the ordered phases are shown in Fig. 3. For the periodic phase (Φ > 0), we obtain from eqn (24) the chemical potential shape resembling simple fluids, with an unstable region for small T*. This leads to a coexistence of two periodic phases with the same period, 2π/k0 ≈ 4.7, but different volume fractions. | ||
| Fig. 3 The dimensionless chemical potential, βμ, as a function of the volume fraction in MF approximation. The dashed line corresponds to the disordered phase (eqn (16)), and the solid lines correspond to the periodic phases (eqn (24)). From the top to the bottom solid line T* = 0.11, 0.09, and 0.086, where temperature is in reduced units, T* = kBT/|Ṽ(k0)|, k0 is the wave number corresponding to the minimum of the interaction potential V = (6/π)2u in Fourier representation and ζ = πρ/6 is the dimensionless volume fraction, with the density ρ = (N1 + N2)/V. | ||
To compute the phase diagram, we compare βΩg (eqn (15)) with βΩc (eqn (25)) for fixed T*, and with ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) (βμ) obtained from eqn (16) and (24). The intersection point between βΩg(μ) and βΩc(μ) gives the coexistence of the two phases. The phase diagram in this MF approximation has the universal shape when the reduced temperature T* is used, and is shown in Fig. 4.
(βμ) obtained from eqn (16) and (24). The intersection point between βΩg(μ) and βΩc(μ) gives the coexistence of the two phases. The phase diagram in this MF approximation has the universal shape when the reduced temperature T* is used, and is shown in Fig. 4.
Beyond MF, in the Brazovskii-type approximation, the chemical potential of the disordered phase is temperature-dependent (see eqn (36)), and for low T* the unstable region of the volume fraction appears (see Fig. 5). The presence of the instability leads to the gas–liquid separation that turns out to be metastable with respect to the phase transition between the disordered and ordered phases. The metastable gas–liquid transition with the asociated critical point is shown in Fig. 6 as the dashed line. The order–disorder transition obtained by equating Ω(μ) for the disordered and periodic phases is shown as the solid lines in Fig. 6. The ordering due to the packing effects of the particles cannot be predicted by our theory in the considered approximation, and we do not expect agreement between our theory and simulations for large densities, where the packing effects lead to formation of a solid crystal.
 | ||
| Fig. 5 The dimensionless chemical potential βμ as a function of the volume fraction ζ in the disordered phase. Dashed and solid lines represent the MF (eqn (16)) and the Brazovskii-type approximation (eqn (36) with Φ = Ψ = 0), respectively. From the top to the bottom solid line T* = 0.065, 0.0325, and 0.025. | ||
According to our theory, the phase diagram in Fig. 6 corresponds to any system with hard-core particles interacting for r > 1 with Vii = V = −V12, such that Ṽ(k0)′′/Ṽ(k0) ≈ −3. For different values of Ṽ(k0)′′/Ṽ(k0), we expect similar coexistence lines on the qualitative level. However, the theory is based on the assumption of a deep minimum of Ṽ(k). For very small values of Ṽ(k0)′′/Ṽ(k0) the minimum can be shallow, and in such a case we cannot make any predictions based on our theory.
At low T*, the phase diagrams obtained in the MF and in the Brazovskii-type approximations are similar, but at higher T* the two phase diagrams are qualitatively different. The continuous order–disorder transition becomes fluctuation-induced first-order, and the dashed line in Fig. 4 is shifted to larger ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) and transformed into the pair of lines enclosing the narrow two-phase region in Fig. 6. The coexistence between the two periodic phases in MF is replaced by the order–disorder phase transition. Interestingly, the narrow two-phase region between the disordered and ordered phases broadens rapidly for T* decreasing from the value corresponding to the MF critical point of the phase coexistence between the two ordered phases. We can identify the low-density ordered phase obtained in MF with the disordered phase in which the aggregates are self-assembled, but are not localized due to the presence of fluctuations.
and transformed into the pair of lines enclosing the narrow two-phase region in Fig. 6. The coexistence between the two periodic phases in MF is replaced by the order–disorder phase transition. Interestingly, the narrow two-phase region between the disordered and ordered phases broadens rapidly for T* decreasing from the value corresponding to the MF critical point of the phase coexistence between the two ordered phases. We can identify the low-density ordered phase obtained in MF with the disordered phase in which the aggregates are self-assembled, but are not localized due to the presence of fluctuations.
Let us focus on the large-density branch of the phase coexistence,  . For the low T*, the slope of this line is negative, and it changes sign for
. For the low T*, the slope of this line is negative, and it changes sign for ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) very close to its value at the MF critical point (see Fig. 4 and 6). This shape of the large-density branch of the phase coexistence has a strong effect on the structural evolution of a system with a fixed number of particles for increasing T*. For
very close to its value at the MF critical point (see Fig. 4 and 6). This shape of the large-density branch of the phase coexistence has a strong effect on the structural evolution of a system with a fixed number of particles for increasing T*. For ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) < 0.3, for example for
< 0.3, for example for ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) = 0.2, the density of the periodic phase and its volume decrease, and the density and volume of the coexisting gas increase when T* increases. Finally, when the low-density branch of the coexistence line is reached, the periodic phase disappears. When
= 0.2, the density of the periodic phase and its volume decrease, and the density and volume of the coexisting gas increase when T* increases. Finally, when the low-density branch of the coexistence line is reached, the periodic phase disappears. When ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) > 0.3, however, for example for
> 0.3, however, for example for ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) = 0.35, the scenario is different. As long as the slope of the
= 0.35, the scenario is different. As long as the slope of the  line is negative, the system evolution upon heating resembles the scenario in the case of the gas–liquid coexistence. Namely, upon heating the density of the denser phase decreases, but its volume increases. When the high-density branch of the phase coexistence is reached, the coexisting fluid disappears and the concentration oscillations are present in the whole volume. The low-density periodic phase has many defects, mainly vacancies, in this temperature regime. Further heating leads to a nucleation of the disordered phase when the Tc*(
line is negative, the system evolution upon heating resembles the scenario in the case of the gas–liquid coexistence. Namely, upon heating the density of the denser phase decreases, but its volume increases. When the high-density branch of the phase coexistence is reached, the coexisting fluid disappears and the concentration oscillations are present in the whole volume. The low-density periodic phase has many defects, mainly vacancies, in this temperature regime. Further heating leads to a nucleation of the disordered phase when the Tc*(![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) ) line with the positive slope is reached (see Fig. 6 for
) line with the positive slope is reached (see Fig. 6 for ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) = 0.35). The density of both the disordered and ordered phases increases with further increase of T*, and the volume of the periodic phase decreases, until the disordered-phase branch of the coexistence line is met and the periodic phase disappears. In this temperature range, the disordering effect of the entropy of mixing plays a more important role, and the periodic phase becomes denser upon heating, in contrast to the temperature region corresponding to the negative slope of
= 0.35). The density of both the disordered and ordered phases increases with further increase of T*, and the volume of the periodic phase decreases, until the disordered-phase branch of the coexistence line is met and the periodic phase disappears. In this temperature range, the disordering effect of the entropy of mixing plays a more important role, and the periodic phase becomes denser upon heating, in contrast to the temperature region corresponding to the negative slope of  , where the increase of T* leads to formation of vacancies and less dense packing of the particles. The amplitude Φ of the concentration oscillations decreases with increasing T*, indicating less ordered states at higher T*.
, where the increase of T* leads to formation of vacancies and less dense packing of the particles. The amplitude Φ of the concentration oscillations decreases with increasing T*, indicating less ordered states at higher T*.
5.2 Simulation results for the phase diagram
Let us focus on the results obtained in the MD simulations. The coexistence lines between the low- and high-density phases obtained in the simulations (see Table 1) are shown in Fig. 7. In the dense phase, we find oscillations of c(r) in one direction, in full agreement with assumptions of our theory. The period of the oscillations is very close to the theoretical prediction. The negative slope of the high-density branch of the phase coexistence agrees with the low temperature-part of the theoretical phase diagram. The total volume fraction oscillations in the dense phase are not visible, again in agreement with the theory, where we get Ψ ≪ Φ for the amplitudes of ζ and c. The volume fraction of the dense phase at the coexistence with the gas is lower than predicted in our theory. Note, however that the volume of the particle with the soft core is not uniquely defined, and the interaction potential takes a minimum for r ≈ 1.14. Thus, the volume per particle is effectively larger than π/6 (length is in a-units), and it may lead to a larger volume fraction occupied by the particles than as shown in Fig. 7. The coexistence lines obtained in the theory and in the simulations lie in a very similar range of temperature, when the units kT/u(rmin) and kT/uMDii(rmin) are used.
as shown in Fig. 7. The coexistence lines obtained in the theory and in the simulations lie in a very similar range of temperature, when the units kT/u(rmin) and kT/uMDii(rmin) are used.
 | ||
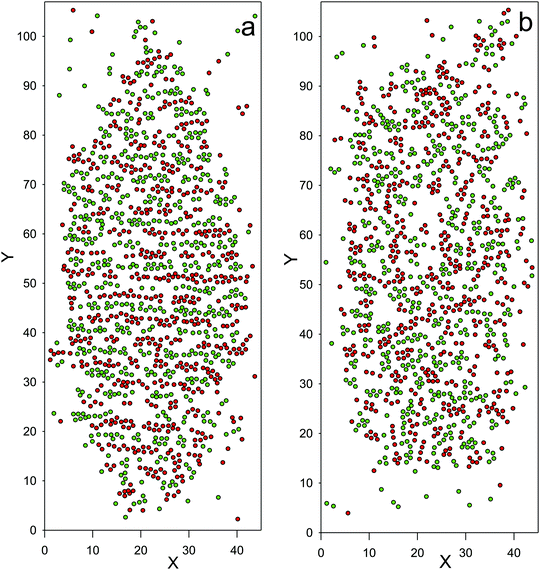
Fig. 7 The coexistence lines between the low- and high-density phases (open and filled symbols, respectively), obtained in the MD simulations. ζ is the average volume fraction of the particles, and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε. For comparison with the theory, note that kT/uMDii(rmin) ≈ 1.7 = kT/ε. For comparison with the theory, note that kT/uMDii(rmin) ≈ 1.7![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) . The structure of the dense phase at coexistence with the gas is shown for the state points indicated by the green triangles down and up in Fig. 9a and b, respectively, and for the state points indicated by the blue square and diamond in Fig. 10a and b, respectively. For simulation details see Section 4. . The structure of the dense phase at coexistence with the gas is shown for the state points indicated by the green triangles down and up in Fig. 9a and b, respectively, and for the state points indicated by the blue square and diamond in Fig. 10a and b, respectively. For simulation details see Section 4. | ||
At a very low ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε, a very dilute gas coexists with a solid crystal, with the structure shown in the snapshots in Fig. 8. In Fig. 8a, alternating bilayers of particles of the first species followed by bilayers of particles of the second species can be seen. The shown bilayers are perpendicular to the direction of the oscillations of c. In Fig. 8b, one layer belonging to the bilayer of particles of one species is shown. Note the hexagonal pattern formed by the particles.
= kT/ε, a very dilute gas coexists with a solid crystal, with the structure shown in the snapshots in Fig. 8. In Fig. 8a, alternating bilayers of particles of the first species followed by bilayers of particles of the second species can be seen. The shown bilayers are perpendicular to the direction of the oscillations of c. In Fig. 8b, one layer belonging to the bilayer of particles of one species is shown. Note the hexagonal pattern formed by the particles.
At ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.27, another periodic phase appears. This phase has a significantly lower density than the solid crystal (see Fig. 7 and Table 1), and has a structure of a soft or liquid crystal, with alternating layers rich in particles of the first and the second components, but without positional order of the centers of the particles. The structure of the crystal phase coexisting with the gas for
= 0.27, another periodic phase appears. This phase has a significantly lower density than the solid crystal (see Fig. 7 and Table 1), and has a structure of a soft or liquid crystal, with alternating layers rich in particles of the first and the second components, but without positional order of the centers of the particles. The structure of the crystal phase coexisting with the gas for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.26 is compared with the structure of the periodic phase coexisting with the gas for
= 0.26 is compared with the structure of the periodic phase coexisting with the gas for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.27 in Fig. 9. In this work we focus only on the coexistence between the dilute and dense phases, and the total volume fractions larger than 0.3 were not studied. The very large density gap indicates that a triple point gas–liquid crystal–crystal may exist at
= 0.27 in Fig. 9. In this work we focus only on the coexistence between the dilute and dense phases, and the total volume fractions larger than 0.3 were not studied. The very large density gap indicates that a triple point gas–liquid crystal–crystal may exist at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≈ 0.27, and that at higher
≈ 0.27, and that at higher ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) the liquid crystal and the crystal phases may coexist. Determination of the high-density part of the phase diagram goes beyond the scope of this work and should be a subject of future studies.
the liquid crystal and the crystal phases may coexist. Determination of the high-density part of the phase diagram goes beyond the scope of this work and should be a subject of future studies.
 | ||
Fig. 9 The configurations obtained in the MD simulations for System 1, with N = 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 and the mean density ρ = 0.178 (a) 566 and the mean density ρ = 0.178 (a) ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.26 and (b) = kT/ε = 0.26 and (b) ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.27 (kT/uMDii(rmin) ≈ 0.46). Red and green circles with the diameter σ = 1.12 (in a-units) represent particles of the first and second components, respectively. The alternating layers rich in the first and in the second components are perpendicular to the shown planes. The particles for = kT/ε = 0.27 (kT/uMDii(rmin) ≈ 0.46). Red and green circles with the diameter σ = 1.12 (in a-units) represent particles of the first and second components, respectively. The alternating layers rich in the first and in the second components are perpendicular to the shown planes. The particles for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≤ 0.26 form a crystal. For ≤ 0.26 form a crystal. For ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≥ 0.27, the particle centers are disordered. Note the smaller density and larger volume of the dense phase at ≥ 0.27, the particle centers are disordered. Note the smaller density and larger volume of the dense phase at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.27, with the shape of the droplet swollen in directions perpendicular to the direction of oscillations of c. The discontinuity of the density at the coexistence with the gas is clearly seen in Fig. 7 and Table 1. For simulation details see Section 4. = 0.27, with the shape of the droplet swollen in directions perpendicular to the direction of oscillations of c. The discontinuity of the density at the coexistence with the gas is clearly seen in Fig. 7 and Table 1. For simulation details see Section 4. | ||
Another structural change can be seen in Fig. 10, where snapshots showing the droplet of the dense phase at coexistence with the gas are shown for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.31 and
= 0.31 and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.32. The structure of the dense phase at
= 0.32. The structure of the dense phase at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.31 is of the same type as at
= 0.31 is of the same type as at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.27 (Fig. 9b), and it differs noticeably from the structure at
= 0.27 (Fig. 9b), and it differs noticeably from the structure at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≥ 0.315. In the latter case, the microsegregation of the components into aggregates of thickness 1 or 2 still takes place, but the concentration oscillations in one direction are no longer evident based on the visual inspection of the simulation snapshots. More empty regions than those at lower
≥ 0.315. In the latter case, the microsegregation of the components into aggregates of thickness 1 or 2 still takes place, but the concentration oscillations in one direction are no longer evident based on the visual inspection of the simulation snapshots. More empty regions than those at lower ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) occur, leading to a relatively large change of the density for temperature increasing by
occur, leading to a relatively large change of the density for temperature increasing by ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ∼ 0.005.
∼ 0.005.
Weak order may be identified only on the level of ensemble-averaged quantities, due to a large number of defects in individual states. At this high ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) and low density, the droplet of the denser phase can undergo deformations, or even move as a whole during the simulations, which may strongly influence the average concentration. In order to pin-point the droplet, we consider a wall attracting strongly the first component, and repulsing weakly the second component. The wall induces periodic ordering, and the range of the wall-induced order is comparable with the bulk correlation length. For distances from the wall significantly larger than the correlation length, the structure of the crystal should not be strongly affected by the wall. The amplitude of the concentration profile should remain constant up to the distance where the interface with the gas appears. Since the interface with the gas phase is free, and the densities between the two phases are significantly different, we assume that the constant-amplitude oscillations in the center of the dense phase are similar to the structure of this phase in the bulk. In simulations, N was sufficiently large to form an interior of the crystal weakly affected by the wall and by the interface with the gas. The density and concentration profiles averaged over the planes (X,Y) parallel to the wall are shown in Fig. 11. The ordering effect of the wall on the total density extends to short distances, while the concentration exhibits damped oscillations up to Z ∼ 40, and for Z > 40, the amplitude of the oscillations of c remains almost constant, although quite small, in the denser phase. In the low density phase the oscillations of the concentration are not visible. The density profile is influenced by the shape of the droplet, since for increasing Z, the area in the (X,Y) plane occupied by the dense phase decreases. For this reason, for Z > 60 the amplitude of the oscillations decreases. We can conclude that the low-density phase is isotropic, but the weak periodic order of the denser phase may still be present above
and low density, the droplet of the denser phase can undergo deformations, or even move as a whole during the simulations, which may strongly influence the average concentration. In order to pin-point the droplet, we consider a wall attracting strongly the first component, and repulsing weakly the second component. The wall induces periodic ordering, and the range of the wall-induced order is comparable with the bulk correlation length. For distances from the wall significantly larger than the correlation length, the structure of the crystal should not be strongly affected by the wall. The amplitude of the concentration profile should remain constant up to the distance where the interface with the gas appears. Since the interface with the gas phase is free, and the densities between the two phases are significantly different, we assume that the constant-amplitude oscillations in the center of the dense phase are similar to the structure of this phase in the bulk. In simulations, N was sufficiently large to form an interior of the crystal weakly affected by the wall and by the interface with the gas. The density and concentration profiles averaged over the planes (X,Y) parallel to the wall are shown in Fig. 11. The ordering effect of the wall on the total density extends to short distances, while the concentration exhibits damped oscillations up to Z ∼ 40, and for Z > 40, the amplitude of the oscillations of c remains almost constant, although quite small, in the denser phase. In the low density phase the oscillations of the concentration are not visible. The density profile is influenced by the shape of the droplet, since for increasing Z, the area in the (X,Y) plane occupied by the dense phase decreases. For this reason, for Z > 60 the amplitude of the oscillations decreases. We can conclude that the low-density phase is isotropic, but the weak periodic order of the denser phase may still be present above ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.31 on the level of the average concentration. Definite conclusions concerning the nature of the structural change at
= 0.31 on the level of the average concentration. Definite conclusions concerning the nature of the structural change at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≈ 0.31, however, are not possible yet. The influence of the finite size of the system on the structural evolution of the weakly microsegregated system cannot be ruled out. As we are interested in the coexistence between the dilute and dense phases, we leave this question open. Our simulation procedure does not allow for a determination of the coexistence lines for
≈ 0.31, however, are not possible yet. The influence of the finite size of the system on the structural evolution of the weakly microsegregated system cannot be ruled out. As we are interested in the coexistence between the dilute and dense phases, we leave this question open. Our simulation procedure does not allow for a determination of the coexistence lines for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) > 0.35.
> 0.35.
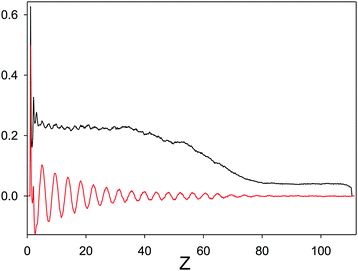 | ||
Fig. 11 The total volume fraction (black line) and the concentration c (red line), averaged over the (X,Y) planes, at a distance Z from the wall attracting the first component with 2Vattr (eqn (37)) and repulsing the second component (eqn (38)) for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.33 (kT/uMDii(rmin) ≈ 0.56). All the remaining walls of the simulation box are repulsive (eqn (38)). N = 85 = 0.33 (kT/uMDii(rmin) ≈ 0.56). All the remaining walls of the simulation box are repulsive (eqn (38)). N = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184, Lx = Ly = 76.5, and Lz = 111.5. For simulation details see Section 4. 184, Lx = Ly = 76.5, and Lz = 111.5. For simulation details see Section 4. | ||
As the number of particles in the simulations is fixed, we can observe the shape of the monocrystal or the droplet coexisting with the gas, as shown in Fig. 8–10. The shape of the crystal or droplet for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≤ 0.31 indicates that the surface tension of the interface parallel to the microsegregated layers is much larger than the surface tension of the interface perpendicular to these layers. The droplet at
≤ 0.31 indicates that the surface tension of the interface parallel to the microsegregated layers is much larger than the surface tension of the interface perpendicular to these layers. The droplet at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.32 has a different shape, but it is still different from a sphere, expected for an isotropic liquid.
= 0.32 has a different shape, but it is still different from a sphere, expected for an isotropic liquid.
5.3 Structure at high temperature
Let us focus on the structure of the disordered phase, and consider the correlation function. In Fig. 12a, we present![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) cc(k) obtained in the Brazovskii-type approximation for three values of the volume fraction and for T* = 0.11. We can clearly see the structure on the length scale 2π/k0 developing for increasing volume fraction, when the phase transition to the periodic phase is approached. For these thermodynamic states,
cc(k) obtained in the Brazovskii-type approximation for three values of the volume fraction and for T* = 0.11. We can clearly see the structure on the length scale 2π/k0 developing for increasing volume fraction, when the phase transition to the periodic phase is approached. For these thermodynamic states, ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) MFcc(k) given in eqn (12) does not exist, since in MF the disordered phase is unstable. In order to compare theoretical and simulation results, we plot the correlation function gcc related to the pair distribution functions gij = Gij
MFcc(k) given in eqn (12) does not exist, since in MF the disordered phase is unstable. In order to compare theoretical and simulation results, we plot the correlation function gcc related to the pair distribution functions gij = Gij![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) i−1
i−1![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) j−1 + 1 according to the formula
j−1 + 1 according to the formula | (39) |
![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) = 0.255. This thermodynamic state is close to the transition to the periodic phase, where the two-phase region becomes narrow.
= 0.255. This thermodynamic state is close to the transition to the periodic phase, where the two-phase region becomes narrow.
 | ||
Fig. 12 The correlation function for the concentration obtained in the Brazovskii-type theory. (a) ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) cc(k) in Fourier representation for T* = 0.11 (kT/u(rmin) ≈ 0.7). From the bottom to the top line, cc(k) in Fourier representation for T* = 0.11 (kT/u(rmin) ≈ 0.7). From the bottom to the top line, ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) = 0.1, 0.15, and 0.2. (b) gcc(r) (see eqn (39)) in real-space representation for T* = 0.12 (kT/u(rmin) ≈ 0.76) and = 0.1, 0.15, and 0.2. (b) gcc(r) (see eqn (39)) in real-space representation for T* = 0.12 (kT/u(rmin) ≈ 0.76) and ![[small zeta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c7.gif) = 0.255. = 0.255. | ||
The pair distribution functions obtained in MD for three values of density at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.4 (kT/uMDii(rmin) ≈ 0.68) are shown in Fig. 13. We can see increasing correlations when the volume fraction increases. For comparison with the theoretical results, we plot in Fig. 13bgcc at ζ = 0.1π/6 and
= kT/ε = 0.4 (kT/uMDii(rmin) ≈ 0.68) are shown in Fig. 13. We can see increasing correlations when the volume fraction increases. For comparison with the theoretical results, we plot in Fig. 13bgcc at ζ = 0.1π/6 and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.4. This thermodynamic state corresponds to the low-density phase not far from the phase transition. Note the very similar period and decay length close to the transition to the ordered phase in theory and simulations (Fig. 12b and 13b). For comparison of the thermodynamic states shown in Fig. 12b and 13b, see Fig. 6 and 7.
= 0.4. This thermodynamic state corresponds to the low-density phase not far from the phase transition. Note the very similar period and decay length close to the transition to the ordered phase in theory and simulations (Fig. 12b and 13b). For comparison of the thermodynamic states shown in Fig. 12b and 13b, see Fig. 6 and 7.
 | ||
Fig. 13 MD simulation results for (a) the correlation functions between like and different particles obtained in simulations with PBC for N = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184, and ρ = N/V = 0.4, 0.2, and 0.1 (red, green and grey lines, respectively) and 184, and ρ = N/V = 0.4, 0.2, and 0.1 (red, green and grey lines, respectively) and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.4 (kT/uMDii(rmin) ≈ 0.68). Representative configurations corresponding to ρ = 0.1 and ρ = 0.4 are shown in Fig. 14. (b) The correlation function for concentration, gcc (see eqn (39)), at ζ = 0.1π/6 and = kT/ε = 0.4 (kT/uMDii(rmin) ≈ 0.68). Representative configurations corresponding to ρ = 0.1 and ρ = 0.4 are shown in Fig. 14. (b) The correlation function for concentration, gcc (see eqn (39)), at ζ = 0.1π/6 and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.4. For simulation details see Section 4. = 0.4. For simulation details see Section 4. | ||
 | ||
Fig. 14 A projection of a layer of thickness 1 on the (X,Y) plane showing the configuration obtained in the MD simulations with PBC for N = 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 184, and 184, and ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.4 (kT/uMDii(rmin) ≈ 0.68). (a) N/V = 0.1 and (b) N/V = 0.4. The corresponding pair distribution functions are presented in Fig. 13. = kT/ε = 0.4 (kT/uMDii(rmin) ≈ 0.68). (a) N/V = 0.1 and (b) N/V = 0.4. The corresponding pair distribution functions are presented in Fig. 13. | ||
6 Discussion and summary
We have studied phase behavior and structure in a binary mixture of particles with competing interactions, assuming hard cores of the particles in the theory, and core-softened particles in the MD simulations. The assumed interactions favor close neighbors of the same kind, but at larger distances the presence of different particles is favorable. We have obtained good agreement between the theory developed in this work and MD simulations. In our theory, local fluctuations of the concentration are taken into account for the first time in the formalism that allows one to determine the phase diagram in microsegregating mixtures.At low T, the simulations show formation of the crystal phase with perfectly separated particles in alternating bilayers composed of the first and second components. We did not obtain the crystal in our mesoscopic theory, because we assumed weak order that is present at higher T.
At ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.27, the liquid-crystalline phase with periodic concentration appears in the simulations, and this phase coexists with the gas at
= 0.27, the liquid-crystalline phase with periodic concentration appears in the simulations, and this phase coexists with the gas at ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) ≥ 0.27. In this periodic phase, alternating layers rich in the first and second components are formed, but the crystalline order of the centers of mass of the particles is absent. Further heating leads to lower density and smaller degree of order of the periodic phase at the coexistence with the disordered phase. At these intermediate temperatures, the theoretical and simulation results are in good agreement.
≥ 0.27. In this periodic phase, alternating layers rich in the first and second components are formed, but the crystalline order of the centers of mass of the particles is absent. Further heating leads to lower density and smaller degree of order of the periodic phase at the coexistence with the disordered phase. At these intermediate temperatures, the theoretical and simulation results are in good agreement.
The phase diagram at large temperatures cannot be reliably determined in our simulations. For this reason, the theoretical predictions for the high-temperature part of the phase diagram are not supported by simulations yet. The periodic structure with weak order, expected at a high T, is characterized by the ensemble-averaged concentration that is periodic in space with a small amplitude. Small amplitude means a large number of different defects in instantaneous states due to thermally induced fluctuations. More subtle simulation methods are necessary for detection of the weak order and determination of its nature.
On the quantitative level, the volume fractions and temperature at the phase diagrams obtained in the theory and in the simulations are significantly different. This is partially because of the approximate nature of the theory, and partially because of the softer core in simulations. The diameter of the particle core in simulations is not uniquely defined, and the potential takes the minimum for a distance noticeably larger than the diameter of the hard core considered in the theory. Thus, we should remember that the actual volume occupied by the particles is larger than that shown in Fig. 7. The difference in temperature corresponding to the phase coexistence of the gas and the dense liquid crystal is as large as one order of magnitude. For example, ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = kT/ε = 0.31 in simulations corresponds to T* ≈ kT/(31ε) ≈ 0.01 in the units used in our theory. The corresponding thermodynamic state in Fig. 6, however, occurs for T* ∼ 0.1. This discrepancy is related mainly to the minimum of the interaction potential that for hard cores is about 10 times deeper than in the case of the softer core (compare Fig. 1a and 2a). Because of that, the thermal energy kT becomes comparable with the depth of the attractive well for T that in the case of hard cores is about 10 times larger than in the case of the softer core. This means that we need ∼10 times larger temperature at the order–disorder transition when the softer core is replaced by the hard one. Note that when the shape of the interactions at short distances is taken into account, our theoretical and simulation predictions are in good agreement. Also, the correlation function calculated for T* = 0.12 in the theory and for
= kT/ε = 0.31 in simulations corresponds to T* ≈ kT/(31ε) ≈ 0.01 in the units used in our theory. The corresponding thermodynamic state in Fig. 6, however, occurs for T* ∼ 0.1. This discrepancy is related mainly to the minimum of the interaction potential that for hard cores is about 10 times deeper than in the case of the softer core (compare Fig. 1a and 2a). Because of that, the thermal energy kT becomes comparable with the depth of the attractive well for T that in the case of hard cores is about 10 times larger than in the case of the softer core. This means that we need ∼10 times larger temperature at the order–disorder transition when the softer core is replaced by the hard one. Note that when the shape of the interactions at short distances is taken into account, our theoretical and simulation predictions are in good agreement. Also, the correlation function calculated for T* = 0.12 in the theory and for ![[T with combining macron]](https://www.rsc.org/images/entities/i_char_0054_0304.gif) = 0.4 in the simulations, correspond to a very similar temperature, if kT is in units of the minimum of the potential between like particles.
= 0.4 in the simulations, correspond to a very similar temperature, if kT is in units of the minimum of the potential between like particles.
The strong effect of the softness (or hardness) of the particle core on the temperature at the order–disorder phase transition should be taken into account in experiments searching for spontaneously formed ordered patterns on the nanometer or micrometer length scale.
Experimental observation of ordered patterns in binary colloidal mixtures concerns colloidal crystals formed by oppositely charged particles41 with cubic symmetry. The same crystals with a rich variety of unit cells were found in computer simulations.41 Another example of pattern formation in binary mixtures concerns colloidal gels.42 As far as we know, however, colloidal crystals and liquid crystals with the components microsegragated into alternating planar layers have not been observed yet. This new type of ordered phases may be found, for example in a mixture with the mermaid potential between like particles (attractive head repulsive tail), and the peacock potential between different ones (repulsive head attractive tail). From the theory developed here it follows that the topology of the phase diagram is common for many systems with this type of interactions. The strength of the interactions should be carefully designed to obtain the ordered phases at room temperature. Also the thickness of the microsegragated layers can be controlled by tuning the interaction potential.
Author contributions
OP: investigation, visualization, validation, and writing – original draft; ML: investigation, software, visualization, and writing – original draft; AC: conceptualization, investigation, and writing – original draft.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This project has received funding from the European Union Horizon 2020 research and innovation under the Marie Skłodowska-Curie grant agreement no. 734276 (CONIN). Additional funding was received from the Polish Ministry of Science and Higher Education for the implementation of the project No. 734276 in the years 2017–2021.References
- M. Rey, R. Elnathan, R. Ditcovski, K. Geisel, M. Zanini, M.-A. Fernandez-Rodriguez, V. V. Naik, A. Frutiger, W. Richtering, T. Ellenbogen, N. H. Voelcker and L. Isa, Nano Lett., 2016, 16, 157 CrossRef.
- A. Rauh, M. Rey, L. Barbera, M. Zanini, M. Karg and L. Isa, Soft Matter, 2017, 13, 158 RSC.
- V. S. Grishina, V. S. Vikhrenko and A. Ciach, J. Phys.: Condens. Matter, 2020, 32, 405102 CrossRef CAS.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. Poon, S. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492 CrossRef CAS.
- A. I. Campbell, V. J. Anderson, J. S. van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301 CrossRef.
- P. Bartlett and A. I. Campbell, Phys. Rev. Lett., 2005, 95, 128302 CrossRef.
- C. P. Royall, Soft Matter, 2018, 14, 4020 RSC.
- A. Ciach, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061505 CrossRef CAS.
- A. Ciach and W. T. Góźdź, Condens. Matter Phys., 2010, 13, 23603 CrossRef.
- A. Ciach, J. Pekalski and W. T. Góźdź, Soft Matter, 2013, 9, 6301 RSC.
- Y. Zhuang, K. Zhang and P. Charbonneau, Phys. Rev. Lett., 2016, 116, 098301 CrossRef.
- Y. Zhuang and P. Charbonneau, J. Phys. Chem. B, 2016, 120, 6178–6188 CrossRef CAS.
- M. Edelmann and R. Roth, Phys. Rev. E, 2016, 93, 062146 CrossRef.
- D. Pini and A. Parola, Soft Matter, 2017, 13, 9259 RSC.
- B. A. Lindquist, R. B. Jadrich and T. M. Truskett, Soft Matter, 2016, 12, 2663–2667 RSC.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031402 CrossRef.
- A. de Candia, E. D. Gado, A. Fierro, N. Sator, M. Tarzia and A. Coniglio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 010403(R) CrossRef.
- A. I. Campbell, V. J. Anderson, J. S. van Duijneveldt and P. Bartlett, Phys. Rev. Lett., 2005, 94, 208301 CrossRef.
- H. Sedgwick, S. U. Egelhaaf and W. C. K. Poon, J. Phys.: Condens. Matter, 2004, 16, S4913–S4922 CrossRef CAS.
- C. J. Dibble, M. Kogan and M. J. Solomon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041403 CrossRef.
- Y. Guo, B. G. P. van Ravensteijn and W. K. Kegel, Chem. Commun., 2020, 56, 6309–6312 RSC.
- K. Marolt, M. Zimmermann and R. Roth, Phys. Rev. E, 2019, 100, 052602 CrossRef CAS.
- K. Marolt and R. Roth, Phys. Rev. E, 2020, 102, 042608 Search PubMed.
- C. Hertlein, L. Helden, A. Gambassi, S. Dietrich and C. Bechinger, Nature, 2008, 451, 172 CrossRef CAS.
- A. Gambassi, A. Maciołek, C. Hertlein, U. Nellen, L. Helden, C. Bechinger and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 061143 CrossRef CAS.
- A. Ciach, Adv. Biomembr. Lipid Self-Assem., 2016, 23, 61 CAS.
- A. Ciach, O. Patsahan and A. Meyra, Condens. Matter Phys., 2020, 23, 23601 CrossRef.
- A. Ciach, Mol. Phys., 2011, 109, 1101 CrossRef CAS.
- R. Evans, Adv. Phys., 1979, 28, 143 CrossRef CAS.
- S. A. Brazovskii, J. Exp. Theor. Phys., 1975, 41, 85 Search PubMed.
- A. Ciach, Soft Matter, 2018, 14, 5497 RSC.
- N. B. Wilding, F. Schmid and P. Nielaba, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1998, 58, 2201 CrossRef CAS.
- O. Patsahan, R. Melnyk and M. Kozlovskii, Condens. Matter Phys., 2001, 4, 235 CrossRef.
- E. Schöll-Paschinger and G. Kahl, J. Chem. Phys., 2003, 118, 7414 CrossRef.
- A. Ciach and O. Patsahan, Condens. Matter Phys., 2012, 15, 23604 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer Simulations of Liquids, Clarendon Press, Oxford, 1990 Search PubMed.
- M. Litniewski and A. Ciach, J. Chem. Phys., 2019, 150, 234702 CrossRef CAS.
- H. Watanabe, N. Ito and C.-K. Hu, J. Chem. Phys., 2012, 136, 204102 CrossRef.
- J. R. Morris and X. Song, J. Chem. Phys., 2002, 116, 9352–9358 CrossRef CAS.
- M. A. Barroso and A. L. Ferreira, J. Chem. Phys., 2002, 116, 7145–7150 CrossRef CAS.
- M. Leunissen, C. Christova, A.-P. Hynninen, C. Royal, A. Campbell, A. Imhof, M. Dijkstra, R. van Roji and A. van Blaaderen, Nature, 2005, 437, 235 CrossRef CAS.
- J. Appel, N. de Lange, H. M. van der Kooij, T. van de Laar, J. B. ten Hove, T. E. Kodger and J. Sprakel, Part. Part. Syst. Charact., 2015, 32, 764 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |