Open Access Article
Open Access ArticleEmergence and stabilization of transient twisted defect structures in confined achiral liquid crystals at a phase transition†
Jose X.
Velez‡
a,
Zhaofei
Zheng‡
a,
Daniel A.
Beller
 b and
Francesca
Serra
b and
Francesca
Serra
 *a
*a
aJohns Hopkins University, Dept. Physics and Astronomy, Baltimore, USA. E-mail: francesca.serra@jhu.edu
bUniversity of California, Merced, Dept. Physics, Merced, USA
First published on 26th March 2021
Abstract
Spontaneous emergence of chirality is a pervasive theme in soft matter. We report a transient twist forming in achiral nematic liquid crystals confined to a capillary tube with square cross section. At the smectic–nematic phase transition, intertwined disclination line pairs are observed with both helical and kinked lozenge-like contours, configurations that we promote through capillary cross-section geometry and stabilize using fluorescent amphiphilic molecules. The observed texture is similar to that found in “exotic” materials such as chromonics, but it is here observed in common thermotropic nematics upon heating from the smectic into the nematic phase. Numerical modeling further reveals that the disclinations may possess winding characters that are intermediate between wedge and twist, and that vary along the defect contours. In our experiments, we utilize a phase transition to generate otherwise elusive defect structures in common liquid crystal materials.
1 Introduction
In many soft matter and biological systems, a spontaneous emergence of chirality occurs in achiral systems and is responsible for important effects. Chirality can emerge, for example, in spheres confined within a cylinder,1 in the assembly of rigid rods in a membrane,2 in the stacking of disc-like molecules,3–7 and in the self-selection of one component in a racemic system.8–11 It is hypothesized that a similar mechanism drove the selection of chiral macromolecules in a pre-biotic environment.12In this context, liquid crystal (LC) systems have attracted a great deal of attention as testing grounds for physical principles of emergent chirality. LCs are complex fluids composed of anisotropic molecules, which possess long-range orientational order. Distorting LCs costs elastic energy. In the simplest LC phase, the nematic phase, the bulk elastic energy is given by the sum of the energy penalties due to splay, twist and bend deformations.13 Earlier work showed how a twisted configuration is favored if the twist elastic constant is significantly smaller than the other two.14,15 More recently, the work of Jeong et al. shows how chirality emerges in the equilibrium configuration of an achiral lyotropic chromonic LC droplet in oil.16 Here, the twist elastic constant of chromonic LCs is one order of magnitude smaller than the bend elastic constant.17 The high energy cost of bend in the droplets induces the LCs to twist instead. Similarly, when lyotropic chromonics are confined in round capillary tubes with homeotropic (perpendicular) molecular anchoring on the surface of the capillary, the low twist constant causes the nematic director to twist from the walls to the center of the capillary (twisted escaped radial, or TER, configuration) or to form two intertwined disclination lines (twisted polar, or TP, configuration).18 More recently, lyotropic micellar LCs and polymeric LCs have been investigated,19,20 leading to similar results and showing that the observation of large chiral domains is not uncommon in achiral LC systems whenever twist is energetically cheaper compared to bend and splay.
Achiral thermotropic LCs confined in capillary tubes have been studied extensively.21–28 In the smectic-A phase, adjacent LC rods form stacked fluid layers. If a cylinder imposes homeotropic molecular anchoring on its walls, the smectic layers are arranged like the concentric layers of a leek29 in the so-called planar radial (PR) configuration. This can be easily observed with polarized microscopy. When the smectic–nematic phase transition occurs, the system breaks from discrete to continuous translational symmetry, maintaining orientational order. Deep in the nematic phase, LCs experience a frustration in the alignment, which gives rise to two possible configurations: the planar polar (PP) configuration, with two disclination lines running parallel to the side of the capillary, or the escaped radial (ER) configuration, where the LC bends from the walls toward the center of the capillary, without topological defects.23,25 While the PP configuration is stable in thin capillaries, ER is stable in capillaries with radius larger than a micron.23 Both these solutions contain no twist deformation, as is typically observed for achiral thermotropic LCs.
Here we show that even for very common achiral thermotropic LCs such as CCN-47 and 8CB confined in large capillaries we can observe intertwined disclinations with spontaneous twist propagating over long length-scales. Such textures, similar to those observed in chromonics and in lyotropics,16,18–20,30–33 are transient near the smectic-A to nematic phase transition. The Frank elastic constants for twist and bend decrease abruptly in the transition from smectic-A, which cannot accommodate those distortion modes, to the nematic phase. Most importantly, the twist elastic constant decreases more rapidly than the bend. This forms the basis for our hypothesized mechanism. In this paper, we describe the emergence of twist at the phase transition, we show the configurations that can be obtained and we explore ways to stabilize the twisted structure. Through Landau-de Gennes numerical modeling, we elucidate the director field structure around the observed defect morphologies. Finally, we discuss the influence of the elastic anisotropy and of the channel geometry on the LC behavior.
2 Methods
For the experiments, 4′-butyl-4-heptyl-bicyclohexyl-4-carbonitrile (CCN-47, Nematel GmbH) and 4-octyl-4′-cyanobiphenyl (8CB, Sigma Aldrich) (chemical structures are shown in ESI,† Fig. S1) are incorporated in square capillaries (VitroTubes.com) of sides 50 μm or in cylindrical capillaries with diameter 50 μm. Addition of 0.1% didecyldimethylammonium bromide (DDAB, Sigma Aldrich),34 or a pretreatment with a solution of 1.0% octadecyltrichlorosilane (OTS, Sigma Aldrich) guarantee homeotropic anchoring. The mixture of CCN-47 and DDAB has a phase transition from smectic to nematic LC at 29.4 °C and a transition from nematic to isotropic phase at 59 °C. 8CB has a transition from smectic to nematic at 33 °C and a transition from nematic to isotropic at 40.5 °C. The elastic constants of CCN47 are similar to 8CB35 and of the order of 10−11 N. The capillaries are studied with polarized optical microscopy (POM) with a Nikon LV Pol microscope, where temperature is controlled with a INSTEC mK2000 heating stage and images are taken with a Nikon DS-Ri2 camera.For the computer simulations, we numerically minimize the Landau-de Gennes free energy with a finite difference scheme on a regular cubic mesh (further details can be found in ESI† and in previous works36,37). For the simulations shown in this paper, we utilize non-periodic boundary conditions, with strong homeotropic anchoring on the capillary walls and weak degenerate planar anchoring on the two ends of the capillary. Here, we vary the elastic constants K1, K2, K3 where the indices 1, 2 and 3 indicate respectively splay, twist and bend. The connection between the simulation parameters and the elastic constants is reported in detail in ESI,† Section 2.1.
The director field n(x) is obtained from the Q-tensor as the eigenvector associated with the leading eigenvalue S. The winding character of disclinations is given by the angle β between the local unit tangent ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) to the disclination contour and the Frank (unit) vector
to the disclination contour and the Frank (unit) vector 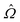 about which
about which ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) rotates at the disclination. Wedge disclinations of winding number +1/2 or −1/2 have β = 0 or π, respectively, while twist disclinations have β = π/2, and any intermediate value of β is geometrically possible. To estimate
rotates at the disclination. Wedge disclinations of winding number +1/2 or −1/2 have β = 0 or π, respectively, while twist disclinations have β = π/2, and any intermediate value of β is geometrically possible. To estimate 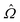 from simulated data, we adapt a method introduced in ref. 38: first, disclinations are found by thresholding for small values of S, identifying two clusters of defect points at each value of z (capillary axis direction), whose centers of mass provide the defect core location. Then, for each disclination and at each z value,
from simulated data, we adapt a method introduced in ref. 38: first, disclinations are found by thresholding for small values of S, identifying two clusters of defect points at each value of z (capillary axis direction), whose centers of mass provide the defect core location. Then, for each disclination and at each z value, 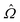 is estimated to be the unit vector parallel to
is estimated to be the unit vector parallel to ![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif) =
= ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) × [(
× [(![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ·∇)
·∇)![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ] as calculated by finite differences at nearest-neighbor sites to the defect core point on the cubic mesh. A weighted average of
] as calculated by finite differences at nearest-neighbor sites to the defect core point on the cubic mesh. A weighted average of ![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif) estimates is constructed with weights 1 − (δr·
estimates is constructed with weights 1 − (δr·![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) )2 dependent on the separation δr from the defect core and the local tangent
)2 dependent on the separation δr from the defect core and the local tangent ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) . Finally, a sign check is performed on
. Finally, a sign check is performed on 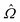 , multiplying it by −1 if ∇·[
, multiplying it by −1 if ∇·[![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) (∇·
(∇·![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ) − (
) − (![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ·∇)
·∇)![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ] has a different sign than
] has a different sign than 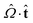 . For disclinations with β near π/2, a second sign check multiplies
. For disclinations with β near π/2, a second sign check multiplies 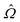 by −1 if the twist
by −1 if the twist ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ·(∇ ×
·(∇ × ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) ) is decreasing rather than increasing along the direction
) is decreasing rather than increasing along the direction 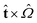 .
.
3 Results
3.1 Smectic phase
Before we explore the twisted structure, which occurs at the transition between smectic and nematic, we describe the behavior of LC CCN-47 in the smectic phase confined in a glass capillary tube with square cross-section (50 μm each side) and homeotropic anchoring. While in round capillaries the smectic layers can be accommodated with a central topological defect line, the edges of the square capillaries induce the formation of geometric defects (Fig. 1a–c). Previous studies of confined smectics highlight the presence of focal conic domains with high eccentricity in rectangular channels.39 Here, we verify that by rotating the capillary by 90° around its main axis we observe very similar images, indicating that the configuration has approximately a four-fold symmetry. All the domains have similar size. The maximum size of each domain (i.e. their major axis length) is equal to half the channel side. We observe, however, that the cooling rate from nematic to smectic affects the defect formation. A slow and regular cooling rate of 1 °C min−1 leads to a smectic phase with evenly spaced defects near the four corners of the capillary (Fig. 1a). A faster cooling, on the other hand (exponential cooling with time constant τ = 400 s), creates a more irregular series of defects (Fig. 1b). An even faster cooling (exponential cooling with time constant τ < 250 s), obtained in our case by quenching the sample from the heating stage onto a cold metal surface, creates a uniformly aligned region in the middle of the capillary with smaller defects concentrated near the four corners of the capillary (Fig. 1c).3.2 Phase transition
As we increase the temperature up to the smectic–nematic transition, we observe the onset of the twisted configuration, an example of which is shown in the bottom panel of Fig. 1. Here, heating from 25 °C to 34 °C at a rate of 0.2 °C min−1, we see the twisted configuration. Initially, the onset of the new texture is characterized by the formation of a lozenge-like pattern. At the phase transition (29.4 °C), the smectic defects disappear and the nematic LC adopts a twisted configuration with two defect lines. The structure closely resembles that reported in ref. 18 and 19 for chromonic and lyotropic LCs, respectively, in capillaries with homeotropic anchoring. In our setting, this configuration is transient: eventually, the structure is replaced by an escaped radial (ER) domain, which typically forms at one end of the capillary and expands through the capillary, as shown in Video S1 (ESI†). The ER configuration, as seen in ref. 23,25, is stable up until the isotropic phase transition. Notably, when the sample is cooled down into the nematic phase from the isotropic phase, only the (achiral) ER texture is observed. This strongly indicates that the emergence of twist is a consequence of the reorganization that happens at the smectic–nematic phase transition. The twisted defect lines are not exclusive to CCN-47. In fact we observe a similar structure in the common LC 8CB at the smectic–nematic phase transition, as shown in Fig. 1g and in ESI,† Fig. S2.While the transient twisted structure can only be observed if the heating rate from smectic to nematic is sufficiently slow, we notice that also the cooling rate from the nematic into the smectic phase plays an important role. The three different smectic configurations shown in Fig. 1a–c, obtained with different cooling rates, have a different fate when they are then re-heated into the nematic phase. All three configurations show evidence of twist, but the smectic textures obtained with slow or intermediate cooling develop disclination lines (Fig. 1d and e) that cross the capillary at irregular intervals, while for the fastest-quenched LC there are no detectable defect lines crossing the capillary (Fig. 1f). In the case of very slow cooling, the twisted lines are compressed in short segments (Fig. 1d), while the smectic structures quenched at intermediate rate can melt into a smooth double helical structure (Fig. 1e) very similar to the twisted polar (TP) configuration observed in lyotropic LCs.19 Thus, this system's behavior depends on the cooling rate and the nematic director is influenced by the configuration prior to the phase transition, a possible indication of a memory effect similar to those observed in thin films.40
3.3 Twisted defects
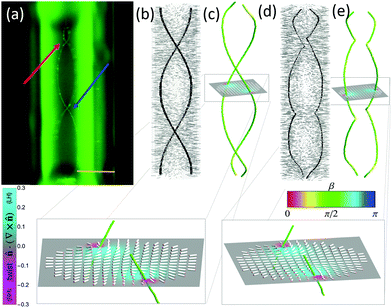
To confirm the presence and configuration of the disclination lines, we stabilize them using a CCN-47 and DDAB (0.1%) mixture with BODIPY-C5 fluorophores (Fig. 2a). Following the work by Wang et al.,41 we use amphiphilic fluorescent molecules that self-assemble in disclination lines above a critical concentration. We thus unambiguously confirm the presence of disclinations (Fig. 2a, line indicated by arrows) and we can measure accurately their average distance. In the 50 μm channels, their distance when they appear to intersect while crossing the channel is between 15 and 20 μm. Using the fluorescent amphiphiles is also helpful to stabilize the TP configuration. If the temperature is kept constant very near the phase transition, the twisted configuration persists, and does not turn into an achiral ER configuration for several hours. If the temperature is then increased, the ER structure grows to eventually occupy most of the channel as the defect lines shrink. The defect lines always close into a short-pitched helix (red arrow in Fig. 2a), and shrink until they are coiled into a highly distorted structure that resembles the cord of a landline telephone.Using Landau-de Gennes numerical modeling of a nematic LC in a cylindrical capillary, we can reproduce the observed double-helix and lozenge-like defect configurations, but only for K2 < K3 with a ratio below 0.5 (Fig. 2b–d). In particular, the regular twisted structure in Fig. 2b was obtained using a bend and splay constant K1 = K3 = 10−11N and K2/K3 = 0.2, while the irregular twist in Fig. 2d was obtained with K2/K3 = 0.13. For K2/K3 > 0.5, simulations show an achiral PP configuration as expected. More details on the simulations and the parameters used can be found in ESI.† The size of the simulation (up to hundreds of nanometers) is very different from that of the experiments (tens of microns); therefore in simulations the TP or PP state with two defect lines running along the capillary are always favorable, while in experiment we observe the ER configuration as the stable one. Despite this intrinsic difference, the simulations show many similarities in the shape of the defect lines in the TP state (Fig. 2b and d).
Within the range explored in simulations (i.e. smaller than experiments), varying the radius of the capillary does not qualitatively change the behavior, as reported in ESI,† Fig. S3. In addition, we have tested the dependence on the anchoring strength and verified that by reducing the anchoring constant down to 1/20 of its initial value Wh = 10−2 N m−1 does not affect the behavior of the defects, as shown in ESI,† Fig. S4.
The elastic constants used so far are consistent with those utilized to describe other twisted achiral systems such as chromonics and lyotropics. However, we have also numerically modeled the case K1 = K2 < K3. The results are reported in ESI,† Fig. S5 and S6, which show the effect of varying the capillary radius/elastic anisotropy and the anchoring constant, respectively. We find once again a qualitative similarity to the experimental observations, with twist emerging and becoming progressively more irregular at higher elastic anisotropy. This indicates that the parameter K2/K3 is responsible for the TP configuration, whereas it is not crucial for K2 to be the smallest elastic constant.
Our numerical findings also highlight a subtlety about the winding character of the disclinations in our system, as compared with recent findings on lyotropic nematics. For the chromonic nematic LCs in a round capillary, a disclination double-helix was reported and suggested to be a twisted planar polar (TPP) state, meaning the director has no component along the capillary long axis.18 In contrast, the TP structure observed in a non-chromonic, micellar lyotropic nematic was modeled as a double-helix of twist disclinations, in which a small measuring circuit around either disclination sees the director wind by π about an axis ![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif) making a right angle β = π/2 with the local disclination tangent.19
making a right angle β = π/2 with the local disclination tangent.19
Neither the TP nor the TPP structure contains wedge disclinations, the ±1/2 defects familiar from 2D nematic point-defects. In wedge disclinations, a measuring circuit around a disclination sees the director rotate by π about a Frank vector parallel or antiparallel to the local disclination tangent, a situation clearly in contrast to the TPP's twist disclinations, but also impossible in the TP: there, the Frank vector must point along the capillary long axis, which never matches the disclination tangent. Instead, the TPP disclinations have a winding character intermediate between wedge and twist, characterized by an oblique angle β between the Frank vector and the defect tangent.
Does the TP or TPP model describe the disclinations in our system? Both models assume a screw symmetry along the capillary axis, meaning the structure is the same everywhere up to a rotation, consistent with the smooth double-helix defects observed in those works.18,19 In contrast, our numerical models, which reproduce the kinked and pinned defect configurations observed in our experiments, indicate that the winding character itself varies along the contour length of each disclination. We observe the following general trends: along segments where the disclination is smoothly undulating and not pinned at an edge, the disclination tends to have twist winding character, or nearly so, consistent with the TP model at a local level (Fig. 2c and e). Twist distortions of both handedness are prominent in the director field on opposite sides of both disclinations, a signature of twist disclinations as noted in ref. 19 (details in Fig. 2c and e). However, near kinks, the winding character becomes somewhat more wedge-like, taking on an intermediate winding character, and kinks are the sites where opposing domains of the spontaneously broken reflection symmetry meet. On one side, the disclinations follow right-handed helices, and the director undergoes right-handed twist in the interior and left-handed twist between the disclinations and the boundary. On the other side of the kink, left-handed and right-handed swap roles in both the director field and the defect contours. (ESI,† Fig. S7).
In certain regions of parameter space, another configuration appears. It is the twisted escaped radial (TER) configuration, observed in chromonics and lyotropic LCs, where the director twists and bends without creating defect lines. Due to the size of the capillary the TP state is always more energetically favorable than the TER configuration, but the latter can be obtained by carefully controlling the initial configuration for the simulation, as detailed in ESI,† Fig. S8. The reason why the size of the simulation is so important is that the diameter of the defect core depends on the molecular size and is therefore not scalable as other length-scales. This was also discussed for LCs near colloidal particles, as detailed in ref. 42.
3.4 The role of edges
In capillaries with a round cross-section, we only rarely observe experimentally the onset of the transient twisted configuration. Some examples of such observations are shown in ESI,† Fig. S9, both for CCN-47 and 8CB. However, the twisted structure is rarely observed and extremely short-lived, up to a few minutes. This indicates that the presence of edges in capillaries with square cross section plays an important role. In nematics, the two disclination lines with half-integer charge are attracted by edges, as this helps reduce the total elastic distortion.43 The cross section of the capillary has six possible arrangements of the two defects lines. We refer to the corners by compass directions: NW (northwest), NE (northeast), SE (southeast), SW (southwest). Of these configurations, four have the two lines sitting near adjacent corners and have therefore a higher energy, while two configurations have defects sitting in opposite corners, NW–SE and NE–SW (Fig. 3a and b).44 Defect lines can run along the same edge and never cross the capillary; however, the director also twists along the capillary. Consequently, defect lines sometimes switch to a neighboring edge. The configurations with lines in NW–SE and NE–SW corners are the most stable. The line in NW may move to NE or to SW, while the line in SE moves to SW or NE, respectively. As the light is incident in the north-south direction, if the two lines move along the north and south walls we can see them crossing, while if they move along the east and west walls we cannot. This is indeed observed and the two cases are shown in Fig. 3c and in ESI,† Videos S2 and S3.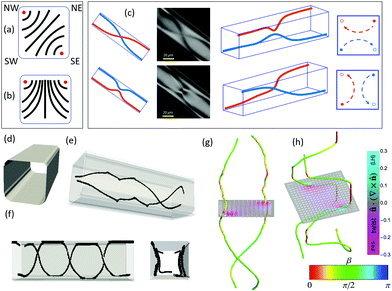 | ||
| Fig. 3 (a and b) Cross section schematic of possible configurations with two defect lines in the nematic phase. (c) Mode of twisting of the lines in the capillary with square cross-section, observed with polarized microscopy. The two lines switch corners and as they switch they approach each other. Given the direction of the light propagation and the geometry of our observation, this switch appears either as a real crossing or as an approaching of the lines near the center. By changing the microscope focus, we follow the fate of each line. (d) Simulated capillary boundary surface with square cross section and rounded corners. (e) Simulation of liquid crystal with high elastic anisotropy K2/K3 = 0.1, K1 = K3 = 10−11 N, in a capillary with rounded corners. The side of the square capillary corresponds to 225 nm and the length to 675 nm. The radius of curvature of the corners is 45 nm. All the side walls impose strong homeotropic anchoring while the top and bottom impose weak degenerate planar anchoring. The configuration is analogous to that shown in Fig. 2c. (f) Simulation of LCs in a capillary with sharper corners. The parameters used are as in panel (e) but the radius of curvature is 18 nm. The disclination lines follow the edges, occasionally crossing the capillary. (g) Twist-wedge winding character of the disclination shown in (e). (h) Twist-wedge character of the disclination shown in (f), where the disclination lines are wedge lines when they are close to the capillary edges (red sections) and twist lines when they cross the capillary (green sections). | ||
We can simulate capillaries with square cross section giving corners a small nonzero rounding radius to investigate the role of the edges (Fig. 3d). If the radius of curvature at the corner is large enough compared to the defect core size, the system behaves like the round capillaries (e.g.Fig. 3e). If the corners are sharper, each twisted defect line is often not smooth and continuous, but it runs straight along an edge until a point where it crosses the capillary and continues at the opposite edge (Fig. 3f). Furthermore, we observe that along segments pinned at edges, the winding character of each disclination is closer to that of a +1/2 wedge disclination in order to match the corner's anchoring condition, while it is a twist disclination when it crosses the capillary (Fig. 3g and more evident in Fig. 3h). A systematic variation of the corner radius is shown in ESI,† Fig. S10 for capillaries of various sizes. The results indicate that progressively sharper edges favor edge-switching rather than a uniform twist. This behavior is clear in simulations with K1 = K3 > K2.
We investigate the role of corners also for K1 = K2 < K3 (ESI,† Fig. S11). Reducing the splay constant with respect to the twist constant has the effect of pushing the defect lines more towards the center of the capillary; therefore the edge switching, while still present, is less promiment when K1 is reduced. Another consequence of the defect lines being closer to each other is that their winding character becomes predominantly wedge, as shown in ESI,† Fig. S12.
In the simulations, however, the ratio between twist and bend constants needed to stabilize configurations such as that in Fig. 3f is at least two times smaller for a square cross section than for a cylindrical capillary. This is in apparent disagreement with the experimental results that show double twist lines appearing preferentially in square capillaries, but it is explained considering the different size of simulations and experiments, as previously discussed. In simulations, the equilibrium configuration has always two defect lines, which can either twist or run straight along the edges. In experiments, however, the most stable structure is the ER configuration. The presence of the edges reduces the energy difference between the ER and the TP states by stabilizing the defect lines.
3.5 Discussion
So, what is responsible for the transient TP configuration in our system? We believe that three effects contribute to this phenomenon: the transient lowering of the twist elastic constant near the phase transition, the memory of the smectic phase and the pinning of the defects in the smectic phase near the capillary edges. The de Gennes theory states that the elastic constants K2 (twist) and K3 (bend) near the smectic–nematic transition scale as power laws with the rescaled temperature (TNA–T).45 Two theories have been proposed: in one, the two exponents characteristic for the fluctuations parallel and perpendicular to the director are identical, while in the second hypothesis they are anisotropic.46,47 Early measurements showed that the exponent of the bend constant is slightly bigger than the exponent characteristic of the twist constant. Neubert and collaborators measured the twist and bend elastic constants near the smectic-A-nematic phase transition. They measured this difference in the exponent to be between 0.2 and 0.6.48,49 The measurements suggest that below a certain temperature the twist constant is lower than the bend. Experimental measurements on 8CB show a more dramatic divergence of K3 near the smectic transition compared to K2,50,51 but no conclusive experiments are available for CCN-47. However, recent simulations by Schlotthauer do not detect a difference in the scaling of the elastic constants near the phase transition.52 Part of the difficulty in determining the ratio K3/K2 is that the twist and bend elastic constants cannot be measured simultaneously, and that the experimental error in the elastic constant measurements, especially the twist elastic constant, are quite significant. Our results seem to confirm the difference between twist and bend constants, and they also confirm the findings of Pergamenchik et al.,53 who found an instability next to the smectic-A to nematic transition: the instability created a striped pattern which was justifiable if K2/K3 was small near the phase transition. Such an effect has also been reported by Torza and Cladis,54 who showed twisting under extreme confinement near the smectic to nematic phase transition in hybrid cells. It is possible that our system is apt to probe an elusive transient phenomenon. Further investigation will also be needed to understand the role of the ratio K1/K2 that we have investigated in simulations, but very recent results by Lucchetti et al.57 indicate that near the smectic–nematic phase transition the twist constant of CCN-47 quickly becomes smaller than the splay constant as suggested by our simulations.The second consideration is that these results should be viewed also in the light of the papers by Suh et al.40 and Hare et al.,55 as effects of memory at the phase transition between smectic-A and nematic LCs. The defect lines in the nematic emerge from the defected smectic phase and they are heavily influenced by the smectic texture, as shown in Fig. 1. The capillary geometry is ideal to reveal the effect of twist, which is hard to observe, for example, in thin films.
Finally, our results show that not solely the elastic anisotropy is responsible for the twisted lines, and that this system is enriched by the presence of the corners of the capillary, sites that favor the formation of defects and stabilize them. The growth of the planar polar and the escaped radial modes from a single defect line in a capillary was studied by Svenšek and Žumer.56 Their theory suggests that the planar polar mode always grows faster than the escaped radial, but this phenomenon has been elusive in experiments so far. In our system, in the smectic phase the defects form next to the edges, which are a source of strong splay deformation, and favor the formation of disclination lines at the phase transition. The combination of elastic anisotropy and corners also imparts large oscillations between wedge and twist winding character along the disclinations' undulating contours, as indicated by our numerical modeling. This emphasizes the need for a fully three-dimensional model, without screw symmetry, to understand effective strain on defects induced by the bulk's preference for twist.
4 Conclusions
In conclusion, we report our observations on square capillaries filled with common LC materials such as 8CB and CCN-47. Near the smectic to nematic phase transition, LCs transiently exhibit a twisted state that, to our knowledge, was previously observed only in lyotropic or chiral LCs. We hypothesize that the spontaneous emergence of chirality here is due to a different rate of change of the twist and bend elastic constants at the phase transition, a phenomenon that was predicted theoretically and that led to key observations in different experimental systems. The LC, previously in a phase where twist is suppressed (smectic-A), has a transient relaxation of stresses at the phase transition via twist. The use of the square capillaries helps stabilize the twisted defect lines near the edges of the capillaries, so that the lines only twist by discrete steps and alternate sections with wedge or twist winding character. This experimental system is an interesting one for the study of reversible aggregates in disclination lines. Moreover, it offers new insight both on the spontaneous emergence of chirality in thermotropic liquid crystals and, indirectly, on the behavior of the elastic constants at the smectic-A to nematic phase transition. Finally, this work suggests a general principle of using phase transitions to generate, and then stabilize, textures that could not be obtained spontaneously within one single phase.Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. S. and Z. Z. gratefully acknowledge the donors of the Americal Chemical Society Petroleum Research Fund grant 59931-DNI10.References
- L. Fu, W. Steinhardt, H. Zhao, J. E. S. Socolar and P. Charbonneau, Soft Matter, 2016, 12, 2505–2514 RSC.
- L. Kang and T. C. Lubensky, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E19–E27 CrossRef CAS PubMed.
- P. Prybytak, W. J. Frith and D. J. Cleaver, Interface Focus, 2012, 2, 651–657 CrossRef CAS PubMed.
- J. R. Brandt, F. Salerno and M. J. Fuchter, Nat. Rev. Chem., 2017, 1, 0045 CrossRef CAS.
- S. Pieraccini, S. Masiero, A. Ferrarini and G. P. Spada, R. Soc. Chem., 2011, 40, 258–271 RSC.
- M. Kang, P. Zhang, H. Cui and S. M. Loverde, Macromolecules, 2016, 3, 994–1001 CrossRef PubMed.
- A. M. Sarotti, I. Fernandez, R. A. Spanevello, M. A. Sierra and A. G. Suarez, Org. Lett., 2008, 10, 3389–3392 CrossRef CAS PubMed.
- A. R. Fassihi, Int. J. Pharm., 1993, 92, 1–14 CrossRef CAS.
- A. N. L. Batista, F. M. dos Santos, J. M. Batista and Q. B. Cass, Molecules, 2018, 23, 492 CrossRef PubMed.
- C. P. Brock, W. B. Schweizer and J. D. Dunitz, J. Am. Chem. Soc., 1991, 113, 9811–9820 CrossRef CAS.
- L. A. Nguyen, H. He and C. Pham-Huy, Int. J. Biomed. Sci., 2006, 2, 85–100 CAS.
- D. G. Blackmond, Cold Spring Harbor Perspect. Biol., 2010, 2, a002147 Search PubMed.
- F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19–28 RSC.
- G. E. Volovik and O. D. Lavrentovich, Sov. Phys. JETP, 1983, 58, 1159 Search PubMed.
- R. D. Williams, J. Phys. A: Math. Gen., 1986, 19, 3211 CrossRef.
- J. Jeong, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1742–1747 CrossRef CAS PubMed.
- E. Romani, A. Ferrarini and C. De Michele, Macromolecules, 2018, 51, 5409–5419 CrossRef CAS.
- J. Jeong, L. Kang, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E1837–E1844 CrossRef CAS PubMed.
- C. F. Dietrich, P. Rudquist, K. Lorenz and F. Giesselmann, Langmuir, 2017, 33, 5852 CrossRef CAS PubMed.
- C. F. Dietrich, P. Rudquist, P. J. Collings and F. Giesselmann, Langmuir, 2021, 37, 2749–2758 CrossRef CAS PubMed.
- D. Melzer and F. R. N. Nabarro, Philos. Mag. A, 1977, 35, 901–906 CrossRef CAS.
- D. Melzer and F. R. N. Nabarro, Philos. Mag. A, 1977, 35, 907–915 CrossRef CAS.
- G. P. Crawford, D. W. Allender and J. W. Doane, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 8693–8708 CrossRef CAS PubMed.
- S. Kralj and S. Z. Žumer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 366–379 CrossRef CAS PubMed.
- M. Kleman and O. D. Lavrentovich, Philos. Mag., 2006, 86, 4117–4137 CrossRef.
- G. De Luca and A. D. Rey, J. Chem. Phys., 2007, 127, 104902 CrossRef PubMed.
- H.-L. Liang, J. Noh, R. Zentel, P. Rudquist and J. P. F. Lagerwall, Philos. Trans. R. Soc., A, 2013, 371, 20120258 CrossRef PubMed.
- F. Serra, Liq. Cryst., 2016, 43, 1920–1936 CrossRef CAS.
- R. Pratibha and N. Madhusudana, J. Phys. II, 1992, 2, 383–400 CrossRef CAS.
- J. Fu, K. Nayani, J. O. Park and M. Srinivasarao, NPG Asia Mater., 2017, 9, e393 CrossRef CAS.
- K. Nayani, R. Chang, J. Fu, P. W. Ellis, A. Fernandez-Nieves, J. O. Park and M. Srinivasarao, Nat. Commun., 2015, 6, 8067 CrossRef CAS PubMed.
- Z. S. Davidson, L. Kang, J. Jeong, T. Still, P. J. Collings, T. C. Lubensky and A. G. Yodh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 050501 CrossRef PubMed.
- L. Tortora and O. D. Lavrentovich, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 5163–5168 CrossRef CAS PubMed.
- F. Serra, K. C. Vishnubhatla, M. Buscaglia, R. Cerbino, R. Osellame, G. Cerullo and T. Bellini, Soft Matter, 2011, 7, 10945–10950 RSC.
- D. V. Sai, T. H. Yoon and S. Dhara, J. Mol. Liq., 2020, 312, 113410 CrossRef CAS.
- D. A. Beller, Controlling defects in nematic and smectic liquid crystals through boundary geometry, PhD thesis, University of Pennsylvania, 2014 Search PubMed.
- D. M. Sussman and D. A. Beller, Front. Phys., 2019, 7, 204 CrossRef.
- G. Duclos, R. Adkins, D. Banerjee, M. Peterson, M. Varghese, I. Kolvin, A. Baskaran, R. Pelcovits, T. Powers, A. Baskaran, F. Toschi, M. Hagan, S. Streichan, V. Vitelli, D. A. Beller and Z. Dogic, Science, 2020, 367, 1120 CrossRef CAS PubMed.
- M. C. Choi, T. Pfohl, Z. Wen, Y. Li, M. W. Kim, J. N. Israelachvili and C. R. Safinya, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17340–17344 CrossRef CAS PubMed.
- A. Suh, M.-J. Gim, D. A. Beller and D. K. Yoon, Soft Matter, 2019, 15, 5835 CAS.
- X. Wang, D. S. Miller, E. Bukusoglu, J. J. de Pablo and N. L. Abbott, Nat. Mater., 2015, 15, 106–112 CrossRef PubMed.
- Y. Luo, D. A. Beller, G. Boniello, F. Serra and K. J. Stebe, Nat. Commun., 2018, 9, 3841 CrossRef PubMed.
- Y. Luo, F. Serra, D. A. Beller, M. Gharbi, N. Li, S. Yang, R. Kamien and K. J. Stebe, Phys. Rev. E, 2016, 93, 032705 CrossRef PubMed.
- C. Luo, A. Majumdar and R. Erban, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061702 CrossRef PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 2nd edn, 1993 Search PubMed.
- C. Garland and G. Nounesis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 2964 CrossRef CAS PubMed.
- B. Andereck and B. Patton, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 1393 CrossRef CAS PubMed.
- R. Mahmood, I. Brisbin, C. Gooden, A. Baldwin, D. Johnson and M. Neubert, Phys. Rev. Lett., 1985, 54, 1031 CrossRef CAS PubMed.
- C. Gooden, R. Mahmood, I. Brisbin, A. Baldwin, D. Johnson and M. Neubert, Phys. Rev. Lett., 1985, 54, 1035 CrossRef CAS PubMed.
- H. Hakemi, Liq. Cryst., 1989, 5, 327 CrossRef CAS.
- S. Srigengan, H. Liu, M. Osipov, R. Mandle, S. Cowling and H. Gleeson, Liq. Cryst., 2020, 47, 895–907 CrossRef CAS.
- S. Paschel-Schlotthauer, V. Meiwes Turrain, T. Stieger, R. Grotjahn, C. K. Hall, M. G. Mazza and M. Schoen, J. Chem. Phys., 2016, 145, 164903 CrossRef PubMed.
- V. Pergamenshchik, I. Lelidis and V. Uzunova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041703 CrossRef CAS PubMed.
- P. Cladis and S. Torza, J. Appl. Phys., 1975, 46, 584 CrossRef.
- S. M. Hare, B. Lunsford-Poe, M. Kim and F. Serra, Materials, 2020, 13, 3761 CrossRef CAS PubMed.
- D. Svensšek and S. Z. Žumer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061707 CrossRef PubMed.
- L. Lucchetti, G. Nava, R. Barboza, F. Ciciulla and T. Bellini, J. Mol. Liq., 2021, 329, 115520 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm02040k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |