Poroelastic shape relaxation of hydrogel particles†
Jean-François
Louf
 and
Sujit S.
Datta
and
Sujit S.
Datta
 *
*
Department of Chemical and Biological Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: ssdatta@princeton.edu
First published on 29th March 2021
Abstract
Hydrogels are commonly used in research and energy, manufacturing, agriculture, and biomedical applications. These uses typically require hydrogel mechanics and internal water transport, described by the poroelastic diffusion coefficient, to be characterized. Sophisticated indentation-based approaches are typically used for this purpose, but they require expensive instrumentation and are often limited to planar samples. Here, we present Shape Relaxation (SHARE), an alternative way to assess the poroelastic diffusion coefficient of hydrogel particles that is cost-effective, straightforward, and versatile. This approach relies on first indenting a hydrogel particle via swelling within a granular packing, and then monitoring how the indented shape of the hydrogel relaxes after it is removed from the packing. We validate this approach using experiments in packings with varying grain sizes and confining stresses; these yield measurements of the poroelastic diffusion coefficient of polyacrylamide hydrogels that are in good agreement with those previously obtained using indentation approaches. We therefore anticipate that the SHARE approach will find broad use in a range of applications of hydrogels and other swellable soft materials.
1 Introduction
Hydrogels are cross-linked networks of hydrophilic polymers that can absorb large amounts of aqueous solvent while retaining their integrity.1,2 Their versatility, ease of manufacture, and biocompatibility make them attractive for use in energy,3–7 manufacturing,8 agriculture,9–14 and biomedical applications.15–24 These applications often require hydrogel mechanics and internal water transport to be finely tuned. Thus, a range of approaches have been developed to characterize the mechanical properties of bulk hydrogels under different forms of loading.25–52 Unlike many other materials, hydrogels are poroelastic: compressing a hydrogel not only deforms its elastic polymer network, but also forces the solvent through the pores of this network. Thus, compression is resisted by both the network elasticity and the viscous drag on the solvent. For deformations over length scales much larger than the network mesh size, spatial variations in solvent concentration smooth out diffusively, with a poroelastic diffusion coefficient D ∼ Ek/μ, where E and k are the Young's modulus and permeability of the elastic network, respectively, and μ is the solvent dynamic shear viscosity.50–58 The poroelastic diffusion coefficient is therefore a fundamental descriptor of hydrogel mechanics and water transport.It is now well established that macroscopic measurements of dynamics associated with large-scale deformations of poroelastic materials can be used to determine D.50–60 Thus, sophisticated approaches to characterize poroelastic diffusion have been developed for planar hydrogels attached to flat underlying substrata. These approaches typically use an indenter to abruptly compress a hydrogel to a fixed indentation depth and measure the relaxation of the associated normal force over time; D can then be computed given the indentation depth, indenter geometry, and measured characteristic time scale of the force relaxation.47,48,61–63 However, while they provide tremendous insight into hydrogel mechanics and water transport, such approaches also have several limitations. First, due to a lack of models required to interpret the experimental data, these measurements are typically restricted to samples on hard planar substrata—despite the fact that many key applications of hydrogels involve their use as discrete particles.1,3–24 Second, these measurements are sensitive to the indentation velocity and hydrogel thickness. Lastly, such measurements often require the use of expensive instruments such as rheometers or Atomic Force Microscopes (AFM) to access the force precision required. Ongoing work is beginning to explore how to overcome the first limitation by extending indentation measurements to the case of discrete hydrogel particles;64 nevertheless, alternative approaches for characterizing hydrogel poroelastic diffusion are necessary to overcome all of these limitations. Another simple and well-established approach is to track the shape evolution of a hydrogel during swelling, starting from the dry state.53 However, because the mesh size of the hydrogel changes dramatically during this process, modeling this highly dynamic process requires a sophisticated poromechanical treatment.2 Moreover, the non-uniform swelling dynamics can give rise to transient surface instabilities that complicate the tracking of the overall hydrogel shape.2,65 As a result, extracting a poroelastic diffusion coefficient using this approach can be complicated.
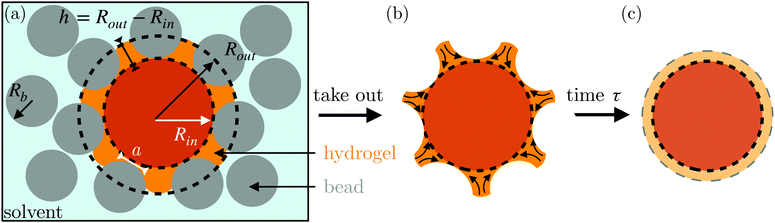
Here, we describe an alternative approach to assess the poroelastic diffusion coefficient of hydrogel particles without requiring specialized instrumentation for performing force measurements. We term our approach the Shape Relaxation (SHARE) approach. As schematized in Fig. 1, SHARE employs the following steps:
(1) Embed a dry hydrogel particle within an unconsolidated, three-dimensional (3D) granular packing of spherical beads with mean radii Rb that is confined in a sealed container (Fig. 1a).
(2) Saturate the packing with the solvent.
(3) Tune the confining stress exerted by the beads on the hydrogel, σ, by either varying the height Htop of the packing overlying the hydrogel or placing a load of mass m on top of the packing.
(4) Allow the hydrogel to absorb the solvent and swell over a fixed duration of time, τswell.
(5) Remove the hydrogel from the packing; its swollen surface will be indented by the surrounding beads to a depth whose magnitude can be tuned by Rb and σ (Fig. 1b).
(6) Monitor the shape relaxation of the hydrogel surface over time (Fig. 1c); measuring the initial indentation size and the characteristic timescale over which the surface indentations relax then enables the poroelastic diffusion coefficient D to be determined.
We validate the SHARE approach using measurements performed on well-characterized and widely-used polyacrylamide hydrogels in packings of varying Rb and σ. In particular, our measurements of D are in excellent agreement with previous reports obtained using indentation measurements. A key feature of the SHARE approach is that it is straightforward and cost-effective, only requiring a collection of beads, a container to confine them in, and a conventional camera. We therefore expect that SHARE will find broad use in characterizing hydrogel poroelasticity.
2 Hydrogel swelling in a granular packing
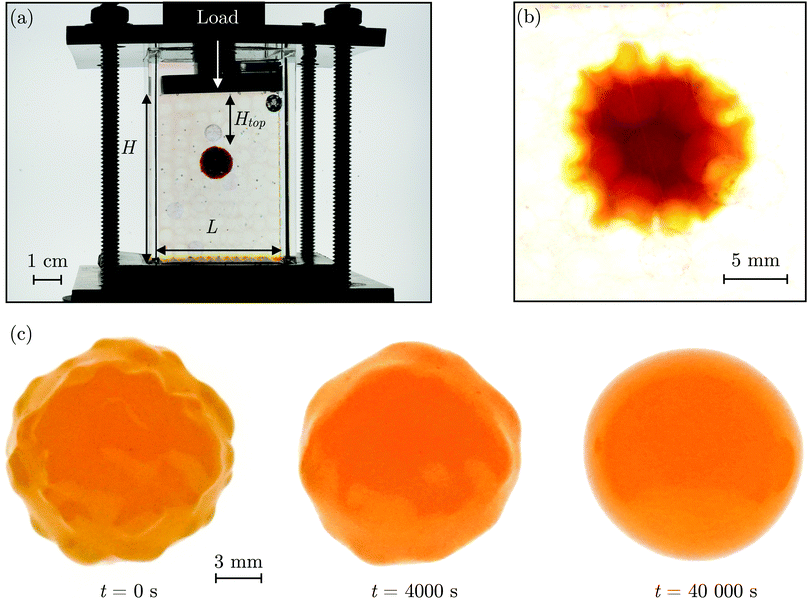
The SHARE approach utilizes a surrounding granular packing as a means of controllably indenting a hydrogel as it swells. In each experiment, we prepare a 3D close-packed, disordered, granular packing using borosilicate glass beads (Sigma-Aldrich) of mean radii Rb = 1, 1.5, 2.5, or 3 mm in a transparent, sealed, acrylic box L × L = 4.3 cm × 4.3 cm across. During addition of the beads, we also embed a colored polyacrylamide hydrogel sphere (Jangostor) of initial radius Ri ≈ 5.9 mm near the center of the packing at a height Htop ≈ 2 cm from its top surface. We then repeatedly tap the box using a metal rod for ∼20 s; therefore, the packing approaches the random close packing limit from the initial random loose packed state, with a porosity approximately between 36 and 41%. To impose an additional confining stress, we also place a weighted piston of mass m on top of the packing, ensuring that a slight gap around the edges of the piston enables liquid to move freely when the packing is saturated with solvent. The confining stress on the hydrogel is then σ ≈ ΔρgHtop + mg/L2, where Δρ is the density difference between the beads and the solvent and g is gravitational acceleration. We then overfill the box with 54.1 wt% aqueous solution of NH4SCN (Sigma-Aldrich). This solvent matches the refractive index of the glass beads, rendering the packing transparent. While the use of a refractive index-matched solvent is not necessary for SHARE measurements, it enables us to directly visualize the subsequent hydrogel swelling in situ using a Nikon Micro-NIKKOR 55 mm f/2.8 lens mounted on a Sony α6300 camera. A picture of the overall apparatus with the hydrogel in the center is shown in Fig. 2a.Confinement hinders hydrogel swelling.66,67 In a granular packing, the confining force is transmitted to the hydrogel surface only where it contacts surrounding grains, over a region of radius a. As a result, hydrogel swelling is hindered at these regions, but proceeds in between them, ultimately causing the hydrogel to have an indented shape as schematized in Fig. 1a and b and shown experimentally in Fig. 2b. Given that the elastic modulus of the glass beads (∼1010 Pa) is six orders of magnitude larger than that of the swollen hydrogel (∼104 Pa), we consider the beads to be undeformable; however, we expect that bead deformability would provide another way to tune the indentation magnitude, which will be an interesting direction to explore in future work.
In our previous work,67 we demonstrated how σ, Rb, and the hydrogel physico-chemical properties determine the indented hydrogel shape; in general, the geometry of the indentations is determined by a complex interplay between hydrogel swelling, hydrogel–bead interactions, force transmission within the packing, and possible frictional effects at the boundary of the packing. However, for our experiments here, this interplay is given by a simple balance between the osmotic swelling force exerted by the hydrogel at its contacts with surrounding grains and the confining force transmitted through the packing. Due to the granularity of the packing, this force balance varies spatially over the surface of the hydrogel—leading to the “dimpled” shape of the hydrogel. As a result, the osmotic swelling pressure varies along the surface of the hydrogel; it is larger in the indented regions, where the hydrogel has not swollen as much and its internal polymer network is more concentrated, and is smaller in between indentations, where the hydrogel has swollen more and its internal polymer network is more expanded and less concentrated.
Here, we take this swollen indented shape as the starting condition, and instead focus on the subsequent shape relaxation dynamics after the hydrogel is removed from the packing. We hypothesize that given an indentation geometry, tracking how this shape subsequently relaxes after the hydrogel is removed from the packing enables the poroelastic diffusion coefficient D to be determined. To enable us to test this hypothesis, for each experiment, we use direct visualization to characterize the indented hydrogel shape before removing it from the granular packing. Specifically, we obtain a two-dimensional (2D) projection of the swollen hydrogel shape within each granular packing after a duration of τswell ≈ 100 h, sufficiently long to equilibrate swelling.67 From this projection, we measure the radii of the circumscribed and inscribed circles Rin and Rout, respectively, as schematized in Fig. 1a and shown in Fig. S1 (ESI†). These quantities yield the characteristic indentation depth h ≡ Rout − Rin for each experiment. A similar measurement can be performed on the hydrogel immediately after it is removed from the packing, as may be needed when not using a refractive index-matched solvent; we have verified that such a protocol yields comparable results. For simplicity, we then approximate the characteristic radius of the hydrogel–grain contacts that cause indentations as 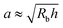 .68
.68
3 Hydrogel shape relaxation outside the packing
Having characterized the indented hydrogel shape, in each experiment, we then gently remove the overlying piston, beads, and hydrogel from the packing and place the hydrogel on an LED light panel under ambient room conditions. We track the subsequent evolution of the hydrogel shape again using a Sony α6300 camera with a Nikon Micro-NIKKOR 105 mm lens. Because it is no longer under the stress imposed by the granular packing, the indentations in the hydrogel surface progressively smooth out, as shown in Fig. 2c. Computer analysis of these images yields a 2D projection of the overall hydrogel shape, characterized by a projected area A and a perimeter P that we directly determine from the binarized images. We do not observe any indication of plastic deformations in the shape relaxation; the hydrogels regain a spherical shape at long times. Furthermore, while the local strain experienced by an indented hydrogel can be as large as ≈50%, this strain is nevertheless well within the regime of linear elasticity of the hydrogels we use, which exhibit linear elastic behavior to strains as large as ≈100%.69One way of characterizing this shape relaxation is to track the position of individual points at fixed radial orientations on the hydrogel surface over time. For multiple different points, we find that the variation in the radial position R of a point with time t is in all cases consistent with an exponential with a well-defined characteristic time scale τ, shown by the black dashed line in the plot of normalized distance moved relative to the fixed camera (R(t) − Ri)/(Rf − Ri) versus dimensionless time t/τ in Fig. 3a; here, Ri and Rf represent the initial and final positions. The measurements of an example point on the surface of the hydrogel in Fig. 2 are shown by the orange symbols. For this example, we find τ = 3900 ± 800 s.
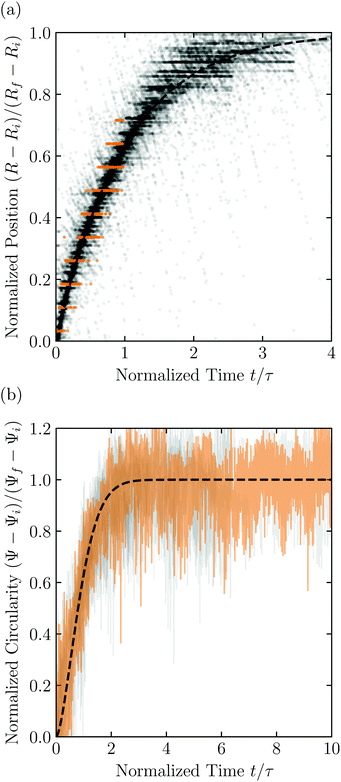 | ||
| Fig. 3 Characterization of hydrogel shape relaxation over time after removal from a granular packing. (a) Measurements of radial position R of surface points versus time t for all the experiments; the vertical axis shows the normalized distance moved relative to the fixed camera, where Ri and Rf are the initial and final positions for each dataset, and the horizontal axis shows the dimensionless time, where τ is the characteristic relaxation time obtained using an exponential fit (black dashed line) for each dataset. The data corresponding to one point on the surface of the hydrogel in Fig. 2 are shown by the orange symbols, while measurements for other points and other experiments are shown by the symbols in varying shades of gray. For each hydrogel tested, we track three different points, correcting for hydrogel drying or movement as described in the ESI.† (b) Measurements of circularity Ψ versus time t for all the experiments; the vertical axis shows the normalized circularity, where Ψi and Ψf are the initial and final measured circularity for each experiment, and τ is the characteristic relaxation time obtained using a stretched-exponential fit in each experiment.† The data corresponding to Fig. 2 are shown by the orange curve, while the other experiments are shown by the curves in varying shades of gray. The black dashed line shows the fit to the orange dataset. | ||
However, in some cases, slight drying or movement of the hydrogel may preclude reliable tracking of individual points on its surface (ESI†). An alternative way of characterizing the hydrogel shape relaxation that circumvents these issues is by tracking the evolution of the circularity Ψ ≡ 4πA/P2; for a perfect sphere, Ψ = 1, whereas for a sphere with indentations of increasing depth, Ψ decreases below 1. Indeed, Ψ monotonically increases from an initial value Ψi as the hydrogel smooths, eventually fluctuating around a fixed plateau value Ψf. The absolute values of Ψi and Ψf depend on the resolution and magnification of the images used—a well known consequence of pixelization.70 However, we again find that the relative variation of circularity between Ψi and Ψf has a well-defined characteristic time scale τ, as exemplified by the plot of the normalized circularity (Ψ(t) − Ψi)/(Ψf − Ψi) versus dimensionless time t/τ in Fig. 3b. In this case, we find that the data are better fit by a phenomenological stretched exponential function 1 − e−(t/τ)β (ESI†), consistent with the findings of some previous studies of poroelastic relaxation.63,71–73 The representative example of Fig. 2 is shown by the orange curve, with τ = 3300 ± 300 s—in good agreement with the time scale obtained by tracking the relaxation of individual point. The influence of hydrogel drying is minimal over this time scale, as shown in Fig. S2 (ESI†); moreover, a useful feature of the circularity used as our descriptor of hydrogel shape is that it is invariant under isotropic shrinkage or translation—as confirmed by the measurements shown in Fig. 3b, which fluctuate around a well-defined mean value at large times.
Repeating these measurements for thirteen different experiments, each performed on a different hydrogel and exploring values of σ and Rb varying from ≈7 to 40 kPa and 1 to 3 mm, respectively, yields indented hydrogels having a ranging from ≈1 to 2 mm and shape relaxation times τ ranging from ≈1000 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s. All the measurements of τ obtained by tracking either individual points or the overall circularity consistently show similar relaxation dynamics, as shown by the data collapse in Fig. 3a and b. Moreover, measurements obtained using either approach are all consistent with the same quadratic scaling τ ∝ a2, as shown by the circles and squares in Fig. 4, respectively—characteristic of a diffusive process.
000 s. All the measurements of τ obtained by tracking either individual points or the overall circularity consistently show similar relaxation dynamics, as shown by the data collapse in Fig. 3a and b. Moreover, measurements obtained using either approach are all consistent with the same quadratic scaling τ ∝ a2, as shown by the circles and squares in Fig. 4, respectively—characteristic of a diffusive process.
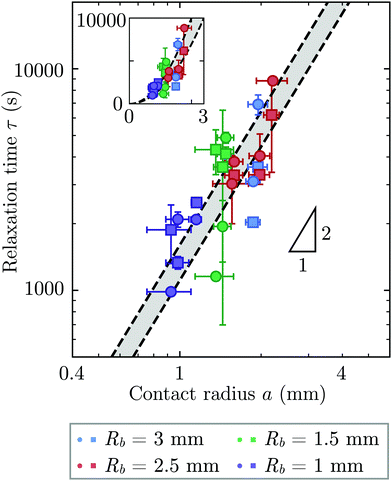 | ||
| Fig. 4 The time scale of hydrogel shape relaxation is set by poroelastic relaxation. Circles and squares show shape relaxation time τ obtained from two different approaches: tracking the positions of individual points or the overall circularity over time, respectively. Dashed lines show upper and lower bounds of the poroelastic relaxation time τporo ≈ a2/D obtained using the variation in the predicted poroelastic diffusion coefficient D. Triangle shows quadratic scaling characteristic of a diffusive process. Main panel shows the data on logarithmic axes, while inset shows the same data on linear axes. The points are obtained from thirteen separate experiments performed on thirteen different hydrogels using varying confining stresses σ and bead radii Rb, resulting in indented hydrogels having contact radii a ranging from ≈1 to 2 mm; both approaches to determining τ yield consistent results. For three of the experiments, our measurements only permit reliable determination of τ using one of the two approaches due to e.g., slight movement of the hydrogel or noise in the imaging, and thus for these experiments only one circle or square is shown. The vertical error bars indicate the uncertainty in τ obtained separately for each data point, as detailed further in the ESI.† The horizontal error bars indicate the uncertainty in a obtained by propagating the uncertainty in the measurement of h again obtained separately for each experiment. The uncertainty in Rb given by the standard deviation in measurements of different beads having the same mean Rb is 1%, and we therefore neglect this minimal uncertainty from the analysis. The uncertainty in h is given by the sum of the uncertainty in our measurements of the inscribed and circumscribed radii Rin and Rout, each of which we estimate using the largest and smallest possible circles that can be circumscribed and inscribed for each hydrogel imaged within the granular packing. | ||
What processes drive hydrogel shape relaxation? Within a granular packing, hydrogel swelling is hindered at the contacts with surrounding grains—ultimately reaching an equilibrium state determined by the balance between the osmotic swelling force exerted by the hydrogel and the confining force transmitted by the grains.67 When the hydrogel is removed from the granular packing, this confining force is no longer exerted, resulting in spatial variations in solvent concentration and therefore osmotic pressure along the hydrogel surface. Our previous measurements of the swelling-dependent hydrogel Young's modulus indicate that this unbalanced osmotic pressure difference is of magnitude ∼10 kPa.67 By contrast, the capillary pressure difference associated with the curved liquid-air interface along the surface of the hydrogel is over two orders of magnitude smaller: it is at most 2γ/a ∼ 0.1 kPa, where γ ≈ 70 mN m−1 represents the liquid-air surface tension. Thus, the primary contributor to shape smoothing is the unbalanced osmotic pressure difference across indentations arising from the initial hydrogel swelling in the granular packing. As established by typical indentation measurements, these spatial variations in osmotic pressure force the solvent to diffusively redistribute over each contact of radius ≈a,47,48,61–63 as schematized by the arrows in Fig. 1b, with a poroelastic diffusion coefficient 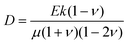 , where E is the hydrogel Young's modulus, k is the internal hydrogel permeability, ν ≈ 0.45 is Poisson's ratio,74 and μ ≈ 1 mPa s is the fluid dynamic shear viscosity. The poroelastic relaxation time scale is therefore given by τporo ≈ a2/D.
, where E is the hydrogel Young's modulus, k is the internal hydrogel permeability, ν ≈ 0.45 is Poisson's ratio,74 and μ ≈ 1 mPa s is the fluid dynamic shear viscosity. The poroelastic relaxation time scale is therefore given by τporo ≈ a2/D.
We determine D directly using independent mechanical testing. In particular, we use planar compression experiments, performed at different compression rates, of a hydrogel swollen in the refractive index-matched solvent to measure E.67 Because the modulus depends on the hydrogel degree of swelling, which varies across indentations and between different experiments, we use the minimum and maximum values of E measured at the different degrees of swelling that arise in the experiments—≈8 and 24 kPa, respectively—in our calculation of D. These values can also be related to the hydrogel mesh size ξ using the prediction of network elasticity theory75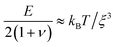 ; here, kB is Boltzmann's constant and T = 300 K is temperature. We find ξ ≈ 8 to 11 nm, in good agreement with previous measurements on polyacrylamide hydrogels.76–78 Furthermore, these values of ξ can be used to estimate the internal hydrogel permeability using the empirical relation k ≈ 0.2ξ2 determined previously;79 we find k varying between ≈1 and 3 × 10−17 m2, in good agreement with previous measurements on polyacrylamide hydrogels.80,81 Taken together, these measurements yield a hydrogel poroelastic diffusion coefficient D ≈ 6 to 9 × 10−10 m2 s−1, in good agreement with the results of indentation measurements.42,44,46,63,64,73,82 Finally, we use this estimate of D to test the hypothesis that the measured shape relaxation time τ is given by the poroelastic relaxation time τporo ≈ a2/D. For the range of a explored in our experiments, the corresponding τporo is shown by the gray region in Fig. 4. We find close agreement between all the measurements of τ and the corresponding τporo, with both showing the quadratic scaling ∼a2 characteristic of a diffusive process. This agreement validates that the SHARE approach provides a straightforward way to determine the poroelastic diffusion coefficient of hydrogel particles. While our experiments utilize beads whose size varies by a factor of three, future implementations of this approach can explore a much broader range, leading to indentations of sizes that vary over an even broader range.
; here, kB is Boltzmann's constant and T = 300 K is temperature. We find ξ ≈ 8 to 11 nm, in good agreement with previous measurements on polyacrylamide hydrogels.76–78 Furthermore, these values of ξ can be used to estimate the internal hydrogel permeability using the empirical relation k ≈ 0.2ξ2 determined previously;79 we find k varying between ≈1 and 3 × 10−17 m2, in good agreement with previous measurements on polyacrylamide hydrogels.80,81 Taken together, these measurements yield a hydrogel poroelastic diffusion coefficient D ≈ 6 to 9 × 10−10 m2 s−1, in good agreement with the results of indentation measurements.42,44,46,63,64,73,82 Finally, we use this estimate of D to test the hypothesis that the measured shape relaxation time τ is given by the poroelastic relaxation time τporo ≈ a2/D. For the range of a explored in our experiments, the corresponding τporo is shown by the gray region in Fig. 4. We find close agreement between all the measurements of τ and the corresponding τporo, with both showing the quadratic scaling ∼a2 characteristic of a diffusive process. This agreement validates that the SHARE approach provides a straightforward way to determine the poroelastic diffusion coefficient of hydrogel particles. While our experiments utilize beads whose size varies by a factor of three, future implementations of this approach can explore a much broader range, leading to indentations of sizes that vary over an even broader range.
4 Discussion and conclusions
This work provides a proof-of-principle demonstration of the SHARE approach. The approach itself is versatile: it can be used to characterize the poroelasticity of diverse swellable soft materials, having varying geometries and employing a broad range of solvents, simply using a packing of beads, a container to confine them in, and a camera to image how indentations caused by the beads smooth over time. An even simpler implementation of SHARE could be accomplished using indentation/stress–relaxation measurements performed using an inexpensive load cell. Because hydrogel particles are utilized in diverse energy, manufacturing, agriculture, and biomedical applications—all of which typically require their poroelastic properties to be characterized—we expect that the SHARE approach will find broad use as a complement to existing approaches to characterizing hydrogel poroelasticity.Our experiments track the circularity of hydrogel particles as a means of quantifying the shape relaxation; the poroelastic diffusion coefficient is then given by D ≈ a2τ. While force transmission in disordered granular packings is known to be heterogeneous, likely resulting in contact radii a that slightly vary over the surface of the hydrogel, previous work83 has shown that the distribution of contact forces is not long-tailed, but is exponentially bounded above the mean, suggesting that a mean-field picture employing a single characteristic value is a reasonable starting point. Indeed, this mean-field assumption can capture the extent of hydrogel swelling within a granular packing, as we demonstrated in our previous work.67 We therefore use the characteristic value 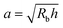 calculated using a single measured characteristic value of the indentation depth h for simplicity. Using a more sophisticated non-linear treatment of the hydrogel-grain contact geometry could yield a more accurate determination of D, and would therefore be a useful direction for future work. Moreover, we note that the smoothing of individual indentations could alternatively be tracked to characterize the shape relaxation—yielding similar relaxation dynamics, as shown by our measurements in Fig. 2.
calculated using a single measured characteristic value of the indentation depth h for simplicity. Using a more sophisticated non-linear treatment of the hydrogel-grain contact geometry could yield a more accurate determination of D, and would therefore be a useful direction for future work. Moreover, we note that the smoothing of individual indentations could alternatively be tracked to characterize the shape relaxation—yielding similar relaxation dynamics, as shown by our measurements in Fig. 2.
The SHARE method does have some limitations. First, it requires that the initial radius of the swellable particle be larger than the radius of the pore bodies in the granular packing, so that the beads are able to indent the particle as it swells. Second, to adequately capture the hydrogel shape relaxation dynamics, the time required to remove the hydrogel from the packing and begin imaging (τi ≈ 1 min) must be much shorter than the poroelastic relaxation time τporo ≈ a2/D, and thus, the contact radius a must be larger than ≈200 mm for the value of D considered here. We note, however, that because D is a material property and is not hydrogel size dependent, in principle one could use SHARE measurements performed on larger hydrogel particles to deduce the relaxation dynamics of smaller hydrogel particles. Third, our experiments only utilize spherical hydrogels—which are indeed the most commonly-used shapes due to their spatial uniformity; however, practitioners may want to use the SHARE approach to characterize the poroelasticity of non-spherical hydrogel particles as well. While our approach can in principle still be used in this case, extra care will be required in the imaging to more clearly characterize the relaxation dynamics of individual indentations, versus measuring the change in circularity over time.
Author contributions
J.-F. L. performed all the experiments; J.-F. L. and S. S. D. designed the experiments, analyzed the data, designed and performed the theoretical analysis, discussed the results and implications, and wrote the manuscript; S. S. D. designed and supervised the overall project.Conflicts of interest
The SHARE approach is the subject of a patent application in the process of being filed by Princeton University on behalf of J.-F. L. and S. S. D.Acknowledgements
It is a pleasure to acknowledge Nancy Lu for her help in setting up the relaxation experiments, and B. B. Browne for stimulating conversations. This work was supported by the Grand Challenges Initiative of the High Meadows Environmental Institute, the Princeton E-ffiliates Partnership of the Andlinger Center for Energy and the Environment, and in part by funding from the Princeton Center for Complex Materials, a Materials Research Science and Engineering Center supported by NSF grant DMR-2011750.References
- A. Fernandez-Nieves, H. Wyss, J. Mattsson and D. A. Weitz, Microgel suspensions: fundamentals and applications, John Wiley & Sons, 2011 Search PubMed.
- T. Bertrand, J. Peixinho, S. Mukhopadhyay and C. W. MacMinn, Phys. Rev. Appl., 2016, 6, 064010 CrossRef.
- M. G. O'Connell, N. B. Lu, C. A. Browne and S. S. Datta, Soft Matter, 2019, 15, 3620–3626 RSC.
- C. Yao, G. Lei, L. Li and X. Gao, Energy Fuels, 2012, 26, 5092–5101 CrossRef CAS.
- C. Yao, G. Lei, J. Hou, X. Xu, D. Wang and T. S. Steenhuis, Ind. Eng. Chem. Res., 2015, 54, 10925–10934 CrossRef CAS.
- B. Bai, Y. Liu, J.-P. Coste and L. Li, et al. , SPE Reserv. Eval. Eng., 2007, 10, 176–184 CrossRef CAS.
- V. Kapur, J. C. Charkoudian, S. B. Kessler and J. L. Anderson, Ind. Eng. Chem. Res., 1996, 35, 3179–3185 CrossRef CAS.
- M. J. Krafcik, N. D. Macke and K. A. Erk, Gels, 2017, 3, 46 CrossRef PubMed.
- Y. Wei and D. J. Durian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 053013 CrossRef CAS PubMed.
- Y. Wei, C. M. Cejas, R. Barrois, R. Dreyfus and D. J. Durian, Phys. Rev. Appl., 2014, 2, 044004 CrossRef.
- Y. Wei and D. Durian, Eur. Phys. J. E, 2014, 37, 97 CrossRef CAS.
- J. Woodhouse and M. Johnson, Agric. Water Manage., 1991, 20, 63 CrossRef.
- K. Lejcuś, M. Śpitalniak and J. Dabrowska, Polymers, 2018, 10, 271 CrossRef PubMed.
- J. Misiewicz, K. Lejcuś, J. Dabrowska and D. Marczak, Sci. Rep., 2019, 9, 1–9 Search PubMed.
- J. P. Best, J. Cui, M. Mullner and F. Caruso, Langmuir, 2013, 29, 9824–9831 CrossRef CAS PubMed.
- N. M. Pinkerton, S. W. Zhang, R. L. Youngblood, D. Gao, S. Li, B. R. Benson, J. Anthony, H. A. Stone, P. J. Sinko and R. K. Prudhomme, Biomacromolecules, 2014, 15, 252–261 CrossRef CAS PubMed.
- R. F. Pagels and R. K. Prud'homme, J. Controlled Release, 2015, 219, 519–535 CrossRef CAS PubMed.
- M. Dolega, M. Delarue, F. Ingremeau, J. Prost, A. Delon and G. Cappello, Nat. Commun., 2017, 8, 1–9 CrossRef PubMed.
- I. M. El-Sherbiny and M. H. Yacoub, Glob. Cardiol. Sci. Pract., 2013, 2013, 316–342 Search PubMed.
- S. Mantha, S. Pillai, P. Khayambashi, A. Upadhyay, Y. Zhang, O. Tao, H. M. Pham and S. D. Tran, Materials, 2019, 12, 3323 CrossRef CAS PubMed.
- J. Li and D. J. Mooney, Nat. Rev. Mater., 2016, 1, 1–17 CrossRef PubMed.
- R. Narayanaswamy and V. P. Torchilin, Molecules, 2019, 24, 603 CrossRef PubMed.
- M. Schaffner, P. A. Rühs, F. Coulter, S. Kilcher and A. R. Studart, Sci. Adv., 2017, 3, eaao6804 CrossRef PubMed.
- W. Lee, N. Kalashnikov, S. Mok, R. Halaoui, E. Kuzmin, A. J. Putnam, S. Takayama, M. Park, L. McCaffrey and R. Zhao, et al. , Nat. Commun., 2019, 10, 1–14 CrossRef PubMed.
- K. Urayama, T. Takigawa and T. Masuda, Macromolecules, 1993, 26, 3092–3096 CrossRef CAS.
- S. Marra, K. Ramesh and A. Douglas, Mater. Sci. Eng., C, 2001, 14, 25–34 CrossRef.
- B. Johnson, D. Beebe and W. Crone, Mater. Sci. Eng., C, 2004, 24, 575–581 CrossRef.
- E. C. Muniz and G. Geuskens, Macromolecules, 2001, 34, 4480–4484 CrossRef CAS.
- X. Zhao, N. Huebsch, D. J. Mooney and Z. Suo, J. Appl. Phys., 2010, 107, 063509 CrossRef PubMed.
- S. Cai, Y. Hu, X. Zhao and Z. Suo, J. Appl. Phys., 2010, 108, 113514 CrossRef.
- X. Zhang, Z. Hu and Y. Li, J. Chem. Phys., 1996, 105, 3794–3800 CrossRef CAS.
- G. W. Scherer, J. Am. Ceram. Soc., 2000, 83, 2231–2239 CrossRef CAS.
- W. Vichit-Vadakan and G. W. Scherer, J. Am. Ceram. Soc., 2000, 83, 2240–2246 CrossRef CAS.
- J. A. Stammen, S. Williams, D. N. Ku and R. E. Guldberg, Biomaterials, 2001, 22, 799–806 CrossRef CAS.
- J. A. Zimberlin, N. Sanabria-DeLong, G. N. Tew and A. J. Crosby, Soft Matter, 2007, 3, 763–767 RSC.
- T. G. Mason and D. A. Weitz, Phys. Rev. Lett., 1995, 74, 1250 CrossRef CAS PubMed.
- F. MacKintosh and C. Schmidt, Curr. Opin. Colloid Interface Sci., 1999, 4, 300–307 CrossRef CAS.
- A. Mukhopadhyay and S. Granick, Curr. Opin. Colloid Interface Sci., 2001, 6, 423–429 CrossRef CAS.
- D. M. Ebenstein and L. A. Pruitt, Nano Today, 2006, 1, 26–33 CrossRef.
- G. Constantinides, Z. I. Kalcioglu, M. McFarland, J. F. Smith and K. J. Van, Vliet, J. Biomech., 2008, 41, 3285–3289 CrossRef PubMed.
- J. D. Kaufman, G. J. Miller, E. F. Morgan and C. M. Klapperich, J. Mater. Res., 2008, 23, 1472 CrossRef CAS PubMed.
- M. Galli, K. S. Comley, T. A. Shean and M. L. Oyen, J. Mater. Res., 2009, 24, 973–979 CrossRef CAS.
- C.-Y. Hui, Y. Y. Lin, F.-C. Chuang, K. R. Shull and W.-C. Lin, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 359–370 CrossRef CAS.
- Y.-Y. Lin and B.-W. Hu, J. Non-Cryst. Solids, 2006, 352, 4034–4040 CrossRef CAS.
- W.-C. Lin, K. R. Shull, C.-Y. Hui and Y.-Y. Lin, J. Chem. Phys., 2007, 127, 094906 CrossRef PubMed.
- M. Galli and M. Oyen, Comput. Model. Eng. Sci., 2009, 48, 241–269 Search PubMed.
- Y. Hu, X. Zhao, J. J. Vlassak and Z. Suo, Appl. Phys. Lett., 2010, 96, 121904 CrossRef.
- Y. Hu, X. Chen, G. M. Whitesides, J. J. Vlassak and Z. Suo, J. Mater. Res., 2011, 6, 785–795 CrossRef.
- A. O. Moghaddam, J. Wei, J. Kim, A. C. Dunn and A. J. W. Johnson, J. Mech. Behav. Biomed. Mater., 2020, 103, 103539 CrossRef PubMed.
- Q. Xu, L. A. Wilen, K. E. Jensen, R. W. Style and E. R. Dufresne, Phys. Rev. Lett., 2020, 125, 238002 CrossRef CAS PubMed.
- M. Zhao, F. Lequeux, T. Narita, M. Roché, L. Limat and J. Dervaux, Soft Matter, 2018, 14, 61–72 RSC.
- J. D. Berman, M. Randeria, R. W. Style, Q. Xu, J. R. Nichols, A. J. Duncan, M. Loewenberg, E. R. Dufresne and K. E. Jensen, Soft Matter, 2019, 15, 1327–1334 RSC.
- T. Tanaka and D. J. Fillmore, J. Chem. Phys., 1979, 70, 1214–1218 CrossRef CAS.
- Y. Li and T. Tanaka, J. Chem. Phys., 1990, 92, 1365–1371 CrossRef CAS.
- M. Doi, J. Phys. Soc. Jpn., 2009, 78, 052001 CrossRef.
- S. K. De, N. Aluru, B. Johnson, W. Crone, D. J. Beebe and J. Moore, J. Microelectromech. Syst., 2002, 11, 544–555 CrossRef CAS.
- T. Traitel, Y. Cohen and J. Kost, Biomaterials, 2000, 21, 1679–1687 CrossRef CAS PubMed.
- H. J. Cho, N. B. Lu, M. P. Howard, R. A. Adams and S. S. Datta, Soft Matter, 2019, 15, 4689–4702 RSC.
- M. A. Biot, J. Appl. Phys., 1941, 12, 155 CrossRef.
- E. Detournay and A. Cheng, Comprehens. Rock Eng., 1993, 2, 113–171 Search PubMed.
- J. Delavoipière, Y. Tran, E. Verneuil and A. Chateauminois, Soft Matter, 2016, 12, 8049–8058 RSC.
- M. H. Esteki, A. A. Alemrajabi, C. M. Hall, G. K. Sheridan, M. Azadi and E. Moeendarbary, Acta Biomater., 2020, 102, 138–148 CrossRef CAS PubMed.
- Z. I. Kalcioglu, R. Mahmoodian, Y. Hu, Z. Suo and K. J. Van Vliet, Soft Matter, 2012, 8, 3393–3398 RSC.
- J. D. Berry, M. Biviano and R. R. Dagastine, Soft Matter, 2020, 16, 5314–5324 RSC.
- T. Tanaka, S.-T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose and T. Amiya, Nature, 1987, 325, 796–798 CrossRef CAS.
- S. Cai and Z. Suo, J. Mech. Phys. Solids, 2011, 59, 2259–2278 CrossRef CAS.
- J.-F. Louf, N. B. Lu, M. G. O'Connell, H. J. Cho and S. S. Datta, Sci. Adv., 2021, 7, eabd2711 CrossRef PubMed.
- K. L. Johnson and K. L. Johnson, Contact Mechanics, Cambridge University Press, 1987 Search PubMed.
- C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nature, 2005, 435, 191–194 CrossRef CAS.
- Y. Takashimizu and M. Iiyoshi, Progr. Earth Planet. Sci., 2016, 3, 1–16 CrossRef.
- Y. Hu, E. P. Chan, J. J. Vlassak and Z. Suo, J. Appl. Phys., 2011, 110, 086103 CrossRef.
- E. P. Chan, Y. Hu, P. M. Johnson, Z. Suo and C. M. Stafford, Soft Matter, 2012, 8, 1492–1498 RSC.
- E. P. Chan, B. Deeyaa, P. M. Johnson and C. M. Stafford, Soft Matter, 2012, 8, 8234–8240 RSC.
- N. Traeber, K. Uhlmann, S. Girardo, G. Kesavan, K. Wagner, J. Friedrichs, R. Goswami, K. Bai, M. Brand and C. Werner, et al. , Sci. Rep., 2019, 9, 1–14 CAS.
- M. Rubinstein and R. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- J. M. Urueña, E. O. McGhee, T. E. Angelini, D. Dowson, W. G. Sawyer and A. A. Pitenis, Biotribology, 2018, 13, 30–35 CrossRef.
- A. Bhattacharyya, C. O'Bryan, Y. Ni, C. D. Morley, C. R. Taylor and T. E. Angelini, Biotribology, 2020, 22, 100125 CrossRef.
- Y. Lai and Y. Hu, Soft Matter, 2018, 14, 2619–2627 RSC.
- C. A. Grattoni, H. H. Al-Sharji, C. Yang, A. H. Muggeridge and R. W. Zimmerman, J. Colloid Interface Sci., 2001, 240, 601–607 CrossRef CAS PubMed.
- M. Tokita and T. Tanaka, J. Chem. Phys., 1991, 95, 4613–4619 CrossRef CAS.
- G. S. Offeddu, E. Axpe, B. A. C. Harley and M. L. Oyen, AIP Adv., 2018, 8, 105006 CrossRef CAS PubMed.
- A. Hecht, E. Geissler and A. Chosson, Polymer, 1981, 22, 877–881 CrossRef CAS.
- D. M. Mueth, H. M. Jaeger and S. R. Nagel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 3164 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of determination of characteristic indentation depth, minimal influence of drying, measurements of individual indentation location versus time, measurements of circularity versus time. See DOI: 10.1039/d0sm02243h |
| This journal is © The Royal Society of Chemistry 2021 |