Open Access Article
Open Access ArticleCrowded solutions of single-chain nanoparticles under shear flow†
Maud
Formanek
ab and
Angel J.
Moreno
 *ac
*ac
aCentro de Física de Materiales (CSIC, UPV/EHU) and Materials Physics Center MPC, Paseo Manuel de Lardizabal 5, E-20018 San Sebastián, Spain. E-mail: angeljose.moreno@ehu.es
bSainsbury Laboratory, University of Cambridge, 47 Bateman Street, Cambridge CB2 1LR, UK
cDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, E-20018 San Sebastián, Spain
First published on 14th January 2021
Abstract
Single-chain nanoparticles (SCNPs) are ultrasoft objects obtained through purely intramolecular cross-linking of single polymer chains. By means of computer simulations with implemented hydrodynamic interactions, we investigate for the first time the effect of the shear flow on the structural and dynamic properties of SCNPs in semidilute and concentrated solutions. We characterize the dependence of several conformational and dynamic observables on the shear rate and the concentration, obtaining a set of power-law scaling laws. The concentration has a very different effect on the shear rate dependence of the former observables in SCNPs than in simple linear chains. Whereas for the latter the scaling behaviour is marginally dependent on the concentration, two clearly different scaling regimes are found for the SCNPs below and above the overlap concentration. At fixed shear rate SCNPs and linear chains also respond very differently to crowding. Whereas, at moderate and high Weissenberg numbers the linear chains swell, the SCNPs exhibit a complex non-monotonic behaviour. We suggest that these findings are inherently related to the topological interactions preventing concatenation of the SCNPs, which lead to less interpenetration than for linear chains, and to the limitation to stretching imposed by the permanent cross-links in the SCNPs, which itself limits the ways to spatially arrange in the shear flow.
1. Introduction
Single-chain nanoparticles (SCNPs) are synthesized through purely intramolecular bonding of functionalized polymer chains.1 These fully polymeric nano-objects are the basis of the single-chain technology, a rapidly growing research area due to the recent advances demonstrating their promising application in fields so diverse as catalysis, drug delivery, biosensing or nanocomposite design.2–10 Taking inspiration from biological systems such as proteins or enzymes, it is a long term goal to design SCNPs with precise control over the chemical sequence and molecular architecture, high performance and quick response to environmental changes. Most of the current research on SCNPs is devoted to improve synthesis routes and to the implementation of advanced functionalities (catalytic, luminescence, etc.). The knowledge of their physical properties has significantly improved in recent years. This is a crucial question, since the functionality of SCNPs should be in part related to their internal structure and dynamics (allowing, e.g., for fast responses to changes in pH, or temperature, and for adaptation to multiple substrates). Moreover, structure and dynamics can be strongly altered in e.g., flow, confinement or crowding conditions,11 which are ubiquitous in multiple problems of practical interest, as e.g., diffusion in blood, membranes or cell environments.A series of investigations by simulations, small-angle X-ray and neutron scattering12–15 have revealed that the molecular topology of SCNPs obtained through conventional routes is far from a compact, globular nano-object.16,17 In the usual good solvent conditions of synthesis the linear precursors universally adopt self-avoiding conformations.18 Such conformations strongly promote bonding of reactive groups that are separated by short contour distances, while those distant in the backbone sequence are statistically far from each other in the real space. Thus, the fraction of cross-links involving long loops is very low (decaying as a power-law with the loop size) and insufficient to fold the precursor into a compact object.12,19–23 For the same molecular weight and fraction of reactive groups in the precursor, the obtained SCNPs are topologically polydisperse12,19,21,23 but the distribution of network topologies is largely dominated by sparse structures.12,24
The particular internal structure of SCNPs, containing loops and clusters of loops of different sizes, leads to a peculiar response in solution when the concentration is increased above the overlap density and up to the melt state. Whereas simple linear chains show a crossover from self-avoiding to Gaussian conformations, SCNPs collapse to more compact conformations15,24,25 that resemble those of the so-called fractal or ‘crumpled’ globule26,27 and are characterized by loose cores and outer protrusions. As a consequence of the topological interactions (loops cannot be concatenated without bond breaking), the SCNPs in concentrated solutions and melts show a weaker interpenetration than linear chains and some microsegregation from neigbouring SCNPs, in close analogy to the well-known case of ring polymers – a feature that has been invoked to explain the formation of chromosome territories.28
The particular architecture of SCNPs also leads to a characteristic response to flow. In a recent computational study29 we have investigated the effect of shear flow on the structural and dynamic properties of isolated SCNPs (mimicking highly dilute conditions). We have characterized the dependence of several observables of interest (size, orientation, intrinsic viscosity, etc.) on the applied shear rate. The obtained power-laws have characteristic exponents that are clearly different from those found in other architectures (linear chains, rings, stars, dendrimers, combs, etc.29–40). Thus, SCNPs constitute a novel class of macromolecules with a distinct response to shear. Interestingly, this response is, at most, weakly dependent on the specific topology of the SCNP, and it seems inherently related to its network-like architecture.29
There is a vast literature on the conformations and intramolecular dynamics of polymeric systems under shear flow at high dilution (experimental) or for isolated polymers (simulations). The effect of shear flow on such properties in semidilute and concentrated solutions have received less attention, though some very detailed studies have been reported, including e.g., experiments in solutions of DNA and common polymers,41–43 and simulations of flexible linear chains,44–47 end-functionalized semiflexible linear chains,48 stars (simple,49,50 telechelic51 and block copolymer52), and cluster-forming semiflexible rings.53,54 There is a broad interest in the characterization of the structure and dynamics of complex macromolecules (stars, dendrimers, nanogels, etc.) for which softness can be tuned (e.g., through the number of branches or cross-linking degree). This interest includes the case of crowded solutions in flow, because their use in related applications is partially due to their architecture, which can be deformed, functionalized and can encapsulate small molecules.
With this motivation in mind, in this article we investigate, for the first time, the structural and dynamic properties of crowded solutions of SCNPs under shear flow. We employ large-scale simulations with implemented hydrodynamic interactions, by using the same model as in the simulations of linear chains by Huang et al.45 This choice allows us to critically compare the response to shear flow in two simulated systems (linear vs. SCNP) that, by construction, only differ in their molecular architecture. In this way we discriminate the role of the molecular architecture from other contributions (mass polydispersity, solvent quality, chain stiffness, charges, etc.) that are usually different in each experiment and can complicate the interpretation of the results.43 We have characterized the dependence of several conformational and dynamic observables of the simulated SCNPs on the shear rate and the concentration. We find that, when compared to simulations of simple linear chains, SCNPs exhibit a very different response to shear and crowding. Unlike in the simulations of linear chains, which essentially show a single power-law dependence on the shear rate, the SCNPs exhibit two distinct regimes with a crossover around the overlap concentration. At fixed shear rate, the size of the SCNPs shows a complex dependence on the concentration. Whereas crowding at fixed moderate and high shear rate leads to swelling of linear chains, the SCNPs may show both swelling and shrinking, as well as reentrant behaviour. We suggest that these findings are inherently related to the topological interactions preventing concatenation of the SCNPs, which lead to less interpenetration than for linear chains, and to the limitations to stretching imposed by the permanent cross-links in the SCNPs, which itself limits the ways to spatially arrange in the shear flow.
2. Model and simulation details
The simulated SCNPs were based on the bead-spring model with purely repulsive interactions,55 which mimicks implicit good solvent conditions and capture the basic ingredients of the system: monomer excluded volume, connectivity, and chain uncrossability (which moreover prevents concatenation of the permanent loops of the SCNPs). The SCNPs were generated in our previous work29 through irreversible cross-linking of isolated (mimicking the limit of high dilution) linear precursors of N = 200 monomers, of which a 25% were reactive groups randomly distributed along the chain contour, with the condition of not being consecutively placed to avoid trivial cross-links. A total of 200 fully reacted SCNPs were used for the simulations of the solutions. The generated SCNPs were topologically polydisperse. See typical equilibrium conformations of different SCNPs at high dilution in Fig. S1 of the ESI,† sorted from lowest to highest values of the asphericity paramemeter a0, which quantifies deviations from spherical shape.29 Though some of the SCNPs were relatively compact ‘nanogel-like’ networks, most of them were sparse objects.29 Two kind of solutions were investigated in the simulations reported here: (i) topologically polydisperse, where different SCNPs were taken from the generated set and were placed in the simulation box, (ii) topologically monodisperse, where all the SCNPs were replicas of the same one. Three monodisperse solutions were investigated, formed by SCNPs with a low, middle and high asphericity parameter, at the extremes and center of the obtained distribution of equilibrium asphericities,29i.e., representative SCNPs of the most compact, mean and sparsest architectures. In all cases the SCNPs were initially placed in a large box by keeping intermolecular distances that prevented violation of topological constraints through accidental concatenations. After a short equilibration, the box was very slowly compressed (rescaling the coordinates by a factor 0.99 every 104 MD steps) to the dimensions required by each selected shear rate and concentration.We will use the indices x, y, z to denote the directions of the flow, gradient and vorticity, respectively (see setup in Fig. S2 in the ESI†). After equilibration at zero shear, a linear shear profile was imposed by Lees–Edwards boundary conditions.56 The hydrodynamic interactions were implemented through the multi-particle collision dynamics (MPCD) technique.57 Both the interactions of the bead-spring model and the details of the MPCD implementation are the same as in the simulations of linear chains by Huang et al.,45 no bending or torsional barriers are imposed and the only relevant difference between both simulations is the molecular architecture (linear vs. SCNP). When the studied observables (see below) reached steady states (several millions MD steps after the compression run), accumulation runs were performed and the generated configurations were used in the analysis. To improve statistics, several independent realizations of the box were simulated for each couple of values of the shear rate and concentration. The number of independent runs was higher in the polydisperse systems, varying, for a same shear rate, between 20 at the lowest simulated concentration and 5 at the highest one. The number of SCNPs in the simulation box varied, respectively, between 8 and the full set of 200. Further details about the bead-spring model, the generation of the SCNPs, and the simulation method can be found in ref. 29. In what follows molecular sizes and number densities will be given in units of σ and σ−3 respectively, where σ is the bead size and qualitatively represents a Kuhn kength.
If Rg = 〈Rg2〉1/2 is the radius of gyration at equilibrium (zero shear rate), we define the overlap density as ρ* = N(2Rg)−3, i.e., as the number density of a cube of size 2Rg containing the N monomers of a SCNP.58 For the investigated SCNPs Rg = 7.4 and ρ* = 0.062. For concentrations higher than ρ* the clouds of monomers of the surrounding macromolecules enter in the cube, distorting the conformations with respect to dilute conditions. Linear chains and SCNPs experience a crossover to Gaussian and crumpled globular conformations, respectively.15,24 In what follows the concentration of the solution, ρ = Nm/V, with Nm the total number of monomers in the simulation box and V the volume of the box, will be given in reduced units, ρ/ρ*. We explored concentrations in the range 0.25 ≤ ρ/ρ* ≤ 6.24. The highest concentration corresponds to a monomer density ρ = 0.38, qualitatively corresponding to 300–400 mg mL−1.24 The SCNPs are unentangled even at the highest concentration. For linear chains of the same N = 200 in good solvent the concentration for the onset of entanglements can be obtained as18ρe ≈ (Ne/N)3νF−1, with Ne the entanglement length in the melt state and νF = 0.59 the Flory exponent. Since for the used bead-spring model Ne ≳ 65,59,60 the entanglement concentration is ρe ≳ 0.42, which is above the highest simulated concentration of SCNPs. For the SCNPs, which are less penetrable than linear chains, a reduction of entanglements with respect to their linear counterparts is expected,61 so that their ρe will be even higher.
We investigate shear rates 5 × 10−5 ≤ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 2 × 10−2 in the simulation units.29 In the rest of the article the shear rates will be given in units of the dimensionless Weissenberg number, Wi =
≤ 2 × 10−2 in the simulation units.29 In the rest of the article the shear rates will be given in units of the dimensionless Weissenberg number, Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τ, where τ is the relaxation time at equilibrium and high dilution ρ = 0. The value of τ is determined from the decay of the correlator of Rg.29 We find τ ≈ 104 as the mean value of the polydisperse distribution, and τ ≈ 2 × 103, 104 and 8 × 104 for the SCNPs with, respectively, low (a0 = 0.18), middle (a0 = 0.34) and high (a0 = 0.47) asphericity parameter (values at
τ, where τ is the relaxation time at equilibrium and high dilution ρ = 0. The value of τ is determined from the decay of the correlator of Rg.29 We find τ ≈ 104 as the mean value of the polydisperse distribution, and τ ≈ 2 × 103, 104 and 8 × 104 for the SCNPs with, respectively, low (a0 = 0.18), middle (a0 = 0.34) and high (a0 = 0.47) asphericity parameter (values at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0 and high dilution)29 that we select for generating the topologically monodisperse solutions. For low Weissenberg numbers Wi ≪ 1 the characteristic time for intramolecular relaxation is much shorter than the characteristic time of the shear flow, and the conformations are weakly perturbed with respect to equilibrium. For Wi ≫ 1 the macromolecule cannot relax its conformations in the fast flow and is strongly elongated most of the time, though it may experience more compact transient conformations due to tumbling motion,29,62,63 where the polymer contracts, flips around and extends again, with the head and tail having switched sides.
= 0 and high dilution)29 that we select for generating the topologically monodisperse solutions. For low Weissenberg numbers Wi ≪ 1 the characteristic time for intramolecular relaxation is much shorter than the characteristic time of the shear flow, and the conformations are weakly perturbed with respect to equilibrium. For Wi ≫ 1 the macromolecule cannot relax its conformations in the fast flow and is strongly elongated most of the time, though it may experience more compact transient conformations due to tumbling motion,29,62,63 where the polymer contracts, flips around and extends again, with the head and tail having switched sides.
3. Results
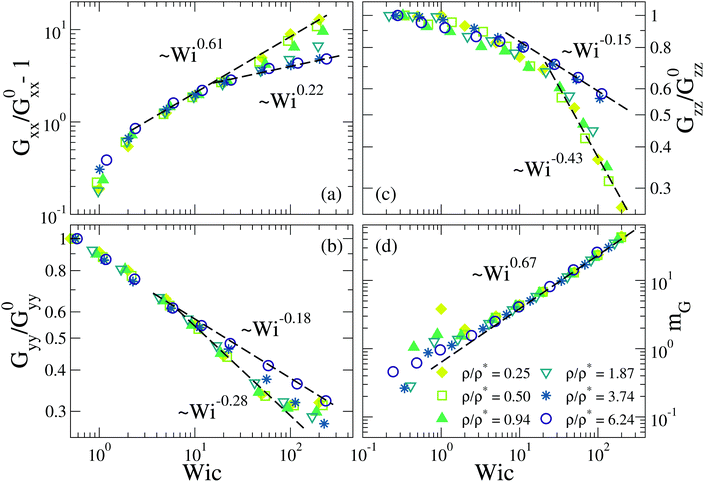
We start our analysis by characterizing static observables adapted to the geometry of the shear flow. The panels (a–c) of Fig. 1 show the Wi-dependence of the diagonal components Gμμ of the gyration tensor, along the flow (x), gradient (y) and vorticity (z) directions, in the topologically polydisperse solutions. The gyration tensor is computed as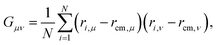 | (1) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 5 × 10−5. The panel (d) shows the corresponding data sets for the Wi-dependence of the orientational resistance mG.64 This is defined as mG = Wi
= 5 × 10−5. The panel (d) shows the corresponding data sets for the Wi-dependence of the orientational resistance mG.64 This is defined as mG = Wi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) tan(2θ) = 2WiGxy/(Gxx − Gyy), where θ is the angle between the direction of the largest eigenvector of the gyration tensor and the direction of the flow. Thus, for a fixed Wi lower values of mG mean stronger alignment with the flow. In all panels each Wi has been rescaled by a factor (in the range 1–3) to obtain the best overlap of the data sets. This representation as a function of the rescaled Weissenberg number (Wic) is made to highlight the emergence of master curves and scaling behaviour.
tan(2θ) = 2WiGxy/(Gxx − Gyy), where θ is the angle between the direction of the largest eigenvector of the gyration tensor and the direction of the flow. Thus, for a fixed Wi lower values of mG mean stronger alignment with the flow. In all panels each Wi has been rescaled by a factor (in the range 1–3) to obtain the best overlap of the data sets. This representation as a function of the rescaled Weissenberg number (Wic) is made to highlight the emergence of master curves and scaling behaviour.
A remarkable feature is observed in the components of the gyration tensor: whereas at low and moderate shear rates a single scaling is apparently observed, at high rates (Wi ≫ 1) two clearly different power-law scaling regimes are found for low (ρ/ρ* ≪ 1) and high (ρ/ρ* ≫ 1) concentration. This observation is rather different from that observed in analogous simulations of linear chains.45,47 In such systems increasing the density even far beyond the overlap concentration has, at most, a very weak effect in the Wi-dependence of the Gμμ components, which essentially keep the power-laws found at dilute conditions. In the SCNPs the crossover between the low and high concentration scaling regimes takes place at concentrations of the order of the equilibrium overlap density, though the specific value changes with the component of the gyration tensor. This is not surprising because conformations stretch or shrink differently along the three directions and therefore effectively overlap at a different concentration for each direction. The results in panels (a–c) reveal the strong effect of crowding on the scaling of the SCNP size under shear. However, crowding has little or no effect on the Wi-dependence of the orientation in shear flow. As can be seen in Fig. 1d, data for mG at all the concentrations are consistent with the same power law, i.e., the orientation of the inertia ellipsoid reacts to shear in the same way below and above the overlap concentration, irrespective of the specific effect of crowding on the molecular size and shape.
Panels (a) and (b) of Fig. 2 show the Wi-dependence of the rotational frequency ωz and the viscosity ηp (polymer contribution), respectively, for the polydisperse solution. The rotational frequency has been determined by using the relation 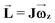 , where
, where ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_004c_20d1.gif) and J are the angular momentum and inertia tensor, respectively. The polymer contribution to the viscosity is obtained as ηp = σxy
and J are the angular momentum and inertia tensor, respectively. The polymer contribution to the viscosity is obtained as ηp = σxy![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1, where σxy is the xy-component of the Kramers–Kirkwood stress tensor:66
−1, where σxy is the xy-component of the Kramers–Kirkwood stress tensor:66
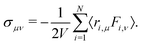 | (2) |
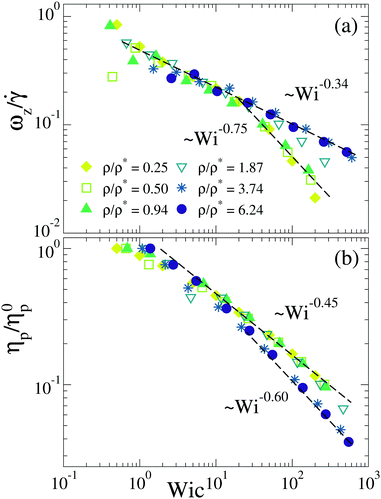 | ||
Fig. 2 As Fig. 1 for the rotational frecuency scaled by ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1 (a) and the polymer contribution to the viscosity (b). The values of η0p are, from the lowest to the highest concentration, 12, 26, 47, 131, 380 and 796 in units of65 (mkBT)1/2σ−2, with m the mass of a solvent particle. −1 (a) and the polymer contribution to the viscosity (b). The values of η0p are, from the lowest to the highest concentration, 12, 26, 47, 131, 380 and 796 in units of65 (mkBT)1/2σ−2, with m the mass of a solvent particle. | ||
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/b_char_0046_20d1.gif) i
is the total force exerted by the rest of the monomers on the monomer i and μ,ν denote the Cartesian components. It should be noted that the data of ηp reported here do not include the collisional contribution from the stochastic forces,67 and only account for the contribution of the conservative forces. As in Fig. 1, each data set in Fig. 2 corresponds to a fixed concentration, and the Weissenberg numbers are rescaled to obtain the best overlap with the data for ρ/ρ* = 0.25. We find the same qualitative behaviour as for the components of the gyration tensor: data at low Wi show the same scaling, whereas at high Wi two different scaling regimes are found, and the crossover between both regimes takes place when ρ is increased above the overlap concentration. The general trend for the diagonal components of the inertia tensor and the rotational frequency is to follow a weaker dependence on the shear rate at high concentrations (lower exponents). Thus, in crowded solutions the same relative increase in the shear rate is less efficient for the relative deformation of the equilibrium conformations than at high dilution, suggesting that deformation and rotation are hindered by the steric interactions with the surrounding crowders. The polymer contribution to the viscosity shows the opposite effect: increasing the shear rate at high densities leads to a stronger reduction of ηp. The number of side contacts at high concentration is large, so that progressively stretching the SCNPs removes many more contacts and is more efficient to reduce the viscosity than at lower concentrations.
i
is the total force exerted by the rest of the monomers on the monomer i and μ,ν denote the Cartesian components. It should be noted that the data of ηp reported here do not include the collisional contribution from the stochastic forces,67 and only account for the contribution of the conservative forces. As in Fig. 1, each data set in Fig. 2 corresponds to a fixed concentration, and the Weissenberg numbers are rescaled to obtain the best overlap with the data for ρ/ρ* = 0.25. We find the same qualitative behaviour as for the components of the gyration tensor: data at low Wi show the same scaling, whereas at high Wi two different scaling regimes are found, and the crossover between both regimes takes place when ρ is increased above the overlap concentration. The general trend for the diagonal components of the inertia tensor and the rotational frequency is to follow a weaker dependence on the shear rate at high concentrations (lower exponents). Thus, in crowded solutions the same relative increase in the shear rate is less efficient for the relative deformation of the equilibrium conformations than at high dilution, suggesting that deformation and rotation are hindered by the steric interactions with the surrounding crowders. The polymer contribution to the viscosity shows the opposite effect: increasing the shear rate at high densities leads to a stronger reduction of ηp. The number of side contacts at high concentration is large, so that progressively stretching the SCNPs removes many more contacts and is more efficient to reduce the viscosity than at lower concentrations.
Data in Fig. 1 and 2 correspond to the topologically polyisperse solutions. Similar results (including the two scaling regimes below and above the overlap concentration) are found in the three investigated monodisperse solutions, with just quantitative changes in the values of the scaling exponents. As an example, Fig. S3–S5 in the ESI† show the components of the gyration tensor and the polymer viscosity vs. the Weissenberg number for the monodisperse solutions at all the investigated concentrations. Fig. S6 and S7 in the ESI,† show, for the monodisperse solutions of SCNPs with low and high asphericity, respectively, typical snapshots of the simulation box for different concentrations and Weissenberg numbers. All the SCNPs in the solution are represented. The color codes are assigned according to the instantaneous value of Rg. The snapshots for the polydisperse systems (not shown) display similar features. As can be seen, at high concentrations and moderate Wi the SCNPs maintain the structural characteristics found in equilibrium. As has been shown in the equilibrium (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0) simulations of ref. 24, due to the topological interactions that prevent concatenation of the loops the SCNPs adopt more compact conformations and are less interpenetrated than linear chains. Regarding high values of the concentration and Weissenberg number, Fig. S6 and S7 (ESI†) show microsegregation of SCNPs with stretched (blue) and compressed (red) instantaneous configurations. It should be noted that these SCNPs are topologically monodisperse, so these conformations just originate from the molecular fluctuations and mobility in the flow. The qualitative picture of such figures sheds light on the origin of the two scaling regimes (at low and high concentration) for the Wi-dependence of the size and viscosity of the SCNPs, in contrast with the single scaling behaviour (independent of the concentration) found for linear chains.68 At high concentrations and in equilibrium (
= 0) simulations of ref. 24, due to the topological interactions that prevent concatenation of the loops the SCNPs adopt more compact conformations and are less interpenetrated than linear chains. Regarding high values of the concentration and Weissenberg number, Fig. S6 and S7 (ESI†) show microsegregation of SCNPs with stretched (blue) and compressed (red) instantaneous configurations. It should be noted that these SCNPs are topologically monodisperse, so these conformations just originate from the molecular fluctuations and mobility in the flow. The qualitative picture of such figures sheds light on the origin of the two scaling regimes (at low and high concentration) for the Wi-dependence of the size and viscosity of the SCNPs, in contrast with the single scaling behaviour (independent of the concentration) found for linear chains.68 At high concentrations and in equilibrium (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0) the linear chains are strongly interpenetrated and their conformations are much less perturbed with respect to high dilution than in the SCNPs.24 In the sheared solution, and for fixed Wi, the linear chains at high concentration are still weakly perturbed with respect to high dilution, since unlike in SCNPs, chain stretching in the flow is not limited by permanent cross-links and non-concatenability with loops of neighboring molecules. As a consequence, for the linear chains crowding has no significant effect in the Wi-dependence of the relative change of their molecular size and viscosity. Crowding at a fixed Wi has a much stronger effect in the ability of the SCNPs to stretch and to spatially arrange in the shear flow, as will be discussed later, leading to very different responses to shear below and above the overlap concentration.
= 0) the linear chains are strongly interpenetrated and their conformations are much less perturbed with respect to high dilution than in the SCNPs.24 In the sheared solution, and for fixed Wi, the linear chains at high concentration are still weakly perturbed with respect to high dilution, since unlike in SCNPs, chain stretching in the flow is not limited by permanent cross-links and non-concatenability with loops of neighboring molecules. As a consequence, for the linear chains crowding has no significant effect in the Wi-dependence of the relative change of their molecular size and viscosity. Crowding at a fixed Wi has a much stronger effect in the ability of the SCNPs to stretch and to spatially arrange in the shear flow, as will be discussed later, leading to very different responses to shear below and above the overlap concentration.
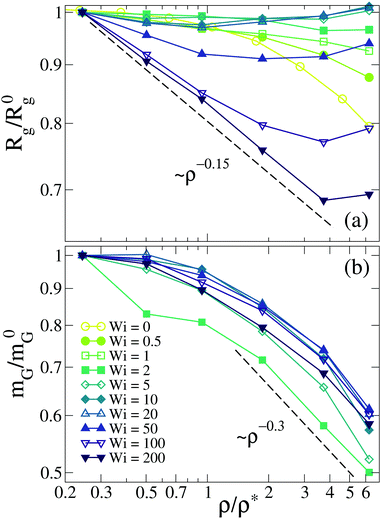
Fig. 3 shows the gyration radius Rg and the orientational resistance mGvs. the normalized concentration for the polydisperse solution. Fig. S8 in the ESI,† shows analogous results for the components of the gyration tensor. In all cases each data set corresponds to a fixed value of the Weissenberg number, and it is normalized by its corresponding value (R0g, m0G, G0μμ) at ρ/ρ* = 0.25. For any fixed Weissenberg number, increasing the concentration leads to a reduction of the orientational resistance mG, i.e., the SCNPs tend to be more aligned with the flow as the solution becomes more crowded. The data for Rg in Fig. 3a reveals a more complex behaviour. As expected, increasing the concentration of the solution above the overlap density leads, in equilibrium (Wi = 0), to shrinking of the SCNPs. This behaviour is still found in the weakly and moderately sheared solutions (Wi ≤ 1), though a much weaker shrinking is observed as Wi is increased. For 1 ≤ Wi ≤ 20 the concentration has essentially no effect: adding more SCNPs to the sheared solution, even up to ρ/ρ* ∼ 6, does not change the molecular size, or even leads to some weak swelling. Unlike at lower shear rates, the SCNPs are, in average, sufficiently elongated to fill the space without significant contact with their neighbours even at high concentrations, and their size is unaltered with respect to high dilution. This effect is partially reversed by further increasing the shear rate, for which a non-monotonic dependence of the molecular size on the concentration is found. At Wi > 20 adding more SCNPs to the solution leads to shrinking (with a stronger effect for higher Wi), but the SCNPs start to swell if the concentration is further increased.
Since the radius of gyration is given by Rg2 = Gxx + Gyy + Gzz, one expects that the scenario displayed in Fig. 3a for the SCNPs elongated under shear flow essentially comes from the largely dominant x-contribution of the gyration tensor. This is confirmed by panel (a) of Fig. S8 (ESI†), where Gxx shows all the qualitative trends found for Rg. On the contrary, the component along the gradient direction, Gyy, monotonically shrinks with increasing concentration for all the Weissenberg numbers, which is consistent with the stronger alignment with the flow reflected in the behaviour of the orientational resistance (Fig. 3b). Crowding at low and moderate Wi shrinks the molecular size along the vorticity direction z, as can be seen for Gzz in panel (c) or Fig. S8 (ESI†). At high Wi the behaviour is non-monotonic, the SCNPs initially swell along the z-direction and above some concentration they start to shrink. As can be seen in panels (a) and (c) of Fig. S8 (ESI†), Gxx and Gzz at fixed Wi qualitatively show opposite dependences on the concentration. Thus, increasing the concentration at fixed shear rate both leads to a stronger alignment with the flow and a redistribution of the monomers within the SCNP, through stretching along one of the x,z-directions and shrinking along the other one.
It is worth mentioning that the emerging scenario displayed in Fig. 3a is not related to a complex interplay of contributions of the different molecular topologies present in the polydisperse solution, each of them responding in a different way to crowding under shear. Fig. S9 in the ESI† shows the corresponding results for the topologically monodisperse solutions. For the three (low, middle and high) asphericities investigated the same qualitative scenario is found and the differences are only quantitative. Not surprisingly, the most deformable SCNPs, i.e., those with the highest asphericity and most sparse structures, are more affected by crowding the solution (note the highest exponent in the approximate scaling Rg ∼ ρ−α at Wi = 200 in Fig. S9, ESI†).
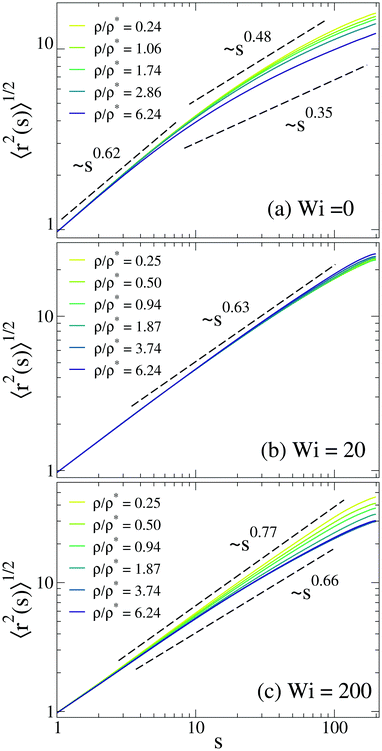
Further insight on the microscopic origin of the complex dependence of the SCNP size on concentration and shear rate can be obtained by analyzing their intramolecular correlations. Fig. 4 shows the real space distance r(s) = 〈r2(s)〉1/2vs. the contour distance s in equilibrium (Wi = 0)15 and for Wi = 20 and 200. By labelling the monomers as i = 1,2,…,N according to their position in the linear backbone of the precursor, the contour distance is defined as s = |i − j|, and the real distance is just 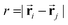 . The quantity r(s) provides insight on the conformational statistics of the SCNPs, through the exponent ν of the scaling law r(s) ∼ sν. It should be noted that the investigated SCNPs with N = 200 are not large enough to develop a well-defined power law regime over a broad s-range. Moreover a significant fraction of SCNPs have some long loop of countour length N/2 < l < N.24 Obviously, by moving forward along the contour of such a loop the real distance r(s) will stop growing at some point when the path starts to go back to the origin. The presence of SCNPs containing such long loops rationalizes the observed flattening of r(s) at large s. At short scales (s < 10) the SCNPs in equilibrium (Wi = 0, panel (a)) show a scaling exponent ν ∼ 0.6 similar to the Flory exponent for self-avoiding walks, indicating that at such scales the SCNPs effectively behave as linear chains with excluded volume interactions. The effect of the cross-links on the scaling of r(s) becomes evident at larger distances. In dilute conditions (ρ/ρ* = 0.25) at equilibrium (Wi = 0) an exponent ν ∼ 0.5 is observed. This is similar to the exponent expected for linear chains in θ-solvent conditions (ν = 1/2), where only local compaction occurs and the large-scale statistics is that of a random-walk.18 In the case of SCNPs in the simulated good solvent conditions this local compaction is mediated by a majority of permanent cross-links between reactive groups close in the chain contour.12,24 By increasing the concentration above the overlap density a crossover to a lower exponent ν ∼ 0.35 is observed. This is rather different from the well-know transition in linear chains from the Flory (νF = 0.59) to the Gaussian value (ν = 1/2).18 The exponent found for the SCNPs in crowded solutions in equilibrium is similar to the value ν = 1/3 for fractal globules.26,27 It should be noted that this is very different from the compact globular structure adopted by linear chains collapsed in bad solvent, for which polymer paths connecting two points of the spherical surface keep Gaussian scaling ν = 1/2. Rather the fractal globule is a mathematical idealization to describe objects with loose cores and outer protrusions where globular structures are present at all (local and global) scales.27
. The quantity r(s) provides insight on the conformational statistics of the SCNPs, through the exponent ν of the scaling law r(s) ∼ sν. It should be noted that the investigated SCNPs with N = 200 are not large enough to develop a well-defined power law regime over a broad s-range. Moreover a significant fraction of SCNPs have some long loop of countour length N/2 < l < N.24 Obviously, by moving forward along the contour of such a loop the real distance r(s) will stop growing at some point when the path starts to go back to the origin. The presence of SCNPs containing such long loops rationalizes the observed flattening of r(s) at large s. At short scales (s < 10) the SCNPs in equilibrium (Wi = 0, panel (a)) show a scaling exponent ν ∼ 0.6 similar to the Flory exponent for self-avoiding walks, indicating that at such scales the SCNPs effectively behave as linear chains with excluded volume interactions. The effect of the cross-links on the scaling of r(s) becomes evident at larger distances. In dilute conditions (ρ/ρ* = 0.25) at equilibrium (Wi = 0) an exponent ν ∼ 0.5 is observed. This is similar to the exponent expected for linear chains in θ-solvent conditions (ν = 1/2), where only local compaction occurs and the large-scale statistics is that of a random-walk.18 In the case of SCNPs in the simulated good solvent conditions this local compaction is mediated by a majority of permanent cross-links between reactive groups close in the chain contour.12,24 By increasing the concentration above the overlap density a crossover to a lower exponent ν ∼ 0.35 is observed. This is rather different from the well-know transition in linear chains from the Flory (νF = 0.59) to the Gaussian value (ν = 1/2).18 The exponent found for the SCNPs in crowded solutions in equilibrium is similar to the value ν = 1/3 for fractal globules.26,27 It should be noted that this is very different from the compact globular structure adopted by linear chains collapsed in bad solvent, for which polymer paths connecting two points of the spherical surface keep Gaussian scaling ν = 1/2. Rather the fractal globule is a mathematical idealization to describe objects with loose cores and outer protrusions where globular structures are present at all (local and global) scales.27
Results in Fig. 4b for relatively high Weissenberg numbers (Wi = 20) show, that in contrast to the equilibrium case, the chain statistics of the SCNPs is almost unaffected by the concentration. This is consistent with the very weak effect observed in the molecular size (see data for Wi = 20 in Fig. 3a). The exponent ν = 0.63 indicates that the typical conformations are more elongated than self-avoiding random walks (νF = 0.59) but still very far from straight rods (νR = 1). At the highest investigated Weissenberg number (Wi = 200), rod-like conformations are approached at high dilution (ν ∼ 0.8). Unlike for the case Wi = 20, the concentration has a strong effect on the conformations of the SCNPs. Concomitant and consistently with the shrinking found in the gyration radius (see data for Wi = 200 in Fig. 3a), the increase of the concentration above the overlap density leads to lower effective exponents ν ≳ 0.6.
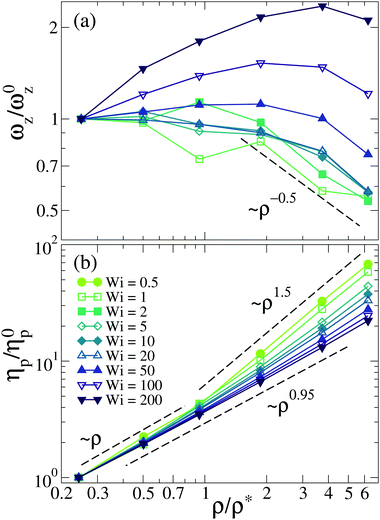
Fig. 5 shows the rotational frequency and polymer contribution to the viscosity vs. the concentration in the polydisperse solution. Each data set corresponds to a fixed Weissenberg number, and data are normalized by the value (ω0z,η0p) at that Wi and  . The concentration dependence of ωz at the different fixed values of Wi shows a good correlation with the z-component of the gyration tensor (Fig. S8c, ESI†). Thus, swelling along the z-direction combined with the concomitant shrinking in the xy-plane (Fig. S8a and b, ESI†) seems to facilitate rotations of the SCNPs around the vorticity axis. Rotations are instead hindered when swelling and shrinking occur along the x and z-direction, respectively. As expected, the polymer contribution to the viscosity (Fig. 5b) is just proportional to the concentration for
. The concentration dependence of ωz at the different fixed values of Wi shows a good correlation with the z-component of the gyration tensor (Fig. S8c, ESI†). Thus, swelling along the z-direction combined with the concomitant shrinking in the xy-plane (Fig. S8a and b, ESI†) seems to facilitate rotations of the SCNPs around the vorticity axis. Rotations are instead hindered when swelling and shrinking occur along the x and z-direction, respectively. As expected, the polymer contribution to the viscosity (Fig. 5b) is just proportional to the concentration for  . At low and moderate values of Wi it shows, around the overlap density, a crossover from the linear to a power-law dependence, ηp ∼ ρx. The exponent at Wi ≲ 1 is x = 1.5, which is intermediate between the values for linear chains in equilibrium and semidilute solution at good (x = 1.3) and θ-solvent (x = 2) conditions.18 No significant crossover in the concentration dependence of the viscosity is found for the largest Weissenberg numbers Wi ≳ 100, for which a quasi-linear dependence x = 0.95 is found. Similar results for ηp are found in the topologically monodisperse solutions (see Fig. S10 in the ESI†).
. At low and moderate values of Wi it shows, around the overlap density, a crossover from the linear to a power-law dependence, ηp ∼ ρx. The exponent at Wi ≲ 1 is x = 1.5, which is intermediate between the values for linear chains in equilibrium and semidilute solution at good (x = 1.3) and θ-solvent (x = 2) conditions.18 No significant crossover in the concentration dependence of the viscosity is found for the largest Weissenberg numbers Wi ≳ 100, for which a quasi-linear dependence x = 0.95 is found. Similar results for ηp are found in the topologically monodisperse solutions (see Fig. S10 in the ESI†).
 | ||
| Fig. 5 As Fig. 3 for the rotational frequency (a) and the polymer contribution to the viscosity (b). | ||
The trends in the observed exponents can be rationalized by a rough scaling argument for unentangled semidilute solutions.18 For macromolecular objects scaling as R ∼ Nν, with R and N their size and number of monomers respectively, their overlap concentration scales as 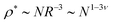 . Since above the overlap concentration
. Since above the overlap concentration 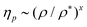 , then we have ηp ∼ ρxN(3ν−1)x. In semidilute conditions the hydrodynamic interactions are screened beyond the mesh size and, as aforementioned, we have simulated SCNPs that are unentangled even at the highest investigated concentrations. As a consequence of both conditions the viscosity should scale in a linear Rouse-like fashion18 with the macromolecular mass, ηp ∼ N. Therefore the exponents x and ν are related as (3ν − 1)x = 1. According to this relation, the exponents for the viscosity x = 1.5, 1.1, 0.95 found at the representative values Wi = 1, 20, 200 should originate from exponents for the molecular size ν = 0.56,0.64 and 0.68, respectively. These values are in good agreement with the analysis of r(s), which gives ν = 0.52 for Wi = 1 (not shown) and ν = 0.63 and 0.66 for Wi = 20 and 200, respectively (Fig. 4). Still, this agreement should be taken with some caution due to the uncertainties in the determination of the ν-values.
, then we have ηp ∼ ρxN(3ν−1)x. In semidilute conditions the hydrodynamic interactions are screened beyond the mesh size and, as aforementioned, we have simulated SCNPs that are unentangled even at the highest investigated concentrations. As a consequence of both conditions the viscosity should scale in a linear Rouse-like fashion18 with the macromolecular mass, ηp ∼ N. Therefore the exponents x and ν are related as (3ν − 1)x = 1. According to this relation, the exponents for the viscosity x = 1.5, 1.1, 0.95 found at the representative values Wi = 1, 20, 200 should originate from exponents for the molecular size ν = 0.56,0.64 and 0.68, respectively. These values are in good agreement with the analysis of r(s), which gives ν = 0.52 for Wi = 1 (not shown) and ν = 0.63 and 0.66 for Wi = 20 and 200, respectively (Fig. 4). Still, this agreement should be taken with some caution due to the uncertainties in the determination of the ν-values.
4. Discussion
The complex behaviour of the concentration dependence of the size and viscosity of the SCNPs is inherent to their molecular architecture. Fig. S11 in the ESI† shows the corresponding results for semidilute of solutions of linear chains under shear (data from ref. 45, see SI for details). As expected, in equilibrium (Wi = 0) crowding leads to shrinking. However, once the Weissenberg number is sufficiently high (Wi > 2) the linear chains swell by increasing the concentration. Unlike in the SCNPs, no reentrant behaviour is observed, and should not be found at higher Wi. Though the swelling ratio Rg/Rg0 at the highest investigated Wi ≈ 2400 is lower than at moderate Wi's, it should be noted that at such a high Wi swelling is just limited by the fact that the linear chains at high dilution are already close to rod-like objects and cannot be stretched much more. Increasing the concentration has a weaker effect on the viscosity of the sheared solutions of linear chains (Fig. S11b, ESI†) than in those made of SCNPs. According to the proposed relation (3ν − 1)x = 1 (see above), the observed exponents x = 1.2 (low concentration, low Wi) and 0.8 (high concentration, high Wi) correspond to values ν = 0.61 and 0.75, respectively. This is consistent with the limits of self-avoiding random walk (νF = 0.59) and rod (νR = 1) that should be approached in the former regimes.We propose a tentative explanation for the very different trends observed for SCNPs and linear chains in Fig. 3a and Fig. S8a (ESI†). When Wi is high and the polymers are stretched, they respond to an increase of the concentration by further stretching. This mechanism is favoured because the ‘pseudonematic’ ordering that emerges in the dense solution of stretched polymers leads to a gain in vibrational (through side oscillations) and translational entropy, which compensates the loss of intramolecular (conformational) entropy induced by the stretching. This effect persists in the case of linear chains if the concentration is further increased because there are no limitations for stretching up to the limit of rod-like conformations. Moreover tumbling motions in the shear flow are not hindered by neigbouring chains, since they can be performed by sliding one piece of the linear chain over the other without thickening significantly the cross-section. However, in the case of the SCNPs stretching at high Wi is limited by their network-like architecture (25% of cross-linking in the investigated systems), and beyond some concentration they will not be able to further stretch without violating topological constraints (loop concatenation). Because of this limitation, SCNPs have a larger cross-section in the flow than linear chains, and tumbling cycles of the SCNPs involve adopting transient conformations that are relatively compact (see right bottom panels in Fig. S6 and S7, ESI†). These conformations coexist, even in the topologically monodisperse solutions, with the elongated ones, hindering the extension of the latter (particularly through the non-concatenability of their respective loops) and leading, in average, to smaller molecular sizes than at lower concentration.
The presence of transient compact conformations of SCNPs across the solution and at all times is illustrated in Movies M1–M3 in the ESI,† which show the dynamics of the monodisperse solution with middle asphericity, at Wi = 200 and 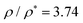 . The SCNPs are colored according to their instantaneous values of Rg as in Fig. S6 and S7 (ESI†). Movie M1 (ESI†) displays all the SCNPs in the solution. Movie M2 (ESI†) shows, for the sake of clarity, only the SCNPs whose instantaneous position of the center-of-mass is within a fixed slice perpendicular to the z-axis and of width Δz = 10. Movie M3 shows the trajectory of a selected SCNP. The big beads in M3 are the couple of monomers of this SCNP that are, in average, most distant in the real space, and are depicted in different colors to highlight the tumbling motion.
. The SCNPs are colored according to their instantaneous values of Rg as in Fig. S6 and S7 (ESI†). Movie M1 (ESI†) displays all the SCNPs in the solution. Movie M2 (ESI†) shows, for the sake of clarity, only the SCNPs whose instantaneous position of the center-of-mass is within a fixed slice perpendicular to the z-axis and of width Δz = 10. Movie M3 shows the trajectory of a selected SCNP. The big beads in M3 are the couple of monomers of this SCNP that are, in average, most distant in the real space, and are depicted in different colors to highlight the tumbling motion.
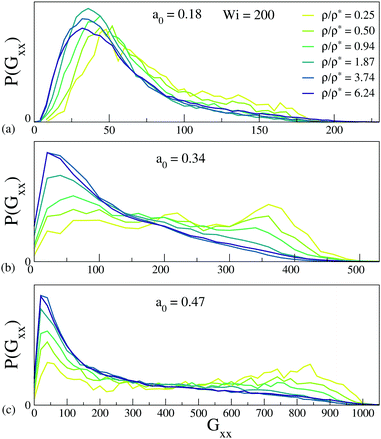
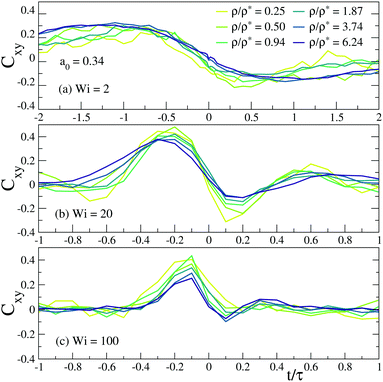
More insight about the reduction of the SCNP size by increasing the concentration at high Wi can be obtained by analyzing the distribution of instantaneous configurations and characterizing the tumbling dynamics. Fig. 6 shows the distribution of the instantaneous values of the x-component of the gyration tensor, Gxx, at fixed Wi = 200 in the monodisperse solutions of low, middle and high asphericity. As can be seen, crowding leads to a higher presence of the least elongated conformations (low Gxx), and in particular breaks the flat distribution (expected for well-defined tumbling motion) found at low concentration for the sparse SCNPs (panels (b) and (c)). Fig. 7 shows the cross-correlator Cxy of the x- and y-components of the gyration tensor for the monodisperse solutions with middle asphericity, at Wi = 2,20 and 100. The correlator is calculated as
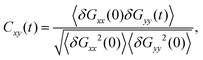 | (3) |
5. Conclusions
In summary, we have investigated for the first time the effect of the shear flow on the structural and dynamic properties of SCNPs in crowded solutions. We have characterized the dependence of several conformational and dynamic observables on the shear rate and the concentration. The emerging physical scenario exhibits remarkable differences with those of topologically simple objects such as linear chains. Such differences originate from the particular architecture of the SCNPs, since we have implemented the same interactions as in previous simulations works for linear chains.45 Thus, we have discriminated the specific role of the molecular architecture from other contributions (mass polydispersity, chain stiffness, solvent quality, charges, etc.) that are usually different in each experiment and can complicate the interpretation of the behaviour in flow. Whereas in simulations of linear chains45 the shear-rate dependence of structural and dynamic properties is marginally dependent on the concentration, two clearly different scaling regimes are found for the SCNPs below and above the overlap concentration. Furthermore, crowding the solutions of SCNPs at fixed shear rate leads to a complex non-monotonic scenario for the molecular size, in contrast to the case of linear chains, for which increasing the concentration at moderate or high shear rate always leads to swelling. The fractal globular conformations adopted by the SCNPs in equilibrium, originating from the topological interactions that reduce interpenetrability in comparison with linear chains, have their counterpart in the strongly sheared solutions as transient compact conformations, which hinder the stretching of the most elongated ones. These compact conformations naturally arise from the cross-linked character of the SCNPs, which limit their maximum extension far below the rod-like limit, and have a longer lifetime at high concentration due to partial suppression of tumbling. This effect, together with the lower penetrability of the SCNPs arising from the topological interactions (non-concatenation of loops), may be at the origin of the rather different response to shear and crowding of solutions of SCNPs with respect to solutions of simple linear chains.Beyond the consequences on the field of non-linear rheology of complex macromolecules, our system may have applications as a simple model of intrinsically disordered proteins (IDPs) in shear flow. SANS experiments and equilibrium simulations have revealed some structural similarities between IDPs and SCNPs.24 Though SCNPs lack of the ordered regions present in IDPs, they still contain weakly deformable compact domains connected by flexible strands, suggesting that SCNPs in concentrated solutions can be used as model systems, free of specific interactions, to shed light on the effect of excluded volume on IDPs in crowded environments. IDPs should share more analogies with SCNPs in shear flow than in equilibrium: shear may break69 the ordered domains of IDPs (this order being absent in SCNPs), which in equilibrium are stabilized through physical interactions (hydrogen bonds, electrostatic, assembly of hydrophobic groups, etc.), whereas the common ingredient with the SCNPs, i.e., the chemical ‘cross-links’ mediating loops in the IDP backbone (such as disulfide bonds) will remain.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from the projects PGC2018-094548-B-I00 (MCIU/AEI/FEDER, UE) and IT-1175-19 (Basque Government, Spain). We acknowledge support of the publication fee by the CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI). We thank Arash Nikoubashman for useful discussions.References
- Single-Chain Polymer Nanoparticles: Synthesis, Characterization, Simulations, and Applications, ed. J. A. Pomposo, John Wiley & Sons, Weinheim, Germany, 2017 Search PubMed.
- T. Terashima, T. Mes, T. F. A. De Greef, M. A. J. Gillissen, P. Besenius, A. R. A. Palmans and E. W. Meijer, J. Am. Chem. Soc., 2011, 133, 4742–4745 CrossRef CAS.
- I. Perez-Baena, F. Barroso-Bujans, U. Gasser, A. Arbe, A. J. Moreno, J. Colmenero and J. A. Pomposo, ACS Macro Lett., 2013, 2, 775–779 CrossRef CAS.
- E. Huerta, P. J. M. Stals, E. W. Meijer and A. R. A. Palmans, Angew. Chem., Int. Ed., 2013, 52, 2906–2910 CrossRef CAS.
- C. A. Tooley, S. Pazicni and E. B. Berda, Polym. Chem., 2015, 6, 7646–7651 RSC.
- S. K. Hamilton and E. Harth, ACS Nano, 2009, 3, 402–410 CrossRef CAS.
- A. Sanchez-Sanchez, S. Akbari, A. J. Moreno, F. Lo Verso, A. Arbe, J. Colmenero and J. A. Pomposo, Macromol. Rapid Commun., 2013, 34, 1681–1686 CrossRef CAS.
- M. A. J. Gillissen, I. K. Voets, E. W. Meijer and A. R. A. Palmans, Polym. Chem., 2012, 3, 3166–3174 RSC.
- M. E. Mackay, T. T. Dao, A. Tuteja, D. L. Ho, B. V. Horn, H.-C. Kim and C. J. Hawker, Nat. Mater., 2003, 2, 762–766 CrossRef CAS.
- P. Bačová, F. Lo Verso, A. Arbe, J. Colmenero, J. A. Pomposo and A. J. Moreno, Macromolecules, 2017, 50, 1719–1731 CrossRef.
- E. Verde-Sesto, A. Arbe, A. J. Moreno, D. Cangialosi, A. Alegría, J. Colmenero and J. A. Pomposo, Mater. Horiz., 2020, 7, 2292–2313 RSC.
- A. J. Moreno, F. Lo Verso, A. Sanchez-Sanchez, A. Arbe, J. Colmenero and J. A. Pomposo, Macromolecules, 2013, 46, 9748–9759 CrossRef CAS.
- S. Basasoro, M. Gonzalez-Burgos, A. J. Moreno, F. Lo Verso, A. Arbe, J. Colmenero and J. A. Pomposo, Macromol. Rapid Commun., 2016, 37, 1060–1065 CrossRef CAS.
- A. Arbe, J. Pomposo, A. Moreno, F. LoVerso, M. Gonzalez-Burgos, I. Asenjo-Sanz, A. Iturrospe, A. Radulescu, O. Ivanova and J. Colmenero, Polymer, 2016, 105, 532–544 CrossRef CAS.
- M. Gonzalez-Burgos, A. Arbe, A. J. Moreno, J. A. Pomposo, A. Radulescu and J. Colmenero, Macromolecules, 2018, 51, 1573–1585 CrossRef CAS.
- J. A. Pomposo, I. Perez-Baena, F. Lo Verso, A. J. Moreno, A. Arbe and J. Colmenero, ACS Macro Lett., 2014, 3, 767–772 CrossRef CAS.
- J. A. Pomposo, J. Rubio-Cervilla, A. J. Moreno, F. Lo Verso, P. Bacova, A. Arbe and J. Colmenero, Macromolecules, 2017, 50, 1732–1739 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press: Oxford, UK, 2003, vol. 23 Search PubMed.
- F. Lo Verso, J. A. Pomposo, J. Colmenero and A. J. Moreno, Soft Matter, 2014, 10, 4813–4821 RSC.
- H. Rabbel, P. Breier and J.-U. Sommer, Macromolecules, 2017, 50, 7410–7418 CrossRef CAS.
- M. Formanek and A. J. Moreno, Soft Matter, 2017, 13, 6430–6438 RSC.
- B. Oyarzun and B. M. Mognetti, J. Chem. Phys., 2018, 148, 114110 CrossRef.
- A. J. Moreno, P. Bacova, F. L. Verso, A. Arbe, J. Colmenero and J. A. Pomposo, J. Phys.: Condens. Matter, 2018, 30, 034001 CrossRef.
- A. J. Moreno, F. Lo Verso, A. Arbe, J. A. Pomposo and J. Colmenero, J. Phys. Chem. Lett., 2016, 7, 838–844 CrossRef CAS.
- J. Oberdisse, M. González-Burgos, A. Mendia, A. Arbe, A. J. Moreno, J. A. Pomposo, A. Radulescu and J. Colmenero, Macromolecules, 2019, 52, 4295–4305 CrossRef CAS.
- A. Y. Grosberg, S. K. Nechaev and E. I. Shakhnovich, J. Phys., 1988, 49, 2095–2100 CrossRef CAS.
- L. A. Mirny, Chromosome Res., 2011, 19, 37–51 CrossRef CAS.
- J. D. Halverson, J. Smrek, K. Kremer and A. Y. Grosberg, Rep. Prog. Phys., 2014, 77, 022601 CrossRef.
- M. Formanek and A. J. Moreno, Macromolecules, 2019, 52, 1821–1831 CrossRef CAS.
- C. Aust, M. Kröger and S. Hess, Macromolecules, 1999, 32, 5660–5672 CrossRef CAS.
- C. M. Schroeder, R. E. Teixeira, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2005, 38, 1967–1978 CrossRef CAS.
- M. Ripoll, R. G. Winkler and G. Gompper, Phys. Rev. Lett., 2006, 96, 188302 CrossRef CAS.
- A. Nikoubashman and C. N. Likos, Macromolecules, 2010, 43, 1610–1620 CrossRef CAS.
- W. Chen, J. Chen, L. Liu, X. Xu and L. An, Macromolecules, 2013, 46, 7542–7549 CrossRef CAS.
- W. Chen, J. Chen and L. An, Soft Matter, 2013, 9, 4312–4318 RSC.
- W. Chen, Y. Li, H. Zhao, L. Liu, J. Chen and L. An, Polymer, 2015, 64, 93–99 CrossRef CAS.
- W. Chen, K. Zhang, L. Liu, J. Chen, Y. Li and L. An, Macromolecules, 2017, 50, 1236–1244 CrossRef CAS.
- S. H. Jeong, J. M. Kim and C. Baig, Macromolecules, 2017, 50, 4491–4500 CrossRef CAS.
- M. Liebetreu, M. Ripoll and C. N. Likos, ACS Macro Lett., 2018, 7, 447–452 CrossRef CAS.
- D. Jaramillo-Cano, M. Formanek, C. N. Likos and M. Camargo, J. Phys. Chem. B, 2018, 122, 4149–4158 CrossRef CAS.
- J. S. Hur, E. S. G. Shaqfeh, H. P. Babcock, D. E. Smith and S. Chu, J. Rheol., 2001, 45, 421–450 CrossRef CAS.
- S. Pan, D. A. Nguyen, B. Dünweg, P. Sunthar, T. Sridhar and J. R. Prakash, J. Rheol., 2018, 62, 845–867 CrossRef CAS.
- J. R. Prakash, Curr. Opin. Colloid Interface Sci., 2019, 43, 63–79 CrossRef CAS.
- C. Stoltz, J. J. de Pablo and M. D. Graham, J. Rheol., 2006, 50, 137–167 CrossRef CAS.
- C.-C. Huang, R. G. Winkler, G. Sutmann and G. Gompper, Macromolecules, 2010, 43, 10107–10116 CrossRef CAS.
- C.-C. Huang, G. Sutmann, G. Gompper and R. G. Winkler, EPL, 2011, 93, 54004 CrossRef.
- C.-C. Huang, G. Gompper and R. G. Winkler, J. Phys.: Condens. Matter, 2012, 24, 284131 CrossRef.
- J. S. Myung, R. G. Winkler and G. Gompper, J. Chem. Phys., 2015, 143, 243117 CrossRef.
- D. A. Fedosov, S. P. Singh, A. Chatterji, R. G. Winkler and G. Gompper, Soft Matter, 2012, 8, 4109–4120 RSC.
- S. P. Singh, A. Chatterji, G. Gompper and R. G. Winkler, Macromolecules, 2013, 46, 8026–8036 CrossRef CAS.
- E. Moghimi, I. Chubak, A. Statt, M. P. Howard, D. Founta, G. Polymeropoulos, K. Ntetsikas, N. Hadjichristidis, A. Z. Panagiotopoulos, C. N. Likos and D. Vlassopoulos, ACS Macro Lett., 2019, 8, 766–772 CrossRef CAS.
- D. Jaramillo-Cano, M. Camargo, C. N. Likos and I. C. Garlea, Macromolecules, 2020, 53, 10015–10027 CrossRef CAS.
- M. Liebetreu and C. N. Likos, ACS Appl. Polym. Mater., 2020, 2, 3505–3517 CrossRef CAS.
- M. Liebetreu and C. N. Likos, Soft Matter, 2020, 16, 8710–8719 RSC.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- A. Lees and S. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921 CrossRef.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS.
- We use this definition instead of the standard ρ* = N[(4πRg)3/3]−1 because its value is closer to the inflection point in the concentration dependence of the equilibrium radius of gyration (ref. 24).
- R. Everaers, S. K. Sukumaran, G. S. Grest, C. Svaneborg, A. Sivasubramanian and K. Kremer, Science, 2004, 303, 823–826 CrossRef CAS.
- R. S. Hoy, K. Foteinopoulou and M. Kröger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 031803 CrossRef.
- A. Arbe, J. Rubio-Cervilla, A. Alegría, A. J. Moreno, J. A. Pomposo, B. Robles-Hernández, P. Malo de Molina, P. Fouquet, F. Juranyi and J. Colmenero, Macromolecules, 2019, 52, 6935–6942 CrossRef CAS.
- S. I. Dalal, A. Albaugh, N. Hoda and R. G. Larson, Macromolecules, 2012, 45, 9493–9499 CrossRef.
- P. S. Lang, B. Obermayer and E. Frey, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022606 CrossRef.
- J. Bossart and H. C. Oettinger, Macromolecules, 1995, 28, 5852–5860 CrossRef CAS.
- K. Mussawisade, M. Ripoll, R. G. Winkler and G. Gompper, J. Chem. Phys., 2005, 123, 144905 CrossRef CAS.
- R. Bird, C. Curtiss, R. Armstrong and O. Hassager, Dynamics of Polymer Liquids Vol. 2 Kinetic Theory, Wiley, 1987 Search PubMed.
- G. Gompper, T. Ihle, D. M. Kroll and R. G. Winkler, Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids, Springer Berlin Heidelberg, Berlin, Heidelberg, 2009, pp. 1–87 Search PubMed.
- The experiments in DNA solutions of ref. 41 are consistent with the simulations of ref. 44 and 45, which reveal a scaling behaviour of the polymer viscosity with the Weissenberg number ηp ∼ Wi−x that is at most marginally dependent on the concentration, showing a value x ≈ 0.5 from high dilution up to 10 times the overlap concentration. Recent experiments in other DNA solutions (see ref. 42) apparently contradict the simulation and experimental results of the mentioned references, reporting scaling exponents x that are strongly dependent on the concentration, changing from x ∼ 0.3 at dilute conditions to an apparent saturation at x ≈ 0.5 for concentrations far above the overlap density. Ref. 42 also includes results for polystyrene solutions, showing much lower exponents in the range x ∼ 0.05–0.2. In our view the exponents found in the analysis of the data of ref. 42 should be taken with caution. In the simulations of ref. 45 and experiments of ref. 41 the scaling regime with exponent x ≈ 0.5 starts at high Weissenberg numbers Wi ≳ 100 for which the normalized viscosity
![[small eta, Greek, macron]](https://www.rsc.org/images/entities/char_e0c8.gif) = ηp(ρ)/ηp(ρ= 0) has decayed to values
= ηp(ρ)/ηp(ρ= 0) has decayed to values ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) ≲ 0.2. After the low- Wi plateau
≲ 0.2. After the low- Wi plateau ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) ≲ 1 and before the onset of the x ≈ 0.5-regime there is a smooth crossover at intermediate Wi that can be effectively described with much lower exponents (see ref. 45). Close inspection of the data of ref. 42 shows that in the DNA solutions values
≲ 1 and before the onset of the x ≈ 0.5-regime there is a smooth crossover at intermediate Wi that can be effectively described with much lower exponents (see ref. 45). Close inspection of the data of ref. 42 shows that in the DNA solutions values ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) < 0.2 and Wi > 100 are only reported at the highest concentrations, fow which exponents x ≈ 0.5 consistent with the simulations and former experiments are indeed found. In the polystyrene solutions measurements are performed at Wi < 30 and the observed maximum decay is just
< 0.2 and Wi > 100 are only reported at the highest concentrations, fow which exponents x ≈ 0.5 consistent with the simulations and former experiments are indeed found. In the polystyrene solutions measurements are performed at Wi < 30 and the observed maximum decay is just ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) ∼ 0.7. Therefore, it might be that most of the exponents reported in ref. 42 actually correspond to the crossover regime at intermediate Wi, and there is no real contradiction with the findings of ref. 41, 44 and 45.
∼ 0.7. Therefore, it might be that most of the exponents reported in ref. 42 actually correspond to the crossover regime at intermediate Wi, and there is no real contradiction with the findings of ref. 41, 44 and 45. - I. B. Bekard, P. Asimakis, J. Bertolini and D. E. Dunstan, Biopolymers, 2011, 95, 733–745 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01978j |
| This journal is © The Royal Society of Chemistry 2021 |