How a water drop removes a particle from a hydrophobic surface

Abstract

To understand the removal of particles from surfaces by water drops, we used an inverted laser scanning confocal microscope to image the collision between a water drop and a particle on a flat polydimethylsiloxane (PDMS) surface. The dynamic drop–particle contact line was monitored by fixing the drop directly above the objective lens while moving the sample stage at well-defined speeds (10–500 μm s⁻¹). The lateral force acting on the drop during the collision was measured as a function of speed, using a force sensor mounted on the microscope. Depending on the collision speed, the particle either stays attached at the rear of the drop or detaches from it. We propose a criterion to determine whether the particle remains attached to the drop based on the capillary and resistive forces acting on the particle during the collision. The forces measured when the particle crosses the air–water interface are compared to existing models. We adapted these to account for rolling of the particle. By comparing our experimental measurements with an analytical model for the capillary torque acting on a particle rolling at an interface, we provide detailed insights on the origins of the resistive force acting on the particle when it is pushed or pulled by the drop. A low friction force between the surface and the particle increases the likelihood of particle removal.

---

1 Introduction

Dust particles adhere to surfaces, such as windows, leaves and solar panels. Outdoors, there is a chance that these surfaces get cleaned when dew, fog or raindrops move over the surface and collide with the particles.^1–5 But how and when does a drop remove a particle? The mechanism is still poorly understood. In particular, it is unclear which forces are involved when a moving drop hits a single particle and how the drop deforms during the collision. A better understanding of this process is not only of fundamental interest but also guides the design of self-cleaning surfaces.

The collision of liquid–air interfaces with a large number of particles has been monitored on various surfaces, using optical or fluorescence microscopy.^6–11 On superhydrophobic surfaces, particles are lifted and removed at the receding side of the rolling drop.¹² However, in all previous studies, the focus was on using a large number of particles and on describing averages. Results were expressed in terms of the removal efficiency or the average friction force due to multiple particles. There are no studies that focus on an individual particle. Therefore, it is not clear why some particles are usually left behind, despite having similar sizes and surface chemistry as the ones that are removed. To study this problem, we used an inverted laser scanning confocal microscope to image the process with microscopic resolution (1 μm or better) and to measure lateral forces (resolution ≈200 nN) in situ [Fig. 1(a)]. Measuring the forces acting on a particle allows us to test existing models quantitatively. We performed force measurements by using a force sensor to fix the drop above the objective lens whilst moving the sample stage at well-defined speeds. This method allows us to dynamically monitor the collision between a drop and a particle. The technique can also be used to study a wide range of problems where the combination of microscopic imaging with lateral force measurements is desirable.

Fig. 1 Experimental setup and possible collision outcomes. (a) Experimental setup to image the collision and to measure lateral forces using a confocal microscope. The surface moves to the right, while the drop's (blue) position is fixed by the blade (grey). (b) Possible outcomes of a head-on collision (bottom view). The red arrows indicate the direction of motion of the particle. F^push_γ (F^pull_γ) is the maximum capillary force that the air–water interface exerts on the particle when the latter is to the left (right) of the drop. F^push_R (F^pull_R) is the resistive force acting on the particle when it is pushed (pulled) by the drop.

A particle in contact with a surface experiences adhesion forces such as the van der Waals force,^13,14 and capillary forces when in a humid environment.^15–17 Due to the finite elasticity of materials, these adhesion forces deform the contacting bodies.¹⁸ The normal adhesion force and the resulting deformation influence the lateral friction force when the particle moves relative to the surface.^19,20 Furthermore, the friction force depends on whether the particle rolls or slides. All these forces must be considered together with the capillary force between drop and particle to predict particle removal. Providing a general prediction for whether a particular liquid can remove a specific type of particle is a complex problem combining expertise in tribology, surface forces, and capillary interactions. For example, a hydrophilic particle is more strongly attracted to water compared to a hydrophobic particle. However, this property alone is insufficient to predict which particle is more likely to be removed by a drop since the shape and hydrophobicity of the particle also influences the adhesion force between the particle and the surface. Here, we focus on a system comprising of a flat polydimethylsiloxane (PDMS) surface, a spherical glass particle, and water.

Although PDMS is a widely used material, it should be noted that crosslinked PDMS contains a small fraction of uncrosslinked chains (≈5% for Sylgard 184).²¹ When a water drop moves on a PDMS surface, the air–water interface accumulates uncrosslinked PDMS to minimise its surface tension.²² When drops are covered by a thin layer of an immiscible liquid, they are referred to as being ‘cloaked’. Since surface tension influences the capillary force that a drop exerts on a particle, we quantified the surface tension of a cloaked drop by performing a pendant drop experiment directly on a PDMS substrate.

The possible outcomes of a head-on collision between a particle moving to the right and a stationary drop, both lying on a PDMS surface, are summarised in [Fig. 1(b)]. When the particle hits the air–water interface, it either remains attached to it or enters the drop. If it enters, it moves through the drop, reaching the rear side. There, it either stays attached to the interface or exits the drop. We observed that the particle rolled when pulled by the drop. We discuss the implications of rolling on the capillary and friction forces. Due to contact angle hysteresis, the maximum capillary force acting on a rolling particle is lower than on a sliding particle. Analytical expressions for the maximum capillary forces acting on a rolling particle when it crosses the interface are provided and compared with experimental results. The experimentally measured forces were around 50% lower than the forces predicted by existing models⁶ (ignoring rolling) and our proposed model. When a particle rolls at an interface, it experiences a resistive capillary torque. We derived an expression to estimate the magnitude of this resistive torque and show that it is a significant contribution to the resistive force experienced by a particle when it is pushed or pulled by a water drop.

2 Materials and methods

2.1 Substrate

Glass slides (thickness 270 μm) were coated with polydimethylsiloxane (PDMS) (thickness ≈ 50 μm). We prepared the PDMS layer by mixing Sylgard 184 (10 parts base to 1 part crosslinker) in a glass vial and degassed the mixture under vacuum for 10 minutes. Meanwhile, glass slides were cleaned with ethanol, dried in a nitrogen stream, and placed in an oxygen plasma oven (300 W, 0.4 bar) for 5 minutes. Then, the Sylgard 184 mixture was spin-coated onto the glass slides at 1000 rpm for 60 s. The coated surfaces were cured in an oven at 60 °C for 15 hours. The contact angle of water on the resulting surfaces was between 80° and 120°.²¹

2.2 Particles

Glass particles (Polysciences Europe GmbH) with radii between 115 μm and 182 μm were used. The particles were spherical, with some having occasional defects. The contact angle of water on the particle was imaged using laser scanning confocal microscopy.

2.3 Drops

We used ultra-pure (Milli-Q) water with volumes between 3 μL and 10 μL. The drop volume was chosen such that the force exerted by the particle on the drop during the collision was clearly visible when plotted on the same scale as the force required to push the drop alone.

2.4 Laser scanning confocal microscope

The drop–particle collisions were imaged with an inverted laser scanning confocal microscope (Leica TCS SP8) using a Leica HC PL APO CS 10×/0.40 objective lens. To image the drop in fluorescence mode, we used water containing a fluorescent dye (ATTO 488). The focus was in a horizontal plane going across the centre of the particle, and imaging was done in transmission, fluorescent and reflection modes simultaneously. The final image was constructed by overlaying all three channels. The collision of the drop with the particle was initiated by moving the surface to the right at a constant speed while keeping the drop's position fixed by the blade [Fig. 1(a)]. To control the motion of the sample stage, a program was written in LabVIEW. Since the objective lens is fixed and has a limited field of view, moving the surface instead of the drop is advantageous as it allows us to continuously image the drop throughout the collision over a range of speeds (10 to 500 μm s⁻¹).

We measured lateral forces on the same setup by mounting a metal blade on the microscope. The metal blade (Orion stainless steel feeler gauge tape, ≈3 mm wide, 40–70 μm thick, 5–10 cm long) was clamped at the top and the focal plane was set at the lower edge of the blade. A laser beam was incident on lower edge, and the reflected light was captured by the objective lens. When a drop presses against the blade with a time-dependent force F(t), the resulting deflection Δx(t) is given by Hooke's law F(t) = kΔx(t), where k is the spring constant of the blade. The spring constant was determined by gently deflecting the blade, releasing it, and measuring the natural angular frequency of the resulting oscillations, ω. The angular frequency was then inserted into the relation k = 0.243mω², where m is the mass of the freely hanging blade.²³ The pre-factor accounts for the uniform mass distribution of the blade. The blade dimensions were chosen such that the deflection could be clearly imaged while staying within the maximum measurable range at all times. The noise level due to ambient vibrations was below 200 nN, which was negligible compared to fluctuations due to surface inhomogeneities (≈2 μN) (ESI,† Fig. S1). The time resolution was 5 ms or better. The main difference between our setup and previous ones^24–26 is that we measure the deflection using a commercial laser scanning confocal microscope rather than using a separate camera^25,26 or a home-built laser system.²⁴ Performing the force measurements directly on the microscope enables us to image the drop with micrometre resolution and to measure the corresponding forces along the same track on the surface.

2.5 Imaging cloaked drops

A drop (diameter ≈ 500 μm) was placed on fluorescent PDMS and imaged using laser scanning confocal microscopy. Fluorescent dye (absorption wavelength 663 nm, emission wavelength 712 nm) was added to the PDMS when mixing the Sylgard 184 mixture. The drop consisted of 57% water (containing ATTO 488) and 43% glycerol. Glycerol was added to suppress evaporation and to match the refractive index between the drop (1.41) and PDMS (1.41). The image was taken 30 minutes after placing the drop on the surface. Evaporation was insignificant over the waiting period.

2.6 Measurement of the interfacial tension of cloaked drops

Holes of diameter 2 mm were drilled into a glass slide, which was then coated with PDMS. We added 25% of PDMS lubricant (tri-methylsiloxyl terminated, molecular weight 14 000 g mol^-1, density 970 kg m⁻³) to the Sylgard 184 PDMS when stirring the base and the crosslinker in order to speed up the cloaking process. The surface was positioned with the PDMS-coated side facing down. The following steps were automated using on a Krüss Drop Shape Analyzer (DSA100). A syringe tip (outer diameter 1.8 mm) was lowered into the hole until it was a few millimetres below the PDMS surface. A 25 μL drop of ultra-pure water (Milli-Q) was dosed and held by the syringe tip. After waiting for 10 s for vibrations from the dosing process to subside, the syringe was moved upwards until the drop came into contact with the surface and the three-phase contact line was pinned by the hole. Then, the surface tension measurement was initiated and the drop volume was increased to 38 μL at 5 μL s⁻¹. The drop volume was increased to 38 μL since larger drops lead to more precise surface tension measurements using the pendant drop method.

3 Results and discussion

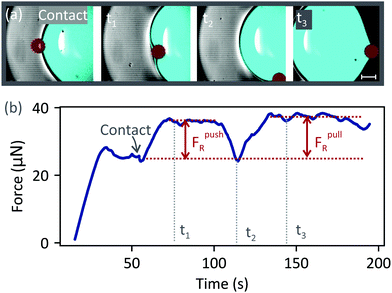
To characterise the PDMS surface, we measured the force required to move a water drop (volume 3 μL) relative to the surface at 500 μm s⁻¹ (without a particle). The force needed to repeatedly move the drop along the same track was highly reproducible, demonstrating that the noise level was negligible. Fluctuations due to surface inhomogeneities were around 5% (ESI,† Fig. S1). As the drop moved over the surface, the air–water interface accumulated uncrosslinked PDMS chains.²² We confirmed the presence of a PDMS layer around the drop by imaging the drop–air interface using confocal microscopy [Fig. 2(a)]. A fluorescent glycerol–water drop (cyan) was placed on a PDMS substrate containing a different fluorescent dye (yellow). Glycerol was added to the drop to match the refractive index between PDMS and the drop, and to suppress evaporation. The drop's apex was imaged after 30 minutes, and a PDMS layer was observed around the drop. To measure the surface tension, γ, of water cloaked with PDMS, we suspended a pure water drop from a PDMS surface [Fig. 2(b)]. Initially, the surface tension was 72 mN m⁻¹, which corresponds to the value expected for pure water. Then, the surface tension decreased and plateaued at 64 mN m⁻¹ after around 200 s. Thus, the surface tension of a cloaked drop is 64 mN m⁻¹. To speed up the cloaking process, PDMS lubricant was added to the Sylgard 184 mixture prior to cross-linking. Without added lubricant, cloaking takes longer than 25 minutes and drop evaporation becomes significant. However, the drop should eventually have the same final surface tension (64 mN m⁻¹) due to the uncrosslinked PDMS chains. A moving drop, however, accumulates PDMS much faster²² than a suspended drop as it rolls into contact with the surface. In all the experiments described below, PDMS surfaces without added lubricant were used. All drops were rolled on the surface for a few millimetres before the collision to ensure that their surface tension was constant during the collision. Therefore, throughout this paper, we use γ = 64 mN m⁻¹ as the surface tension of the drop–air interface.

Fig. 2 Cloaking. (a) PDMS cloak (yellow) covering a drop (cyan, 57% water, 43% glycerol). Flourescent dye was added to Sylgard 184 PDMS mixture prior to cross-linking. The three-dimensional image above the schematic was taken with confocal microscopy 30 minutes after the drop was placed on the substrate. Only the top part of the drop is shown, as highlighted by the white dotted rectangle in the schematic. (b) Change in the surface tension of a water drop suspended from a PDMS surface as shown the inset. To speed up cloaking, 25% of PDMS lubricant was added to the Sylgard 184 mixture, prior to cross-linking.

Next, we describe the drop–particle collision experiments. A particle (radius 115 μm) was placed a few millimetres in front of the drop on the substrate. Then, the substrate was moved while keeping the drop fixed. We first consider the case when the particle stayed attached to the drop–air interface [50 μm s⁻¹, Fig. 3(a), Video 1, ESI†]. Before the collision, the force increased until it reached a steady value at ≈ 30 s [Fig. 3(b)]. The plateau between 30 s and 55 s corresponds to the friction force between the drop and the surface.^24,27 At ≈55 s the particle (dark red) made contact with the drop (cyan) and a water meniscus formed around the particle. The action of capillary force acting at the three-phase contact line is seen as a small dip, labelled ‘contact’. Subsequently, the force increased due to resistive forces (F^push_R = 10 ± 1 μN) acting on the particle when it was in front of the drop. The plateau between contact and t₂ corresponds to the force required to push the particle [Fig. 3, t₁]. However, this configuration is unstable due to the convex curvature of the meniscus around the particle. Any deviation from a head-on collision axis will result in an asymmetry in the capillary force, causing the particle to move sideways. Experimentally, even when a perfect head-on collision is achieved, an asymmetry arises when the particle moves over a surface inhomogeneity. Therefore, the particle moved around the drop's base. At t₂, the particle was at the lateral side of the drop. The force decreased to the same value as before the collision since, in this position, the capillary force has no component acting along the x-axis [defined in Fig. 1(a)]. After t₂, the particle was at the rear side of the drop. The particle stayed attached to the drop, while the surface continued to move at 50 μm s⁻¹ [Fig. 3, t₃]. The force required to pull the particle was F^pull_R = 12 ± 2 μN.

Fig. 3 Drop–particle collision on a PDMS surface at 50 μm s⁻¹. (a) A collision between a drop (cyan; 3 μL dyed with ATTO 488) and a glass particle (radius 115 μm, dark red). The focus was in a horizontal plane going through the centre of the particle. Scale bar: 250 μm. (b) Lateral force acting on the drop before and during the collision. F^push_R (F^pull_R) is the resistive force acting on the particle when it is pushed (pulled) by the drop.

To determine whether the particle rolled or slid over the surface, we zoomed into a particle (radius R = 125 μm) that had microscopic defects while it was pulled by a drop [Fig. 4(a), Video 2, ESI†]. The time taken for the defects to perform a complete revolution was 16 s. 16 s corresponds to the time period of rolling (2πR/v, where v is the speed of the surface), assuming that the particle rolls at the same speed as the surface. Therefore, we conclude that the particle was rolling on the surface without any noticeable slip. The defects caused the particle to roll unevenly, resulting in a periodic motion of the water–air–particle contact line. We tracked the contact angle, Θ, of water on the particle and the position, x_CL, of the contact line along the x-axis, relative to the centre of the particle [Fig. 4(b)]. Each data point for Θ and x_CL corresponds to an average value of the upper and lower contact points [two green dots in Fig. 4(a), middle column]. Both the contact line position and the contact angle oscillated with a time period equal to that of rolling (16 s). The advancing angle refers to the maximum angle (Θ_A ≈ 100°) when the contact line advanced [positive gradient of x_CL in Fig. 4(b)] on the particle. The receding angle refers to the minimum angle (Θ_R ≈ 75°) when the contact line receded on the particle. The contact angles are higher than what would typically be expected for water on glass because uncrosslinked PDMS molecules from the flat substrate adhere to silica, lowering the surface energy of the particle.²⁸

Fig. 4 Water drop pulling a particle (radius 125 μm) with defects. (a) The highlighted defects appear in focus every 16 s. The green dots in the middle image highlight the position of the contact line of diameter L. Θ is the contact angle and β is the angle between the drop–air interface and the x-axis. (b) Position of the contact line (x_CL) and contact angle (Θ) as a function of time. x_CL is defined relative to the centre of the particle. Both Θ and x_CL are averages of the values measured at the two green dots in (a). (c) Capillary force acting on the particle, calculated from the image series (Video 2, ESI†) in (a), using eqn (1). The points were averaged every 0.8 s.

We estimated the component of the capillary force pulling the particle horizontally along x from the image series shown in Fig. 4(a). The net capillary force, F⃑_γ, is obtained by integrating the surface tension vector around the contact line, which we assume to be a circle of diameter L [Fig. 4(a)]. Furthermore, we assume a constant contact angle around the contact line. Due to symmetry about the xz plane, the force components along the y-axis cancel, leaving only the components parallel to the xz plane, 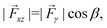where β is the angle between the surface tension vector and the x-axis [defined in Fig. 4(a)]. The x-component of the force is obtained by taking the projection of F⃑_xz along x,

F_x = |F⃑_xz|sin A = πLγ cos β sin A, (1)

where πL is the circumference of the contact line, A is the angle between the flat substrate and the plane containing the contact line, and γ is the magnitude of the surface tension vector. F_x is plotted as a function of time in Fig. 4(c) (refer to Video 2 for a live plot, ESI†). In Fig. 4(c), we used A ≈ 40°. This approximation was obtained by imaging the water meniscus around a particle in contact with a static drop, in three-dimensions [Fig. 5(a)]. The shape of the three-phase contact line around the bottom half of the particle was circular (radius 117 μm), and the angle between the contact line and the substrate was A ≈ 40° [Fig. 5(b) and (c)]. Therefore, the horizontal component of the capillary force is obtained by multiplying the |F⃑_xz| by sin 40°. In general, however, we expect the shape of the water meniscus surrounding the particle to change with speed and therefore expect A to deviate from 40° when the surface moves. Nevertheless, the average force calculated using eqn (1) [15 μN, Fig. 4(c)] shows good agreement with the force measured with the blade [F^pull_R = 12 ± 2 μN, Fig. 3(b)].

Fig. 5 Water meniscus around a particle. (a) Three-dimensional confocal image of the water meniscus (cyan) surrounding a stationary particle (not drawn) of radius 125 μm. Note that above the particle's centre, the image is subject to an optical artefact since the particle obstructs fluorescent light emitted by the drop. Therefore, the shape of the meniscus is only accurate below the red dots (drawn). (b) Shape of the lower half of the three-phase contact line around the particle, extracted from (a). (c) Schematic side view showing the capillary force and its horizontal projection.

When the collision was performed at 500 μm s⁻¹, the particle entered and exited the drop [Fig. 6(a), Video 3, ESI†]. The particle fully crossed the front drop–air interface and the force reached a maximum of F^push_γ = 16 μN [Fig. 6(b)]. The force decreased when the particle was inside the drop [Fig. 6(b), t₂], suggesting that viscous drag is negligible. The viscous drag is given by F_drag = 1.7 × 6πηR²(dτ/dt),²⁹ where η is the dynamic viscosity of water and R is the particle's radius. dτ/dt ≈ v_D/H is the shear rate of the flow, where v_D is the speed of the drop relative to the surface and H is the drop's height. F_drag is of the order of 10⁻⁹ N – negligible compared to the capillary force. Consequently, a particle that crosses the front side of the drop will easily move through the drop, reaching the rear interface. The particle detached from the drop just after t₃ [Fig. 6(b)], exerting a maximum force of F^pull_γ = 13 μN.

Fig. 6 Drop–particle collision on a PDMS surface at 500 μm s⁻¹. (a) Collision between a drop (cyan, 3 μL dyed with ATTO 488) and a particle (radius 115 μm, dark red). The focus was on a horizontal plane through the particle's centre. (b) Lateral force acting on the drop. The particle was initially 1.2 cm away from the drop and collided with the drop at ≈23 s.

3.1 Criterion for particle removal

For a particle to remain attached to a drop–air interface, it has to slide or roll over the substrate such that its centre of mass is at rest relative to the drop. When the particle moves relative to the surface, it experiences resistive forces F_R. The particle stays attached to the drop when

F^max_γ ≥ F_R, (2)

where F^max_γ is the maximum capillary force that the drop–air interface can exert on the particle. We will refer to F^max_γ as F^push_γ (F^pull_γ) when the particle is attached to the air–water interface at the front (rear) side of the drop since capillary force acts to push (pull) the particle out of (into) the drop.

3.2 Maximum capillary forces

To estimate F^max_γ, we first consider a spherical particle going through an air–water interface perpendicularly, neglecting the PDMS substrate. F^max_γ depends on whether the particle rolls or slides, the contact line geometry, and the contact angle Θ between the particle and water. For a perfectly smooth and homogeneous particle, Θ has a unique value given by Young's law cos Θ = (γ_SA − γ_SD)/γ, where γ_SA, γ_SD and γ are the solid–air, solid–drop and drop–air interfacial tensions, respectively.³⁰ However, for real materials, the contact angle lies between the advancing and receding angles (Θ_R ≤ Θ ≤ Θ_A). When a particle moves from the air phase into the water phase, the contact angle of water on the particle corresponds to the advancing angle Θ_A. The maximum force F^push_γ acting on a non-rolling particle during entry is^31,32where R is the particle's radius and γ is the surface tension of the interface. When the particle is pulled away from the water phase, the corresponding maximum capillary force is^31,33

However, when the particle is slowly pushed across an air–water interface while rolling, half of it moves out of the water (receding) while the other half moves into water (advancing). The three-phase contact line on the rotating particle is divided into two regions: one having a contact angle of Θ_R and the other, an angle of Θ_A. Below we derive expressions for the maximum capillary forces on a rolling particle. When a particle is pushed across a horizontal air–water interface, the vertical component of surface tension (along +z) acting on the particle is

Here, γ is the air–water surface tension, R is the radius of the particle, α is the azimuthal angle in the xy plane, and φ is the angle between the xy plane and a line joining the three-phase contact line to the centre of the particle [Fig. 7 (a)]. φ is defined to be positive (negative) above (below) the xy plane. In general, for a rotating particle, φ and Θ are functions of α due to contact angle hysteresis. To evaluate eqn (5), we introduce a simplifying approximation by splitting the contact-line into two separate regions. On the right of the rotational axis (0 < α < π), Θ = Θ_R and φ = φ_R. On the left (π < α < 2π), Θ = Θ_A and φ = −φ_A. eqn (5) then evaluates to

F_γ = −πγR[cos(Θ_R + φ_R)cosφ_R+ cos(−Θ_A + φ_A)cosφ_A]. (6)

Fig. 7 Maximum force acting on a particle (Θ_A = 100° and Θ_R = 75°) as it enters and exits a drop. (a) Schematic of a particle rolling at an air–water interface. (b) Maximum force measured on a 182 μm particle during entry (red squares) and exit (blue circles) at 500 μm s⁻¹. The error bars correspond to the standard deviations of the drop friction due to surface inhomogeneities. The solid horizontal lines correspond to the predicted maximum capillary force on a sliding particle [eqn (3) (red) and eqn (4) (blue)]. The broken lines correspond to a rolling particle [eqn (11) (red) and eqn (12) (blue)].

To find the maximum force, we first write the differential of F:

= πγR[sin(φ_A − Θ_A)cosφ_A+ cos(φ_A − Θ_A)sinφ_A]dφ_A (8)

+ πγR[sin(φ_R + Θ_R)cos φ_R + cos(φ_R + Θ_R)sin φ_R]dφ_R.

Assuming that φ_A and φ_R are independent, dF is zero when φ_A = Θ_A/2 + nπ/2 and φ_R = −Θ_R/2 + mπ/2, where n = −1 or 0, and m = 0 or 1 such that −π/2 ≤ φ_A ≤ π/2 and −π/2 ≤ φ_R ≤ π/2, respectively. To determine whether these solutions correspond to a minimum (downward capillary force pulling particle towards liquid) or a maximum (upward capillary force pushing particle out of liquid), we calculate the second derivatives of F:

Therefore, φ_A = Θ_A/2 corresponds to a minimum and φ_A = Θ_A/2 − π/2 to a maximum. Similarly, we find that φ_R = −Θ_R/2 corresponds to a minimum whereas φ_R = −Θ_R/2 + π/2 corresponds to a maximum. By substituting φ_A = (Θ_A − π)/2 and φ_R = (−Θ_R + π)/2 in eqn (6), we obtain the maximum upwards capillary force acting on a rolling particle when it is pushed across the interface:

To obtain the maximum downwards capillary force that the air–water interface exerts on the particle when the latter is pulled away from the water phase, we substitute φ_A = Θ_A/2 and φ_R = −Θ_R/2 in eqn (6):

Since Θ_R < Θ_A, the maximum capillary force for a rolling particle (eqn (11) and (12)) is lower than that for a non-rolling particle (eqn (3) and (4)). We expect the contact line approximation used here to be valid for small contact angle hysteresis (Θ_A − Θ_R ≈ 25° for our case). For large differences between Θ_A and Θ_R, the assumption about φ_A and φ_R being independent will no longer be valid. An exact calculation of the maximum capillary force requires precise knowledge of the contact line geometry, in particular how φ and Θ vary around the contact line.

Fig. 7(b) compares the predicted maximum forces to the maximum forces measured when a particle entered (red squares) and exited (blue circles) a drop. The solid lines correspond to a sliding particle [eqn (3) (red) and eqn (4) (blue)], and the broken lines correspond to a rolling particle [eqn (11) (red) and eqn (12) (blue)]. All the experiments were performed at 500 μm s⁻¹ on the same track and with the same particle. The particle (radius 182 μm) and the drop (volume 8–10 μL) were carefully aligned such that they collided head-on. The predictions are around two times larger than the measured forces. This discrepancy is likely because eqn (3), (4), (11) and (12) assume that the angle, A [Fig. 5(c)], between the substrate and the water–air–particle contact line is 90°. However, in general, A differs from 90° [Fig. 5(b)]. Since the measurements only capture the horizontal component of the capillary force, the predictions provided by eqn (3), (4), (11) and (12) are indeed expected to be higher. To reconcile the predicted forces with the measured forces, only the horizontal projection of the predicted force has to be considered when calculating the maximum force. Therefore, |F⃑_γ|sin A has to be maximised. An expression for the maximum horizontal component of the capillary force (ignoring rolling) has been proposed.^6,8 It was suggested that eqn (4) should be multiplied by sin Θ_S, where Θ_S is the contact angle between the drop and the flat substrate (80° in our case, at the rear side). However, our experiments demonstrate that this correction still overestimates the exit force since Θ_S is, in general, not equal to A (40° in Fig. 5).

3.3 Resistive forces

In this section, we provide insights on the physical origins of the resistive force, F_R, experienced by a rolling particle when it is attached to the drop–air interface and is pushed or pulled by the drop. First, there is a contribution due to the friction force, F_S (‘S’ for surface), experienced by the particle as it rolls over the surface. F_S originates from viscoelastic dissipation in the elastomeric substrate and from molecular attraction forces between the particle and the substrate.^34–36 As the particle rolls, the energy required to peel the rear contact is greater than the energy recovered when closing the front contact, thus giving rise to a rolling resistance.³⁴ To determine F_S, we measured the force to push a particle (radius 182 μm) by the blade (without the drop) on the surface at various speeds [Fig. 8(a)]. F_S increased with speed, at a decreasing rate. During these experiments, the particle rolled on the PDMS substrate while sliding relative to the blade. Thus, the measured force is influenced by friction between the blade and the particle. However, we expect the friction contribution due to the blade to only be ≈10% of the measured F_S since the coefficient of sliding friction between PDMS-coated stainless steel (blade) and PDMS-coated glass (particle) is low (≈0.1³⁷). The blade accumulated PDMS when it pushed cloaked drops and the particle accumulated PDMS as it rolled over the substrate.

Fig. 8 Contributions to the resistive force. (a) Force required to push a particle on a dry PDMS surface at different speeds. Error bars correspond to the standard deviation of the measurements due to surface inhomogeneities. (b) Calculated resistive force due to contact angle hysteresis on a particle (radius 182 mm) rolling at an air–water interface. The inset shows the shape of the assumed contact line.

Second, there is a viscous contribution as particle rolls at the interface while being partially submerged in the drop. However, viscous effects turn out to be negligible compared to capillary forces due to the small capillary number, Ca = ηv/γ ≈ 10⁻⁵ ≪ 1, where η is the dynamic viscosity of water, v is the rolling speed of the particle, and γ is the surface tension of the drop. Assuming a Stoke's drag, we obtain a viscous force 6πηRv ≈ 10⁻⁸ N.

A third contribution to the resistive force is due to capillary torque (M_ΔΘ, the subscript stands for ‘contact angle hysteresis’) opposing rolling at the drop–air interface. To understand the origins of M_ΔΘ, consider a cylinder (radius R) quasi-statically spinning counter-clockwise about its equilibrium position at a horizontal air–water interface. Due to contact angle hysteresis, the right side will make an angle Θ_R with the interface, whereas the left side, an angle Θ_A [Fig. 8(b), inset]. This asymmetry gives rise to a resistive torque γR(cos Θ_R − cos Θ_A) per unit length of the cylinder, about the central axis. For a sphere, we obtain the total torque by integrating over the contact line:

where r⃑ is the perpendicular vector from the rotational axis to the surface tension vector , × denotes the vector cross product, and the contour integral is around the contact line (CL). To obtain an analytical estimate of the above integral, we assume a circular contact line of radius R whose centre coincides with the centre of the particle, as drawn in the inset of Fig. 8(b). The surface tension vector acts at a perpendicular distance R sin α from the rotational axis, where α is the azimuthal angle in the xy plane about the centre of the particle. The force acting on an infinitesimal contact line element of length Rdα is . Only the tangential component, , where Θ = Θ_R (right) and Θ_A (left), produces a net moment about the rotational axis. The normal component produces no moment since the surface tension vector is symmetric about the yz plane. Therefore, the net moment acting on the particle has a magnitude

= 2γR²(cos Θ_R − cos Θ_A). (15)

Here, R is the radius of the particle, α is the azimuthal angle [Fig. 7(a)], and Θ_R and Θ_A are the receding and advancing angles of water on the particle. The tangential force corresponding to this torque is

F_ΔΘ = 2γR(cos Θ_R − cos Θ_A). (16)

For a particle of radius 182 μm with a contact angle hysteresis of 25°, F_ΔΘ ≈ 10 μN [Fig. 8(b)]. Note that, eqn (16) is valid when the contact line radius is equal to the particle radius. For our case, this approximation is valid when the particle (mean contact angle ≈90°) rotates about its equilibrium position such that half is in water and the other half in air. Fig. 9 compares F_S + F_ΔΘ (red line and circles) to the measured values of F_R when a particle (radius 182 μm) was pushed (orange triangles) or pulled (blue squares) by a water drop. To ensure a systematic comparison, F_S, F^push_R and F_R^pull were measured along the same track on the substrate and with the same particle. There is good agreement between the sum of the two contributions and the measured F_R, particularly at low speeds. However, unlike F_S, F_R showed no clear dependence on speed. We speculate this is because F_ΔΘ decreases with speed and balances the increase in F_S such that their sum, F_R, is approximately constant. To understand why F_ΔΘ could decrease with speed, we consider a particle attached to the rear side of the drop. When the particle is in equilibrium at the drop–air interface, half of it will lie inside the water phase since the contact angle of water on the particle is approximately 90°. In this configuration, the contact line radius is equal to the radius of the particle and F_ΔΘ is given by eqn (16). However, when the particle moves with the drop, the net capillary force has a component pulling the particle to the drop. To produce this force, the contact line has to slide over the particle such that the net capillary force has a component pointing towards the drop, as in Fig. 5(c). As the contact line slides, the particle moves further out of the drop and the contact line radius decreases. Therefore, eqn (16) is no longer valid. Replacing the radius, R, in eqn (16) by a smaller effective radius, would lead to a smaller F_ΔΘ. Furthermore, it is likely that the angular tilt of the contact line [A in Fig. 5(c)] changes with speed, causing both the magnitude and the direction of the net capillary force vector to change with speed. Another important consideration is that when the particle is attached to the drop, F_S may no longer take the same values as measured in dry conditions [Fig. 8(a)]. The normal adhesion force between the particle and the surface will be influenced by the vertical component of capillary force acting at the air–water–particle contact line and by van der Waals forces which act through water instead of air. Since rolling friction on elastomers depends on the normal force,³⁴ it is likely that F_S will also change. Given all the complexity, it is indeed surprising that F_S + F_ΔΘ ≈ F_R [Fig. 9].

Fig. 9 Resistive force experienced by a particle (radius 182 μm) when it is pushed (orange triangles) or pulled (blue squares) by a water drop. The red line and circles were obtained by adding the two dominant resistive contributions, F_R and F_ΔΘ. Error bars correspond to the standard deviation of the measurements due to surface inhomogeneities.

4 Summary and conclusions

When a particle collides with a water drop on a PDMS surface, it either enters the drop (fast collision) or stays attached at the drop–air interface (slow collision). Intuitively, this may seem expected since a fast particle has a high kinetic energy and therefore interfacial forces have to do more work to stop the particle. However, balancing the kinetic and interfacial energies reveals that if a particle (radius 182 mm; average contact angle 90° with water) and a water drop collide in free space, the relative speed must be at least around a few centimetres per second for the particle to cross the drop–air interface. In contrast, on a hydrophobic (PDMS) surface, the minimum speed of entry is reduced by approximately two orders of magnitude (300 μm s⁻¹).

On PDMS, the particle remained attached to the drop–air interface for speeds <300 μm s⁻¹ and rolled without noticeable slip. When a particle is pushed or pulled by a water drop, it experiences resistive forces F_R. F_R has two main contributions. First, there is a friction force F_S due to rolling hysteresis between the particle and the substrate. The second contribution, F_ΔΘ, has capillary origins and is due to contact angle hysteresis at the air–water interface – an effect which has been overlooked so far. We provide an analytical expression to estimate F_ΔΘ and show that F_S + F_ΔΘ ≈ F_R, particularly at low speeds.

At high speeds, the particle entered and exited the drop. We measured the force that the particle exerted on the drop when it crossed the drop–air interface. The measured values were lower than predicted by existing models describing the attachment of a particle sliding (ignoring rolling) through an interface. We propose a model to account for rolling of the particle. The model predicts that a rolling particle experiences a smaller capillary force than a sliding particle when it crosses the interface. Accounting for rolling leads to a better agreement between the predicted and measured forces. However, the predicted forces remain too high, likely due to the angular tilt, A, of the air–water–particle contact line with respect to the substrate, which was assumed to be 90° in the models. Although we expect A to depend on the contact angle between the drop and the substrate, and the advancing and receding angles between the drop and the particle, it is not clear what the relationship between these quantities is. Additionally, A will depend on how the drop locally deforms as the particle crosses the interface.

Particle removal by water drops on hydrophobic surfaces is conceptually different to particle removal on superhydrophobic surfaces. On a hydrophobic (PDMS) surface, a water drop pulls a glass particle horizontally along the surface. In contrast, on superhydrophobic surfaces, particles are removed in the vertical direction due to the low normal adhesion between the particle and the surface.^8,12 Despite this difference, a unifying principle to enhance self-cleaning of both surfaces is to minimise the adhesion and friction forces between the particle and the surface.

Author contributions

D. V. and A. N. conceptualised the research. A. N., A. K. and D. V. designed the setup for measuring forces on the inverted confocal microscope. A. N. and W. S. Y. W. prepared the substrates. A. N. performed the experiments, analysed the data, and performed the calculations. All the authors discussed the models and checked the calculations. A. N. and D. V. wrote the manuscript. All the authors reviewed and edited the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank A. Saal for writing the LabVIEW script to move the microscope stage. We thank A. Laroche, M. Kappl, K. Hegner, M. D’Acunzi, S. Karpitschka, P. Baumli, A. Sharifi, R. Berger, and L. V. Hyde for stimulating discussions and/or for technical support. We thank an anonymous reviewer for insightful suggestions. This work was supported by the European Union's Horizon 2020 research and innovation program LubISS No. 722497 (A. N., W. S. Y. W., D. V.), the German Research Foundation (DFG) with the Collaborative Research Center 2171 (L. H., D. V., H.-J. B.) and the Collaborative Research Center (H.-J. B.). Open Access funding provided by the Max Planck Society.

References

1. W. Barthlott and C. Neinhuis, Planta, 1997, 202, 1–8.
2. R. Blossey, Nat. Mater., 2003, 2, 301–306.
3. R. Fürstner, W. Barthlott, C. Neinhuis and P. Walzel, Langmuir, 2005, 21, 956–961.
4. A. Nakajima, K. Hashimoto, T. Watanabe, K. Takai, G. Yamauchi and A. Fujishima, Langmuir, 2000, 16, 7044–7047.
5. I. P. Parkin and R. G. Palgrave, J. Mater. Chem., 2005, 15, 1689–1695.
6. A. Leenaars and S. O'Brien, Philips J. Res., 1989, 44, 183–209.
7. P. Aussillous and D. Quéré, Nature, 2001, 411, 924–927.
8. T. Heckenthaler, S. Sadhujan, Y. Morgenstern, P. Natarajan, M. Bashouti and Y. Kaufman, Langmuir, 2019, 35, 15526–15534.
9. S. Aramrak, M. Flury and J. B. Harsh, Langmuir, 2011, 27, 9985–9993.
10. J. Noordmans, P. J. Wit, H. C. Van Der Mei and H. J. Busscher, J. Adhes. Sci. Technol., 1997, 11, 957–969.
11. J. Visser, Part. Sci. Technol., 1995, 13, 169–196.
12. F. Geyer, M. D’Acunzi, A. Sharifi-Aghili, A. Saal, N. Gao, A. Kaltbeitzel, T.-F. Sloot, R. Berger, H.-J. Butt and D. Vollmer, Sci. Adv., 2020, 6, eaaw9727.
13. H. C. Hamaker, Physica, 1937, 4, 1058–1072.
14. R. Tadmor, J. Phys.: Condens. Matter, 2001, 13, L195.
15. X. Xiao and L. Qian, Langmuir, 2000, 16, 8153–8158.
16. M. Farshchi-Tabrizi, M. Kappl, Y. Cheng, J. Gutmann and H.-J. Butt, Langmuir, 2006, 22, 2171–2184.
17. H.-J. Butt and M. Kappl, Adv. Colloid Interface Sci., 2009, 146, 48–60.
18. K. L. Johnson, K. Kendall and A. D. Roberts, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313.
19. H. Yoshizawa, Y. L. Chen and J. Israelachvili, J. Phys. Chem., 1993, 97, 4128–4140.
20. K. L. Johnson, Proc. R. Soc. London, Ser. A, 1997, 453, 163–179.
21. W. S. Y. Wong, L. Hauer, A. Naga, A. Kaltbeitzel, P. Baumli, R. Berger, M. D’Acunzi, D. Vollmer and H.-J. Butt, Langmuir, 2020, 36, 7236–7245.
22. A. Hourlier-Fargette, A. Antkowiak, A. Chateauminois and S. Neukirch, Soft Matter, 2017, 13, 3484–3491.
23. H.-J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152.
24. D. W. Pilat, P. Papadopoulos, D. Schaffel, D. Vollmer, R. Berger and H.-J. Butt, Langmuir, 2012, 28, 16812–16820.
25. D. Daniel, J. V. I. Timonen, R. Li, S. J. Velling and J. Aizenberg, Nat. Phys., 2017, 13, 1020–1025.
26. D. Daniel, A. Y. T. Chia, L. C. H. Moh, R. Liu, X. Q. Koh, X. Zhang and N. Tomczak, Commun. Phys., 2019, 2, 105.
27. R. Tadmor, P. Bahadur, A. Leh, H. E. N'guessan, R. Jaini and L. Dang, Phys. Rev. Lett., 2009, 103, 266101.
28. H. Teisala, P. Baumli, S. A. L. Weber, D. Vollmer and H.-J. Butt, Langmuir, 2020, 36, 4416–4431.
29. A. J. Goldman, R. G. Cox and H. Brenner, Chem. Eng. Sci., 1967, 22, 637–651.
30. T. Young, Philos. Trans. R. Soc. London, 1805, 95, 65–87.
31. A. Scheludko and D. Nikolov, Colloid Polym. Sci., 1975, 253, 396–403.
32. J. Ally, M. Kappl, H.-J. Butt and A. Amirfazli, Langmuir, 2010, 26, 18135–18143.
33. F. Schellenberger, P. Papadopoulos, M. Kappl, S. A. L. Weber, D. Vollmer and H.-J. Butt, Phys. Rev. Lett., 2018, 121, 048002.
34. M. Barquins, J. Adhes., 1988, 26, 1–12.
35. H. She, D. Malotky and M. K. Chaudhury, Langmuir, 1998, 14, 3090–3100.
36. J. A. Greenwood, K. L. Johnson, S.-H. Choi and M. K. Chaudhury, J. Phys. D: Appl. Phys., 2008, 42, 035301.
37. W. Beare and F. P. Bowden, Philos. Trans. R. Soc., A, 1935, 234, 329–354.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01925a

---