Chains of cubic colloids at fluid–fluid interfaces

Abstract

Inspired by recent experimental observations of spontaneous chain formation of cubic particles adsorbed at a fluid–fluid interface, we theoretically investigate whether capillary interactions can be responsible for this self-assembly process. We calculate adsorption energies, equilibrium particle orientations, and interfacial deformations, not only for a variety of contact angles but also for single cubes as well as an infinite 2D lattice of cubes at the interface. This allows us to construct a ground-state phase diagram as a function of areal density for several contact angles, and upon combining the capillary energy of a 2D lattice with a simple expression for the entropy of a 2D fluid we also construct temperature–density or size–density phase diagrams that exhibit large two-phase regions and triple points. We identify several regimes with stable chainlike structures, in line with the experimental observations.

---

I. Introduction

Capillary-driven self-assembly of colloidal particles trapped at a fluid–fluid interface has recently gained a great deal of attention in the soft-matter community.^1–3 Indeed, by controlling the strength and the directionality of capillary interactions, quasi-2D ordered structures at interfaces can be obtained, which have interesting applications ranging from the stabilization of foams and Pickering emulsions⁴ to the development of new materials.⁵ Several strategies to control capillarity have been elaborated in recent years. These include the use of particles with surface chemical heterogeneities, i.e. patchy and Janus particles,^6–10 the application of external electric or magnetic fields,¹¹ and the employment of interfaces with a finite curvature.¹² Another popular method to control capillarity consists of considering particles with anisotropic shapes. Indeed, because of the constraint imposed by Young's law,¹³ nonspherical colloidal particles adsorbed at a fluid–fluid interface induce interfacial deformations that determine their orientations and generate mutual capillary interactions. Different anisotropic shapes induce different deformation fields such that the particles shape plays a key role in regulating the self-assembly of colloids trapped at an interface.

Since a large variety of colloidal particles is nowadays available, with tunable shapes and surface functionalizations,^14,15 the behavior at interfaces of nm- and μm-sized particles with several anisotropic shapes, e.g. rods, cylinders, cubes, dumbbells and discs^16–22 has been widely studied in the past few years. Among the several shapes studied so far, cubic particles have been proven to form 2D structures with striking features. In recent experiments^23,24 for example, polystyrene cubes with 30 μm edge length have been reported to self-assemble at a water–air interface into three distinct structures, namely square close-packed, linear, and hexagonal structures. Furthermore, the relative stability of these three phases has been shown to strongly depend on their wettability, which is specified by the so-called Young contact angle θ.¹³ While hydrophilic cubes with a small θ ∼ 0 give rise to square close-packed aggregates, by increasing θ first linear aggregates and finally hexagonal aggregates are observed. Cases of coexistence between linear and hexagonal aggregates have also been reported.^23,24

By noting that the cubes display different single-particle configurations in the different observed structures, i.e. a “face up” configuration in the square close-packed structure, an “edge up” configuration in the linear structure, and a “vertex up” configuration in the hexagonal structure, the authors of ref. 23 and 24 have argued that the formation of each 2D structure could be caused by a different kind of deformation field induced by the cubes at the interface. In particular these authors have proposed that cubes adsorbed in the “face up”, “edge up”, and “vertex up” configurations would induce monopolar, quadrupolar and hexapolar deformation fields, respectively.

The scenario experimentally found in ref. 23 and 24 represents, at the same time, a confirmation and an extension of the theoretical predictions previously presented in ref. 25 and 26. Here it was shown that cubic colloidal particles with a Young contact angle θ = π/2 indeed adsorb at a fluid–fluid interface with one vertex pointing upward with respect to the interface plane (“vertex up” configuration), and induce a hexapolar deformation field in the interface height profile which causes nm-sized cubes to self-assemble into thermodynamically-stable “vertex up” honeycomb, square, and hexagonal lattices. Crucial for these findings was the development of a numerical method²⁷ that takes into account interfacial deformations. This method allows to go beyond the so-called Pieranski approximation²⁸ which assumes the fluid–fluid interface to be flat even when a particle is adsorbed. Although often used in the literature,^29–33 Pieranski's approximation can lead to erroneous predictions, and in the case of cubes it cannot predict the equilibrium hexapolar-generating “vertex up” configuration when θ = π/2.²⁵

Despite the importance that linear aggregates of cubes trapped at a fluid–fluid interface appear to have in technological applications,^23,24 no theoretical investigation on this kind of aggregates has been performed so far. To fill this gap, we extend in this paper the theoretical calculations of ref. 25 and 26 in order to understand under what conditions linear chains of cubes could be more stable than other 2D structures. To this aim we first study the deformation field induced by a single adsorbed cube as a function of the Young contact angle θ and of the particle configuration. We find that, below θ = π/2, a regime of contact angles exists in which the speculation of ref. 23 and 24 concerning a quadrupolar deformation field induced by a particle adsorbed in the “edge up” configuration is correct. Then, by computing the capillary interactions acting among a 2D lattice of N → ∞ cubes, we find that in this regime the quadrupolar deformation field leads to the formation of stable linear aggregates which replace the hexagonal patterns observed at θ = π/2. Besides the linear chains we also find stable “edge up” square structures. However, for θ below a certain threshold, we find that both the linear and “edge up” square structures become metastable with respect to close-packed square aggregates, in line with the experimental findings. Nevertheless, in contrast to speculations in ref. 23 and 24, the stabilization of the close-packed square aggregates appears to be driven by packing entropy rather than by a monopolar deformation field. Finally, we introduce a simple free-energy model to estimate the interplay between capillary interactions and particle entropy. In this way we aim to include in our analysis the case of nm-sized particles for which, in contrast with μm-sized particles, entropic effects cannot be neglected. We summarize our results in a series of temperature–density or size–density phase diagrams.

The paper is organized as follows: after briefly reviewing our numerical method in Section II, we report our results in Section III, and present our conclusions and a discussion in Section IV.

II. Numerical method

In this section, we briefly review the numerical method developed in ref. 27. We refer to ref. 34 for more details, and to ref. 25, 26 and 35–38 for other examples of its application to colloidal particles at fluid–fluid interfaces and to a droplet in contact with heterogeneous surfaces.

We consider two immiscible, homogeneous, and incompressible fluids, separated by a fluid–fluid interface of surface tension γ. We introduce a Cartesian coordinate system x, y, z, and by convention call fluid 1 and fluid 2 the fluid at z → +∞ and z → −∞, respectively. We assume the fluid–fluid interface as a 2D, possibly curved surface with zero thickness, coinciding with a plane parallel to z = 0 when no particles are adsorbed. In the case that colloidal particles are adsorbed, the equilibrium shape of the fluid–fluid interface is given by the Young–Laplace equation, with Young's law as a boundary condition for the Young contact angle θ.²⁷ This is the angle formed by the fluid–fluid interface along the three-phase contact line, i.e. where the fluid–fluid interface encounters the solid surface of the adsorbed particles. Calling γ₁ and γ₂ the solid–fluid surface tension of the particles with fluid 1 and fluid 2, respectively, Young's law states that θ (measured inside fluid 2) is given by cos θ = (γ₁ − γ₂)/γ.

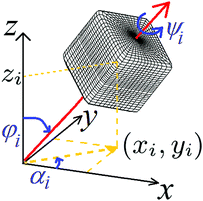
In our formalism we rewrite the force balance described by the Young–Laplace equation as a minimum condition of a suitable (free) energy, and perform the minimization numerically. To this aim we represent the fluid–fluid interface as a grid of points, and the fixed position and orientation of N adsorbed particles by a 6N-dimensional vector Ω = (Ω₁,…Ω_N), with Ω_i = (x_i, y_i, z_i, φ_i, ψ_i, α_i) defining the configuration of the i-th particle (i = 1,…N). As shown in Fig. 1, we consider smooth-edge cubic particles in this paper. The in-plane Cartesian coordinates of the center of mass of the i-th particle is denoted by x_i and y_i, z_i denotes the difference between the Cartesian coordinate z of the center of mass and the interface height far away from the particle, φ_i the polar angle of the vertical axis with respect to the far-field interface normal, ψ_i the angle of the particle around its vertical axis, and α_i is the azimuthal angle of the vertical axis in the interface plane. Moreover we write the free energy E_N of a system of N colloidal particles adsorbed at a fluid–fluid interface as²⁷

E_N(Ω) = γ(S(Ω) − A + W(Ω)cos θ), (1)

where S(Ω) is the total fluid–fluid surface area, W(Ω) is the total surface area between fluid 1 and the particles, and the constant A is the planar fluid–fluid surface area when no particle is adsorbed, and is included in eqn (1) to set the energy level E_N = 0 when all particles are desorbed from the interface and are immersed in fluid 2. Finally we use L and Σ ∼ 5.65L² to indicate the side and the surface area of each particle, respectively, where Σ ≠ 6L² because the cubes are slighlty rounded. Note that the input parameters θ and γ characterise the two fluids and the material of the particles, and that γ is a mere scaling factor of the energy E_N at this point.

Fig. 1 Sketch of the single-particle configuration (x_i, y_i, z_i, φ_i, ψ_i, α_i) of the generic i-th (smooth-edge) cube adsorbed at the fluid–fluid interface, with i = 1,…N and N the total number of adsorbed cubes. The i-th cube has a center of mass with Cartesian coordinates x_i, y_i, z_i, a polar angle φ_i between its vertical axis (sketched with a red arrow) and the z axis, an internal Euler angle ψ_i around its vertical axis, and an azimuthal angle α_i in the z = 0 plane. The plane z = 0 corresponds to the flat fluid–fluid interface when no particle is adsorbed.

We now adopt the following protocol: first we fix the contact angle θ. Then, by varying Ω to minimize E_N, we obtain the equilibrium particle configuration and the corresponding shape of the fluid–fluid interface, at fixed contact angle θ. We repeat this protocol for several θ in order to investigate different particle wettabilities. However, it is important to note that in this paper we are interested in the deformation fields induced by equilibrium configurations as well as by (metastable) non-equilibrium ones.

III. Results

In this section we investigate whether we can find conditions for colloidal cubes to assemble into stable linear chains rather than into other 2D structures, like square, hexagonal, or honeycomb lattices. We first study the deformation field induced by a single adsorbed cube as a function of the Young contact angle θ and of the particle configuration. Then we numerically compute the capillary interactions acting among a 2D lattice of N → ∞ cubes adsorbed at an interface and perform a stability analysis among the several phases that the cubes can form. Finally, by using a simple free-energy model, we summarize our results in a series of density–temperature phase diagrams. Here the temperature is actually the dimensionless combination k_BT/(γΣ), which in practise is seen as an inverse particle size.

Following ref. 25 and 26 we will refer to the “vertex up”, “edge up”, and “face up” configurations, as the {111}, {110}, and {100} configurations, respectively.

A. Hexapolar and quadrupolar deformation fields

As stated in the introduction, in ref. 23 and 24 it has been suggested that the self-assembly of micronscale cubes trapped at a fluid–fluid interface into hexagonal aggregates and linear ones would be caused by two different kinds of deformation fields induced by the adsorbed particles. More specifically, the stabilization of the hexagonal phase would be caused by a hexapolar deformation field generated by cubes in the {111} configuration while the stabilization of the linear phase would be caused by a quadrupolar deformation field generated by cubes in the {110} configuration. While these suggestions agree with the theoretical calculations performed so far in the former case, they disagree in the latter case. Indeed, in ref. 25 and 26 it has been theoretically predicted that the deformation field induced by a cube adsorbed in the {111} configuration is dominated by the hexapolar mode, but it has also been found that the same cube adsorbed in the {110} configuration does not induce any interfacial deformation. However, these calculations have been performed only for cubes with contact angle θ = π/2. Since the wettability has been experimentally proven to play a decisive role in the stabilization of the various phases at the interface, we here extend the calculations performed in ref. 25 and 26 of the deformation field induced by a single cube adsorbed at a fluid–fluid interface, from the case θ = π/2 to smaller values of θ.

As explained in Section II, the configuration of a single adsorbed cube at the interface, is given by Ω = (x, y, z, φ, ψ, α), where the subscript “1” can be omitted since we consider only a single particle (i.e. N = 1), and the equilibrium shape of the fluid–fluid interface is the one that minimizes the free energy E₁ (eqn (1)), for fixed values of Ω and θ. We note that symmetry considerations in the case of a single particle show that the energy E₁ is independent of x, y, and α, such that the particle configuration is specified by only φ, ψ, and z. Furthermore the equilibrium height z of the cube at the interface is automatically found by our numerical method, for each fixed φ, ψ, and θ, by allowing the two fluids to exchange volume while minimizing E₁.³⁸ The {111} configuration is specified by ψ_{111} = π/4, φ_{111} = π/3.29, while the {110} configuration by ψ_{110} = 0, φ_{110} = π/4. Note that we consider φ_{111} = π/3.29 rather than φ_{111} = π/4 since the former configuration has a (slightly) lower energy than the latter one.^25,26 In the following we will indicate the energies of a single cube adsorbed in the {111} and {110} configurations with E^{111}₁ and E^{110}₁, respectively.

The results of the minimization procedure for cos θ ∈ {0, 0.2, 0.4, 0.6} are shown in Fig. 2 and 3. We find that the deformation field induced by the adsorption process strongly depends on the contact angle θ. In agreement with ref. 25 and 26, we find that for cos θ = 0 a cube adsorbed in the {111} configuration generates a hexapolar deformation field consisting of three rises and three depressions, exhibiting a 3-fold symmetry around the particle (see Fig. 2(a) and 3(a)), while the same particle adsorbed in the {110} configuration does not induce any deformation (see Fig. 2(e) and 3(e)). The situation changes by changing the contact angle. By decreasing θ, the intensity of the hexapolar deformation field decreases until it essentially vanishes for cos θ = 0.6 (see Fig. 2(d) and 3(d)). In this case the fluid–fluid interface becomes actually flat. By contrast, the flat interface observed for the {110} configuration at cos θ = 0 evolves into a quadrupolar deformation field consisting of two rises and two depressions, showing a 2-fold symmetry around the particle, for larger cos θ. In particular the intensity of the quadrupole increases with increasing cos θ. Note that the quadrupolar deformation field for cos θ = 0.6 has two depressions that are more spread and less intense than the two rises. As a consequence the depressions can hardly be appreciated in the contour plot of Fig. 3(h). Nevertheless the presence of the quadrupole at cos θ = 0.6 can clearly be seen in the 3D plot of Fig. S1 of the ESI.†

Fig. 2 3D plot of the deformation field induced by a single cube of side length L adsorbed at a fluid–fluid interface in the “vertex up” {111} and “edge up” {110} configuration, respectively, for several Young contact angles θ. For cos θ = 0 (no preference for either of the two fluids), a cube adsorbed in the {111} configuration (a) generates a hexapolar deformation field, while a cube adsorbed in the {110} configuration (e) does not induce any deformation. By increasing cos θ (such that the cube favours the lower fluid) the intensity of the hexapolar deformation field of the {111} configuration decreases (b and c) until it essentially vanishes in (d) where cos θ = 0.6, while the flat interface of the {110} configuration evolves into a quadrupolar deformation field whose intensity increases with cos θ (f–h).

Fig. 3 Contour plot of the deformation field induced by a single cube of side length L adsorbed at a fluid–fluid interface in the “vertex up” {111} and “edge up” {110} configuration, respectively, for the same Young contact angles θ as in Fig. 2.

In addition to the deformation fields induced by a single cube adsorbed in the {111} and {110} configurations, we employ our numerical method to compute the deformation field induced by a single cube adsorbed in the {100} configuration (ψ_{100} = 0, φ_{100} = 0), for several values of the contact angle θ. We indicate the energy of a single cube adsorbed in this configuration with E^{100}₁. As shown in Fig. S2 of the ESI,† we find that in these cases the cube never deforms the interface. This finding disagrees with the speculation of ref. 23 and 24, where it was suggested that cubes with 30 μm edge length and a very small contact angle θ ∼ 0 would induce a monopolar deformation field at the interface, when adsorbed in the {100} configuration. This does not appear to be the case. Indeed, by considering typical values for the mass density difference between the particle and the fluids δ ∼ 10³ kg m⁻³, the fluid–fluid surface tension γ ∼ 10⁻² N m⁻¹, and (the modulus of) the gravitational acceleration g on planet Earth, we obtain a Bond number for a cubic particle with side length L ≪ 1 mm. It follows that a monopolar mode is not expected for a sub-mm sized particle at its equilibrium adsorption configuration, unless non-gravitational external forces act on the particle.

We plot E^{111}₁, E^{110}₁, and E^{100}₁ as a function of the contact angle θ in Fig. 4. We observe that the particle configurations discussed above are not always equilibrium configurations. Indeed, the minimal single-particle adsorption energy is E^{111}₁ for cos θ ≤ 0.25 and E^{100}₁ for cos θ > 0.25. It follows that the equilibrium (minimal (free) energy) configuration of a single adsorbed cube is the {111} in the former case, and the {100} in the latter case. One could therefore naively think that the linear-chain phase will never be stable at an interface since the quadrupolar-generating {110} single-particle configuration is always metastable with respect to the {111} and the {100} ones. However, this is not necessarily true because when more particles are adsorbed at an interface, capillary interactions have to be considered such that an equilibrium phase of many particles can be stabilized even though the corresponding single-particle configuration is not the stable one. In particular we will see that a regime exists for cos θ ≥ 0.35 in which the quadrupolar and the hexapolar deformation fields induced by cubes in the {110} and {111} configurations, respectively, have comparable intensities. As we will show in the next subsection it is in this regime that the linear-chain phase of {110} particles is stable, even though the single-particle equilibrium configuration is the {100} one in this regime of contact angles θ.

Fig. 4 Adsorption energies E^{111}₁, E^{110}₁ and E^{100}₁ of a single cube in the {111}, {110} and {100} configuration, respectively, as a function of the Young contact angle θ. The energies are expressed in units of γΣ, with γ the fluid–fluid surface tension and Σ the surface area of the particle. The inset shows a zoom of the graph in the region cos θ ≥ 0.55, where E^{100}₁ ≪ E^{110}₁ < E^{111}₁; for cos θ ≤ 0.25, the {111} configuration has the lowest free energy.

Furthermore we observe that for cos θ ≥ 0.55, E^{100}₁ ≪ E^{110}₁ < E^{111}₁, with E^{110}₁ and E^{111}₁ approaching zero. In other words the adsorption energies of cubes in the {111} and {110} configuration are very weak in this regime of contact angles and, as we will show, this results in weak capillary interactions.

B. Stable chains of cubes at a fluid–fluid interface

Two or more cubes adsorbed in the hexapolar-generating {111} and in the quadrupolar-generating {110} configurations give rise to different kinds of energetically-favorable bonds. This can be understood by considering that a pair of cubes (N = 2) adsorbed at a fluid–fluid interface can attract or repel each other, depending on their relative azimuthal orientation |α₁ − α₂|. Attractive relative orientations are those that allow overlap of interfacial deformations with the same sign, i.e. rises with other rises and depressions with other depressions. In this case the fluid–fluid surface area, and hence the energy E₂ (eqn (1)), decrease as the particles approach each other. Repulsive relative orientations, instead, are those in which interfacial deformations with the opposite sign, i.e. rises with depressions, overlap. In this case, the fluid–fluid surface area, and hence the energy E₂ (eqn (1)), increase as the particles approach each other.

As already explained in ref. 25 and 26 and as shown in Fig. 5, it follows that N = 2 cubes adsorbed in the {111} configuration can form two different kinds of energetically-favorable bonds: a dipole–dipole bond, when a rise-depression dipole of one hexapole overlaps with a rise-depression dipole of the other hexapole (see Fig. 5(a)), and a tripole–tripole bond, when either a rise-depression-rise or a depression-rise–depression tripole of one hexapole overlaps with, respectively, a rise-depression-rise or a depression-rise–depression tripole of the other hexapole (see Fig. 5(b)). By contrast, two cubes adsorbed in the {110} configuration can only form a monopole–monopole bond, when a rise monopole of one quadrupole overlaps with a rise monopole of the other quadrupole (see Fig. 5(c)), or when a depression monopole of one quadrupole overlaps with a depression monopole of the other quadrupole (see Fig. 5(d)).

Fig. 5 Energetically-favorable capillary bonds induced by N = 2 cubes adsorbed at a fluid–fluid interface in the {111} (a and b), and {110} (c and d) configuration, respectively, where red denotes a rise and blue a depression. (a) Dipole–dipole bond, when a rise-depression dipole of one hexapole overlaps with a rise-depression dipole of another hexapole. (b) Tripole–tripole bond, when a depression-rise–depression tripole of one hexapole overlaps with a depression-rise–depression tripole of the other hexapole. (c) Monopole–monopole bond, when a rise monopole of one quadrupole overlaps with a rise monopole of the other quadrupole. (d) Monopole–monopole bond, when a depression monopole of one quadrupole overlaps with a depression monopole of the other quadrupole.

The different energetically-favorable bonds induced by cubes in the {111} and {110} configuration, respectively, lead in turn to the formation of different phases at the interface, as illustrated in Fig. 6. In particular, a regular lattice of N → ∞ cubes adsorbed in the {111} configuration can lead to the formation of three distinct 2D phases, namely hexagonal (x), honeycomb (h), and “vertex up” square (s_v) phases. In the x phase each particle forms a dipole–dipole bond with each of its six nearest neighbors (see Fig. 6(a)), in the h phase each particle forms a tripole–tripole bond with each of its three nearest neighbors (see Fig. 6(b)), in the s_v phase each particle forms a dipole–dipole bond with two opposite nearest neighbors and a tripole–tripole bond with the two remaining neighbors (see Fig. 6(c)). By constrast, N → ∞ cubes adsorbed in the {110} configuration can lead to the formation of two distinct phases, namely chains (c), and “edge up” square (s_e) phases. In the c phase each particle forms a monopole–monopole bond with only two neighbors, along a single linear “preferred” direction (see Fig. 6(d)), where the particles do not interact along the direction perpendicular to the principal one. In the s_e phase, each particle forms a monopole–monopole bond with four nearest neighbors, i.e. the cubes not only interact along a “preferred” direction as in the case of the chains, but also perpendicularly to this (see Fig. 6(e)).

Fig. 6 Phases formed by a 2D lattice of N → ∞ colloidal cubes adsorbed at a fluid–fluid interface with schematic capillary rises (red) and depressions (blue). Cubes adsorbed in the hexapolar-generating {111} configuration can give rise to hexagonal x (a), honeycomb h (b), and “vertex up” square s_v (c) phases, while cubes adsorbed in the quadrupolar-generating {110} configuration can give rise to chains c (d), and “edge up” square s_e (e) phases. No capillary interactions act among cubes in the {100} configuration, as cubes in this configuration do not deform the interface. The formation of a “face up” square s_f phase (f) would then be driven by packing entropy.

We find that in principle two different chain phases exist. In the first case the chains are obtained by overlapping rises with rises, in the second case by overlapping depressions with depressions. As shown in Fig. S3 of the ESI,† we find that the pair interaction acting between two cubes with overlapping rises is much stronger than the pair interaction acting between two cubes with overlapping depressions. As a consequence it is more favorable for cubes to assemble into chains with overlapping rises rather than overlapping depressions, and we will only consider the former case throughout the paper.

Finally no capillary interactions act among N → ∞ cubes adsorbed in the {100} configuration, since cubes in this configuration do not deform the interface. The formation of a “face up” square phase s_f (see Fig. 6(f)) is then entropy-driven at sufficiently high areal densities.

The intensity of the (capillary) interaction energy E_N acting among a 2D lattice of N → ∞ cubes in the several phases indicated above changes with the contact angle θ, and consequently different phases stabilize at different θ. To show this, we compute E_N for the various phases as a function of θ. To this aim we apply the numerical method described in section II to a lattice unit cell, and impose periodic boundary conditions (PBCs) to the interface height profile. The size of the cell determines the particle packing fraction η in the lattice, while the shape of the unit cell and the PBCs specify the particular phase under considerations. Details on the lattice unit cells and the PBCs used to define the several phases sketched in Fig. 6 can be found in Fig. S4–S6 of the ESI.†

We observe that while the x, h, s_v, s_e and s_f phases are 2D phases, the c phase is essentially a 1D phase. It follows that the definition of the 2D packing fraction η is rather arbitrary in this latter case. In order to overcome this problem, we describe the c phase as a “gas” of chains that do not interact laterally (see Fig. 6(d)). As explained in Fig. S4 of the ESI,† to define the c phase we choose one side of the unit lattice cell such that the lateral distance D_L among the chains corresponds to the smallest distance for which two cubes in the {110} configuration do not interact. The case corresponds to laterally interacting chains, i.e. the s_e phase. On the other hand, as shown in Fig. S7 of the ESI,† considering 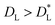does not significantly affect the η dependence of the capillary interaction energy per unit area ηE_N in the c phase, at sufficiently low η.

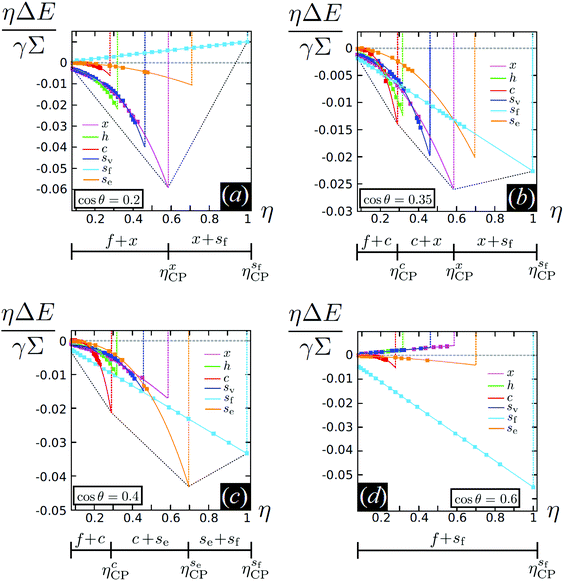
We present our results for cos θ ∈ {0.2, 0.35, 0.4, 0.6} in Fig. 7. The horizontal axis represents the dimensionless areal density η = NL²/A, which we will call packing fraction for convenience below, even though L² is only (close to) the areal coverage of a cube in the {100} configuration. We indicate the closest-packing of a specific phase with η^ξ_CP, where ξ = x, h, s_v, c, s_e, s_f. As explained in Fig. S4 of the ESI† these correspond to η^x_CP = 0.59, η^h_CP = 0.32, , η^c_CP = 0.28, , and . Note that the s_f phase is the densest-packed state. The vertical axis of Fig. 7 represents the dimensionless energy per unit area ηΔE/(γΣ), where ΔE ≡ E_N/N − E^{110}₁ is the capillary interaction energy per particle minus a conveniently but arbitrary constant that we set to the adsorption energy of a single particle in the {110} configuration, for each of the phases described above. In Fig. 7 we employ the common tangent construction as represented by the convex envelope (dashed black line), to determine the ground state (T = 0) phase diagram.

Fig. 7 Dimensionless (capillary) interaction energy per unit area ηΔE/(γΣ) as a function of the particle packing fraction η, for cos θ ∈ {0.2, 0.35, 0.4, 0.6}. η^ξ_CP indicates the closest-packing of the ξ = x, c, s_e, s_f phases. ΔE ≡ E_N/N − E^{110}₁ is the (capillary) interaction energy per particle minus the adsorption energy of a single particle in the {110} configuration, and is expressed in units of γΣ, where γ is the fluid–fluid interfacial tension and Σ is the surface area of a particle. We show results for the phase with chains c (red), the hexagonal phase x (magenta), the “face up” square phase s_f (light-blue), the “edge up” square phase s_e (yellow), the “vertex up” square phase s_v (blue), and the honeycomb phase h (green). Dotted black lines indicate the common tangent construction. At cos θ = 0.2 (see (a)) an extremely dilute disordered fluid phase f coexists with the close-packed x phase for η < η^x_CP, while for η > η^x_CP the close-packed x phase coexists with the close-packed s_f phase. At cos θ = 0.35 (see (b)), for η < η^c_CP the f phase coexists with the close-packed c phase, for η^c_CP < η < η^x_CP the close-packed c phase coexists with the close-packed x phase, while for η > η^x_CP the x phase coexists with the close-packed s_f phase. Instead, at cos θ = 0.4 (see (c)) for η < η^c_CP the f phase coexists with the close-packed c phase, for the close-packed c phase coexists with the close-packed s_e phase, while for the s_e phase coexists with the close-packed s_f phase. Finally, at cos θ = 0.6 (see (d)) the s_f phase is the only stable phase, besides the f phase.

We find several scenarios by changing θ. At cos θ = 0.2 (Fig. 7(a)) the capillary interaction energy among cubes adsorbed in the {111} configuration, i.e. cubes in the x, h, and s_v phases, is much stronger (more negative) than the capillary interaction energy among cubes adsorbed in the {110} configuration, i.e. cubes in the c and s_e phases. As a consequence, we find that for η < η^x_CP an extremely dilute disordered fluid phase f coexists with the close-packed x phase, while for η > η^x_CP the close-packed x phase coexists with the close-packed s_f phase. By increasing cos θ, instead, the intensity of the capillary interaction energy among cubes in the {110} configuration becomes stronger while the capillary interaction energy among cubes in the {111} configuration simultaneously becomes weaker. This leads to the scenarios observed at cos θ = 0.35 and cos θ = 0.4. At cos θ = 0.35 (Fig. 7(b)), for η < η^c_CP the f phase coexists with the close-packed c phase, for η^c_CP < η < η^x_CP the close-packed c phase coexists with the close-packed x phase, while for η > η^x_CP the x phase coexists with the close-packed s_f phase. Instead, at cos θ = 0.4 (Fig. 7(c)) for η < η^c_CP the f phase coexists with the close-packed c phase, for the close-packed c phase coexists with the close-packed s_e phase, while for the s_e phase coexists with the close-packed s_f phase. Finally, at cos θ = 0.6 (Fig. 7(d)) the s_f phase has the lowest energy per unit area ηΔE for each η, and the capillary interactions among cubes in the {111} as well as in the {110} configuration are very weak. It follows that at this contact angle the s_f phase is the only stable phase, besides the f phase. Since in the s_f phase no capillary interactions act among the cubes, its stabilization is completely driven by packing entropy.

We note that the cubes display different orientations in the dilute fluid phase f, as a function of the Young contact angle θ. They are indeed adsorbed in the minimum energy configuration at the θ of interest: the {111} configuration at cos θ = 0, the {100} configuration at the other contact angles.

Finally, we summarize the results of Fig. 7 in the ground state (T = 0) phase diagram of Fig. 8. In this diagram we report the packing density η on the horizontal axis, and the cosine of the contact angle θ on the vertical axis. We note that three regimes of θ exist, in which different phases stabilize by varying η. In the regime of large contact angles (cos θ < 0.35) the f, x, and s_f phases stabilize, in the regime of intermediate contact angles (0.35 ≤ cos θ ≤ 0.4) the f, x, c, s_e and s_f phases stabilize, in the regime of small contact angles (cos θ > 0.4) the f, and s_f phases are stable. We note that in Fig. 8 we included the case of cos θ = 0.0, for which a graph similar to those of Fig. 7 is reported in Fig. S8 of the ESI.†

Fig. 8 Ground state (T = 0) phase diagram reporting the particle packing fraction η on the horizontal axis, and the Young contact angle θ on the vertical axis. With light-pink we represent the dilute fluid phase f, with magenta the hexagonal phase x, with red the phase with linear chains c, with yellow the “edge up” square phase s_e, and with light-blue the “face up” square phase s_f. η^ξ_CP indicates the closest-packing of ξ = x, c, s_e, s_f. Dashed lines indicate regions of phase coexistence.

In the analysis performed so far we only have considered the effect of capillary interactions while we have completely neglected entropic contributions. Although this approximation is correct when studying the phase behaviour of μm-sized particles as those of ref. 23 and 24, it is less accurate when smaller particles are considered. We now extend the analysis to the case of nm-sized particles and introduce an approximate model to estimate the interplay between capillary interactions and particle entropy. We write the (Helmholtz) free energy F^ξ of a system of N colloidal particles adsorbed at a fluid–fluid interface of area A and temperature T, in a particular phase ξ, as

where η, η^ξ_CP and ΔE have been defined above while k_B is the Boltzmann constant. We express F^ξ in terms of γΣ, with γ the fluid–fluid surface tension, and Σ the surface area of the particle. The second term on the right side of eqn (2) is added in order to include entropic effects. It consists of the free energy of an ideal gas³⁹ plus the extra term −(Nk_BT/(γΣ))ln(1 − η/η^ξ_CP), which ensures the free energy to diverge at the close-packed density η^ξ_CP of phase ξ. Note that we include in our model entropic effects only in an approximated way, without any explicit reference to the particle shape and orientation entropy. Nevertheless, as we will show, this approximation reproduces remarkably well results, especially in the limit γΣ ≫ k_BT. This is the limit of low temperatures or large particles, where the free energy (2) is dominated by the capillary contribution ΔE^ξ while the entropic term only contributes significantly close to the close-packed limit η → η^ξ_CP.

By considering k_BT/(γΣ) ≠ 0 in eqn (2), we map out the phase diagrams depicted in Fig. 9 for cos θ ∈ {0.2, 0.35, 0.4}. Here we represent the particle density η on the horizontal axis, and the dimensionless temperature k_BT/(γΣ) on the left vertical axis. The right vertical axis represents the corresponding value of the particle size L at room temperature (T = 300 K) using a typical surface tension γ = 0.01 N m⁻¹. We find that our results reproduce remarkably well the experimental observations in ref. 23 and 24. Indeed for μm-sized L we find that, by decreasing θ, first hexagonal x structures and then linear chains c stabilize. In agreement with experiments we also predict regions in which the x and the c phases coexist, as well as the stabilization of “face up: square s_f patterns at very small θ ∼ 0. Furthermore we see that for cos θ = 0.4 regions exist in which “edge up” square s_e aggregates stabilize in coexistence with either f, c, or s_f phases. For cubes with nm-sized L we also find the presence of f–c–x, and f–c–s_e triple-points. Note that in the limit of high temperature T our model for the free energy becomes less accurate and only the phase f survives. For k_BT/(γΣ) = 0, instead, the scenario depicted in Fig. 9 coincides with the ground states depicted in Fig. 7 and 8.

Fig. 9 Temperature–density phase diagram for cos θ ∈ {0.2, 0.35, 0.4}. The left vertical axis is the dimensionless temperature k_BT/(γΣ), with γ the fluid–fluid surface tension, Σ the total surface area of a particle, k_B the Boltzmann constant, and T the temperature. The right vertical axis represents the corresponding value of the particle size L at room temperature (300 K) and using a typical surface tension γ = 0.01 N m⁻¹. The horizontal axis is the particle density η, which is equal to 1 for the close-packed “face up” square phase s_f. The colored areas indicate stable 2D one-phase regions at the fluid–fluid interface: light-pink indicates a disordered fluid phase f, while red, magenta, yellow, and light-blue the chains c, hexagonal x, “edge up” square s_e, and “face up” square s_f phases, respectively. The gray areas indicate coexistence between two phases of different η, and the horizontal lines connect three phases coexisting at the f–c–x, and f–c–s_e triple points, respectively.

As a final remark we observe that we cannot build a proper phase diagram in the case of cos θ = 0.6, where the capillary interactions become so weak that the phase behaviour is governed by packing entropy among cubes in the adsorbed “face up” {100} configuration. A more accurate theoretical model of the free energy that takes into account the particle shape and excluded volume is then required to describe the entropy-driven phase transitions.

IV. Conclusions and discussion

In this paper, we numerically studied the adsorption and self-assembly of cubic colloidal particles at a fluid–fluid interface, as a function of the Young contact angle θ. For values of θ close to π/2, we confirmed the scenario already found in a series of previous papers: a single cube prefers to adsorb with one vertex pointing upward with respect to the interface plane (“vertex up” configuration) and induces a hexapolar deformation field in the interface height profile which causes a lattice of N → ∞ adsorbed cubes to assemble into “vertex up” hexagonal structures. At the same time, a cube with θ = π/2 adsorbed with one edge pointing upward (“edge up” configuration) or with one face pointing upward (“face up” configuration), does not induce any deformation in the interface height profile. By decreasing θ, however, we found that the intensity of the hexapolar deformation field induced by a cube in the “vertex up” configuration decreases, while a cube in the “edge up” configuration induces a finite quadrupolar deformation field. The intensity of this quadrupole increases with decreasing θ, and a regime exists in which it causes a lattice of N → ∞ adsorbed cubes to assemble into stable “edge up” chains and square aggregates. Finally we observed that, by decreasing θ even further, the cubes give rise to “face up” square patterns, whose stabilization is driven by packing entropy as the capillary interactions become very weak.

Our results are in agreement with the findings of recent experiments performed on μm-sized polystyrene cubes. In particular they give strong theoretical support to the idea of a capillary-driven stabilization of chains of cubic colloids at fluid–fluid interfaces, in addition to the stabilization of other, already found, 2D structures. Our analysis also explains the linear aggregates of “edge up” cubes observed in the case of the cubic nanocrystals (of roughly 5-to-10 nm size) studied in ref. 40–42. Nevertheless for these experiments the true underlying mechanism (capillarity, van der Waals forces, steric interactions due to capping ligands,…) that drives the self-assembly is still under investigation.

We note that chains of cubic colloids have also been observed in systems of magnetic cubes with a fixed magnetic dipole moment and in suspensions of colloidal cubes in an electric field,^43–48 inducing dipolar interactions between the cubes. As the physical mechanism behind the chain formation is very different from the capillary-induced chain formation of colloidal cubes at an interface, the structure of the chains can also be very different. Depending on the orientation of the fixed dipole moment of the magnetic cubes, the cubes within the chains can have different orientations, and in the case of dipolar cubes in an electric field, the cubes can even freely rotate along the field axis.⁴⁸

Finally several extensions of the work presented in this paper could be considered. First it could be interesting to investigate the effects of slightly tuning the shape of the cubic particles (i.e. considering cubes with edges truncated at different levels) on the self-assembly at the interface, as a function of the Young contact angle θ. In addition, the simple model used here for the free energy could be improved to take into account, for instance the orientational entropy of the cubes in each phase. In ref. 25 and 26 it was shown that considering this contribution can lead to stable honeycomb and “vertex up” square patterns coexisting with hexagonal ones, for nm-sized cubes with θ = π/2. For smaller θ it could reveal the presence of coexistence regions between the chains with honeycomb and “vertex up” square patterns. We plan to address these issues in future work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support by the “Nederlandse Organisatie voor Wetenschappelijk Onderzoek” (NWO) TOPPUNT. This work is part of the D-ITP consortium, a program of the NWO that is funded by the Dutch Ministry of Education, Culture and Science (OCW).

References

1. E. M. Furst, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 20853 , ISSN 0027-8424, https://www.pnas.org/content/108/52/20853.
2. R. McGorty, J. Fung, D. Kaz and V. N. Manoharan, Mater. Today, 2010, 13, 34 , ISSN 1369-7021, http://www.sciencedirect.com/science/article/pii/S1369702110701073.
3. A. Böker, J. He, T. Emrick and T. P. Russell, Soft Matter, 2007, 3, 1231,  10.1039/B706609K.
4. S. Sacanna, W. K. Kegel and A. P. Philipse, Phys. Rev. Lett., 2007, 98, 13 , ISSN 00319007.
5. K. Stratford, R. Adhikari, I. Pagonabarraga, J.-C. Desplat and M. E. Cates, Science, 2005, 309, 2198 , ISSN 0036-8075, https://science.sciencemag.org/content/309/5744/2198.
6. B. J. Park and D. Lee, Soft Matter, 2012, 8, 7690,  10.1039/C2SM25775K.
7. B. J. Park and D. Lee, ACS Nano, 2012, 6, 782,  DOI:10.1021/nn204261w.
8. L. C. Bradley, W.-H. Chen, K. J. Stebe and D. Lee, Curr. Opin. Colloid Interface Sci., 2017, 30, 25 , ISSN 1359-0294, http://www.sciencedirect.com/science/article/pii/S1359029417300146.
9. A. Kumar, B. J. Park, F. Tu and D. Lee, Soft Matter, 2013, 9, 6604,  10.1039/C3SM50239B.
10. Q. Xie, G. B. Davies, F. Günther and J. Harting, Soft Matter, 2015, 11, 3581 , ISSN 17446848, 1501.07707.
11. M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591,  DOI:10.1021/nn100869j , pMID: 20568710.
12. D. Ershov, J. Sprakel, J. Appel, M. A. Cohen Stuart and J. van der Gucht, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9220 , ISSN 0027-8424, https://www.pnas.org/content/110/23/9220.
13. P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827,  DOI:10.1103/RevModPhys.57.827.
14. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557,  DOI:10.1038/nmat1949 , ISSN 1476-4660.
15. S. Sacanna and D. J. Pine, Curr. Opin. Colloid Interface Sci., 2011, 16, 96 , ISSN 1359-0294, http://www.sciencedirect.com/science/article/pii/S1359029411000069.
16. E. P. Lewandowski, J. A. Bernate, A. Tseng, P. C. Searson and K. J. Stebe, Soft Matter, 2009, 5, 886,  10.1039/B812257A.
17. E. P. Lewandowski, M. Cavallaro, L. Botto, J. C. Bernate, V. Garbin and K. J. Stebe, Langmuir, 2010, 26, 15142,  DOI:10.1021/la1012632.
18. L. Botto, E. P. Lewandowski, M. Cavallaro and K. J. Stebe, Soft Matter, 2012, 8, 9957,  10.1039/C2SM25929J.
19. I. B. Liu, N. Sharifi-Mood and K. J. Stebe, Annu. Rev. Condens. Matter Phys., 2018, 9, 283,  DOI:10.1146/annurev-conmatphys-031016-025514.
20. B. Madivala, J. Fransaer and J. Vermant, Langmuir, 2009, 25, 2718,  DOI:10.1021/la803554u.
21. S. Dasgupta, M. Katava, M. Faraj, T. Auth and G. Gompper, Langmuir, 2014, 30, 11873,  DOI:10.1021/la502627h , ISSN 0743-7463.
22. S. Dasgupta, T. Auth and G. Gompper, J. Phys.: Condens. Matter, 2017, 29, 373003,  DOI:10.1088/1361-648x/aa7933.
23. Q. Song, M. Steuber, S. I. Druzhinin and H. Schönherr, Angew. Chem., Int. Ed., 2019, 58, 5246,  DOI:10.1002/anie.201814076.
24. Q. Song and H. Schönherr, Langmuir, 2019, 35, 6742,  DOI:10.1021/acs.langmuir.9b00792 , ISSN 0743-7463.
25. G. Soligno, M. Dijkstra and R. van Roij, Phys. Rev. Lett., 2016, 116, 258001,  DOI:10.1103/PhysRevLett.116.258001.
26. G. Soligno, M. Dijkstra and R. van Roij, Soft Matter, 2018, 14, 42,  10.1039/C7SM01946G.
27. G. Soligno, M. Dijkstra and R. van Roij, J. Chem. Phys., 2014, 141, 244702,  DOI:10.1063/1.4904391.
28. P. Pieranski, Phys. Rev. Lett., 1980, 45, 569,  DOI:10.1103/PhysRevLett.45.569.
29. J. de Graaf, M. Dijkstra and R. van Roij, J. Chem. Phys., 2010, 132, 164902,  DOI:10.1063/1.3389481.
30. A. R. Morgan, N. Ballard, L. A. Rochford, G. Nurumbetov, T. S. Skelhon and S. A. F. Bon, Soft Matter, 2013, 9, 487,  10.1039/C2SM26556G.
31. W. van der Stam, A. P. Gantapara, Q. A. Akkerman, G. Soligno, J. D. Meeldijk, R. van Roij, M. Dijkstra and C. de Mello Donega, Nano Lett., 2014, 14, 1032,  DOI:10.1021/nl4046069.
32. B. Peng, G. Soligno, M. Kamp, B. de Nijs, J. de Graaf, M. Dijkstra, R. van Roij, A. van Blaaderen and A. Imhof, Soft Matter, 2014, 10, 9644,  10.1039/C4SM01989J.
33. N. Ballard and S. A. F. Bon, J. Colloid Interface Sci., 2015, 448, 533 , ISSN 0021-9797, http://www.sciencedirect.com/science/article/pii/S0021979715002453.
34. G. Soligno, Droplets, Capillary Interactions and Self-assembly, 2017, ISBN 9789463321242.
35. M. Vis, J. Opdam, I. S. J. van't Oor, G. Soligno, R. van Roij, R. H. Tromp and B. H. Erné, ACS Macro Lett., 2015, 4, 965,  DOI:10.1021/acsmacrolett.5b00480.
36. I. Dević, G. Soligno, M. Dijkstra, R. van Roij, X. Zhang and D. Lohse, Langmuir, 2017, 33, 2744,  DOI:10.1021/acs.langmuir.7b00002.
37. M. Kamp, G. Soligno, F. Hagemans, B. Peng, A. Imhof, R. van Roij and A. van Blaaderen, J. Phys. Chem. C, 2017, 121, 19989,  DOI:10.1021/acs.jpcc.7b04188.
38. C. Anzivino, F. Chang, G. Soligno, R. van Roij, W. K. Kegel and M. Dijkstra, Soft Matter, 2019, 15, 2638,  10.1039/C8SM02361A.
39. P. M. Chaikin and T. C. Lubensky, Principles of Condensed Matter Physics, Cambridge University Press, 1995, ISBN 9780521432245, https://www.cambridge.org/core/product/identifier/9780511813467/type/book.
40. W. H. Evers, B. Goris, S. Bals, M. Casavola, J. de Graaf, R. van Roij, M. Dijkstra and D. Vanmaekelbergh, Nano Lett., 2013, 13, 2317,  DOI:10.1021/nl303322k , ISSN 1530-6984.
41. M. P. Boneschanscher, W. H. Evers, J. J. Geuchies, T. Altantzis, B. Goris, F. T. Rabouw, S. A. P. van Rossum, H. S. J. van der Zant, L. D. A. Siebbeles and G. Van Tendeloo, et al. , Science, 2014, 344, 1377 , ISSN 0036-8075, https://science.sciencemag.org/content/344/6190/1377.
42. J. J. Geuchies, C. van Overbeek, W. H. Evers, B. Goris, A. de Backer, A. P. Gantapara, F. T. Rabouw, J. Hilhorst, J. L. Peters and O. Konovalov, et al. , Nat. Mater., 2016, 15, 1248,  DOI:10.1038/nmat4746 , ISSN 1476-4660.
43. J. G. Donaldson and S. S. Kantorovich, Nanoscale, 2015, 7, 3217,  10.1039/C4NR07101H.
44. J. G. Donaldson, P. Linse and S. S. Kantorovich, Nanoscale, 2017, 9, 6448,  10.1039/C7NR01245D.
45. P. Linse, Soft Matter, 2015, 11, 3900,  10.1039/C5SM00338E.
46. L. Rossi, J. G. Donaldson, J. M. Meijer, A. V. Petukhov, D. Kleckner, S. S. Kantorovich, W. T. Irvine, A. P. Philipse and S. Sacanna, Soft Matter, 2018, 14, 1080 , ISSN 17446848.
47. L. Abelmann, T. A. G. Hageman, P. A. Löthman, M. Mastrangeli and M. C. Elwenspoek, Sci. Adv., 2020, 6, eaba2007.
48. H. R. Vutukuri, F. Smallenburg, S. Badaire, A. Imhof, M. Dijkstra and A. Van Blaaderen, Soft Matter, 2014, 10, 9110 , ISSN 17446848.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01815e

---