 Open Access Article
Open Access ArticleGrowth of gas-filled penny-shaped cracks in decompressed hydrogels†
Yansheng
Zhang
 ,
Merlin A.
Etzold
,
Merlin A.
Etzold
 and
Adrien
Lefauve
and
Adrien
Lefauve
 *
*
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK. E-mail: lefauve@damtp.cam.ac.uk
First published on 7th January 2021
Abstract
We report that the decompression of soft brittle materials can lead to the growth of internal gas-filled cracks. These cracks are oblate spheroids (‘penny shape’), whose major radius grows linearly in time, irreversibly fracturing the surrounding material. Our optical measurements in hydrogels characterise and quantify the three-dimensional crack geometry and growth rate. These results are in good agreement with our analytical model coupling fracture mechanics and gas diffusion, and predicting the dependence on the mechanical properties, gas diffusivity and super-saturation conditions (gas pressure, solubility, temperature). Our results suggest a new potential mechanism for decompression sickness in scuba diving and for indirect optical measurements of the fracture properties of hydrogels.
1 Introduction
It is well-known that dissolved gases can form bubbles following a reduction in solubility caused by a reduction in ambient pressure (decompression). This general phenomenon spans a variety of materials (liquids and solids) and applications, ranging from fizzy drinks (e.g. champagne1), industrial high-pressure gas containers (cavitation damage of rubber seals2), and volcanic eruptions (fragmentation of rising magma3). A related phenomenon occurs in polymer networks saturated by liquid–liquid mixtures. Liquid droplets may form within the polymer following a reduction in miscibility caused by temperature4–6 or composition,4 thus causing the polymer to deform in order to accommodate the new phase. However, perhaps the best-studied application of the gas–liquid phenomenon is the decompression sickness experienced by human scuba‡ divers. Gases breathed while at depth dissolve in body tissues (blood, skin, muscles, joints, nerves, etc.) at concentrations exceeding saturation at atmospheric pressure, and can form bubbles upon resurfacing. These bubbles can, for inert gases (chiefly N2) and under certain ‘extreme’ circumstances, grow numerous and large enough to be painful, seriously pathological, and even fatal (see ref. 7 Section 2.2 for a short review of the complex pathophysiology).Significant research and debate exist on the conditions under which bubble populations can form and grow; in particular on the questions of bubble nucleation at liquid/solid interfaces,8–10 the competition between perfusion and diffusion in soft tissues,11–13 and the role of tissue elasticity.14,15 However, these studies have in common to assume that gas bubbles are spherical in shape, and that when they grow in soft materials, they do so by elastic (and therefore reversible) deformation. These assumptions are broadly consistent with the limited number of observations of small (≲ 1 mm) bubbles in hydrogels mimicking artificial tissues.15,16 However, the forced syringe injection of liquid17,18 or gas19 into hydrogels is known to cause large (≫ 1 mm) cracks that are non-spherical and that grow by irreversible fracture of the material.
In this paper we demonstrate and explain that the growth of large, non-spherical, gas-filled cracks can also generically occur as a result of decompression.
We study hydrogels super-saturated in dissolved CO2 by swelling cross-linked polyacrylamide beads in carbonated water at modest absolute pressures (≈2–4 bar). Upon decompression to atmospheric pressure, no gas-filled bubble or crack forms spontaneously; instead we drop a hydrogel bead (weighing ≈10 g) directly onto a solid surface (from a modest height ≈0.1–1 m) in order to initiate or enlarge microscopic internal fractures (invisible to the naked eye). For sufficiently high concentrations of dissolved gas (proportional to the gas pressure during swelling) and impact heights, a number of gas-filled cracks (typically one to five) start growing inside the bead.
What follows is illustrated in Fig. 1. The spherical hydrogel bead is imaged almost fully immersed in water, against a high-contrast grid background (the edge of the bead is outlined in black). At time 32 s after impact, two millimetre-sized, circular thin cracks are clearly visible near the centre of the bead. Until time t = 82 s (second panel) these cracks grow independently of one another at similar speeds (≈2 mm radius gain in 50 s). Until t = 132 s, these ‘penny-shaped’ (or ellipsoidal) cracks grow in increasing proximity, slightly distorting each other. Over the next 10 s, they partially merge, before the ‘left’ crack deflates after reaching and breaking through the surface of the bead. As a result, the ‘right’ crack partially deflates as well, and both cracks undergo a few oscillations in size before coming to a relative rest. The whole process is evidently irreversible. The corresponding movie is available as ESI.†
In the remainder of this paper, we focus on the more elementary problem of the growth of a single gas-filled crack in an apparently infinite elastic brittle material following sudden decompression and impact.
Our objectives and outline are as follows. In Section 2 we explain how we used optical measurements to accurately measure the three-dimensional shape of a crack during its growth. In Section 3 we derive a predictive model for the crack shape and growth from first principles. In Section 4 we validate this model with our experimental measurements, covering a range of pressures and mechanical properties. In Section 5 we discuss implications of our work and conclude.
2 Experiments
2.1 Protocol
Our experiments were conducted as follows.First, bottled water was carbonised with pure CO2 using a home soda maker, at variables absolute pressures in the range 2–4 bar (the water was first chilled to reach the highest pressures).
Second, a few commercial-grade cross-linked polyacrylamide dry beads (Soil MoistTM, JRM Chemical, USA, as in ref. 20) were swollen at room temperature with this carbonated water in a sealed bottle for at least 48 hours.
Third, the seal cap was broken, and swapped with a pressure gauge cap. The bottle was vigorously shaken in order to stabilise the pressure of the small pocket of CO2 above the water, which we take as the equilibrium ‘super-saturation’ pressure ps to determine the dissolved gas concentration in the beads cs = khps (where kh is Henry's law solubility constant).§ The water temperature inside the bottle was measured within 0.5 °C and used as the representative experimental temperature T of the hydrogel.
Fourth, a bead was taken out of the bottle, and its diameter, mass, and elastic Young modulus E were measured. For the latter we used the standard Hertz contact model and fitted the force/displacement curve obtained by compressing the spherical bead between two rigid glass plates using an accurate translation stage and balance (for more details about this method, see the ESI,† Section 2). Inherent variability in the polymer/water volume fraction among the beads caused a range of E = 12–28 kPa, which we will use to our advantage in order to validate our model in Section 4.
Fifth, directly afterwards, the bead was individually dropped from ≈0.2 m onto a flat glass plate (as described in the introduction).¶ The bead was then inspected by eye, and, if no visible gas-filled crack had formed, it was dropped again from incremental heights, until a single crack formed or two cracks formed far enough from one another to remain largely independent for sufficiently long times. If the crack was too close to the surface of the bead, or if multiple cracks formed too close to one another, the bead was discarded, another bead was taken out of the bottle, and these steps were repeated.
Sixth, the ‘successful’ bead was swiftly positioned in a (non-carbonated) water bath at the same temperature T as the bead. Imaging started typically at t ≈ 5–20 s (recorded from the moment of the successful impact) and continued until the crack reached the surface of the bead or became visibly influenced by it.
2.2 Imaging
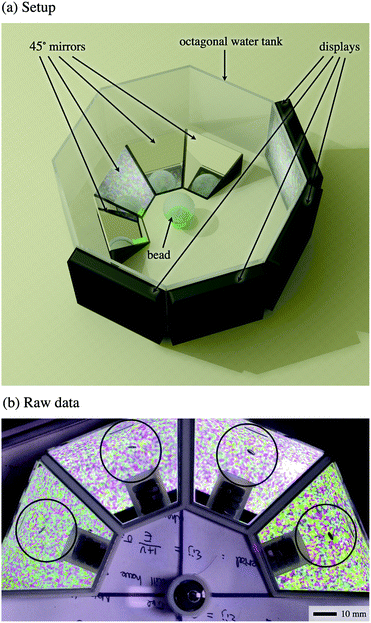 | ||
| Fig. 2 (a) Experimental setup to capture four views at 45° of a single crack growing inside the bead. The camera (not displayed here) is placed directly over the bead. The water level (not displayed here) is such that the mirrors are fully submersed, and the bead almost submersed, as in Fig. 1 (the bead is not fully submersed to prevent it from floating). (b) Snapshot illustrating the raw data obtained by the camera, ready for analysis in Fig. 3 (the edge of the bead is outlined in black). | ||
This allowed a single video camera, which had a top view of these mirrors, to capture simultaneously four different and complementary views of the growth of a single ‘isolated’ crack, as shown in Fig. 2b. These four views were then combined during image analysis to reconstruct the time-resolved, three-dimensional geometry of the crack.
A bright and high contrast colour background was displayed by LCD screens placed directly across each mirror (see Fig. 2a). To avoid undesirable reflections and loss of background brightness, an octagonal water tank was used to immerse the bead and mirrors.
Images were captured by an 8.3 MPixels video camera with good depth of field and negligible parallax. The resulting spatial resolution was 40 μm Pixel−1 (although the combination of four views could achieve sub-pixel resolution). The frame rate of 25 Frame s−1 was sufficient given our growth rates in the range 0.5–4.5 Pixel s−1, corresponding to 0.02–0.18 Pixel Frame−1.
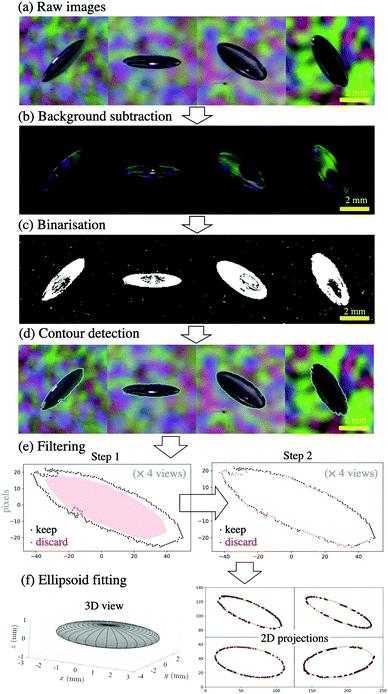 | ||
| Fig. 3 Key steps of the image analysis, from (a) the acquisition of raw images (four views at 45° angles) to (f) the three-dimensional ellipsoid best fitting the crack (more details in the ESI,† Section 3). | ||
The raw images (panel a) first underwent background subtraction (panel b), binarisation (panel c), and contour detection (panel d).
These raw contours were invariably noisy, and were thus filtered in two steps (panel e). In step 1, their convex hull was computed, shrunk to 80% (shown in red shade), and any points inside this region were discarded (shown in red). In step 2, two-dimensional ellipses were fitted to the remaining points, and the points furthest away from the fitted ellipse were in turn discarded (shown in red). A further set of two-dimensional ellipses were fitted to the final set of remaining points, which were then centred based on this last two-dimensional fit (this centering is crucial in order to ensure that all views have a common origin for the next step).
Finally, a three-dimensional ellipsoid was fitted (panel f) by minimising the distance between the four projections of this ellipsoid (at 45°) and the four sets of remaining points centred on a common origin. Our choice of fitting a three-dimensional ellipsoid to the crack was influenced by our observations (see Fig. 1), as well as theoretical expectations (as will become clear in Section 3.1). The adequacy of this choice is confirmed by the excellent agreement between the two-dimensional projections of the fitted ellipsoid and the four filtered contours (see panel f, right hand side).
The absolute position of the crack within the bead could be and was computed, but it is not discussed in this paper since we focus exclusively on the crack geometry. More details about the image acquisition and analysis are given in the ESI,† Section 3.
2.3 Qualitative observations
Fig. 4 shows the results obtained from image processing in a typical experiment (quantitative results for this particular experiment will be discussed in Section 4.1).In panel a, we plot four snapshots (i = 1–4) of the three-dimensional ellipsoid best fitting the crack geometry at t = iΔt where Δt = 24.5 s (for visualisation purposes, the ‘base’ of successive cracks is arbitrarily set as the z = −3i plane). In panel b, we reveal further details by plotting two-dimensional projections of the crack: a ‘top view’ (x–y plane) and a ‘side view’ (y–z plane). These ellipses are plotted successively so that they create a continuous spatio-temporal trace, whose edge allows us to infer the growth rate (the four snapshots of panel a are also highlighted in white in panel b for comparison).
First, we confirm the observations of Fig. 1 that the crack is not spherical; it is circular but thin. In other words it has two approximately equal major axes (here along x,y by convention) and a much smaller minor axis (here along z).
Second, sets of straight dashed lines prove to be excellent guides to the growth of the crack along its major axes (panel a and top view in panel b), suggesting linear growth of the radius in time. However, straight lines prove to be poor guides to the growth of the crack along its minor axis (side view in panel b), suggesting that the thickness grows with sub-linear scaling (the growth slows down with time). In other words, the aspect ratio is not conserved; the crack becomes relatively thinner with time.
3 Model
In this section we introduce an analytical model to account for the above observations and provide quantitative predictions. We establish the link between crack geometry and gas pressure within the crack in Section 3.1, add the diffusion of gas into the crack in Section 3.2, and finally deduce its temporal growth in Section 3.3. The model is sketched in Fig. 5 and the key constants and variables used in the remainder of the paper are summarised in Table 1.| Name | Description/definition | SI unit | Value |
|---|---|---|---|
| p a | Atmospheric pressure | Pa | 1.013 × 105 |
| p s | Partial gas pressure in vessel during the swelling of the hydrogel | Pa | Varied (2.3–4.1 × 105) |
| p b(t) | Absolute pressure inside growing bubble (uniform) | Pa | — |
| Δp(t) | Pressure in bubble relative to atmospheric = pb(t) − pa | Pa | — |
| R(t) | Radius of the penny-shaped (spheroidal) crack (R ≪ R∞) | m | Measured (Fig. 4 and 6) |
| w(r,t) | Width of the crack | m | Measured (Fig. 4) |
| A(t) | Area of the crack | m2 | Measured (Fig. 4) |
| V(t) | Volume of the crack | m3 | Measured (Fig. 6) |
| E | Young modulus of the gel | Pa | Measured (Fig. 7) |
| ν | Poisson ratio of the gel | — | 0.5 (incompressible) |
| K I(t) | Stress intensity factor at the crack tip (‘opening’ mode I loading) | Pa m1/2 | — |
| K IC | Critical stress intensity factor (mode I), also called material toughness | Pa m1/2 | Estimated by V, R, E (Fig. 7) |
| G C | Critical strain energy release rate (mode I) = 3KIC2/(4E) | Pa m | Estimated by V, R, E (Fig. 7) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) |
Elasto-fracture length of the gel = 9KIC2/(4πE2) = 3GC/(πE) | m | Estimated by V, R (Fig. 7) |

|
Ideal gas constant | J K−1 mol−1 | 8.314 |
| T | Temperature during swelling of the gel and crack growth | K | Measured (295–299) |
| k h | Henry's solubility constant in water (here for CO2) | mol m−3 Pa−1 | 3.4 × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{2400(T−1 – 298.15−1)} exp{2400(T−1 – 298.15−1)} |
| D | Diffusivity of the gas in water (here for CO2) | m2 s−1 | 1.9 × 10−9+ 4.8 × 10−11(T – 298.15) |
| c(r,z,t) | Dissolved gas concentration in the hydrogel, i.e. (r,|z|) > (R,w) | mol m−3 | — |
| c b(r,t) | Dissolved gas concentration at the crack boundary = khpb(t) | mol m−3 | — |
| c s | Dissolved gas concentration far from the crack = khps | mol m−3 | — |
| Δc | Gas concentration difference driving the diffusion = kh(ps − pa) > 0 | mol m−3 | — |
| S | Non-dimensional super-saturation ‘strength’ = ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) TΔc/pa TΔc/pa |
— | varied through ps (1.07–2.67) |
| α | Growth rate of the crack radius = dR/dt | m s−1 | measured and estimated by D, S, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (Fig. 8) (Fig. 8) |
3.1 Fracture mechanics
 | (1) |
Mathematically, this ‘penny’-shaped crack is an oblate spheroid (sketched in Fig. 5a and b). Since our hydrogel is primarily made of (incompressible) water, we use ν = 0.5 throughout the remainder of the paper.
 | ||
| Fig. 5 Model sketch. (a and b) Top and side view of the general crack geometry. (c) Axial diffusion (along z) of the gas concentration between the ‘far-field’ cs and the crack flat boundary cb ≈ cs − Δc, the gas flux being proportional to the gradient ∂c/∂z at the growing boundary. (c) Principle of the time integration of the diffusive flux during crack growth as explained in (13)–(16). In (c and d) the bottom half of the crack z < 0 is implicit by mirror symmetry. | ||
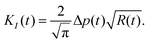 | (2) |
The crack propagates when KI reaches the critical stress intensity factor (or toughness) KIC, a material property.** This quasi-static propagation criterion allows us to link, at all times, crack pressure and radius as
 | (3) |
Inserting (3) into (1), we link the crack geometry to the mechanical properties
 | (4) |
 | (5) |
We recognise that this fundamental V(t) ∝ R5/2(t) scaling relation predicted for penny-shaped cracks can be equivalently written as
 | (6) |
In other words, the maximum width (thickness) of the crack is the geometric mean of R and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , the elasto-fracture length27 of the material defined as
, the elasto-fracture length27 of the material defined as
 | (7) |
This penny-shaped crack geometry has been used extensively, in particular in the geophysical literature on the hydraulic fracturing of rocks.17,18,28
 | (8) |
We interpret this as the main condition under which the above fracture mechanics model is valid, and under which ‘large’ (R > ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) gas-filled penny-shaped cracks are expected, as opposed to the ‘small’ (R <
) gas-filled penny-shaped cracks are expected, as opposed to the ‘small’ (R < ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) spherical bubbles considered elsewhere in the literature.8–15
) spherical bubbles considered elsewhere in the literature.8–15
3.2 Gas diffusion
We now add the diffusion of dissolved gas, as sketched in Fig. 5c, to obtain a dynamical equation for the volume V(t) and the radius R(t). .
.
 | (9) |
We convert the above molar flux of dissolved gas into the following volume flux of ideal gas inside the crack:
 | (10) |
Importantly, we note that it represents the flux per unit area at a time t after this unit area was created.
As the crack grows, new area is continually created, such that the instantaneous flux (10) across ‘new areas’ close to the crack tip (r ≲ R) is always higher than that across ‘old areas’ close to the centre (r ≈ 0) as sketched in Fig. 5c.‡‡ For a unit area created at t = 0, the total change in volume per unit area after time t is thus given by the integral
 | (11) |
We define the convenient effective diffusivity Deff, which can also be expressed in terms of the non-dimensional ‘super-saturation’ S that we define as
 | (12) |
• At t0 = 0 the area is A(t0) ≈ 0 and the volume is V(t0) ≈ 0.
• At t1 = δt (small) the crack surface is an infinitesimal disk of area  and the crack volume is
and the crack volume is
 | (13) |
• At t2 = 2δt the cumulative flux through the ‘old’ area A1 slowly increases (thicker arrow in Fig. 5d), while we now have an additional flux through the ‘new’ infinitesimal annulus of area  The total volume is thus given by
The total volume is thus given by
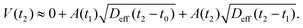 | (14) |
• At ti = iδt, we generalise this sum by mathematical induction
 | (15) |
Note that ti stays constant in the sum over tj.
In the limit δt → 0 we recover the following convolution integral
 | (16) |
3.3 Deducing the growth dynamics
We now assume that the crack grows with power law R(t) = αtn, and we seek the growth rate α and exponent n.Combining the V–R scaling relation of fracture mechanics (6), the total area A = 2πR2 (thin crack), and the gas diffusion history (16), we find
 | (17) |
Using the power law ansatz, we find
 | (18) |
Since α is independent of t, the last equation requires n = 1, thus our model predicts linear growth
| R(t) = αt. | (19) |
By evaluating the integral in (18) as = 4/15 we find the growth rate
 | (20) |
We conclude that the growth rate is given analytically by the dimensional speed D![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −1 (gas diffusivity/material elasto-fracture length), modulated by S2 (square of the non-dimensional super-saturation), and a pre-factor ≈0.81. This is the main result of our model.
−1 (gas diffusivity/material elasto-fracture length), modulated by S2 (square of the non-dimensional super-saturation), and a pre-factor ≈0.81. This is the main result of our model.
Note that the time scaling of diffusion-driven cracks (dV/dt ∝ t3/2 and R ∝ t) differs from that of fluid-driven cracks created by a constant injection rate (dV/dt = const. and R ∝ t2/5 in the toughness-dominated limit).17,18
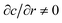 due to the crack growth history (see Fig. 5c). The full two-dimensional axisymmetric diffusion problem does not admit an analytical solution because it requires mixed boundary conditions at z = 0 (fixed c = cb for r < R and no flux for
due to the crack growth history (see Fig. 5c). The full two-dimensional axisymmetric diffusion problem does not admit an analytical solution because it requires mixed boundary conditions at z = 0 (fixed c = cb for r < R and no flux for  for r > R by symmetry) as well as moving boundaries R(t) = αt.
for r > R by symmetry) as well as moving boundaries R(t) = αt.
However, by a simple advection–diffusion scaling argument we consider the ratio of maximum length-scales achieved by advection ατ and diffusion  where τ is the total experimental run time. The resulting Péclet number is
where τ is the total experimental run time. The resulting Péclet number is  (in terms of maximum crack radius achieved Rmax = R(τ)). Using our experimental values (discussed later), we find a range of Pe ≈ 40–800, which is indeed high enough (≫1) to neglect radial gradients.
(in terms of maximum crack radius achieved Rmax = R(τ)). Using our experimental values (discussed later), we find a range of Pe ≈ 40–800, which is indeed high enough (≫1) to neglect radial gradients.
Numerical solutions of the full problem confirmed that even for values as low as Pe = 15 (corresponding to a crack growth slower and longer than in any of our experiments) purely axial diffusion under-estimates the actual final gas flux across the crack boundary by less than 1%. For more details on these scaling arguments and numerical solutions, see the ESI,† Section 4.
Using (19) we recast this Pe ≫ 1 validity condition of purely axial diffusion as
Rmax ≫ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) S−2 S−2 | (21) |
In other words, the maximum radius achieved by the crack must greatly exceed ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) S−2, otherwise radial diffusion will noticeably reduce the gas flux, and therefore the pre-factor in (20).
S−2, otherwise radial diffusion will noticeably reduce the gas flux, and therefore the pre-factor in (20).
4 Results and model validation
We now turn to experimental results to validate the model, which can be summarised by four equations only: the shape of the crack (6); the relation between shape and mechanical properties (7); the linear growth of its radius (19); and the dependence of the growth rate on system parameters (20). We examine (6) and (19) in Section 4.1, (7) in Section 4.2, and (20) in Section 4.3.4.1 Crack shape and linear growth
To illustrate our analysis of the data, we focus in this section on a single representative experiment (identical to that of Section 2.3 and Fig. 4).Both measures of the radius are in good agreement and grow linearly to a very good approximation (as anticipated in Fig. 4), which validates the key model eqn (19). Linear fits (dashed lines) give similar growth rates α = 0.0410 mm s−1 (from here on quoted using the more direct ‘orange’ contour data, but within a few percents of the ‘black’ ellipsoid data). In this and other experiments, the standard error of the linear fit is typically negligible (<0.1%), such that we consider this measured α virtually exact. We defer the comparison between this value and that predicted by the model in (20) to Section 4.3, because the predicted α will suffer from errors in S and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) that we have not yet addressed.
that we have not yet addressed.
From the intercept of the fit R(t = 0) ≈ 0.4 mm we conjecture that, immediately upon impact, the radius was <0.4 mm and grew more rapidly than αt (i.e. sub-linear in time). However, more detailed observations would be needed to clarify the early-time behaviour, which falls outside the scope of this paper.
We see that the crack geometry closely follows the penny shape scaling V ∝ R2.5 assumed in the model, since the best power law fit gives an exponent 2.54. This is typical of our other experiments, which had an average exponent 2.55 with standard deviation 0.12. This validates the key model eqn (6).
![[small script l]](https://www.rsc.org/images/entities/b_char_e146.gif) Value.
The intercept of the fit, V(R = 1 mm) = 1.23 mm3, provides a first straightforward optical measurement of the elasto-fracture length of the material
Value.
The intercept of the fit, V(R = 1 mm) = 1.23 mm3, provides a first straightforward optical measurement of the elasto-fracture length of the material ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = {(3 × 1.23)/(4π)}2 ≈ 0.0862 mm (assuming the V ∝ R2.5 scaling). More rigorously, we apply (6) directly to all the data and plot
= {(3 × 1.23)/(4π)}2 ≈ 0.0862 mm (assuming the V ∝ R2.5 scaling). More rigorously, we apply (6) directly to all the data and plot  (shown in the inset in blue). The mean value across the full range of R is
(shown in the inset in blue). The mean value across the full range of R is ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 0.0931 mm (solid line), and the standard deviation is 0.0044 mm = 4.7% of the mean (dashed lines). Henceforth we take these values as the measured
= 0.0931 mm (solid line), and the standard deviation is 0.0044 mm = 4.7% of the mean (dashed lines). Henceforth we take these values as the measured ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and its error (the error being primarily caused by apparent deviation from the exact scaling V ∝ R2.5).
and its error (the error being primarily caused by apparent deviation from the exact scaling V ∝ R2.5).
4.2 Mechanical properties
In Fig. 7 we present results from 70 independent experiments in which![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) was measured from R(t), V(t) data as explained in the previous section, E was measured as explained in Section 2.1 (and ESI,† Section 2), and KIC, GC were deduced from
was measured from R(t), V(t) data as explained in the previous section, E was measured as explained in Section 2.1 (and ESI,† Section 2), and KIC, GC were deduced from ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , E using (7). We plot
, E using (7). We plot ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , KIC, GC (respectively in panel a, b, c) against E (common horizontal axis) to investigate potential correlations between elastic and fracture properties.
, KIC, GC (respectively in panel a, b, c) against E (common horizontal axis) to investigate potential correlations between elastic and fracture properties.
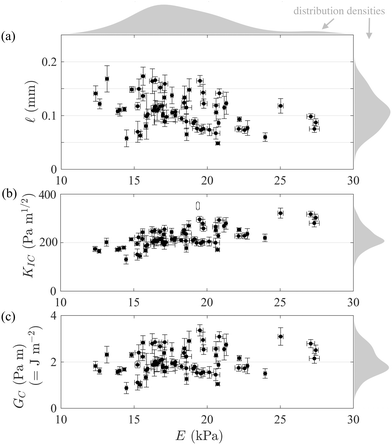 | ||
Fig. 7 Linear elastic fracture mechanical properties in 70 independent experiments: (a) elasto-fracture length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (determined as in Fig. 6b); (b) critical stress intensity factor (or toughness) KIC = (2π1/2/3)E (determined as in Fig. 6b); (b) critical stress intensity factor (or toughness) KIC = (2π1/2/3)E![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1/2; (c) critical strain energy release rate GC = (π/3)E 1/2; (c) critical strain energy release rate GC = (π/3)E![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . All are plotted against the Young modulus E. The grey shaded areas represent their distributions (estimates of the probability densities). Error bars in KIC, GC were propagated from those in E, . All are plotted against the Young modulus E. The grey shaded areas represent their distributions (estimates of the probability densities). Error bars in KIC, GC were propagated from those in E, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (respectively (respectively 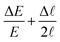 and and  ). ). | ||
First, we see that E covers a broad range ≈12–28 kPa (see its distribution in grey on top of panel a), despite the fact that we did not intentionally vary it (only ps was intentionally varied in these experiments). Beads were left to swell in similar conditions for ≈50–150 hours (but swelled little beyond the first ≈24 hours), and had a polymer/water volume fraction ϕ ≈ 0.3–2% (using extreme values of their dry radius 2.5–3 mm and wet radius 11–17 mm). We attribute theses variations in E to inherent variability in the manufacturing of our commercial-grade polyacrylamide gel beads, resulting in slightly different ϕ and relative weight of cross-linkers/monomers.29 This is qualitatively consistent with two previous studies on fractures in polyacrylamide gels at higher ϕ: ref. 19 reported a range E ≈ 1.5–600 kPa sharply increasing with ϕ ≈ 3–9% (see their Fig. 5), while ref. 30 reported E ≈ 50–700 kPa for ϕ ≈ 8–15% and varying cross-linkers/monomers weight fractions ≈2.5–6% (see their Fig. 4).
Second, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) covers a range of ≈0.05–0.2 mm (see its distribution in grey on the right of panel a). This remains an order of magnitude below the minimum crack radius measured in our experiments (Rmin ≈ 1 mm), which confirms the validity condition (8) of the penny-shaped model.
covers a range of ≈0.05–0.2 mm (see its distribution in grey on the right of panel a). This remains an order of magnitude below the minimum crack radius measured in our experiments (Rmin ≈ 1 mm), which confirms the validity condition (8) of the penny-shaped model.
Third, the corresponding range for the fracture properties is KIC ≈ 100–300 Pa m1/2 and GC ≈ 1–4 Pa m (or J m−2). The latter is at least an order of magnitude larger than the surface tension of water (≈0.07 Pa m) which justifies that we neglected surface tension in the model.
4.3 Growth rate predictions
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (Fig. 7a), allowed us to cover a range of α ≈ 0.01–0.15 mm s−1 (an order of magnitude). We find that the predicted α is on average 27% below the measured value (see the green dashed linear fit ‘y = 0.733x’). However, the discrepancy between predicted and measured α is highly variable (extreme values are ≈±50%).
(Fig. 7a), allowed us to cover a range of α ≈ 0.01–0.15 mm s−1 (an order of magnitude). We find that the predicted α is on average 27% below the measured value (see the green dashed linear fit ‘y = 0.733x’). However, the discrepancy between predicted and measured α is highly variable (extreme values are ≈±50%).
 | ||
Fig. 8 Comparison of growth rates: measured from dR/dt (linear fit of the orange data in Fig. 6a) vs. predicted from (20). The fit of the data has slope 0.733 (green dashed line), lower than the expected unit value (black solid line). Errors in the measured α are smaller than the symbol size, while errors in the predicted α (vertical error bars) were propagated from those in S, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (the relative error is thus (the relative error is thus  ). The error in the measured temperature T (±0.2%), involved in the calculation of D, S, is small enough to be neglected. ). The error in the measured temperature T (±0.2%), involved in the calculation of D, S, is small enough to be neglected. | ||
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (representing an average of 13%, primarily due to the imperfect V ∝ R5/2 scaling). These error bounds are such that the measured and predicted α are consistent for a quarter of our data (i.e. error bars cross the 1
(representing an average of 13%, primarily due to the imperfect V ∝ R5/2 scaling). These error bounds are such that the measured and predicted α are consistent for a quarter of our data (i.e. error bars cross the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 black solid line). However, it is clear that these uncertainties are not sufficient to account for the observed discrepancy. In other words, our model is essentially validated by our measurements, but it appears to systematically under-estimate the growth rate.
1 black solid line). However, it is clear that these uncertainties are not sufficient to account for the observed discrepancy. In other words, our model is essentially validated by our measurements, but it appears to systematically under-estimate the growth rate.
First, an imperfect equilibrium between the concentration of dissolved CO2 in the beads cs and the gas pressure ps measured above the solution (due to the surface tension barrier to bubble nucleation explained in the ESI,† Section 1.3) would cause our application of Henry's law cs = khps to slightly under-estimate cs and therefore S (through (12)).
Second, a more quantitatively plausible reason lies in the fact that some cracks do not grow in a perfectly flat plane as we assumed; instead minor inhomogeneities in the gel cause the crack plane to warp slightly. This warped plane, even when barely detectable by the naked eye, can cause our fitting to over-estimate the true crack thickness, its volume, and therefore our measured ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) (through (6)).
(through (6)).
Third, note that we may not invoke the finite size of the hydrogel bead as a possible reason. It is true that our finite surrounding medium may be felt by the crack, and oppose slightly less resistance than the assumed infinite medium. This would indeed cause us to under-estimate the true crack thickness, and therefore ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , and therefore to over-estimate the predicted α; but only if we obtained
, and therefore to over-estimate the predicted α; but only if we obtained ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from the mechanical properties E, KIC. However, in this paper we obtain
from the mechanical properties E, KIC. However, in this paper we obtain ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) from the observed crack geometry instead (and deduce KIC from it), which should effectively account for possible finite-size effects of the surrounding medium already. Finally, it is possible that the CO2 diffusivity D and solubility kh within the hydrogel are not identical to those in pure water (as assumed, see Table 1). Limited evidence appears to suggest that the polymer may slightly decrease D31 and increase kh.32 Both effects would thus tend to compensate one another, but details remain speculative.
from the observed crack geometry instead (and deduce KIC from it), which should effectively account for possible finite-size effects of the surrounding medium already. Finally, it is possible that the CO2 diffusivity D and solubility kh within the hydrogel are not identical to those in pure water (as assumed, see Table 1). Limited evidence appears to suggest that the polymer may slightly decrease D31 and increase kh.32 Both effects would thus tend to compensate one another, but details remain speculative.
5 Conclusions
Key result. We have shown and explained how initially microscopic (invisible) defects in decompressed hydrogels can, through diffusion and irreversible fracturing, grow as a penny-shaped crack with linear scaling in time R(t) = αt, where α ∝ DS2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −1 ∝ D(TkhpsE/KIC)2 (in terms of the basic parameters in Table 1), provided that R ≫ max(
−1 ∝ D(TkhpsE/KIC)2 (in terms of the basic parameters in Table 1), provided that R ≫ max(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) S−2). This key result has at least two applications.
S−2). This key result has at least two applications.
Optical measurements of fracture properties. It allows fracture properties of hydrogels (the toughness KIC, or equivalently its fracture energy GC) to be estimated indirectly by optical measurements of dR/dt = α (assuming that all other quantities D, T, kh, ps, E can be measured accurately). This new method represents an interesting alternative to that proposed in ref. 30 who used the forced syringe injection of liquid and optical dye attenuation to measure the penny-shaped crack thickness. This new method also complements previous cavitation rheology methods,33 based on the growth of spherical elastic (non-fracturing) bubbles to estimate material properties such as E.34
Decompression sickness. Our key result also suggests a new potential mechanism for decompression sickness: the growth of inert gas pockets with a potentially catastrophic linear scaling, and a thin penny-shaped geometry that irreversibly fractures body tissues. Future work is undoubtedly needed to assess the relevance of this mechanism in the very complex pathophysiology of decompression sickness.
Open questions. Our work raises at least three open questions.
First, what is the importance of tissue perfusion and of the potential presence of multiple cracks? Both phenomena would limit the available dissolved gas and therefore the crack growth. In particular, we would only expect to find ‘large’ cracks (say of a given radius R0) in poorly-perfused tissues in which the ‘flushing’ time-scale is ≫R0/α ∝ R0D−1S−2![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .
.
Second, what is the range of parameters involved in the physiology of decompression sickness? It is apparent that N2-filled cracks would grow much more slowly than our analogue CO2-filled cracks due to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio in solubilities kh (causing α to be reduced by a factor ≈502 = 2500 for a given temperature). We also expect body temperature (at least 10 °C larger than in any of our experiments) to further decrease α (since kh decays with T faster than 1/T). However, we also need to consider the potentially large (and poorly known) range of body tissue elasticity and toughness, and in particular their ratio, i.e. the elasto-fracture length
50 ratio in solubilities kh (causing α to be reduced by a factor ≈502 = 2500 for a given temperature). We also expect body temperature (at least 10 °C larger than in any of our experiments) to further decrease α (since kh decays with T faster than 1/T). However, we also need to consider the potentially large (and poorly known) range of body tissue elasticity and toughness, and in particular their ratio, i.e. the elasto-fracture length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∝ (KIC/E)2. Tissues with particularly small
∝ (KIC/E)2. Tissues with particularly small ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) could still be subject to appreciable growth rates.
could still be subject to appreciable growth rates.
Third, what is the early-time behaviour of this crack growth? This includes understanding the conditions in which micro-cracks are formed at t = 0. In these experiments we chose mechanical impact; in the body this could be micro-traumata in muscles, tendons, ligaments, joints, bones, or nerves. It also includes investigating the pathway by which initially small, ‘classical’ spherical bubble micro-nuclei might grow large enough (R ≫ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) to initiate fracture and bifurcate to the penny-shaped crack regime.
) to initiate fracture and bifurcate to the penny-shaped crack regime.
This last direction is also relevant to the growth of liquid cavities in polymer matrices mentioned in the introduction.4,5 Irreversible cavity formation has been reported in ref. 6 and attributed to a ductile response of the material, although, in principle at least, the brittle regime we described could also occur in these systems. An important difference between gas–liquid and liquid–liquid systems is the compressibility of the gas phase and the connection between gas solubility and pressure within the cavity. This may be the reason why liquid–liquid systems show spontaneous cavity growth after quenching, whereas our system requires an impact. We would also expect much slower crack growth in liquid–liquid systems due to the absence of volume change upon phase separation (compared to gas–liquid systems), perhaps making them ideal to study the early stages of crack formation.
Supporting data
The data and codes associated with this paper can be freely downloaded from the repository doi.org/10.17863/CAM.60212.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Mr Zhiyuan Wei for discussions about the modelling. This research was conducted while Y. Z. was an undergraduate student at Trinity College, Cambridge, supported by a Trinity Overseas Bursary. A. L. was supported by an Early Career Fellowship funded by the Leverhulme Trust and Isaac Newton Trust.Notes and references
- G. Liger-Belair, G. Polidori and P. Jeandet, Chem. Soc. Rev., 2008, 37, 2490–2511 RSC.
- A. N. Gent and D. A. Tompkins, J. Appl. Phys., 1969, 40, 2520–2525 CrossRef CAS.
- K. Ittai, L. Vladimir and N. Oded, Bull. Volcanol., 2011, 73, 39–54 CrossRef.
- R. W. Style, T. Sai, N. Fanelli, M. Ijavi, K. Smith-Mannschott, Q. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. X, 2018, 8, 011028 CAS.
- K. A. Rosowski, T. Sai, E. Vidal-Henriquez, D. Zwicker, R. W. Style and E. R. Dufresne, Nat. Phys., 2020, 16, 422–425 Search PubMed.
- J. Y. Kim, Z. Liu, B. M. Weon, T. Cohen, C.-Y. Hui, E. R. Dufresne and R. W. Style, Sci. Adv., 2020, 6, eaaz0418 Search PubMed.
- C. Walsh, PhD thesis, University College London, 2017.
- V. Papadopoulou, R. J. Eckersley, C. Balestra, T. D. Karapantsios and M.-X. Tang, Adv. Colloid Interface Sci., 2013, 191-192, 22–30 CrossRef CAS.
- M. Chappell and S. Payne, Respir. Physiol. Neurobiol., 2006, 153, 166–180 CrossRef CAS.
- O. R. Enríquez, C. Sun, D. Lohse, A. Prosperetti and D. van der Meer, J. Fluid Mech., 2014, 741, R1 CrossRef.
- H. D. Van Liew and M. P. Hlastala, Respir. Physiol., 1969, 7, 111–121 CrossRef CAS.
- S. R. Srinivasan, W. A. Gerth and M. R. Powell, Ann. Biomed. Eng., 2002, 30, 232–246 CrossRef.
- S. A. Mohammadein and K. G. Mohamed, ESAIM: Math. Modell. Numer. Anal., 2016, 21, 762–773 Search PubMed.
- S. Goldman, J. Chem. Phys., 2009, 131, 184502 CrossRef.
- C. Walsh, E. Stride, U. Cheema and N. Ovenden, J. R. Soc., Interface, 2017, 14, 20170653 CrossRef.
- D. E. Yount and R. H. Strauss, J. Appl. Phys., 1976, 47, 5081–5089 CrossRef CAS.
- C.-Y. Lai, Z. Zheng, E. Dressaire and H. A. Stone, Philos. Trans. R. Soc., A, 2016, 374, 20150425 CrossRef.
- N. J. OKeeffe, H. E. Huppert and P. F. Linden, J. Fluid Mech., 2018, 844, 435–458 CrossRef CAS.
- S. Kundu and A. J. Crosby, Soft Matter, 2009, 5, 3963 RSC.
- T. Bertrand, J. Peixinho, S. Mukhopadhyay and C. W. MacMinn, Phys. Rev. Appl., 2016, 6, 064010 CrossRef.
- R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981 CrossRef CAS.
- in CRC Handbook of Chemistry and Physics: a Ready-Reference Book of Chemical and Physical Data, ed. W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Press, 97th edn, 2016 Search PubMed.
- I. N. Sneddon, Philos. Trans. R. Soc., A, 1946, 187, 229–260 Search PubMed.
- T. Kundu, Fundamentals of Fracture Mechanics, CRC Press, 2008 Search PubMed.
- G. R. Irwin, J. Appl. Mech., 1962, 29, 651–654 CrossRef.
- M. F. Kanninen and C. H. Popelar, Advanced Fracture Mechanics, Oxford University Press, 1985 Search PubMed.
- S. Rattan and A. J. Crosby, ACS Macro Lett., 2019, 8, 492–498 CrossRef CAS.
- E. Detournay, Annu. Rev. Fluid Mech., 2016, 48, 311–339 CrossRef.
- A. K. Denisin and B. L. Pruitt, ACS Appl. Mater. Interfaces, 2016, 8, 893–902 CrossRef.
- N. J. OKeeffe and P. F. Linden, Exp. Mech., 2017, 57, 1483–1493 CrossRef.
- L. Liu, A. Chakma and X. Feng, J. Membr. Sci., 2008, 310, 66–75 CrossRef CAS.
- Y. Zhao, Y. Shen, L. Bai and S. Ni, Appl. Surf. Sci., 2012, 261, 708–716 CrossRef CAS.
- C. W. Barney, C. E. Dougan, K. R. Mcleod, A. Kazemi-Moridani, Y. Zheng, Z. Ye, S. Tiwari, I. Sacligil, R. A. Riggleman, S. Cai, J.-H. Lee, S. R. Peyton, G. N. Tew and A. J. Crosby, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9157–9165 CrossRef CAS.
- J. A. Zimberlin, N. Sanabria-DeLong, G. N. Tew and A. J. Crosby, Soft Matter, 2007, 3, 763 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: See DOI: 10.1039/d0sm01795g |
| ‡ SCUBA = Self-Contained Underwater Breathing Apparatus. |
| § The cap swap was necessary because the available pressure gauge fittings did not provide a sufficiently good seal for >48 hours. Unfortunately this swap caused the system to lose a small amount of CO2, which we corrected for as described in the ESI,† Section 1. |
| ¶ This impact proved necessary since cracks did not grow spontaneously upon decompression in the range of pressures ps investigated here. However, preliminary experiments in which the beads were heated well above room temperature proved that thermal shock could also be sufficient to initiate crack growth. This method was not pursued in this work because of the need to carefully control and measure temperature for the validation of our model. |
| || This axisymmetry in isotropic materials is expected theoretically: the energy derivation of ref. 25 (eqn (24)) shows that any crack base that is initially non-circular will quickly become circular, even before the crack grows in thickness. |
| ** Here we present the (local) stress intensity factor approach. In linear elasticity, it is equivalent to the (global) energy approach, originally due to Griffith and improved by Irwin, which considers that fracture occurs when the rate of release per unit area of strain energy G stored in the surrounding material exceeds the material's critical value GC = 3KIC2/(4E) (under incompressible, axisymmetric i.e. plane strain conditions, see ref. 24 eqn (3.54) and ref. 26 eqn. (3.3)–(3.18)). Note that the surface tension of water is negligible compared to GC. |
†† We use (3) to estimate the maximum excess pressure inside the crack:  using our extreme experimental values (see Fig. 7b). At larger radii R(t) ≫ 1 mm, assuming Δp(t) ≪ ps is very reasonable for the diffusion problem. using our extreme experimental values (see Fig. 7b). At larger radii R(t) ≫ 1 mm, assuming Δp(t) ≪ ps is very reasonable for the diffusion problem. |
| ‡‡ This creates a radial gradient in the gas concentration c(r,z,t) inside the gel, which we neglected (this is validated later in Section 3.3). |
| This journal is © The Royal Society of Chemistry 2021 |



