Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaporation-driven colloidal cluster assembly using droplets on superhydrophobic fractal-like structures†
Carola
Seyfert
 *a,
Erwin J. W.
Berenschot
*a,
Erwin J. W.
Berenschot
 b,
Niels R.
Tas
b,
Niels R.
Tas
 b,
Arturo
Susarrey-Arce
b,
Arturo
Susarrey-Arce
 b and
Alvaro
Marin
b and
Alvaro
Marin
 *a
*a
aPhysics of Fluids Group, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands. E-mail: c.seyfert@utwente.nl; a.marin@utwente.nl
bMesoscale Chemical Systems, Faculty of Science and Technology, Mesa+ Institute, University of Twente, 7500 AE Enschede, The Netherlands
First published on 24th November 2020
Abstract
Microparticles can be considered building units for functional systems, but their assembly into larger structures typically involves complex methods. In this work, we show that a large variety of macro-agglomerate clusters (“supra-particles”) can be obtained, by systematically varying the initial particle concentration in an evaporating droplet, spanning more than 3 decades. The key is the use of robust superhydrophobic substrates: in this study we make use of a recently discovered kind of patterned surface with fractal-like microstructures which dramatically reduce the contact of the droplet with the solid substrate. Our results show a clear transition from quasi-2D to 3D clusters as a function of the initial particle concentration, and a clear transition from unstable to stable 3D spheroids as a function of the evaporation rate. The origin of such shape transitions can respectively be found in the dynamic wetting of the fractal-like structure, but also in the enhanced mechanical stability of the particle agglomerate as its particle packing fraction increases.
1 Introduction
Agglomerating small solid particles in clusters of a particular shape and size has been an intriguing challenge of fundamental soft matter research for decades. Precise knowledge of the underlying mechanisms and the governing factors of, for example, grain size and morphology, is a necessity for many fields of modern microtechnology, such as spray drying of colloidals,1,2 (3D) printing,3 coating processes,4 and drug delivery.5Handling micro- or nanoparticles in a dry state is challenging for many applications, due to adhesion forces and electrostatic charges. Often, it is easier to first suspend the particles in a liquid and then gain control over the evaporation of the suspending phase. At controlled evaporation, the particles can agglomerate into clusters of bigger size, which are easier to handle. Evaporating suspensions is a powerful tool for particle deposition, as was observed in works as early as Brown's, deepening his understanding of the motion now named after him.6 In those early works, Brown already observed “…those currents from centre to circumference [of the droplet], at first hardly perceptible, then more obvious, and at last very rapid, which constantly exist in drops exposed to the air…”. More than a century later, Deegan et al.7 explained the phenomenon, which is now popularly known as the coffee-stain effect: particles are being transported to the rim of a sessile evaporating droplet by “currents from centre to circumference”, and form a stain-like deposit, once the evaporation is complete. A crucial condition for this phenomenon to occur, is a stationary droplet perimeter at a contact angle below 90° with respect to the substrate. This leads to a replenishment of liquid at the outer rim in order to maintain a minimal liquid–air interface. The droplet perimeter, also described as the (three-phase) contact line, remains stationary or pinned as long as surface defects or surface-adhered particles prevent the contact line motion.8 However, if the contact line of the droplet is unpinned and moves freely across a pristine substrate, the coffee-stain effect will be mostly suppressed.9,10
In order to agglomerate particle clusters from suspension droplets via evaporation, all particles should ideally end up agglomerated around one point, e.g. at the centre of the droplet. To avoid the irreversible transport of particles away from the droplet centre, an unpinned contact line and high contact angles are therefore essential requirements for a particle cluster formation. Both requirements can be met by evaporating the droplets on superhydrophobic substrates.11–17 On a superhydrophobic substrate, water-based droplets minimize their contact area with the solid due to the considerably higher solid–liquid surface energy than the droplet's liquid–gas energy. The increased energy difference is often induced by a chemical treatment of the solid substrate (see Section 3.1 for more details). To reduce the contact between liquid and solid as far as possible, the substrate is often decorated with micro- or nano-scopic asperities, which lead to a composite solid–liquid–gas interface underneath the droplet. The droplet then lays on top of a forest of microstructures, like a fakir, laying on a bed of needles.18–20 Such a droplet features high macroscopic contact angles with the substrate and little or no contact line pinning, as long as the pattern of microstructures is homogeneous and does not suffer from impurities or irregularities.
This superhydrophobic state of almost floating droplets is well described by the Cassie–Baxter model.12 Consequently, a droplet following this model is said to be in a Cassie–Baxter (CB) state. In contrast, when the droplet is fully engulfing the microstructures, the model developed by Wenzel11 applies, and the state in which the droplet is impaled on the asperities is called the Wenzel (W) state.
CB states typically involve larger surface energies than W states. This translates to a certain degree of metastability and larger contact angles in CB states than observed in W states. Droplets transition between the higher energy CB to the lower energy W by impaling on the asperities.21,22 However, this transition is rarely spontaneous and requires a certain input of energy due to the complex energy landscape.23 Impaling can happen due to, for example, evaporation and a consequent pressure increase inside the droplet,21 or due to mechanical force, pushing the droplet down into the substrate.24 Re-entrant features on the asperities14,25,26 can help to prevent the droplet from impaling.
Water droplets on superhydrophobic substrates are therefore ideal vessels for (non-volatile) colloidals, such as e.g. particles, polymers, and biological matter, due to the reduced contact with the solid substrate and the reduced interaction with the gas phase. But when the droplet evaporates, such ideal containers can become rather complex systems. Water evaporation leads to a continuous increase in volume concentration of non-volatile contents. As the droplet's volume reduces, non-volatile content can eventually aggregate in different structures depending on their nature.27,28 As a result, generating particle clusters from sessile suspension droplets is a simple way (due to the low energy input) to achieve agglomeration of particles on a very small length scale.
Despite the abundant literature on such systems, most of these studies are typically very narrow in the parameter space explored, and therefore there is a lack of understanding on which are the most important parameters to control the shape of the resulting colloidal structures via droplet evaporation.
In our study, we demonstrate that, using a robust superhydrophobic substrate and a stable colloidal solution, one can obtain a vast variety of particle assemblies by simply controlling the initial particle concentration (and to a lesser extent, humidity). Our results show two extreme kinds of cluster shapes: spherically-shaped (3D) clusters and flattened (2D) clusters, which we classify quantitatively based on their shape. On the one hand, 3D clusters offer high particle packing fraction and feature low surface area to volume ratios. On the other hand, 2D clusters offer direct access to the majority of particles in the deposit, and are of special interest for 2D printing applications.29
2 Methods
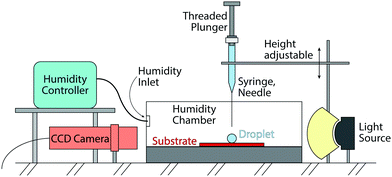
The performed experiments involve the evaporation of sessile droplets on a superhydrophobic substrate. The experiments take place inside a closed (not pressurized) chamber to minimize environmental influence. See Fig. 1 for a schematic of the set-up. The substrate is placed in line with the CCD camera (Ximea MQ013MG-ON) to capture the side view of the experiment. To deposit a droplet on top of the superhydrophobic substrate, we use a threaded-plunger syringe (glass syringe from Hamilton, Model 1750 LT Threaded Plunger SYR) with a blunt cut needle with a nominal outer diameter of 0.21 mm (also supplied from Hamilton, 33 gauge, Metal Hub Needle).In order to gently deposit the droplet, the needle is brought close to the substrate. We then form a droplet at the needle tip by slowly turning the threaded plunger, until the droplet touches the substrate and the needle at the same time. Once the droplet volume is big enough, we force the detachment of the droplet by retracting the needle upwards. The droplet consequently comes to rest on top of the substrate. With this method, used for all experiments, we reach droplet volumes between 3 μl and 4 μl. Our analysis show that such variation in initial volume does not affect the results.
The deposited droplets are either purified water droplets (Milli-Q® IQ 7000 Water Purification System), or water droplets with suspended fluorescent polystyrene particles of 0.98 ± 0.04 μm in diameter. We use suspensions of different particle concentrations, ranging from 0.0009 vol% to 1.66 vol% (the error margin for all concentrations stated in this work are ±10%). The fluorescent polystyrene particles (distributed by Microparticles GmbH) are functionalized with sulphate groups that convey electrostatic stability to the suspension with no need of additional surfactants. Prior to the experiments, the particle solutions are washed twice by diluting, centrifuging and extracting the supernatant. After the washing process, the particles stay homogeneously suspended for longer than 24 hours. The suspensions are stored in the fridge and are immersed in an ultrasound bath for 10 minutes prior to each experiment.
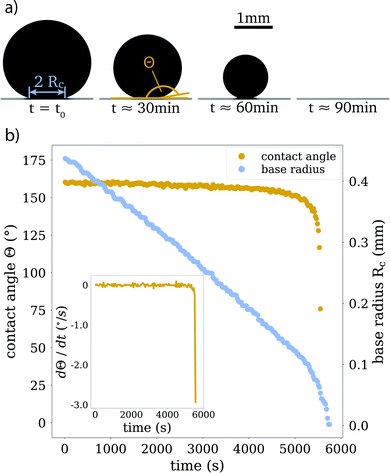
In every experiment, the evaporation process is captured from the side view with the CCD camera, with a frame rate of 0.5 frames per second (see Fig. 2 for sample images). From these images, we extract contact angles and droplet volumes as functions of time, as well as aspect ratios of particle clusters, after the liquid has completely evaporated. We categorize the clusters based on their morphology (see Section 4.2). For this classification, we also rely on scanning electron microscopy (SEM), see for example Fig. 5.
The role of the chamber is to shield the droplets against spurious air currents or sudden changes in temperature and humidity. For a number of experiments, we also use a humidity controller (HGC 30 from DataPhysics) to keep the humidity in the chamber at a constant value. The values for humidity and temperature within the chamber were monitored throughout all experiments.
3 Materials
3.1 Fractal-like substrates
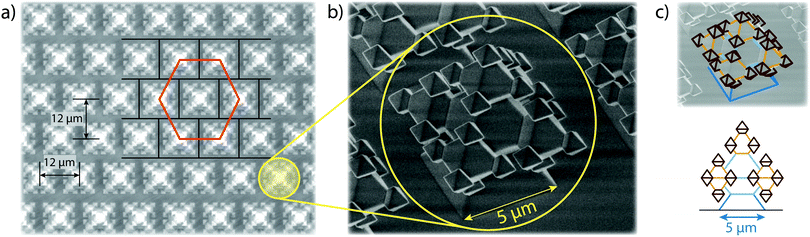
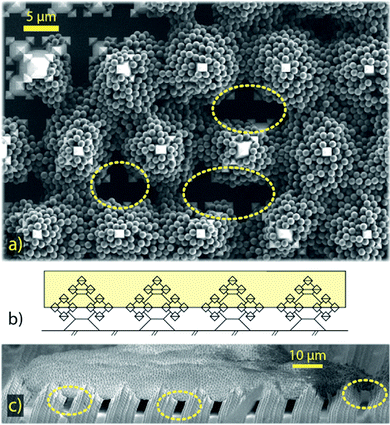
Typical superhydrophobic substrates have two components which render them superhydrophobic:26,30,31 a mechanical component, consisting of microscopic structures, that enlarge the surface area and enhance air entrapment, and a chemical component, consisting of a low-surface-energy coating. The substrates in our research were fabricated with oxide-only corner lithography and an anisotropic etching process of silicon,32,33 which delivers SiO2 substrates with microscopic fractal-like structures (see Fig. 3). The fractal-like structures consist of stacked octahedra, resulting from the crystalline structure of silicon. The intricate shape of the fractal-like asperities features several re-entrant geometries (see Fig. 3c). These “overhanging” steps are known to considerably improve the stability of the floating CB state of droplets.14,25,34,35 The base width of one fractal-like structure is 5 μm, the structures are ordered in a hexagonal pattern on the substrate and the pitch between structures is 12 μm. The actual surface area of this substrate is 13 times bigger than the projected one.Following Young's law of surface tensions,36,37 the high surface energy of SiO2 renders substrates of this material generally hydrophilic. Decorating the surface with microscopic structures, and therefore adding a roughness, will increase the wettability further,38 much like wetting a porous medium. However, applying a low surface energy coating to the surface renders the substrate superhydrophobic. To achieve this, we applied a vapour deposition protocol to coat our fractal-like decorated substrates with Fluoroctatrichlorosilane (FOTS),‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 which yielded static contact angles of ≥155° and roll-off angles as low as 1.2° ± 0.25°.
39 which yielded static contact angles of ≥155° and roll-off angles as low as 1.2° ± 0.25°.
4 Results
4.1 Experimental results
Since the evaporation process is the driving force for particle agglomeration, we first analyse the droplet evaporation process. Evaporating sessile droplets either shrink with a constant contact radius of the wetted area on the solid substrate (CCR mode), or with a constant contact angle, while the wetted area is decreasing (CCA mode).41,42 A droplet evaporating in a CCA mode maintains an unpinned contact line, with the radius of the wetted area decreasing due to decreasing droplet volume. If the contact line pins (and the droplet enters a CCR mode), the contact angle will need to decrease due to the continued volume loss. If the contact line de-pins again, the contact angle will jump back up to its original receding value. We do not observe significant pinning events on our substrates throughout the evaporation of the droplets, as is shown in Fig. 2 and its inset, where we can see that the change in contact angle as a function of time is negligible until the last instants. Our experiments therefore follow, for the majority of their duration, the CCA mode with contact angles of ≈155° due to the superhydrophobicity of the substrate, which prevented the droplet perimeter from pinning.Both modes of evaporation have been extensively studied. In this analysis, we will make use of the celebrated work by Popov,40 who investigated spatial deposition patterns of particles during the evaporation of sessile suspension droplets in CCR mode. However, since the derivation of evaporation rates is valid for arbitrary contact angles, this model has also been adapted for cases with droplets in CCA mode, e.g. by Nguyen et al.43 and Dash and Garimella15 and we implement their analytic approach in the following.
The evaporation rate can be described as a function of contact radius and contact angle:
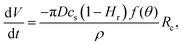 | (1) |
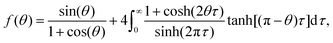 | (2) |
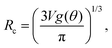 | (3) |
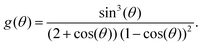 | (4) |
We want to emphasize that for all our experiments, the contact angle stays approximately constant and well above 150° throughout 90% of the droplet's lifetime. We therefore consider the functions f(θ) and g(θ), (eqn (2) and (4)) also constant for the majority of the duration of the experiments.
By numerically integrating eqn (2), and combining the result with eqn (3) into eqn (1), we obtain the following relation for the volume of the droplet in time:
| V(t)2/3 = V02/3 − kt, | (5) |
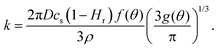 | (6) |
In order to make a prediction of the droplet volume evolution, we require empirical input from the initial droplet volume, the initial contact angle and the relative humidity in the chamber during the experiment. However, we noticed that the measured relative humidity does not seem to be representative of the far field vapour concentration felt by the droplet, and therefore we choose to use Hr as a fitting parameter. We find that our measured values are consistently off for all experiments by a factor of roughly ∼1.2, which might be caused by the fixed position of the humidity sensor.
In Fig. 4 we present the results of the measurements, expressed as volume loss over time, based on eqn (5). Fig. 4a shows data from droplets with and without added particles, conducted at similar relative humidities. As the plots overlap within the experimental error, we can safely conclude that the presence of particles at these initial concentrations does not influence the evaporation process. This holds even for the last stages, when the particle concentration reaches its highest values.
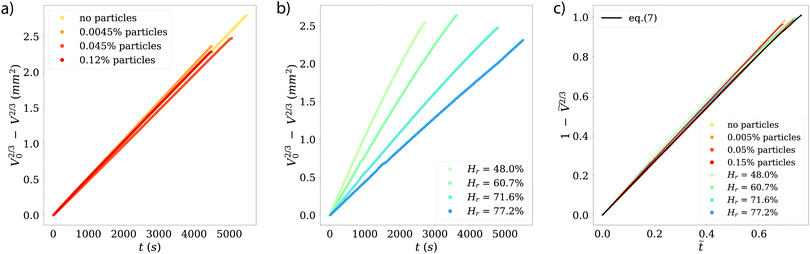 | ||
| Fig. 4 (a) Comparison of experiments with and without added particles, at similar relative humidities (Hr ≈ 71%). The results are plotted as the volume loss over time, following eqn (5). No influence of the particles is visible. (b) Experimental results in the same form as in panel (a), for experiments of pure water droplets (i.e. no particles) at different relative humidities. With an increase of relative humidity, the evaporation of the droplet takes longer. Note that all droplet have slightly different initial sizes (see Section 2), as can be seen in the different end points of the data. (c) Data from panels (a) and (b), now presented in dimensionless units, following eqn (7), which is plotted making use of the mean θ found in the experiments. All plots collapse, indicating that our experiments are governed by a diffusion-limited evaporation regime which can be described by the analytical solution by Popov.40 | ||
In Fig. 4b, we show experiments with pure water droplets, conducted at different relative humidities. An increase in relative humidity reflects in a decrease in evaporation rate, manifested in smaller slopes of the curves. In order to test the validity of the modelled evaporation rate for all experiments, we write eqn (5) in dimensionless form as
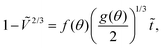 | (7) |
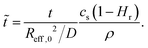 | (8) |
R eff,0 is the effective radius of the droplet at time t = 0. Note that since g(θ) and f(θ) are only functions of θ, they can be considered constant for the majority of the droplet's lifetime.
In Fig. 4c, we show the same experimental data from panels (a) and (b) in dimensionless form. Eqn (7) is plotted making use of the mean θ found in the experiments. The experimental data from the different experimental settings clearly collapses onto a single curve, matching also the theoretical predictions from eqn (7), and therefore we can conclude that our experiments are all governed by a diffusion-limited regime.
4.2 Morphological categories
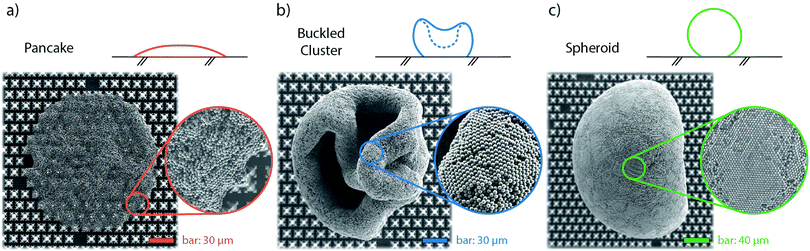
By varying the initial particle concentration of the evaporating droplets within more than three decades, we find a variety of shapes in the resulting particle clusters. We categorize them in three groups, depending on shape and formation, which are shown in Fig. 5. The two extreme shapes are on the one hand thin, flattened clusters (“pancakes”) and on the other hand, spheroid-shaped clusters with a smoothly curved surface, which we will describe as “spheroids”. In between these two extreme cases, we find clusters with irregular shapes which we will refer to as “buckled clusters”. This latter category of agglomerates experiences a sudden buckling instability in a late stage of evaporation.In order to better quantify the classification, we introduce the aspect ratio AR of the final cluster as AR = dv/dh, calculated from the side view images, where dv is the maximum vertical extend of the cluster (normal to the substrate) and dh the maximum horizontal one (parallel to the substrate).
The main control parameter is the initial particle concentration or initial particle packing fraction Φ0, defined as the fraction of volume taken up in the droplet by the solid particles. As the evaporation process takes the place, the particle packing fraction Φ(t) will increase until its maximum, which will change depending on the final particle arrangement. A perfectly ordered arrangement of the particles in close packing would yield a Φ|max of approximately 0.74. Unfortunately, due to the irregular shapes of the agglomerates and inaccuracies in the total number of particles per droplet, we are unable to compute their final packing fraction with sufficient precision.
Fig. 6 a shows the resulting aspect ratio AR as a function of the initial particle concentration Φ0. Starting with the lowest AR (Φ0 = 0.0009%, about 8 × 104 particles in 4 μl), at the left side of the figure, we find the pancake category, with aspect ratios well below 0.4.
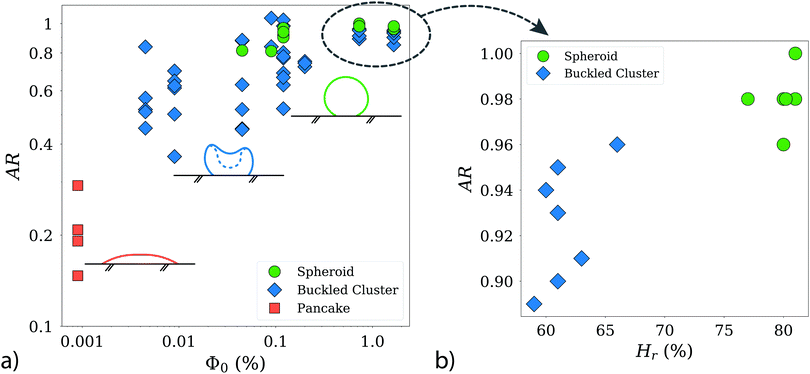 | ||
| Fig. 6 (a) Characterization of the clusters according to aspect ratio AR = dv/dh, and the initial particle concentration Φ0. Note the logarithmic scaling of the axes. The inset schematics and the denominations correspond to Fig. 5. With increasing Φ0 the final clusters present with higher aspect ratios. The distinction between buckles clusters and spheroids is not always sharp, as can be seen in the overlap of particle concentrations, where both categories co-exist. The data for high Φ0 is plotted again in panel (b), as AR = dv/dh over relative humidity Hr. Note here the linear scaling of the axes. We can see a clear trend for buckled clusters to present for lower Hr than spheroids. This trend is not as clear in lower Φ0. Therefore, we assume that a sufficiently high initial particle concentration is crucial for the influence of humidity to become quantifiable. | ||
Increasing the initial particle concentration to the range from 0.0045% to 0.009%, we start to find buckled clusters, which results in AR values of up to 0.9 in this range of packing fractions. As we continue further along the x-axis of the plot, towards the largest initial particle concentrations (Φ0 ≥ 1.66%), buckled clusters and spheroids, are both found in a similar range of AR values. Buckled clusters present a large variety of shapes, which explains their larger dispersion in AR. Note however, that the AR measurements are based only on a single side view image of each object, and therefore such measurements should be interpreted with caution. While spheroids and buckled clusters are found with similar probabilities for initial concentrations in the range from 0.009% up to 0.5%, regardless the humidity values, we do see a sharp dependence on the evaporation rate for the largest initial concentrations. This is shown in Fig. 6b, where spheroids are obtained with the highest probability at high humidity (slower evaporation rates), while buckled clusters are found with their larger dispersion in AR for lower humidity values (faster evaporation rate).
The adherence of the clusters to the substrates is an interesting property and worth mentioning: whereas the flattened pancakes stick to the substrates, clusters that consolidate a more 3D shape detach easily from the substrate after evaporation. Simple tilting of the substrate out of the horizontal plane will be enough to displace the clusters from their original position. Such lack of adherence was also observed by Wooh et al.17 for titanium oxide nanoparticles over soot-template superhydrophobic substrates.
In summary, our analysis indicates that the initial particle concentration in the droplet is a (if not the most) crucial factor in determining the final shape of the agglomerate. There are two interesting transitions that we will discuss in the following section: First, the fact that only flattened clusters are observed below packing fractions of 0.004%. Second, the puzzling transition from buckled clusters to stable spheroids, which does not occur for a certain critical initial particle concentration, but rather for a combination of Φ0 and humidity.
5 Discussion
Our results show that capillary water droplets (i.e. where the dominant length scale is smaller or comparable to the capillary length) evaporate following a CCA mode on surfaces decorated with fractal-like micropillars. The evaporation process follows a purely diffusive model, based on a modified version of the Popov model.40The presence of particles does neither affect the droplet evaporation, nor the contact line motion. Even the droplets containing the highest initial particle concentration still evaporate following a diffusion-limited process (Fig. 4a), and the contact line still follows a smooth CCA motion. As an indication of smooth contact line motion, we want to highlight the fact that no particles can be found outside the bounds of the final cluster. The suspended solid phase in our droplets is therefore completely recovered in a single agglomerate (supraparticle) via the evaporation of the suspending liquid phase. This is an important difference to previous studies on supraparticles on microstructured substrates14,20,44 in which – after reaching a certain particle concentration in the droplet – particles were deposited on top of pillars in the wake of the receding droplet perimeter, as a consequence of a regular stick-and-slip contact line motion.
We do not observe any stick-and-slip motion of the contact line (also see Fig. 2, inset) and instead, the droplet's movement across the substrate is smooth, until a final pinning event occurs at the end of the evaporation process. This final pinning event also limits the 3D cluster agglomeration. Droplets with the lowest initial particle concentration (Φ0 = 0.0009%) do not consolidate a robust particle cluster before the final pinning event occurs. The particle deposit then adopts a flattened circular shape (as seen in Fig. 5a), where the perimeter is determined by the final pinning event, however the height keeps decreasing further after the pinning happened.
The evaporation in CCA mode, with the droplet's base radius steadily decreasing until the final pinning event, gives an indication, that the droplet remains in a Cassie–Baxter state during the whole evaporation process. SEM close-ups of pancake clusters (see Fig. 7) show that the particles are partially engulfing the fractal-like structures. Since there is no evidence for particles at the bottom of the substrate between the fractal-like structures, the liquid seems to never fully penetrate the microstructured substrate. The pancake deposits indicate that the droplet gets partially impaled on the microstructures in a late stage of the evaporation. The particles, wrapping the fractal-like structures only on the top half, then indicate the liquid penetration level. As the final pinning event determines the extent of the pancake perimeter, final pinning and partial impalement possibly happen at the same time and are actually part of the same phenomenon: droplets in this small size range must be partially impaled by the structure,22 which eventually hinders the contact line motion. Wrapping the top half of the microstructures locks the pancakes in their final drying position, which also leads to these clusters to not easily detach, but to stick to the solid substrate.
As the initial concentration of particles increases from Φ0 = 0.0009% to 0.0045%, we observe a transition in cluster shapes: particles begin to consolidate three-dimensional clusters, without influence of the final pinning event.
Buckled clusters appear with variable probabilities for all initial concentrations above Φ0 = 0.0045%. In comparison to the pancakes, these clusters maintain a 3D shape, even though their height can decrease considerably during the buckling event. This leads to folded rims and hollow cores, as can be seen in Fig. 5b. Buckling instabilities in evaporating droplets have often been described as mechanical shell instabilities.45–48 Predictions for critical buckling conditions can be found for spray drying49 and Leidenfrost drying;45,46 as well as for the dissolution of water-based suspension droplets in oil.50,51 SEM images of buckled clusters (e.g.Fig. 5b) indicate that the buckling in the experiments of this study also has its origin in a shell formation at the interface of the droplet.52,53 However, a rigorous quantification of the mechanical shell (in-)stability during the evaporation process is outside of the scope of this work.
All 3D clusters (buckled or unbuckled) reveal highly-ordered particle patches at their surface (see the zoom-in views in Fig. 5), similar to those previously found for clusters of similar size.20 We interpret this as evidence of a predominant particle accumulation at the droplet surface (or in its vicinity). To confirm this we compare the particle diffusive time scale tB = rp2/Dp – where rp is the particle radius and Dp its Brownian diffusivity – with the time scale at which the interface approaches the particles. To construct the time scale of the interface we use the inwards radial velocity of the interface Usurf(t) – which increases non-linearly with time – as well as the particle radius for a length scale, which yields tsurf = rp/Usurf(t). Comparing the two time scales yields a maximum value of tB/tsurf ∼ 0.5, from which we interpret that the interfacial motion is always slower than (but close to) the particles' Brownian motion. Particle–particle ordering, which leads to the hexagonally-ordered facets we see at the cluster surfaces, is therefore not directly influenced by the motion of the interface. However, the comparison of time scales reaches values close to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1). Therefore, the inwards motion of the interface is fast enough to have a sweeping effect on the bulk particles in its way. With time, the particle concentration increases in the region ahead of the moving droplet interface. This picture is consistent with the presence of a loose shell being formed during the evaporation close to the droplet's interface. The hexagonally-ordered facets on the clusters surface originate in this loose shell, which bends and eventually buckles.52
(1). Therefore, the inwards motion of the interface is fast enough to have a sweeping effect on the bulk particles in its way. With time, the particle concentration increases in the region ahead of the moving droplet interface. This picture is consistent with the presence of a loose shell being formed during the evaporation close to the droplet's interface. The hexagonally-ordered facets on the clusters surface originate in this loose shell, which bends and eventually buckles.52
For initial particle concentrations above Φ0 = 0.045%, some of the clusters assemble into spheroids, for which no buckling event can be detected. Considering that buckling is based on a mechanical shell instability, the particle clustering of spheroids has to be mechanically stable enough to withstand rising tensions. In this study, where spheroids only occur for Φ0 ≥ 0.045%, experiments suggest that a higher initial particle concentration favours the agglomeration into spheroids. With a higher initial particle concentration, the sweeping effect of the interface on the particles in the bulk will lead to a shell, which can extend further into the bulk and therefore convey mechanical stability.
In principle, buckling events, i.e. unstable shells, are likely to occur for all the initial particle concentrations explored. However, for experiments with high initial particle concentrations Φ0 ≥ 0.5%, we observe a strong influence of the relative humidity, see panel (b) in Fig. 6, which is absent for lower concentrations. Spheroids are then found with the highest probability when the humidity is increased from approximately 60% to about 80%. This increase corresponds to a proportional decrease in the evaporation rate, and consequently in the time scale ratio tB/tsurf to values closer to 0.3. We conclude from this result that the sweeping effect, too, substantially decreases, which only has a significant impact in those cases, where the inter-particle distance is shortest (i.e. for highest particle concentrations).
Other studies on evaporation-driven colloidal agglomerates have obtained other cluster shapes, like the “doughnut” shapes in Rastogi et al.,16 which we have not observed in our experiments. It is difficult to point to one specific reason to explain such a difference, but we can definitively point out that their doughnut shapes were found for heavier particles (silica is almost twice as dense as our polystyrene particles), much larger initial concentrations and, as explicitly mentioned by the authors, an early pinning of the contact line. Nonetheless, the colloidal agglomerates found by Rastogi et al.16 at their lowest particle concentrations seem very similar to the spheroidal clusters in our work. Wooh et al.17 also occasionally found doughnut shapes in their titanium oxide particle clusters, for small droplets in which the contact line motion cannot keep up with the fast evaporation. Our clusters however are very different from those by Wooh et al.17 In their case, the final particle packing is rather low due to the complex inter-particle structures resulting from the attractive interaction among the particles.
In summary, the data in Fig. 6 shows that, for high initial particle concentrations, a slower evaporation leads to a higher packing of particles inside the shell, conveying stability to the cluster. Interestingly, such a dependence on the evaporation rate has also been observed in spray drying systems for silica nano-particle solutions with particle sizes in the range of 10 nm, with initial volume fractions in the range of 2%,49 but with completely different evaporation rates. Furthermore, in a similar system as ours, Sperling et al.53 directly observed with confocal microscopy such shell formation, using fused silica nano-particle solutions at slightly higher initial particle concentrations, as the ones used here (around 1.7% volume fraction).
6 Conclusions
We have shown that, using a stable droplet suspension and a robust superhydrophobic substrate, we can obtain a large variety of particle agglomerates depending only on the initial particle fraction within the droplet. The fractal-like microstructures employed have proved to be a powerful tool yielding high contact angles and minimized pinning of evaporating water droplets. Although wetting transitions from CB to W states were not observed, final pinning events for minimal droplet sizes seem to be unavoidable,22,35 and prevent the formation of spheroid-shaped particle clusters with low number of particles. We distinguish three different categories of cluster shapes based on their aspect ratio (i.e. their three-dimensional character), for a wide range of initial particle packing fractions in the droplet, spanning over 3 decades. From low to high initial particle concentration we found: pancakes, flattened clusters which engulf the upper part of the micropillars, buckled clusters, which adopt their shape due to a sudden collapse of the cluster's shell structure, and spheroids, unbuckled 3D clusters with smooth surfaces.The controlled assembly of shell structures by exploiting a simple process, such as the evaporation of particle suspensions, is a very exciting goal. Applications such as spray drying,1 drug delivery,5 or advanced detection techniques54,55 utilize shell geometries down to the nano-scale. The ability to control the shell thickness and stability is crucial, as well as insights about stratification56 and/or cavity formation on the inside of the cluster.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. S. and A. M. acknowledge financial support from the European Research Council, Starting Grant No. 678573 NanoPacks. The authors thank Eva Krolis for performing preliminary experiments and for the measurement of the roll-off angle, as well as Sander G. Huisman for developing a surface model of the fractal-like structures. The authors furthermore thank H. Gelderblom, M. Jalaal and R. Ezeta for helpful and productive discussions. Finally, the authors would like to thank Mark Smithers for creating breathtaking SEM images of the samples.Notes and references
- D. E. Walton and C. J. Mumford, Chem. Eng. Res. Des., 1999, 77, 21–38 CrossRef CAS.
- E. Lintingre, F. Lequeux, L. Talini and N. Tsapis, Soft Matter, 2016, 12, 7435–7444 RSC.
- A. Corker, H. C.-H. Ng, R. J. Poole and E. Garca-Tuñón, Soft Matter, 2019, 15, 1444–1456 RSC.
- G. Berteloot, A. Daerr, F. Lequeux and L. Limat, Chem. Eng. Process., 2013, 68, 69–73 CrossRef CAS.
- N. Tsapis, D. Bennett, B. Jackson, D. A. Weitz and D. A. Edwards, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12001–12005 CrossRef CAS.
- R. Brown, Philos. Mag., 1829, 6, 161–166 CrossRef.
- R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829 CrossRef CAS.
- T. Pham and S. Kumar, Langmuir, 2017, 33, 10061–10076 CrossRef CAS.
- Y.-F. Li, Y.-J. Sheng and H.-K. Tsao, Langmuir, 2013, 29, 7802–7811 CrossRef CAS.
- D. Mampallil, H. B. Eral, D. van den Ende and F. Mugele, Soft Matter, 2012, 8, 10614–10617 RSC.
- R. N. Wenzel, Ind. Eng. Chem., 1936, 28, 988–994 CrossRef CAS.
- A. B. D. Cassie and S. Baxter, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- D. Quéré, Rep. Prog. Phys., 2005, 68, 2495–2532 CrossRef.
- A. Susarrey-Arce, Á. G. Marín, H. Nair, L. Lefferts, J. G. E. Gardeniers, D. Lohse and A. van Houselt, Soft Matter, 2012, 8, 9765 RSC.
- S. Dash and S. V. Garimella, Langmuir, 2013, 29, 10785–10795 CrossRef CAS.
- V. Rastogi, A. A. Garcia, M. Marquez and O. D. Velev, Macromol. Rapid Commun., 2010, 31, 190–195 CrossRef CAS.
- S. Wooh, H. Huesmann, M. N. Tahir, M. Paven, K. Wichmann, D. Vollmer, W. Tremel, P. Papadopoulos and H. J. Butt, Adv. Mater., 2015, 27, 7338–7343 CrossRef CAS.
- D. Quéré, Nat. Mater., 2002, 1, 14–15 CrossRef.
- M. Reyssat, J. M. Yeomans and D. Quéré, EPL, 2008, 81, 2–7 Search PubMed.
- A. G. Marin, H. Gelderblom, A. Susarrey-Arce, A. van Houselt, L. Lefferts, J. G. E. Gardeniers, D. Lohse and J. H. Snoeijer, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16455–16458 CrossRef CAS.
- P. Tsai, R. G. Lammertink, M. Wessling and D. Lohse, Phys. Rev. Lett., 2010, 104, 2–3 CrossRef.
- P. Papadopoulos, L. Mammen, X. Deng, D. Vollmer and H.-J. Butt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3254–3258 CrossRef CAS.
- A. Marmur, C. Della Volpe, S. Siboni, A. Amirfazli and J. W. Drelich, Surf. Innovations, 2017, 5, 3–8 CrossRef.
- H.-M. Kwon, A. T. Paxson, K. K. Varanasi and N. A. Patankar, Phys. Rev. Lett., 2011, 106, 036102 CrossRef.
- A. Tuteja, C. Wonjae, M. Ma, J. M. Mabry, S. A. Mazzella, G. C. Rutledge, G. H. McKinley and R. E. Cohen, Science, 2007, 318, 1618–1623 CrossRef CAS.
- A. Tuteja, W. Choi, J. M. Mabry, G. H. McKinley and R. E. Cohen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18200–18205 CrossRef CAS.
- L. Pauchard, J.-P. Hulin and C. Allain, Europhys. News, 2005, 36, 9–10 CrossRef.
- K. A. Baldwin, S. Roest, D. J. Fairhurst, K. Sefiane and M. E. Shanahan, J. Fluid Mech., 2012, 695, 321–329 CrossRef CAS.
- A. Susarrey-Arce, K. M. Czajkowski, I. Darmadi, S. Nilsson, I. Tanyeli, S. Alekseeva, T. J. Antosiewicz and C. Langhammer, Nanoscale, 2019, 11, 21207–21217 RSC.
- M. Callies and D. Quéré, Soft Matter, 2005, 1, 55–61 RSC.
- X. Deng, L. Mammen and D. Vollmer, Science, 2012, 502, 67–71 CrossRef.
- E. J. Berenschot, H. V. Jansen and N. R. Tas, J. Micromech. Microeng., 2013, 23, 1–10 CrossRef.
- J. W. Berenschot, R. M. Tiggelaar, J. Geerlings, J. G. E. Gardeniers, N. R. Tas, M. Malankowska, M. P. Pina and R. Mallada, 2016 Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS (DTIP), 2016, pp. 1–4.
- W. Li and A. Amirfazli, Soft Matter, 2008, 4, 462–466 RSC.
- X. Deng, M. Paven, P. Papadopoulos, M. Ye, S. Wu, T. Schuster, M. Klapper, D. Vollmer and H. J. Butt, Angew. Chem., Int. Ed., 2013, 52, 11286–11289 CrossRef CAS.
- T. Young, Philos. Trans. R. Soc. London, 1805, 95, 65–87 CrossRef.
- P.-G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena, Springer New York, 2004 Search PubMed.
- A. M. Cazabat and M. A. Stuart, J. Phys. Chem., 1986, 90, 5845–5849 CrossRef CAS.
- A. Susarrey-Arce, Á. Marín, S. Schlautmann, L. Lefferts, J. G. E. Gardeniers and A. van Houselt, J. Micromech. Microeng., 2012, 23, 1–6 Search PubMed.
- Y. O. Popov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 1–17 Search PubMed.
- R. G. Picknett and R. Bexon, J. Colloid Interface Sci., 1977, 61, 336–350 CrossRef CAS.
- H. Gelderblom, Á. G. Marín, H. Nair, A. Van Houselt, L. Lefferts, J. H. Snoeijer and D. Lohse, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 1–6 Search PubMed.
- T. A. Nguyen, A. V. Nguyen, M. A. Hampton, Z. P. Xu, L. Huang and V. Rudolph, Chem. Eng. Sci., 2012, 69, 522–529 CrossRef CAS.
- P. Brunet, Soft Matter, 2012, 8, 11294–11301 RSC.
- N. Tsapis, E. Dufresne, S. Sinha, C. Riera, J. Hutchinson, L. Mahadevan and D. Weitz, Phys. Rev. Lett., 2005, 94, 018302 CrossRef CAS.
- E. Lintingre, G. Ducouret, F. Lequeux, L. Olanier, T. Périé and L. Talini, Soft Matter, 2015, 11, 3660–3665 RSC.
- E. Lintingre, F. Lequeux, L. Talini and N. Tsapis, Soft Matter, 2016, 12, 7435–7444 RSC.
- M. S. Tirumkudulu, Soft Matter, 2018, 14, 7455–7461 RSC.
- D. Sen, O. Spalla, O. Taché, P. Haltebourg and A. Thill, Langmuir, 2007, 23, 4296–4302 CrossRef CAS.
- J. Wang, C. F. Mbah, T. Przybilla, B. A. Zubiri, E. Spiecker, M. Engel and N. Vogel, Nat. Commun., 2018, 9, 1–10 CrossRef.
- V. N. Manoharan, Solid State Commun., 2006, 139, 557–561 CrossRef CAS.
- L. Pauchard and Y. Couder, Europhys. Lett., 2004, 66, 667–673 CrossRef CAS.
- M. Sperling, P. Papadopoulos and M. Gradzielski, Langmuir, 2016, 32, 6902–6908 CrossRef CAS.
- J. B. Jackson, S. L. Westcott, L. R. Hirsch, J. L. West and N. J. Halas, Appl. Phys. Lett., 2003, 82, 257–259 CrossRef CAS.
- N. Halas, MRS Bull., 2005, 30, 362–367 CrossRef CAS.
- W. Liu, J. Midya, M. Kappl, H. J. Butt and A. Nikoubashman, ACS Nano, 2019, 13, 4972–4979 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: See DOI: 10.1039/d0sm01346c |
| ‡ For details of the vapour deposition protocol, see the supplementary material. |
| This journal is © The Royal Society of Chemistry 2021 |