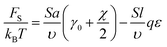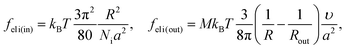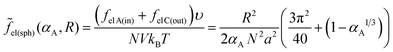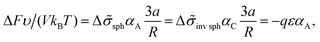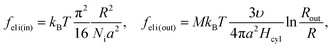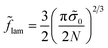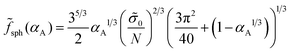Microphase separation in the melts of diblock copolymers with amphiphilic blocks
Dmitry A.
Filatov
ab and
Elena N.
Govorun
 *bc
*bc
aA. N. Nesmeyanov Institute of Organoelement Compounds RAS, Vavilova ul. 28, Moscow 119991, Russia
bA. V. Topchiev Institute of Petrochemical Synthesis RAS, Leninsky Prosp. 29, Moscow 119991, Russia
cFaculty of Physics, M. V. Lomonosov Moscow State University, Leninskie Gory, Moscow 119991, Russia. E-mail: govorun@polly.phys.msu.ru
First published on 12th October 2020
Abstract
Self-assembly of graft diblock copolymers is an actual topic in the development of materials with desirable properties. In the paper, microphase separation in a melt of the diblock copolymer with amphiphilic and non-amphiphilic blocks is investigated using the analytical theory in the strong segregation approximation. Non-amphiphilic blocks are strongly immiscible with the backbone chains of amphiphilic ones but miscible with their side chains. In the theory, the amphiphilic units are considered as dimers, which can easily orient at interfaces. In the case of weakly amphiphilic dimers, the interfacial tension at a flat interface is calculated using density-functional theory. The amphiphilicity effect leads to a decrease in the surface tension and, hence, to weakening of the block stretching and decrease of the spatial period of the structure. In the case of strongly amphiphilic dimers, the phase diagrams are calculated taking into account basic morphological types (spheres and inverse spheres of amphiphilic blocks, cylinders and inverse cylinders, and lamellae). If the amphiphilicity effects dominate, the characteristic size of the amphiphilic block domain is equal to the side chain length, spherical and cylindrical micelles are formed only at very low fractions of the amphiphilic blocks, the lamellae are formed at slightly larger factions, and the micelles from non-amphiphilic blocks are separated by thin interconnected layers from amphiphilic blocks in the broad range of compositions.
1 Introduction
Linear diblock copolymers are widely used as constructing blocks for polymer self-assembly. Different spatial patterns can be created in bulk or on substrates, which strongly affect the material properties.1–4 For the copolymers possessing pendant groups or grafted side chains, the morphological behavior of the melt becomes quite complicated. Up to now, great progress has been achieved in the field of synthesis, characterization and structural investigations of various graft copolymers, such as comb-like polymers, bottlebrushes, or molecular brushes.5–9 Mixed graft block copolymers and, in particular, diblock copolymers with two types of grafted blocks demonstrate a topologically controlled polymorphism in melts.10–14 The mechanical characteristics of such melts vary in a wide range and, besides, their applications as photonic crystals are discussed.A backbone and side parts of a copolymer block can be chemically different, i.e. one of the blocks or both blocks can be amphiphilic. In that case, hierarchical structure-within-structure morphologies can be formed in melts.15–17 A small-scale structure corresponds to the segregation of side chains or groups from the backbone, whereas a large-scale structure corresponds to the separation of the blocks of two types from each other.
Microphase separation in the melts of diblock copolymers with the backbone chains from chemically identical groups and the side chains or groups of the different type was considered in computer simulations18,19 and numerically via the self-consistent field theory.20,21 It was found that the phase diagrams are asymmetric, and a relatively small fraction of side groups is able to form continuous regions across all the box. The morphological behavior differs considerably from that of the melts of usual diblock copolymers with homogeneous blocks.22–25
Such differences are related to the surface activity of amphiphilic constituents and with chain architecture, however, the understanding of controlling factors is lacking. One of those factors should be the interfacial tension and its dependence on the domain size and shape.
The surface interactions depend on the side group orientations in the vicinity of the surface. An important role of the orientational effect reveals itself, for example, in the anomalous behavior of a liquid–vapor surface tension of liquid crystals in the vicinity of the clearing point.26 In particular, the surface-induced orientational ordering of molecules can lead to an increase in the surface tension with temperature.27
The dependence of the interfacial tension on molecular parameters and the interplay between the interfacial tension and the polymer block stretching for different macromolecular-architecture parameters can be analyzed in terms of an analytical theory. Besides, the strongest effect of the surface activity of amphiphilic constituents on the morphological behavior can be expected for the macromolecular architecture, where the pendant parts of amphiphilic blocks are miscible with the non-amphiphilic blocks and can be incorporated in their domains rather than being segregated from both the block backbones.22–25 It is this case which is analyzed in the present paper.
We use a simple dimer model for the description of amphiphilic monomer units or amphiphilic parts of amphiphilic blocks containing oligomeric side chains. One part of a dimer is incorporated into the backbone chain and connected to the second part with a spacer of certain length. This length is a crucial parameter in the control of amphiphilicity effects, since the interaction energies are self-averaged on a small spatial scale and the amphiphilicity is lost for short spacers.
Using a dimer model, a number of self-assembly peculiarities of amphiphilic molecules was successfully analyzed. The surface tension at a flat surface of a collapsed amphiphilic macromolecule in solution was calculated in the cases of weakly amphiphilic and highly amphiphilic monomer units.28 For highly amphiphilic monomer units, the possible shapes of a single compact macromolecule were found assuming that the globule surface is thin, i.e., the monomer unit concentration is stepwise.28,29 In a more recent paper,29 the curvature effects on the surface tension are exactly calculated and the computer simulations with the classical molecular dynamics are carried out for different values of molecular parameters. The surface tension was also calculated at a thin surface in a wide range of degrees of dimer amphiphilicity taking into account the curvature effects.30 For a solution of amphiphilic macromolecules, the possible types of morphological diagrams are presented in terms of the surface bending moduli.30 In a dense layer of macromolecules grafted at a plane surface, the lateral microphase separation can be induced by the monomer unit amphiphilicity, as was predicted by the analytical theory and in the molecular dynamics simulations.31
In the present paper, we use, for the first time, an analytical theory to investigate microphase separation in the melts of diblock copolymers with amphiphilic blocks. Diblock copolymers consisting of non-amphiphilic blocks and amphiphilic blocks with the chemically different backbone and side parts being affine with the non-amphiphilic blocks are considered. In the model section, the macromolecular parameters are introduced and the interfacial tension at a flat interface is calculated in the strong segregation regime for weakly amphiphilic and strongly amphiphilic monomer units. The interfacial tension for slightly amphiphilic monomer units is calculated in terms of density-functional theory taking into account the orientational entropy of dimer monomer units. In the microphases section, the free energies of all the basic structure types are written out and the phase diagram of linear non-amphiphilic diblock copolymers is constructed. In the Results and discussion section, the phase diagrams for the melt of the diblock copolymers with amphiphilic blocks are presented and their morphological behavior is discussed. In the Conclusions and outlook section, the results are summarized and the peculiarities of structured materials from the considered type of diblock copolymers are revealed.
2 The model
We consider a melt of flexible diblock copolymer chains containing amphiphilic A blocks and non-amphiphilic C blocks. The backbone of an amphiphilic block consists of NA beads of type A, from which qNA ones (0 < q < 1) are connected with the side beads of type B; a block C consists of NC monomer units (Fig. 1). According to the Flory theorem, the conformations of linear macromolecules in a polymer melt can be described as random walks, i.e. the volume interactions are screened out. We consider macromolecules containing flexible side chains or quite large side parts assuming that their junctions with a backbone are not completely rigid, so that the end groups of the side parts can freely rotate around the backbone. The volumes of the monomer units of both blocks are equal to υ and the volume of a bead A is much larger than the volume of a bead B, υA ≫ υB. Therefore, υA ≈ υ.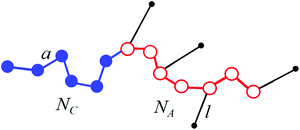 | ||
| Fig. 1 Scheme of a macromolecule with amphiphilic (A) and non-amphiphilic (C) blocks. An amphiphilic block contains amphiphilic monomer units represented as dimers AB. | ||
We assume that amphiphilic blocks A and blocks C are incompatible so that microphase separation can proceed. The melt volume is equal to V. Pair interactions between A and C beads are described by the Flory–Huggins parameter χAC. The interaction energy of a B bead with surrounding A beads and with C beads is designated as εBA and εBC, respectively. The difference ε = εBA − εBC > 0 is the interaction energy benefit (in units of kBT) for a transfer of the B bead from layer A to layer C.
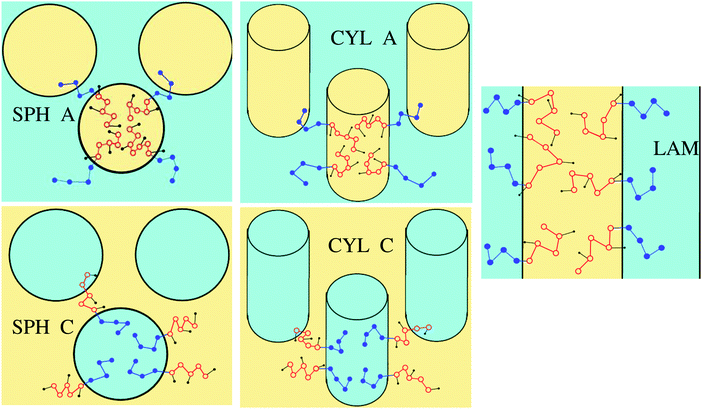
Microphase segregation into the structures of basic types (lamellar structures, micelles and cylinders consisting of A or C blocks) is considered (Fig. 2). The interface thickness is assumed to be quite small, so that chemically different blocks are strongly segregated. The interfacial properties and structure parameters are analyzed for the particular macromolecular structure described above and, for comparison, in the case, when chemically different groups A and B are not separated in space (as if l = 0) in the amphiphilic blocks.
If a melt is homogeneous under certain conditions, the chains are unrestricted in conformations and the free energy of the system in both the cases is equal to the energy of pairwise interactions:
F0 = E0 = kBTmdNA(χAC![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) C + q(εBA C + q(εBA![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) + εBC + εBC![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) C − εBA)), C − εBA)), |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) C and
C and ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) are the average volume fractions of C and A beads, respectively. The interaction energy of a reference state with completely separated blocks is subtracted in the last term. In the considered case of equal volumes υ of monomer units of both blocks and of approximately equal volumes υA ≈ υ, the average volume fractions can be found as
are the average volume fractions of C and A beads, respectively. The interaction energy of a reference state with completely separated blocks is subtracted in the last term. In the considered case of equal volumes υ of monomer units of both blocks and of approximately equal volumes υA ≈ υ, the average volume fractions can be found as![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) = NA/(NA + NC) ≡ αA, = NA/(NA + NC) ≡ αA, ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) C = NC/(NA + NC) ≡ αC. C = NC/(NA + NC) ≡ αC. |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) 0 = F0υ/V = (χAC − qε)αAαC. 0 = F0υ/V = (χAC − qε)αAαC. |
If microphase separation is considered in the strong segregation limit, the bulk interaction energy is equal to zero, but copolymer blocks are deformed and, besides, the interfacial free energy begins to play an important role. To analyze the structure parameters, first, the interfacial tension should be found for the simplest case of a planar interface. We consider two opposite limits of weakly amphiphilic (ε ≪ 1) and strongly amphiphilic (ε ≫ 1) monomer units.
2.1 Interfacial tension for weakly amphiphilic monomer units
We consider a planar boundary between layer A of amphiphilic A blocks and a layer of C blocks. Let ϕ(r) be the volume fraction of A beads at point r and f(θ,r) be the orientational distribution of A–B bond vectors over angle θ between the bond vector l and the axis z, which is directed from an A layer to C layer perpendicular to the interfacial plane. The normalization conditions for the function f(θ,r) is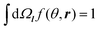 . The volume fraction of C beads is assumed to be equal to ϕC(r) = 1 − ϕ(r), where the excluded volume of B beads is neglected. The volume fractions of beads are assumed to change smoothly at the scale of A–B bond length l: l|∇ϕ| ≪ 1, where l is taken to be much larger than the monomer size a, l ≫ a.
. The volume fraction of C beads is assumed to be equal to ϕC(r) = 1 − ϕ(r), where the excluded volume of B beads is neglected. The volume fractions of beads are assumed to change smoothly at the scale of A–B bond length l: l|∇ϕ| ≪ 1, where l is taken to be much larger than the monomer size a, l ≫ a.
The interfacial free energy F consists of the interfacial interaction energy E and entropic terms:
| F(ϕ,f) = E(ϕ,f) − TSconf(ϕ) − TSorient(ϕ,f), | (1) |
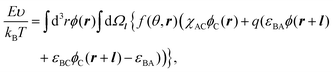 | (2) |
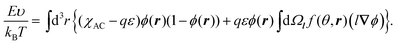 | (3) |
The conformational entropy that contains the contributions from the backbones of the copolymer blocks can be written out in the form proposed by Lifshitz:32
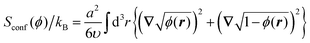 | (4) |
The orientational entropy reads as in the Onsager theory of liquid crystals:33
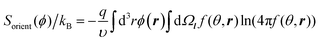 | (5) |
Minimization of the free energy F (eqn (1)) with respect to the orientational distribution f(θ,r) gives the dependence
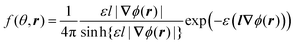 | (6) |
Then, the interfacial tension σ = F/S, where S is the interface area, can be represented as a functional, which depends on the one-dimensional volume fraction ϕ(z) only:
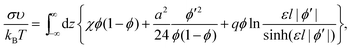 | (7) |
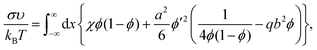 | (8) |
If b = 0, then the minimum of functional (8) corresponds to the known expressions for the volume fraction profile and the surface tension derived by Helfand and Tagami:34
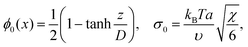 | (9) |
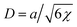 is the characteristic interface thickness. The value z = 0 is taken at the point, where ϕ0 = 1/2, and the boundary conditions are ϕ0(−∞) = 1 and ϕ0(+∞) = 0.
is the characteristic interface thickness. The value z = 0 is taken at the point, where ϕ0 = 1/2, and the boundary conditions are ϕ0(−∞) = 1 and ϕ0(+∞) = 0.
If b is a small parameter, b ≪ 1, substituting the volume fraction profile (9) into expression (8) gives a decrease in the interfacial tension as a correction to the value of σ0:
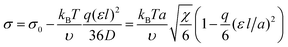 | (10) |
By analyzing the expression for the surface tension in form (8), one can conclude that the role of the gradient dependent term is diminished. As a result, the equilibrium profile of the volume fraction ϕ(z) should possess higher gradients, so that the interface becomes thinner. Similar conclusions about the volume fraction profile and the interfacial tension were reported earlier for the surface properties of a polymer globule formed in solution by a macromolecule with amphiphilic monomer units.28
2.2 Interfacial tension for highly amphiphilic monomer units
Now we address the opposite limit of highly amphiphilic monomer units, ε ≫ 1. In this case, the effects discussed above for weakly amphiphilic monomer units should become much stronger. The amphiphilicity leads to a considerable decrease in the interfacial tension and thinning of the interface, its thickness is assumed to be of the order of monomer unit size a (≈Kuhn segment length). It is worth noting that for highly amphiphilic monomer units the microphase separation can take place only for highly incompatible A and C beads, when χAC > qε.The interfacial free energy FS includes contributions describing the elastic deformation of polymer chains and the interfacial interaction energy of beads. The entropic contribution from the side bond orientation is negligible in comparison with the interaction energy of highly amphiphilic monomer units.
Backbone conformations of the both block types are geometrically constrained on one of the sides of the interfacial plane, therefore, the conformational elastic free energy should be of the order of kBT per monomer unit in the interfacial layer. The interfacial interaction energy of the beads separated by the interfacial plane can be found using the lattice representation. The number of monomer units at the interface can be estimated as NS = Sa/υ. If all the B beads were located in A domains, then the excess interaction energy would be equal to the product of NS/2 and the effective Flory–Huggins parameter χ = χAC − qε. In this case, the reference value of the interfacial free energy without accounting for amphiphilicity is equal to FS0 = kBTNS(γ0 + χ/2), where γ0 describes the elastic energy of a backbone chain per monomer unit at the interface; the value of γ0 should be of the order of unity.
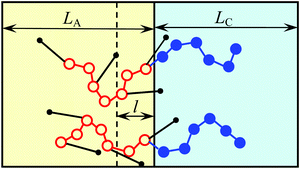
Since AB monomer units are assumed to be highly amphiphilic, all the side bonds in the vicinity of the interface are oriented so that the B beads of those units are located in C domains. The number of such beads is equal to the number qSl/υ of A beads of amphiphilic monomer units in the layer of thickness l adjacent to the planar interface (Fig. 3). Here it is assumed that the layer thickness of amphiphilic blocks LA > 2l. Then, the interfacial free energy is equal to
The interfacial tension σlam can be represented as a sum of the primary contribution σ0, which does not include the effect of amphiphilic unit orientation (as if l = 0), and the negative term Δσlam originated from the B bead interactions with C ones:
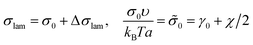 | (11) |
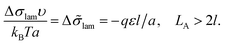 | (12) |
Δ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) lam = −LAqε/(2a), LA < 2l. lam = −LAqε/(2a), LA < 2l. | (13) |
3 The microphases
3.1 Lamellar microphase
The alternating flat lamellae A of thickness LA formed by amphiphilic blocks and lamellae C of thickness LC formed by C blocks are considered (Fig. 3). The equilibrium structure parameters are controlled by a balance of the free energy of polymer block deformation Fconf and the interfacial free energy FS. The total free energy F is the sum of those contributions:| F = md(fel A + fel C) + FS, | (14) |
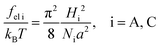 | (15) |
The interfacial free energy
| FS = σlamS, | (16) |
| S = 2mlS1, | (17) |
The volume ratio of two phases is equal to the ratio of block lengths: VA/VC = NA/NC. Therefore, the HA/HC ratio = NA/NC, and the layers of blocks A and C are of the thickness Hi = αiL/2, i = A, C. Then, the free energy F can be considered as a function of a single variable, HA. The interfacial tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) lam =
lam = ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 + Δ
0 + Δ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) lam is independent of HA at HA > l, whereas at HA < l all B beads are in the C phase and expression (13) for the addition Δσlam should be used. Then, expression (14) for the free energy reads
lam is independent of HA at HA > l, whereas at HA < l all B beads are in the C phase and expression (13) for the addition Δσlam should be used. Then, expression (14) for the free energy reads
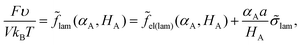 | (18) |
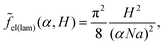 | (19) |
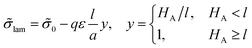 | (20) |
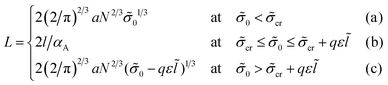 | (21) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) cr = π2
cr = π2![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) 3/(4αA3N2),
3/(4αA3N2), ![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) = l/a.
= l/a.
At ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 <
0 < ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) cr the thickness of layer A HA < l, at
cr the thickness of layer A HA < l, at ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 >
0 > ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) cr + qε
cr + qε![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) the thickness HA > l, and at the intermediate values of σ0,
the thickness HA > l, and at the intermediate values of σ0, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) cr ≤
cr ≤ ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 ≤
0 ≤ ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) cr + qε
cr + qε![[l with combining tilde]](https://www.rsc.org/images/entities/i_char_006c_0303.gif) , the thickness HA = l.
, the thickness HA = l.
The free energy minimum is given by the expressions:
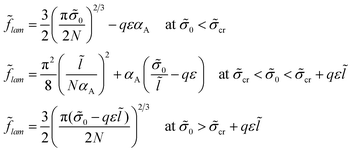 | (22) |
If both blocks of macromolecules were chemically homogeneous and their monomer units were characterized by the value χ of the Flory–Huggins parameter, the interfacial tension would be equal to σ0. Then, the lamellar structure period would be given by expression (21a), as for the amphiphilic units at small enough values of σ0. If the chemical groups of different types are separated by a certain distance l in an amphiphilic monomer unit, the structure period L could be much smaller than that for the diblock copolymers with homogeneous blocks at high enough σ0, the value L being given by expression (21c).
Below we consider the other structure types in the strong segregation limit and compare their free energies to find a most energetically favorable structure.
3.2 Micelles
We consider microphase separation into the system of mm spherical micelles of radius R formed by the amphiphilic blocks surrounded by C blocks. The surface area of a micelle S1 = 4πR2 and the volume V1 = 4πR3/3. The volume of an inner spherical layer of thickness l adjacent to the micelle surface is equal to Vlayer = 4πR2l(1 − l/R + (l/R)2/3) (for R > l). The total volume of the system and the total interface area are equal to V = mdNυ and S = mmS1. The elastic free energies of two blocks are assumed to be the same as if they are enclosed in a sphere of radius R and in an adjacent spherical layer of external radius Rout, respectively. For a block of type i inside and outside a sphere,23where M = md/mm is the number of blocks per micelle.
The number of A beads in a spherical layer adjacent to the surface is equal to Vlayer/υ, and the contribution of all the B beads bound to those A beads to the interfacial tension is given by
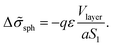 | (23) |
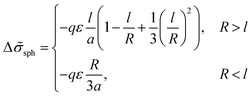 | (24) |
The free energy of the system is given by expression (14). Assuming that the volume fraction of micelles αA = mmV1/V = NA/N is equal to the volume fraction of the sphere of radius R in the sphere of radius Rout, αA = (R/Rout)3, one can write expression (14) as
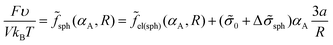 | (25) |
If micelles are packed into a cubic lattice with an edge of length b, the structure period is equal to Lsph = b. For a body-centered cubic phase (bcc), the volume fraction of micelles is equal to αA = 2V1/b3 thus yielding the relation between Lsph and the radii:
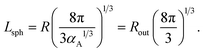 | (26) |
For an inverse phase with micelles of C blocks surrounded by amphiphilic blocks, the B beads bound to A ones in the outer spherical layer adjacent to a micelle contribute to the interfacial free energy. The layer volume is equal to Vlayer = 4πR2l(1 + l/R + (l/R)2/3) at large enough value of the thickness of amphiphilic block regions, ΔRout = Rout− R > l, and the addition (23) to the interfacial tension is equal to
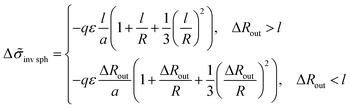 | (27) |
The free energy within the same approximation can be written as
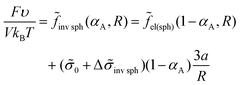 | (28) |
It is worth noting that the contribution of B bead interactions to the free energy in the case when all B beads are in C domains is equal to
3.3 Cylinders
Now the system of mcyl cylinders of radius R formed by amphiphilic blocks is addressed. Let Hcyl be the cylinder height equal to the system size and M = md/mcyl be the number of blocks per cylinder. The cylinder volume V1 = πR2Hcyl and the surface area S1 = 2πRHcyl. The total interface area is equal to S = mcylS1, the volume of the inner layer of thickness l adjacent to the surface is equal to Vlayer = 2πRHcyll((1 − l/(2R)), R > l.The elastic free energies of A and C blocks are assumed to be the same as if they are enclosed in a cylinder of radius R and in an outer adjacent layer of external radius Rout. For a block of type i inside and outside a cylinder, one finds that23
The B bead contribution to the interfacial tension is given by the expression (23) of the same form as for the spherical micelles. Then,
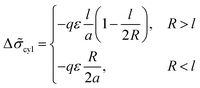 | (29) |
Taking into account that the volume fraction of cylinders is equal to αA = mcylV1/V = (R/Rout)2 = NA/N, one can write expression (14) for the free energy as
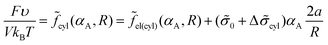 | (30) |
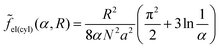 | (31) |
The period Lcyl of the hexagonal structure is equal to the distance between the nearest cylinder axes, so that 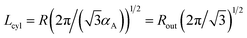 .
.
For the structure of inverse cylinders, the B bead contribution to the interfacial tension is determined by the volume of the outer adjacent layer, Vlayer = 2πRHcl(1 + l/(2R)) at ΔRout > l, thus giving the interfacial tension decrease
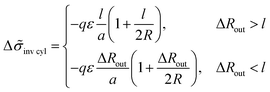 | (32) |
The free energy eqn (14) for an inverse micellar structure can be represented as
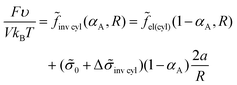 | (33) |
3.4 Morphological diagram for diblock copolymers with homogeneous blocks
To reveal the effect of the monomer unit structure on the morphological behavior of the diblock copolymer melt, we first calculate the equilibrium characteristics for the AC diblock copolymer with homogeneous blocks. In other words, the monomer units A can contain different chemical groups but they are not spatially separated (l = 0). The interactions of A and C monomer units are characterized by the Flory–Huggins parameter χ and the interfacial tension between A and C domains is equal to σ0.A similar morphological behavior of a diblock copolymer melt in the strong segregation limit was studied earlier by Semenov.23 The free energies of the lamellar (18), micellar (25) and cylindrical (30) phases at l = 0 (Δσ = 0) can be found analytically by means of minimization over the geometrical sizes of the domains. They are equal to
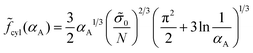 | (34) |
For the inverse cylindrical (28) and spherical (33) structures, which can be described as cylindrical and spherical ones with monomer units of type A exchanged with monomer units of type C, the free energies can be found as
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) inv cyl(αA) = inv cyl(αA) = ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) cyl(1 − αA), cyl(1 − αA), ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) inv sph(αA) = inv sph(αA) = ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) sph(1 − αA). sph(1 − αA). | (35) |
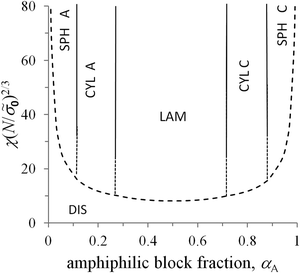
The free energies (34) and (35) depend on the surface tension σ0 and polymerization degree in the same way, that is, they are proportional to (σ0/N)2/3. Therefore, the critical values of αA corresponding to the possible coexistence of different types of microphases do not depend on σ0 and N. If the microphase separation takes place, the structure type corresponding to the minimal value of the free energy is determined by the value of αA only. The crossover values of αA are universal: αsph-cyl ≈ 0.125 for the transition between spheres and cylinders, αcyl-lam ≈ 0.283 for cylinders and lamellae, αinv cyl-lam = 1 − αcyl-lam ≈ 0.717 for lamellae and inverse cylinders, and αinv sph-inv cyl = 1 − αsph-cyl ≈ 0.875 for inverse cylinders and spheres. It is convenient to describe the inverse cylinders of amphiphilic blocks as the normal cylinders of blocks C surrounded by blocks A (“CYL C” structure in all the figures below) and the inverse spheres as the C spheres as well.
Under the conditions near the order–disorder transition, the segregation of polymer blocks A and C is not strong. Using the approach of strong segregation, we can only roughly estimate the value of χ, for which a homogeneous state becomes the most favorable. The free energy of the homogeneous melt is equal to ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) 0 = χαA(1 − αA). Comparing the value of
0 = χαA(1 − αA). Comparing the value of ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) 0 with the free energies (34) and (35) of different microstructures, one can calculate the transition value of the universal parameter χ(N/
0 with the free energies (34) and (35) of different microstructures, one can calculate the transition value of the universal parameter χ(N/![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0)2/3. The dependence of this value on αA is depicted by the dashed curve in the morphological diagram (Fig. 4). It is worth noting that the strong separation approach is not valid in the vicinity of the order–disorder transition so that only solid curves are within the validity limits of the theory.
0)2/3. The dependence of this value on αA is depicted by the dashed curve in the morphological diagram (Fig. 4). It is worth noting that the strong separation approach is not valid in the vicinity of the order–disorder transition so that only solid curves are within the validity limits of the theory.
4 Results and discussion
The interfacial activity of amphiphilic monomer units of A blocks can change the melt morphology considerably. Aside from the elasticity of polymer blocks and the interfacial tension characterized by the “bare” value σ0, the negative interfacial contribution of oriented monomer units AB also influence the self-assembly of the diblock copolymer.By minimizing the melt free energy with respect to the geometrical parameter of every considered structure, we calculate the equilibrium values of the free energy and radius R or thickness HA for the basic structure types: spherical and cylindrical micelles, inverse micelles, and lamellae. After that, we choose the morphology with the minimum value of the free energy. It is worth noting that a homogeneous melt without interfaces is always unfavorable in the considered limit of strongly amphiphilic monomer units and their large negative contribution in the interfacial free energy.
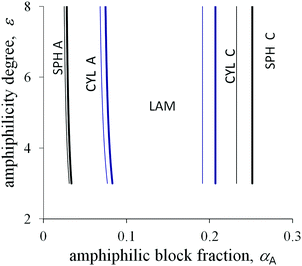
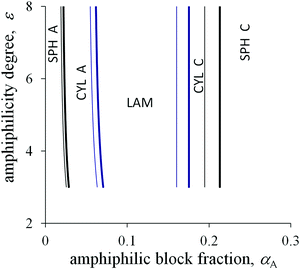
The degree of amphiphilicity can be characterized by the shift ε in the interaction energy of a B group upon changing its surrounding. The morphological diagrams in the coordinates the fraction αA of amphiphilic blocks–the amphiphilicity degree ε are plotted in Fig. 5 and 6 for the moderate value of the interfacial tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 = 1.25. With increasing fraction αA under the other fixed parameters, the sequence of structural transitions appears to be the same as for the non-amphiphilic copolymer (Fig. 4): spheres A → cylinders A → lamellae → cylinders C → spheres C. However, those transitions proceed at much smaller values of the fraction αA: the spherical micelles A transform into cylinders A at αA < 0.05, cylinders A transform into lamellae at αA < 0.1, then inverse morphologies appear beginning at αA ≈ 0.2 or less under the typical values of the chain length N and the side bond length l.
0 = 1.25. With increasing fraction αA under the other fixed parameters, the sequence of structural transitions appears to be the same as for the non-amphiphilic copolymer (Fig. 4): spheres A → cylinders A → lamellae → cylinders C → spheres C. However, those transitions proceed at much smaller values of the fraction αA: the spherical micelles A transform into cylinders A at αA < 0.05, cylinders A transform into lamellae at αA < 0.1, then inverse morphologies appear beginning at αA ≈ 0.2 or less under the typical values of the chain length N and the side bond length l.
Crossover values of the fraction αA weakly depend on the amphiphilicity degree ε or even do not depend on it as for the non-amphiphilic diblock copolymer (the vertical lines in the diagrams in Fig. 5 and 6). However, unlike the diagram of the non-amphiphilic copolymer, those values are determined mostly by the geometrical parameters. All B groups could be located in C domains if the size of the A domains does not exceed the length l. At the same time, further thinning of A domains followed by growth in the interface area is unfavorable because of the positive value of the primary interfacial tension σ0. As a result, the structure type corresponds to a possible arrangement of A domains of size l under the given value of αA.
Upon increasing the side bond length l, the favorable thickness of A domains becomes larger, so that the crossover values of αA increase (thin and thick lines in Fig. 5). The A block length NA, which is sufficient for the formation of A domains of fixed size l, is independent of the total chain length N. Hence, for larger N the structural transitions proceed at smaller values of αA (thin and thick lines in Fig. 6).
If the characteristic size l of A domains does not exceed the gaussian size 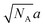 of A blocks, then those blocks are not stretched perpendicularly to the interface and their conformations are close to random ones. The dimer bonds are predominantly oriented perpendicularly to the interfaces, their orientations being uncorrelated with those of the main chains.
of A blocks, then those blocks are not stretched perpendicularly to the interface and their conformations are close to random ones. The dimer bonds are predominantly oriented perpendicularly to the interfaces, their orientations being uncorrelated with those of the main chains.
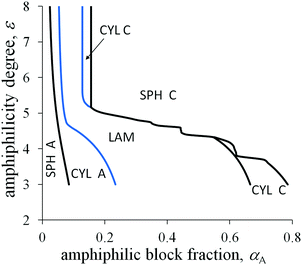
If A and C blocks are strongly immiscible and the value ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 is quite large, the topology of the morphological diagram in the coordinates αA and ε changes (Fig. 7). At quite small values of ε (ε ≈ 3), the interfacial tension decreases moderately in comparison with the primary interfacial tension σ0, and the crossover values of αA are not very far from those of the non-amphiphilic diblock copolymer. However, the shift in the crossover values of αA between the inverse spheres and cylinders, αinv.
0 is quite large, the topology of the morphological diagram in the coordinates αA and ε changes (Fig. 7). At quite small values of ε (ε ≈ 3), the interfacial tension decreases moderately in comparison with the primary interfacial tension σ0, and the crossover values of αA are not very far from those of the non-amphiphilic diblock copolymer. However, the shift in the crossover values of αA between the inverse spheres and cylinders, αinv.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cyl–inv.
cyl–inv.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sph, is markedly larger than that for the usual micellar morphologies, αsph-cyl, and the shift in αlam–inv.
sph, is markedly larger than that for the usual micellar morphologies, αsph-cyl, and the shift in αlam–inv.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cyl is larger than in αcyl–lam. The differences originate from the absolute values of the interfacial contribution of amphiphilic monomer units: the largest one (eqn (26)) is for inverse spheres, the second one at the same radius R (eqn (31)) is for inverse cylinders, then for lamellae (eqn (20)), and, even smaller, are the values for cylinders and spheres (eqn (28) and (23)).
cyl is larger than in αcyl–lam. The differences originate from the absolute values of the interfacial contribution of amphiphilic monomer units: the largest one (eqn (26)) is for inverse spheres, the second one at the same radius R (eqn (31)) is for inverse cylinders, then for lamellae (eqn (20)), and, even smaller, are the values for cylinders and spheres (eqn (28) and (23)).
For moderate values of ε, the A domain size is larger than l and the backbone and dimer orientations are not correlated in the middle parts of those domains. At the same time, vectors directed along the A backbone from the junction point with the C block to the chain end and along dimer bonds from A to B make an obtuse angle or they can be almost oppositely oriented in the interfacial layer of thickness l. If the junctions between side chains and the backbone were rigid, some side B groups from the interfacial layer would reach C domains developing an additional bond stress, whereas the rest of the B groups would stay in A domains. As a result, a decrease in the surface tension originating from the dimer orientation would be much smaller and the phase diagrams would be closer to those for a diblock copolymer with homogeneous blocks.
With increasing ε, the amphiphilicity factors begin to compete with the block elasticity and the primary interfacial tension. This leads to a decrease in the crossover values of αA and considerable broadening of the region of inverse spherical micelles (spheres C). The region of inverse cylinders can even be absent at the intermediate values of ε under the certain conditions. It is worth noting that for any real systems the boundary curves would be smooth rather than being jagged like the curve limiting the domain of C spheres at the intermediate values of ε in Fig. 7. The steps can be considered as an artifact of a simplified definition of the surface tension σ dependence on size H (eqn (20)) or on the values of R, ΔRout (eqn (24), (27), (29) and (32)) in the limit of high amphiphilicity. The derivative of σ with respect to H (or R, ΔRout) is stepwise thus leading to a stability gap for the morphologies with the amphiphilic domain size equal to l (as with HA = l in eqn (21)). There are such gaps that correspond to the vertical parts of “steps” on the curve.
For strongly amphiphilic monomer units (the large value of ε), the morphology of inverse micelles is commonly observed except for the copolymers with very short A blocks. A rich set of morphological types upon changing the external conditions is possible only for the copolymer with an intermediate value of αA. Furthermore, we consider the copolymer with the amphiphilic block fraction αA = 0.18.
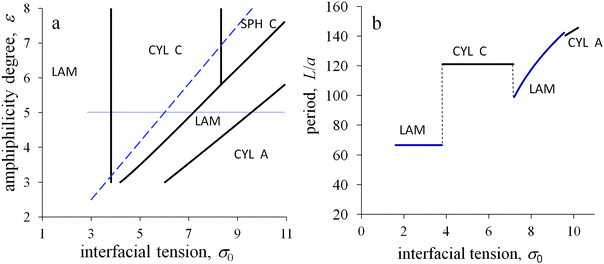
With increasing temperature, the dimensionless energy ε and interfacial tension ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 decrease. The morphological diagram in these coordinates is presented in Fig. 8a. Assuming that a temperature change corresponds to a shift along imaginary straight lines plotted from the origin of coordinates ε,
0 decrease. The morphological diagram in these coordinates is presented in Fig. 8a. Assuming that a temperature change corresponds to a shift along imaginary straight lines plotted from the origin of coordinates ε, ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 = 0, it is possible to follow the structural transitions. Two different regimes can be predicted depending on the slope of such a line. The lamellar structure or cylinders from amphiphilic blocks are kept with changing temperature for a small slope. In contrast, the structure types are thermally sensitive for a large slope: inverse micelles can transform into inverse cylinders and inverse cylinders into lamellae with increasing temperature.
0 = 0, it is possible to follow the structural transitions. Two different regimes can be predicted depending on the slope of such a line. The lamellar structure or cylinders from amphiphilic blocks are kept with changing temperature for a small slope. In contrast, the structure types are thermally sensitive for a large slope: inverse micelles can transform into inverse cylinders and inverse cylinders into lamellae with increasing temperature.
The above two regimes correspond to the domination of the primary interfacial tension or the amphiphilicity effects in the interfacial free energy, respectively. The threshold conditions can be roughly estimated from the comparison of the primary interfacial tension σ0 and the interfacial contribution of amphiphilic monomer units at a flat interface εql(kBT/υ). Then, the amphiphilicity of the monomer units of A blocks should determine the morphological behavior of the melt if the parameter qεl/a exceeds the value ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0. In the coordinates
0. In the coordinates ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0 and ε, the threshold corresponds to the dashed line. For domains A with concave surfaces, the number of B groups per unit interface area is larger than for a flat surface, therefore the inverse structures are even more favorable and their regions at the diagrams are larger than those predicted by that threshold.
0 and ε, the threshold corresponds to the dashed line. For domains A with concave surfaces, the number of B groups per unit interface area is larger than for a flat surface, therefore the inverse structures are even more favorable and their regions at the diagrams are larger than those predicted by that threshold.
To monitor the melt structure under the different conditions, the spatial period L is plotted depending on the value of the primary interfacial tension σ0 at the other fixed parameters (Fig. 8b). For the conditions above the threshold line in Fig. 8a, the amphiphilic properties dominate. With increasing σ0, the period of the lamellar structure equals to L = 2HA/αA, where HA = l, until the morphological transformation to the inverse cylinders occurs. Then, the period of the inverse cylinders also keeps constant until the interfacial tension attains its threshold value and a new transformation takes place. The structure period of the hexagonally packed inverse cylinders corresponds to the thickness of the outer adjacent layer ΔRout = l. For larger values of σ0, the period grows with increasing σ0 as it is typical for the melts of non-amphiphilic diblock copolymers.
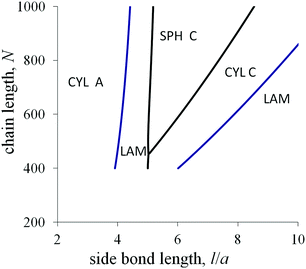
The last diagram (Fig. 9) in the axes l–N at the fixed value of the fraction αA demonstrates how the macromolecular architecture can control the melt morphology. For the moderate values of l, the transitional conditions almost do not depend on the chain length N and the crossover curves are close to vertical lines. The transition from cylinders A to lamellae upon an increase in l can be related to a larger decrease in the interfacial tension for lamellae (eqn (20)) compared with the analogous decrease for cylinders (eqn (28)).
For the values of l, which are larger than the threshold value lth = ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) 0a/(qε), the amphiphilicity factors dominate and almost all the side groups of amphiphilic monomer units are situated in C domains. For large l, the sequence of morphological transitions with increasing N and decreasing l is: lamellae → cylinders C → spheres C. This sequence is the same as for the non-amphiphilic diblock copolymer with increasing αA (Fig. 4). The favorable morphology should be determined by the comparing the contributions from the elastic free energy of blocks and the “bare” interfacial free energy. The domain sizes are determined by the side bond length l. For larger N, the block elasticity decreases, and, for smaller l, the block stretching decreases. Both effects lead to a decrease in the conformational free energy relative to the interfacial free energy and can cause the above morphological transitions.
0a/(qε), the amphiphilicity factors dominate and almost all the side groups of amphiphilic monomer units are situated in C domains. For large l, the sequence of morphological transitions with increasing N and decreasing l is: lamellae → cylinders C → spheres C. This sequence is the same as for the non-amphiphilic diblock copolymer with increasing αA (Fig. 4). The favorable morphology should be determined by the comparing the contributions from the elastic free energy of blocks and the “bare” interfacial free energy. The domain sizes are determined by the side bond length l. For larger N, the block elasticity decreases, and, for smaller l, the block stretching decreases. Both effects lead to a decrease in the conformational free energy relative to the interfacial free energy and can cause the above morphological transitions.
With increasing fraction αA, the region of inverse spheres at the morphological diagram in the axes l–N broadens. Besides inverse spheres, a lamellar structure and inverse cylinders can be favorable at moderate values of the chain length and the side bond length.
By analyzing the peculiarities of all the morphological diagrams for the diblock copolymers with amphiphilic A blocks, it can be concluded that the structures with concave surfaces of A domains are energetically favorable. The advantage or penalty of a surface shape is due to the dependence of the interfacial tension on the domain size, which varies for the different surface shapes. All the side groups belonging to the amphiphilic monomer units at the interfaces are located in the alien C domains. The number of such groups is determined by the volume of the adjacent surface layer in A domains. At the same value of the characteristic domain size, this volume and the number of side groups per unit surface area of A domains are maximum for inverse spheres. In the decreasing order of this number, the other structure types are inverse cylinders, lamellae, cylinders, and spheres.
In the present study, microphase separation leading to the domains of the backbone chains of amphiphilic macromolecules results from the interactions of side chains with other polymer blocks. It is worth noting that the same effect was reported for the polymer with a rigid backbone and junction groups of the side chains, presumably due to the volume interactions of side chains.35
In our approach, the excluded volume interactions of the side groups of amphiphilic monomer units are not taken into consideration for simplicity. If these interactions were taken into account, the curvature dependent factors would be less important, thus making the amphiphilicity effects less pronounced than predicted with the present theory. However, even for equal volumes of A groups in the main chain and side B groups in amphiphilic blocks (the fraction q = 1), the phase diagram was considerably asymmetric, as it was studied via solving the self-consistent-field equations for the melt of diblock copolymers with an A main chain and gaussian B side chains grafted at one of the blocks.20 It was found that the majority domains tend to be surrounded by the minority domains if the fraction of side groups is not too low.
The second consequence of the model assumption that side groups do not interact with each other is that they cannot segregate into separate domains, and we can predict only the type of a large scale structure in the case of the hierarchical structure-within-structure morphology. In our consideration, the side groups are present in both A and C domains for large enough A domains, whereas all the side groups are located in C domains if the size of A domains does not exceed the side bond length l. We do not analyze also the possibility of more complex morphologies, such as perforated or crossed lamellae. Intuitively, those morphologies can be favorable under certain conditions, especially finite cylinders of non-amphiphilic blocks surrounded by amphiphilic blocks arranged in layers.
5 Conclusions and outlook
We considered the morphological behavior of the diblock copolymer melt with the particular macromolecular architecture. One type of the blocks was assumed to be locally amphiphilic, so that the side chains grafted at those blocks or the large pendant groups are immiscible with the backbone groups but miscible with the non-amphiphilic blocks. The analytical mean-field theory was applied to describe the interfacial effect of amphiphilicity in the case of strong segregation of different blocks.For the small degree of amphiphilicity, the interfacial tension with the additional contribution originating from the orientation of side bonds at the interface has been calculated with density functional theory. The decrease in the interfacial tension is proportional to the fraction of side groups and to the square of the amphiphilicity parameter, which is equal to the product of the side bond length and the difference in the interaction energy of side groups with the backbone groups of different types. The decrease in the interfacial tension leads to the weakening of the polymer block stretching and decrease of the spatial period of the microstructure.
It is worth noting that the spatial segregation of the chemical groups of different types in amphiphilic blocks is very important for their interfacial activity. If the different groups are neighboring, all the interaction energies are locally averaged and the melt morphology is described as for non-amphiphilic diblock copolymers.
The decrease in the interfacial tension is promoted by the thinning of the interface, so that a very thin interface is expected to be formed for the diblock copolymer with strongly amphiphilic monomer units. Assuming that all the side groups are placed in the alien domains for the monomer units close to the interface, the interfacial tension was calculated at the flat and basic curved interfaces. The microphase separation into spherical and inverse spherical micelles from amphiphilic blocks, cylindrical and inverse cylindrical micelles, and lamellae is analyzed.
If the effect of amphiphilicity is essential but the interfacial tension remains positive, the sequence of structural transitions with increasing amphiphilic block fraction αA is the same as for a non-amphiphilic diblock copolymer. However, all the transitional values of αA decrease and the region of the inverse spherical micelles essentially broadens in the morphological diagrams.
If the interfacial activity of the amphiphilic monomer units dominates over the chain elasticity and the primary interfacial tension (without the amphiphilicity effect), then the melt morphology is determined by the chain composition and spatial characteristics. The size of the domains of amphiphilic blocks is approximately equal to the side bond length of amphiphilic units, which can be related to the length of side chains grafted at one type of the blocks or the pendant group length. Spherical and cylindrical micelles from amphiphilic blocks are formed only at very low fractions of these blocks, the lamellar structure is formed at quite small factions, and the broad range of compositions with the moderate or large fraction of amphiphilic blocks corresponds to a continuous domain from amphiphilic blocks enveloping the micelles from non-amphiphilic blocks.
At the interfaces, amphiphilic monomer units are oriented so that their side groups are placed in the alien domains. An advantage of the inverse structure types originates from the higher number of such groups per unit surface area for the concave surfaces of amphiphilic domains relatively to the flat surface, or, to even higher extent, to the convex surfaces.
In the simplest realization of the polymer architecture addressed in this work, only two types of monomers can be used. It should be possible to treat both polymers made from those monomers under the same conditions in a melt and the polymers should be strongly immiscible. For example, a non-polar A block can be connected to an amphiphilic block with polar B backbone and non-polar A side chains, which can be incorporated into the domains formed by blocks of the same A type.
The features of the morphological behavior of the considered diblock copolymer suggest a strategy to create fine dispersed systems. In particular, dispersed domains from the non-amphiphilic blocks with a volume fraction of 0.5, or even more, can be surrounded by the amphiphilic blocks with side groups or grafted side chains affine to non-amphiphilic blocks. The characteristic thickness of a continuous domain from amphiphilic blocks is close to the side group size, whereas the domains of non-amphiphilic blocks can be several times larger.
The revealed structural features suggest the directions for searching the possible applications. Such composites have quite small but continuous amphiphilic regions that could provide permeability or conductivity properties of the material. If the amphiphilic blocks are degradable, such materials could be easily utilized being transformed into a powder of small particles of non-amphiphilic blocks.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was financially supported by the Russian Science Foundation (project no. 19-13-00398).References
-
P. Alexandridis and B. Lindman, Amphiphilic Block Copolymers: Self-Assembly and Applications, Elsevier Science B.V., Amsterdam, 2000 Search PubMed
.
- B. M. Boyle, T. A. French, R. M. Pearson, B. G. McCarthy and G. M. Miyake, ACS Nano, 2017, 11, 3052 CAS
.
- C. M. Bates, M. J. Maher, D. W. Janes, C. J. Ellison and C. G. Willson, Macromolecules, 2014, 47, 2 CrossRef CAS
.
- I. Ya. Erukhimovich, M. V. Belousov, E. N. Govorun, V. Abetz and M. V. Tamm, Macromolecules, 2010, 43, 3465 CrossRef CAS
.
- J. Zhang, Z. Wang, X. Wang and Z. Wang, Chem. Commun., 2019, 55, 13904 RSC
.
- V. A. Ivanov, T. K. Meleshko, A. V. Kashina and A. V. Yakimansky, Russ. Chem. Rev., 2019, 88, 1248 CrossRef
.
- G. Xie, M. R. Martinez, M. Olszewski, S. S. Sheiko and K. Matyjaszewski, Biomacromolecules, 2019, 20, 27 CrossRef CAS
.
- R. Verduzco, X. Li, S. L. Pesek and G. E. Stein, Chem. Soc. Rev., 2015, 44, 405 Search PubMed
.
- X. Leng, Z. Wei, Y. Ren, Y. Bian, Q. Wang and Y. Li, RSC Adv., 2016, 6, 40371 RSC
.
- A. N. Le, R. Liang and M. Zhong, Chem. – Eur. J., 2019, 25, 8177 CrossRef CAS
.
- E. B. Zhulina, S. S. Sheiko, A. V. Dobrynin and O. V. Borisov, Macromolecules, 2020, 53, 2582 CrossRef CAS
.
- E. B. Zhulina, S. S. Sheiko and O. V. Borisov, ACS Macro Lett., 2019, 8, 1075 CrossRef CAS
.
- A. L. Liberman-Martin, C. K. Chu and R. H. Grubbs, Macromol. Rapid Commun., 2017, 38, 1700058 CrossRef
.
- B. M. Yavitt, Y. Gai, D.-P. Song, H. H. Winter and J. J. Watkins, Macromolecules, 2017, 50, 396 CrossRef CAS
.
- M. A. Ayoubi, K. Zhu, B. Nystrom, K. Almdal, U. Olsson and L. Piculell, Soft Matter, 2013, 9, 1540 RSC
.
- S. Valkama, T. Ruotsalainen, A. Nykanen, A. Laiho, H. Kosonen, G. ten Brinke, O. Ikkala and J. Ruokolainen, Macromolecules, 2006, 39, 9327 CrossRef CAS
.
- S.-H. Tung and T. Xu, Macromolecules, 2009, 42, 5761 CrossRef CAS
.
- A. R. Khokhlov and P. G. Khalatur, Chem. Phys. Lett., 2008, 461, 58 CrossRef CAS
.
- A. A. Glagoleva, V. V. Vasilevskaya and A. R. Khokhlov, Pol. Sci. A, 2010, 52, 182 CrossRef
.
- Yu. A. Kriksin, P. G. Khalatur, I. Ya. Erukhimovich, G. ten Brinke and A. R. Khokhlov, Soft Matter, 2009, 15, 2896 RSC
.
- L. Wang, J. Lin and L. Zhang, Langmuir, 2009, 25, 4735 CrossRef CAS
.
- L. Leibler, Macromolecules, 1980, 13, 1602 CrossRef CAS
.
- A. N. Semenov, Sov. Phys. JETP, 1985, 61, 733 Search PubMed
.
- M. W. Matsen and F. S. Bates, J. Chem. Phys., 1997, 106, 2436 CrossRef CAS
.
- E. W. Cochran, C. J. Garcia-Corvera and G. H. Fredrickson, Macromolecules, 2006, 39, 2449 CrossRef CAS
.
-
S. Chandrasekhar, Liquid Crystals, Cambridge University Press, Cambridge, 2nd edn, 1992 Search PubMed
.
- Y. Martínez-Ratón, E. Velasco, A. M. Somoza, L. Mederos and T. J. Sluckin, J. Chem. Phys., 1998, 108, 2583 CrossRef
.
- A. S. Ushakova, E. N. Govorun and A. R. Khokhlov, J. Phys.: Condens. Matter, 2006, 18, 915 CrossRef CAS
.
- D. E. Larin, A. A. Glagoleva, E. N. Govorun and V. V. Vasilevskaya, Polymer, 2018, 146, 230 CrossRef CAS
.
- E. A. Maresov and A. N. Semenov, Macromolecules, 2008, 41, 9439 CrossRef CAS
.
- D. E. Larin, A. A. Lazutin, E. N. Govorun and V. V. Vasilevskaya, Langmuir, 2016, 32, 7000 CrossRef CAS
.
- I. M. Lifshits, A. Yu Grosberg and A. R. Khokhlov, Rev. Mod. Phys., 1978, 50, 683 CrossRef
.
- L. Onsager, Ann. N. Y. Acad. Sci., 1949, 51, 627 CrossRef CAS
.
- E. Helfand and Y. Tagami, J. Polym. Sci., Polym. Lett., 1971, 9, 741 CrossRef CAS
.
- B. Kang, R. Kim, S. B. Lee, S.-K. Kwon, Y.-H. Kim and K. Cho, J. Am. Chem. Soc., 2016, 138, 3679 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2021 |