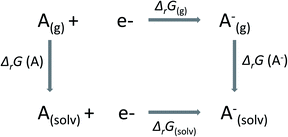Open Access Article
Open Access ArticleCarbon dioxide reduction mechanism on Ru-based electrocatalysts [Ru(bpy)2(CO)2]2+: insights from first-principles theory†
Giane B.
Damas
 *ab,
Dmytro A.
Ivashchenko
c,
Ivan
Rivalta
*ab,
Dmytro A.
Ivashchenko
c,
Ivan
Rivalta
 cd and
C. Moyses
Araujo
cd and
C. Moyses
Araujo
 *ae
*ae
aMaterials Theory Division, Department of Physics and Astronomy, Uppsala University, Box 530, Uppsala, S75121, Sweden
bDepartment of Physics, Chemistry and Biology, Linköping University, 581 83 Linköping, Sweden. E-mail: giane.benvinda.damas@liu.se
cUniv. Lyon, Ens de Lyon, CNRS, Laboratoire de Chimie, UMR 5182, Université Lyon 1, Lyon, France
dDipartimento di Chimica Industriale “Toso Montanari”Università di Bologna, Bologna, Italy
eDepartment of Engineering and Physics, Karlstad University, 65188 Karlstad, Sweden. E-mail: moyses.araujo@kau.se
First published on 3rd November 2021
Abstract
Solar fuel production through the so-called artificial photosynthesis has attracted a great deal of attention to the development of a new world energy matrix that is renewable and environmentally friendly. This process is characterized by light absorption with enough photon energy to generate conduction electrons, which drive the carbon dioxide reduction to produce organic fuels. It is also common to couple Ru-complex electrocatalysts to form a more efficient and selective hybrid system for this application. In this work, we have undertaken a thorough investigation of the redox reaction mechanism of Ru-based electrocatalysts by means of density functional theory (DFT) methods under the experimental conditions that have been previously reported. More specifically, we have studied the electrochemistry and catalytic activity of the [Ru(bpy)2(CO)2]2+ coordination complex. Our theoretical assessment supports the following catalytic cycle: (i) [Ru(bpy)2(CO)2]2+ is transformed into [Ru(bpy)2(CO)]0 upon two-electron reduction and CO release; (ii) [Ru(bpy)2(CO)]0 is protonated to form the [Ru(bpy)2(CO)H]+ hydride complex; (iii) CO2 is activated by the hydride complex through an electrophilic addition to form the [Ru(bpy)2(CO)(OCHO)]+ intermediate; (iv) the resulting formic acid ligand is released in solution; and, finally, (v) the CO ligand is reattached to the complex to recover the initial [Ru(bpy)2(CO)2]2+ catalyst.
1. Introduction
In recent years, the use of carbon dioxide as a starting material for organic fuel production has offered an exciting possibility to conciliate economic development with the urge for a more environmentally friendly society.1–8 For instance, carbon monoxide,9,10 low-weight hydrocarbons,11–15 formic acid6,16–24 and alcohols11,25–27 are among the products that have been obtained following this concept, also referred to as carbon dioxide conversion. The high stability of carbon dioxide does not facilitate its direct conversion into useful products, but indirect approaches have been successful in accomplishing this task.5,6 In this context, the use of photochemical and/or electrochemical techniques involves a proton-coupled multielectron transfer that can significantly reduce the overpotential necessary for product formation.5,6 In a hybrid system comprising a semiconductor as a light harvesting unit and a metal-complex working as an electrocatalyst, the electron transfer rate is then expected to be determined by the thermodynamic driving force,18,20 density of accepting states, reorganization energy and the photo-electrocatalyst electron coupling.1,28,29In 2010, Sato et al. reported the development of a hybrid system consisting of an N-doped Ta2O5 p-type semiconductor and Ru-complex, namely [Ru(bpy)2(CO)2]2+, [Ru(dcbpy)(bpy)(CO)2]2+ and [Ru(dcbpy)2(CO)2]2+, where bpy = 2,2′ bipyridine, for carbon dioxide conversion in an acetonitrile/triethanolamine mixture. In these systems, the electron transfer has been enhanced by the combined effect of the photo-electrocatalyst thermodynamic driving force and the linkage with Ru-complex carboxyl groups. The latter Ru-complex has been associated with an improved selectivity of 75% for formic acid production against CO and H2 under the same conditions.18 In their follow-up reports, phosphonate has also been tested as linking groups for improvement of the photocatalytic efficiency and selectivity in formic acid production,19 and NH3 adsorption effects have been evaluated over the photocatalytic performance based on the idea that this species might be present during the nitrogen-doping process with ammonia.30 Since then, much attention has been given to the development of novel hybrid systems containing Ta-based semiconductors, such as oxygen-doped Ta3N5,31 Ag-loaded TaON,32,33, yttrium-Ta oxide (YTON)34 and perovskite Ta-oxide (CaTaO2N).35 In addition, Co-36 and Fe-based oxides,37 Zn-based sulfides,38 fibrous phosphosilicates39 and carbon-nitride (C3N4)21,23,24,40–43 have been largely utilized as light harvesting semiconductors alongside different Ru–metal complexes acting as electron transfer mediators to drive the reduction reaction.39,41
From a theoretical standpoint, the role played by anchor groups in the photocatalytic efficiency has been previously investigated by Akimov et al.28 By using PO3H2, COOH, and OH as the anchor functionalities in an undoped-Ta2O5/neutral Ru(di-X-bpy)(CO)2Cl2 hybrid system, they have found a direct influence from the local interactions to establish the donor–acceptor coupling and the characteristics associated with the acceptor states. In this sense, the lower efficiency verified with the –COOH group has been attributed to the electron trapping in these moieties, instead of a preferred localization in the catalytic center that is verified for the –PO3H2 case.28
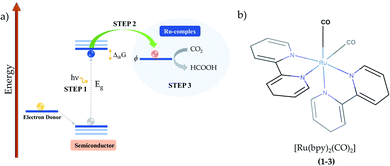
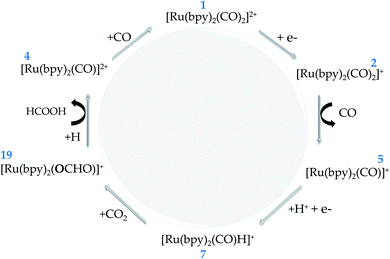
In hybrid systems, the reaction mechanism for photocatalytic conversion of carbon dioxide into formic acid involves three main steps as schematized in Fig. 1. Firstly, it is essential that the incident light has photon energy that is equal to or higher than the band gap of the semiconductor material. The photo-driven excitation then promotes an electron initially lying in the valence band maximum or in shallow defect states to higher-level states, while the former is filled with a positively charged quasiparticle, i.e. the hole (Step 1).34 At this point, it is important to emphasize that the intrinsic electrostatic attraction held by the electron–hole pair usually leads to a decreased photocatalytic efficiency, as photoexcited electrons are compelled to return to their initial state.22 Therefore, it is essential to use an electron donor that can fill in the state promptly after photoexcitation, such as triethanolamine, ethylenediamine-tetraacetic acid disodium salt dihydrate (EDTA)21 and water.20,44,45
From this point, the occurrence of the direct electron transfer from the semiconductor to the metal-complex upon the existence of a favourable driving force has been generally assumed (Step 2).45,46 However, recent TR-IR spectroscopy measurements have demonstrated that anchoring groups linking N-Ta2O5 and Ru-complex photo-electrocatalysts induce the formation of non-radiative charge-transfer states that concentrate the photoelectrons immediately after photoexcitation, thus implying a non-direct charge transfer process that is enhanced alongside the electron coupling.29 At this point, it is crucial that the first unoccupied molecular orbital (LUMO) energy is lower than that of the photoelectron, which is confined in the conduction band maximum or the charge-transfer state.19 By a more accurate definition,47 the Ru-complex energy level is assessed through the reduction potential ϕ, a quantity that accounts for the internal relaxation that is expected to occur upon electron injection. Finally, the electron transfer to carbon dioxide promotes formic acid production along with the electrocatalyst recovery at the end of the process (Step 3). In this context, the present study focuses on the last two steps to shed light on the reaction mechanism implied in the formic acid production catalyzed by Ru-based complexes.
It is also worth mentioning that other studies have focused on using Ru-complexes for CO2 reduction in an electrochemical cell, thus not involving a photocatalyst. In 1991, Meyer and collaborators48 reported formate production catalyzed by a polypyridyl Ru-complex in tetra-n-butylammonium hexafluorophosphate and acetonitrile. They have suggested that the carbon dioxide molecule is inserted into the Ru–H bond of the [Ru(bpy)2(CO)H]+ complex, which is later recovered through water reduction. These processes are activated by the initial reduction in the bipyridine (bpy) ligand, which subsequently increases the electron density at the metal/metal-hydride bond to enable the CO2 attack as an electrophile.48 Noblat et al.49 have verified that the bpy ligand is released during the process with subsequent formation of a polymeric film (ϕ = −0.91 V vs. SHE) and a small amount of hydride complex [Ru(bpy)2(CO)H]+ in pure acetonitrile solution. Under such conditions, the main role in the reduction reaction is played by the hydride complex, while in aqueous acetonitrile, the conversion efficiency of 3% has been attributed to the polymeric film.49 Kuramochi and collaborators50 have proposed that the low supply of electrons promoted the dimerization of Ru-complexes, i.e. Ru(I)–Ru(I), leading to formate production, while CO formation is favoured at a lower catalyst concentration. Based on that, they have synthesized trans-(Cl–Ru(6-Mes-bpy)(CO)2Cl2), a Ru-complex that exhibits a higher selectivity for CO production by suppressing the dimer formation. The present study also addresses this reaction pathway, although to a lesser extent.
Herein, we aim at assessing multiple reduction pathways that Ru-complexes can pursue upon electron injection from a photo-driven or electrocatalytic excitation. Hence, we evaluate the electrochemistry of Ru-based electrocatalysts with a focus on the coordination complexes [Ru(bpy)x(CO)2]y where bpy = 2,2′ bipyridine, and x and y correspond to the number of ligands and total charge of the complex, respectively. The theoretical framework is based on density functional theory (DFT) interplayed with Born–Haber thermodynamics cycles and implicit solvation models, providing information on the catalytic cycle of carbon dioxide conversion into formic acid.
2. Computational details
2.1. The photocatalytic process
In the introductory section, the main steps involved in the carbon dioxide conversion into formic acid photocatalyzed by a hybrid system have been illustrated (see Fig. 1). The present study sheds light on Steps 2 and 3 in order to provide a detailed understanding of the conversion reaction mechanism in acetonitrile solution, with the electrocatalyst (Ru-complex) energy levels assessed through the reduction potential ϕ to account for the electronic relaxation occurring upon electron transfer.47 In the additional evaluation of polymerization in aqueous medium, Step 1 is replaced by the application of an external bias. The computational methods are detailed in the following subsections.2.2. Thermodynamics
In this work, we have calculated the redox potentials of selected Ru-complexes in solution with reference to the standard hydrogen electrode (SHE, ϕref = 4.26 V). According to thermodynamics, the relation between the standard redox potential ϕ of an A/A− redox couple and the Gibbs free energy of reaction in the solvated phase (ΔrG(solv)) is given by| ϕ = −ΔrG(solv)/nF, | (1) |
In Scheme 1,
| ΔrG(solv) = ΔrG(g) − ΔsolvG(A) + ΔsolvG(A−), | (2) |
| ΔrG(g) = G(A(g)−) − G(A(g)). | (3) |
In eqn (2), ΔsolvG is the Gibbs solvation energy of the individual species, while ΔrG(g) is the Gibbs free energy of reaction in the gas phase. In eqn (3), A and A− stand for oxidized and reduced species, respectively. The Gibbs free energy in the gas phase of each species, G, is decomposed into entropic (S) and enthalpic (H) contributions, as follows:
| G(g) = H − T(Svib + Srot + Strans), | (4) |
| H = Eelect + Uvib + Urot + Utrans + PV, | (5) |
Here, we have performed theoretical calculations in Gaussian 09 (ref. 51) within the framework of DFT. The Jaguar code52 has also been employed to benchmark the results, but these outcomes will not be presented for clarity reasons. Optimizations and frequency calculations were carried out in the gas phase at the B3LYP53/6-31G* level of theory, while the electronic total energies were taken from additional single-point calculations with the 6-311++G(2df,2p) basis set, a higher level basis set that includes polarization and diffusion functions. Additionally, we have tested the LAND2DZ and SDD models of effective core potentials for the ruthenium atom (Ru), which aims to replace the chemically inert core electrons to diminish the computational cost. Dispersion effects were considered through the use of the M06 functional,54 but no significant changes have been observed. Solvation energies were obtained by applying the polarizable continuum (PCM)55 and SMD56 solvent models.
2.3. Electronic structure assessment
We have assessed the electronic structure of selected Ru-complexes by computing the total and partial density of states (t- and p-DOS) within the projected augmented wave (PAW) scheme that is implemented in the VASP code.57 The Perdew–Burke–Ernzerhof (PBE)58 functional has been used to perform these calculations, also including the D3 correction method by Grimme et al.59 to account for weak interactions. The plane wave basis set has been determined with a cutoff energy of 500 eV, while the Brillouin zone has been sampled in the Γ-point. In this approach, the molecular system has been placed in the middle of an empty box with lattice parameters a ≈ 32 Å, b ≈ 28 Å, c ≈ 27 Å and α = β = γ, which could relax until the convergence criterion for energy was reached for the ionic steps (10−3 eV).3. Results and discussion
3.1. The Ru-Complex catalyst: [Ru(bpy)2(CO)2]2+
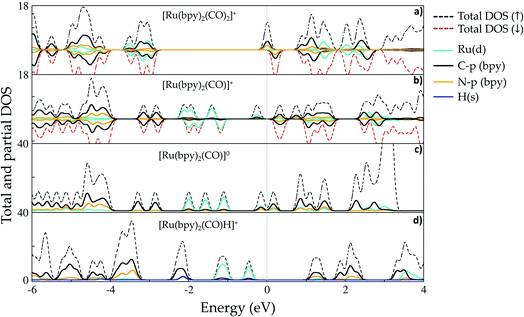
Ruthenium (Ru) is a transition metal element that features a rich chemistry, as it possesses a 4d7 5s1 ground-state electronic configuration with possible oxidation states varying from VIII to 0. In this study, the starting Ru-complex, [Ru(bpy)2(CO)2]2+, is stabilized as an 18-electron octahedral system that could be attached to a semiconductor to act as a charge-transfer mediator between the photosensitizer and carbon dioxide. In this complex, Ru exhibits a +2 oxidation state that leads to a [Kr] 4d6 electronic configuration with electron occupancy given by t3↑↓2ge0g, i.e. low-spin configuration with no electrons unpaired.60,61 Bipyridine ligands have a bidentate chelating bonding with the Ru metal-center, which is also bound to CO ligands lying in the axial and equatorial positions that complete the octahedral coordination (see Fig. 1(b)).Fig. 2 depicts the total and partial density of states (t- and p-DOS, respectively) of this compound in the energy range from −20 to +9 eV relative to the Fermi level (at 0 eV) to provide more details about its electronic structure. Right below the Fermi energy, the Ru 4d orbitals have the highest contribution for the HOMO, with the π-orbitals from the bpy ligand being dominant from −0.6 to −4.7 eV, while their π*-orbitals constitute the first unoccupied orbitals. This is an important feature because the electronic charge is assimilated by this ligand during the first reduction process and concentrated over the carbon atoms, with secondary contributions from N p orbitals. On the other hand, the p orbitals from the CO ligand only contribute in a significant way at energies lower than −5.0 eV until about −6.0 eV in the valence states. Thus, CO acts as a spectator ligand, as its unoccupied p-states are just available at about 3.9 eV. However, loss of CO is an important step to open a coordination site on the Ru-complex for further protonation.
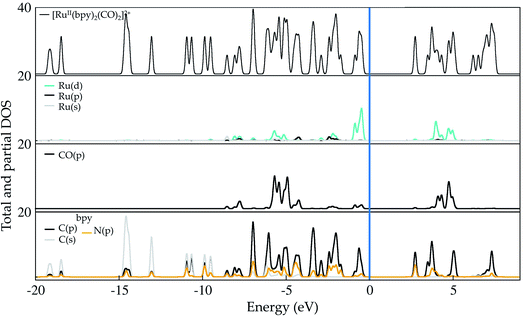 | ||
| Fig. 2 Total and partial density (pDOS) for the starting complex [Ru(bpy)2(CO)2]2+, also labeled as 1 in the text. Level of theory: PBE/500 eV, VASP code.57 The fermi energy is set at zero. | ||
3.2. Ru-Complex reduction pathways
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solution, although still displaying a turnover number lower than 10.18 Sato et al.18 have measured a redox potential (ϕ) of −0.7 V vs. SHE for this complex in acetonitrile purged with Ar and −1.0 V vs. SHE in the presence of CO2. Here, the B3LYP/6-311++G(2df,2p) theory level and implicit solvation model (PCM) provided a calculated potential (ϕ = −0.69 V vs. SHE, see Fig. 3) that is in excellent agreement with the experimental result. This redox potential has been used as a reference value for method validation. Therefore, all outcomes throughout this work will be given within this choice of exchange–correlation functional and basis set. Hereafter, the standard hydrogen electrode (SHE) will not be mentioned along with the redox potentials, for simplicity reasons.
1) solution, although still displaying a turnover number lower than 10.18 Sato et al.18 have measured a redox potential (ϕ) of −0.7 V vs. SHE for this complex in acetonitrile purged with Ar and −1.0 V vs. SHE in the presence of CO2. Here, the B3LYP/6-311++G(2df,2p) theory level and implicit solvation model (PCM) provided a calculated potential (ϕ = −0.69 V vs. SHE, see Fig. 3) that is in excellent agreement with the experimental result. This redox potential has been used as a reference value for method validation. Therefore, all outcomes throughout this work will be given within this choice of exchange–correlation functional and basis set. Hereafter, the standard hydrogen electrode (SHE) will not be mentioned along with the redox potentials, for simplicity reasons.
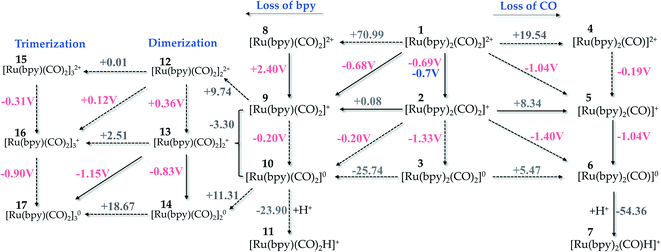 | ||
| Fig. 3 Possible pathways for reduction of Ru-complexes alongside the loss of CO or bpy ligands as presented in the right- and left-hand side, respectively. ΔrG(solv) and ϕ are given in kcal mol−1 and volts, respectively. The value in blue indicates the experimental result by Sato et al.18 Level of theory: B3LYP/6-311++G(2df,2p)/PCM solvent model. | ||
Fig. 3 depicts different reduction pathways for the starting complex 1, which includes the loss of a CO or bpy ligand. The dashed arrows represent the processes that are not likely to occur. From this picture, it is easy to see that the second reduction from 2 →3 is not a feasible pathway, since this step exhibits a more negative potential (ϕ = −1.33 V) than that verified experimentally (ϕ = −1.0 V).18 Instead, 2 can overcome the energetic barrier of +8.34 kcal mol−1 to release a CO ligand and form 5, followed by a second reduction process at ϕ = −1.04 V that is supported by the experimental findings.18 Although pKa calculations are out of the scope of this work, our results show a thermodynamically favourable protonation step with ΔG = −54.36 kcal mol−1 suggesting that the carbon dioxide activation process originated from complex 7.
Noblat et al.49 have previously carried out the electrocatalytic reduction of carbon dioxide in acetonitrile solution, with 1 used as an electrocatalyst to produce formate. They have verified, at −0.96 V, an irreversible peak associated with the formation of the Ru(0)-polymer {[Ru(bpy)(CO)2]0}n, a process that takes place upon release of a bpy ligand in solution. In another study,62 the polymerization has been suggested to occur through a step of dimerization of Ru(I)–Ru(I) monomers, followed by oligomerization of Ru-monomers with a mixed valence. In aqueous acetonitrile (20% v/v H2O), the polymer species was found to play the major role in the reduction to formate, with 3% efficiency at −1.01 V. Nevertheless, the hydride complex [Ru(bpy)2(CO)H]+ is the active species in the reduction process in pure acetonitrile, being formed after the CO release step. In this case, the cathodic current regarding the formate production by the reduced form of the hydride complex started at −1.36 V.49 This pathway is reported in Fig. 3 – left, where the formation of the Ru(0) complex (10) from the Ru(I)-complex 2 or 9 has a very low potential (ϕ = −0.20 V).
From this step (2 → 9), our calculations exhibit a more thermodynamically favourable result for the dimerization taking place between Ru-complexes with a mixed valence (9 and 10), as indicated by a ΔG = −3.30 kcal mol−1 for this step. We have not verified the whole polymerization process because large systems might require a better solvation method to accurately reproduce the experimental values, but the trimerization process occurring at ϕ = −0.90 V is quite close to the experimental value (ϕ = −0.96 V). This pathway is reported in Fig. 3 – left for completeness, since such process is likely to be dominated by diffusion that drives aggregation of the reduced complexes and here, we are dealing with an electrocatalyst that is anchored to the semiconductor photosensitizer, making the polymerization in such hybrid photo-electrocatalysts largely limited by diffusion.
We can also verify that the release of a ligand – either bpy or CO – is thermodynamically favoured with the electrocatalyst reduction. For instance, ΔrG(solv) of the bpy release is diminished from +70.99 to +0.08 kcal mol−1 upon reduction of 1 to 2, a trend that is also verified for the CO loss pathway. This effect results from the instability generated with the electron injection, which facilitates the ligand release and subsequent protonation of the metallic center.
| Variation in charge (Δe) | ||||
|---|---|---|---|---|
| (1–2) | (2–5) | (5–6) | (6–7) | |
| Ru | 0.00 | −0.12 | −0.04 | +0.05 |
| CO(1) | −0.05 | −0.14 | +0.07 | +0.11 |
| CO(2) | −0.05 | — | — | — |
| bpy(1) | −0.46 | +0.14 | −0.45 | +0.49 |
| bpy(2) | −0.46 | +0.14 | −0.45 | +0.49 |
| H | — | −0.12 | ||
| Total charge | ||||
|---|---|---|---|---|
| Ru | 0.00 | −0.12 | −0.04 | +0.05 |
| CO | −0.10 | −0.14 | +0.07 | +0.11 |
| bpy | −0.92 | +0.28 | −0.90 | +0.98 |
Fig. 4(a) shows that the first reduction process introduces a peak in the DOS that is centered at the Fermi level (Ef = −4.73 eV, set as a reference at 0 eV) in complex 2. This band is naturally composed of π-orbitals from the bpy ligand that assimilates an extra electron, but the spin-down contribution (at ∼0.2 eV) reveals the availability of such orbitals to take another electron later in the process. The separation between the rest of the valence band starting from ∼ −3.0 eV is also noticeable, indicating the lack of distribution of the added electron over the other atoms of the Ru-complex, which instead remains localized over the bpy ligands. The Hirshfeld charge analysis confirms the total assimilation of −0.92e by bpy ligands, implying that the charge is well distributed over both entities. This is an interesting point for discussion, since chemical intuition suggests that the reduction would be expected to take place at one of the ligands,49 but there is no geometric asymmetry that would justify a possible separation of these π-orbitals in energy, which would make them equally able to receive the extra charge. On the other hand, the self-interaction problem leading to artificial delocalization in DFT calculations is solved, at least partially, by using a certain amount of exact exchange to compose the exchange–correlation term, which is set at 20% in the hybrid method B3LYP.63,64 Therefore, these outcomes suggest that both bpy ligands participate in the first reduction process by taking an equal amount of the extra charge. In addition, the Ru–N bond length is stretched from 1.127–1.151 Å at [Ru(bpy)2(CO)2]+2 to 2.111–2.147 Å, suggesting that this bond is significantly weakened.
As shown in Fig. 4(b), the CO loss after the first reduction results in significant changes in the Ru-complex electronic structure (5). First, bonding Ru 4d states from −0.1 to about −2.3 eV exhibit localization due to the opening of a coordination site. The unpaired electron at the metal center has its state localized near the Fermi level, with a peak centered at ∼−0.3 eV and slight hybridization with bpy molecular orbitals. The fingerprints of π-backbonding between the t2g (Ru) and CO molecular orbitals lie in the range −1.8 to −2.3 eV, while the π-bonding with bpy orbitals is verified at energies −1.1 to −2.3 eV. Lying lower in energy, the C 2p states from the bpy ligand do not show any hybridization with other N 2p orbitals. The partial charges also indicate the occurrence of charge redistribution after ligand release. The five-coordinated complex has an increased positive charge of +0.28e on its bidentate chelating ligand, altering the bond strength of the Ru–N bonds. On the other hand, Ru has a slightly increased negative charge (−0.12e) that is also verified for the CO ligand.
After the second reduction process, the resulting complex [Ru(bpy)2(CO)]0 features a band right below the Fermi energy indicating that the added electron lowers the C 2p and N 2p states from the bpy ligand for an effective π-backbonding interaction with the Ru atom (see Fig. 4(c)). The charge assimilated by the bpy ligand (−0.90e) also shows that its capacity of taking electrons is indeed not affected after the first reduction process with as many unoccupied π*-orbitals still available at this step.
The formation of the hydride complex [Ru(bpy)2(CO)H]+ containing a hydrogen atom with position adjacent to the CO ligand at the axial position implies addition of a positive charge that is mostly taken by the bpy ligand (+0.98e), while the hydrogen itself receives −0.12e, a value that is in line with Ru-hydride formation. The H 1s states are mixed with both Ru 4d and C 2p and N 2p to generate the band centered at about −2.2 eV in Fig. 4(d), with a Ru–H bond length of 1.609 Å. In Fig. 4(d), it is also possible to note that the H 1s orbital also hybridizes with C p orbitals from bpy ligands, as indicated by the overlapping energies from −2.0 to about −2.2 eV. Here, it is relevant to mention that the hydride ligand is assumed to be responsible for activating the highly stable carbon dioxide molecule, as detailed in the next section.
3.3. Carbon dioxide conversion thermodynamics
| Atom | Ru–H (7) | –COOH (18) | –OCHO (19) | Δe | Δe |
|---|---|---|---|---|---|
| Ru | +0.155 | +0.202 | +0.257 | +0.050 | +0.100 |
| H (…Ru) | −0.122 | — | — | — | — |
| H (…O) | — | +0.143 | +0.041 | — | — |
| C | +0.074 | +0.070 | +0.102 | −0.004 | +0.028 |
| O | −0.146 | −0.137 | −0.117 | +0.010 | +0.029 |
| CO2 (gas) | –COOH (18) | –OCHO (19) | Δe | Δe | |
|---|---|---|---|---|---|
| C | +0.327 | +0.071 | +0.143 | −0.256 | −0.184 |
| O | −0.163 | −0.289 | −0.274 | −0.126 | −0.111 |
| O | −0.163 | −0.187 | −0.298 | −0.024 | −0.135 |
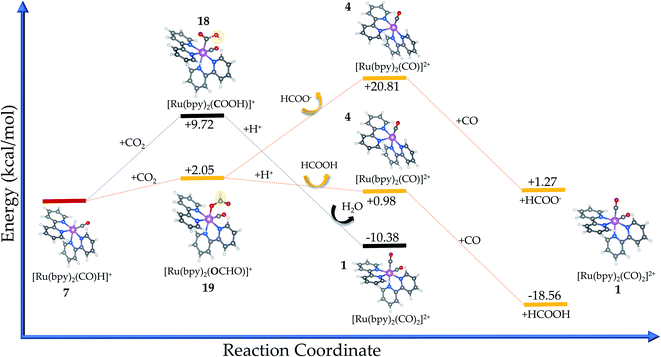
The carbon-bound intermediate in [Ru(bpy)2(CO)(COOH)]+ (18) is formed with a minimum energy cost of ΔrG(solv) = +9.72 kcal mol−1 from 7. Here, the carbon dioxide insertion step leads to a change in the carbon hybridization (sp → sp2) that is responsible for breaking the CO2 molecular linearity in the so-called activation process. In addition, the O–C–O angle is bent by 63.7°, while a natural stretching in the single C–O bond (dC–O = 1.39 Å, Δd = 0.18 Å) is seen along with a weaker bond. The internal charge transfer between the electrocatalyst and carbon dioxide is evidenced by the now negative charge carried by the bound –COO (−0.41e), while Ru has its internal charge almost unaltered. Therefore, the complex positive charge (+1) is mainly distributed over the bpy ligands (∼+0.87e).
The oxygen-bound [Ru(bpy)2(CO)(OCHO)]+ intermediate (complex 19) has a formation pathway that is thermodynamically favoured by 7.67 kcal mol−1 in comparison with that of 18. In this case, the CO2 molecule exhibits lower bending (aO–CH–O = 53°) to form –OCHO because the surrounding oxygen and hydrogen atoms impose lower steric hindrance compared to ruthenium in 18. The internal charge transfer between the electrocatalyst and carbon dioxide is very similar to that verified for complex 19 but the charge carried by the oxygen atom is naturally more negative (−0.27e) when bonded to ruthenium instead of the positive hydrogen.
To clarify the role exerted by the transition state (TS) structures in defining the most likely pathway, we have performed additional calculations regarding the formation of the C-bound and O-bound species from complex 7 (see Fig. S1 and S2 available in the ESI†). To accomplish this task, we have used the synchronous transit-guided quasi-Newton (QST3)65 methodology implemented in Gaussian 16. The TSs have been confirmed through the negative frequency along their specific pathways. For the C- and O-bound species, the activation energy (Ea) is calculated, respectively, as +52.03 and +32.91 kcal mol−1. Hence, the formation of the O-bound species is the most favorable from a kinetic standpoint, corroborating our thermodynamics assessment. Nevertheless, the complex nature of such chemical reactions could require the inclusion of the explicit solvent or the consideration of other pathways for a better assessment, which is currently being studied.
In this sense, the C-bound [Ru(bpy)2(CO)(COOH)]+ complex (18) is preferentially protonated at the oxygen (O–H) site to release water. This is justified by the electrostatic attraction from this atom (−0.29e) in comparison with the carbon site (+0.07e), with the protonation being a favoured process with ΔrG(solv) = −20.10 kcal mol−1 from the intermediate species (18). Thereafter, the initial electrocatalyst 1 is recovered and the primary product is CO,60 an overall reaction that is energetically favoured ΔrG(solv) = −10.38 kcal mol−1, but it requires a higher Ea = + 52.03 kcal mol−1 to form the intermediate. Additional calculations including acetonitrile as a coordinating ligand, namely [Ru(bpy)2(CO)(NCCH3)]2+, have returned a lower value for ΔrG(solv) = −11.67 kcal mol−1. Therefore, the higher amount of acetonitrile in the solvent medium could contribute to decrease the efficiency of this electrocatalyst, even though the reaction is slightly less favourable.
From the thermodynamic point of view, the Ru-complex 19 has an overall reaction that involves a favoured stabilization of formic acid by ΔrG(solv) = −18.56 kcal mol−1, with further CO reattachment to the complex to recover the initial complex 1 (see Fig. 5 and 6). This reaction pathway is driven through the low-energy intermediate 19, which requires +32.91 kcal mol−1 to be formed from the hydride complex (7). Hence, the production of formic acid is more likely to occur when the hydride complex works as the active species. These results corroborate the selectivity toward production of formic acid that has been observed experimentally.18 On the other hand, the formate formation in solution is likely to occur if the medium pH is basic, with a minimum energy cost of 20.81 kcal mol−1 to form 4. The electrocatalytic cycle is summarized in Fig. 6.
4. Conclusions
In this work, we have performed density functional theory calculations along with thermodynamics cycles and implicit solvation models to shed light on the mechanism of the CO2 reduction reaction electro-catalysed by the coordination complex [Ru(bpy)2(CO)2]2+. Initially, we have assessed the electrochemistry of such complex along with its reduction reaction pathway in acetonitrile solution. It was found that the release of either a CO or bpy ligand in solution is energetically favourable. Furthermore, the calculated redox potential of −0.69 V vs. SHE displays very good agreement with the experimental finding (around −0.7 V vs. SHE) for the first reduction step. The tendency towards polymerization upon bpy release has also been evaluated. However, this is a process that may take place at more negative potentials and is hampered if the Ru complexes are anchored to the semiconductor surfaces. Hence, the CO release is more likely to occur in a hybrid system according to our theoretical assessment within the experimentally measured potentials.Furthermore, we have investigated the electronic structure of these complexes at different reduction stages by means of calculated total and partial density of states. For the complex [Ru(bpy)2(CO)2]2+, the Ru 4d states have the highest contribution for the HOMO, while the antibonding states from C sp2 atoms play the major role in composing the LUMO, showing also some contribution from N 2p antibonding orbitals. This is consistent with the fact that the bpy species are non-innocent ligands during the reduction process. This result is further confirmed from the analysis of the DOS on the reduced complexes.
In a further step, we have investigated different reaction pathways for CO2 reduction catalyzed by Ru-complexes. Firstly, we have found that the protonation of the [Ru(bpy)2(CO)]0 complex is energetically favourable, with this system being prone to forming a metal-hydride complex. Then, we have assessed the energetics of two primary pathways for CO2 insertion into the electrocatalyst, where the connection is given through either O–Ru or C–Ru bond formation. In this sense, we have shown that the former is favoured energetically and the production of formic acid is the most likely reaction pathway that corroborates the previous experimental findings. More specifically, CO2 reduction to CO would demand the stabilization of the higher energy intermediate [Ru(bpy)2(CO)(COOH)]+ at a cost of 52.03 kcal mol−1. On the other hand, formic acid production involves the stabilization of [Ru(bpy)2(CO)(OCHO)]+ at a lower cost (Ea = 32.91 kcal mol−1), with an overall reaction free energy (ΔrG(solv) = −18.56 kcal mol−1) that is expected to lead to a higher thermodynamic driving force. Nonetheless, the inclusion of acetonitrile as a coordinating ligand is also favourable thermodynamically (ΔrG(solv) = −11.67 kcal mol−1), which should contribute to decrease the efficiency of this electrocatalyst. Thus, from thermodynamics considerations we propose the following catalytic cycle:
(i) [Ru(bpy)2(CO)2]2+ is transformed into [Ru(bpy)2(CO)]0 with two-electron reduction and CO release;
(ii) [Ru(bpy)2(CO)]0 is protonated to form the hydride complex [Ru(bpy)2(CO)H]+, which is actually the catalytically active species;
(iii) CO2 is incorporated into the complex through an electrophilic addition to form the intermediate [Ru(bpy)2(CO)(OCHO)]+, with the formation of the C–H bond;
(iv) The formate ion is protonated and released in solution;
(v) Then, the CO ligand is reattached to the complex in order to recover the initial complex [Ru(bpy)2(CO)2]2+.
Conflicts of interest
The authors declare no conflict of interest in this project.Acknowledgements
This project is supported by the Swedish Research Council (VR) and STandUP for energy collaboration, with computational resources provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Center for High Performance Computing and National Supercomputer Centre at Linköping University (NSC). CAPES (Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior) financially supports the author GBD.Notes and references
- G. Sahara and O. Ishitani, Efficient Photocatalysts for CO2 Reduction, Inorg. Chem., 2015, 54(1), 5096–5104, DOI:10.1021/ic502675a.
- S. Das and W. M. A. Wan Daud, A Review on Advances in Photocatalysts towards CO2 Conversion, RSC Adv., 2014, 4(40), 20856, 10.1039/c4ra01769b.
- J. R. Bolton, Solar Fuels, Science, 1978, 202(4369), 705–711, DOI:10.1126/science.202.4369.705.
- World Meteorological Organization, Greenhouse Gas Bulletin, World Meteorol. Organ. Bull., 2017, vol. 12, pp. 1–4, ISSN 2078-0796 Search PubMed.
- D. Xiang, D. Magana and R. B. Dyer, CO2 Reduction Catalyzed by Mercaptopteridine on Glassy Carbon, J. Am. Chem. Soc., 2014, 136(40), 14007–14010, DOI:10.1021/ja5081103.
- G. B. Damas, C. R. Miranda, R. Sgarbi, J. M. Portela, M. R. Camilo, F. H. B. Lima and C. M. Araujo, On the Mechanism of Carbon Dioxide Reduction on Sn-Based Electrodes: Insights into the Role of Oxide Surfaces, Catalysts, 2019, 9(8), 636, DOI:10.3390/catal9080636.
- V. Kumaravel, J. Bartlett and S. C. Pillai, Photoelectrochemical Conversion of Carbon Dioxide (CO2) into Fuels and Value-Added Products, ACS Energy Lett., 2020, 5(2), 486–519, DOI:10.1021/acsenergylett.9b02585.
- W. Zhang, Y. Hu, L. Ma, G. Zhu, Y. Wang, X. Xue, R. Chen, S. Yang and Z. Jin, Progress and Perspective of Electrocatalytic CO2 Reduction for Renewable Carbonaceous Fuels and Chemicals, Adv. Sci., 2018, 5, 1700275, DOI:10.1002/advs.201700275.
- Y. Kuramochi, J. Itabashi, M. Toyama and H. Ishida, Photochemical CO2 Reduction Catalyzed by Trans(Cl)-[Ru(2,2′-Bipyridine)(CO)2Cl2] Bearing Two Methyl Groups at 4,4′-, 5,5′- or 6,6′-Positions in the Ligand, ChemPhotoChem, 2018, 2, 314–322, DOI:10.1002/cptc.201700201.
- H. Ishida and A. Sakaba, Temperature Dependence of Photocatalytic CO2 Reduction by: Trans (Cl)–Ru(Bpy)(CO)2Cl2: Activation Energy Difference between CO and Formate Production, Faraday Discuss., 2017, 198, 263–277, 10.1039/c6fd00242k.
- H. Yuan, X. Qian, B. Luo, L. Wang, L. Deng and Y. Chen, Carbon Dioxide Reduction to Multicarbon Hydrocarbons and Oxygenates on Plant Moss-Derived, Metal-Free, in Situ Nitrogen-Doped Biochar, Sci. Total Environ., 2020, 739, 140340, DOI:10.1016/j.scitotenv.2020.140340.
- Z. Yin, G. T. R. Palmore and S. Sun, Electrochemical Reduction of CO2 Catalyzed by Metal Nanocatalysts, Trends Chem., 2019, 1(8), 739–739, DOI:10.1016/j.trechm.2019.05.004.
- M. R. Gonçalves, A. Gomes, J. Condeço, R. Fernandes, T. Pardal, C. A. C. Sequeira and J. B. Branco, Selective Electrochemical Conversion of CO2 to C2 Hydrocarbons, Energy Convers. Manage., 2010, 51(1), 30–32, DOI:10.1016/j.enconman.2009.08.002.
- N. Li, X. Chen, W. J. Ong, D. R. Macfarlane, X. Zhao, A. K. Cheetham and C. Sun, Understanding of Electrochemical Mechanisms for CO2 Capture and Conversion into Hydrocarbon Fuels in Transition-Metal Carbides (MXenes), ACS Nano, 2017, 11(11), 10825–10833, DOI:10.1021/acsnano.7b03738.
- A. Engelbrecht, M. Hämmerle, R. Moos, M. Fleischer and G. Schmid, Improvement of the Selectivity of the Electrochemical Conversion of CO2 to Hydrocarbons Using Cupreous Electrodes with In-Situ Oxidation by Oxygen, Electrochim. Acta, 2017, 224, 642–648, DOI:10.1016/j.electacta.2016.12.059.
- Q. Wang, H. Dong and H. Yu, Development of Rolling Tin Gas Diffusion Electrode for Carbon Dioxide Electrochemical Reduction to Produce Formate in Aqueous Electrolyte, J. Power Sources, 2014, 271, 278–284, DOI:10.1016/j.jpowsour.2014.08.017.
- T. Baran, S. Wojtyła, A. Dibenedetto, M. Aresta and W. Macyk, Zinc Sulfide Functionalized with Ruthenium Nanoparticles for Photocatalytic Reduction of CO2, Appl. Catal., B, 2015, 178, 170–176, DOI:10.1016/j.apcatb.2014.09.052.
- S. Sato, T. Morikawa, S. Saeki, T. Kajino and T. Motohiro, Visible-Light-Induced Selective CO2 Reduction Utilizing a Ruthenium Complex Electrocatalyst Linked to a p-Type Nitrogen-Doped Ta2O5 Semiconductor, Angew. Chem., 2010, 49(30), 5101–5105, DOI:10.1002/anie.201000613.
- T. M. Suzuki, H. Tanaka, T. Morikawa, M. Iwaki, S. Sato, S. Saeki, M. Inoue, T. Kajino and T. Motohiro, Direct Assembly Synthesis of Metal Complex-Semiconductor Hybrid Photocatalysts Anchored by Phosphonate for Highly Efficient CO2 Reduction, Chem. Commun., 2011, 47, 8673–8675, 10.1039/c1cc12491a.
- T. Morikawa, S. Sato, T. Arai, K. Uemura, K. I. Yamanaka, T. M. Suzuki, T. Kajino and T. Motohiro, Selective CO2 Reduction Conjugated with H2O Oxidation Utilizing Semiconductor/Metal-Complex Hybrid Photocatalysts, AIP Conf. Proc., 2013, 1568, 11–15, DOI:10.1063/1.4848080.
- R. Kuriki, H. Matsunaga, T. Nakashima, K. Wada, A. Yamakata, O. Ishitani and K. Maeda, Nature-Inspired, Highly Durable CO2 Reduction System Consisting of a Binuclear Ruthenium(II) Complex and an Organic Semiconductor Using Visible Light, J. Am. Chem. Soc., 2016, 138, 5159–5170, DOI:10.1021/jacs.6b01997.
- K. Muraoka, J. J. M. Vequizo, R. Kuriki, A. Yamakata, T. Uchiyama, D. Lu, Y. Uchimoto, O. Ishitani and K. Maeda, Oxygen-Doped Ta3N5 Nanoparticles for Enhanced Z-Scheme Carbon Dioxide Reduction with a Binuclear Ruthenium(II) Complex under Visible Light, ChemPhotoChem, 2019, 3, 1027–1033, DOI:10.1002/cptc.201900120.
- K. Maeda, R. Kuriki and O. Ishitani, Photocatalytic Activity of Carbon Nitride Modified with a Ruthenium(II) Complex Having Carboxylic- or Phosphonic Acid Anchoring Groups for Visible-Light CO2 Reduction, Chem. Lett., 2016, 45, 182–184, DOI:10.1246/cl.151061.
- K. Maeda, D. An, C. S. Kumara Ranasinghe, T. Uchiyama, R. Kuriki, T. Kanazawa, D. Lu, S. Nozawa, A. Yamakata, Y. Uchimoto and O. Ishitani, Visible-Light CO2 Reduction over a Ruthenium(II)-Complex/C3N4 Hybrid Photocatalyst: The Promotional Effect of Silver Species, J. Mater. Chem. A, 2018, 6, 9708–9715, 10.1039/c8ta03245a.
- H. Han, Y. Noh, Y. Kim, S. Park, W. Yoon, D. Jang, S. M. Choi and W. B. Kim, Selective Electrochemical CO2 Conversion to Multicarbon Alcohols on Highly Efficient N-Doped Porous Carbon-Supported Cu Catalysts, Green Chem., 2020, 22, 71–84, 10.1039/c9gc03088c.
- Q. Zhang, J. Du, A. He, Z. Liu and C. Tao, High-Selectivity Electrochemical Conversion of CO2 to Lower Alcohols Using a Multi-Active Sites Catalyst of Transition-Metal Oxides, J. CO2 Util., 2019, 34, 635–645, DOI:10.1016/j.jcou.2019.08.005.
- J. Liu, H. Shi, X. Huang, Q. Shen and G. Zhao, Efficient Photoelectrochemical Reduction of CO2 on Pyridyl Covalent Bonded Ruthenium(II) Based-Photosensitizer, Electrochim. Acta, 2016, 216, 228–238, DOI:10.1016/j.electacta.2016.08.135.
- A. V. Akimov, R. Jinnouchi, S. Shirai, R. Asahi and O. V. Prezhdo, Theoretical Insights into the Impact of Ru Catalyst Anchors on the Efficiency of Photocatalytic CO2 Reduction on Ta2O5, J. Phys. Chem. B, 2015, 119(24), 7186–7197, DOI:10.1021/jp5080658.
- S. Sato, S. Tanaka, K. Yamanaka, S. Saeki, K. Sekizawa, T. M. Suzuki, T. Morikawa and K. Onda, Study of Excited States and Electron Transfer of Semiconductor-Metal-Complex Hybrid Photocatalysts for CO2 Reduction by Using Picosecond Time-Resolved Spectroscopies, Chem.–Eur. J., 2021, 27, 1127–1137, DOI:10.1002/chem.202004068.
- S. Shirai, S. Sato, T. M. Suzuki, R. Jinnouchi, N. Ohba, R. Asahi and T. Morikawa, Effects of Ta2O5 Surface Modification by NH3 on the Electronic Structure of a Ru-Complex/N-Ta2O5 Hybrid Photocatalyst for Selective CO2 Reduction, J. Phys. Chem. C, 2018, 122(4), 1921–1929, DOI:10.1021/acs.jpcc.7b09670.
- K. Muraoka, T. Uchiyama, D. Lu, Y. Uchimoto, O. Ishitani and K. Maeda, A Visible-Light-Driven Z-Scheme CO2 Reduction System Using Ta3N5 and a Ru(II) Binuclear Complex, Bull. Chem. Soc. Jpn., 2019, 92, 124–126, DOI:10.1246/bcsj.20180239.
- A. D. Handoko, K. Li and J. Tang, Recent Progress in Artificial Photosynthesis: CO2 Photoreduction to Valuable Chemicals in a Heterogeneous System, Curr. Opin. Chem. Eng., 2013, 200–206, DOI:10.1016/j.coche.2012.12.003.
- A. Nakada, T. Nakashima, K. Sekizawa, K. Maeda and O. Ishitani, Visible-Light-Driven CO2 Reduction on a Hybrid Photocatalyst Consisting of a Ru(II) Binuclear Complex and a Ag-Loaded TaON in Aqueous Solutions, Chem. Sci., 2016, 7, 4364–4371, 10.1039/c6sc00586a.
- K. Muraoka, H. Kumagai, M. Eguchi, O. Ishitani and K. Maeda, A Z-Scheme Photocatalyst Constructed with an Yttrium-Tantalum Oxynitride and a Binuclear Ru(II) Complex for Visible-Light CO2 Reduction, Chem. Commun., 2016, 52, 7886–7889, 10.1039/c6cc03627a.
- F. Yoshitomi, K. Sekizawa, K. Maeda and O. Ishitani, Selective Formic Acid Production via CO2 Reduction with Visible Light Using a Hybrid of a Perovskite Tantalum Oxynitride and a Binuclear Ruthenium(II) Complex, ACS Appl. Mater. Interfaces, 2015, 7(23), 13092–13097, DOI:10.1021/acsami.5b03509.
- X. Huang, Q. Shen, J. Liu, N. Yang and G. Zhao, A CO2 Adsorption-Enhanced Semiconductor/Metal-Complex Hybrid Photoelectrocatalytic Interface for Efficient Formate Production, Energy Environ. Sci., 2016, 9, 3161–3171, 10.1039/c6ee00968a.
- K. Sekizawa, S. Sato, T. Arai and T. Morikawa, Solar-Driven Photocatalytic CO2 Reduction in Water Utilizing a Ruthenium Complex Catalyst on p-Type Fe2O3 with a Multiheterojunction, ACS Catal., 2018, 8(2), 1405–1416, DOI:10.1021/acscatal.7b03244.
- T. M. Suzuki, T. Takayama, S. Sato, A. Iwase, A. Kudo and T. Morikawa, Enhancement of CO2 Reduction Activity under Visible Light Irradiation over Zn-Based Metal Sulfides by Combination with Ru-Complex Catalysts, Appl. Catal., B, 2018, 224, 572–578, DOI:10.1016/j.apcatb.2017.10.053.
- R. Zhiani, M. Khoobi and S. M. Sadeghzadeh, Ruthenium–Birhodanine Complex Supported over Fibrousphosphosilicate for Photocatalytic CO2 Reduction to Formate, Catal. Today, 2020, 340, 197–203, DOI:10.1016/j.cattod.2018.09.034.
- K. Maeda, K. Sekizawa and O. Ishitani, A Polymeric-Semiconductor-Metal-Complex Hybrid Photocatalyst for Visible-Light CO2 reduction, Chem. Commun., 2013, 49, 10127–10129, 10.1039/c3cc45532g.
- R. Kuriki, M. Yamamoto, K. Higuchi, Y. Yamamoto, M. Akatsuka, D. Lu, S. Yagi, T. Yoshida, O. Ishitani and K. Maeda, Robust Binding between Carbon Nitride Nanosheets and a Binuclear Ruthenium(II) Complex Enabling Durable, Selective CO2 Reduction under Visible Light in Aqueous Solution, Angew. Chem., Int. Ed., 2017, 56, 4867–4871, DOI:10.1002/anie.201701627.
- R. Kuriki, K. Sekizawa, O. Ishitani and K. Maeda, Visible-Light-Driven CO2 Reduction with Carbon Nitride: Enhancing the Activity of Ruthenium Catalysts, Angew. Chem., Int. Ed., 2015, 54, 2406–2409, DOI:10.1002/anie.201411170.
- C. Tsounis, R. Kuriki, K. Shibata, J. J. M. Vequizo, D. Lu, A. Yamakata, O. Ishitani, R. Amal and K. Maeda, Copolymerization Approach to Improving Ru(II)-Complex/C3N4 Hybrid Photocatalysts for Visible-Light CO2 Reduction, ACS Sustainable Chem. Eng., 2018, 6(11), 15333–15340, DOI:10.1021/acssuschemeng.8b03782.
- S. Sato, T. Arai, T. Morikawa, K. Uemura, T. M. Suzuki, H. Tanaka and T. Kajino, Selective CO2 Conversion to Formate Conjugated with H2O Oxidation Utilizing Semiconductor/Complex Hybrid Photocatalysts, J. Am. Chem. Soc., 2011, 133(39), 15240–15243, DOI:10.1021/ja204881d.
- T. M. Suzuki, S. Yoshino, T. Takayama, A. Iwase, A. Kudo and T. Morikawa, Z-Schematic and Visible-Light-Driven CO2 Reduction Using H2O as an Electron Donor by a Particulate Mixture of a Ru-Complex/(CuGa)1−xZn2xS2 Hybrid Catalyst, BiVO4 and an Electron Mediator, Chem. Commun., 2018, 54, 10199–10202, 10.1039/c8cc05505j.
- K. I. Yamanaka, S. Sato, M. Iwaki, T. Kajino and T. Morikawa, Photoinduced Electron Transfer from Nitrogen-Doped Tantalum Oxide to Adsorbed Ruthenium Complex, J. Phys. Chem. C, 2011, 115(37), 18348–18353, DOI:10.1021/jp205223k.
- G. Damas, C. F. N. Marchiori and C. M. Araujo, On the Design of Donor-Acceptor Conjugated Polymers for Photocatalytic Hydrogen Evolution Reaction: First-Principles Theory-Based Assessment, J. Phys. Chem. C, 2018, 122(47), 26876–26888, DOI:10.1021/acs.jpcc.8b09408.
- J. R. Pugh, M. R. M. Bruce, B. P. Sullivan and T. J. Meyer, Formation of a Metal-Hydride Bond and the Insertion of CO2. Key Steps in the Electrocatalytic Reduction of Carbon Dioxide to Formate Anion, Inorg. Chem., 1991, 30(1), 86–91, DOI:10.1021/ic00001a016.
- S. Chardon-Noblat, M. N. Collomb-Dunand-Sauthier, A. Deronzier, R. Ziessel and D. Zsoldos, Formation of Polymeric [{Ru0(Bpy)(CO)2}n] Films by Electrochemical Reduction of [Ru(Bpy)2(CO)2](PF6)2: Its Implication in CO2 Electrocatalytic Reduction, Inorg. Chem., 1994, 33(19), 4410–4412, DOI:10.1021/ic00097a034.
- Y. Kuramochi, J. Itabashi, K. Fukaya, A. Enomoto, M. Yoshida and H. Ishida, Unexpected Effect of Catalyst Concentration on Photochemical CO2 Reduction by Trans(Cl)-Ru(Bpy)(CO)2Cl2: New Mechanistic Insight into the CO/HCOO- Selectivity, Chem. Sci., 2015, 6(5), 3063–3074, 10.1039/c5sc00199d.
- M. J. Frisch, et al., Gaussian 09, Revision D.01, 2009, DOI:10.1159/000348293.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Jaguar: A High-Performance Quantum Chemistry Software Program with Strengths in Life and Materials Sciences, Int. J. Quantum Chem., 2013, 113(18), 2110–2142, DOI:10.1002/qua.24481.
- A. Becke, B3LYP, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function, Theor. Chem. Acc., 2008, 120(1–3), 215–241, DOI:10.1007/s00214-007-0310-x.
- B. Mennucci, Polarizable Continuum Model, Wiley Interdisciplinary Reviews: Computational Molecular Science, 2012, pp. 386–404, DOI:10.1002/wcms.1086.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396, DOI:10.1021/jp810292n.
- G. Kresse, M. Marsman and J. Furthmüller, Vienna Ab-Initio Package Vienna Simulation: VASP the GUIDE, VASP Man, 2014, p. 237 Search PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344.
- R. Sánchez-De-Armas, B. Brena, I. Rivalta and C. M. Araujo, Soft X-Ray Spectroscopic Properties of Ruthenium Complex Catalyst under CO2 Electrochemical Reduction Conditions: A First-Principles Study, J. Phys. Chem. C, 2015, 119(40), 22899–22907, DOI:10.1021/acs.jpcc.5b05626.
- P. W. Atkins, T. L. Overton, J. P. Rourke and M. T. Weller, Shriver and Atkins' Inorganic Chemistry, Fifth edn, 2010, DOI:10.1016/0375-9601(91)90960-G.
- S. Chardon-Noblat, A. Deronzier, D. Zsoldos, R. Ziessel, M. Haukka, T. Pakkanen and T. Venäläinen, Mode of Formation of Polymeric [{Ru(Bipy)(CO)2}n] (Bipy = 2,2′-Bipyridine) Films, J. Chem. Soc., Dalton Trans., 1996, 2581–2583, 10.1039/DT9960002581.
- M. Lundberg and P. E. M. Siegbahn, Quantifying the Effects of the Self-Interaction Error in DFT: When Do the Delocalized States Appear?, J. Chem. Phys., 2005, 122, 224103, DOI:10.1063/1.1926277.
- E. I. Ioannidis and H. J. Kulik, Towards Quantifying the Role of Exact Exchange in Predictions of Transition Metal Complex Properties, J. Chem. Phys., 2015, 143, 034104, DOI:10.1063/1.4926836.
- C. Peng and H. Bernhard Schlegel, Combining Synchronous Transit and Quasi-Newton Methods to Find Transition States, Isr. J. Chem., 1993, 33(4), 449–454, DOI:10.1002/ijch.199300051.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1se01315g |
| This journal is © The Royal Society of Chemistry 2021 |