Open Access Article
Open Access ArticleUnexpected inverse correlations and cooperativity in ion-pair phase transfer†
Nitesh
Kumar
 *a and
Aurora E.
Clark
*a and
Aurora E.
Clark
 *ab
*ab
aDepartment of Chemistry, Washington State University, Pullman, Washington 99164, USA
bPacific Northwest National Laboratory, Richland, Washington 99354, USA. E-mail: nitesh.kumar@wsu.edu; auclark@wsu.edu
First published on 29th September 2021
Abstract
Liquid/liquid extraction is one of the most widely used separation and purification methods, where a forefront of research is the study of transport mechanisms for solute partitioning and the relationships that these have to solution structure at the phase boundary. To date, organized surface features that include protrusions, water-fingers, and molecular hinges have been reported. Many of these equilibrium studies have focused upon small-molecule transport – yet the extent to which the complexity of the solute, and the competition between different solutes, influence transport mechanisms have not been explored. Here we report molecular dynamics simulations that demonstrate that a metal salt (LiNO3) can be transported via a protrusion mechanism that is remarkably similar to that reported for H2O by tri-butyl phosphate (TBP), a process that involves dimeric assemblies. Yet the LiNO3 out-competes H2O for a bridging position between the extracting TBP dimer, which in-turn changes the preferred transport pathway of H2O. Examining the electrolyte concentration dependence on ion-pair transport unexpectedly reveals an inverse correlation with the extracting surfactant concentration. As [LiNO3] increases, surface adsorbed TBP becomes a limiting reactant in correlation with an increased negative surface charge induced by excess interfacial NO3−, however the rate of transport is enhanced. Within the highly dynamic interfacial environment, we hypothesize that this unique cooperative effect may be due to perturbed surface organization that either decreases the energy of formation of transporting protrusion motifs or makes it easier for these self-assembled species to disengage from the surface.
1 Introduction
Solvent extraction, also known as liquid/liquid extraction (LLE), is one of the most industrially prevalent methods for the separation and purification of complex metal mixtures – whether in ore refinement, recycling, or environmental remediation. It is a particularly relevant technology for the separation of heavy metals, including actinides and rare earths, that are critical materials to energy and communication technologies.1–4 LLE involves the partitioning of metal ions between the aqueous and organic phases and often involves the use of a chelating amphiphilic extractant that binds the hydrated metal ion at the water/oil interface to create a hydrophobic species that migrates from the interface into the organic phase. Understanding the changes to metal ion speciation within the interfacial region, the distribution of ions, and organizational features of the instantaneous water/oil interface are an active and vibrant ongoing area of research.5–10 Yet the specific mechanisms of transport (particularly under equilibrium conditions) are at their nascent stages of being understood. Surface sensitive experimental techniques like vibrational sum-frequency generation (VSFG)11,12 and X-ray diffraction13 can provide an ensemble average depiction of molecular orientation and species distributions, however these do not characterize dynamic phenomena.14–16 The instantaneous water/oil interface is often interpreted in terms of capillary waves that derive from thermal fluctuations and interfacial anisotropy,13,17 yet on top of this rough and dynamically evolving surface other architectures have been predicted that are modulated by the presence of surfactants. These include protrusions that extend from the aqueous to organic phase, “islands” of surfactant bilayers, and budding micellar-like structures.7,18,19 Atomistic molecular simulations have implicated these hierarchically organized features within transport mechanisms under equilibrium conditions,20 but it is anticipated that several different pathways may exist that simultaneously depend upon the self-assembly of the surfactant at the instantaneous surface, as well as the solute that is being transported. For example, it is entirely unclear if transport pathways for simple solutes like H2O are capable of partitioning more complex solutes like ion-pairs or metal-extractant complexes.Background electrolytes, LiNO3 for example, play an important role within LLE and are often employed to increase the distribution ratio of metal ions of interest,21–23 though the mechanism of how this occurs is not understood. Interestingly, these electrolytes are often co-extracted alongside other unwanted species, like HNO3 and H2O. This is a well-known occurrence with tributyl phosphate (TBP) in the PUREX (Plutonium Uranium Reduction EXtraction) process.24,25 Recent work has elucidated the mechanism of H2O extraction by TBP through the formation of water protrusions at the TBP laden interface. These structures are related to an increase in the concentration of water-bridged TBP dimers that can effectively desorb from the instantaneous water/oil surface and migrate into the organic phase.18 Presumably, strong ion–dipole interactions between charge dense Li+ ions and TBP are a prominent factor in LiNO3 extraction, especially at high electrolyte and extractant concentrations.26–28 However, it is important to recognize that the presence of electrolytes can affect extractant driven interfacial chemistry through additional ion–ion, ion–dipole, and dipole–dipole interactions between ions, extractant, solvent, and the diluent molecules.29,30
This work employs molecular dynamics simulations to probe the equilibrium complexation of LiNO3 by TBP under PUREX-like conditions.31 This includes the subsequent extraction mechanism. The impact of the background electrolyte concentration upon competing extraction processes (notably the extraction of H2O) has been investigated alongside the distribution coefficient and transfer rates. Unlike prior studies that have employed free energy methods with pre-identified ion transport reaction coordinates, the equilibrium studies here provide a new and unbiased perspective of how the transport mechanisms may change as a function of solute size and solution conditions. LiNO3 is observed to follow a similar extraction mechanism as H2O extraction by TBP, although the rate of phase transfer is significantly dampened. The distribution of TBP-assembled species is significantly more complex in the presence of an electrolyte and varies depending on the position within the capillary wave front of the instantaneous surface. At crest regions of the surface that extend into the organic phase, Li+ replaces H2O within TBP(H2O)TBP dimers to form a TBP(Li+)TBP complex that then associates with NO3− to form TBP(LiNO3)TBP, subsequently disengaging from the instantaneous surface and migrating into the organic phase. Yet this competition between Li+ and H2O within the dimeric TBP assembly changes the mechanism of H2O transport from being facilitated by TBP(H2O)TBP to TBP(H2O) adducts within the crest region. Importantly, the TBP concentration at the instantaneous surface is highly sensitive to the [LiNO3] – where potential of mean force simulations demonstrate a decrease in surface sorption energy with increasing aqueous LiNO3 concentration. We presume this behavior to be due to a complex suite of electrostatic effects induced by excess interfacial NO3− (as supported by the calculated surface charge). Counterintuitively, the rate of LiNO3 transport increases in spite of the observation that interfacially sorbed TBP becomes a limiting reactant for the formation of the transporting TBP(LiNO3)TBP species – meaning that the encounter frequency on the surface is dramatically reduced. This indicates that when a protrusion is formed, it has a higher probability of successfully transporting these solutes, a feature that may result from more favorable energetics for protrusion formation or decreased barriers for disengagement from the surface to promote migration into the organic phase. Although it is conceptually convenient that the LiNO3 extraction mechanism follows the same process as simple H2O transport, the fact that LiNO3 alters the mechanistic pathway for H2O transport, in combination with the concentration-dependent observations of cooperative behavior for transport efficiency, certainly demonstrates the complex collective behavior of these interfaces that are still far from being understood.
2 Computational methods and analysis
2.1 System setup and simulation details
Initial system configurations for all-atom classical molecular dynamics simulations (pictured in Fig. S1†), using the compositions and cell sizes presented in Table S1,† were constructed using Packmol.32 Three different TBP-containing systems with 10%, 30% & 50% v/v (TBP/hexane) organic phase compositions were studied (corresponding to 0.05 M, 0.15 M and 0.25 M respectively), where the electrolyte (LiNO3(aq)) concentrations were varied from 1 to 5 M. In similar experimental conditions Zhou et al.33 reported the highest extraction of lithium salts at TBP concentration of 50% v/v in the organic phase. Using GROMACS 2016.2,34 each system was equilibrated for at least 100 ns in the NPT ensemble followed by at least 40 ns of NVT simulation, using a 2 fs time-step at 298 K and the leap frog integrator. After equilibration, production runs were performed for 150 ns in the NVT ensemble. Computations were performed with a 16 Å cutoff for both van der Waals and short-range electrostatic interactions. Ewald summation35 was used for the computation of long-range interactions.36 The Nose–Hoover thermostat37 was employed for temperature coupling and Parrinello–Rahman barostat38 for pressure coupling with 1 ps coupling time.2.2 Force fields and benchmarking
The Li+ and NO3− ions were modeled using parameters from Joung et al.39 and Ye et al.40,41 but with a 90% electrostatic continuum correction (ECC) to account for the polarization effects (charges scaled by 10%), as recently reported by Kumar et al.42 to reproduce the interactions with metal ions (e.g. UO22+) in PUREX-like conditions up to 5 M [LiNO3]. We employ this modified ECC potential for Li+ and NO3− for consistency across multiple works that are ongoing for PUREX systems. The modified all-atom Generalized Amber Force Field (GAFF)43,44 was employed to describe TBP and hexane, along with the TIP3P water model,45 which yields a water solubility (concentration in TBP) of 4.53 ± 0.08 g L−1 that is in good agreement with the experimental value of 5.80 g L−1.44,46,47 All LJ terms and charges are provided in Table S2.† The Lorentz–Berthelot combination rules were employed for the calculation of collision diameter and well depth cross terms. Extensive benchmarking was performed to ensure that the system reproduced the known aqueous solvation behavior in the bulk, the distribution coefficients for LiNO3 into the organic phase, as well as trends in interfacial tension, width, and surface activity of the TBP. These procedures are discussed in the ESI† (including Fig. S2–S7†).2.3 Chemical species identified by intermolecular networks
The identification of ion–water, water–extractant, and ion–extractant solvated or complexed species was achieved with a graph-theoretical approach using the ChemNetworks package.48 Molecular or ion vertices within a network of intermolecular interactions were constructed wherein an edge occurs via a geometric criterion of the intermolecular interaction of interest. The geometric cutoffs are derived from the position of the first minima in the respective pair correlation functions associated with each vertex (Table S3†). In the case of hydrogen bonding (HB), the H2O⋯H2O and H2O⋯TBP HBs are defined by an O⋯H distance < 2.5 Å and an O⋯H–O angle of ∼145–180°.2.4 The instantaneous liquid/liquid interface
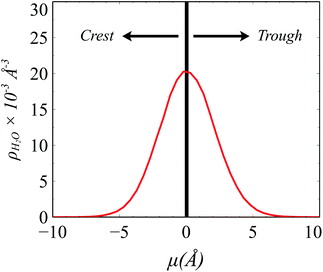
The instantaneous surface comprises those solvent and solute molecules that are in direct contact with the immiscible cosolvent. The Identification of Truly Interfacial Molecules49,50 algorithm (ITIM) is employed for this purpose, yet the distribution of H2O and LiNO3 between the two phases caused by TBP extraction complicates the analysis (e.g., H2O(org) are counted as interfacial water) and requires a slightly modified approach as illustrated in Fig. S8.† The procedure of identification of interfacial ions, solvent, and extractant involves first determining the H-bonding network of water using the aforementioned edge criteria. Cluster analysis is then used to separate the extracted water molecules from the bulk and dangling interfacial H2O using the connected components module of the NetworkX package.51 The largest molecular cluster in the simulated system is formed by the bulk water, whereas the extracted water forms sub-graphs.52,53 Water molecules that are directly connected to the largest water cluster are part of the bulk electrolyte network, whereas all other subgraphs in the organic phase are termed as extracted H2O. Ions interacting with the largest cluster of water are included in the bulk electrolyte network. ITIM analysis is then performed on the molecules and ions that comprise the bulk electrolyte network for the identification of truly interfacial molecules/ions using a probe sphere of radius 1.5 Å.10,50 Using the mean of the density of the waters within the instantaneous surface the z-axis is modified such that the mean is set to μ = 0 (Fig. 1). Molecules within the instantaneous surface with negative μ are considered to be in extending into the organic phase and within the “crest” region of the capillary wave front, while those with positive μ values extend into the aqueous phase and are part of the “trough” region. TBP molecules are divided into two subcategories: surface adsorbed TBP and interfacial region TBP. The TBP molecules that are directly in contact with the electrolyte phase are termed as surface adsorbed TBP, whereas the TBPs present in the interfacial region (−5 to 5 Å on the μ axis), but are not in direct contact with the aqueous phase, are called interfacial region TBP.2.5 Density profiles of molecular complexes
The density profiles of different chemical species were analyzed along the μ-axis and the xy plane to understand the distribution of species within the interfacial region, and changes to speciation in going from the aqueous phase, through the instantaneous surface, and into the organic phase. The time-averaged densities of chemical species of interest were binned in 2 Å increments, with the density normalized by the volume formed by the bin multiplied by the xy box lengths. For Li+-containing species, the position of the Li+-center was used to assign the position of the complex, while for the H2O(TBP)H2O species the position of the phosphoryl O-atom was employed, and for the TBP(H2O)TBP complex the position of OW was used (these atoms being closest to the center of mass). In the case of TBP, to understand organization within the plane of the instantaneous surface, the two dimensional density distributions of the adsorbed TBPs were computed by projecting the Cartesian coordinates to the phosphoryl O-atoms to an xy plane (using 100 × 100 pixel resolution).2.6 Potential of mean force
Umbrella sampling was used to characterize the free energy of a single TBP adsorption at the electrolyte/hexane interface as a function of [LiNO3]. Although this omits TBP⋯TBP interactions that may influence adsorption energetics, the sampling of the environments at the instantaneous surface is greatly simplified while still capturing the affect of the aqueous electrolyte upon adsorption characteristics. The potential of mean force (PMF) was computed along the μ axis in the NPT ensemble at 298 K. A harmonic potential of form, 1/2κ(μ − μ0)2 with κ = 1000 kcal nm−2 was employed to constrain the TBP (P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O headgroup) in the sampling windows near μ0. Fifty equally spaced windows explored a 25 Å region (in 0.5 Å increments) along μ. Each sampling window was first equilibrated for 2 ns in NPT, followed by a 10 ns production run. Statistical uncertainties were computed using the bootstrapping methodology implemented in gwham.54
O headgroup) in the sampling windows near μ0. Fifty equally spaced windows explored a 25 Å region (in 0.5 Å increments) along μ. Each sampling window was first equilibrated for 2 ns in NPT, followed by a 10 ns production run. Statistical uncertainties were computed using the bootstrapping methodology implemented in gwham.54
2.7 Convergence and equilibration
Multiple timescale behaviors are observed in biphasic systems and a such it is important to note their equilibrium characteristics on the timescale of the simulations performed. Several different system features were monitored, including (1) equivalent distribution of chemical species at both interfaces within the simulation box, (2) converged interfacial tension, (3) steady state concentrations of chemical species in both phases (as measured by the distribution ratios), and (4) converged forward and reverse migration rates of solutes. Pertaining to (1), the average density distributions of each species are plotted in Fig. S5.† Normalized density profiles (ρ/ρ0) are computed for all systems with 50% TBP in the organic phase and for various [LiNO3]. For (2), the interfacial tension (γ) was calculated using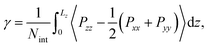 | (1) |
The bulk aqueous and organic densities after equilibration were used to compute the distribution ratio (D) of LiNO3, labelled DLiNO3, as
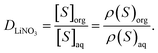 | (2) |
The concentration of LiNO3 was counted in the organic phase irrespective of its location relative to the instantaneous surface. Therein, DLiNO3 reached equilibrium after 60 ns (Fig. S10†). The experimental DLiNO3 is generally measured to be less than ≤0.1 depending upon the ionic strength and specific extractant employed. Using malonamide extractants in n-heptane and 3 M LiNO3, a D value of 0.05 has been measured,57 while a value of 0.104 is observed using ionic extractants.58 In the case of TBP, DLiNO3 has been reported to be 0.02 at 2 M LiNO3.21,59 Within the current work, DLiNO3 is predicted to be 0.0179 ± 0.003 from 1–4 M [LiNO3] which increases to 0.048 ± 0.004 at 5 M LiNO3 (Fig. S7†). It is important to mention that the equilibrium phase transfer of ion-pairs at low [LiNO3] (1–3 M) is much slower than the 4–5 M [LiNO3] system, which challenges sampling within the timescale of the simulation. As such, the possibility of the variations in the DLiNO3 at longer timescales cannot be neglected.
To quantify the dynamical phenomena of water and ions in the context of equilibration, we delineate two different processes: (1) migration of water and ions to the instantaneous surface and amongst the subjacent layers in the aqueous phase, and (2) transport of water and ions from the instantaneous surface to the organic phase (where the organic phase may be in the immediate vicinity of the instantaneous surface (μ = −10 Å to −25 Å), the interfacial region (μ = −10 to 10 Å), or the bulk (μ < −25 Å)). In the case of (1), the reversible adsorption/desorption of H2O, Li+, and NO3− to the instantaneous surface (Layer 1 in the ITIM algorithm, denoted L1), was examined by studying the rate of exchange between the instantaneous surface and the subjacent layer L2. Further, the L2 ⇔ L3, L3 ⇔ L4, and L4 ⇔ L5 exchange processes were identified. Ions present at the instantaneous interface at time t were tagged and their migration between subjacent layers were noted at time t + Δt. To identify transport into the organic phase we presume that if a H2O or ion was present at the instantaneous surface at t and was absent in either L2–L5 at t + Δt, it was identified as moving into the organic phase (thus, it takes more than 1 ps to migrate beyond L5 starting at L1). Two different sampling times were employed so as to balance total sampling time and the amount of data generated. First, a Δt of 1 ps over a total of 60 ns was examined. Using this sampling, the reversible rates of exchange for H2O, Li+ and NO3− between L1 ⇔ L2 are measured to be 126, 2, and 2 events per ps respectively – with the L1 → L2 and L2 → L1 having values within 0.5 events per ps of each other. This data supports the well-equilibrated aqueous dynamics of all species for the adsorption and desorption with respect to the instantaneous surface (Fig. S11†). In contrast, the transport of H2O and ions from L1 into the organic phase is significantly slower, vide infra. Only 0.027 and 10.45 events per ps are observed for Li+ and H2O, respectively in a system with 1 M LiNO3 and 50% TBP, which precludes highly accurate statistics, and further, no transport events of H2O or the ions from the organic phase into L1 was observed. These data were then compared to a 20 fs sampling time over 4 ns in which similar trends hold. Focusing upon the transport into the organic phase, using the 20 fs sampling, 5.5 H2O transport events are observed per ps while 0.07 Li+ events per ps are observed. Necessarily this points to the fact that converged rates require sampling that is faster than the exchange processes and that are sampled long enough time for convergence. We do not presume that the bulk organic phase (i.e., the region <−30 Å on the μ axis) solute transport dynamics is well-equilibrated and instead focuses upon a detailed study of the mechanistic observations of the L1 → organic transport processes, with trends in rate information presented rather than absolute values.
3 Results and discussion
3.1 Adsorption and molecular speciation within the instantaneous surface
The molecular speciation within the instantaneous surface is dependent upon both the adsorbed concentrations as well as the distribution amongst the crest and trough regions of the capillary wavefronts. As observed in Table 1, there is a consistent anionic excess observed in the instantaneous surface relative to Li+, irrespective of the [LiNO3]. TBP is known to form surfactant monolayers, and at 50% v/v TBP a surfactant monolayer is observed with a coverage of c.a. 0.03 TBP/Å2 (1 M LiNO3), a value similar to the 0.02 reported for a pure water/hexane interface at the TBP sorption saturation limit.5,18,60| [LiNO3] M | Li+ | NO3− | TBP |
|---|---|---|---|
| 1 | 06.48 ± 0.65 | 10.81 ± 0.22 | 79.25 ± 0.95 |
| 2 | 10.52 ± 0.53 | 18.20 ± 0.54 | 58.31 ± 1.90 |
| 3 | 14.81 ± 0.33 | 26.15 ± 0.24 | 49.74 ± 0.24 |
| 4 | 20.24 ± 0.43 | 36.06 ± 0.11 | 31.89 ± 0.95 |
| 5 | 25.84 ± 0.14 | 42.72 ± 0.34 | 30.22 ± 1.19 |
This saturation limit is only observed under the 50% v/v conditions, as the surface coverage of TBP decreases by 50% in going to the 30% v/v total TBP concentration, and at 10% v/v total TBP concentration, only ∼12% of the surface contains TBP (at 1 M LiNO3). Turning to the effect of [LiNO3] upon the adsorbed TBP concentration, Table 1 and S4† indicate a very interesting trend of decreased monolayer coverage with increased electrolyte concentration. This is consistent with prior dynamic interfacial tension measurements of phosphine oxide surfactants like trioctylphosphine oxide (TOPO) that also indicate decreased surface activity with increased aqueous ionic strength.61 At the 50% v/v TBP conditions, going from 1 M to 5 M [LiNO3] decreases the TBP coverage from ∼0.03 to ∼0.01 TBP/Å2 or by 60%. The distribution of the adsorbed TBP (projected into the xy plane) is graphically illustrated in (Fig. 2). The loss of TBP coverage with increasing [LiNO3] is supported by the decrease in the free energy of TBP adsorption as indicated by the potential of mean force simulations and is strongly correlated with an increase in the negative surface charge in the interfacial region as a result of interfacial NO3− excess relative to Li+ (Fig. S6 and S12†).
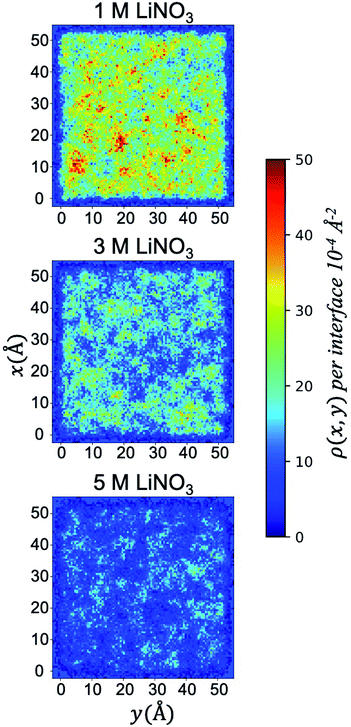 | ||
| Fig. 2 Two dimensional density distribution ρ(x, y) per interface of adsorbed TBP molecules present in the system with 50% TBP at 1, 3, and 5 M LiNO3. | ||
Necessarily, the statistical interpretation of transport processes is enhanced under conditions that have significant adsorbed TBP concentration and the remainder of the discussion focuses upon the 50% TBP v/v conditions. Therein, we focus upon two inter-related phenomena (1) the comparison of the TBP interactions and assembled species with H2O, Li+, and NO3− within the instantaneous surface and (2) the mechanisms of transport of H2O and LiNO3 as a function of aqueous electrolyte concentration. Prior study of water extraction by TBP has demonstrated that transport is intimately related to the formation of non-covalently bound (H2O)n(TBP)m species at the instantaneous surface.5,18,62,63 Specifically, the TBP(H2O)TBP assembly is the major species associated with surface protrusions that can disengage H2O as a solute and transport it to the organic phase.
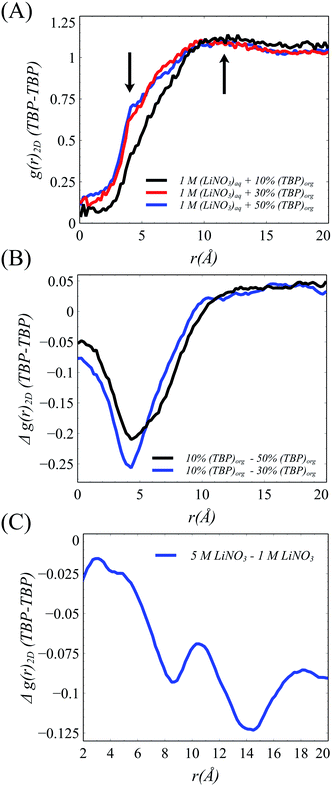
The xy surface TBP⋯TBP spatial adsorption interactions were first examined in terms of 2-dimensional pair correlation functions. In prior work at the water/hexane interface,18 two peaks, one at ∼4 Å and a broad peak at ∼12 Å were observed wherein the 4 Å correlation resulted from TBP(H2O)TBP species. This work reproduces those general features in the 1 M LiNO3 50% v/v conditions, though the 4 Å peak is slightly less pronounced (Fig. 4). The 2-D correlations are highly sensitive to the interfacial TBP concentration. Under 1 M [LiNO3], changing the TBP concentration from 50% to 30% to 10% v/v clearly leads to a decrease in the 4 Å correlation while the longer-range correlation is essentially unchanged. This indicates as the TBP concentration is decreased, there is a relatively homogeneous redistribution of TBP on the instantaneous surface. In comparison, under the 50% TBP v/v conditions, increasing the [LiNO3] causes a decrease in the mid- and long-range correlations (above 7 Å) while keeping much of the local TBP⋯TBP interactions.
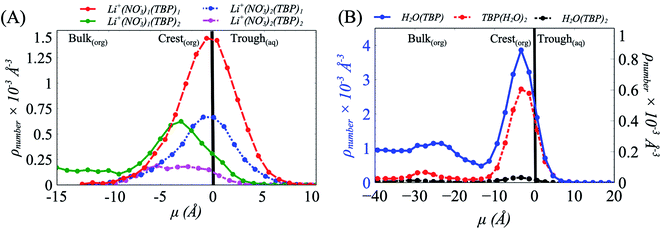
To understand this behavior further we then consider the number densities of Li+, NO3−, and TBP in the instantaneous surface (L1), with comparisons to the four subjacent layers as a function of [LiNO3]. Recall that each layer is obtained using the ITIM algorithm and represents a sequential distribution that moves into the bulk region. The average thickness of these layers is represented by the full-width at half maximum and is approximately 5 Å. As observed in (Fig. 3 and S14†), the NO3− ions distribute equally between the crest (negative μ) and trough (positive μ) regions of the instantaneous surface, while Li+ adsorb primarily in the crest region at all electrolyte concentrations. Furthermore, Li+ is depleted in the instantaneous surface relative to the subjacent layers as indicated by the growth of density in moving from L1 to L2, etc. under the 5 M conditions illustrated in Fig. 3A. At the same time, TBP also distributes preferentially to the crest region (Fig. S15†). Compared to the bulk aqueous electrolyte, there is a loss of one of the four solvating H2O about the Li+ irrespective of whether or not the Li+ exists as the ion-paired species (Fig. S16 and S17†). Yet the distribution of Li+ is into the crest regions is in sharp contrast to prior observations in the absence of a strongly interacting surfactant and it is well-known that loss of solvating H2O is thermodynamically unfavorable for the Li+.10,64,65
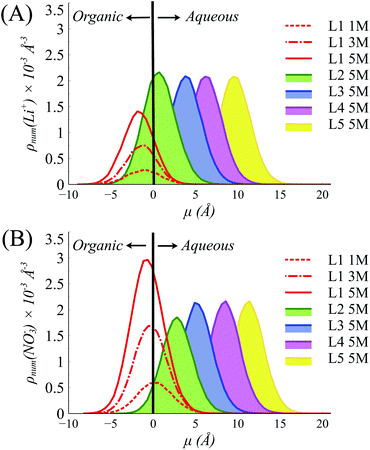 | ||
| Fig. 3 Distributions of (A) Li+ and (B) NO3− in the interfacial layers (Layer 1 to Layer 5 (L1–L5)) at various [LiNO3] (1–5 M) in the systems with 10% TBP in the organic phase. | ||
In combination, these data provide indirect evidence of strong Li+⋯TBP interactions within the crest region of the instantaneous surface, where TBP replaces one H2O in the first coordination shell (Fig. S18†). Direct analysis of the density of Li(NO3)m(TBP)n−m+1 species along the μ axis reveals a predominance of Li(NO3) (TBP)2 that systematically grows from the trough to the crest region of the instantaneous surface (Fig. 5A). Interestingly, the Li+⋯NO3−⋯TBP complexes undergo a further chemical transformation during the transition from the trough to crest region of the capillary wave front, where at the peaks of the crest region there is a high likelihood of the addition of a second TBP to form TBP(LiNO3)TBP. This is consistent with the extracted TBP(LiNO3)TBP molecular complexes being experimentally observed in the organic phase.24
With the formation of the TBP(LiNO3)TBP dimer within the crest region of the instantaneous surface, it is reasonable to question how this influences the formation of the aforementioned TBP(H2O)TBP species reported in prior work. Does the LiNO3 compete with H2O for interaction with TBP and does this impact the distribution of TBP–H2O assembled species? The density of the TBP(H2O)2, H2O(TBP) and H2O(TBP)2 species along the μ axis reveal an interesting change to the interactions of H2O with TBP within the 5 M LiNO3 50% TBP system (Fig. 5B). Specifically, the highest density of TBP⋯H2O complexes are formed in the crest region of the interface ranging from 0 to −10 Å. This differs from systems without electrolyte, where most of the TBP⋯H2O complexes were predominantly formed in the trough region, except the extracting TBP(H2O)TBP complex.18 Further, in the presence of LiNO3, the primary species is the TBP(H2O) singly hydrogen bonded complex rather than the solvent bridged dimer. Importantly, this implies that within the 2D TBP–TBP radial distribution function, it is the LiNO3-bridged TBP dimer that contributes to the observed peak at 4 Å presented in Fig. 4 and S13.†
3.2 H2O and LiNO3 extraction
The aforementioned speciation within the instantaneous surface portends interesting observations regarding the transport processes of both LiNO3 and H2O as solutes migrate from the aqueous to the organic phase. First and foremost, the TBP(LiNO3)TBP dimer formed at the crest region is the extracted species – as observed from the density profile of the LiNO3 species in the bulk organic phase (Fig. 5A). The ion-pair dimeric assemblies disengage from the instantaneous surface through a protrusion pathway identical to the H2O transport pathway in a non-electrolyte containing system as illustrated in Fig. 6A. The transport process is highly dynamic with many unsuccessful protrusions observed before disengagement and often taking up to 10 ns to leave the instantaneous surface. As illustrated in Fig. 6A, the initial formation of Li(NO3)(TBP)2 complex occurs at the crest region (t = 18.0 ns within this example), then the excess NO3− within the instantaneous surface supports formation of the Li(NO3)n(TBP)m complex alongside interfacial H2O via H-bonding interactions causing an elongation of the underlying protrusion at t = 23.7 ns. The interfacial water-nitrate H-bonding interactions promotes migration of H2O and LiNO3 (t = 25.7 ns) to the organic phase. The organic phase structure of the experimentally observed24 stable LiNO3(TBP)2(H2O) complex is shown in the final frame of Fig. 6A. In comparison, H2O transport via a protrusion is much more rapid – on the order of 1 ns (Fig. 6B). Although there is a distribution of H2O⋯TBP adducts in the crest region of the capillary wave front, it is the (TBP)H2O complex that is the major water extracting species. These data are in stark contrast to the TBP(H2O)TBP that was quantified as the major extracting species in the absence of electrolytes and indicates that the competition between extraction of LiNO3 and H2O by TBP fundamentally alters the H2O extraction mechanism.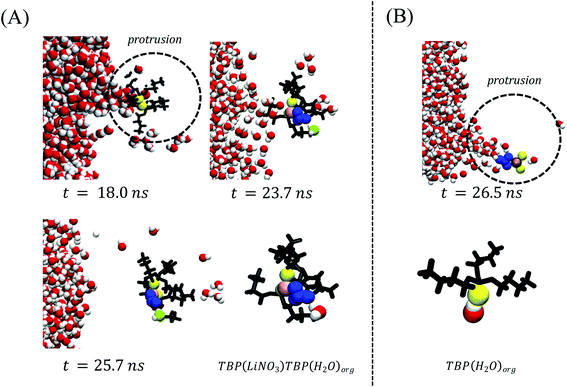 | ||
Fig. 6 (A) A microscopic mechanism for LiNO3 ion-pair extraction by tri-butyl phosphate. This includes formation of the ion-pair–TBP complex within a protrusion and disengagement during the phase transport. Note that the Li+ and NO3− ions are represented by pink and blue colors respectively. TBP oxygen (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P) is shown by yellow and the remaining part by black color. The H2O extracted during the ion-pair extraction is green. (B) A schematic representation of observed water protrusion66 In both cases the TBP tail-groups are hidden for visual clarity. P) is shown by yellow and the remaining part by black color. The H2O extracted during the ion-pair extraction is green. (B) A schematic representation of observed water protrusion66 In both cases the TBP tail-groups are hidden for visual clarity. | ||
Perhaps most intriguing is the observed change in transfer rates for both LiNO3 and H2O as a function of electrolyte concentration. As noted in Table 1, moving from 1–5 M [LiNO3] systematically increases the number of sorbed ions at the instantaneous surface, while at the same time decreasing the number of TBP available to first form the observed LiNO3(TBP) complex in the trough region and then the TBP(LiNO3)TBP in the crest region. From a stoichiometry perspective, Li+ is the limiting reactant from 1–3 M, however, at 4–5 M the TBP becomes the limiting reactant as a two-fold excess of TBP is required relative to the surface ion concentration. Yet surprisingly, the rate of transfer of LiNO3via the TBP(LiNO3)TBP adduct increases dramatically in going from 1 M to 5 M electrolyte. At 1 M [LiNO3] 0.027 transfer events are observed per ps, while at 5 M 0.53 events per ps are observed (using the 1 ps sampling frequency, see Computational methods). These data indicate a fundamental change to the efficacy of protrusions as transporting architectures under high-ionic strength conditions. Although the encounter frequency associated with the formation of the TBP(LiNO3)TBP species is likely comparable with the 1–3 M conditions, the increase in rate suggests that when protrusions do form they have a higher probability of successfully disengaging from the surface.
4 Summary
Amphiphiles like TBP are employed for the extraction of a wide array of metals during separations and purification processes, not the least of which is the selective partitioning of UO22+ within the PUREX process. As in many liquid/liquid extraction systems, TBP extracts both wanted metal ions and unwanted polar solutes (like H2O) and salts from the aqueous electrolyte (as in LiNO3). This phenomenon is highly sensitive to the electrolyte concentration and complex relationships between this variable and the metal distribution ratio and surface activity of amphiphiles have been previously reported. Although the equilibrium mechanism of H2O transport has been identified through protrusion surface structures that are based upon a TBP(H2O)TBP self-assembled adduct, the extent to which such structures can transport larger electrolyte salts or metal–ligand complexes has not been explored.Herein, we demonstrate that while LiNO3 is extracted via a similar mechanism to H2O (through TBP(LiNO3)TBP assemblies in protrusion architectures), there is significant competition between LiNO3 and H2O and as a result the mechanism of H2O transport is modified. Although H2O transport still occurs by protrusions, the transported species are TBP(H2O) adducts. This MD study reproduces the changes in surface activity that have been previously reported for phosphine-oxide amphiphiles, providing a molecular rationale that is based upon the buildup of surface charge at the instantaneous surface through excess adsorption of NO−3. In turn, as the [LiNO3] concentration is increased, surface adsorbed TBP becomes a limiting reactant for the formation of transporting TBP(LiNO3)TBP species. Yet surprisingly, the rate of transport of TBP(LiNO3)TBP increases by an order of magnitude, indicating that the aqueous electrolyte concentration significantly impacts the energetics of the transport. This may occur by reducing the barrier for protrusion formation or disengagement of the self-assembled adducts.
Data availability
Data processing scripts and molecular dynamics simulation files are available at https://gitlab.com/aurora-clark-public/lino3-tbp-extraction-2021-chemsci. ChemNetworks package is available at https://gitlab.com/aurora-clark-public/chemnetworksv2-2.Author contributions
NK performed the simulations, curated data and validated the methodology, created the original draft and collaborated in manuscript revisions. AC conceptualized the project and acquired funding, supervised the research, supported manuscript drafting and collaborated with revisions and final edits.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the Department of Energy, Basic Energy Sciences Separations program (DE-SC0001815) for funding. This research used resources from the Center for Institutional Research Computing at Washington State University. NK is grateful for support from the Pacific Northwest National Laboratory (PNNL)-Washington State University (WSU) Distinguished Graduate Research Program (DGRP) Fellowship.References
- K. L. Nash and M. P. Jensen, Sep. Sci. Technol., 2001, 36, 1257–1282 CrossRef CAS.
- K. L. Nash, C. Madic, J. N. Mathur and J. Lacquement, The Chemistry of the Actinide and Transactinide Elements, Springer, 2008, pp. 2622–2798 Search PubMed.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- D. Sholl and R. Lively, Nature, 2016, 532, 435–437 CrossRef PubMed.
- M. Baaden, M. Burgard and G. Wipff, J. Phys. Chem. B, 2001, 105, 11131–11141 CrossRef CAS.
- B. Qiao, J. V. Muntean, M. Olvera de la Cruz and R. J. Ellis, Langmuir, 2017, 33, 6135–6142 CrossRef CAS PubMed.
- Z. Liang, W. Bu, K. J. Schweighofer, D. J. Walwark, J. S. Harvey, G. R. Hanlon, D. Amoanu, C. Erol, I. Benjamin and M. L. Schlossman, Proc. Natl. Acad. Sci. U.S.A., 2019, 116, 18227–18232 CrossRef CAS PubMed.
- P. Jungwirth and D. J. Tobias, Chem. Rev., 2006, 106, 1259–1281 CrossRef CAS PubMed.
- S. Vembanur, A. J. Patel, S. Sarupria and S. Garde, J. Phys. Chem. B, 2013, 117, 10261–10270 CrossRef CAS PubMed.
- N. Kumar, M. J. Servis, Z. Liu and A. E. Clark, J. Phys. Chem. C, 2020, 124, 10924–10934 CrossRef CAS.
- M. Bonn, Y. Nagata and E. H. Backus, Angew. Chem., Int. Ed., 2015, 54, 5560–5576 CrossRef CAS PubMed.
- S. K. Reddy, R. Thiraux, B. A. W. Rudd, L. Lin, T. Adel, T. Joutsuka, F. M. Geiger, H. C. Allen, A. Morita and F. Paesani, Chem, 2018, 4, 1629–1644 CAS.
- D. M. Mitrinović, A. M. Tikhonov, M. Li, Z. Huang and M. L. Schlossman, Phys. Rev. Lett., 2000, 85, 582 CrossRef PubMed.
- S. Nayak, K. Lovering, W. Bu and A. Uysal, J. Phys. Chem. Lett., 2020, 11, 4436–4442 CrossRef CAS PubMed.
- X. Chen, W. Hua, Z. Huang and H. C. Allen, J. Am. Chem. Soc., 2010, 132, 11336–11342 CrossRef CAS PubMed.
- D. Bagchi, T. D. Nguyen and M. O. de la Cruz, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 19677–19684 CrossRef CAS PubMed.
- G. Luo, S. Malkova, J. Yoon, D. G. Schultz, B. Lin, M. Meron, I. Benjamin, P. Vanỳsek and M. L. Schlossman, Science, 2006, 311, 216–218 CrossRef CAS PubMed.
- M. J. Servis and A. E. Clark, Phys. Chem. Chem. Phys., 2019, 21, 2866–2874 RSC.
- Z. Liu and A. E. Clark, Chem. Sci., 2021, 12, 2294–2303 RSC.
- R. J. Ellis, Y. Meridiano, J. Muller, L. Berthon, P. Guilbaud, N. Zorz, M. R. Antonio, T. Demars and T. Zemb, Chem.–Eur. J., 2014, 20, 12796–12807 CrossRef CAS PubMed.
- E. Hesford and H. McKay, Trans. Faraday Soc., 1958, 54, 573–586 RSC.
- T. Healy and H. McKay, Recl. Trav. Chim. Pays-Bas, 1956, 75, 730–736 CrossRef CAS.
- E. Mowafy and H. Aly, Solvent Extr. Ion Exch., 2002, 20, 177–194 CrossRef CAS.
- N. Isaac, P. Fields and D. Gruen, J. Inorg. Nucl. Chem., 1961, 21, 152–168 CrossRef CAS.
- R. Chiarizia, K. L. Nash, M. P. Jensen, P. Thiyagarajan and K. C. Littrell, Langmuir, 2003, 19, 9592–9599 CrossRef CAS.
- B. Mokili and C. Poitrenaud, Solvent Extr. Ion Exch., 1995, 13, 731–754 CrossRef CAS.
- O. A. Francisco, H. M. Glor and M. Khajehpour, ChemPhysChem, 2020, 21, 484–493 CrossRef CAS PubMed.
- B. Qiao, F. Jiménez-Ángeles, T. D. Nguyen and M. O. De La Cruz, Proc. Natl. Acad. Sci. U.S.A., 2019, 116, 19274–19281 CrossRef CAS.
- L. I. Katzin and J. C. Sullivan, J. Phys. Chem., 1951, 55, 346–374 CrossRef CAS PubMed.
- I. Benjamin, Chem. Rev., 1996, 96, 1449–1476 CrossRef CAS PubMed.
- W. Lanham and T. Runion, PUREX Process for Plutonium and Uranium Recovery, Oak ridge national lab., tenn. technical report, 1949 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- Z. Zhou, S. Liang, W. Qin and W. Fei, Ind. Eng. Chem. Res., 2013, 52, 7912–7917 CrossRef CAS.
- M. Abraham, T. Murtol, R. Schulz, S. Pall, J. Smith, B. Hess and E. Lindhal, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- D. J. Price and C. L. Brooks III, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef CAS PubMed.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- I. S. Joung and T. E. Cheatham III, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- X. Ye, S. Cui, V. F. de Almeida, B. P. Hay and B. Khomami, Phys. Chem. Chem. Phys., 2010, 12, 15406–15409 RSC.
- G. Benay and G. Wipff, J. Phys. Chem. B, 2014, 118, 3133–3149 CrossRef CAS PubMed.
- N. Kumar, M. J. Servis and A. E. Clark, Solvent Extr. Ion Exch., 2021, 1–23 CrossRef.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- X. Ye, S. Cui, V. F. de Almeida and B. Khomami, J. Phys. Chem. B, 2013, 117, 14835–14841 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- Q. N. Vo, C. A. Hawkins, L. X. Dang, M. Nilsson and H. D. Nguyen, J. Phys. Chem. B, 2015, 119, 1588–1597 CrossRef CAS PubMed.
- Q. N. Vo, L. X. Dang, M. Nilsson and H. D. Nguyen, J. Phys. Chem. B, 2016, 120, 6985–6994 CrossRef CAS PubMed.
- A. Ozkanlar and A. E. Clark, J. Comput. Chem., 2014, 35, 495–505 CrossRef CAS PubMed.
- L. B. Pártay, G. Hantal, P. Jedlovszky, Á. Vincze and G. Horvai, J. Comput. Chem., 2008, 29, 945–956 CrossRef PubMed.
- G. Hantal, M. Darvas, L. B. Partay, G. Horvai and P. Jedlovszky, J. Phys.: Condens. Matter, 2010, 22, 284112 CrossRef PubMed.
- A. Hagberg, P. Swart and D. S. Chult, Exploring Network Structure, Dynamics, and Function using NetworkX, Los alamos national lab.(lanl), los alamos, nm (united states) technical report, 2008 Search PubMed.
- M. E. Newman, Nat. Phys., 2012, 8, 25–31 Search PubMed.
- M. E. Newman, SIAM Rev., 2003, 45, 167–256 CrossRef.
- J. S. Hub, B. L. De Groot and D. Van Der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- J. Alejandre, D. J. Tildesley and G. A. Chapela, J. Chem. Phys., 1995, 102, 4574–4583 CrossRef CAS.
- S. Senapati and M. L. Berkowitz, Phys. Rev. Lett., 2001, 87, 176101 CrossRef CAS PubMed.
- Y. Meridiano, L. Berthon, X. Crozes, C. Sorel, P. Dannus, M. Antonio, R. Chiarizia and T. Zemb, Solvent Extr. Ion Exch., 2009, 27, 607–637 CrossRef CAS.
- R. A. Hernandez and J. M. Martinez, Ind. Eng. Chem. Process Des. Dev., 1981, 20, 698–704 CrossRef CAS.
- H. Naganawa and S. Tachimori, Anal. Sci., 1994, 10, 309–314 CrossRef CAS.
- P. Beudaert, V. Lamare, J.-F. Dozol, L. Troxler and G. Wipff, Solvent Extr. Ion Exch., 1998, 16, 597–618 CrossRef CAS.
- K. Prochaska, M. Walczak and K. Staszak, J. Colloid Interface Sci., 2002, 248, 143–148 CrossRef CAS PubMed.
- X. Ye, S. Cui, V. d. Almeida and B. Khomami, J. Phys. Chem. B, 2009, 113, 9852–9862 CrossRef CAS PubMed.
- J. Mu, R. Motokawa, K. Akutsu, S. Nishitsuji and A. J. Masters, J. Phys. Chem. B, 2018, 122, 1439–1452 CrossRef CAS PubMed.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2001, 105, 10468–10472 CrossRef CAS.
- J. L. Thomas, M. Roeselová, L. X. Dang and D. J. Tobias, J. Phys. Chem. A, 2007, 111, 3091–3098 CrossRef CAS PubMed.
- J. J. Karnes and I. Benjamin, J. Chem. Phys., 2016, 145, 014701 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc04004a |
| This journal is © The Royal Society of Chemistry 2021 |