In silico design to enhance the barrier height for magnetization reversal in Dy(III) sandwich complexes by stitching them under the umbrella of corannulene

Abstract

Lanthanide based single molecular magnets (SMMs), particularly dysprocenium based SIMs, are well known for their high energy barrier for spin reversal (U_eff) and blocking temperatures (T_B). Enhancing these two parameters and at the same time obtaining ambient stability is key to realising end-user applications such as compact storage or as qubits in quantum computing. In this work, by employing an array of theoretical tools (DFT, ab initio CASSCF and molecular dynamics), we have modelled six complexes [(η⁵-corannulene)Dy(Cp)] (1), [(η⁵-corannulene)Dy(C₆H₆)] (2), [(η⁶-corannulene)Dy(Cp)] (3), [(η⁶-corannulene)Dy(C₆H₆)] (4), [(exo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] (5), and [(endo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] (6) containing corannulene as a capping ligand to stabilise Dy(III) half-sandwich complexes. Our calculations predict a strong axiality exerted by the Dy–C interactions in all complexes. Ab initio calculations predict a very large barrier height for all six molecules in the order 1 (919 cm⁻¹) ≈ 3 (913 cm⁻¹) > 2 (847 cm⁻¹) > 4 (608 cm⁻¹) ≈ 5 (603 cm⁻¹) ≈ 6 (599 cm⁻¹), suggesting larger barrier heights for Cp ring systems, followed by six-membered arene systems and then corannulene. DFT based molecular dynamics calculations were performed on complexes 3, 5 and 6. For complexes 3 and 5, the geometries that are dynamically accessible are far fewer. The range of U_eff computed for molecular dynamics snapshots is high, indicating a possibility of translating the large U_eff obtained into attractive blocking temperatures in these complexes, but the converse is found for 6. Furthermore, an in-depth C–H bond vibrational analysis performed on complex 3 suggests that the vibration responsible for reducing the blocking temperature in dysprocenium SIMs is absent here as the C–H bonds are stronger and corannulene steric strain prevents the C(Cp)–Dy–C(Cor) bending. As [(η⁶-corannulene)TM(X)]⁺ (TM = Ru, Zr, Os, Rh, Ir and X = C₅Me₅, C₆Me₆) are known, the predictions made here have a higher prospect of yielding stability under ambient conditions, a very large U_eff value and a high blocking temperature – a life-giving combination to new generation SMMs.

---

Introduction

Molecular magnets with bulk magnet-like features have fascinating applications, for instance, in high-dense memory storage devices, spintronics, multiferroics and molecular qubits, to name a few.^1–9 While different applications demand various criteria, several stumble blocks that exist need to be addressed before achieving end-user applications. Attaining a very high energy barrier height for spin reversal (U_eff) and blocking barrier (T_B) on a molecule that is stable under device fabrication conditions is crucial to realise the proposed applications.¹⁰ Three decades of enthralling studies on countless transition and lanthanide mono and polynuclear complexes reveal mononuclear lanthanide complexes as one of the most promising candidates to achieve this goal.^10–15 Among lanthanides, the Dy(III) ion is known to have the largest free-ion magnetic moment among half-integer spins due to the combination of a high total angular momentum (J = 15/2) and large Ising g-anisotropy.^10,16 It is an ideal candidate to produce single-ion magnets (SIMs) with a large U_eff in the presence of a strong axial ligand field due to the equatorially expanded electron density of the m_J = ±15/2 state.^13–15,17 Particularly, recent developments in dysprocenium based magnets have garnered attention with the achievement of blocking temperatures even beyond liquid nitrogen temperatures.^13–15

Dysprocenium magnets are unstable under ambient conditions.^13,15 Previous theoretical work has predicted that in the presence of the linear 2-coordinate Dy(III) ion, relaxation is expected to occur through the highest possible excited state.¹⁸ Most of these low coordinate Dy(III) complexes are not stable under ambient conditions. To overcome this, we have predicted the use of lanthanide encapsulated fullerenes (endohedral metallofullerenes (EMFs)) as one of the potential routes. Later, this was proved by experiments, offering a new generation of lanthanide encapsulated fullerenes as SMMs.^19–24 Particularly, the exchange interaction and magnetic anisotropy computed for Gd₂@C₇₉N and their analogues yield Q-bits/high blocking SMMs.^19,23,25 These fullerene cages offer a stable environment around the metal and can be easily fabricated on surfaces such as graphene/HOPG etc. They can also be functionalised with a tethering group to adsorb them on metallic surfaces without altering their magnetic characteristics.²⁶ Despite these advantages, EMFs are synthetically challenging and often suffer from very low yield, making them the world's costliest materials.²⁷

In search of an ideal ligand field environment that mimics dysprocenium chemistry and EMF chemistry and at the same time offers stability to the molecule under ambient conditions, we arrived at the lanthanide–corannulene moiety. Corannulene, with fivefold symmetry, consists of five benzene rings joined together through a five-membered ring in the centre, featuring one-third of the buckybowl structure (C₆₀).²⁸ To further extend our studies, we have included η⁶-benzene and cyclopentadienyl ligands in the presence of one of the corannulene molecules. While such complexes based on lanthanides are not known, we are motivated by the fact that [(η⁶-corannulene)TM(X)]⁺ (TM = Ru, Zr, Os, Rh, Ir and X = C₅Me₅, C₆Me₆) complexes are reported with several variations, and some of the complexes reported are air-stable for several months.^29–32 Keeping this in mind, we have performed DFT/ab initio CASSCF/RASSI-SI/SINGE_ANISO calculations on six such complexes [(η⁵-corannulene)Dy(Cp)] (1), [(η⁵-corannulene)Dy(C₆H₆)] (2), [(η⁶-corannulene)Dy(Cp)] (3), [(η⁶-corannulene)Dy(C₆H₆)] (4), [(exo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] (5), and [(endo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] (6) (see Fig. 1, S1, S2† and Table S1† for optimized cordinate) with the aim of finding a suitable match between arenes and corannulenes that yield attractive barrier height values. Frequency calculations reveal that all the complexes computed here are minima (see Table S2†). Also, it is worth mentioning that the charge on Dy is +3 in all these complexes studied with corannulene, and the C₆H₆ ligand is considered neutral, whereas the Cp ligand is considered to be monoionic. Moreover, molecular dynamics simulations have been performed within the DFT framework to assess various geometries that offer a shortcut to the relaxation mechanism and are likely correlated with the blocking temperatures.

Results and discussion

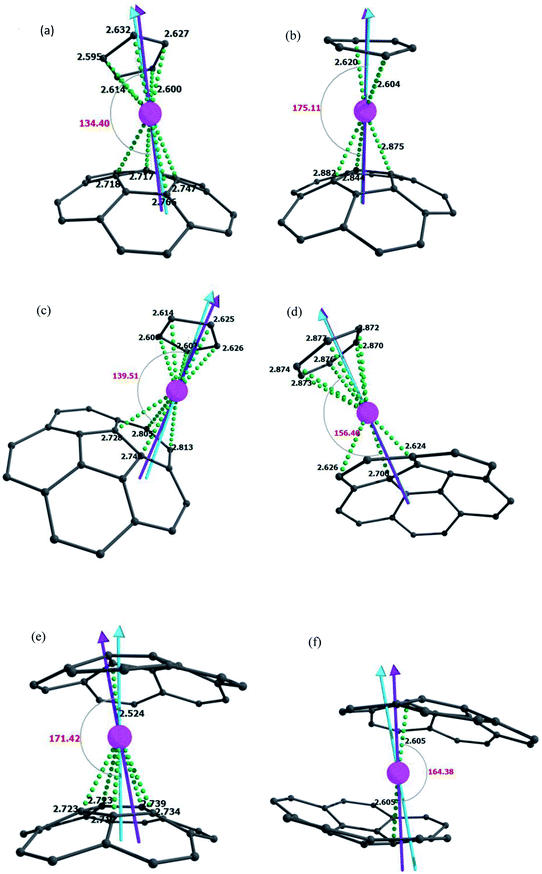
For corannulene complexes, one can expect the Dy(III) ion to coordinate either via hexagonal (η⁶) or pentagonal (η⁵) rings, and if lower hapticity is chosen, it can bind to various positions such as the hub, spoke, flank, and rim positions (Fig. S1†). To ascertain the effect of the pentagonal/hexagonal ring on the magnetic anisotropy, we have modelled six complexes (Fig. 1, see computational details, and Table S1† for details). The optimised structures were used to perform CASSCF + RASSI-SO/SINGLE_ANISO calculations using MOLCAS 8.2 to estimate magnetic anisotropy parameters together with the magnetic relaxation mechanism.¹⁵ This methodology has been established as a reliable tool to predict g-tensors and energies of low lying states for 4f, 3d–4f, and 4f–4f complexes.^{11,19,20,30,33–40} We have computed eight low lying Kramer's Doublets (KDs) corresponding to the ⁶H_15/2 state. For all these complexes, the eight low-lying KDs lie within an energy span of 717–1092 cm⁻¹ (see Table 1). The Dy–C distances with the corannulene ring in 1 were found to be in the range of 2.715–2.766 Å, while with Cp ring carbon, the distances are shorter (2.595–2.627 Å). For complex 2, on the other hand, the Dy–C(corannulene) distances are longer (2.844–2.940 Å), while the Dy–C(C₆H₆) distances are similar. This suggests that the ring size attached to the Dy(III) ion influences the Dy–C(corannulene) distances. In complex 3, the Dy–C distances are longer than those in model 1 but shorter than those in 2, while the Dy–C(C₅H₅) is similar to that in 1. Particularly, the shortest Dy–C(corannulene) distance is found to be linked to the rim carbon atom, which is reported to possess a greater negative charge density.⁴¹ Complex 4 has Dy–C(cor) distance in the range of 2.624–2.700, while in 5 and 6, the distances are shorter. To quantify the nature of Ln–C interaction, we turn to AIM analysis,^42,43 which suggests stronger Dy–C(Cp) interactions for 1 and 3 than Dy–C(C₆H₆) interactions for 2 and 4. The Dy–C interaction in 6 is the weakest among all, but in 5, these are moderate. For 1–6, AIM analysis yields mostly positive H(r) values suggesting the Ln–C bond to be dominantly ionic in nature (Table S3†). For 1 and 3, the strong Dy–C interactions (higher ρ values) can be seen as a reason behind the higher crystal field and hence a large gap between the first KD and eighth KD. Among complexes 1–4, 1–3 have a strong Dy–C interaction with the Cp/C₆H₆ ring and weaker interaction with the carbon atoms of the corannulene, while for complex 4, Dy–C(cor) interactions are found to be the strongest and Dy–C(C₆H₆) interactions are weaker, which weakens the crystal field effects.

Fig. 1 DFT optimized structures with all interacting Gd(III)–C bonds for models (a) [(η⁵-corannulene)Dy(Cp)] 1, (b) [(η⁵-corannulene)Dy(C₆H₆)] 2, (c) [(η⁶-corannulene)Dy(Cp)] 3, (d) [(η⁶-corannulene)Dy(C₆H₆)] 4, (e) [(exo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] 5, and (f) [(endo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] 6, with all the Gd(III)–C interactions obtained from the atoms in molecules (AIM) analysis. Colour code: Gd(III) = magenta, C = dark grey. Here, exo = Gd(III) interacts with corannulene through the exohedral side, endo = Gd(III) interacts with corannulene through the endohedral side. Gd–C bonds are assigned from the atoms in molecules (AIM) analysis. Bond distances and bond angles are marked in black and red respectively. The cyan arrows and violet arrows represent the direction of g_zz corresponding to ground KD and first KD respectively.

Table 1 CASSCF + RASSI-SO computed relative energies of eight low lying KDs and g tensors of eight low lying KDs for models 1–6 along with deviations from the principal magnetization axes of the first KD

KDs	1			2			3
	E, cm^−1	g x , gy, gz	(°)	E, cm^−1	g x , gy, gz	(°)	E, cm^−1	g x , gy, gz	(°)
1	0.0	0.000, 0.000, 19.976	—	0.0	0.000, 0.000, 20.007	—	0.0	0.000, 0.000, 19.983	—
2	302.0	0.000, 0.000, 17.217	5.9	352.5	0.000, 0.000, 17.138	1.3	301.6	0.000, 0.000, 17.201	4.8
3	513.6	0.003, 0.003, 14.519	5.3	512.7	0.003, 0.003, 14.512	3.5	509.3	0.007, 0.008, 14.504	4.7
4	676.5	0.008, 0.014, 11.827	0.9	614.5	0.024, 0.029, 11.866	0.3	668.3	0.042, 0.058, 11.814	2.4
5	812.7	0.219, 0.262, 9.303	9.1	724.8	0.017, 0.066, 9.186	1.3	803.1	0.334, 0.416, 9.204	7.6
6	919.5	1.778, 2.274, 6.778	26.4	846.8	0.806, 0.918, 6.440	1.5	912.9	3.319, 3.372, 6.397	22.5
7	991.7	9.557, 7.568, 2.507	0.2	956.3	3.551, 3.855, 5.959	88.8	994.2	2.549, 5.026, 11.217	89.2
8	1092.9	0.257, 0.841, 18.314	89.9	998.1	1.027, 5.526, 15.307	90.0	1078.9	0.389, 1.373, 17.938	90.4

---

KDs	4			5			6
	E, cm^−1	g x , gy, gz	(°)	E, cm^−1	g x , gy, gz	(°)	E, cm^−1	g x , gy, gz	(°)
1	0.0	0.000, 0.000, 19.960	—	0.0	0.000, 0.000, 19.871	—	0.0	0.000, 0.000, 19.927	—
2	232.6	0.000, 0.001, 17.169	0.7	137.3	0.004, 0.004, 17.312	12.3	170.6	0.001, 0.001, 17.404	7.8
3	391.1	0.004, 0.004, 14.567	4.1	298.3	0.024, 0.029, 14.659	9.1	301.8	0.024, 0.028, 14.552	10.1
4	508.1	0.319, 0.041, 11.913	8.5	441.7	0.006, 0.077, 11.864	5.7	425.2	0.193, 0.258, 12.070	2.7
5	608.3	0.782, 0.874, 9.060	14.0	546.3	0.058, 0.514, 8.977	19.3	517.9	0.053, 0.321, 9.760	0.5
6	690.4	6.443, 6.028, 4.906	11.4	603.1	8.532, 7.493, 4.431	23.8	598.8	0.619, 1.218, 6.874	1.5
7	768.9	1.494, 3.163, 13.432	90.0	640.7	0.797, 1.427, 18.732	85	670.7	3.304, 3.746, 5.173	89.9
8	873.2	0.131, 0.369, 18.763	90.0	717.1	0.017, 0.047, 19.478	90	717.5	1.102, 6.287, 16.645	88.6

---

For complexes 5 and 6, the Dy–C(cor) bonding is relatively weaker compared to similar bonding detected in 1 (η⁵). Also, the |V(r)|/|G(r)| ratio in all these cases is close to 1, which further confirms that these interactions are mostly ionic in nature. However, both the complexes have a strong interaction with one of the hub carbon atoms, and this has not been seen in earlier models. The overall CF splitting of the eight KDs are in the range of ∼800 cm⁻¹ for these complexes compared to ∼1000 cm⁻¹ for complexes 1–4 (Table 1), and this moderate drop in the CF splitting is due to the weaker binding of corannulene, and the absence of smaller (five/six) arene rings that tend to offer stronger interactions.

To understand the nature of Ln–C interaction further, we have performed energy decomposition analysis (EDA) using {(ligand)₂ + Ln} as fragments (Table S4†), and this reveals a strong Ln–C bonding in complexes 1 and 3, with 1 being slightly stronger compared to 3. Though the orbital interactions in 3 are very favourable, the steric contributions are significantly less compared to 1 leading to the observed difference. The next set of interaction energies are found for complexes 5 and 6, where the orbital interaction energies are found to be the largest among all the complexes, but the steric energy is very unfavourable due to the presence of two bulky corannulene units, leading to moderate interaction energy. Complexes 2 and 4 have the smallest overall interaction energy due to the weak orbital interaction contribution coupled with unfavourable steric energy (Table S4†). For all the studied models, m_J = ±15/2 is found to be the ground state with pure Ising type anisotropy making the ligand field suitable for the oblate Dy(III) ion (g_xx/yy = 0.000 and g_zz ≥ 19.960, see Table 1).

It is worth mentioning here that for most of the reported Dy@EMFs, which have η⁵ or η⁶ Dy–C interaction with the fullerene cage, the ground state is found to be pure m_J = ±15/2. Similar to the computed ground state, the first excited KD is also purely Ising in nature for all these complexes (g_xx ≤ 0.004, g_yy ≤ 0.004 and g_zz ≥ 17.138, see Table 1), signifying the calculated small quantum tunnelling of magnetisation (QTM) and thermally assisted QTM (TA-QTM) within the ground and first excited KDs (in the range of 10⁻⁴ to 10⁻⁷μ_B, see Fig. 2). The second, third, and fourth excited KDs are strongly axial (g_xx ≤ 0.782, g_yy ≤ 0.874, and g_zz ≥ 8.977, see Table 1) with a very small operative TA-QTM (in the range of 10⁻¹ to 10⁻⁴μ_B, see Fig. 2). The fifth excited KD has a significant transverse anisotropy (g_xx ≤ 8.532, g_yy ≤ 7.493 and g_zz ≥ 4.431, see Table 1) with substantial operative TA-QTM (in the range of 0.28 to 2.6 μ_B see Fig. 2). In all these models, the relaxation takes place from the fifth excited state except in 4, where relaxation takes place from the fourth excited KD. For 1, Orbach and QTM/TA-QTM up to the fourth excited state are found to be very small (in the range of 10⁻⁷ to 10⁻²μ_B); the TA-QTM from fifth excited state KDs of opposite magnetisation is found to be large enough (0.72 μ_B, see Fig. 2), causing relaxation via the fifth excited KD (−1 → −2 → −3 → −4 → −5 → −6 → +6 → +5 → +4 → +3 → +2 → +1, see Fig. 2), which yields a U_cal value of 919.5 cm⁻¹. For 2, the Orbach/Raman process related to the ground and first-excited KDs as well as between first and second-excited KDs of opposite magnetisation is found to be small (in the range of 10⁻⁷ to 10⁻⁵μ_B, see Fig. 2). The Orbach/Raman process and TA-QTM up to the fourth excited state vary in the order of 10⁻⁴ to 10⁻²μ_B. There is a significant TA-QTM in the fifth excited state (0.29 μ_B), and hence relaxation takes place from this state, setting the energy barrier as 846.8 cm⁻¹. For 3, the Orbach/Raman process is small till the fifth excited state. For 3, collinearity of KDs is maintained till the fourth-excited state, causing relaxation via the fifth excited state (−1 → −2 → −3 → −4 → −5 → −6 → +6 → +5 → +4 → +3 → +2 → +1, see Fig. 2) with a U_cal value of 912.9 cm⁻¹, whereas for 4, the collinearity of KDs is maintained till the fourth excited state. As mentioned earlier, the strong transverse anisotropy witnessed for the fourth excited state causes relaxation via this state (−1 → −2 → −3 → −4 → +4 → +3 → +2 → +1, see Fig. 2) which set the U_cal value to 608.3 cm⁻¹. For 5 and 6, eight KDs are separated by an energy range of ≈717 cm⁻¹. The relaxation mode is TA-QTM and Orbach through the fifth excited state in 5 and 6, respectively, and this sets the U_cal values to 603.1 cm⁻¹ and 598 cm⁻¹, respectively. Furthermore, the highest U_cal values observed are for 1 and 3, and in both cases, one of the ligands is Cp, whereas the other is corannulene. It can be seen that LoProp charges on carbons in the Cp ring in 1 and 3 are comparatively higher than their counterparts, i.e., the carbons of the C₆H₆ ring in 2 and 4, and hence it offers a higher crystal field and consequently larger U_cal values. Between 2 and 4, the C–Ln–C angle in 2 is larger than that in 4 (175.1° vs. 156.4°), and this lower angle reduces the axiality in 4, leading to smaller U_cal values. The difference of 20° bending leads to relaxation via a lower excited state in 4 compared to 2 (4th excited state vs. 5th excited state). In 5 and 6, there are only corannulene ligands, and from LoProp charges, it is ascertained that these offer a weaker ligand field, and hence comparatively lower U_cal values.

Fig. 2 Ab initio computed magnetic blockade diagrams for (a–f) 1–6, respectively. The arrows show the connected energy states with the number representing the matrix element of the transverse moment (see the text for details). Here, QTM = quantum tunnelling of the magnetisation, TA-QTM = thermally assisted QTM, O/R = Orbach/Raman process. The numbers above each arrow represent corresponding transverse matrix elements for the transition magnetic moments.

The mechanism developed here considered only static magnetic relaxation while the dynamic part is not taken into consideration. Addressing the dynamic part of the relaxation is challenging, and here we have followed two approaches: (i) perform molecular dynamics to ascertain various possible conformers which are energetically accessible and compute their magnetic anisotropy to ascertain the lowest possible effective energy barrier that could offer clues about the blocking temperature; (ii) look at the vibrational modes of the molecules to ascertain vibrational motions that are most likely to cause relaxation of magnetisation.

In the first approach, we have performed Molecular Dynamics (MD) calculations for 3, 5, and 6 using DFT methodology at 300 K employing the CP2K suite (see the Computational details section for more information). The MD trajectories computed for 3, 5, and 6 are shown in Fig. 3. From the computed trajectories, geometries which are in an energy window of less than ∼80 kJ mol⁻¹ were taken for CASSCF calculations to assess the geometric conformation that could reduce the blocking barrier/temperatures assuming these conformers would be present at room temperature. We performed calculations on several such snapshots from the MD trajectory (Fig. 3a for 3), and only small variations in the crystal field and U_cal values are noticed for complex 3. The U_cal values are found to be in the range of 784.2 (femtosecond f33) to 936.7 cm⁻¹ (f248) (see Tables S5 and S6†). In all these snapshots, the relaxation was found to occur via the 5th excited state similar to the original geometry, suggesting a more robust U_cal estimate that could offer a larger blocking temperature as well (Fig. 3 and S3†).

Fig. 3 (a, c and e) Time (in fs) evolution of energy (ΔE in cm⁻¹), (b, d and f) together with the U_cal values for the thermally accessible structures for models 3, 5 and 6, respectively. In (b), (d) and (f), black hollow circle = relaxation though 7th KD via Orbach; black solid triangle = relaxation through 6th KD via Orbach; black solid square = relaxation through 5th KD via Orbach; red hollow triangle = relaxation through 6th KD via TA-QTM; red hollow square = relaxation through 5th KD via TA-QTM and red hollow circle = relaxation through 7th KD via TA-QTM; black hollow pentagon = relaxation through 2nd KD via Orbach.

The MD study suggests fewer structures for model 5 whereas several structures for model 6 within the energy window (Table S5†). The geometries of 5 and 6 reveal conformational changes where the hapticity of the bonding alters among the donor atoms leading to smaller variations in the crystal field and U_cal values. It is worth noting that [(η⁶-corannulene)TM(X)]⁺ (TM = Ru, Zr, Os, Rh, Ir and X = C₅Me₅, C₆Me₆) complexes were also reported to exhibit fluxional behaviour detected from NMR. In complexes 5 and 6, the geometric changes are expected to alter the Ln–C (corannulene) interaction and Ln–C(Cp) interactions and, thus, the U_cal value. There are four snapshots that yield a U_cal value range of 641–652 cm⁻¹, while another two snapshots yield smaller U_cal values (503–533 cm⁻¹ see Fig. 3d, Tables S5 and S6†), setting the lower bound U_cal value to 5. The reduction in U_cal in two of the snapshots is due to the relaxation via the 6th excited state, unlike the other snapshots and the original molecule, which relaxes via the 7th excited state. The two snapshots that yield lower U_cal have smaller C–Dy–C angles causing relaxation via lower excited states and hence a reduction in the U_cal values. The MD trajectory for model 6 suggests several snapshots (126) in the energy window with a substantial change of Ln–C(corannulene) interaction (see Fig. 3f, Tables S5 and S6†). Considering the large number of snapshots available, a few representative structures have been chosen for each energy well to estimate the anisotropy. As all the structures in the same energy well do not differ significantly, their magnetic behaviour is expected to be similar. For 6, a substantial variation of ligand field around the metal centre is noticed, and this results in relaxation via Orbach (1st, 4th, 5th, and 6th excited states) and TA-QTM (4th, 5th, and 6th excited KDs) process for various snapshots leading to U_cal value in the range of 69–751 cm⁻¹ (see Fig. 3d, Tables S5 and S6†). The geometry, which yields a very small U_cal value (69 cm⁻¹), was analysed further, and here the Dy^III ion was found to move to the spoke carbon atoms and interact with three rings of the corannulene; this offers a strong equatorial ligand field leading to relaxation via the first excited state.

The second approach of following the vibration mode for the possible relaxation mechanism was performed on complex 3 as it shows more robust SIM characteristics among all tested examples. The C–H bond vibration of the cyclopentadienyl ring is found to cause the relaxation in dysprocenium SIMs, leading to a reduction in the blocking temperature. The C–H bond vibration causes relaxation in the dysprocenium SIMs, coupled with the bending of the Cp ring during the vibrational mode, and this vibration offers a shortcut for the magnetisation blockade to relax. In model 3, the presence of a larger corannulene ring is likely to block this relaxation as bending of the rings is not possible due to the steric strain imposed. We have performed frequency calculation on the optimised geometry of complex 3 and have performed vibrational mode analysis with a displacement of x_J = +1.0 to −1.0 (see Table S7 in the ESI†) and this reveals minor variation in the U_cal values (Table S7†). No significant changes are noted in the computed CF parameters (see Fig. S4 in the ESI†). This suggests that the C–H vibrations are unlikely to cause relaxation of magnetisation in this molecule, boosting the hope for obtaining larger blocking temperatures and ambient stability.

Conclusions

In search of EMFs like traditional coordination complexes with high energy barriers for spin reversal, we have performed a theoretical study on several Dy(III)–corannulene complexes using an array of theoretical tools such as DFT for geometries, ab initio CASSCF/SINGLE_ANISO for barrier height of magnetisation reversal and DFT based molecular dynamics to gain understanding on various relaxation processes that are likely to be correlated with the blocking temperatures. The conclusions derived from this work are summarised below.

(i) Stabilising Dy(III)-half-sandwich complexes using corannulene capping: six half-sandwich Dy(III) complexes containing both five and six-membered arenes and stitching them up with corannulene on one side or utilising two corannulenes as ligands are modelled [(η⁵-corannulene)Dy(Cp)] (1), [(η⁵-corannulene)Dy(C₆H₆)] (2), [(η⁶-corannulene)Dy(Cp)] (3), [(η⁶-corannulene)Dy(C₆H₆)] (4), [(exo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] (5), and [(endo-η⁵-corannulene)Dy(endo-η⁵-corannulene)] (6). The atoms in molecules method predicts that the Dy–C bond is strong and ionic in nature offering strong axiality. The energy decomposition analysis reveals the strength of Dy–C bonding in the following order 1 ≈ 3 > 5 ≈ 6 > 4 ≈ 2. Complexes 1 and 3 have favourable sterics as well as orbital interaction energies, while 5 and 6 have favourable orbital interaction energy but not the sterics, and for 2 and 4, both are unfavourable, placing them at the bottom of the list in terms of overall stabilisation energy.

(ii) Very large U_eff SIMs unveiled: ab initio computed U_cal values are in the following order 1 (U_cal = 919 cm⁻¹) ≈ 3 (913 cm⁻¹) > 2 (847 cm⁻¹) > 4 (608 cm⁻¹) ≈ 5 (603 cm⁻¹) ≈ 6 (599 cm⁻¹). Attachment of the Dy–cyclopentadienyl moieties to corannulene, irrespective of having a five or six-membered ring, yields a much larger barrier height compared to the rest. The Dy–C₆H₆ moiety, on the other hand, shows two different U_cal values depending on their position of binding to corannulene. This is due to the difference in the C–Dy–C angles observed (175° vs. 156°). If corannulene is solely used as a ligand, this combination yields moderate U_cal values due to the diminished axiality from weaker crystal fields than other systems.

(iii) Structural dynamics and its relationship to blocking temperatures: molecular dynamics based on the DFT method reveals fewer thermally accessible structures for 3 and 5 as Dy(III) ion movement is restricted. For complex 6, on the other hand, many thermally accessible structures with the Dy(III) moving across the C₅/C₆ rings of corannulene are detected. This resulted in U_cal values in the range of 69–751 cm⁻¹, and such a large variation suggests that the large U_cal is unlikely to translate into a higher blocking temperature in this example. For complexes 3 and 5, the computed U_cal lies in the range of 784–936 cm⁻¹ and 503–641 cm⁻¹, respectively. Here the gaps are smaller and suggest that the larger U_cal estimated is likely to translate into attractive blocking temperatures. Further vibrational analysis performed on 3 suggests that the corannulene ring could block the C–H vibrations and the associated ring bendings. Moreover, here, the C–H bonds are strong, and these C–H vibrations of the five-membered ring have been found not to influence the blocking temperature. This offers a higher prospect for this molecule to exhibit stability under ambient conditions, a very large U_eff value and a large blocking temperature – a dream achievement in the area of SMMs.

Computational details

All geometry optimisations are carried out using the Gaussian 09 suite of programs⁴⁴ at the UB3LYP functional^45,46 with a 6-31G* basis set⁴⁷ for H and C atoms and Stuttgart–Dresden ECPs (SDDs)⁴⁸ for the Y atom. The ab initio calculations were performed using the MOLCAS 8.0 code. Here, we have used the Dy: ANO⋯RCC VTZP⁴⁹ basis set for all elements for calculating the magnetic properties of all six molecules. For the vibrational conformers coming from MD, there was a slight difference in the basis set, i.e. Dy: ANO⋯RCC VTZP for Dy and X: ANO⋯RCC VDZP for remaining elements. This is adapted after benchmarking the basis set on three structures that were found only marginally to alter the properties computed. The ground state f-electron configuration for Dy(III) is 4f⁹ with ⁶H_15/2 multiplet as a ground state. Generation of guess orbitals is followed by the CASSCF calculations,⁵⁰ where guess orbitals served as starting orbitals. The CASSCF calculations have been performed with nine electrons in the seven active orbitals with an active space of CAS(9,7). In this active space, full configuration interaction (CI) calculations were performed to achieve 21 sextet states. These 21 sextet states being spin free states, the RASSI module was performed to compute spin–orbit (SO) states from these states. Furthermore, SINGLE_ANISO⁵¹ was carried out to calculate the values of g-tensors of the low-lying eight Kramer's Doublets (KDs). Also, the anisotropy in g-factors, U_cal values, crystal field parameters, and direction of g_zz of ground KD were extracted from this set of calculations.

Atoms in molecules (AIM) calculations were performed for investigation of the nature of bonding in the molecules between the Dy(III) ion and the carbons of the ligand system. According to the AIM theory, the sign of H gives the nature of interactions, either electrostatic or ionic such that H > 0 indicates electrostatic interactions and the dominant H < 0 indicates covalent interactions. Multiwfn suite, a multiconfigurational wavefunction analyser, was used to carry out EDA analysis. For AIM and EDA analysis, DFT computed wave functions are employed. A triple zeta basis set employing the Cundari–Stevens (CS) relativistic effective core potential⁵² for Gd atoms has been used along with the TZV basis set for rest of the atoms.

Born Oppenheimer molecular dynamics (BOMD) simulation was performed at the PBE⁵³/DZVP level for Y and PBE/TZVP level for C and H in CP2K code^54,55 and the velocity Verlet algorithm with a time step of 1 fs and a Nosé–Hoover thermostat set at 300 K were employed. Molecular structures and BOMD trajectories were visualised using the Visual Molecular Dynamics (VMD) package.⁵⁶ DFT-based Born–Oppenheimer molecular dynamics (BOMDs) simulations of optimised systems were performed to analyse their dynamics. For 5 and 6, the BOMD trajectory propagated for 2000 femtoseconds at 300 K. For complex 3, MD simulations were restricted to 300 femtoseconds to reduce the computational cost. Interactions between valence electrons and atomic cores are described using Goedecker–Teter–Hutter (GTH) pseudopotentials.⁵⁷ The time constant for the thermostat is taken to be 50 fs. A small-time constant will result in strong thermosetting, which is useful for initial equilibrations. This is an NVT simulation where the number of particles in the system N, the volume of the system V and temperature T remain constant. The thermostat is used to maintain a constant temperature of 300 K.

Data availability

The xyz coordinates as well as the input files of the calculations are given in the ESI.†

Author contributions

GR designed the project and supervised the investigations; TS, MKS and RG performed DFT, AIM, EDA and ab initio calculations. TS and MK performed BOMD calculations. All authors contributed to the writing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the DST/SERB (CRG/2018/00430, DST/CSA-03/2018-19, SB/SJF/2019-20/12, SPR/2019/001145) and IIT-Bombay. MKS thanks UGC-INDIA for a research fellowship. TS is thankful to the Council of Scientific and Industrial Research (CSIR) India for a fellowship.

References

1. G. Aromí, E. J. McInnes and R. E. Winpenny, Molecular Cluster Magnets, ed. R. E. P. Winpenny, World Scientific, 2012, vol. 3, p. 59.
2. S. J. Bartolome, F. Luis and J. F. Fernández, Molecular magnets, Springer, 2016.
3. A. Caneschi, D. Gatteschi, R. Sessoli, A. L. Barra, L. C. Brunel and M. Guillot, J. Am. Chem. Soc., 1991, 113, 5873–5874.
4. G. Christou, D. Gatteschi, D. N. Hendrickson and R. Sessoli, MRS Bull., 2000, 25, 66–71.
5. E. Coronado, P. Delhaès, D. Gatteschi and J. S. Miller, Molecular magnetism: from molecular assemblies to the devices, Springer Science & Business Media, 2013.
6. G. Karotsis, S. Kennedy, S. J. Teat, C. M. Beavers, D. A. Fowler, J. J. Morales, M. Evangelisti, S. J. Dalgarno and E. K. Brechin, J. Am. Chem. Soc., 2010, 132, 12983–12990.
7. C. Marrows, L. Chapon and S. Langridge, Mater. Today, 2009, 12, 70–77.
8. R. Sessoli, D. Gatteschi, A. Caneschi and M. Novak, Nature, 1993, 365, 141–143.
9. N. A. Spaldin, Magnetic materials: fundamentals and applications, Cambridge university press, 2010.
10. A. K. Bar, P. Kalita, M. K. Singh, G. Rajaraman and V. Chandrasekhar, Coord. Chem. Rev., 2018, 367, 163–216.
11. A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380.
12. M. Feng and M. L. Tong, Chem.–Eur. J., 2018, 24, 7574–7594.
13. C. A. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
14. F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., 2017, 129, 11603–11607.
15. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403.
16. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
17. A. Zabala-Lekuona, J. M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984.
18. L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090.
19. M. K. Singh, N. Yadav and G. Rajaraman, Chem. Commun., 2015, 51, 17732–17735.
20. M. K. Singh and G. Rajaraman, Chem. Commun., 2016, 52, 14047–14050.
21. C.-H. Chen, D. S. Krylov, S. M. Avdoshenko, F. Liu, L. Spree, R. Yadav, A. Alvertis, L. Hozoi, K. Nenkov and A. Kostanyan, Chem. Sci., 2017, 8, 6451–6465.
22. F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. Wolter and B. Büchner, Nat. Commun., 2017, 8, 1–9.
23. G. Velkos, D. Krylov, K. Kirkpatrick, X. Liu, L. Spree, A. Wolter, B. Büchner, H. Dorn and A. Popov, Chem. Commun., 2018, 54, 2902–2905.
24. G. Velkos, W. Yang, Y.-R. Yao, S. M. Sudarkova, X. Liu, B. Büchner, S. M. Avdoshenko, N. Chen and A. A. Popov, Chem. Sci., 2020, 11, 4766–4772.
25. Z. Hu, B.-W. Dong, Z. Liu, J.-J. Liu, J. Su, C. Yu, J. Xiong, D.-E. Shi, Y. Wang and B.-W. Wang, J. Am. Chem. Soc., 2018, 140, 1123–1130.
26. C. H. Chen, L. Spree, E. Koutsouflakis, D. S. Krylov, F. Liu, A. Brandenburg, G. Velkos, S. Schimmel, S. M. Avdoshenko and A. Fedorov, Adv. Sci., 2021, 8, 2000777.
27. A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113.
28. E. Nestoros and M. C. Stuparu, Chem. Commun., 2018, 54, 6503–6519.
29. P. A. Vecchi, C. M. Alvarez, A. Ellern, R. J. Angelici, A. Sygula, R. Sygula and P. W. Rabideau, Organometallics, 2005, 24, 4543–4552.
30. J. S. Siegel, K. K. Baldridge, A. Linden and R. Dorta, J. Am. Chem. Soc., 2006, 128, 10644–10645.
31. B. Zhu, A. Ellern, A. Sygula, R. Sygula and R. J. Angelici, Organometallics, 2007, 26, 1721–1728.
32. A. S. Filatov, N. J. Sumner, S. N. Spisak, A. V. Zabula, A. Y. Rogachev and M. A. Petrukhina, Chem.–Eur. J., 2012, 18, 15753–15760.
33. Y. Peng, M. K. Singh, V. Mereacre, C. E. Anson, G. Rajaraman and A. K. Powell, Chem. Sci., 2019, 10, 5528–5538.
34. A. B. Canaj, M. K. Singh, E. R. Marti, M. Damjanović, C. Wilson, O. Céspedes, W. Wernsdorfer, G. Rajaraman and M. Murrie, Chem. Commun., 2019, 55, 5950–5953.
35. S. Ghosh, S. Mandal, M. K. Singh, C.-M. Liu, G. Rajaraman and S. Mohanta, Dalton Trans., 2018, 47, 11455–11469.
36. A. B. Canaj, M. K. Singh, C. Wilson, G. Rajaraman and M. Murrie, Chem. Commun., 2018, 54, 8273–8276.
37. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer and S. Gao, J. Am. Chem. Soc., 2016, 138, 5441–5450.
38. Y. S. Ding, N. F. Chilton, R. E. Winpenny and Y. Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074.
39. S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Chem. Commun., 2014, 50, 15513–15516.
40. J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310–3316.
41. T. Sato, A. Yamamoto and T. Yamabe, J. Phys. Chem. A, 2000, 104, 130–137.
42. Atoms in Molecules: A Quantum Theory, ed. R. F. W. Bader, Clarendon Press, Oxford, 1990, vol. 95, pp. 1–2.
43. I. S. Bushmarinov, K. A. Lyssenko and M. Y. e. Antipin, Russ. Chem. Rev., 2009, 78, 283–302.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2016.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
46. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
47. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
48. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
49. B. r. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431–11435.
50. P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
51. L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112.
52. T. R. Cundari and W. J. Stevens, J. Chem. Phys., 1993, 98, 5555–5565.
53. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891.
54. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
55. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
56. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
57. C. Hartwigsen, S. Gœdecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641.

---

Footnotes

† Electronic supplementary information (ESI) available: Optimised structures, CASSCF + RASSI-SO energies, energy decomposition analysis, AIM analysis, frequency calcualtions, input files of optimisation, molcas calculations and BOMD calculations. See DOI: 10.1039/d1sc03160k

‡ Both authors contributed equally.

---