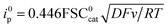Open Access Article
Open Access ArticleHomogeneous molecular catalysis of the electrochemical reduction of N2O to N2: redox vs. chemical catalysis†
Rana
Deeba
a,
Sylvie
Chardon-Noblat
 *a and
Cyrille
Costentin
*a and
Cyrille
Costentin
 *ab
*ab
aUniv Grenoble Alpes, DCM, CNRS, 38000 Grenoble, France. E-mail: cyrille.costentin@univ-grenoble-alpes.fr
bUniversité de Paris, 75013 Paris, France
First published on 24th August 2021
Abstract
Homogeneous electrochemical catalysis of N2O reduction to N2 is investigated with a series of organic catalysts and rhenium and manganese bipyridyl carbonyl complexes. An activation-driving force correlation is revealed with the organic species characteristic of a redox catalysis involving an outer-sphere electron transfer from the radical anions or dianions of the reduced catalyst to N2O. Taking into account the previously estimated reorganization energy required to form the N2O radical anions leads to an estimation of the N2O/N2O˙− standard potential in acetonitrile electrolyte. The direct reduction of N2O at a glassy carbon electrode follows the same quadratic activation driving force relationship. Our analysis reveals that the catalytic effect of the mediators is due to a smaller reorganization energy of the homogeneous electron transfer than that of the heterogeneous one. The physical effect of “spreading” electrons in the electrolyte is shown to be unfavorable for the homogeneous reduction. Importantly, we show that the reduction of N2O by low valent rhenium and manganese bipyridyl carbonyl complexes is of a chemical nature, with an initial one-electron reduction process associated with a chemical reaction more efficient than the simple outer-sphere electron transfer process. This points to an inner-sphere mechanism possibly involving partial charge transfer from the low valent metal to the binding N2O and emphasizes the differences between chemical and redox catalytic processes.
Introduction
Direct electrochemical activation of small molecules, without a catalyst, operates at large overpotential owing to the thermodynamic penalty resulting from the necessity to reach highly energetic intermediates and from the kinetic penalty associated with the large reorganization energy required to form these intermediates. One emblematic case is CO2 for which direct reduction in aprotic solvents at inert electrodes requires the formation of the bent radical anion whose standard potential is −2.21 V vs. SCE in dimethylformamide (DMF) associated with a small standard rate constant (6 × 10−3 cm s−1) of electron transfer (ET).1 Ways to circumvent this general problem are developed via the use of electrocatalytic electrode materials or molecular catalysts.2 In the latter case, the problem can be circumvented only if the active form of the catalyst (reduced or oxidized), generated at the electrode, leads to the transient formation of an adduct with the substrate, i.e. “chemical catalysis” or inner-sphere electron transfer. Indeed, if the active form of the catalyst only transfers electrons to the substrate through the outer sphere, formation of a highly energetic intermediate is not skipped, thus leading to “redox catalysis”.3 Being able to distinguish if a given catalyst is acting as a redox mediator or a chemical catalyst is therefore of prime importance in the endeavour to design efficient molecular catalysts for given small molecule activation.4 It is in particular crucial to understand how the catalytic effect is related to the nature of the catalyst, a subject of debate in O2 or CO2 reduction for example.5–8 We have recently emphasized the potential of the nitrous oxide (N2O) electrochemical reduction reaction leading to inert dinitrogen (N2)9 since N2O is a greenhouse gas presenting a long lifetime, a higher global warming potential than CO2 and CH4 and playing a major role in the cycles of ozone destruction.10 It should be underlined that N2O is a potentially good oxidant but its reductive deoxygenation leading to N2 is kinetically slow,11 unless using very strong reductive conditions as in pulse radiolysis where hydrated electrons generate N2O radical anions that rapidly evolve via reaction in water to produce N2 and hydroxyl radicals.12 Therefore finding efficient molecular catalysts to reduce N2O and deciphering the mechanisms are important tasks. We have already discovered that low valent rhenium bipyridyl carbonyl complexes catalyse the N2O reductive deoxygenation reaction.9 Here we investigate the electrochemical reduction of N2O in acetonitrile (CH3CN) electrolyte using a series of organic aromatic catalysts and we compare their activity with low valent rhenium (Re) and manganese (Mn) bipyridyl carbonyl complexes.Results
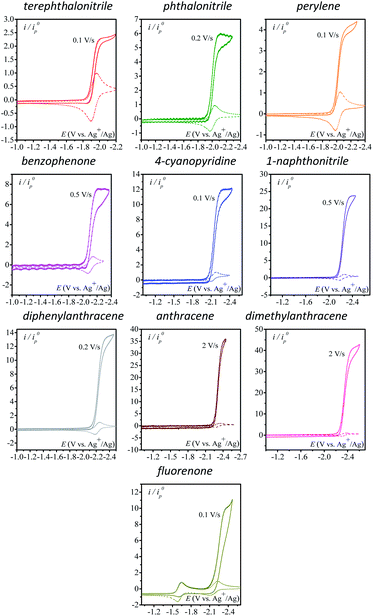
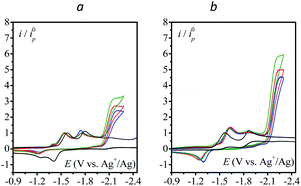
We first use as catalysts organic molecules (structures are shown in Table S1 in the ESI†) leading to either radical anion or dianion reduced species upon one or two successive one-electron reductions. The corresponding standard potentials are obtained from the midpoint of the cathodic and anodic peak potentials recorded from cyclic voltammograms (CVs) at 0.1 V s−1 at a 3 mm diameter glassy carbon (GC) electrode in CH3CN + 0.1 M n-NBu4PF6 (Table 1). We reasoned that the electrogenerated radical anion or dianion reduced species with negative enough standard potentials should be able to reduce N2O. Indeed, in the presence of N2O (saturated solution 1 atm), a catalytic current is observed with catalysts whose standard potentials (1st or 2nd one-electron reduction) are negative to ca. −1.90 V vs. Ag+/Ag. No catalytic current is observed with dicyanoanthracene or phenazine (Fig. S2†). In all cases where a catalytic current is observed, raising the scan rate allows reaching a plateau independent of scan rate, indicating pure kinetics conditions with negligible substrate consumption (Fig. 1). The CVs at different scan rates are shown in Fig. S3.† The catalytic CVs have been corrected for ohmic drop considering a resistance of 120 ohms (Fig. S4†).| Catalyst | E 0 (V vs. Ag+/Ag) |
|---|---|
| Terephthalonitrile | −1.93 |
| Phthalonitrile | −2.01 |
| Perylene | −2.01 (5) |
| Benzophenone | −2.10 |
| 4-Cyanopyridine | −2.13 (5) |
| 1-Naphthonitrile | −2.22 |
| 9,10-Diphenylanthracene | −2.21 (5) |
| Anthracene | −2.31 |
| 9,10-Dimethylanthracene | −2.33 |
| 9,10-Dicyanoanthracene | −1.23/−1.84 |
| Phenazine | −1.49/−1.83 |
| Fluorenone | −1.61/−2.16 |
The effect of addition of water as a proton source was then investigated. Addition of water has no to very little effect on the catalytic current (Fig. 2) except for 4-cyanopyridine and fluorenone, for which a deleterious effect on catalysis is observed. In each case, the scan rate is adjusted so as to reach the steady-state plateau current.
The case of fluorenone (Fig. 2) is more striking and different than the others in several ways: the catalytic activity is observed on the second reduction wave (Fig. 2, red CV) and addition of 100 mM water suppresses the catalytic current and its potential peak becomes less negative by ca. 100 mV (Fig. 2, blue CV). This latter observation can be rationalized assuming a reaction of the intermediate radical anions, probably with water, or a fast reaction of the dianions, also with water, preventing its ability to reduce N2O. The effect is less drastic with 4-cyanopyridine for which a substantial decrease of the catalytic current, ca. 50%, is observed upon addition of 200 mM water. Reaction of the radical anions with water might be in competition with the reaction with N2O. This reaction might lead to a neutral radical that is immediately reduced (ECE or DISP process13) corresponding to the deactivation of the catalyst.
The stoichiometry and selectivity of the reaction were checked by running short-time controlled potential electrolysis in the presence of 100 mM H2O (see the ESI† for details and results) for the reduction catalysed by representative catalysts, namely phthalonitrile, 4-cyanopyridine, benzophenone, and perylene, as well as for the direct electrochemical reduction on a GC electrode and with [Re(bpy)(CO)3Cl] as a catalyst for comparison. In all cases, N2 is the only product formed in a quantitative faradaic yield (FY) corresponding to the consumption of two electrons per molecule of N2 formed, thus leading to the overall reaction:
| N2O + 2e− + H2O → N2 + 2OH− |
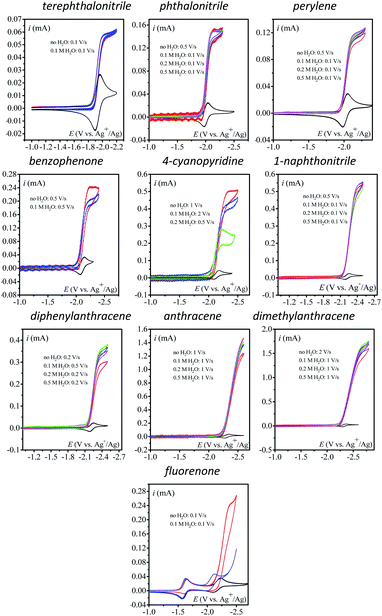
The initial chemical step rate constant k for the reduction of N2O by electrogenerated radical anions or dianions is obtained from the plateau current measured in cyclic voltammetry:
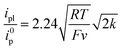 | (1) |
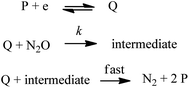
Here a two-electron process is considered with the second electron reduction taking place in solution rather than at the electrode surface (Scheme 1). This assumption is justified a posteriori: given the slowness of the overall process, the one-electron reduced N2O intermediate is produced far away from the electrode so that it is further reduced in solution and not at the electrode surface (see the ESI for details†). Fig. S5† shows a good agreement of the fit of the forward catalytic response with eqn (2):
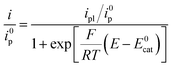 | (2) |
This indicates that the half-wave potential is equal to the standard potential of the catalyst, an established criterion for two-electron processes where the initial chemical step of the catalysis is actually the rate-determining step.3 Therefore the mechanism that we are investigating is depicted in Scheme 1. We note that a deviation of the fit with eqn (2) is observed with the fluorenone dianion used as a reductant. It is presumably because the corresponding redox couple (radical anion/dianion) is not Nernstian.
The variation of the rate constant with the standard potential of the catalyst couple is shown in Fig. 3. It appears that there is a correlation between the standard potential of the catalyst and the rate constant: the more negative the standard potential, the larger the rate constant.
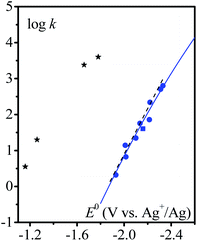 | ||
Fig. 3 Homogeneous catalysis of the electrochemical reduction of N2O by radical anions ( ) or dianions ( ) or dianions ( ) and by [M(L)(CO)3X] (black stars) complexes (M = Mn or Re, L = bpy or dmbpy, X = Cl or Br). Variation of the rate constant of the rate-determining step with the standard potential of the outer (blue) or inner (black) sphere electron donor. Dashed line: fitting with eqn (3), see the text. Full line: fitting with eqn (4) and (5), see the text. ) and by [M(L)(CO)3X] (black stars) complexes (M = Mn or Re, L = bpy or dmbpy, X = Cl or Br). Variation of the rate constant of the rate-determining step with the standard potential of the outer (blue) or inner (black) sphere electron donor. Dashed line: fitting with eqn (3), see the text. Full line: fitting with eqn (4) and (5), see the text. | ||
Rate constants obtained with transition metal complex catalysts [MI(L)(CO)3X] (M = Re and X = Cl or Mn and X = Br, L = 2,2′-bipyridine (bpy) or 4,4′-dimethyl-2,2′-bipyridine (dmbpy)) are also reported in Fig. 3. The rate constants for these metallic based catalysts are obtained considering the mechanism recently reported and depicted in Scheme 2 for the Re complexes.9 The two-step process is triggered by the formation of [Re0(L˙−)(CO)3]− upon one electron reductive dehalogenation of mono reduced [ReI(L˙−)(CO)3Cl]−. Addition of N2O is characterized by a rate constant (k2) determined from the effect of added water and corresponds to the addition of N2O on a reduced form of the catalyst [Re0(L˙−)(CO)3]−. It is the maximal apparent rate constant for catalysis. We note that the addition of N2O can be a ligand substitution as the vacant site on Re0 could be occupied by a solvent molecule. It is important to note that the standard potential of the catalysts to be considered in such a case corresponds to [ReI(L˙−) (CO)3]/[Re0(L˙−)(CO)3]− couples.9 These standard potentials have been estimated as −1.66 and −1.78 V vs. Ag+/Ag for L = bpy and dmbpy, respectively, by running CV measurements on solution of [Re0(L˙−)(CO)3]− obtained from two-electron bulk electrolysis of [ReI(L)(CO)3Cl] initial compounds (see the ESI for details†).
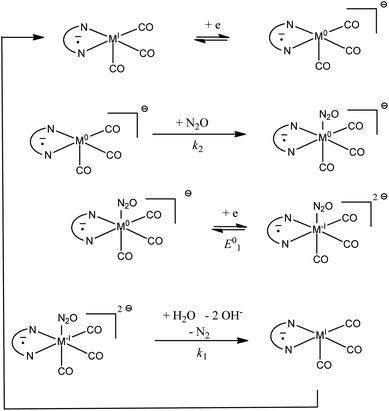 | ||
| Scheme 2 Proposed mechanism for the catalytic reduction of N2O with [ReI(L˙−)(CO)3] and [MnI(L˙−)(CO)3]. | ||
In the case of [Mn(L)(CO)3Br] complexes, the catalytic wave is observed at potentials more negative than that for the formation of [Mn−I(L)(CO)3]−. Mn−I(L)(CO)3]− is obtained after reductive cleavage of the [Mn0(L)(CO)3]2 dimer formed via a parent–child reaction on the first reduction wave.14 The catalytic wave is only slightly sensitive to the addition of water (Fig. 4). The apparent catalytic rate constant evaluated from the plateau current viaeqn (1) can thus be assumed to be the rate constant for the reaction of N2O with the Mn complex. The value is reported in Fig. 3. The proposed mechanism (Scheme 2) is thus akin to the mechanism at play with a bulky manganese carbonyl complex for CO2 reduction in the presence of weak acids.15 The standard potential of [Mn0(L)(CO)3]/[Mn−I(L)(CO)3]− is estimated to be more positive than the peak potentials corresponding to reductive debromination, i.e. −1.16 and −1.26 V vs. Ag+/Ag for L = bpy and dmbpy, respectively.14
Finally, the direct reduction of N2O on a glassy carbon electrode is reported in Fig. 5 (see Table S2† for bulk electrolysis results). Due to the slow reduction rate, the current is purely kinetic, i.e. not perturbed by mass transport and thus independent of scan rate (Fig. S6†). Once corrected for ohmic drop, the kinetics can be represented in the form of a Tafel plot, i.e. log(i) vs. E. The plot is restricted to potentials negative to −2.2 V vs. Ag+/Ag for the current to be significantly above the background current, i.e. larger than 1 μA.
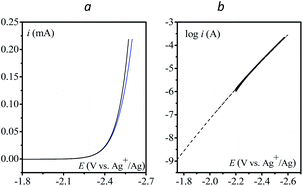 | ||
| Fig. 5 (a) Direct reduction of N2O in acetonitrile with n-Bu4NPF6 (0.1 M) on a 3 mm diameter GC electrode; v = 0.1 V s−1, blue: no ohmic drop correction; black: with ohmic drop correction. (b) Tafel plot obtained from (a). Dashed line: fitting with eqn (6), see the text. | ||
Discussion
It clearly appears that organic radical anionic and dianionic species can be considered as a different category of molecular catalysts than Re and Mn bipyridyl carbonyl complexes vis-à-vis their reactivity with N2O. In the organic catalyst series, the rate constant decreases when going to less negative potential following an activation-driving force correlation (dashed line in Fig. 3). The average slope: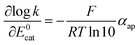 | (3) |
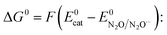
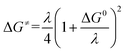 | (4) |
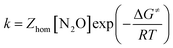 | (5) |
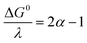 and taking the averaged value αap ≈ 0.35, we obtain that
and taking the averaged value αap ≈ 0.35, we obtain that 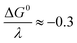 in the range of the driving force investigated with the considered series of electron donors (reduced organic species). The reorganization energy is the sum of the contribution of the internal reorganization energy λi and the solvent contribution λ0. The internal reorganization energy required for the reduction of N2O to N2O˙− has been evaluated from theoretical calculations18 as λi ≈ 1.8 eV due to the bending of the N–N–O angle from 180° to 133° and due to the stretching of both N–N and N–O bonds. The solvent reorganization energy is also expected to be quite large due to the small radius of the molecule. Taking, λ0 (eV) ≈ 3/a (Å)16 and a ≈ 2 Å, we obtain λ ≈ 3.3 eV and therefore ΔG0 is in the range of −1 eV. Such a large driving force is required to overcome the intrinsic activation energy ΔG≠0 = λ/4. As the standard potentials of the electron donors are around −2.1 V vs. Ag+/Ag, a rough estimation of the standard potential of the N2O/N2O˙− redox couple is
in the range of the driving force investigated with the considered series of electron donors (reduced organic species). The reorganization energy is the sum of the contribution of the internal reorganization energy λi and the solvent contribution λ0. The internal reorganization energy required for the reduction of N2O to N2O˙− has been evaluated from theoretical calculations18 as λi ≈ 1.8 eV due to the bending of the N–N–O angle from 180° to 133° and due to the stretching of both N–N and N–O bonds. The solvent reorganization energy is also expected to be quite large due to the small radius of the molecule. Taking, λ0 (eV) ≈ 3/a (Å)16 and a ≈ 2 Å, we obtain λ ≈ 3.3 eV and therefore ΔG0 is in the range of −1 eV. Such a large driving force is required to overcome the intrinsic activation energy ΔG≠0 = λ/4. As the standard potentials of the electron donors are around −2.1 V vs. Ag+/Ag, a rough estimation of the standard potential of the N2O/N2O˙− redox couple is 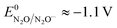 vs. Ag+/Ag. Taking this value and λ ≈ 3.3 eV, the experimental data are fitted with eqn (4) and (5) leading to Zhom[N2O] ≈ 3 × 108 s−1 (Fig. 3).
vs. Ag+/Ag. Taking this value and λ ≈ 3.3 eV, the experimental data are fitted with eqn (4) and (5) leading to Zhom[N2O] ≈ 3 × 108 s−1 (Fig. 3).
Given the large reorganization energy, it is not surprising that the direct electroreduction of N2O proceeds with a considerable overpotential at the non-electrocatalytic GC electrode (Fig. 4).19 It is in line with the observation that the electrochemical transfer coefficient αelec, obtained from the averaged slope of the Tafel plot, is much below 0.5, i.e.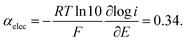 Therefore, in the context of electrochemical electron transfer theory,20 the direct electroreduction of N2O can be expressed as:
Therefore, in the context of electrochemical electron transfer theory,20 the direct electroreduction of N2O can be expressed as:
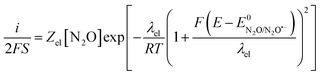 | (6) |
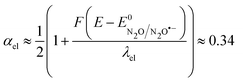 at potentials around −2.4 V vs. Ag+/Ag and taking the standard potential evaluated above, we obtain λel ≈ 4 eV and the fitting of the Tafel plot with eqn (6) leads to Zel[N2O] = 0.16 mol cm−2 s−1 (Fig. 4).
at potentials around −2.4 V vs. Ag+/Ag and taking the standard potential evaluated above, we obtain λel ≈ 4 eV and the fitting of the Tafel plot with eqn (6) leads to Zel[N2O] = 0.16 mol cm−2 s−1 (Fig. 4).
One may wonder why the current resulting from the reduction of N2O by the electrogenerated homogeneous outer-sphere electron donor characterized by a given standard potential is larger than the current resulting from the reduction of N2O by an outer-sphere electron transfer from the electrode polarized at a potential equal to this standard potential. This amounts to comparing the catalytic current at E = E0cat for a given catalyst, i.e. when half of the catalyst has been transformed to its reduced form at the electrode surface, i.e.
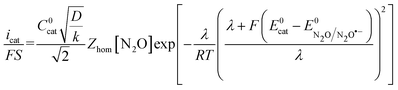 | (7) |
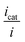 is thus the product of two terms. The first term is
is thus the product of two terms. The first term is 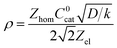 and takes into account the number of active catalysts, i.e. outer-sphere molecular reductants, in the diffusion reaction layer whose size is
and takes into account the number of active catalysts, i.e. outer-sphere molecular reductants, in the diffusion reaction layer whose size is 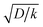 . It thus compares the effect of spreading out electrons in the diffusion-reaction layer with the necessity for the substrate N2O to pick up electrons from the electrode at the Helmholtz outer plane for the direct reduction. Taking C0cat = 1 mM, D = 10−5 cm2 s−1, the ratio ρ is plotted as a function of the catalyst standard potential (Fig. 6b). This reveals that spreading electrons in a diffusion-reaction layer is only beneficial in terms of collision efficiency between the substrate and the electron donor at potentials positive to −2 V vs. Ag+/Ag. The decrease of this physical catalytic effect as the standard potential of the catalyst becomes more negative is due to the increase of the homogeneous rate constant and the corresponding decrease of the diffusion-reaction layer size and hence of the number of electrons spread out in the solution. In other words, there is a self-limitation of the physical catalytic effect. As a consequence, comparison of Fig. 6a (which shows that redox catalysis is more efficient than direct reduction at potentials negative to −2 V vs. Ag+/Ag) and Fig. 6b (which shows that the term ρ is unfavourable for redox catalysis vs. direct reduction at potentials negative to −2 V vs. Ag+/Ag) reveals that the second term of the ratio icat/i is responsible for icat/i being larger than 1 at potentials negative to −2 V vs. Ag+/Ag. In other words, the main catalytic effect of the homogeneous donors resides in the fact that λ < λel, making the exponential term of the icat/i ratio much larger than 1.
. It thus compares the effect of spreading out electrons in the diffusion-reaction layer with the necessity for the substrate N2O to pick up electrons from the electrode at the Helmholtz outer plane for the direct reduction. Taking C0cat = 1 mM, D = 10−5 cm2 s−1, the ratio ρ is plotted as a function of the catalyst standard potential (Fig. 6b). This reveals that spreading electrons in a diffusion-reaction layer is only beneficial in terms of collision efficiency between the substrate and the electron donor at potentials positive to −2 V vs. Ag+/Ag. The decrease of this physical catalytic effect as the standard potential of the catalyst becomes more negative is due to the increase of the homogeneous rate constant and the corresponding decrease of the diffusion-reaction layer size and hence of the number of electrons spread out in the solution. In other words, there is a self-limitation of the physical catalytic effect. As a consequence, comparison of Fig. 6a (which shows that redox catalysis is more efficient than direct reduction at potentials negative to −2 V vs. Ag+/Ag) and Fig. 6b (which shows that the term ρ is unfavourable for redox catalysis vs. direct reduction at potentials negative to −2 V vs. Ag+/Ag) reveals that the second term of the ratio icat/i is responsible for icat/i being larger than 1 at potentials negative to −2 V vs. Ag+/Ag. In other words, the main catalytic effect of the homogeneous donors resides in the fact that λ < λel, making the exponential term of the icat/i ratio much larger than 1.
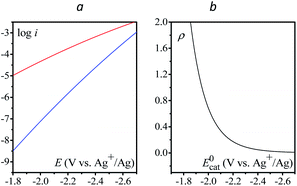 | ||
Fig. 6 (a) Comparison of the calculated direct reduction of N2O (blue) from eqn (6) with S = 0.07 cm2, Zel[N2O] = 0.16 mol cm−2 s−1, λel ≈ 4 eV and EN2O/N2O˙−0 ≈ −1.1 V vs. Ag+/Ag, and of the redox catalytic current (red) from eqn (7) with C0cat = 1 mM, D = 10−5 cm2 s−1, S = 0.07 cm2, Zhom[N2O] = 3 × 108 s−1, λ = 3.3 eV and 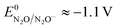 vs. Ag+/Ag considering an infinity of catalysts with E = E0cat. (b) Plot of ρ as a function of E = E0cat, k is obtained from eqn (4) and (5). vs. Ag+/Ag considering an infinity of catalysts with E = E0cat. (b) Plot of ρ as a function of E = E0cat, k is obtained from eqn (4) and (5). | ||
We now consider the comparison of outer-sphere redox catalysts and transition metal complexes [Re(L)(CO)3Cl] and [Mn(L)(CO)3Br]. It appears that the catalytic rate constants are much larger than the outer-sphere rate constants (Fig. 3). As already reported,9 two chemical processes are involved in the catalytic cycle, and at large concentration of water, it is predicted that the overall process is limited by the reaction of N2O with the low valent [M0(L˙−)(CO)3]− species (step k2 in Scheme 2). This binding step is faster than an outer-sphere electron transfer from [M0(L˙−)(CO)3]− to N2O which could be in principle possible because of the charge partially localized on the bipyridine ligand. This observation further emphasizes that understanding the reactivity of transition metal complexes requires to understand the electronic structure in the context of experimental catalytic data.21 Partial electron transfer from the low valent metal to N2O is not unlikely as an activation-driving force trend similar to that of outer-sphere electron transfer is observed. This could make the binding process a formal inner-sphere electron transfer. Interestingly, the species thus formed is stable enough so that no catalytic process is triggered at this stage. A further reduction is required at a more negative potential. As a consequence, the kinetic advantage observed in Fig. 3 for low valent transition metal complexes over aromatic radical anions and dianions does not necessarily definitively lead to an advantage of chemical catalysis over redox catalysis. In the present case, additional driving force is indeed necessary for the intermediate formed via chemical catalysis to evolve into the product. In other words, chemical catalysis is framed by the classical Sabatier principles.22 However, lower potentials may be possible if one finds ways to boost the N–O bond cleavage, as shown in the case of CO2 electroreduction activation by manganese carbonyl complexes.23
Conclusions
Molecular catalysis of nitrous oxide electrochemical reduction to dinitrogen was investigated with both a series of organic catalysts and rhenium and manganese bipyridyl carbonyl complexes. In the first case, the initial formation of N2O radical anions is the rate-determining step thus corresponding to redox catalysis. Due to the large reorganization energy, an important driving force is required to drive the reaction. From the activation-driving force quadratic relationship, the standard potential of N2O/N2O˙− is evaluated in acetonitrile electrolyte. Comparison with direct reduction of N2O at a glassy carbon electrode following the same outer-sphere mechanism reveals that redox catalysis is more efficient mostly because of a smaller reorganization energy. Compared to aromatic radical anions and dianions, low valent rhenium and manganese bipyridyl carbonyl complexes follow a different mechanism: once electrogenerated they react with N2O more rapidly. However, the intermediate thus formed requires additional driving force, here via reduction at a more negative potential, to evolve into the product via an associated decoordination reaction. This emphasizes that the competition between redox and chemical catalysis is a subtle balance between skipping high energy intermediates and over-stabilization of intermediates.Author contributions
R. D. performed the experiments. S. C-N. and C. C. designed the project. R. D., S. C-N. and C. C. analysed the results and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The MITI (Mission pour les Initiatives Transverses et Interdisciplinaires) program of the CNRS is gratefully acknowledged for doctoral financial support for R. D. This work is supported by the French National Research Agency in the framework of the “Investissements d’avenir” program (ANR-15-IDEX-02) and Labex ARCANE, CBH-EUR-GS, ANR-17-EURE-0003. The NanoBio ICMG (UAR 2607) is acknowledged for providing facilities for analyses.Notes and references
- E. Lamy, L. Nadjo and J.-M. Savéant, J. Electroanal. Chem., 1977, 78, 403 CrossRef CAS.
- J.-M. Savéant, Chem. Rev., 2008, 108, 2348 CrossRef PubMed.
- (a) C. Costentin and J.-M. Savéant, Elements of Molecular and Biomolecular Electrochemistry, Wiley, 2nd edn, 2019, ch. 5 Search PubMed; (b) L. Eberson and S. S. Shaik, J. Am. Chem. Soc., 1990, 112, 4484 CrossRef CAS; (c) H. Lund, K. Daasbjerg, T. Lund and S. U. Pedersen, Acc. Chem. Res., 1995, 28, 313 CrossRef CAS; (d) A. Gennaro, A. A. Isse, J.-M. Savéant, M.-G. Severin and E. Vianello, J. Am. Chem. Soc., 1996, 118, 7190 CrossRef CAS.
- T. Tang, C. Sandford, S. D. Minteer and M. S. Sigman, Chem. Sci., 2021, 12, 4771 RSC.
- C. W. Machan, ACS Catal., 2020, 10, 2640 CrossRef CAS.
- D. J. Martin, C. F. Wise, M. L. Pegis and J. M. Mayer, Acc. Chem. Res., 2020, 53, 1056 CrossRef CAS PubMed.
- C. Costentin and J.-M. Savéant, J. Am. Chem. Soc., 2018, 140, 16669 CrossRef CAS PubMed.
- C. Costentin, ACS Catal., 2021, 11, 5678 CrossRef CAS.
- R. Deeba, F. Molton, S. Chardon-Noblat and C. Costentin, ACS Catal., 2021, 11, 6099 CrossRef CAS.
- S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. Averyt, M. M. B. Tignor and H. L. Miller, Climate Change 2007: The Physical Science Basis. Contribution if Working Group I to the Fourth Assessment Report of the Intergouvernemental Panel on Climate Change, Cambridge University Press, Cambridge, UK, 2007 Search PubMed.
- S. R. Pauleta, M. S. P. Carepo and I. Moura, Coord. Chem. Rev., 2019, 387, 436 CrossRef CAS.
- E. J. Hart and M. Anbar, The Hydrated Electron, Wiley, New York, 1970 Search PubMed.
- C. Costentin and J.-M. Savéant, Elements of Molecular and Biomolecular Electrochemistry, Wiley, 2nd edn, 2019, pp. 100–107 Search PubMed.
- M. H. Ronne, M. R. Madsen, T. Skrydstrup, S. U. Pedersen and K. Daasbjerg, ChemElectroChem, 2021, 8, 2108 CrossRef.
- M. D. Sampson, A. D. Nguyen, A. Grice, C. E. Moore, A. L. Rheingold and C. P. Kubiak, J. Am. Chem. Soc., 2014, 136, 5460 CrossRef CAS PubMed.
- (a) H. Kojima and A. J. Bard, J. Am. Chem. Soc., 1975, 97, 6317 CrossRef CAS; (b) D. Lexa, J.-M. Savéant, K. B. Su and D. L. Wang, J. Am. Chem. Soc., 1987, 109, 6464 CrossRef CAS.
- (a) R. A. Marcus, J. Chem. Phys., 1956, 24, 966 CrossRef CAS; (b) N. S. Hush, J. Chem. Phys., 1958, 28, 962 CrossRef CAS.
- K. Takahashi, S. Ohgami, Y. Koyama, S. Sawamura, T. W. Marin, D. M. Bartels and C. D. Jonah, Chem. Phys. Lett., 2004, 383, 445 CrossRef CAS.
- Glassy carbon behaves as a simple outersphere electron donor with reduction of N2O taking place in the Helmholtz outer plan of the double layer. An electrocatalytic electrode would involve a specific interaction between the electrode material and the substrate and/or the product.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679 CrossRef CAS.
- C. Costentin, J.-M. Savéant and C. Tard, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9104 CrossRef CAS PubMed.
- P. Sabatier, La Catalyse en Chimie Organique, Librairie Polytechnique, Paris, 1913 Search PubMed.
- K. T. Ngo, M. McKinnon, B. Mahanti, R. Narayanan, D. C. Grills, M. Z. Ertem and J. Rochford, J. Am. Chem. Soc., 2017, 139, 2604 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, additional CVS, ohmic drop correction, theoretical framework for catalytic CV analysis, and details of electrolysis. See DOI: 10.1039/d1sc03044b |
| This journal is © The Royal Society of Chemistry 2021 |