Open Access Article
Open Access ArticlePlanar tetracoordinate fluorine atoms†
Gabriela
Castillo-Toraya
a,
Mesías
Orozco-Ic
a,
Eugenia
Dzib
a,
Ximena
Zarate
b,
Filiberto
Ortíz-Chi
 c,
Zhong-hua
Cui
c,
Zhong-hua
Cui
 d,
Jorge
Barroso
d,
Jorge
Barroso
 *a and
Gabriel
Merino
*a and
Gabriel
Merino
 *a
*a
aDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados, Unidad Mérida, Mérida, Yucatán, México. E-mail: gmerino@cinvestav.mx; jorge.barroso@cinvestav.mx
bInstituto de Ciencias Químicas Aplicadas, Facultad de Ingeniería, Universidad Autónoma de Chile, Santiago, Chile
cCONACYT-Universidad Juárez Autónoma de Tabasco, Centro de Investigación de Ciencia y Tecnología Aplicada de Tabasco, Cunduacán 86690, Tabasco, México
dInstitute of Atomic and Molecular Physics, Key Laboratory of Physics and Technology for Advanced Batteries (Ministry of Education), Jilin University, Changchun 130012, China
First published on 8th April 2021
Abstract
Among the list of planar tetracoordinate atoms, fluorine is missing. So far, there are no theoretical or experimental reports suggesting their existence. Herein, we introduce the first six combinations (FIn4+, FTl4+, FGaIn3+, FIn2Tl2+, FIn3Tl+, and FInTl3+) whose global minima contain a planar tetracoordinate fluorine. The bonding analyses indicate that the interactions between the fluorine and the peripheral atoms are significantly electrostatic, which is also reflected in the electronic delocalization. As opposed to other planar tetracoordinate systems with carbon, nitrogen, or oxygen atoms, the fluorine in the ptFs does not act as a σ-acceptor, restraining any back-donation. On the other hand, σ-electrons show a diatropic response, which would characterize these clusters as σ-aromatic.
Introduction
Planar tetracoordinate carbon (ptC) atoms are oddities, they embody a conflict with one of the most important paradigms in organic chemistry, yet some exist in bottles. The long-standing tetrahedral model of van't Hoff and Lebel was first challenged in 1968 when Monkhorst1 suggested a transition state (TS) with a ptC in the stereomutation of a tetrahedral carbon. Two years later, Hoffmann, Alder, and Wilcox2 proposed a few rules for stabilizing such TS based on planar methane's molecular orbital analysis. Schleyer and co-workers adopted this idea to introduce the first structure with a ptC that is energetically more favorable than its tetrahedral counterpart.3 In 1991, Boldyrev and Schleyer predicted various planar tetracoordinate atoms with 18 valence electrons (18ve), such as CAl2Si2, OAl4, NAl3Si, BAlSi3, and NAl4−.4 In fact, the last one was thereafter experimentally characterized by Nayak et al.5 Later, Boldyrev and Simons established that 18ve are required to stabilize a planar form, in which three C-ligand σ-bonds, one C-ligand π-bond, and one ligand–ligand bond take place.6 The first neutral pentaatomic ptC molecules with 17 and 18ve experimentally observed in the gas-phase via anion photoelectron spectroscopy and characterized by ab initio computations were CAl4− and CAl42−, respectively.7–9 Although the 18ve valence rule is not universal (a rule is not a law), it proved useful in predicting new planar hypercoordinate atoms.10–19So, the theory has played a fundamental role in predicting and understanding these peculiar species.20–23 Although the list is long, it does not include a theoretically or experimentally reported planar tetracoordinate fluorine (ptF) atom, which does not make sense since the D4h CAl42−, NAl4−, and OAl4 structures are the global minima on their corresponding potential energy surfaces (PESs). Why is the isoelectronic FAl4+ not planar? Is it possible to introduce fluorine into the flat world? Herein, we systematically explored the PESs of all viable pentaatomic clusters containing a fluorine atom combined with main group elements, totaling 18ve and charges from +2 to −2. This amounts to 440 combinations and around 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 optimizations. Gratifyingly, we found that the global minima of FIn4+, FTl4+, FGaIn3+, FIn2Tl2+, FIn3Tl+, and FInTl3+ contain a ptF atom.
000 optimizations. Gratifyingly, we found that the global minima of FIn4+, FTl4+, FGaIn3+, FIn2Tl2+, FIn3Tl+, and FInTl3+ contain a ptF atom.
Computational details
The systematic exploration of the corresponding PESs was carried out through a modified genetic algorithm, as implemented in the GLobal Optimization of MOlecular Systems (GLOMOS).24–26 GLOMOS is written in Python and includes stochastic and evolutive methodologies to carry out the global optimization of atomic and molecular clusters, where the local optimizations are solved through an electronic structure code. The initial screening was done at the TPSS27/def2-SVP28 level. All the stationary points were re-minimized and characterized at the TPSS/def2-TZVP level, including Grimme's D3 dispersion29 scheme with Becke-Johnson damping. The final energies were refined at the CCSD(T)30/def2-TZVP level, including the zero-point energy correction at the TPSS-D3(BJ)/def2-TZVP. Thus, the energetic discussion is based on the CCSD(T)/def2-TZVP//TPSS-D3(BJ)/def2-TZVP results. All of these computations were performed with Gaussian 16.31The Wiberg Bond Index (WBI)32 and Natural Population Analysis (NPA)33 were estimated following the NBO scheme.34 The AdNDP method, developed by Zubarev and Boldyrev,35 was employed for better insight into the bonding of these systems. The AdNDP leads to a partitioning of the charge density into elements with the lowest possible number of atomic centers per electron pair: n-center-two-electron (nc-2e) bonds, including the Lewis bonding elements as core electrons, lone pairs, and 2c–2e bonds.
Also, the analysis of the induced magnetic field36–38 (Bind) and induced current density (Jind)39–41 was analyzed using the programs Aromagnetic42 and GIMIC,39–41 respectively. The molecular magnetic response to a homogeneous external magnetic field is computed on a rectangular grid with the molecule in its center. These calculations were performed at the TPSS/TZP-DKH43 level.
Bonding and structure
Interestingly, structures with a ptF only arise in clusters formed by substituents exclusively of group 13 (Fig. 1). Let us start with those systems with a single element as ligands, i.e., FX4+ (X = Al, Ga, In, Tl). The planar D4h form of FAl4+, with F–Al bond lengths (rF-Al) of 2.214 Å, has two imaginary frequencies. Apparently, the cavity formed by four aluminum atoms is not large enough to accommodate a fluorine atom. The putative global minimum, 18.7 kcal mol−1 lower in energy, is a C2v aluminum tetrahedron with fluorine at the edge (see Fig. S1†). For the FGa4+ case, the D4h arrangement (rF–Ga = 2.238 Å) is a transition state (νmin = −70 cm−1), 4.5 kcal mol−1 higher in energy than the most stable structure formed by a gallium triangle and a F–Ga fragment. Gratifyingly, the global minimum structures for FIn4+ (rF–In = 2.415 Å) and FTl4+ (rF–Tl = 2.533 Å) have the perfect cavity to stabilize a ptF. In other words, the cavity size is critical.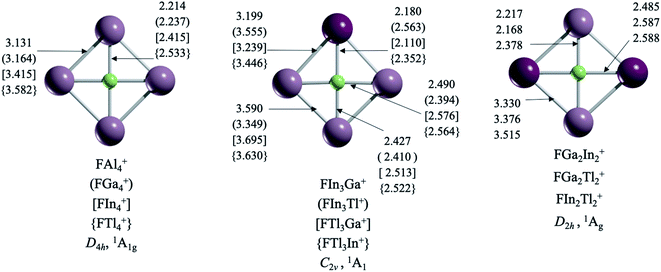 | ||
| Fig. 1 TPSS-D3(BJ)/def2-TZVP structures of the FX4+ (X = Al, Ga, In, Tl) series. Bond lengths are in Å. | ||
With this in mind, we explored the possibility of combining two elements of group 13 (except boron because it creates a small cavity) to produce more clusters with a ptF. Notably, there is no ptF as the global minimum if the structure contains aluminum. The only ptFs, but as local minima, are FIn3Al+ and FTl3Al+. It might be assumed that replacing a Ga atom in FGa4+ with a heavier element should create a cavity large enough to stabilize a ptF, but it is not so obvious (this only occurs for FGaIn3+). Interestingly, while the putative global minimum of FGaIn3+ (rF–Ga = 2.180 Å) is a ptF, the ptF isomer for FGaTl3+ (rF–Ga = 2.110 Å) is 0.6 kcal mol−1 higher in energy than the structure with the tricoordinate fluorine atom. In fact, the F–Ga bond lengths are shortened in clusters containing Tl, reducing the cavity space. So, using larger atoms does not necessarily lead to larger cavities. That is why the three combinations including In and Tl (FIn2Tl2+, FIn3Tl+, and FInTl3+) are the only ones with perfect cavities for stabilizing a true ptF.
Why are ptFs so elusive compared to their isoelectric analogues CAl42−, NAl4−, and OAl4? Table 1 reveals particular trends among planar tetracoordinate atoms surrounded by Al. First, our computations show that going from CAl42− to FAl4+, there is a charge decrease on the central atom (from −2.62 |e| to −0.88 |e|) with a charge increment on the peripheral atoms (from +0.16 |e| to +0.47 |e|). So, the charge transfer from the Al4 skeleton to the central atom is more effective in the fluorine case. In other words, the ionic character between the hypercoordinate center and the metal fragment increases from C to F.
| q | Configuration | WBItotal | Δ H–L (eV) | ν min | |
|---|---|---|---|---|---|
| FAl4+ | −0.88 | 2s1.97 2px1.97 2py1.97 2pz1.97 | 0.24 | 1.15 | −47 |
| FGa4+ | −0.86 | 2s1.97 2px1.96 2py1.96 2pz1.97 | 0.28 | 1.13 | −71 |
| FIn4+ | −0.88 | 2s1.98 2px1.96 2py1.96 2pz1.97 | 0.24 | 0.95 | 33 |
| FTl4+ | −0.87 | 2s1.98 2px1.96 2py1.96 2pz1.97 | 0.25 | 0.86 | 28 |
| FGa3In+ | −0.85 | 2s1.97 2px1.96 2py1.95 2pz1.97 | 0.30 | 0.84 | 26 |
| FGa3Tl+ | −0.84 | 2s1.97 2px1.95 2py1.95 2pz1.96 | 0.32 | 0.79 | 24 |
| FGa2In2+ | −0.84 | 2s1.97 2px1.96 2py1.95 2pz1.96 | 0.31 | 0.80 | 30 |
| FGa2Tl2+ | −0.83 | 2s1.97 2px1.96 2py1.95 2pz1.96 | 0.33 | 0.79 | 25 |
| FGaIn3+ | −0.87 | 2s1.97 2px1.96 2py1.97 2pz1.97 | 0.26 | 0.97 | 42 |
| FGaTl3+ | −0.86 | 2s1.97 2px1.96 2py1.96 2pz1.97 | 0.27 | 0.89 | 33 |
| FIn2Tl2+ | −0.88 | 2s1.98 2px1.96 2py1.96 2pz1.97 | 0.25 | 0.89 | 10 |
| FIn3Tl+ | −0.88 | 2s1.98 2px1.96 2py1.96 2pz1.97 | 0.25 | 0.92 | 25 |
| FInTl3+ | −0.87 | 2s1.98 2px1.96 2py1.96 2pz1.97 | 0.25 | 0.87 | 31 |
| CAl42− | −2.62 | 2s1.60 2px1.76 2py1.76 2pz1.46 | 2.29 | 1.55 | 86 |
| NAl4− | −2.27 | 2s1.79 2px1.88 2py1.88 2pz1.71 | 1.33 | 1.79 | 95 |
| OAl4 | −1.68 | 2s1.91 2px1.94 2py1.94 2pz1.88 | 0.63 | 1.64 | 94 |
This is also supported by the significant reduction in the total values of the WBI32 of the central atom from 2.29 in CAl42− to only 0.24 in FAl4+, which, of course, is a consequence of the electronegativity difference between the peripheral atoms and the corresponding planar tetracoordinate atom. The electron transfer mechanism is less obvious, while carbon acts as σ-acceptor, and this is compensated by the back-donation from its 2pz electrons to the π-bonding (2s1.60 2px1.76 2py1.76 2pz1.46), the back-donation is null in the fluorine compounds. This is the main reason why these species are so rare. While several ptCs have been predicted and even detected experimentally, only six from 440 compositions contain a planar fluorine atom within the established parameters. For all ptFs, global minimum or not, there is a negligible variation of the fluorine charges and orbital occupancies. The only distinction is a subtle increase in the total WBI values of the gallium clusters due to their relatively short Ga–F bonds. However, the charge transfer is more effective for the global minima, i.e., higher than 0.86 |e| on F. The exception is FAl4+ (−0.88 |e|), but the cavity formed by the aluminum atoms is relatively small. In other words, both cavity size and charge transfer are essential to stabilize the ptF.
AdNDP is a powerful tool for understanding the distribution of electron pairs in the system.35 However, in some cases, several solutions are possible. Our strategy for identifying the most viable ones was to determine those schemes with the highest occupation number (ON). Let us compare two bonding schemes, or solutions, for CAl42− and FAl4+. In the first solution (Fig. 2a and b), there are four 2c–2e E-Al σ-bonds (E = C or F), four 3c–2e Al-E-Al σ-bonds, and one π-bond. In both clusters, the σ-bonds remain almost identical, but in the carbon molecule, the π-bond involves the four ligands, whereas, in FAl4+, it is located at the central atom, i.e., it can be reclassified as a lone-pair. The occupation numbers in all cases are higher than 1.95.
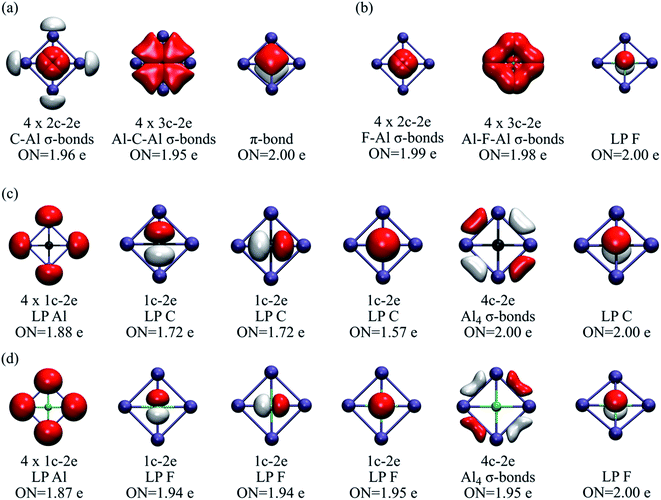 | ||
| Fig. 2 (a) First AdNDP solution for CAl42− and (b) FAl4+. (c) Second AdNDP solution for CAl42− and (d) FAl4+. ON stands for occupation number. | ||
However, a second solution suggests the absence of back-donation from the central to the peripheral atoms (Fig. 2c and d). This bonding layout can be described by a delocalized 4c–2e σ-bond involving the external ring, one lone-pair on each peripheral atom, and four lone-pairs on the central fluorine, i.e., no overlap between fluoride and the X42+ skeleton. This is entirely consistent with the charge analysis and WBI values. The residual electrons for the carbon system are 1.47, and in the case of fluorine, only 0.65. These values, along with the corresponding analysis for N and O (Tables S1–S2†), reveal that, along the row, the “ionic” scheme becomes quite competitive. Besides, it should be emphasized that both systems identify the lone pair on the fluorine atom, and most importantly, the number of residual electrons in the ionic scheme varies from 0.65 to 0.35 as it goes from Al to Tl, indicating a proclivity for the scheme bonding with no orbital overlap, i.e., an electrostatic nature between the fluorine and the peripheral atoms.
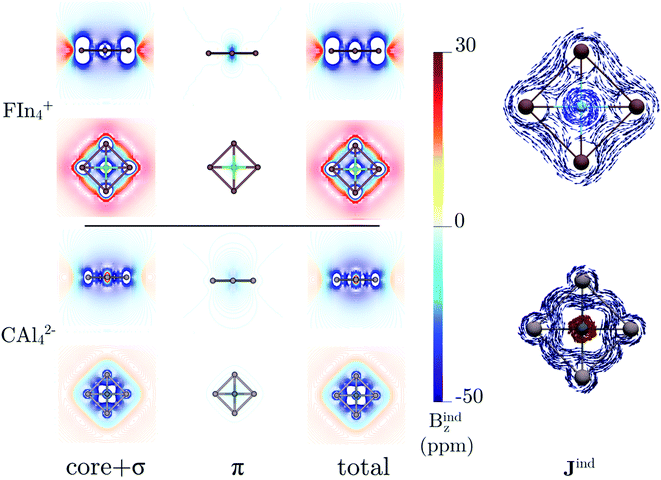
The back-donation absence also has consequences on the magnetic response. Let us compare the induced magnetic field36–38 of FIn4+ and CAl42−. In both cases, the magnetic response of the σ- and π-electrons is diatropic, but the first one much stronger compared to that caused by the π-cloud (almost negligible), as Fig. 3 shows. Note that the σ-electrons response of FIn4+ is stronger than in the carbon structure. So, both clusters could be classified as aromatic, predominantly σ-aromatic.44 More details about the magnetic response are provided by the induced current density (Jind).39–41 For CAl42−, there is a strong diatropic ring current around the Al4 skeleton (in deep blue) and a paratropic (counterclockwise) current around the carbon vicinity (in red, see Fig. 3). In contrast, in FIn4+, a local diatropic current is entirely localized at the fluorine atom (light blue). In order to quantify the ring-current strength, the Jind is integrated into a specific area. For the typical reference system, benzene, the integration plane starts in the center of the ring, intersects the C–C bond ending about 4 Å away. This results in a ring-current strength of 12 nA/T. A ring-current strength of 20.5 (FIn4+) and 13.7 (CAl42−) nA/T are obtained using the same integration domain. However, these values include the currents located at the central atoms. So, it is mandatory to avoid these local ring-current effects to quantify only the peripheral ring current. The selected integration planes start at 1.2 (FIn4+) and 0.7 Å (CAl42−) from the central atom, which are inflection Jind points from the local pathway to a ring current pathway. This provides a ring-current strength of 17.1 nA/T for FIn4+, which is smaller than the corresponding one for CAl42− (22.6 nA/T).
Conclusions
In summary, the exhaustive exploration of the PESs of pentaatomic systems with a fluorine atom and main group elements revealed that only atoms of group 13 as ligands could stabilize a ptF. Among the 440 examined combinations, only six clusters with a ptF are the energy global minimum, two of them with the same element as the ligand, FIn4+ and FTl4+, and the four composite species FGaIn3+, FIn2Tl2+, FIn3Tl+, and FInTl3+. The bonding analyses indicate that the interactions of fluorine with the peripheral atoms are significantly electrostatic, affecting the electronic delocalization. In other words, as opposed to planar tetracoordinate systems with carbon, nitrogen, or oxygen atoms, the fluorine in the ptFs does not act as a σ-acceptor, restraining any back-donation. This is reflected in the magnetic response. Although ptFs could be characterized as σ-aromatic and with a diatropic external current on the X4 ring, they also show a diatropic current entirely localized on the central F, as opposed to systems with a ptC. The above implies that the stabilization of these species is through subtle ionic interactions and an adequate cavity to accommodate the central atom, hence its scarcity. We believe that the design and prediction of these species will stimulate the experimental detection of a larger number of bizarre fluorine-containing structures.45Author contributions
G. M. and J. B. conceived the project and wrote the manuscript. G. C.-T., M. O.-I., E. D., and F. O.-C. performed the computational studies in consultation with X. Z., Z.-h. C.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by Grant SEP-Cinvestav-2018-57. F. O.-C. thanks CONACyT (grant Al-S-26876) for financial support and the Cátedras-CONACyT 1024 project. G. C.-T., E. D., M. O.-I. and J. B. thank Conacyt for their PhD fellowships.References
- H. J. Monkhorst, Chem. Commun., 1968, 1111–1112 RSC.
- R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993 CrossRef CAS.
- J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. v. R. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427 CrossRef CAS.
- P. v. R. Schleyer and A. I. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 21, 1536–1538 RSC.
- S. K. Nayak, B. K. Rao, P. Jena, X. Li and L.-S. Wang, Chem. Phys. Lett., 1999, 301, 379–384 CrossRef CAS.
- A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1998, 120, 7967–7972 CrossRef CAS.
- X. Li, L.-S. Wang, A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1999, 121, 6033–6038 CrossRef CAS.
- L.-S. Wang, A. I. Boldyrev, X. Li and J. Simons, J. Am. Chem. Soc., 2000, 122, 7681–7687 CrossRef CAS.
- X. Li, H.-F. Zhang, L.-S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 112, 3776–3778 CrossRef.
- Z.-H. Cui, Y.-H. Ding, J. L. Cabellos, E. Osorio, R. Islas, A. Restrepo and G. Merino, Phys. Chem. Chem. Phys., 2015, 17, 8769–8775 RSC.
- J. O. C. Jimenez-Halla, Y.-B. Wu, Z.-X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778 RSC.
- R. Grande-Aztatzi, J. L. Cabellos, R. Islas, I. Infante, J. M. Mercero, A. Restrepo and G. Merino, Phys. Chem. Chem. Phys., 2015, 17, 4620–4624 RSC.
- Z.-H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y.-H. Ding and G. Merino, Chem. Commun., 2017, 53, 138–141 RSC.
- S. Pan, J. L. Cabellos, M. Orozco-Ic, P. K. Chattaraj, L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350–12355 RSC.
- M.-H. Wang, X. Dong, Z.-H. Cui, M. Orozco-Ic, Y.-H. Ding, J. Barroso and G. Merino, Chem. Commun., 2020, 56, 13772–13775 RSC.
- A. C. Castro, G. Martínez-Guajardo, T. Johnson, J. M. Ugalde, Y.-B. Wu, J. M. Mercero, T. Heine, K. J. Donald and G. Merino, Phys. Chem. Chem. Phys., 2012, 14, 14764 RSC.
- J.-C. Guo, L.-Y. Feng, J. Barroso, G. Merino and H.-J. Zhai, Chem. Commun., 2020, 56, 8305–8308 RSC.
- J. Xu, X. Zhang, X. Yu, Y.-H. Ding, K. H. Bowen and J. Phys, Chem. Lett., 2017, 8, 2263–2267 CAS.
- J.-C. Guo, L.-Y. Feng, X.-Y. Zhang and H.-J. Zhai, J. Phys. Chem. Lett., 2018, 122, 1138–1145 CAS.
- R. Keese, Chem. Rev., 2006, 106, 4787–4808 CrossRef CAS PubMed.
- V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 1–10 CrossRef.
- L.-M. Yang, E. Ganz, Z. Chen, Z.-X. Wang and P. v. R. Schleyer, Angew. Chem., Int. Ed., 2015, 54, 9468–9501 CrossRef CAS PubMed.
- G. Merino, M. A. Méndez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372 CrossRef CAS PubMed.
- F. Ortiz-Chi and G. Merino, GLOMOS, Mérida, México, 2020 Search PubMed.
- R. Grande-Aztatzi, P. R. Martínez-Alanis, J. L. Cabellos, E. Osorio, A. Martínez and G. Merino, J. Comput. Chem., 2014, 35, 2288–2296 CrossRef CAS PubMed.
- A. Ramirez-Manzanares, J. Peña, J. M. Azpiroz and G. Merino, J. Comput. Chem., 2015, 36, 1456–1466 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, H. Borkent, W. Laarhoven, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- G. Merino, T. Heine and G. Seifert, Chem.–Eur. J., 2004, 10, 4367–4371 CrossRef CAS PubMed.
- T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309 CrossRef CAS PubMed.
- R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228 CrossRef CAS PubMed.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CAS.
- M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, Cinvestav-Mérida, México, 2016 Search PubMed.
- F. E. Jorge, A. Canal Neto, G. G. Camiletti and S. F. Machado, J. Chem. Phys., 2009, 130, 064108 CrossRef CAS PubMed.
- S. Fias, Z. Boisdenghien, T. Stuyver, M. Audiffred, G. Merino, P. Geerlings and F. de Proft, J. Phys. Chem. A, 2013, 117, 3556–3560 CrossRef CAS PubMed.
- P. Pröhm, N. Schwarze, C. Muller, S. Steinhauer, H. Beckers, S. M. Rupf and S. Riedel, Chem. Commun., 2021 10.1039/D1CC01088C.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01325d |
| This journal is © The Royal Society of Chemistry 2021 |