Open Access Article
Open Access ArticleTSNet: predicting transition state structures with tensor field networks and transfer learning
Riley
Jackson
,
Wenyuan
Zhang
and
Jason
Pearson
 *
*
Department of Chemistry, University of Prince Edward Island, Canada. E-mail: jpearson@upei.ca
First published on 23rd June 2021
Abstract
Transition states are among the most important molecular structures in chemistry, critical to a variety of fields such as reaction kinetics, catalyst design, and the study of protein function. However, transition states are very unstable, typically only existing on the order of femtoseconds. The transient nature of these structures makes them incredibly difficult to study, thus chemists often turn to simulation. Unfortunately, computer simulation of transition states is also challenging, as they are first-order saddle points on highly dimensional mathematical surfaces. Locating these points is resource intensive and unreliable, resulting in methods which can take very long to converge. Machine learning, a relatively novel class of algorithm, has led to radical changes in several fields of computation, including computer vision and natural language processing due to its aptitude for highly accurate function approximation. While machine learning has been widely adopted throughout computational chemistry as a lightweight alternative to costly quantum mechanical calculations, little research has been pursued which utilizes machine learning for transition state structure optimization. In this paper TSNet is presented, a new end-to-end Siamese message-passing neural network based on tensor field networks shown to be capable of predicting transition state geometries. Also presented is a small dataset of SN2 reactions which includes transition state structures – the first of its kind built specifically for machine learning. Finally, transfer learning, a low data remedial technique, is explored to understand the viability of pretraining TSNet on widely available chemical data may provide better starting points during training, faster convergence, and lower loss values. Aspects of the new dataset and model shall be discussed in detail, along with motivations and general outlook on the future of machine learning-based transition state prediction.
1 Introduction
The transition state (TS) is central to several important chemical prediction tasks, including reaction mechanism studies, protein investigation, and catalyst design.2–5 The common conception of a TS is a high energy configuration of reaction atoms along a particular reaction coordinate – a threshold along the trajectory from reactant to product which dictates reaction activation energy. Mathematically TS are represented by saddle points, also know as minimax points, on the potential energy surface (PES) of a given quantum system. Saddle points are complex critical points unique to surfaces with two degrees-of-freedom or more where all dimensions are either at a relative minimum or relative maximum. Of interest to most fields of chemistry are first-order saddle points where only a single dimension is at a maximum while all others are minimised. This maximised dimension corresponds to the reaction coordinate, e.g. the bond being broken or formed, and the minima which bookend this maximum represent the reactant and product complexes of the reaction. In other words, the first-order saddle point sits as the maximal energy geometry along the minimum energy pathway (MEP) between reactant and product complexes. Locating a specific TS on any given PES is exceptionally difficult for a handful of reasons. First, since TS are off-equilibrium conformers corresponding to the breaking/forming of chemical bonds, electronic configuration must be considered – i.e. TS search is only viable with quantum mechanics (QM) based ab initio methodologies which are often incredibly costly and scale very poorly with the size of the quantum system.6 Second, existing iterative Hessian-based search algorithms which optimize surfaces for minimax points potentially require many very expensive ab initio calls before convergence – and convergence is never guaranteed. Third, Hessian-based search algorithms are incredibly sensitive to starting point, meaning accurate estimations of true TS geometries must be provided to increase the probability of convergence upon desired structures.7 Over the last several decades many TS search algorithms have been developed to address these listed obstacles. Algorithms of note include Schlegel and Peng's synchronous transit quasi-Newton (STQN) method,8,9 the nudged elastic band (NEB) method,10,11 and Zimmerman's growing string methods (GSM).12–14 Other notable search implementations include eigen-vector following methods15–17 and spline methods.18–21 While implementation, reliability and use-cases differ among these search algorithms, they all largely follow the same schema: (1) generate a “guess” geometry of the TS from provided input structures (2) perform local Hessian-based surface optimization (typically some variation of the Broyden–Fletcher–Goldfarb–Shanno algorithm). Of the noted algorithms, GSMs are often reported as the most reliable,12 however they still require a handful of ab initio force calls at each node. Depending on the number of nodes created along the string, a single search can accrue dozens of force calls – albeit far fewer than NEB and STQN. Peterson reported significantly lowered ab initio force calls with NEB when supplemented with a machine-learned PES, resulting in a much more rapid acquisition of valid structures.22 The use of a machine-learned potential by Peterson is a footnote in the radical paradigm shift over the past decade towards novel machine learning (ML) algorithms for modelling chemical trends.1,23,24 State-of-the-art neural networks (NNs) such as SchNet and PhysNet are capable of achieving energy predictions within error margins much smaller than 1 kcal mol−1 trained upon data obtained using density functional theory (DFT) methods,25,26 and recent work using transfer-learning has allowed for coupled-cluster levels of accuracy with small sets of training data.27 We believe that the success observed mimicking ab initio with ML may be translated to TS search. However, while these milestones are incredibly promising, they all generally fall under the umbrella of “scalar regression”, where some representation of a quantum system serves as input and a single real number representing some aspect of that quantum system is outputted, e.g. internal energy. Less success has been observed developing predictive ML models which are capable of outputting structures – a requirement for modelling TS search.28 Progress has been made creating generative ML models for the purposes of molecular design, which output data structures representative of equilibrium structures, such as SMILES strings.28–31 However, these models are not transferrable to the task of TS prediction for a number of reasons. First, TSs are fundamentally very special non-equilibrium conformers of molecular systems, something not well represented by SMILES strings and simple binary connectivity graphs.32 Second, generative models are often invariant to the translation and rotation, i.e. the orientation, of the input molecules33–35 – meaning the output of the model does not change if the input is rotated and/or translated within its coordinate system. TS prediction ultimately requires equivariance to orientation, meaning the orientation of the output molecule must change equivalently to the orientation of the input molecule(s). The few existing equivariant ML models have only been developed within the last handful of year,36–38 and only much more recently have they been applied to computational chemistry, such as with the very recent Cormorant architecture.39–41 In order to translate the success of molecular predictive ML to structure prediction, effort must be put into the development of novel equivariant models capable of outputting verifiable and human-readable quantum systems. The solution we are proposing is an end-to-end approach – replacing both PES modelling and traditional Hessian-based search. The alternative approach, like that proposed by Peterson, is to replace only PES modelling and utilize traditional saddle point search methods. There are benefits to this semi-learned approach, the main being that accurate ML-based PES generating models already exist.25,26 However, these machine-learned potentials do not include TS structures in their training sets, meaning their performance for TS prediction would be dubious at best. Also, users will still be required to interact with traditional search algorithms which are very sensitive to input quality and often very difficult to operate effectively. Lastly, the success of end-to-end approaches in computer vision and natural language processing have shown considerable success along with other, more niche domains, such that they are quickly becoming the de facto methodologies in their respective fields.42–45 While chances of observing similar success with-respect-to TS prediction are questionable, we believe this approach is worth exploring.1.1 Project contributions
The goal of this study is to develop a ML model to predict accurate transition state structures on a potential energy surface (PES) between reactant and product complexes as input. This is challenging for several reasons. First, such a model requires interpreting molecular systems in multiple coordinate systems. Since reactant and product complexes are necessarily expressed in different coordinate systems (which cannot be unique), our ML models must both be capable of interpreting each of these and generating a third structure in yet another coordinate system. We find that tensor field networks based on the equivariant tensor field networks created by Thomas et al.38 are amenable to this challenge and provide details of our chosen architecture below. Second, the ambiguity of directionality on the potential energy surface is an important challenge. It is, of course, irrelevant whether one labels the reactant complex as “reactants” or “products” and a transition structure prediction must be appropriately invariant. We find that incorporating a Siamese architecture into our network is an effective strategy for incorporating PES directional invariance within our model. Finally, though there are a growing number of examples of ML molecular property predictors and even generative models for whole-molecule prediction, we find a dearth of examples that explicitly treat non-equilibrium molecular structures. Though transition structures are critical for understanding kinetics, intersystem crossings, enzyme function, etc. we find that most (if not all) ML predictors focus on equilibrium structure and properties. As such, there is very little data from which to train on. We use a novel approach to transfer learning as a solution here, where we incorporate the benefits from training on a large equilibrium dataset to training on a small non-equilibrium dataset.1.2 Similar works
While significant success has been observed applying ML to traditional fields of predictive computational chemistry, such as energy and force prediction, little research has been completed with respect to ML applied to TS prediction. While there are many facets of TS search that may be bolstered with ML, truly desirable is the development of a novel ML algorithm capable of outputting TS structure predictions directly, with a high level of accuracy, reliability, and generalizability. Such a feat has been attempted only a handful of times. The earliest found inclusion of ML to TS-based research was the 2012 paper by Pozun et al. The paper detailed the development of a support vector machine (SVM), a type of traditional ML classifier, which classified various non-equilibrium structures as either belonging to a reactant, or product region of a mechanistic pathway. The decision boundary function learned by the SVM, which is a plane through feature space, may serve as an approximation for the dividing surface of the reaction. From this dividing surface, one may determine the rate of reaction as the approximate equilibrium flux out of this surface. While the results of this study could prove useful in a variety of fields, it is unrelated to the proposed work due to its focus on kinetics, and the lack of TS structures in the training dataset.46 Slightly more related is the 2016 paper by Peterson, which described the use of traditional saddle-point search on machine-learned PESs. What is most interesting about this second work is the proposed hybrid QM-ML approach, where a majority of the saddle-point search is carried out upon a PES generated by a NN. While Peterson reported a drastic reduction in the number of required ab initio calls for successful calculations, the reliability of the method, e.g. the number of successfully obtained TSs, was not reported. Peterson's study was deemed dissimilar to the proposed study due to the lack of explicit TS structures in the dataset,47 and the fact that TS predictions are still carried out with traditional search algorithms, just upon machine-learned surfaces.48 Most recently, Pattanaik et al. Built a graph NN capable outputting TS distance matrices, which are used to generate a set of most probable Cartesians following non-linear least squares optimization.49 Our approach is most similar to that followed by Pattanaik et al., however there are a few key differences. First, we directly output Cartesians as opposed to distance matrices. This necessitates model equivariance and a standardized Cartesian dataset, however it affords our model the ability to differentiate enantiomers – something not possible with only a distance matrix. Second, the set of bond features used as input to the model proposed by Pattanaik et al. is a set of length 3 vectors, where the first entry of each vector is the bond distance for that particular bond averaged between reactant and product. The second and third entries indicate whether or not the bond has been broken or formed when going from reactant to product, and whether or not the bond was aromatic, respectively. Our input differs radically for a handful of reasons. First, TSNet is a Siamese architecture which offloads the combination of reactant and product features to the model. TSNet is also theoretically capable of operating on multi-reactant reactions, though the construction of a multi-reactant reaction dataset to test this capability is beyond the scope of this work. Second, we expand our interatomic distances using 800 unique atom-centered symmetry functions originally proposed by Behler, which have been shown to increase the predictive capabilities of chemical ML models.25,26,50 The last major difference between TSNet and Pattanaik's graph NN come from overall architectural differences. TSNet is a rotationally and translationally equivariant convolutional graph NN, while Pattanaik's model is an invariant multi-layer perceptron which operates atom-wise. It is too early in the development of both TSNet and Pattanaik's model to definitively say which model is superior with-respect-to predictive capabilities and computational cost. We leave an extensive benchmarking of TSNet and Pattanaik's model to future studies when larger TS datasets are more readily available.1.3 Anticipated problems
Prior to the development of TSNet three major challenges were anticipated: (1) how should inputs and outputs be represented? (2) How would one present multiple inputs to a model? (3) How would one deal with the lack of readily available TS data? The first question has largely been answered already and is general to most chemical ML projects, while the latter two are much more specific to TS search, meaning they must be answered within this work. In the following sections, the answers to these questions shall be explored.2 Methods
2.1 Construction of the SN2-TS dataset
The semi-automated algorithm for dataset generation was developed using Python 3.6, a programming language well regarded for its utility as an adapter between applications.58 A script written in Python that is capable of transcribing data from common file formats and executing external programs is often more digestible, reliable, and quick to develop than competing languages. Also, Python has become the de facto language for interacting with highly optimized ML backends, so integration between data generation and ML-based prediction is palatable. Seed data was recorded into the common xyz molecular file format by hand from various sources59–73 before being funnelled into the semi-automated TS data generation pipeline, titled Gaussian Manager (GM) (https://github.com/UPEIChemistry/GaussianManager).After TS optimization, GM performs an intrinsic reaction coordinate (IRC) calculation to obtain corresponding reactant and product geometries. To remedy convergence errors, IRC calculations were customized with the following keywords: loose, stepsize = 2, which ensured IRCs ran with very lenient convergence criteria, and the search computed only two steps along the negative mode, thus “pushing” the optimization towards either product or reactant complex. These IRCs are then followed by separate geometry optimizations for each of the reactant and product complexes. While most obtained reactant and product complex geometries appear visually to mimic the expected complexes some differ from expected structures,75 particularly reactions containing atoms capable of hydrogen bonding. The chosen basis set to optimize the structures with was the cc-PVDZ double-zeta basis.76 Calculations were performed at the Møller–Plesset 2 (MP2) level of theory.77 The method and basis set were ultimately chosen to ensure calculations completed in a reasonable amount of time, while not sacrificing a significant amount of computational accuracy.
2.2 Tensor field networks
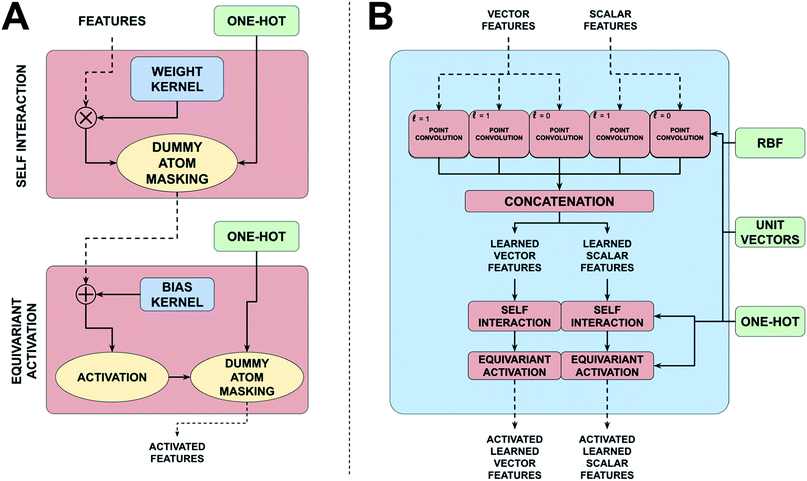
TSNet borrows heavily from TFNs proposed by Thomas et al., complex multifaceted NNs built specifically for equivariant prediction upon point clouds (represented by graphs).38 While other equivariant networks would likely suffice for TS prediction, the architecture from Thomas et al. was the most readily available and easily implemented architecture at the time TSNet was developed. In the following sections, an explanation of each distinct TFN layer, how TSNet differs from the original, and how they are integrated together to create the final learned “block” shall be given. Though based on similar motivations to the original, the overall construction of TSNet is very different. The four greatest differences are: (1) while the original implementation only accepted a single molecule/reaction at a time, TSNet utilizes dummy atoms and masking layers to allow for batching multiple molecule/reactions (2) the model uses residual skip connections (3) TSNet supports shared radial functions rather than only creating new sets of trainable weights every block (4) TSNet is built using a Siamese architecture, allowing it to accept any number of input systems. In the case of TSNet, we accept two inputs (reactant and product), though TSNet could easily be used for unimolecular reactions, or even trimolecular reactions.Input 1 – positional information. Like most state-of-the-art architectures, TSNet utilizes an interatomic distance matrix expanded using Behler's ACSFs, specifically radial basis functions. The shorthand ‘rbf’ is typically used when referring to positional information. The rbf array is of shape (molecules, atoms, atoms, basis functions) – a rank four array.
Input 2 – orientation information. Somewhat unique to TFNs is the use of interatomic unit vectors as input. The set of unit vectors for a single atom are computed as such:
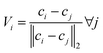 | (1) |
Input 3 – one-hot representation of atomic type. One-hot vectors are a very common binary data structure used in ML to represent the class of an object from a group of choices. For example, in a system that operates on all atoms up to an including fluorine, the one-hot vector representing a carbon atom would be a length nine vector with a one in the sixth position and zeroes everywhere else. An entire molecule or reaction would require a matrix of one-hot vectors, one for each atom. In a nutshell, for TFNs, one-hots are used frequently to represent the types of atoms present in a particular reaction or molecule. This input was not required in the original implementation of TFNs, as they only operated on a single molecule/reaction at a time. In order to operate on collections of molecules at a time, dummy atoms must be utilized to pad out smaller molecules to ensure inputs are rectangular. Dummy atoms have atomic number zero and are all centered at the origin of the molecule's coordinate system. As TFNs operate atom-wise and share weights across all atoms of a molecule, dummy atoms can potentially influence model training in undesirable ways. The new TFN implementation requires one-hot vectors for corresponding positional and feature arrays to track which atoms are dummy atoms and remove any contributions attributed to them during training. TSNet utilizes Profitt and Pearson's implementation of dummy atom masking,79 which require one-hot vectors to track dummy atoms and zero any contribution they make to training. Dummy atoms are masked after every layer.
Input 4 – vertex features represented as a set of tensor fields. Feature arrays are the single way in which information flows between learned blocks in a TFN. Ultimately, TFNs operate upon and output tensor fields, thus vertex features must be represented as sets of tensor fields, i.e. they must be represented as arrays of shape (molecules, atoms, features, representation index). The final axis of a tensor field array, representation index (RI), is related to which set of spherical harmonics functions are required to represent that particular feature array. In other words, RI is the same as the parameter m for the spherical harmonics, e.g. for Y10 RI is one (a scalar field) and for Y31 RI is three (a Euclidean vector field). Like the original implementation, TSNet only supports up to vector fields, however this is easily extendable to higher order tensors with minimal changes to the architecture. It should be noted that TFNs can actually operate on multiple feature arrays of differing RIs at a time. The only true vertex features on hand are atomic types which are only well represented by integers (or one-hot vectors, which are a very common way of representing integers). To translate atomic type to a tensor field one must expand the set of one-hot vectors for a collection of molecules which is of shape (molecules, atoms, highest atomic number) to a scalar field representation of atomic type, which is of shape (molecules, atoms, highest atomic number, 1). This operation is trivial mathematically but is critical to the model. This scalar field is then operated upon by an atom-wise dense layer to produce an array known as an ‘embedding’, which is exclusively machine-interpretable, of shape (molecules, atoms, units, 1) where ‘units’ refers to the number of trainable weights in the atom-wise dense layer. TSNet differs from the original in that it also includes a vector field embedding representation of atomic type which is of shape (molecules, atoms, units, 3) to facilitate residual skip connections between clusters of blocks of the network. Fig. 1 showcases the flow of information through the point convolution layer. All of the point convolution layers' trainable parameters are contained within a NN known as the ‘radial’ which operates interatomic-wise rather than atom-wise – with weights shared across all atoms in a molecule. This is distinct from networks like that proposed by Profitt and Pearson, which utilises a positional array in which the second atoms axis has been summed over to create a set of atomic environment vectors which describe the molecule. The radial extracts learned features from the interatomic distance features, i.e. the basis functions, and the second atoms axis is summed over during the tensor product between the harmonic filter, the vertex features, and the Clebsch–Gordan coefficients. Point convolution layers contain over 90% of the weights in a TFN.
2.2.1.1 Concatenation. The harmonic filter which is combined with vertex features is also a tensor field, and there are mathematical restrictions on how tensor fields of varying irreducible representations must be combined. The combinations TSNet supports are:
(1) Scalar × scalar → scalar.
(2) Scalar × vector → scalar.
(3) Scalar × vector → vector.
(4) Vector × vector → scalar.
(5) Vector × vector → vector.
Combinations (1), (3), and (5) are simply element-wise multiplication, while (2) and (4) are dot products. Since TFNs can accept multiple feature arrays of differing representation order (i.e. differing values of l) and TSNet supports harmonic filters up to l = 1, all five combinations are possible depending on input orders and desired filter orders. For example, providing both scalar field and vector field features and selecting both scalar and vector harmonic filters to be used results in five output feature arrays: three scalar fields, two vector fields. Keeping feature arrays of identical representation order separate is nonsensical, so they are concatenated along the features axis resulting in as many feature arrays as there are differing representation orders.
| ssp(x) = ln(0.5ex − 0.5) | (2) |
2.3 TSNet development
We should also point out that TSNet does not make use of the energy data for our structures. Though this is tempting, we have found in our tests that incorporating electronic energy data leads to a decrease in performance, since that comes with the necessary addition of a new loss function. When loss is split among structural measures and energetic measures, the performance on structure worsens. As such, since there are many excellent models for the rapid prediction of quantum energetics, we have focussed our efforts on structural predictions.
2.3.4.1 SN2-TS dataset. A benefit of adding support for training on batches of molecules rather than one molecule per batch is an increase in the amount of data pushed through the network during a single iteration of the optimizer. In fact, due to the miniscule amount of data in the SN2-TS dataset, training may be performed on the entire trainset rather than in batches, resulting in effectively noiseless steps along the cost landscape and smooth convergence. Selecting a validation split from a small dataset may result in a split comprised entirely of outliers, providing a skewed view on model performance. K-fold cross validation with k = 5 was used to address this. K-fold cross validation reports model performance as the average over k different train/validation splits, reducing the influence of unfortunate splits. Training on the SN2-TS dataset was completed in 1000 epochs using the Adam optimizer with an initial learning rate of 1 × 10−3.82. The learning rate was halved whenever the training reached a plateau to further assure complete convergence upon local minima on the cost landscape. The mean absolute error (MAE) loss function with L2 regularization was utilized for both the QM9 and SN2-TS dataset:
 | (3) |
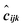 is the corresponding true Cartesian coordinate. The second term of the loss is the L2-norm regularization term, which hinders any single weight from reaching high values to combat overfitting. λ is a tuneable scalar to control the level of regularization used during training typically with a value in the range [0,0.1]. It is common practice to utilize a small amount of regularization regardless of any perceived overfitting, thus a default λ value of 0.01 is used. Models were trained using the Compute Canada HPC cluster Beluga on a single Nvidia 16 Gb Tesla v100 GPU.
is the corresponding true Cartesian coordinate. The second term of the loss is the L2-norm regularization term, which hinders any single weight from reaching high values to combat overfitting. λ is a tuneable scalar to control the level of regularization used during training typically with a value in the range [0,0.1]. It is common practice to utilize a small amount of regularization regardless of any perceived overfitting, thus a default λ value of 0.01 is used. Models were trained using the Compute Canada HPC cluster Beluga on a single Nvidia 16 Gb Tesla v100 GPU.
2.3.4.2 QM9 dataset. The QM9 dataset was obtained from: http://quantum-machine.org/datasets/. Targets for the QM9 were discarded in favour of a new prediction task more closely related to TS structure prediction. For each molecule in the dataset, a single random atom from the first three atoms of the Cartesian array was selected and perturbed by 0.75 Å along the positive and negative x, y, and z axes, while all other atoms were perturbed by 0.15 Å. This resulted in a set of three systems: the reverse structure, the forward structure, and the equilibrium structure, which are labelled as pseudo-reactant, product, and TS, respectively. For the pseudo-reaction double-ended prediction task, reactant, and product Cartesians along with a single atomic number one-hot array (since they are identical for all three systems) serve as input while the TS Cartesian array serves as the target. Training was completed on the QM9 in only 50 epochs – however, due to the size of the QM9 dataset, each epoch contains many more optimizer iterations. Batch size for the QM9 was 48, and training was completed with the Adam optimizer at an initial learning rate of 1 × 10−3 using a 90
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 train/validation ratio. Loss and regularization were performed following the strategies defined in Section 2.3.4.1.
10 train/validation ratio. Loss and regularization were performed following the strategies defined in Section 2.3.4.1.
2.3.4.3 ωB97X-D3 isomerization dataset. The higher theory ωB97X-D3 isomerization dataset developed by Grambow et al. was used following a similar approach to Pattanaik et al. to benchmark TSNet. We split the ωB97X-D3 dataset into an 80
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 train/validation/test split, further following Pattanaik et al. We trained for 100 epochs with a batch size of 32 reactions. Optimization, loss, and regularization were performed following the strategies defined in Section 2.3.4.1.
10 train/validation/test split, further following Pattanaik et al. We trained for 100 epochs with a batch size of 32 reactions. Optimization, loss, and regularization were performed following the strategies defined in Section 2.3.4.1.
3 Results and discussion
3.1 SN2-TS analytics
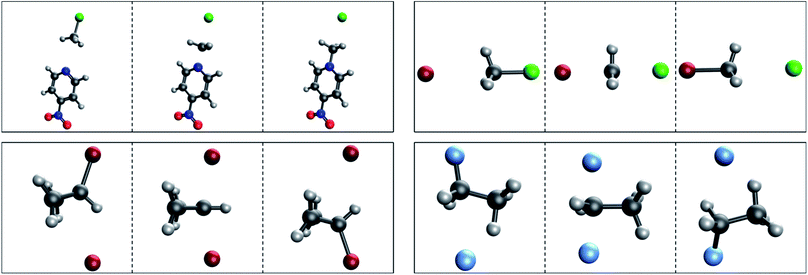
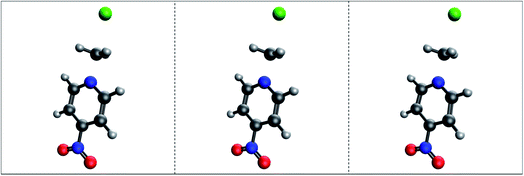
Significant thought was put into selecting the SN2 reaction for generation of a TS dataset. While other saddle points exist upon the PES, such as rotational TSs which only involve the rotation of a particular group of a single species, there was initial concern that such a prediction task may be too trivial. Also, “product” and “reactant” states for rotations may be exceedingly similar in structure, which could cause concern for models which depend on picking out differences between inputs. Ultimately, a greater impact was foreseen from a model capable of performing predictions upon reactions in which bonds are broken and formed. Gas-phase SN2 reactions are some of the most simplistic reaction mechanisms: a nucleophile approaches the center to form a bond, while the bond between the leaving group and the center breaks – all in a single concerted motion. In a nutshell, the decision to use SN2 reactions was made due to their complexity over rotations and other more trivial molecular motions, yet simplicity when compared to other chemical reactions. The SN2-TS dataset was generated using the second order Møller–Plesset perturbation theory method with the cc-pVDZ double-zeta basis set.76,83 This level of theory and basis were chosen strategically to ensure relative accuracy while keeping calculation times low.Only 53 SN2 reactions passed manual validation from a pool of 114 seed structures, the majority of which are small systems of 6–8 atoms. Each reaction includes three structures: reactant complex, TS, and product complex. The dataset as a whole includes 518 atoms and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 226 interatomic distances totalled across all three structures of each reaction. Most reactions are symmetric, e.g. both nucleophile and leaving group are identical. Why so many calculations failed to converge is unknown, but it could relate to the simplicity of many reactions in the dataset. Hessian-based optimization methods are typically quite sensitive to the curvature of the surface being searched. It is possible that the PES around the small, symmetric reactions from the SN2-TS is shallow enough that many steps must be taken before convergence is observed. In other words, the PES may be too flat such that the Hessian does not provide enough of a definitive direction for critical point location. This would lead to the optimizer taking effectively random steps across the surface, where each point is not radically different from the next energetically. Theoretically, an exact critical point representing reactant and product complexes should exist on the “true” surface, however a weak approximation may represent very shallow curvature as flat, hindering convergence. Further testing using methods of higher accuracy than MP2 must be conducted before anything conclusive about IRC convergence failure can be stated. Fig. 4 presents size and atomic type distributions for the dataset. Fig. 5 includes TS structures for four reactions from the SN2-TS dataset, selected to showcase example variety. All structures are presented and saved in standard orientation. IRC calculations for locating product/reactant complexes from optimized TS structures regularly failed during data acquisition. The alternative approach described above in Section 2.1.1 provided some success, however it does not guarantee convergence upon the exact complex, unlike true IRC calculations. This “noisy” optimization procedure is the sole reason for why such a low yield of final reactions were obtained from seed structures. While sufficient at providing a preliminary view of performance for TSNet, the SN2-TS dataset could benefit from a greater number of more diverse structures.
226 interatomic distances totalled across all three structures of each reaction. Most reactions are symmetric, e.g. both nucleophile and leaving group are identical. Why so many calculations failed to converge is unknown, but it could relate to the simplicity of many reactions in the dataset. Hessian-based optimization methods are typically quite sensitive to the curvature of the surface being searched. It is possible that the PES around the small, symmetric reactions from the SN2-TS is shallow enough that many steps must be taken before convergence is observed. In other words, the PES may be too flat such that the Hessian does not provide enough of a definitive direction for critical point location. This would lead to the optimizer taking effectively random steps across the surface, where each point is not radically different from the next energetically. Theoretically, an exact critical point representing reactant and product complexes should exist on the “true” surface, however a weak approximation may represent very shallow curvature as flat, hindering convergence. Further testing using methods of higher accuracy than MP2 must be conducted before anything conclusive about IRC convergence failure can be stated. Fig. 4 presents size and atomic type distributions for the dataset. Fig. 5 includes TS structures for four reactions from the SN2-TS dataset, selected to showcase example variety. All structures are presented and saved in standard orientation. IRC calculations for locating product/reactant complexes from optimized TS structures regularly failed during data acquisition. The alternative approach described above in Section 2.1.1 provided some success, however it does not guarantee convergence upon the exact complex, unlike true IRC calculations. This “noisy” optimization procedure is the sole reason for why such a low yield of final reactions were obtained from seed structures. While sufficient at providing a preliminary view of performance for TSNet, the SN2-TS dataset could benefit from a greater number of more diverse structures.
3.2 TSNet performance
The architectural motivation behind TSNet is multifaceted, pulling inspiration from ResNet,84 SchNet,25 the weight-sharing network from Profitt and Pearson,79 and the original TFN architecture proposed by Thomas et al.38 The decision to use only 64 self-interaction units for embeddings, MCB layers and radials was motivated by the high memory constraints of the new TFN implementation. Despite access to high-end hardware through Compute Canada, TSNet regularly encountered memory errors when using more than 64 units across the entire network architecture – thus limiting the size of each individual MCB. Training a larger version of TSNet will likely require access to GPU hardware with greater than 16 Gb of onboard vRAM. Presence of residual skip connections also motivated architectural decisions, as skip connections allow the model to determine during training which layers are necessary for training, push layer weights which are not necessary towards zero, dropping their involvement in prediction. Ultimately, the largest model within hardware constraints was chosen which trained smoothly and allowed the model to decide which layers were not necessary during training. One of the biggest additions to TSNet over the original TFNs is the support for radial sharing. In addition to TSNet TSNet-shared was tested, which utilizes a single shared radial across all MCBs within the network, resulting in a 10-fold reduction of trainable parameters.Some complications arise from computing loss from Cartesian arrays, as the difference between true and predicted includes coordinate system differences in addition to molecular differences. A separate distance error metric was developed to determine molecular difference within coordinate system difference inclusion, which computes average absolute difference between the distance matrix of true and predicted structures:
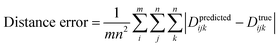 | (4) |
| Model | Train | Validation | ||
|---|---|---|---|---|
| Mean loss | Mean distance error | Mean loss | Mean distance error | |
| TSNet | 0.1455 (0.01) | 0.02672 (0.01) | 0.4576 (0.03) | 0.1831 (0.03) |
| Pre-trained TSNet (midpoint) | 0.06956 (0.004) | 0.07868 (0.006) | 0.3631 (0.04) | 0.2095 (0.03) |
| TSNet-shared | 0.2977 (0.03) | 0.07301 (0.02) | 0.6598 (0.1) | 0.1950 (0.04) |
| Pre-trained TSNet-shared (midpoint) | 0.07941 (0.007) | 0.04978 (0.01) | 0.4181 (0.05) | 0.1925 (0.06) |
| Pre-trained TSNet (energy) | 0.1327 (0.03) | 0.04387 (0.01) | 0.5124 (0.07) | 0.2838 (0.1) |
| TSNet-distance | — | 0.6198 (0.2) | — | 1.828 (0.3) |
• Low MAE, low distance error → model fits structures & coordinate system.
• Low MAE, high distance error → model fits coordinate system, not structures.
• High MAE, low distance error → model fits structures, not coordinate system.
Relationships one and three are ideal, while two is likely indicative of overfitting. In addition to computing distance error, manual validation must be performed in order to obtain the full view of a model's performance, as predicted chemical systems are too complex to score reliably with a single number. A fully automated pipeline including various molecular comparison metrics and sub-graph matching would ideally be utilized in place of manual validation; however, such a complex validation pipeline is beyond the scope of this paper and the SN2-TS dataset is small enough for visualization to be viable.
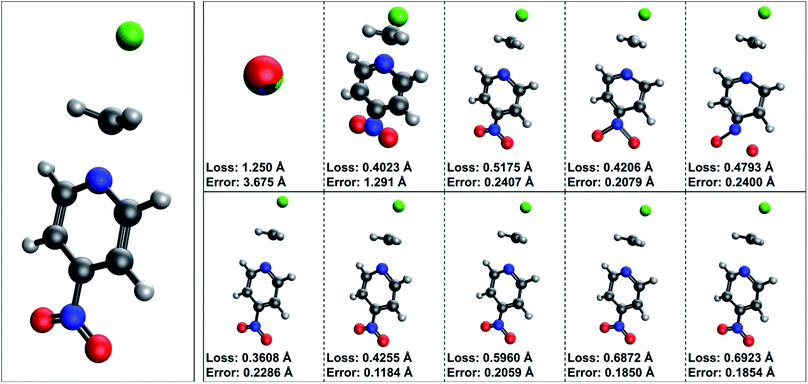
Representative train/validation curves for TSNet may be found in Fig. 7. Output inspection revealed virtually zero noticeable differences between true and predicted structures for both models as well. Validation performance suggests that TSNet is overfitting the SN2-TS dataset, and manual inspection uncovers that validation predictions are worse than train predictions. This overfitting is likely not a flaw of TSNet for a number of reasons. First, the small size and low diversity of the dataset suggests TSNet and TSNet-shared perform worse on the validation set simply because equivalent systems are not abundant within the train set. Second, overfitting behaviour is not observed during the midpoint prediction task with the QM9. TSNet is also trained by default with L2-regularization using a λ value of 0.01, and no noticeable changes to train and validation performance were observed when increasing regularization strength. Boosting TSNet validation performance is likely only possible with a larger, more diverse dataset of reactions. However, the performance of TSNet is promising, and worth further exploration.
| Model | Train | Validation | Test | |||
|---|---|---|---|---|---|---|
| Mean loss | Mean distance error | Mean loss | Mean distance error | Mean loss | Mean distance error | |
| TSNet | 0.1961 | 0.2130 | 0.2099 | 0.2236 | 0.2090 | 0.2236 |
| TSNet-shared | 0.1972 | 0.2131 | 0.2103 | 0.2238 | 0.2098 | 0.2238 |
| Model | Train | Validation | ||
|---|---|---|---|---|
| Mean loss | Mean distance error | Mean loss | Mean distance error | |
| TSNet (midpoint) | 0.1286 | 0.03893 | 0.1355 | 0.05694 |
| TSNet-shared (midpoint) | 0.1962 | 0.03589 | 0.2209 | 0.06257 |
| TSNet (energy) | 0.1575 (eV) | — | 0.3976 (eV) | — |
TSs for reactions are mostly made up of interatomic distances which are at equilibrium, with a handful of critical distances surrounding the reaction center, most notably the bonds being broken/formed. In a sense, by pretraining with the midpoint task, TSNet encodes knowledge about “equilibrium” chemistry within its weights – leading to superior predictions prior to training compared to an equivalent model trained from scratch. In other words, pretraining TSNet and TSNet-shared with the midpoint task allows each model to effectively skip the first approx. 400 epochs of training observed when training from scratch on the SN2-TS dataset. However, there are too few examples within the SN2-TS dataset for TSNet to hook into the underlying pattern which defines the SN2 reaction trajectory and produce highly accurate predictions. This leads to optimizing what is effectively noise, causing overfitting. Following the relationship between loss and distance error defined above in Section 3.3, pre-training with the midpoint task before training on the SN2-TS dataset in its current state creates models which better fit the coordinate system, rather than actual TS structures. Re-iterating the point made in Section 3.3.1, likely the only way of boosting performance is through the acquisition of more data. However, the idea of using TL to pretrain machine-learned TS structure predictors like TSNet is worthy of further investigation. Pretraining can, in a sense, remove the need to learn “equilibrium” chemistry, providing it prior to training on TS data. There is simply a lack of enough TS structures and clean reactant and product complexes to achieve highly accurate predictions during validation (Fig. 9).
4 Conclusion
The innovations of this paper are threefold. First, a novel dataset of SN2 reactions including TS structures has been created, the first of its kind. Second, a new MPNN based on TFNs titled TSNet has been developed which perform admirably on this dataset, given its size. Lastly, a TL method has been tested which allows for pretraining of TSNet using the QM9, a dataset over 4 orders of magnitude larger than the SN2-TS dataset, providing a reduction to loss values and a boost to prediction quality prior to training on the SN2-TS dataset. Already TSNet has outgrown the SN2-TS dataset – and the need for more data is paramount. Also, TS structures for much more complex reactions should be acquired to further test out TSNet's capabilities. While data acquisition is difficult for this particular task, if enough theoreticians make inhouse TS data readily available, data scientists may be able to quickly compile datasets of respectable size for training purposes. Also, in the past decade advancements have been made with respect to better automated saddle point search methods,85–87 meaning better pipelines for data acquisition may be constructed to reduce the need for human intervention. In addition to data generation and acquisition, new TL procedures should be developed to shrink the minimum amount of target TS data necessary to achieve high performance. Pre-training with the QM9 midpoint prediction task has shown that pretraining tasks do not necessarily have to be predicated by the laws of physics so long as the model is ultimately exposed to meaningful chemical structures. Ideally physically motivated prediction tasks would be used for pretraining, such as predicting frames from molecular dynamics trajectories – however, pseudo-physical tasks like the QM9 midpoint task are much easier to generate. While TSNet has been built for TS structure prediction, the framework upon which the model is built is general to many applications in chemistry. Ultimately, TSNet and TFNs are capable of any form of conformer prediction, mean they may be used for machine-learned molecular dynamics algorithms, calculation of stable conformers for known and potentially novel compounds, etc. The lightweight nature of ML vs. QM could also make QM/MM techniques obsolete, as ML can achieve QM level accuracies in a fraction of the compute times. Despite the quick paradigm shift to ML for computational chemistry, the field is still extremely young and full of potential. Hopefully, the very promising performance of TSNet will spark interest in the development of both purely machine-learned TS predictors, and composite methods which blend ML and traditional search, resulting in a new cast of inexpensive methods capable of predicting TS structures with a high degree of fidelity, and reliability.Data availability
The data and code developed in this work is available at https://github.com/UPEIChemistry/tensor-field-networks.Author contributions
RJ and JP designed the study. RJ was responsible for data curation, model design, and the original implementation of TSNet. WZ was reponsible for review and editing of the manuscript in the revision stage. JP was responsible for overall project administration and supervision as well as funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported in part by a Discovery Grant from the Natural Sciences and Engineering Research Council (NSERC) of Canada. Advanced computing resources are provided by Compute Canada, the organization responsible for digital research infrastructure in Canada, and ACENET, the regional partner in Atlantic Canada. ACENET is funded by the Canada Foundation for Innovation (CFI), and the provinces of New Brunswick, Newfoundland & Labrador, and Nova Scotia.References
- Y. Lecun, Y. Bengio and G. Hinton, Deep Learning, Nature, 2015, 436–444, DOI:10.1038/nature14539.
- A. Thawabteh, F. Lelario, L. Scrano, S. A. Bufo, S. Nowak, M. Behrens, A. Di Pizio, M. Y. Niv and R. Karaman, Bitterless Guaifenesin Prodrugs-Design, Synthesis, Characterization, in Vitro Kinetics, and Bitterness Studies, Chem. Biol. Drug Des., 2019, 93(3), 262–271, DOI:10.1111/cbdd.13409.
- E. Karlsson, E. Andersson, J. Dogan, S. Gianni, P. Jemth and C. Camilloni, A Structurally Heterogeneous Transition State Underlies Coupled Binding and Folding of Disordered Proteins, J. Biol. Chem., 2019, 294(4), 1230–1239, DOI:10.1074/jbc.RA118.005854.
- A. J. Neel, M. J. Hilton, M. S. Sigman and F. D. Toste, Exploiting Non-Covalent π Interactions for Catalyst Design, Nature, 2017, 637–646, DOI:10.1038/nature21701.
- Y. Zhu and D. G. Drueckhammer, Transition State Modeling and Catalyst Design for Hydrogen Bond-Stabilized Enolate Formation, J. Org. Chem., 2005, 70(19), 7755–7760, DOI:10.1021/jo0513818.
- E. T. Stewart, Quantum Chemistry, ed. N. Folchetti, K. P. Hamman and C. DuPont, Pearson Prentice Hall, Upper Saddle River, NJ, 6th edn, 1970, vol. 226, DOI:10.1038/226383b0.
- J. Nocedal and S. Wright, Numerical Optimization; Springer Series in Operations Research and Financial Engineering, Springer, New York, 2006 Search PubMed.
- C. Peng and H. B. Schlegel, Combining Synchronous Transit and Quasi-Newton Methods to Find Transition States, Isr. J. Chem., 1993, 33(4), 449–454, DOI:10.1002/ijch.199300051.
- P. Culot, G. Dive, V. H. Nguyen and J. M. Ghuysen, A Quasi-Newton Algorithm for First-Order Saddle-Point Location, Theor. Chim. Acta, 1992, 82, 189–205, DOI:10.1007/BF01113251.
- S. A. Trygubenko and D. J. Wales, A Doubly Nudged Elastic Band Method for Finding Transition States, J. Chem. Phys., 2004, 120(5), 2082–2094, DOI:10.1063/1.1636455.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113(22), 9901–9904, DOI:10.1063/1.1329672.
- P. Zimmerman, Reliable Transition State Searches Integrated with the Growing String Method, J. Chem. Theory Comput., 2013, 9(7), 3043–3050, DOI:10.1021/ct400319w.
- P. M. Zimmerman, Single-Ended Transition State Finding with the Growing String Method, J. Comput. Chem., 2015, 36(9), 601–611, DOI:10.1002/jcc.23833.
- M. Jafari and P. M. Zimmerman, Reliable and Efficient Reaction Path and Transition State Finding for Surface Reactions with the Growing String Method, J. Comput. Chem., 2017, 38(10), 645–658, DOI:10.1002/jcc.24720.
- C. J. Cerjan and W. H. Miller, On Finding Transition States, J. Chem. Phys., 1981, 75(6), 2800–2801, DOI:10.1063/1.442352.
- J. Simons, P. Jørgensen, H. Taylor and J. Ozment, Walking on Potential Energy Surfaces, J. Phys. Chem., 1983, 87(15), 2745–2753, DOI:10.1021/j100238a013.
- A. Banerjee, N. Adams, J. Simons and R. Shepard, Search for Stationary Points on Surfaces, J. Phys. Chem., 1985, 89(1), 52–57, DOI:10.1021/j100247a015.
- S. A. Ghasemi and S. Goedecker, An Enhanced Splined Saddle Method, J. Chem. Phys., 2011, 135(1), 014108, DOI:10.1063/1.3605539.
- R. Granot and R. Baer, A Spline for Your Saddle, J. Chem. Phys., 2008, 128(18), 184111, DOI:10.1063/1.2916716.
- A. C. Vaucher and M. Reiher, Minimum Energy Paths and Transition States by Curve Optimization, J. Chem. Theory Comput., 2018, 14(6), 3091–3099, DOI:10.1021/acs.jctc.8b00169.
- M. A. Heuer, A. C. Vaucher, M. P. Haag and M. Reiher, Integrated Reaction Path Processing from Sampled Structure Sequences, J. Chem. Theory Comput., 2018, 14(4), 2052–2062, DOI:10.1021/acs.jctc.8b00019.
- A. A. Peterson, Acceleration of Saddle-Point Searches with Machine Learning, J. Chem. Phys., 2016, 145(7), 074106, DOI:10.1063/1.4960708.
- J. Behler, Perspective: Machine Learning Potentials for Atomistic Simulations, J. Chem. Phys., 2016, 145(17), 170901, DOI:10.1063/1.4966192.
- A. C. Mater and M. L. Coote, Deep Learning in Chemistry, J. Chem. Inf. Model., 2019, 59(6), 2545–2559, DOI:10.1021/acs.jcim.9b00266.
- K. T. Schütt, P. J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K. R. Müller, SchNet: A Continuous-Filter Convolutional Neural Network for Modeling Quantum Interactions, Adv. Neural Inf. Process. Syst., 2017, 992–1002 Search PubMed.
- O. T. Unke and M. Meuwly, PhysNet: A Neural Network for Predicting Energies, Forces, Dipole Moments, and Partial Charges, J. Chem. Theory Comput., 2019, 15(6), 3678–3693, DOI:10.1021/acs.jctc.9b00181.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Approaching Coupled Cluster Accuracy with a General-Purpose Neural Network Potential through Transfer Learning, Nat. Commun., 2019, 10(1), 2903, DOI:10.1038/s41467-019-10827-4.
- D. C. Elton, Z. Boukouvalas, M. D. Fuge and P. W. Chung, Deep Learning for Molecular Design – A Review of the State of the Art, Mol. Syst. Des. Eng., 2019, 828–849, 10.1039/c9me00039a.
- B. Sanchez-Lengeling, C. Outeiral, G. L. Guimaraes and A. Aspuru-Guzik, Optimizing Distributions over Molecular Space. An Objective-Reinforced Generative Adversarial Network for Inverse-Design Chemistry (ORGANIC), ChemRxiv 2017.
- N. W. A. Gebauer, M. Gastegger and K. T. Schütt, Symmetry-Adapted Generation of 3d Point Sets for the Targeted Discovery of, Molecules, 2019 Search PubMed , arXiv:1906.00957.
- G. N. C. Simm, R. Pinsler and J. M. Hernández-Lobato, Reinforcement Learning for Molecular Design Guided by Quantum Mechanics, 2020, arXiv:2002.07717.
- M. Simonovsky and N. Komodakis, GraphVAE: Towards Generation of Small Graphs Using Variational Autoencoders, 2018, DOI:10.5121/csit.2012.2417.
- G. L. Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. L. C. Farias and A. Aspuru-Guzik, Objective-Reinforced Generative Adversarial Networks (ORGAN) for Sequence Generation, Models, 2017 Search PubMed , arXiv:1705.10843v2.
- M. Benhenda, ChemGAN Challenge for Drug Discovery: Can AI Reproduce Natural Chemical Diversity?, 2017 Search PubMed.
- E. Putin, A. Asadulaev, Q. Vanhaelen, Y. Ivanenkov, A. V. Aladinskaya, A. Aliper and A. Zhavoronkov, Adversarial Threshold Neural Computer for Molecular de Novo Design, Mol. Pharm., 2018, 15(10), 4386–4397, DOI:10.1021/acs.molpharmaceut.7b01137.
- T. S. Cohen and M. Welling, Steerable CNNs, 5th Int. Conf. Learn. Represent. ICLR 2017 – Conf. Track Proc., 2016 Search PubMed.
- M. Weiler, M. Geiger, M. Welling, W. Boomsma and T. Cohen, 3D Steerable CNNs: Learning Rotationally Equivariant Features in Volumetric Data, Adv. Neural Inf. Process. Syst., 2018, 10381–10392 Search PubMed.
- N. Thomas, T. Smidt, S. Kearnes, L. Yang, L. Li, K. Kohlhoff and P. Riley, Tensor Field Networks: Rotation- and Translation-Equivariant Neural Networks for 3D Point Clouds, 2018 Search PubMed.
- B. Anderson, T.-S. Hy and R. Kondor, Cormorant: Covariant Molecular Neural Networks, 2019 Search PubMed.
- G. N. C. Simm, R. Pinsler, G. Csányi and J. M. Hernández-Lobato, Symmetry-Aware Actor-Critic for 3D Molecular Design, 2020, arXiv:2011.12747.
- R. Kondor, N-Body Networks: A Covariant Hierarchical Neural Network Architecture for Learning Atomic, Potentials, 2018 Search PubMed , arXiv:1803.01588.
- G. Trigeorgis, F. Ringeval, R. Brueckner, E. Marchi, M. A. Nicolaou, B. Schuller and S. Zafeiriou, Adieu Features? End-to-End Speech Emotion Recognition Using a Deep Convolutional Recurrent Network, in ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing – Proceedings, Institute of Electrical and Electronics Engineers Inc., 2016, pp. 5200–5204, DOI:10.1109/ICASSP.2016.7472669.
- D. Amodei, S. Ananthanarayanan, R. Anubhai, J. Bai, E. Battenberg, C. Case, J. Casper, B. Catanzaro, Q. Cheng, G. Chen, J. Chen, J. Chen, Z. Chen, M. Chrzanowski, A. Coates, G. Diamos, K. Ding, N. Du, E. Elsen, J. Engel, W. Fang, L. Fan, C. Fougner, L. Gao, C. Gong, A. Hannun, T. Han, L. Vaino Johannes, B. Jiang, C. Ju, B. Jun, P. LeGresley, L. Lin, J. Liu, Y. Liu, W. Li, X. Li, D. Ma, S. Narang, A. Ng, S. Ozair, Y. Peng, R. Prenger, S. Qian, Z. Quan, J. Raiman, V. Rao, S. Satheesh, D. Seetapun, S. Sengupta, K. Srinet, A. Sriram, H. Tang, L. Tang, C. Wang, J. Wang, K. Wang, Y. Wang, Z. Wang, Z. Wang, S. Wu, L. Wei, B. Xiao, W. Xie, Y. Xie, D. Yogatama, B. Yuan, J. Zhan and Z. Zhu, Deep Speech 2: End-to-End Speech Recognition in English and Mandarin, PMLR, 2016 Search PubMed.
- S. Ekins, A. C. Puhl, K. M. Zorn, T. R. Lane, D. P. Russo, J. J. Klein, A. J. Hickey and A. M. Clark, Exploiting Machine Learning for End-to-End Drug Discovery and Development, Nat. Mater., 2019, 18, 435–441, DOI:10.1038/s41563-019-0338-z.
- X. Shi, Z. Chen, H. Wang, D.-Y. Yeung, W.-K. Wong and W.-C. Woo, Convolutional LSTM Network: a machine learning approach for precipitation nowcasting, In Proceedings of the 28th International Conference on Neural Information Processing Systems – Vol. 1 (NIPS'15), MIT Press, Cambridge, MA, 2015, pp. 802–810 Search PubMed.
- Z. D. Pozun, K. Hansen, D. Sheppard, M. Rupp, K. R. Müller and G. Henkelman, Optimizing Transition States via Kernel-Based Machine Learning, J. Chem. Phys., 2012, 136(17), 174101, DOI:10.1063/1.4707167.
- A. A. Peterson, Acceleration of Saddle-Point Searches with Machine Learning, J. Chem. Phys., 2016, 145(7), 074106, DOI:10.1063/1.4960708.
- A. Khorshidi and A. A. Peterson, Amp: A Modular Approach to Machine Learning in Atomistic Simulations, Comput. Phys. Commun., 2016, 207, 310–324, DOI:10.1016/j.cpc.2016.05.010.
- L. Pattanaik, J. B. Ingraham, C. A. Grambow and W. H. Green, Generating Transition States of Isomerization Reactions with Deep Learning, Phys. Chem. Chem. Phys., 2020, 22(41), 23618–23626, 10.1039/d0cp04670a.
- J. Behler, Atom-Centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials, J. Chem. Phys., 2011, 134(7), 074106, DOI:10.1063/1.3553717.
- A. P. Bartók, R. Kondor and G. Csányi, On Representing Chemical Environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 87(18), 184115, DOI:10.1103/PhysRevB.87.184115.
- G. Koch, R. Zemel and R. Salakhutdinov, Siamese Neural Networks for One-Shot Image Recognition, 2015 Search PubMed.
- C. A. Grambow, L. Pattanaik and W. H. Green, Reactants, Products, and Transition States of Elementary Chemical Reactions Based on Quantum Chemistry, Sci. Data, 2020, 7(1), 1–8, DOI:10.1038/s41597-020-0460-4.
- C. Tan, F. Sun, T. Kong, W. Zhang, C. Yang and C. Liu, A Survey on Deep Transfer Learning, in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), LNCS, Springer Verlag, 2018, vol. 11141, pp. 270–279, DOI:10.1007/978-3-030-01424-7_27.
- J. Yosinski, J. Clune, Y. Bengio and H. Lipson, How Transferable Are Features in Deep Neural Networks?, Adv. Neural Inf. Process. Syst., 2014, 3320–3328 Search PubMed.
- L. Ruddigkeit, R. Van Deursen, L. C. Blum and J. L. Reymond, Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17, J. Chem. Inf. Model., 2012, 52(11), 2864–2875, DOI:10.1021/ci300415d.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum Chemistry Structures and Properties of 134 Kilo Molecules, Sci. Data, 2014, 1(1), 1–7, DOI:10.1038/sdata.2014.22.
- G. van Rossum, Python Tutorial, CWI Rep. CS-R9526 1995, No. CS-R9526, 1995, pp. 1–65 Search PubMed.
- S. Wolfe, D. J. Mitchell and H. Bernhard Schlegel, Theoretical Studies of SN2 Transition States. 1. Geometries, J. Am. Chem. Soc., 1981, 7692–7694, DOI:10.1021/ja00415a068.
- I. Lee, C. Kim, D. Chung and B.-S. Lee, J. Org. Chem., 1994, 59(16), 4490–4494 CrossRef CAS.
- Y. S. Park, C. K. Kim, B. -S. Lee, I. Lee, W. M. Lim and W. K. Kim, Theoretical Studies on the Reactions of Substituted Phenolate Anions with Formate Esters, J. Phys. Org. Chem., 1995, 8(5), 325–334, DOI:10.1002/poc.610080502.
- A. Streitwieser, G. S. C. Choy and F. Abu-Hasanayn, Theoretical Study of Ion Pair S(N)2 Reactions: Ethyl vs. Methyl Reactivities and Extension to Higher Alkyls, J. Am. Chem. Soc., 1997, 119(21), 5013–5019, DOI:10.1021/ja961673d.
- Y. A. Borisov, E. E. Arcia, S. L. Mielke, B. C. Garrett and T. H. Dunning, A Systematic Study of the Reactions of OH- with Chlorinated Methanes. 1. Benchmark Studies of the Gas-Phase Reactions, J. Phys. Chem. A, 2001, 105(32), 7724–7736, DOI:10.1021/jp011447c.
- S. Parthiban, G. De Oliveira and J. M. L. Martin, Benchmark Ab Initio Energy Profiles for the Gas-Phase SN2 Reactions Y− + CH3X → CH3Y + X− (X,Y = F,Cl,Br). Validation of Hybrid DFT Methods, J. Phys. Chem. A, 2001, 105(5), 895–904, DOI:10.1021/jp0031000.
- I. Lee, C. K. Kim, C. K. Sohn, H. G. Li and H. W. Lee, A High-Level Theoretical Study on the Gas-Phase Identity Methyl Transfer Reactions, J. Phys. Chem. A, 2002, 106(6), 1081–1087, DOI:10.1021/jp013690h.
- J. Ren and J. I. Brauman, Energy Deposition in SN2 Reaction Products and Kinetic Energy Effects on Reactivity, J. Phys. Chem. A, 2002, 106(15), 3804–3813, DOI:10.1021/jp0141070.
- K. K. Chang, G. L. Hong, B. S. Lee, K. K. Chan, W. L. Hai and I. Lee, Gas-Phase Identity Nucleophilic Substitution Reactions of Cyclopropenyl Halides, J. Org. Chem., 2002, 67(6), 1953–1960, DOI:10.1021/jo0164047.
- T. D. Fridgen and T. B. McMahon, Enthalpy Barriers for Asymmetric SN2 Alkyl Cation Transfer Reactions between Neutral and Protonated Alcohols, J. Phys. Chem. A, 2003, 107(5), 668–675, DOI:10.1021/jp026818j.
- A. Dybała-Defratyka, M. Rostkowski, O. Matsson, K. C. Westaway and P. Paneth, A New Interpretation of Chlorine Leaving Group Kinetic Isotope Effects; a Theoretical Approach, J. Org. Chem., 2004, 69(15), 4900–4905, DOI:10.1021/jo049327z.
- H. J. Zhu, Y. Ren, J. Ren and S. Y. Chu, Theoretical Investigation of Ion Pair SN2 Reactions of Alkali Isothiocyanates with Alkyl Halides. Part 1. Reaction of Lithium Isothiocyanate and Methyl Fluoride with Inversion Mechanism, Int. J. Quantum Chem., 2005, 101(1), 104–112, DOI:10.1002/qua.20213.
- A. P. Bento, M. Solà and F. M. Bickelhaupt, Ab Initio and DFT Benchmark Study for Nucleophilic Substitution at Carbon (SN2@C) and Silicon (SN2@Si), J. Comput. Chem., 2005, 26(14), 1497–1504, DOI:10.1002/jcc.20261.
- S. R. K. Ainavarapu, A. P. Wiita, L. Dougan, E. Uggerud and J. M. Fernandez, Single-Molecule Force Spectroscopy Measurements of Bond Elongation during a Bimolecular Reaction, J. Am. Chem. Soc., 2008, 130, 6479–6487, DOI:10.1021/ja800180u.
- A. P. Bento, M. Sola and F. M. Bickelhaupt, E2 and S2 Reactions of X + CHCHX (X = F, Cl); an Ab Initio and DFT Benchmark Study, J. Chem. Theory Comput., 2008, 4(6), 929–940, DOI:10.1021/ct700318e.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. Hratchian, A. Izmaylov, J. Bloino, G. Zheng, J. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. Montgomery, J. Peralta, F. Ogliaro, M. Bearpark, J. Heyd, E. Brothers, K. Kudin, V. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, P. Rendell, J. Burant, S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. Millam, M. Klene, J. Knox, J. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. Stratmann, O. Yazyev, A. Austin, R. Cammi, C. Pomelli, J. Ochterski, R. Martin, K. Morokuma, V. Zakrzewski, G. Voth, P. Salvador, J. Dannenberg, S. Dapprich, A. Daniels, O. Farkas, J. Foresman, J. Ortiz, J. Cioslowski and D. Fox, Gaussian ∼09 Revision D.01, January 1, 2014 Search PubMed.
- R. J. Ouellette and J. D. Rawn, Nucleophilic Substitution and Elimination Reactions, in Principles of Organic Chemistry, Elsevier, 2015, pp. 189–208, DOI:10.1016/b978-0-12-802444-7.00007-0.
- T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023, DOI:10.1063/1.456153.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, MP2 Energy Evaluation by Direct Methods, Chem. Phys. Lett., 1988, 153(6), 503–506, DOI:10.1016/0009-2614(88)85250-3.
- C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Array Programming with NumPy, Nature, 2020, 357–362, DOI:10.1038/s41586-020-2649-2.
- T. A. Profitt and J. K. Pearson, A Shared-Weight Neural Network Architecture for Predicting Molecular Properties, Phys. Chem. Chem. Phys., 2019, 21(47), 26175–26183, 10.1039/c9cp03103k.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, Google Research, TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems, 2015 Search PubMed.
- F. Chollet, others, Keras, GitHub, 2015 Search PubMed.
- D. P. Kingma and J. L. Ba, Adam: A Method for Stochastic Optimization, in 3rd International Conference on Learning Representations, ICLR 2015 – Conference Track Proceedings; International Conference on Learning Representations, ICLR, 2015 Search PubMed.
- C. Møller and M. S. Plesset, Note on an Approximation Treatment for Many-Electron Systems, Phys. Rev., 1934, 46(7), 618–622, DOI:10.1103/PhysRev.46.618.
- K. He, X. Zhang, S. Ren and J. Sun, Deep Residual Learning for Image Recognition, in Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, IEEE Computer Society, 2016, pp. 770–778, DOI:10.1109/CVPR.2016.90.
- E. Martínez-Núñez, An Automated Method to Find Transition States Using Chemical Dynamics Simulations, J. Comput. Chem., 2015, 36(4), 222–234, DOI:10.1002/jcc.23790.
- L. D. Jacobson, A. D. Bochevarov, M. A. Watson, T. F. Hughes, D. Rinaldo, S. Ehrlich, T. B. Steinbrecher, S. Vaitheeswaran, D. M. Philipp, M. D. Halls and R. A. Friesner, Automated Transition State Search and Its Application to Diverse Types of Organic Reactions, J. Chem. Theory Comput., 2017, 13(11), 5780–5797, DOI:10.1021/acs.jctc.7b00764.
- E. L. Kolsbjerg, M. N. Groves and B. Hammer, An Automated Nudged Elastic Band Method, J. Chem. Phys., 2016, 145(9), 094107, DOI:10.1063/1.4961868.
| This journal is © The Royal Society of Chemistry 2021 |