Open Access Article
Open Access ArticleCoacervate formation studied by explicit solvent coarse-grain molecular dynamics with the Martini model†
Maria
Tsanai
 a,
Pim W. J. M.
Frederix
a,
Pim W. J. M.
Frederix
 a,
Carsten F. E.
Schroer
a,
Paulo C. T.
Souza
a,
Carsten F. E.
Schroer
a,
Paulo C. T.
Souza
 ab and
Siewert J.
Marrink
ab and
Siewert J.
Marrink
 *a
*a
aGroningen Biomolecular Sciences and Biotechnology Institute and Zernike Institute for Advanced Materials, University of Groningen, 9747AG Groningen, The Netherlands. E-mail: s.j.marrink@rug.nl
bMolecular Microbiology and Structural Biochemistry, UMR 5086 CNRS, University of Lyon, Lyon, France
First published on 18th May 2021
Abstract
Complex coacervates are liquid–liquid phase separated systems, typically containing oppositely charged polyelectrolytes. They are widely studied for their functional properties as well as their potential involvement in cellular compartmentalization as biomolecular condensates. Diffusion and partitioning of solutes into a coacervate phase are important to address because their highly dynamic nature is one of their most important functional characteristics in real-world systems, but are difficult to study experimentally or even theoretically without an explicit representation of every molecule in the system. Here, we present an explicit-solvent, molecular dynamics coarse-grain model of complex coacervates, based on the Martini 3.0 force field. We demonstrate the accuracy of the model by reproducing the salt dependent coacervation of poly-lysine and poly-glutamate systems, and show the potential of the model by simulating the partitioning of ions and small nucleotides between the condensate and surrounding solvent phase. Our model paves the way for simulating coacervates and biomolecular condensates in a wide range of conditions, with near-atomic resolution.
1 Introduction
Solutions of oppositely charged polyions may show liquid–liquid phase coexistence. Depending on the state conditions (e.g. salt concentration, polymer concentration, pH and temperature), electrostatically driven complex formation can lead to phase separation between macromolecule-rich and macromolecule-deficient fractions. Already since the early 20th century, this process is known as coacervation, and it is regularly found in naturally occurring charged colloids, such as serum albumin and gum arabic.1 Since then, many combinations of natural or synthetic macro-ions have been shown to form complex coacervates and they have started to find applications in the encapsulation or extraction of small active compounds for biomedicine.2,3 Additionally, the liquid–liquid phase separation leads to formation of liquid droplets that could serve as membraneless compartments in aqueous solution, a potentially important intermediate step in the early formation of living cells.4 Moreover, evidence is mounting that present-day cells feature multiple cellular compartments that are characterized by liquid properties (biomolecular condensates), including high turnover of components and easy deformation.5–14One of the current challenges for the field is to study the dynamics of individual molecules (not only polyelectrolytes, but also solvent, ions and small organic compounds) inside the coacervate phase. Some experimental methods such as Overhauser dynamic nuclear polarization (ODNP) measurements can probe the local dynamics of polymers or water when spin labels are added,15 but explicit molecular simulation techniques such as Molecular Dynamics (MD) are arguably more versatile in addressing this challenge. All-atom MD simulations have so far mainly been restricted to simulating pairs of electrolyte molecules, as simulating systems with multiple polymer chains representative of a coacervate becomes computationally expensive and the sampling of the relevant conformations becomes problematic.16–18 A recent exception is the study by Mintis and Mavrantzas,19 who used a free energy based approach with an explicit solvent all-atom model to study the phase diagram of short acrylic polymer fragments. Neglecting the solvent degrees of freedom remedies this problem to some extent,20,21 but the importance of explicit water in simulating polyelectrolyte complex formation was demonstrated in a number of cases.22–25 Given the limitations of all-atom models, the use of coarse-grain (CG) models is gaining popularity in this field.26 In coarse-graining, groups of atoms are represented by effective interaction sites, drastically reducing the number of particles.27 CG MD allows to describe the diffusive and complexation behavior of all constituents of the coacervate phase at a length scale large enough to have phase separation. This has been demonstrated by several groups, utilizing a one bead per amino acid CG model to study a variety of condensed liquid biomolecular systems.28–34 Although these CG models offer important insight to the physicochemical driving forces of liquid–liquid phase separation, their ability to represent fine chemical details of the constituents is limited. Inherent to their limited resolution, they are more generic in their predictions.
To alleviate this problem, here we use the recently re-parameterized CG Martini force field (version 3) that offers a higher (near-atomic) resolution. Martini maps 2–4 heavy particles to 1 CG bead and is based on oil/water partitioning free energies, as well as miscibility data to describe the various hydrophobic and hydrophilic interactions.35 Previous simulations on poly(diallyldimethylammonium) and poly(styrene sulfonate) complexes with an older version of Martini have demonstrated that this CG approach can correctly deal with excluded volume effects, charge compensation and changes in the dielectric constant of water inside a coacervate.36 We demonstrate the accuracy of the model by reproducing the salt dependent coacervation of poly-L-lysine/poly-L-glutamate (pLys/pGlu) systems, which have been studied extensively by Tirrell, Perry and co-workers,17,20,30,36,37 and show the potential of the model by simulating the partitioning of ions and small nucleotides between the condensate and surrounding solvent phase. The advantage of the Martini model over other CG approaches, in addition to the chemical specificity, is the building block approach offering immediate compatibility of polyelectrolytes with other molecules parameterized using the Martini philosophy, such as lipids,38 proteins,39 sugars,40 nucleotides,41,42 ionic liquids43 and polymers.44 This provides a quick route to the simulation of extraction of valuable compounds in biotechnological applications, as well as to study prebiotic cell precursors and biomolecular condensates in current cells with realistic composition.
2 Results and discussion
2.1 Salt and polymer dependent coacervation
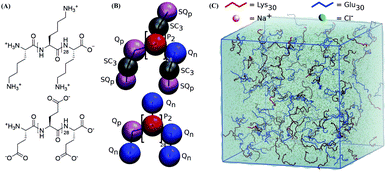
In order to study the complexation of polyelectrolytes, we set up simulation boxes with equal numbers of Lys30 and Glu30 polymers employing the coarse-grain parameters from the “open beta” version of the Martini 3.0 CG force field, as illustrated in Fig. 1.35,45 From this starting point, with a randomized distribution of the polymers, we performed 20 μs simulations at salt concentrations varying from 0.17 to 0.9 M. Equilibration of these systems required between 1 and 2 μs. In particular, systems which phase separated required slightly longer equilibration times (Fig. S1†). The main target for the CG model is reproducing the experimental phase behavior of the pLys/pGlu mixture. Priftis and Tirrell showed for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of these polymers with Npol = 30, coacervation occurs in sodium chloride solutions with concentrations below 0.40 M.36Fig. 2A shows snapshots of the simulated systems and Fig. 2B and C polymer–polymer radial distribution functions (RDFs) from simulations with six different salt concentrations, both below and above this threshold. Two different processes can be observed: firstly, at all salt concentrations positive and negative polymers pair to form dimers. Fig. 2B shows this clearly in the intense first peaks of the pLys–pGlu RDFs at 0.5 nm for all these six salt concentrations, revealing direct contact between the oppositely charged polymers' beads. However, a different behavior is observed for polymers with identical charges, as shown for pGlu–pGlu RDFs (Fig. 2C). As expected, the first neighbor shell (0.5 nm) is almost completely excluded because of charge repulsion, but an enrichment of polymer at larger distances (>1 nm) is clearly observed for the simulations at lower salt concentration, indicative of a large-scale phase separation. Simulations with 0.36 M NaCl concentration only show a negligible enhancement of polymer density compared to the bulk, while with 0.6 and 0.9 M the polymer chains are fully dispersed. Together with the snapshots from the simulations (Fig. 2A), these RDFs show that phase separation into a polymer-dense and a polymer-deficient phase occurs at sodium chloride concentrations of 0.17, 0.21 and 0.25 M, but not at concentrations above 0.36 M. To quantify the salt concentration at which coacervation is observed in our simulations, we calculated the maximum peptide cluster size, normalized by the volume of the system. The results are shown in Fig. 2D. The maximum cluster size seems to decrease with increasing the salt concentration and above 0.36 M it levels off. Taking the inflection point of the maximum cluster size curve as a rough estimate (Fig. 2D), we conclude that, in our simulations, the transition from coacervation to non-coacervation occurs around 0.3 M NaCl concentration. It should be noted that the coacervate formation is a dynamic and reversible process: when additional salt (1.3 M) is added to the coacervate structure formed at 0.17 M sodium chloride solution, the polymers redissolve into pairs over time, as shown in Fig. S2.† Our estimate of the transition point is consistent with the experimental threshold of 0.4 M,30 although it is important to point out that a fair comparison between the experimental and simulated critical salt concentration is difficult, due to a number of reasons. First, the polymer concentrations used in the simulations are much higher than those used in the experiments, to keep the simulations tractable (otherwise mostly water–water interactions would be simulated). Potentially, the miscibility transition depends on the polymer concentration. Unfortunately, the extent of this effect is not known for the system under investigation, but experimental data for similar systems (pHis/pGlu complex coacervate) point to a limited effect.30 Similar to the polymer length, an increase of 2 to 10 times the polymer concentration seems to promote a shift to modestly higher concentrations of salt, in the range of 0.2 to 0.5 M. Second, our simulation boxes are periodic, and limited in size, and therefore finite size effects are likely to play a role. To obtain a more accurate estimate of precise phase boundaries, Gibbs-ensemble simulations are a suitable choice, as demonstrated by several groups in the context of LLPS.19,31,34 However, such simulations are computationally rather demanding as they rely on Monte-Carlo moves, which is not trivial for polymer-based systems with near-atomic detail. Third, the exact transition point is rather sensitive to details of the force field. We noticed a shift of the transition point to higher salt concentration when using the final Martini 3.0 version instead of the beta release (Fig. S3†), which certainly improves the match with the experimental transition point. Keeping these limitations in mind, we conclude that our model captures the experimentally observed salt-dependency of the coacervation, at least at a semi-quantitative level.
1 mixtures of these polymers with Npol = 30, coacervation occurs in sodium chloride solutions with concentrations below 0.40 M.36Fig. 2A shows snapshots of the simulated systems and Fig. 2B and C polymer–polymer radial distribution functions (RDFs) from simulations with six different salt concentrations, both below and above this threshold. Two different processes can be observed: firstly, at all salt concentrations positive and negative polymers pair to form dimers. Fig. 2B shows this clearly in the intense first peaks of the pLys–pGlu RDFs at 0.5 nm for all these six salt concentrations, revealing direct contact between the oppositely charged polymers' beads. However, a different behavior is observed for polymers with identical charges, as shown for pGlu–pGlu RDFs (Fig. 2C). As expected, the first neighbor shell (0.5 nm) is almost completely excluded because of charge repulsion, but an enrichment of polymer at larger distances (>1 nm) is clearly observed for the simulations at lower salt concentration, indicative of a large-scale phase separation. Simulations with 0.36 M NaCl concentration only show a negligible enhancement of polymer density compared to the bulk, while with 0.6 and 0.9 M the polymer chains are fully dispersed. Together with the snapshots from the simulations (Fig. 2A), these RDFs show that phase separation into a polymer-dense and a polymer-deficient phase occurs at sodium chloride concentrations of 0.17, 0.21 and 0.25 M, but not at concentrations above 0.36 M. To quantify the salt concentration at which coacervation is observed in our simulations, we calculated the maximum peptide cluster size, normalized by the volume of the system. The results are shown in Fig. 2D. The maximum cluster size seems to decrease with increasing the salt concentration and above 0.36 M it levels off. Taking the inflection point of the maximum cluster size curve as a rough estimate (Fig. 2D), we conclude that, in our simulations, the transition from coacervation to non-coacervation occurs around 0.3 M NaCl concentration. It should be noted that the coacervate formation is a dynamic and reversible process: when additional salt (1.3 M) is added to the coacervate structure formed at 0.17 M sodium chloride solution, the polymers redissolve into pairs over time, as shown in Fig. S2.† Our estimate of the transition point is consistent with the experimental threshold of 0.4 M,30 although it is important to point out that a fair comparison between the experimental and simulated critical salt concentration is difficult, due to a number of reasons. First, the polymer concentrations used in the simulations are much higher than those used in the experiments, to keep the simulations tractable (otherwise mostly water–water interactions would be simulated). Potentially, the miscibility transition depends on the polymer concentration. Unfortunately, the extent of this effect is not known for the system under investigation, but experimental data for similar systems (pHis/pGlu complex coacervate) point to a limited effect.30 Similar to the polymer length, an increase of 2 to 10 times the polymer concentration seems to promote a shift to modestly higher concentrations of salt, in the range of 0.2 to 0.5 M. Second, our simulation boxes are periodic, and limited in size, and therefore finite size effects are likely to play a role. To obtain a more accurate estimate of precise phase boundaries, Gibbs-ensemble simulations are a suitable choice, as demonstrated by several groups in the context of LLPS.19,31,34 However, such simulations are computationally rather demanding as they rely on Monte-Carlo moves, which is not trivial for polymer-based systems with near-atomic detail. Third, the exact transition point is rather sensitive to details of the force field. We noticed a shift of the transition point to higher salt concentration when using the final Martini 3.0 version instead of the beta release (Fig. S3†), which certainly improves the match with the experimental transition point. Keeping these limitations in mind, we conclude that our model captures the experimentally observed salt-dependency of the coacervation, at least at a semi-quantitative level.
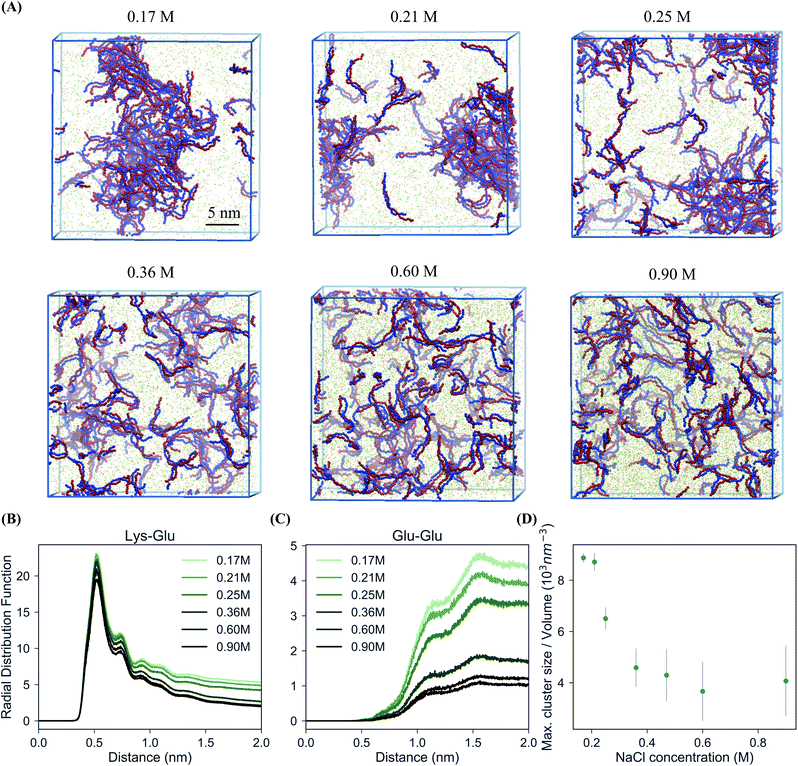 | ||
| Fig. 2 Salt-dependent coacervation. (A) Snapshots of the final state of 100 Lys30 and 100 Glu30 polymers after 20 μs of CG MD simulations at different salt concentrations. Color code is the same as in Fig. 1, water not shown. (B) pLys–pGlu RDFs at different salt concentrations. (C) pGlu–pGlu RDFs at different salt concentrations. (D) Maximum peptide cluster size at different salt concentrations normalized by the volume of each system (for a cut-off of 0.6 nm, which is the largest distance to be considered as a cluster). | ||
To exemplify the effect of polymer concentration to some extent, we performed additional simulations at varying polymer/water weight ratio. We found that polymer concentration did not influence the coacervation as strongly as salt concentration. Simulations with 10, 50, 100 and 150 polymer chains of each charge (0.5–8% w/w) with 0.17 M salt concentration show aggregation in each case (except for the lowest concentration), with the polymer-rich phase taking up a considerable part of the simulation box at the highest polymer concentration (Fig. S4†). Priftis et al. show the formation of coacervate droplets from 0.1 wt% total polymer concentration. With further increase of the total polymer concentration more complex is formed due to the increase of the available charged sites.36
2.2 Ion partitioning and hydration of the coacervate phase
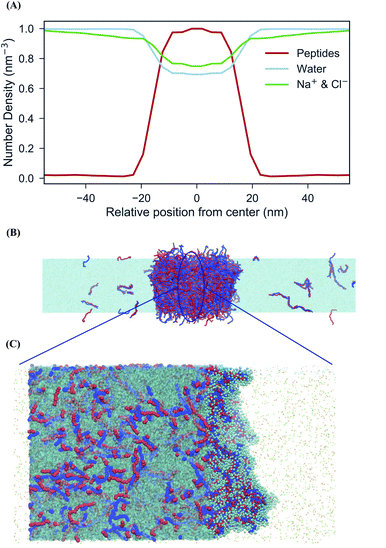
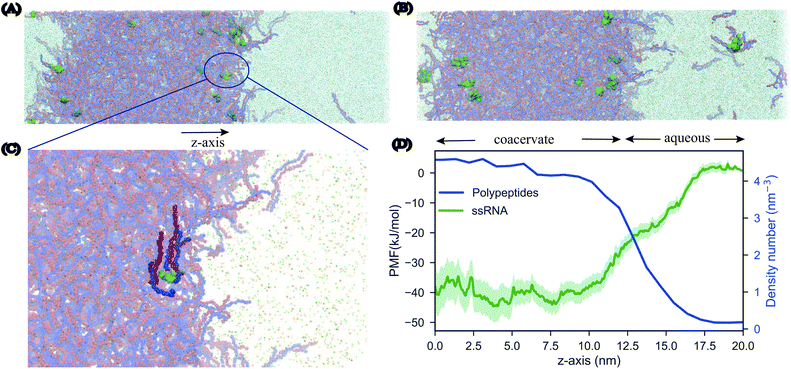
An important driving force behind coacervation is the release of small counter-ions that were initially “bound” to the polymers, although also polymer–polymer contacts play a role.46–48 The MD simulations show a rapid decrease of polymer-ion contacts after complexation compared to the beginning of the simulation where polymers are randomly dispersed, as seen in polymer-ion RDFs (Fig. S5†). While the classical analytical theories predict that ions will preferentially stay in the coacervate phase when they are released from the polymers by complexation, recent discoveries suggest that ions dissolve into the polymer-dilute phase, ascribing the difference to the problems of Voorn–Overbeek-based theories at high polymer and salt concentrations, and the lack of molecular details such as excluded volume effects and the reduced entropy gain from ions release at the polymer ends.47,49,50 We have direct access to the relative concentrations of all components between the two phases. A straightforward way to analyze this data is by computing the densities of the components across the system. To have a clear definition of the two phases, we performed additional simulations of an extended system (see Methods for details). The resulting densities for the peptides can be observed in the density profiles for the peptides, ions and water in the system of 0.17 M salt concentration, as seen in Fig. 3. Although the coacervate phase contains a large amount of water molecules and ions, the ion concentration in the bulk phase is higher than in the coacervate phase which is in line with experimental as well as with results from all-atom simulations.19,30 Note that the density of water inside the coacervate phase is reduced even more compared to the density of ions (Fig. 3A). Therefore, the effective ion concentration (amount of ions per water) is actually increased in this region.Another interesting observation is the broad width of the interface between the condensate and the aqueous solution. The maximum bulk density of the condensate is only reached at the very center of the phase, implying an interfacial width of around 20 nm. This suggests a low surface tension (γ) between the two phases. To quantify this, we computed the surface tension for the extended system based on the pressure differences between the lateral and perpendicular directions (see Methods). Although this is a slowly converging property, we observe convergence to a value of ∼3 bar nm on a time scale of 10 μs (Fig. S6†). This low surface tension is in reasonable agreement with experimental findings performed for the same system with 0.16 M NaCl concentration which report a value of γ = 7 bar nm.51
2.3 Water and peptide diffusion
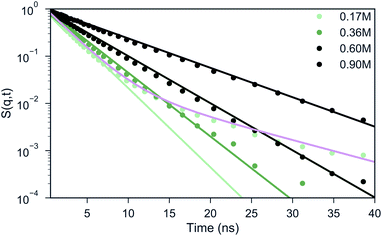
Experimental studies employing ODNP52 have reported a slowing down of water from D = 2.3 × 10−9 m2 s−1 in bulk water to ∼1.3 × 10−9 m2 s−1 at the surface of uncomplexed polymer and to D ∼ 0.25 × 10−9 m2 s−1 inside a coacervate phase of polyaspartate with poly(vinylimidazole).52 Although it is difficult to directly compare diffusion coefficients in CG MD simulations to experiments, due to the smoothness of the CG potential energy landscape,38,53 it would be interesting to see whether a similar qualitative slowdown can be observed in our simulations as well. A standard way of computing the diffusive properties is via the mean square displacement (MSD) of the water beads.In a heterogeneous system, however, this analysis is problematic because of the computation of the particle average which mixes the dynamics of particles in different environments, hence, the MSD only offers an average behavior. An alternative pathway to gain insight into the particle dynamics is the computation of the Incoherent Scattering Function (ISF) that has been frequently studied in the field of supercooled liquids.54,55 The ISF contains information on how long a particle is correlated to a certain distance around its initial position. In case of homogeneous diffusion, the ISF decays exponentially, where the time scale is related to the diffusion coefficient.54,56 One can observe from Fig. 4 that for a salt concentration of 0.60 and 0.90 M, the shape of the curve can be reasonably well described by a single exponential decay. For the systems with 0.17 and 0.36 M salt concentration, a single exponential function (light green) clearly fails to describe the shape of the ISF. Instead, two distinct regimes can be observed: a fast decay that corresponds to the water beads in the bulk and a slow decay that represents the water beads in the coacervate. In order to extract the diffusion coefficients from the curve, we fitted the data points in these cases with a weighted sum of two exponential functions (illustrated with the pink line for 0.17 M salt concentration in Fig. 4), considering ISF curves obtained at different wave vectors q (Fig. S7†). The resulting diffusion coefficients are shown in Table 1. The decrease in diffusion coefficients upon increasing salt concentration can be rationalized by the increase of the salt concentration. This was proven by running simulations in pure water/salt mixtures in 0.17, 0.36, 0.60 and 0.90 M NaCl concentration (Table 1), which show similar diffusion coefficients as observed in the bulk phase of the coacervate systems. Within the coacervate phase, water diffusion is observed at a significantly reduced speed, about 6 times slower than in the bulk, in qualitative agreement with the experimentally observed slow-down.52 The reduced speed of the water molecules in the coacervate phase with respect to the bulk phase was further validated by calculating the short-time MSD of selected water molecules inside the coacervate and inside the bulk phase over a period of 1 ns simulation time for the biphasic system with 0.17 M NaCl concentration (Fig. S8B–D†). From the MSD analysis we found the diffusion coefficients for the bulk and coacervate phase to be Dbulk = (1.60 ± 0.10) × 10−9 m2 s−1 and Dcoac = (0.43 ± 0.04) × 10−9 m2 s−1 respectively (Fig. S8A†), consistent with the results reported in Table 1 given the approximate nature of the MSD analysis.
| Water–NaCl–peptides | Water–NaCl | ||
|---|---|---|---|
| C NaCl | D bulk | D coac | D bulk |
| 0.17 | 1.56 ± 0.01 | 0.26 ± 0.01 | 1.71 ± 0.01 |
| 0.36 | 1.47 ± 0.01 | 0.24 ± 0.02 | 1.36 ± 0.01 |
| 0.60 | 0.86 ± 0.05 | — | 0.96 ± 0.01 |
| 0.90 | 0.56 ± 0.02 | — | 0.62 ± 0.01 |
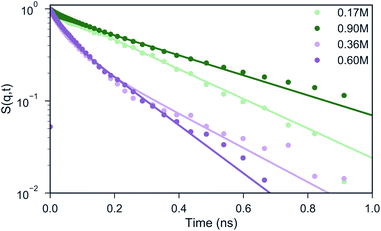
An interesting question is to what extent polymers inside condensates still display liquid-like properties. In order to gain insight into the dynamics of the peptides in our systems, we calculate the ISF pGlu in different salt concentrations and for different wave vectors q. As mentioned earlier, the ISF should decay exponentially in the case of a homogeneous diffusion. From Fig. 5 one can observe that the systems with 0.17 and 0.90 M NaCl concentration, the shape of the curves can be reasonably well described by a single exponential decay. In these systems most of the peptides are either in the coacervate phase (system with 0.17 M) or totally dissolved (system with 0.90 M), in consequence they will show a homogeneous diffusion. However, for the systems with 0.36 and 0.60 M salt concentration, a single exponential function fails to describe the shape of the ISF. Instead, two distinct regimes can be observed: a fast decay that corresponds to the peptides that are dissolved in the bulk and a slow decay that represents the peptides that are part of transient peptide clusters. In order to extract the diffusion coefficients from the curves, we fitted the data points for 0.17 and 0.90 M NaCl concentration with an exponential function (illustrated with the green lines in Fig. 5) and the data points for 0.36, 0.60 M with a weighted sum of two exponential functions (illustrated with the pink lines in Fig. 5), considering ISF curves obtained at different wave vectors q. For q value of ∼0.64 (i.e. a length scale lower than 2.8 particle diameters), we find the diffusion coefficients to plateau at values shown in Table 2. Experimental studies employing proton pulsed field gradient NMR have reported diffusion coefficients of poly(diallyldimethylammonium chloride) to be of the order of 10−12 m2 s−1 to 10−14 m2 s−1 inside a coacervate phase of poly(diallyldimethylammonium chloride) and the protein bovine serum albumin.57 Our peptides diffuse at the faster end of this range, and clearly are in a liquid-like state. The liquid properties and the dynamics of the polypeptides in our systems can be also seen in the Movie S1.†Table 2 shows that poly-Glu peptides diffuse less when they are in the coacervate phase, which is the system with 0.17 M NaCl concentration. By increasing the salt concentration the peptides start to dissolve, therefore the diffusion coefficient of pGlu increases. A much faster component is now also present due to peptides that diffuse as isolated entities. In case of the system with 0.9 M, which is homogeneous (Movie S2†), the dynamics is slowed down due to the formation of a gel-like network at the high peptide concentrations used in this study.
| C NaCl | D 1(pGlu) | D 2(pGlu) |
|---|---|---|
| 0.17 | 27 ± 1 | — |
| 0.36 | 39 ± 2 | 325 ± 7 |
| 0.60 | 38 ± 2 | 355 ± 6 |
| 0.90 | 33 ± 1 | — |
2.4 Partitioning of RNA
According to the RNA world hypothesis,58 RNA, with its ability to self-replicate, could have functioned as the primary genetic material in primitive cells and coacervate systems could have provided the necessary environment for the RNA self-replication. Although this hypothesis has been a popular idea in the origin of life theory59,60 there have been studies that oppose to this idea arguing that the RNA is too complex, unstable and that is difficult for long chains to catalyze chemical reactions.61 Nevertheless, over the years many experimental studies62,63 have shown that membrane-less organelles support RNA catalysis and concentrate oligonucleotides.In order to study the partitioning of the RNA polyelectrolytes, we performed MD simulations of 10 μs of a phase separated pLys/pGlu coacervate system in the presence of single stranded RNA (ssRNA) molecules. We prepared three different systems, differing in the length of the ssRNA: 3-, 5-, or 10-mer, with 20 copies present in each case. All three systems were simulated at two different salt concentrations, 0.17 M and 0.25 M. Starting from randomized placements of the ssRNA in the solution phase, we observed the partitioning of the 20 oligonucleotides into the coacervate phase, at first on the surface and as the simulations proceeded, further inside the coacervate system. The movement of ssRNA into the coacervate phase is most evident for the system with 0.25 M salt, which can be rationalized by the closer vicinity to the phase transition point (estimated at 0.3 M, see above) implying a diffuser interface. Snapshots of the final configurations for the 3-mer ssRNA are shown in Fig. 6, similar results are obtained for the 5-mer and 10-mer ssRNA molecules (Fig. S9†), showing the preference of the ssRNA for the coacervate phase in line with the experimental observations on related systems.62 It should be noted that the systems have not reached full equilibrium. The slow dynamics of the polymers (see above) makes the diffusion of ssRNA in and out of the condensate a slow process. Experimental studies show that exchange of RNA molecules between coacervate droplets occurs on the second time scale.62 This phenomenon cannot be captured with our simulations which are in the order of microseconds.
In order to further quantify the extent to which the ssRNA molecules prefer the coacervate phase or perhaps the interface, we performed umbrella sampling simulations to obtain the free energy of transfer of an RNA molecule from the aqueous phase to the coacervate phase. The resulting profile (Fig. 6C) shows that the transfer of the RNA molecule to coacervate phase is more favorable than the molecule remaining in the aqueous phase by about 40 kJ mol−1. Furthermore, the broad interface does not show a minimum free energy demonstrating that the oligonucleotides do not remain localized at the surface of the phase but have a stronger tendency to move within its interiors.
3 Conclusions
To conclude, we show the validity of coarse-grain MD simulations in studying coacervate dynamics with explicit solvent, ions and polyelectrolytes. Using the Martini model we built a coacervate system which consists of two polypeptides, poly-lysine and poly-glutamate, which have a higher affinity with each other than they do with the solution. This difference in affinities separates them from the aqueous phase through a phenomenon known as liquid–liquid phase separation.Our results demonstrate that, using the Martini 3 force field, we can capture the experimental trends of this complex coacervate system. RDFs and cluster analysis, show that the coacervate formation is strongly affected by the ionic strength. In particular, we observe coacervation at a lower salt concentration than the experiments, but still in semi-quantitative agreement with the phase diagram.
Furthermore, we revealed that the coacervate phase remains well hydrated and ions are depleted from the coacervate phase. Remarkably, the interface between the condensate and surrounding solution is found to be very broad, of the order of 20 nm, with a low surface tension of γ = 3 bar nm consistent with experimental studies.
Additionally, our analysis showed that peptides, water and ions diffuse freely in these complex coacervate systems. A systematic analysis of the diffusion of water molecules, both inside the coacervate and the aqueous phase reveal that the diffusion coefficient for the bulk water is almost one order of magnitude larger than the diffusion coefficient of the water molecules inside the coacervate phase. This trend agrees with the reported experimental findings.
Increasing evidence suggest the localization of biomolecules, and especially nucleic acids, within coacervate droplets. In an attempt to study this phenomenon, we performed 10 μs simulations of single strand RNA molecules in biphasic systems with 0.17 M and 0.25 M NaCl concentration. Our simulations show the partitioning of all RNA molecules inside the coacervate phase. This is also evident from free energy calculations which signify a clear preference of the oligonucleotides for the interiors of the coacervate phase.
Taken together, our results demonstrate that we can capture the experimental behavior of the poly-lysine and poly-glutamate coacervate system with the Martini 3 force field. Consequently, the present explicit-solvent coarse-grain model of complex coacervates can be extended to gain physical insight on the mechanisms that drive the formation of membraneless organelles within cells and provide near-atomic resolution on the structural and dynamic organisation inside the coacervate phase.
4 Computational methods
4.1 System setup
Coarse-grain molecular dynamics simulations were conducted with the “open beta” version of the Martini 3.0 CG force field35,45 using the GROMACS 2016.3 software.64 Lys30 and Glu30 CG polypeptides were generated using the martinize.py script included in the Martini 3.0 beta release, using an extended sheet secondary structure backbone, generating harmonic (“elastic”) bonds between (1,3) and (1,4) backbone beads, with an optimized force constant of 1250 kJ nm−2. This backbone structure was chosen based on experimental and theoretical findings were a β-sheet structure was reported for P(L-lysine)/P(L-glutamate) systems.37 The latest version of the Martini model has also been used to reproduce the conformation of disordered regions in multi-domain proteins65 and has been successfully applied to capture allosteric conformational protein changes as well as protein–ligand binding events.66–68 All amino acid side chains, and the C- and N-terminal beads have a full ±1e charge. It should be noted that the same resolution with the previous versions of the Martini force field was used, albeit avoiding over-mapping for lysine.45 A selection of the GROMACS topology files of Martini models that were used in this study are available to download at our web portal http://cgmartini.nl. For a number of selected systems, additional simulations with the final Martini 3.0 release were also performed (Fig. S3†).Equal numbers of polymers (100 each unless specified otherwise, representing ∼5–7% w/w polymer) were randomly dispersed in a 30 × 30 × 30 nm3 periodic simulation box and solvated using normal Martini water beads. The required number of water beads was replaced with charged TQd and TQa ion particles to represent Na+ and Cl−, respectively. After steepest descent minimization, systems were equilibrated for 10 ns using a 10 fs time step and the Berendsen barostat. 20 μs production runs using a 20 fs timestep were carried out in the NPT ensemble, keeping temperature at 298 K using the v-rescale thermostat69 (τT = 1.0 ps−1) and pressure at 1.0 bar using the isotropic Parrinello–Rahman pressure coupling70 (τP = 12 ps−1). In accordance with the typical settings associated with the Martini force field, electrostatic interactions were treated using a reaction field approach (εrf = 15 beyond the 1.1 nm cut-off) and a shifted van der Waals potential, cut-off at 1.1 nm with the Verlet cut-off scheme.71 The neighbor list was updated every 20 steps and coordinates were saved every 200 ps. Reported salt concentrations are based on the final number of the water molecules and are calculated as C(Na+) = C(Cl−) = (number of ions × 55 mol L−1)/(final number of water beads × 4), small changes in polymer concentration are not deemed significant for the results. In Martini model, one water bead accounts for four water molecules.
In addition, extended systems were generated to compute the surface tension and measure density profiles by constructing a biphasic system of 600 Lys30 and 600 Glu30 polyelectrolyte chains in a 24 × 24 × 176 nm3 simulation box. In particular, accumulative average surface tension was calculated every 200 ns over a 16 μs length trajectory using the GROMACS tool gmx energy.64 This system requires to be equilibrated for long time (around 9 μs) since the surface tension shows huge fluctuations in the beginning of the equilibration but also after the equilibration. Negative values for the surface tension could mean that water tunnels are formed in the coacervate phase which connect the two sides of the aqueous phase. Low positive values for the surface tension indicate that the coacervate phase consists of a large amount of water molecules which form water bubbles inside the phase. RNA partitioning simulations were performed in a 22 × 22 × 74 nm3 simulation box consisting of 581 Lys30, 581 Glu30 polyelectrolyte chains and 20 ss-RNA molecules, whose bonded parameters were based on Uusitalo et al.41 The ssRNA molecules are composed by 3, 5 or 10 monomers of uracil.
4.2 Analysis details
Snapshots of pLys/pGlu systems were obtained using the VMD software.72 Normalized radial distribution functions were calculated using the GROMACS tool gmx rdf64 and by averaging distances from any polymer backbone atom to other atoms (polymer, water or ion) not belonging to the same polymer over the last 50 ns of the trajectory (unless stated otherwise). Both maximum size and number of clusters were computed using the GROMACS tool gmx clustsize,64 using a cut-off of 0.6 nm (which is the largest distance to be considered in a cluster) and after the equilibration (Fig. S1A and B†), during the last 8 μs of 20 μs trajectories. The density profile was computed using the tool gmx energy64 and was normalized by the maximum density of each component. The incoherent scattering function for one dimension was computed55via S(q,t) = 〈cos(q[x(t) − x(0)])〉 where q denotes a wave vector that defines the length scale on which the particle dynamic is probed. In case of homogeneous diffusion, the ISF decays exponentially, where the time scale τq is related to the diffusion coefficient54,56Sdiff(q,t) = exp(−t/τq) with τq = 1/(q2D), the total ISF can be regarded as a superposition of ISF with different τq that can be described via the previous equation.Author contributions
S. J. M., P. W. J. M. F. and P. C. T. S. designed the project. M. T., P. W. J. M. F. and P. C. T. S. performed the simulations. M. T., P. C. T. S. and C. F. E. S. analysed the data. M. T. wrote the manuscript. All the authors discussed the results and revised the final version of the text.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Dr Ignacio Faustino Plo for his contributions in the preliminary Martini 3 model of the RNA molecule. P. Frederix acknowledges support from the Netherlands Organisation for Scientific Research (Veni, 722.015.005). This research is supported by the “BaSyC-Building a Synthetic Cell” Gravitation grant (024.003.019) of the Netherlands Ministry of Education, Culture, and Science (OCW) and the Netherlands Organization for Scientific Research (NWO/OCW).Notes and references
- H. G. Bungenberg de Jong and H. R. Kruyt, Kolloid-Z., 1930, 50, 39–48 CrossRef.
- A. Melnyk, J. Namieśnik and L. Wolska, TrAC, Trends Anal. Chem., 2015, 71, 282–292 CrossRef CAS.
- W. C. Blocher and S. L. Perry, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2017, 9, e1442 Search PubMed.
- D. Zwicker, R. Seyboldt, C. A. Weber, A. A. Hyman and F. Jülicher, Nat. Phys., 2017, 13, 408–413 Search PubMed.
- C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324, 1729–1732 CrossRef CAS PubMed.
- N. Wolf, J. Priess and D. Hirsh, J. Embryol. Exp. Morphol., 1983, 297–306 CAS.
- C. P. Brangwynne, T. J. Mitchison and A. A. Hyman, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4334–4339 CrossRef CAS PubMed.
- A. R. Strom, A. V. Emelyanov, M. Mir, D. V. Fyodorov, X. Darzacq and G. H. Karpen, Nature, 2017, 547, 241–245 CrossRef CAS PubMed.
- S. F. Banani, H. O. Lee, A. A. Hyman and M. K. Rosen, Nat. Rev. Mol. Cell Biol., 2017, 18, 285–298 CrossRef CAS PubMed.
- C. P. Brangwynne, P. Tompa and R. V. Pappu, Nat. Phys., 2015, 11, 899–904 Search PubMed.
- J. A. Riback, L. Zhu, M. C. Ferrolino, M. Tolbert, D. M. Mitrea, D. W. Sanders, M.-T. Wei, R. W. Kriwacki and C. P. Brangwynne, Nature, 2020, 581, 209–214 CrossRef CAS PubMed.
- S. K. Goetz and J. Mahamid, Dev. Cell, 2020, 55, 97–107 CrossRef CAS PubMed.
- G. L. Dignon, R. B. Best and J. Mittal, Annu. Rev. Phys. Chem., 2020, 71, 53–75 CrossRef CAS PubMed.
- Z. Benayad, S. von Bülow, L. S. Stelzl and G. Hummer, J. Chem. Theory Comput., 2021, 17, 525–537 CrossRef CAS.
- J. H. Ortony, D. S. Hwang, J. M. Franck, J. H. Waite and S. Han, Biomacromolecules, 2013, 14, 1395–1402 CrossRef CAS PubMed.
- J. Ziebarth and Y. Wang, Biophys. J., 2009, 97, 1971–1983 CrossRef CAS PubMed.
- K. Q. Hoffmann, S. L. Perry, L. Leon, D. Priftis, M. Tirrell and J. J. de Pablo, Soft Matter, 2015, 11, 1525–1538 RSC.
- A. N. Singh and A. Yethiraj, J. Phys. Chem. B, 2020, 124, 1285–1292 CrossRef CAS PubMed.
- D. G. Mintis and V. G. Mavrantzas, Macromolecules, 2020, 53, 7618–7634 CrossRef CAS.
- L. Chang, T. K. Lytle, M. Radhakrishna, J. J. Madinya, J. Vélez, C. E. Sing and S. L. Perry, Nat. Commun., 2017, 8, 1273 CrossRef PubMed.
- T. K. Lytle, A. J. Salazar and C. E. Sing, J. Chem. Phys., 2018, 149, 163315 CrossRef PubMed.
- J. J. Cerdà, B. Qiao and C. Holm, Soft Matter, 2009, 5, 4412–4425 RSC.
- M. Vögele, C. Holm and J. Smiatek, J. Chem. Phys., 2015, 143, 243151 CrossRef PubMed.
- P. Batys, Y. Zhang, J. L. Lutkenhaus and M. Sammalkorpi, Macromolecules, 2018, 51, 8268–8277 CrossRef CAS PubMed.
- W. Zheng, G. L. Dignon, N. Jovic, X. Xu, R. M. Regy, N. L. Fawzi, Y. C. Kim, R. B. Best and J. Mittal, J. Phys. Chem. B, 2020, 124, 11671–11679 CrossRef CAS PubMed.
- K. J. Bari and D. D. Prakashchand, J. Phys. Chem. Lett., 2021, 12, 1644–1656 CrossRef CAS PubMed.
- H. I. Ingólfsson, C. A. Lopez, J. J. Uusitalo, D. H. de Jong, S. M. Gopal, X. Periole and S. J. Marrink, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 225–248 Search PubMed.
- J. C. Shillcock, M. Brochut, E. Chénais and J. H. Ipsen, bioRxiv, 2020 DOI:10.1101/2019.12.11.873133.
- M. Lísal, K. Šindelka, L. Suchá, Z. Limpouchová and K. Procházka, Polym. Sci., Ser. C, 2017, 59, 77–101 CrossRef.
- L. Li, S. Srivastava, M. Andreev, A. B. Marciel, J. J. de Pablo and M. V. Tirrell, Macromolecules, 2018, 51, 2988–2995 CrossRef CAS.
- G. L. Dignon, W. Zheng, Y. C. Kim and J. Mittal, ACS Cent. Sci., 2019, 5, 821–830 CAS.
- T. J. Welsh, G. Krainer, J. R. Espinosa, J. A. Joseph, A. Sridhar, M. Jahnel, W. E. Arter, K. L. Saar, S. Alberti, R. Collepardo-Guevara and T. P. Knowles, bioRxiv, 2020 DOI:10.1101/2020.04.20.04791.
- H. Jafarinia, E. van der Giessen and P. R. Onck, Biophys. J., 2020, 119, 843–851 CrossRef CAS PubMed.
- G. L. Dignon, W. Zheng, R. B. Best, Y. C. Kim and J. Mittal, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9929–9934 CrossRef CAS PubMed.
- P. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, J. Khan, H. M. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Nat. Methods, 2021, 382–388 CrossRef CAS.
- D. Priftis and M. Tirrell, Soft Matter, 2012, 8, 9396–9405 RSC.
- S. L. Perry, L. Leon, K. Q. Hoffmann, M. J. Kade, D. Priftis, K. A. Black, D. Wong, R. A. Klein, C. F. Pierce Iii, K. O. Margossian, J. K. Whitmer, J. Qin, J. J. de Pablo and M. Tirrell, Nat. Commun., 2015, 6, 6052 CrossRef CAS PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem., 2007, 111, 7812–7824 CrossRef CAS PubMed.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697 CrossRef CAS PubMed.
- C. A. López, A. J. Rzepiela, A. H. de Vries, L. Dijkhuizen, P. H. Hünenberger and S. J. Marrink, J. Chem. Theory Comput., 2009, 5, 3195–3210 CrossRef.
- J. J. Uusitalo, H. I. Ingólfsson, S. J. Marrink and I. Faustino, Biophys. J., 2017, 113, 246–256 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- L. I. Vazquez-Salazar, M. Selle, A. H. de Vries, S. J. Marrink and P. C. T. Souza, Green Chem., 2020, 22, 7376–7386 RSC.
- F. Grünewald, G. Rossi, A. H. de Vries, S. J. Marrink and L. Monticelli, J. Phys. Chem. B, 2018, 122, 7436–7449 CrossRef.
- P. C. T. Souza, http://www.cgmartini.nl/index.php/martini3beta, 31 July 2018.
- C. E. Sing, Adv. Colloid Interface Sci., 2017, 239, 2–16 CrossRef CAS.
- T. K. Lytle and C. E. Sing, Mol. Syst. Des. Eng., 2018, 3, 183–196 RSC.
- A. Salehi and R. G. Larson, Macromolecules, 2016, 49, 9706–9719 CrossRef CAS.
- T. K. Lytle and C. E. Sing, Soft Matter, 2017, 13, 7001–7012 RSC.
- M. Radhakrishna, K. Basu, Y. Liu, R. Shamsi, S. L. Perry and C. E. Sing, Macromolecules, 2017, 50, 3030–3037 CrossRef CAS.
- D. Priftis, R. Farina and M. Tirrell, Langmuir, 2012, 28, 8721–8729 CrossRef CAS.
- R. Kausik, A. Srivastava, P. A. Korevaar, G. Stucky, J. H. Waite and S. Han, Macromolecules, 2010, 43, 3122 CrossRef CAS.
- I. N. Tsimpanogiannis, O. A. Moultos, L. F. M. Franco, M. B. d. M. Spera, M. Erdös and I. G. Economou, Mol. Simul., 2019, 45, 425–453 CrossRef CAS.
- F. Ritort and P. Sollich, Adv. Phys., 2003, 52, 219–342 CrossRef.
- A. Heuer, J. Phys.: Condens. Matter, 2008, 20, 373101 CrossRef.
- L. Berthier, D. Chandler and J. P. Garrahan, Europhys. Lett., 2005, 69, 320–326 CrossRef CAS.
- A. R. Menjoge, A. B. Kayitmazer, P. L. Dubin, W. Jaeger and S. Vasenkov, J. Phys. Chem. B, 2008, 112, 4961–4966 CrossRef CAS.
- M. Neveu, H.-J. Kim and S. A. Benner, Astrobiology, 2013, 13, 391–403 CrossRef.
- A. I. Oparin and S. Morgulis, The Origin of Life, Macmillan, New York, USA, 1938 Search PubMed.
- O. Leslie E, Crit. Rev. Biochem. Mol. Biol., 2004, 39, 99–123 CrossRef.
- H. S. Bernhardt, Biol. Direct, 2012, 7, 23 CrossRef CAS PubMed.
- T. Z. Jia, C. Hentrich and J. W. Szostak, Origins Life Evol. Biospheres, 2014, 44, 1–12 CrossRef CAS PubMed.
- T. Nott, T. Craggs and A. Baldwin, Nat. Chem., 2016, 8, 569–575 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- A. H. Larsen, Y. Wang, S. Bottaro, S. Grudinin, L. Arleth and K. Lindorff-Larsen, PLoS Comput. Biol., 2020, 16, 1–29 CrossRef PubMed.
- P. C. T. Souza, S. Thallmair, P. Conflitti, C. Ramírez Palacios, R. Alessandri, S. Raniolo, V. Limongelli and S. J. Marrink, Nat. Commun., 2020, 11, 3714 CrossRef CAS PubMed.
- I. Faustino, H. Abdizadeh, P. C. T. Souza, A. Jeucken, W. K. Stanek, A. Guskov, D. J. Slotboom and S. J. Marrink, Nat. Commun., 2020, 11, 1763 CrossRef CAS PubMed.
- P. C. T. Souza, S. Thallmair, S. J. Marrink and R. Mera-Adasme, J. Phys. Chem. Lett., 2019, 10, 7740–7744 CrossRef CAS PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- D. H. de Jong, S. Baoukina, H. I. Ingólfsson and S. J. Marrink, Comput. Phys. Commun., 2016, 199, 1–7 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc00374g |
| This journal is © The Royal Society of Chemistry 2021 |