Open Access Article
Open Access ArticleEffects of applied voltage on water at a gold electrode interface from ab initio molecular dynamics†
Zachary K.
Goldsmith
 *,
Marcos F.
Calegari Andrade
*,
Marcos F.
Calegari Andrade
 and
Annabella
Selloni
and
Annabella
Selloni
 *
*
Department of Chemistry, Princeton University, Princeton, NJ 08544, USA. E-mail: zkg@princeton.edu; aselloni@princeton.edu
First published on 18th March 2021
Abstract
Electrode–water interfaces under voltage bias demonstrate anomalous electrostatic and structural properties that are influential in their catalytic and technological applications. Mean-field and empirical models of the electrical double layer (EDL) that forms in response to an applied potential do not capture the heterogeneity that polarizable, liquid-phase water molecules engender. To illustrate the inhomogeneous nature of the electrochemical interface, Born–Oppenheimer ab initio molecular dynamics calculations of electrified Au(111) slabs interfaced with liquid water were performed using a combined explicit–implicit solvent approach. The excess charges localized on the model electrode were held constant and the electrode potentials were computed at frequent simulation times. The electrode potential in each trajectory fluctuated with changes in the atomic structure, and the trajectory-averaged potentials converged and yielded a physically reasonable differential capacitance for the system. The effects of the average applied voltages, both positive and negative, on the structural, hydrogen bonding, dynamical, and vibrational properties of water were characterized and compared to literature where applicable. Controlled-potential simulations of the interfacial solvent dynamics provide a framework for further investigation of more complex or reactive species in the EDL and broadly for understanding electrochemical interfaces in situ.
1. Introduction
Aqueous electrochemical interfaces are central to heterogeneous catalysis1,2 and emerging energy conversion technologies.3–5 Electrical double layers (EDL) of solvated ions notably form at such interfaces, however, water molecules will predominate the immediate interface even for concentrated electrolyte solutions6 and are known to exhibit starkly different properties and reactivity than water in the bulk liquid.7 It is therefore imperative to both characterize water at electrochemical interfaces and develop the computational tools for doing so as a step towards modeling more sophisticated EDL environments.8Experimental studies of the structure of the electrode–water interface, often by X-ray absorption spectroscopy (XAS), have underscored its anomalous structure and hydrogen bonding patterns.9,10 Specifically, water forms at least one structural layer against common electrodes such as Ag and Au with densities higher than bulk and with dangling OH bonds at both positive and negative voltage biases.11 Directly studying electrochemical interfaces in situ has been largely accomplished via surface-specific vibrational spectroscopies such as surface-enhanced infrared absorption (SEIRAS),12,13 plasmon-enhanced Raman spectroscopy,14 and sum-frequency generation (SFG).15,16 These techniques have elucidated dependencies of the vibrational spectra of water at the interface on the voltage applied, consequences of the strong electric fields in the EDL.17 Nonetheless, experimental probes of the structure and composition of the EDL are challenging to perform, incomplete in scope, and would benefit from improvements in atomistic modeling.
Realistic simulation of the EDL and processes therein is an outstanding challenge for theory and computation as well. Classical MD and Monte Carlo simulations of water at electrified surfaces18–20 have been instructive but are limited in their microscopic resolution. Notably, empirical approaches lack instantaneous polarization of species in the interfacial electric field that may give way to novel properties and/or reactivity. Quantum chemical simulations, most practically density functional theory (DFT), are capable of describing molecular polarization and bond-breaking, albeit at greater computational cost. DFT with a posteriori corrections for the thermodynamic effects of the electrode potential21,22 have been useful in elaborating catalytic mechanisms, but neglect specific effects of the strong, induced electric fields at the interface.
Recent advances in periodic DFT with continuum solvation,23–26 self-consistent analytical EDL models,27,28 as well as formally grand-canonical approaches29,30 have enabled studies of more sophisticated systems that include a controlled potential. Applications of such implicit and/or hybrid solvation methods have included potentiostatic simulations along key nuclear coordinates associated with heterogeneous catalysis31–34 and surface-enhanced spectroscopy.35,36 Dynamical ab initio studies including voltage bias have mostly considered just the electrode37 or limited numbers of molecules38–40 and/or monolayers.14,41–44
In this work, we performed ab initio molecular dynamics of water at a Au electrode interface with fixed amounts of charge on the Au electrode as a means of modulating the electrode potential. The electrode potentials were measured at frequent times for each simulation and their converged average values yielded a physically reasonable differential capacitance for the system. The recovery of the system's electronic properties enabled analyses of the structure and dynamics of interfacial water under quantifiable potentials. In particular, we elucidated the effect of voltage on the density of water with respect to surface normal as well as the characteristic orientations of water molecules near the electrode as a function of the voltage bias. Furthermore, our computed vibrational densities of states of the interfacial water under bias corroborated phenomena previously reported by surface-enhanced spectroscopies. Moreover, we realized ab initio-quality simulations of an electrode under quantifiable voltage biases in contact with several layers of explicit solvent, a long outstanding benchmark for computation. We anticipate that atomistic modeling of electrochemical interfaces will be a powerful tool for understanding how chemical mechanisms are shaped by the polarization and statistical dynamics of the EDL.
2. Methods
2.1 Computational system
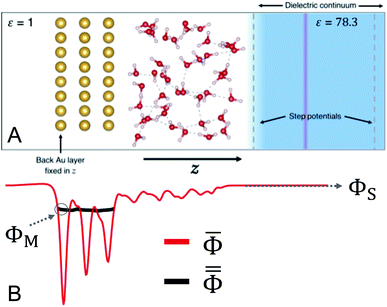
We devised a model system that was small enough to enable several AIMD trajectories while maintaining the essential physical chemistry of both phases at the interface. In addition, Au(111)/water was chosen so that no faradaic charge transfer would occur on the timescale of the simulations, maintaining our focus on the interfacial system near equilibrium. The lack of faradaic charge transfer furthermore allowed for the constant charge ensemble employed to best approximate that of a constant potential,45 which is the more practical experimental condition. The 3D-periodic computational unit cell was therefore comprised of a 4 × 4 × 3 Au(111) slab (48 Au atoms) interfaced with 56 molecules of water. The surface-parallel cell dimensions as determined by the Au(111) slab's size were approximately 10.2 Å × 11.8 Å and the total height of the orthorhombic cell was 36 Å. The computational cell is depicted in Fig. 1.The inactive back side of the Au(111) slab was in contact with vacuum (ε = 1) and the surface atoms on this side were held fixed in the direction perpendicular to the surface (z). A region of dielectric continuum representative of bulk water (ε = 78.3) was imposed beyond the region of explicit water molecules. This hybrid explicit/implicit approach enabled us to use a smaller system in expensive electronic structure calculations than a fully explicit system. More critically, this hybrid approach made it possible to establish both a region of “bulk solution” and a vacuum on the inactive side of the Au slab. The presence of the vacuum ensured the selective localization of excess charge at the interface with water.33 The continuum solvent was included using the Environ24,46 plug-in to Quantum-ESPRESSO,47,48 which solves the Poisson equation for the dielectric continuum in contact with the atomistic system self-consistently with the Kohn–Sham equation. Specifically, we employed a “solvent-aware”49 implementation of the self-consistent continuum solvation method24 and solved the relevant Poisson equation using periodic boundary conditions only in the surface-parallel dimensions to avoid solvation interactions between unit cells. A plane of charge equal and opposite that on the electrode was positioned within the region of implicit water to maintain the overall neutrality of the periodic cell. In addition, a dipole correction was employed in the vacant region near the boundary of the cell50 to negate spurious electrostatic interactions via periodicity.
Additionally, a planar step function potential51 was positioned at a distance from the Au surface that ensured a total density of 1 g mL−1 of the 56 water molecules. The step function, which in practice was error function-shaped, had a height of 0.25 Ry. To maintain 3D periodicity, this region was terminated near the top of the unit cell and beyond the position of the counter-charge plane by a step function of equal size and opposite directionality. These features are illustrated in Fig. 1.
2.2 Ab initio molecular dynamics calculations
We performed DFT-based Born–Oppenheimer molecular dynamics (BOMD) trajectories using the PWscf code of the Quantum-ESPRESSO package.47,48 We employed optimized norm-conserving Vanderbilt pseudopotentials52 and a plane wave cutoff energy of 60 Ry,53 which is greater than the suggested cutoff for these pseudopotentials. Only the gamma point was used to sample the surface Brillouin zone. We used the PBE functional54 for all DFT calculations with the exception of the BOMD trajectory in which there was no excess charge on the electrode (i.e. at the potential of zero charge (PZC)). For this we used PBE with a Tkatchenko–Scheffler55 correction for van der Waals (vdW) interactions (PBE + TS), which are known to be especially important for unbiased metal–water interfaces.56,57 Contributions from vdW interactions were not expected to be as important for describing water at electrode surfaces carrying excess charge, at which configurations with water oriented parallel to the surface were expected to be disfavored.40 Moreover, we demonstrate herein that the qualitative results of this study were not impacted by the inclusion of vdW correction only at PZC.We carried out five BOMD trajectories of our model electrochemical half-cell, each with a different amount of charge localized at the Au surface. The total electrode charges per unit cell σ used were −0.4e, −0.2e, 0e, +0.2e, and +0.4e, where e is the elementary charge. These amounted to at most ±0.025e per surface Au atom, if distributed evenly. We demonstrate below that these σ represented modest applied potentials smaller in magnitude than ±0.5 V vs. PZC. The BOMD runs were performed with a timestep of ∼0.48 fs, which was made possible by using the mass of D for all H atoms, and at 330 K, as is typical for AIMD simulations of bulk liquid water.58 The results below regarding hydrogen bonding and diffusivity are indicative that water was sufficiently liquid in our simulations. The physical Au and O masses were used otherwise. We employed an NVT ensemble with a velocity-rescaling thermostat with a tolerance of ±100 K. Each trajectory spanned over 10 ps of integration time, which we will later show was sufficient to recover a physical differential capacitance for the system. The initial coordinates were generated via a geometry minimization in a classical force field57 with no excess charges followed by partial DFT-level geometry optimization at each trajectory's respective electrode charge. The 3D electrostatic potential Φ, as obtained by solving the Kohn–Sham equation self-consistently, was recorded every 100 time steps (∼48 fs) of each trajectory.
2.3 Calculation of electrode potential
Here we briefly introduce the absolute electrode potential, its constituent quantities, and demonstrate the simple utility of measuring the computed electrode potentials relative to the system's potential of zero charge (PZC). The absolute electrode potential Φabs can be expressed as,59,60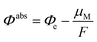 | (1) |
![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) . Then, we took as ΦS the value of
. Then, we took as ΦS the value of ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) deep in the continuum solvent region of the cell,25,36,61 where
deep in the continuum solvent region of the cell,25,36,61 where ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) is unchanging as a function of z (Fig. 1B). To measure the metal potential, we macroscopically-averaged
is unchanging as a function of z (Fig. 1B). To measure the metal potential, we macroscopically-averaged ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) in the Au slab using the optimized layer spacing of 2.4 Å and took as μM the average of this quantity over the back 1 Å of the slab. Utilizing the partially-frozen back layer provided a more stable metal potential (Fig. 1B), although alternative definitions for ΦM did not qualitatively change our results (see Fig. S3†). The resulting values of Φe presented below represent the difference between the quantities ΦM and ΦS for each trajectory.
in the Au slab using the optimized layer spacing of 2.4 Å and took as μM the average of this quantity over the back 1 Å of the slab. Utilizing the partially-frozen back layer provided a more stable metal potential (Fig. 1B), although alternative definitions for ΦM did not qualitatively change our results (see Fig. S3†). The resulting values of Φe presented below represent the difference between the quantities ΦM and ΦS for each trajectory.
For the purposes of analyzing the effects of electrode potential on various properties of water we referred potentials to the system's PZC, i.e. σ = 0 e. The referenced potentials ΔΦe are expressed as,
| ΔΦe = Φabs[σ] − Φabs[σ = 0] = Φe[σ] − Φe[σ = 0] | (2) |
In this expression it is evident that we do not need the bulk metal's Fermi energy to compute the referenced electrode potentials. While certain implementations of e.g. Poisson–Boltzmann boundary conditions may make it possible to obtain the absolute potentials from ab initio calculations of small systems,27,41,62 the PZC-referenced potentials will suffice to quantify the effects of electrode polarization on water. In the present application, the referenced electrode potentials associated with each σ will emerge as the trajectory averages of the Φe, referred to hereafter as φ and computed as,
| φ = Δ〈Φe〉 | (3) |
In the following section we will first present the dynamics and convergence of each trajectory's Φe before subsequently analyzing the structure, dynamics, and vibrational spectra of interfacial water as a function of φ, the trajectory-averaged potentials versus PZC.
3. Results and discussion
3.1 Electrical properties of Au(111)/water
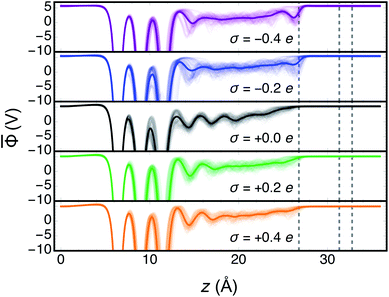
![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) for each electrode charge as well as the full trajectory averages are shown in Fig. 2. The electrostatic potential wells observed include one for each of the layers of the Au slab and at least one characteristic of a structural layer of water at the interface. In the region of dielectric continuum, to the right of the potential energy step in Fig. 2,
for each electrode charge as well as the full trajectory averages are shown in Fig. 2. The electrostatic potential wells observed include one for each of the layers of the Au slab and at least one characteristic of a structural layer of water at the interface. In the region of dielectric continuum, to the right of the potential energy step in Fig. 2, ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) is unchanging in z, making the calculation of ΦS straightforward. The metal potentials as measured at the back of the slab were relatively stable as a function of time, as shown in Fig. S2 and S3.† In the two trajectories with negative electrode charges, and therefore positive counter charges, we observed electrostatic potential wells near the boundary of the region of explicit water. While these are indicative of a spurious interaction between some water molecules and the counter charge plane, the below analyses demonstrate that the system's electrical properties and more immediate interfacial water layers were nonetheless physically realistic.
is unchanging in z, making the calculation of ΦS straightforward. The metal potentials as measured at the back of the slab were relatively stable as a function of time, as shown in Fig. S2 and S3.† In the two trajectories with negative electrode charges, and therefore positive counter charges, we observed electrostatic potential wells near the boundary of the region of explicit water. While these are indicative of a spurious interaction between some water molecules and the counter charge plane, the below analyses demonstrate that the system's electrical properties and more immediate interfacial water layers were nonetheless physically realistic.
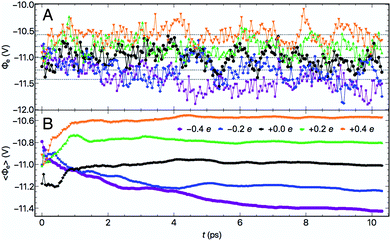
At each electrode charge, ![[capital Phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c1.gif) fluctuated as a consequence of the changing atomic structure during the molecular dynamics, as depicted in Fig. 2. Moreover, for these fixed σ trajectories, motion of both the Au and water atoms yielded changes to the electrode potentials Φe over time, plotted in Fig. 3A. The values of Φe for the five trajectories largely preserve the intuitive ordering according to the electrode charges throughout the dynamics. After at most 5–6 ps of dynamics, the cumulative time averages 〈Φe〉 (shown in Fig. 3B) were well converged. Although the 10 ps trajectories were short relative to molecular dynamics studies of interfacial water,63 the converged electrical properties of the system allowed for a qualitative investigation into water's structure and dynamics under quantifiable voltage bias.
fluctuated as a consequence of the changing atomic structure during the molecular dynamics, as depicted in Fig. 2. Moreover, for these fixed σ trajectories, motion of both the Au and water atoms yielded changes to the electrode potentials Φe over time, plotted in Fig. 3A. The values of Φe for the five trajectories largely preserve the intuitive ordering according to the electrode charges throughout the dynamics. After at most 5–6 ps of dynamics, the cumulative time averages 〈Φe〉 (shown in Fig. 3B) were well converged. Although the 10 ps trajectories were short relative to molecular dynamics studies of interfacial water,63 the converged electrical properties of the system allowed for a qualitative investigation into water's structure and dynamics under quantifiable voltage bias.
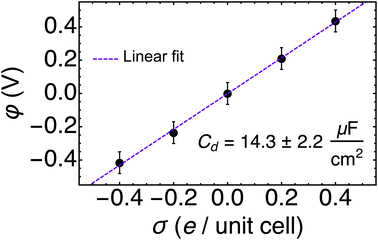
The relationship between the surface charges σ and the full trajectory-averaged electrode potentials versus PZC φ was found to be nearly perfectly linear, as depicted in Fig. 4. We ascribe the observed symmetry of the potentials around PZC to the lack of electrolyte ions in our system. The inverse slope of the linear fit to these five data points represents the differential capacitance Cd of the Au(111)/water system, 14.3 ± 2.2 μF cm−2. This Cd is within the rather large range of experimentally measured values, 11–40 μF cm−2,64–66 which depend significantly on experimental conditions including but not limited to the concentration and identity of the electrolyte ions. In the absence of ions, we are satisfied to recover a reasonable differential capacitance for Au(111)/water towards the bottom of the measured range of Cd.67 Similar values of Cd have been achieved for Au(111)/water with a fully implicit solvent with specifically tuned parameters25 and with a monolayer of water.33 Our results recover this macroscopic electrical property from short AIMD trajectories and an effectively fully explicit solvent.
3.2 Structural and dynamic response of water to applied voltages
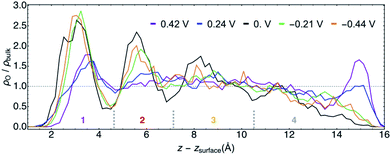
The structural similarities of the first water layers at PZC and at φ > 0 V have been previously observed by XAS.11 Furthermore, the position and maximum of the first density peak at PZC is in agreement with recent AIMD studies of Au(111)/water.68,69 An earlier AIMD study of this system at PZC predicted a narrowly resolved first water layer with a density maximum of ∼4 times that of bulk water,11 although this work was performed with PBE water at 300 K, which is now known to likely be over-structured.70
For the purposes of further analyses, we designated four characteristic layers of water for each trajectory, the approximate positions of which are delineated in Fig. 5. The layer boundaries were chosen at local density minima and differed slightly for each φ. Hereafter we will refer to water in these spatial regions by the numbers shown in Fig. 5, with layer 1 being the most immediate interfacial layer, followed by layer 2. Layer 3 is yet further from the surface and appears in terms of the density to be most similar to bulk water. We will neglect layer 4 in the subsequent analyses given its aforementioned unphysical behavior.
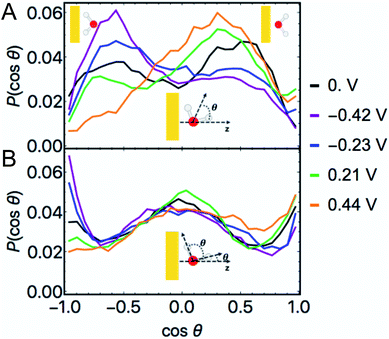
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) at non-zero φ in Fig. 6A demonstrate that when the Au surface was charged positively the bisectors were selectively oriented away from the surface (O atoms oriented towards the surface) and when the surface was negatively charged the water dipoles were selectively oriented towards the surface (O atoms oriented away from the surface). These results follow intuitively from electrostatic attraction of O to the positively charged surface and of H/D to the negatively charged surface. Nonetheless, these maxima appear not at cos
θ) at non-zero φ in Fig. 6A demonstrate that when the Au surface was charged positively the bisectors were selectively oriented away from the surface (O atoms oriented towards the surface) and when the surface was negatively charged the water dipoles were selectively oriented towards the surface (O atoms oriented away from the surface). These results follow intuitively from electrostatic attraction of O to the positively charged surface and of H/D to the negatively charged surface. Nonetheless, these maxima appear not at cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = ±1 but at intermediate positive and negative values, i.e. at these modest voltages water's geometric dipoles are not entirely oriented to the electric fields. We also observed non-negligible probabilities of water molecules being oriented counter to the prevailing electrostatics for both positive and negative φ. At PZC, we observed a bimodal distribution of water bisectors with more being oriented generally away from the surface by a small margin.71 This is in subtle contrast to literature characterizations of room temperature water at the Au(111) interface as being similar to a 2D ice, in which the bisectors would be predominantly parallel to the surface and P(cos
θ = ±1 but at intermediate positive and negative values, i.e. at these modest voltages water's geometric dipoles are not entirely oriented to the electric fields. We also observed non-negligible probabilities of water molecules being oriented counter to the prevailing electrostatics for both positive and negative φ. At PZC, we observed a bimodal distribution of water bisectors with more being oriented generally away from the surface by a small margin.71 This is in subtle contrast to literature characterizations of room temperature water at the Au(111) interface as being similar to a 2D ice, in which the bisectors would be predominantly parallel to the surface and P(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) would be maximal near cos
θ) would be maximal near cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0.11 In general, the bisector orientation statistics in layer 1 appear to smoothly change as a function of φ.
θ = 0.11 In general, the bisector orientation statistics in layer 1 appear to smoothly change as a function of φ.
The histogram of the cosine of the angles formed between all water OD vectors and a unit vector parallel to the z axis in layer 1 is given in Fig. 6B. These plots demonstrate local maxima at −1 for the negative φ and at +1 for the positive φ, i.e. OD bonds pointed perpendicularly towards and away from the surface, respectively, in accordance with the bond's geometric dipole. At each non-zero φ we additionally observe significant frequencies near cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0, indicative of a significant proportion of OD bonds being nearly parallel to the surface in layer 1.
θ = 0, indicative of a significant proportion of OD bonds being nearly parallel to the surface in layer 1.
The complimentary observations of water bisectors not being entirely oriented along the applied fields and the significant proportion of OD bonds being roughly parallel to the surface suggest a general characterization of water's structure in layer 1: water's geometric dipole being partially oriented according to the local field while sustaining hydrogen bonding interactions with neighboring water molecules. Nonetheless, interfacial water at room temperature still exhibits considerable disorder within this paradigm at the modest values of φ studied.
This characterization is further supported by an analysis of the hydrogen bonding properties of water in our simulations that found on average at least 1 and up to more than 2 intra-layer hydrogen bonds among layer 1 water at every potential (Fig. S5†). In addition, our calculations suggest fewer hydrogen bonds formed by water in layer 1 at negative φ than at PZC and positive φ, on average (Fig. S5†). This is consistent with the observation of more dangling OH bonds at negative potentials than at positive potentials by XAS.11 The hydrogen bonding properties of water at an Au(111) interface at PZC are in accordance with a previous BOMD study.71 The average number of hydrogen bonds in layer 3, the most bulk-like water, ranged from 3.42–3.58 (Fig. S7†). This compares favorably to the experimental value for bulk water at 330 K, 3.58.72 Comparable BOMD simulations of bulk water estimate this value to be approximately 3.85, 3.77, and 3.60 for PBE, PBE + TS, and SCAN, respectively.58
The biasing voltage affects the orientation of water in sub-interfacial layers 2 and 3 as well, as shown in Fig. S8 and S9.† We observed little attenuation of the bisector orientation preferences of water in layers 2 and 3 at non-zero φ. In the case of the PZC trajectory, water no longer shows any significant orientation pattern beyond layer 1.
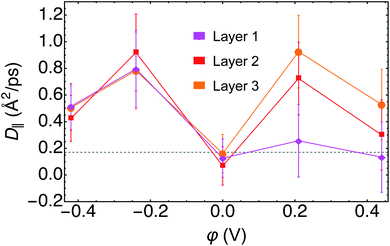
For water in layer 1, we observed an increase in the D‖ at negative φ relative to both PZC and to bulk D2O. At PZC and at positive φ we observed little difference within error of D‖ relative to bulk D2O, further evidence contrary to layer 1 water having ice-like properties. For layer 2, we found a minimum D‖ at PZC, with D‖ at PZC being below, but within the error, of bulk D2O. Furthermore, D‖ at both positive and negative potentials in layer 2 was found to be higher than that of bulk D2O. In layer 3 we observed a similar response of D‖ to φ as in layer 2. Note that in layer 3, the most bulk-like water in our small simulation, D‖ at PZC was nearly identical to that of bulk D2O (Fig. 7).
The observation of increased parallel diffusivity of water in layer 1 at negative φ can be rationalized by the smaller average number of hydrogen bonds observed under these conditions (Fig. S5–S7†). Conversely, the total average numbers of hydrogen bonds were roughly the same for the trajectories of φ ≥ 0, for which the layer 1 parallel diffusion coefficients were similar. The increased D‖ in layers 2 and 3 at φ ≠ 0 are more difficult to rationalize on the basis of hydrogen bonding, given that their total numbers and ratios of intra- and inter-layer hydrogen bonding are not very different from PZC in these layers (Fig. S5–S7†). However, there is literature precedent for water's diffusion being faster in small, oscillatory external electric fields,73 which may describe the sub-interfacial water layer. Recent AIMD simulations demonstrated that such electric fields induced frequent rearrangements of the hydrogen bonding network and consequentially increased water's diffusivity.73 We also note that D‖ in each layer is generally lowest at PZC, the only trajectory in which the vdW correction was included, despite the inclusion of vdW corrections in AIMD being known to increase the diffusivity of bulk water.58
3.3 Water vibrational densities of states versus electrode potential
We computed the vibrational density of states (VDOS) for water in each layer and at each potential from the BOMD trajectories. The VDOS spectra calculated by Fourier transforming the velocity autocorrelation functions for each trajectory are shown in Fig. 8. For the purposes of qualitatively assessing the effects of distance from the electrode and φ on the VDOS spectra, we will focus on the peaks associated with the bending (δDOD, ∼1200 cm−1) and stretching (νOD, ∼2400–2600 cm−1) modes of D2O. The former yielded a single, relatively narrow peak, whereas the latter exhibited a much broader peak that in some cases was evidently bimodal. Bimodal νOH(D) signals at the Au(111) interface have been previously observed by SEIRAS12 and SFG15 and from BOMD of similar systems at PZC.74 We emphasize that VDOS spectra are related to but not exactly coincident with the spectra associated with any surface-enhanced spectroscopy.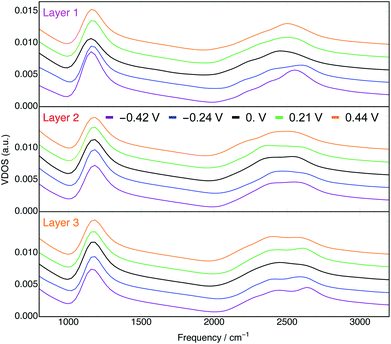 | ||
| Fig. 8 Vibrational density of states of D2O in layers 1 (top), 2 (middle), and 3 (bottom) at every φ. Spectra for each φ are vertically offset by arbitrary amounts in each plot for visual clarity. | ||
In the VDOS spectra for layer 1 water (top panel of Fig. 8) there is a clear dependence on φ. Both positive and negative φ have the effect of blue shifting the peaks associated with the δDOD and νOD vibrations. This phenomenon has been observed experimentally by SEIRAS.12 Moreover, the blue shifts of the two characteristic signatures with both positive and negative φ are consistent with the orientation of water's geometric dipoles with the induced fields vis-à-vis the Stark effect.75 This qualitative conclusion holds despite the vdW correction (only employed at PZC) being known to blue shift both the δDOD and νOD peaks.76,77
Furthermore, the δDOD peaks of layer 1 water appear at lower frequencies relative to those of water in layers 2 and 3 (Fig. S19†). This is suggestive of a weaker hydrogen bonding network78 in layer 1, consistent with our observation of fewer overall hydrogen bonds formed in the interfacial layer (Fig. S5–S7†). In addition to the behavior of the peak positions, the integrated intensities of the δDOD peaks demonstrate a minimum at φ = 0 V (Fig. S21†), consistent with SEIRAS data.12 Further analyses of the VDOS spectra, including the spectra that emerge from the velocities only in z, are presented in the ESI.†
The VDOS spectra for layer 2 water (middle panel of Fig. 8) are significantly less sensitive to φ than are those in layer 1. Nonetheless, we observe in layer 2 small potential dependencies of the νOD peak (Fig. S17†). It is evident from the bottom panel of Fig. 8 and S18† that in layer 3, which is comprised of water even further from the electrode surface, the effects of φ on the VDOS spectra are mostly negligible. This observation is consistent with the electric field associated with the applied potential being nearly entirely screened by the first two layers of water.
4. Conclusions
In this work we studied the interface between electrified Au(111) slabs and heavy water using several BOMD trajectories and a mixed explicit–implicit solvation approach. The electrostatic potential differences between points in the interior of the metal and deep in the continuum solvent, Φe, were computed regularly throughout each BOMD simulation. The cumulative trajectory averages of Φe all converged within 10 ps and the relationship between the total electrode charges and their corresponding average potentials yielded a differential capacitance of 14.3 μF cm−2 for the system, in good agreement with experimental values for Au(111) electrodes with dilute electrolytes. Recovering the differential capacitance was validation for the methodology of utilizing several fixed electrode charge BOMD trajectories to study this inert electrochemical interface.That the BOMD trajectories reliably quantified the potential φ enabled structural and dynamic analyses of water with respect to both φ and distance from the electrode surface. Our calculations demonstrated that water forms at least one structural layer with a density greater than that of bulk against the Au(111) electrode, and more than one such layer at PZC and at positive φ. In addition, an analysis of the orientations of water characterize a general structure of water under bias in layer 1 in which one OD bond is generally oriented towards or away from the electrode depending on the sign of the applied potential whereas the other OD bond is nearly parallel to the surface. We observed that the D‖ of layer 1 water is enhanced only at potentials negative of the PZC, and that D‖ increases for all non-zero values of φ in the second and third layers of water. Lastly, the VDOS were most significantly potential-dependent in layer 1 of water, in which the δDOD and νOD peaks exhibited blue shifts for all trajectories with φ ≠ 0. The δDOD peak positions supported the observation of a weakened hydrogen bonding network at the interface.
This work represents a step towards describing in situ aqueous electrochemistry with ab initio molecular simulation. Water comprises a significant portion of the EDL even for concentrated aqueous electrolyte solutions, necessitating that we intimately understand how its properties are altered by applied voltage at equilibrium and beyond. Looking ahead, the inclusion of ions that constitute the EDL as well as reliable descriptions of driven, faradaic charge transfer processes would vastly enhance the scope of these simulations and offer valuable microscopic insights into electrochemistry and its diverse applications.
Author contributions
Z. K. G. conceived of the project; Z. K. G., M. F. C. A., and A. S. designed the model system and simulations, analyzed the results, and wrote the paper. Z. K. G. and M. F. C. A. carried out BOMD simulations and corresponding post-processing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Marko Melander for a helpful discussion of the electrode potential and Roberto Car for support and inspiration in designing the project. This work was supported by the Computational Chemical Science Center: Chemistry in Solution and at Interfaces under DOE Award DE-SC0019394.Notes and references
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- K. Sakaushi, T. Kumeda, S. Hammes-Schiffer, M. M. Melander and O. Sugino, Phys. Chem. Chem. Phys., 2020, 22, 19401–19442 RSC.
- C. Zhao and W. Zheng, Front. Energy Res., 2015, 3, 23 Search PubMed.
- K. Sivula and R. van de Krol, Nat. Rev. Mater., 2016, 1, 15010 CrossRef CAS.
- V. R. Stamenkovic, D. Strmcnik, P. P. Lopes and N. M. Markovic, Nat. Mater., 2017, 16, 57–69 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods Fundamentals and Applictions, John Wiley & Sons, Inc., New York, 2nd edn, 2001 Search PubMed.
- J. O. Bockris and S. U. Khan, Surface electrochemistry: a molecular level approach, Springer Science & Business Media, 2013 Search PubMed.
- O. M. Magnussen and A. Groß, J. Am. Chem. Soc., 2019, 141, 4777–4790 CrossRef CAS.
- M. F. Toney, J. N. Howard, J. Richer, G. L. Borges, J. G. Gordon, O. R. Melroy, D. G. Wiesler, D. Yee and L. B. Sorensen, Nature, 1994, 368, 444–446 CrossRef CAS.
- S. V. Kalinin, O. Dyck, N. Balke, S. Neumayer, W.-Y. Tsai, R. Vasudevan, D. Lingerfelt, M. Ahmadi, M. Ziatdinov, M. T. McDowell and E. Strelcov, ACS Nano, 2019, 13, 9735–9780 CrossRef CAS PubMed.
- J.-J. Velasco-Velez, C. H. Wu, T. A. Pascal, L. F. Wan, J. Guo, D. Prendergast and M. Salmeron, Science, 2014, 346, 831–834 CrossRef CAS PubMed.
- K.-i. Ataka, T. Yotsuyanagi and M. Osawa, J. Phys. Chem., 1996, 100, 10664–10672 CrossRef CAS.
- N. Garcia-Araez, P. Rodriguez, V. Navarro, H. J. Bakker and M. T. Koper, J. Phys. Chem. C, 2011, 115, 21249–21257 CrossRef CAS.
- C.-Y. Li, J.-B. Le, Y.-H. Wang, S. Chen, Z.-L. Yang, J.-F. Li, J. Cheng and Z.-Q. Tian, Nat. Mater., 2019, 18, 697–701 CrossRef CAS PubMed.
- S. Nihonyanagi, S. Ye, K. Uosaki, L. Dreesen, C. Humbert, P. Thiry and A. Peremans, Surf. Sci., 2004, 573, 11–16 CrossRef CAS.
- W.-T. Liu and Y. R. Shen, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1293–1297 CrossRef CAS PubMed.
- M. Osawa, M. Tsushima, H. Mogami, G. Samjeske and A. Yamakata, J. Phys. Chem. C, 2008, 112, 4248–4256 CrossRef CAS.
- J. I. Siepmann and M. Sprik, J. Chem. Phys., 1995, 102, 511–524 CrossRef CAS.
- A. P. Willard, S. K. Reed, P. A. Madden and D. Chandler, Faraday Discuss., 2009, 141, 423–441 RSC.
- Y. Zhang, H. B. de Aguiar, J. T. Hynes and D. Laage, J. Phys. Chem. Lett., 2020, 11, 624–631 CrossRef CAS PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23–J26 CrossRef.
- K. Letchworth-Weaver and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075140 CrossRef.
- O. Andreussi, I. Dabo and N. Marzari, J. Chem. Phys., 2012, 136, 064102 CrossRef PubMed.
- N. G. Hörmann, O. Andreussi and N. Marzari, J. Chem. Phys., 2019, 150, 041730 CrossRef PubMed.
- J. A. Gauthier, C. F. Dickens, H. H. Heenen, S. Vijay, S. Ringe and K. Chan, J. Chem. Theory Comput., 2019, 15, 6895–6906 CrossRef CAS PubMed.
- G. Fisicaro, L. Genovese, O. Andreussi, N. Marzari and S. Goedecker, J. Chem. Phys., 2016, 144, 014103 CrossRef CAS PubMed.
- F. Nattino, M. Truscott, N. Marzari and O. Andreussi, J. Chem. Phys., 2019, 150, 041722 CrossRef PubMed.
- A. Bouzid and A. Pasquarello, J. Phys. Chem. Lett., 2018, 9, 1880–1884 CrossRef CAS PubMed.
- M. M. Melander, M. J. Kuisma, T. E. K. Christensen and K. Honkala, J. Chem. Phys., 2019, 150, 041706 CrossRef PubMed.
- C. D. Taylor, S. A. Wasileski, J.-S. Filhol and M. Neurock, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165402 CrossRef.
- Y. Ping, R. J. Nielsen and W. A. Goddard, J. Am. Chem. Soc., 2017, 139, 149–155 CrossRef CAS PubMed.
- G. Kastlunger, P. Lindgren and A. A. Peterson, J. Phys. Chem. C, 2018, 122, 12771–12781 CrossRef CAS.
- H. Nong, L. Falling, A. Bergmann, M. Klingenhof, H. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella and A. Knop-Gericke, et al. , Nature, 2020, 587, 408–413 CrossRef CAS PubMed.
- M. L. Clark, A. Ge, P. E. Videla, B. Rudshteyn, C. J. Miller, J. Song, V. S. Batista, T. Lian and C. P. Kubiak, J. Am. Chem. Soc., 2018, 140, 17643–17655 CrossRef CAS PubMed.
- Z. K. Goldsmith, M. Secor and S. Hammes-Schiffer, ACS Cent. Sci., 2020, 6, 304–311 CrossRef CAS PubMed.
- N. Bonnet, T. Morishita, O. Sugino and M. Otani, Phys. Rev. Lett., 2012, 109, 266101 CrossRef PubMed.
- A. Huzayyin, J. H. Chang, K. Lian and F. Dawson, J. Phys. Chem. C, 2014, 118, 3459–3470 CrossRef CAS.
- L. S. Pedroza, A. Poissier and M. V. Fernández-Serra, J. Chem. Phys., 2015, 142, 034706 CrossRef PubMed.
- L. S. Pedroza, P. Brandimarte, A. R. Rocha and M. V. Fernández-Serra, Chem. Sci., 2018, 9, 62–69 RSC.
- M. Otani and O. Sugino, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115407 CrossRef.
- O. Sugino, I. Hamada, M. Otani, Y. Morikawa, T. Ikeshoji and Y. Okamoto, Surf. Sci., 2007, 601, 5237–5240 CrossRef CAS.
- M. Otani, I. Hamada, O. Sugino, Y. Morikawa, Y. Okamoto and T. Ikeshoji, Phys. Chem. Chem. Phys., 2008, 10, 3609–3612 RSC.
- S. Schnur and A. Groß, New J. Phys., 2009, 11, 125003 CrossRef.
- C. Merlet, C. Péan, B. Rotenberg, P. A. Madden, P. Simon and M. Salanne, J. Phys. Chem. Lett., 2013, 4, 264–268 CrossRef CAS PubMed.
- O. Andreussi and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 245101 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- O. Andreussi, N. G. Hörmann, F. Nattino, G. Fisicaro, S. Goedecker and N. Marzari, J. Chem. Theory Comput., 2019, 15, 1996–2009 CrossRef CAS PubMed.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301 CrossRef CAS.
- T. Brumme, M. Calandra and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 245406 CrossRef.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- Y.-C. Lam, A. V. Soudackov, Z. K. Goldsmith and S. Hammes-Schiffer, J. Phys. Chem. C, 2019, 123, 12335–12345 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- J. Carrasco, J. Klimeš and A. Michaelides, J. Chem. Phys., 2013, 138, 024708 CrossRef PubMed.
- A. Berg, C. Peter and K. Johnston, J. Chem. Theory Comput., 2017, 13, 5610–5623 CrossRef CAS PubMed.
- L. Zheng, M. Chen, Z. Sun, H.-Y. Ko, B. Santra, P. Dhuvad and X. Wu, J. Chem. Phys., 2018, 148, 164505 CrossRef PubMed.
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CAS.
- S. Trasatti, Electrochim. Acta, 1990, 35, 269–271 CrossRef CAS.
- S. Sakong and A. Groß, J. Chem. Phys., 2018, 149, 084705 CrossRef PubMed.
- R. Jinnouchi and A. B. Anderson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245417 CrossRef.
- M. F. Calegari Andrade, H.-Y. Ko, R. Car and A. Selloni, J. Phys. Chem. Lett., 2018, 9, 6716–6721 CrossRef CAS PubMed.
- D. M. Kolb and J. Schneider, Electrochim. Acta, 1986, 31, 929–936 CrossRef CAS.
- N. Vasiljevic, T. Trimble, N. Dimitrov and K. Sieradzki, Langmuir, 2004, 20, 6639–6643 CrossRef CAS PubMed.
- B. Garlyyev, S. Xue, S. Watzele, D. Scieszka and A. S. Bandarenka, J. Phys. Chem. Lett., 2018, 9, 1927–1930 CrossRef CAS PubMed.
- E. Lust, in Electrical Double Layers. Double Layers at Single-crystal and Polycrystalline Electrodes, American Cancer Society, 2007 Search PubMed.
- H. H. Heenen, J. A. Gauthier, H. H. Kristoffersen, T. Ludwig and K. Chan, J. Chem. Phys., 2020, 152, 144703 CrossRef CAS PubMed.
- J.-B. Le and J. Cheng, Curr. Opin. Electrochem., 2020, 19, 129–136 CrossRef CAS.
- R. A. DiStasio Jr, B. Santra, Z. Li, X. Wu and R. Car, J. Chem. Phys., 2014, 141, 084502 CrossRef PubMed.
- J. Le, A. Cuesta and J. Cheng, J. Electroanal. Chem., 2018, 819, 87–94 CrossRef CAS.
- A. Soper, F. Bruni and M. Ricci, J. Chem. Phys., 1997, 106, 247–254 CrossRef CAS.
- Z. Futera and N. J. English, J. Chem. Phys., 2017, 147, 031102 CrossRef PubMed.
- J. Le, Q. Fan, L. Perez-Martinez, A. Cuesta and J. Cheng, Phys. Chem. Chem. Phys., 2018, 20, 11554–11558 RSC.
- S. D. Fried and S. G. Boxer, Acc. Chem. Res., 2015, 48, 998–1006 CrossRef CAS PubMed.
- J. Xu, M. Chen, C. Zhang and X. Wu, Phys. Rev. B, 2019, 99, 205123 CrossRef CAS.
- K. Zhong, C.-C. Yu, M. Dodia, M. Bonn, Y. Nagata and T. Ohto, Phys. Chem. Chem. Phys., 2020, 22, 12785–12793 RSC.
- T. Seki, K.-Y. Chiang, C.-C. Yu, X. Yu, M. Okuno, J. Hunger, Y. Nagata and M. Bonn, J. Phys. Chem. Lett., 2020, 11, 8459–8469 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc00354b |
| This journal is © The Royal Society of Chemistry 2021 |