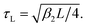Open Access Article
Open Access ArticleEngineering entangled photon pairs with metal–organic frameworks†
Rubén A.
Fritz
 a,
Yamil J.
Colón
a,
Yamil J.
Colón
 b and
Felipe
Herrera
b and
Felipe
Herrera
 *ac
*ac
aDepartment of Physics, Universidad de Santiago de Chile, Av. Ecuador 3493, Santiago, Chile. E-mail: felipe.herrera.u@usach.cl
bDepartment of Chemical and Biomolecular Engineering, University of Notre Dame, IN, USA
cANID – Millennium Science Initiative Program, Millennium Institute for Research in Optics, Chile
First published on 22nd January 2021
Abstract
The discovery and design of new materials with competitive optical frequency conversion efficiencies can accelerate the development of scalable photonic quantum technologies. Metal–organic framework (MOF) crystals without inversion symmetry have shown potential for these applications, given their nonlinear optical properties and the combinatorial number of possibilities for MOF self-assembly. In order to accelerate the discovery of MOF materials for quantum optical technologies, scalable computational assessment tools are needed. We develop a multi-scale methodology to study the wavefunction of entangled photon pairs generated by selected non-centrosymmetric MOF crystals via spontaneous parametric down-conversion (SPDC). Starting from an optimized crystal structure, we predict the shape of the G(2) intensity correlation function for coincidence detection of the entangled pairs, produced under conditions of collinear type-I phase matching. The effective nonlinearities and photon pair correlation times obtained are comparable to those available with inorganic crystal standards. Our work thus provides fundamental insights into the structure–property relationships for entangled photon generation with metal–organic frameworks, paving the way for the automated discovery of molecular materials for optical quantum technology.
I. Introduction
Optical communication and information technology that exploit the quantum properties of light for enhanced performance,1 has enabled the development of quantum-secure communication networks,2,3 fault-tolerant quantum computing,4 and quantum sensing devices.5 In quantum-enhanced applications, the theoretical performance limits can often be related to the quality of the underlying materials used in the implementation of a target protocol. The challenge for materials science is thus being able to tailor the conventional device development workflow such that the performance limits of specific quantum-enhanced protocols can be improved. For example, in several device-independent quantum key distribution protocols, the secure bit rate can be directly related to the flux of entangled photon pairs that can be generated in a nonlinear optical crystal subject to laser driving,6,7 given a detection efficiency. The generation of entangled photon pairs via down-frequency conversion can in turn be mapped directly into a search for highly crystalline birefringent materials with large second-order nonlinearities, which can be used as entangled photon sources with high brightness.8Optical quantum technologies have growing applications in enhanced imaging,9 secure communication,10 and quantum computing.11 However, the prospects for expanding the reach of quantum-enhanced optical devices is limited, as the number of optical materials that are suitable for advanced protocols is relatively small.12 For instance, inorganic crystals such as BaB2O4 (BBO) or KH2PO4 (KDP) are widely used for classical and quantum frequency conversion via three-wave mixing.13 The optical anisotropy and large second-order nonlinear susceptibility of these materials in the visible and near infrared are exploited for spontaneous parametric down-conversion (SPDC),14 a quantum optical process in which a single pump photon at frequency ω splits into two indistinguishable photons at ω/2. The indistinguishability of the down-converted photons leads to entanglement of their degrees of freedom.8 Despite their widespread use in practical quantum communication,15 the Poissonian photon number distribution of the pump laser makes the SPDC photon pair generation events intrinsically probabilistic.8 Deterministic (on-demand) generation of entangled photon pairs can be produced via the cascaded radiative decay of biexcitons in inorganic semiconductors,16,17 cascaded decay of dipole-coupled emitters,18 or by a combination of cascaded SPDC sources with conditional measurement events (heralding).19 Regardless of their physical origin, photon pairs that are entangled in frequency,8 polarization,20 or spatial mode profile,21 are the building blocks of several quantum imaging and secure communication protocols.22
Inorganic crystals, in general, are considered to be robust materials. Zeolites are an example; they can be used in catalysis applications, usually at high temperatures.23 Organic crystals are less stable but can provide great flexibility through molecular interactions and can be used as functional materials in drug delivery, catalysis, photonics, and electronics, and other applications.24 Metal–organic frameworks (MOFs) are hybrid materials that combine the structural stability of inorganic crystals and the versatility of organic materials.25 MOF crystals are very promising for applications in nonlinear optics.12,14,26,27 Recent experimental reports of competitive second-order28–30 and third-order optical nonlinearities31 with polycrystalline MOF crystals, have stimulated the need to develop a computational methodology that is capable of screening the available MOF databases, and generate a list of leading candidate structures with a suitable combination of features in their linear and nonlinear optical responses that make them competitive materials for applications in quantum optics. Large-scale computational MOF screening methods for applications in gas storage and gas separation have been developed,32,33 but extensions of these techniques are needed to discover novel applications of MOF materials in quantum technology.
In this work, we focus on selected non-centrosymmetric MOF crystals assembled from d10 transition metal ions (e.g., Zn2+, Cd2+) as metal nodes, and pyridil-tetrazole (ptz) molecules as organic linkers. Due to the closed d-shell of the metal node, and the high HOMO–LUMO gap of the pyridil-tetrazole ligands,34,35 the MOF crystals that we study are transparent throughout the visible spectrum up to the mid-infrared regime. For the MOF structures considered, the lack of inversion symmetry of their unit cells has enabled the observation of second-order nonlinear frequency conversion in polycrystalline powder samples with particle size in the range of microns.26 Given the availability of low-cost optical testing techniques,36 experiments have so far focused on the second-harmonic generation (SHG) process ω → 2ω from near-infrared to visible frequencies.26 The reverse frequency conversion process 2ω → ω corresponds to SPDC, which has yet to be demonstrated experimentally with MOFs. SPDC and SHG are conjugate processes in nonlinear optics.13 Although their experimental implementation is different, the frequency conversion efficiencies of SHG and SPDC in a given crystal are determined by the same components of the nonlinear susceptibility tensor.8 Therefore, understanding the material factors that determine SHG efficiencies is also relevant for future SPDC experiments.
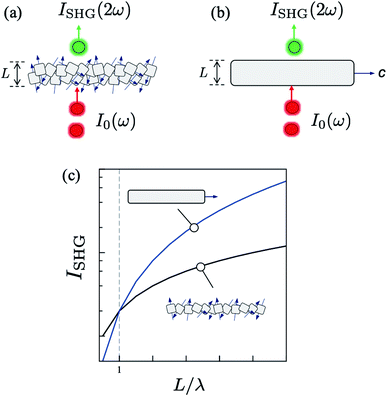
In Fig. 1, we illustrate the qualitative behavior of the SHG signal intensity (ISHG) at frequency 2ω upon illumination with a strong laser at frequency ω of a polycrystalline slab of non-centrosymmetric particles with propagation length L (panel a), and a single non-centrosymmetric crystal of equivalent propagation dimensions (panel b). For a powder sample, propagating optical waves sample an entire distribution of crystal orientations, defined by the direction of the optical axis of individual crystallites relative to the propagation light direction. This is the typical condition in SHG tests carried out with MOFs.26 In this case, the SHG intensity scales linearly with L.36,37 For crystals that support conditions of perfect phase matching (PPM),13 this linear L-scaling is a suboptimal consequence of the random crystal orientation in the medium. In contrast, for a single crystal with same length L, the SHG intensity scales as L2. In other words, the same nonlinear material at the same operating wavelengths has a superior output brightness in a second-order optical process when used as a single crystal. The phase coherence of the waves involved is also superior in single crystals. Fig. 1c shows that is not a critical issue for imaging and spectroscopy applications based on second-harmonic generation, which are typically used to study monolayers and interfaces with thickness L much smaller than the laser pump wavelength λ.38,39 This quadratic scaling is beneficial for quantum nonlinear optical processes, such as SPDC, for two main reasons: (i) to maximize the brightness of the non-classical signal (number of entangled photon pairs) and; (ii) to optimize the degree of temporal correlations in coincidence detection (photon indistinguishability), which leads to the entanglement of photonic degrees of freedom.40 None of these can be achieved using randomly oriented nonlinear crystal powders.
Growing large single crystal MOFs with millimeter dimensions is an experimental challenge. Few groups have reported large centrosymmetric crystals for applications in solid-phase chromatography.41,42 As crystal engineering techniques for MOFs continue to improve,43 we present here the first multi-scale computational design methodology for assessing the entanglement properties of near-infrared entangled photon pairs produced via SPDC in a large non-centrosymmetric single crystal MOF under strong laser pumping. We carry out a detailed analysis of three transparent, non-centrosymmetric, birefringent MOFs having the same ptz ligand in their structure: Zn(3-ptz)2 (MIRO-101, CSD: 184958), [Zn(H2O)6]NO32(3-ptz) (MIRO-102, CSD: 184132) and CdN3(3-ptz)2 (MIRO-103, CSD: 184133). Efforts to grow high-quality single crystals of these MOF species for applications in optics are currently underway.34,35
II. Results
(A) Methodological overview
Starting from its optimized crystal structure, we compute the two-time intensity correlation function G(2)(τ) for coincidence detection of entangled photon pairs generated via SPDC by a non-centrosymmetric MOF subject to strong laser pumping. The multi-scale calculation procedure we propose to achieve this, is described in detail in the ESI.† Briefly, we use solid-state DFT within the Coupled Perturbed Hartree–Fock/Kohn–Sham method (CPHF/KS)44–46 with a PBE functional, to compute the band gap EG, dynamical dielectric tensor εij(ω), and dynamical second-order susceptibility tensor χijk(2)(ω) of a fully optimized MOF crystal structure with non-centrosymmetric unit cell. Lattice disorder models are not implemented. Static disorder due to freely rotating organic groups is corrected from the experimental crystal structures, when needed. All DFT calculations were carried out using the CRYSTAL17 package.47 The Sellmeier equations for ordinary and extraordinary crystal axes are obtained from εij(ω), over a frequency range from the near infrared up to the crystal band gap. These are used to establish conditions for perfect phase matching in collinear type-I SPDC,8 with signal output at 1064 nm. The effective nonlinearity deff is obtained by contracting the χ(2) tensor with the appropriate input and output field polarizations. deff is used to parametrize an effective Hamiltonian for the SPDC process. The number of entangled photon pairs produced by the MOF, as well as the temporal and spectral properties of the entangled pair wavefunction can be computed from the effective Hamiltonian in first order perturbation theory. The G(2) function is fully determined by the photon pair wavefunction and the coincidence detection bandwidth.(B) Phase matching conditions
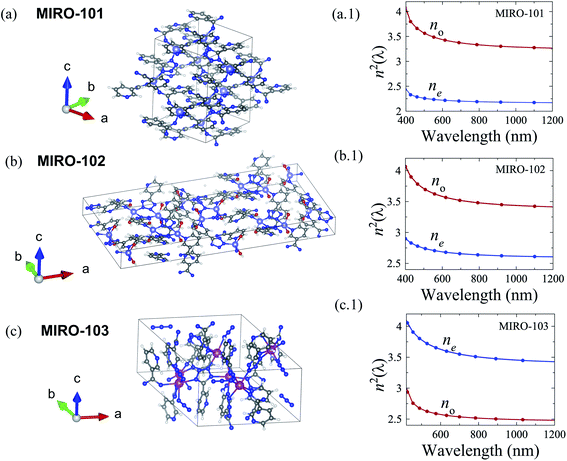
The predicted band gaps EG for the MOFs studied in this work are given in Table 1. The predicted band gap for MIRO 101 agrees well with recent experiments.48 We also compute the band gap of IRMOF-1, to compare with experiments and previous calculations in the literature.49–51 For IRMOF-1, the PBE-GGA functional is found to be in better agreement with experiments than the B3LYP-D calculations used in ref. 52, which overestimate the band gap. As mentioned above, the PBE-GGA functional is used for MIRO-101, MIRO-102, and MIRO-103. As additional validation of our methods, we also compute the band gaps of β-barium borate (BBO) and potassium dihydrogen phosphate (KDP), two widely used inorganic nonlinear crystals. The results are in good agreement with measured band gaps, although further basis set optimization may be needed for KDP.In Fig. 2, we show the unit cell structures and the Sellmeier curves n2(λ) of our target MOFs. We obtain these from the dielectric tensor εij(ω), computed at regular wavelength intervals from λmin = hc/EG to λmax = 1100 nm. For the phase-matching geometry considered below, we are interested in the Sellmeier curves along the ordinary axis (no) and the extraordinary c-axis (ne). For each crystal axis, we fit the ab initio curves to the standard relation
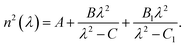 | (1) |
The fitted Sellmeier coefficients for each MOF are given in the ESI.† MIRO-101 is negative uniaxial (ne < no), MIRO-103 is positive uniaxial (ne > no). Although MIRO-102 is biaxial, one can always fix the crystal orientation such that light propagation is influenced by two refractive indices only.55 We aim for obtaining accurate values for the dynamic birefringence Δn(ω) ≡ ne(ω) − no(ω) through the frequency range of interest, as this is the observable that most strongly determines the phase matching conditions in SPDC. The phase matching conditions are invariant with respect to an overall change of the static average refractive index ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = [ne(λ) + no(λ)]/2 for λ → ∞. In other words, we can vertically shift all the Sellmeier curves in Fig. 2 by a constant value, and the phase matching results discussed below would not be affected.
= [ne(λ) + no(λ)]/2 for λ → ∞. In other words, we can vertically shift all the Sellmeier curves in Fig. 2 by a constant value, and the phase matching results discussed below would not be affected.
SPDC is a three-wave mixing process in which photons from a strong pump laser field at frequency ωp are coherently converted into a pair of signal photons with frequencies ω1 and ω2 such that ωp = ω1 + ω2,8 as expected for a perturbative light–matter interaction process that conserves energy. In the photon conversion process, conservation of momentum leads to the condition for perfect phase matching kp = k1 + k2, where k is a wavevector. In general, phase matching is a vectorial condition that together with energy conservation determines the propagation directions and frequencies of the photons generated in an entangled pair. Several possibilities can be analyzed, depending on the polarizations and propagation directions of interest in experiments.56 We consider collinear phase matching, in which the pump and signal photons share the same propagation direction k. The perfect phase matching condition thus reduces to a scalar relation for the refractive indices given by ωpnp(ωp) = ω1n1(ω1) + ω2n2(ω2), where np is the refractive index of the pump wave, n1 and n2 are the refractive indices of the signal photons. We assume that the detected signal photons are degenerate (ω1 = ω2 = ωp/2), thus reducing the condition to np(ωp) = ns(ωp/2), where ns(ω) denotes the refractive index of the signal photons. An additional ambiguity remains regarding the polarizations of the pump and signal waves. For the negative uniaxial MIRO-101 and MIRO-103 crystals, we adopt conventional oee type-I conditions,13 where the entangled signal photons are polarized along the ordinary axis (o), and the pump is polarized along the extraordinary axis (e). For MIRO-102, eoo type-I conditions are used. We focus on degenerate collinear signal photons to simplify the phase matching analysis. Non-degenerate and non-collinear conditions are also possible.8
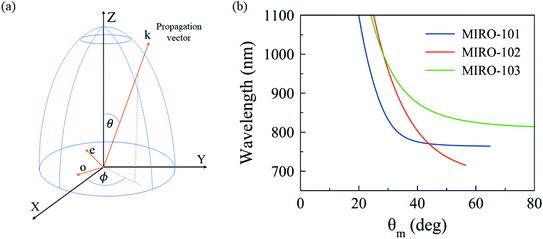
In a collinear configuration, the common propagation vector k of the pump and signal waves has a polar angle θ relative to the optical c-axis and azimuthal angle ϕ with respect to the X-axis, as show in Fig. 3a. Consider now that the waves propagate along the X-axis (θ = ϕ = π/2). Signal photons thus have extraordinary polarization along Z, and the perfect phase matching condition reads no(ωp) = ne(ωp/2). From the Sellmeier curves in Fig. 2, we see that this condition cannot be satisfied for any choice of ωp in the visible spectrum. This is common for materials with large birefringence.13 Perfect phase matching in our uniaxial MOF crystals can still be achieved if the pump and signal waves have propagation components along both ordinary and extraordinary directions. In Fig. 3b, we plot the predicted angle of perfect phase matching θm for MIRO-101, MIRO-102, and MIRO-103, over a range of entangled photon wavelengths λs in the near infrared. We set ϕ = π/2 here for concreteness, but below this constraint is relaxed when we discuss effective nonlinearities.
(C) Entangled photon pair properties
In Fig. 4, we illustrate collinear type-I spontaneous parametric down-conversion (SPDC) in a nonlinear MOF crystal, for the generation of entangled photon pairs in the near infrared. Pump photons from a strong visible laser field are coherently converted into photon pairs described by a wavefunction of the form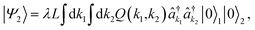 | (2) |
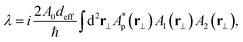 | (3) |
The photon pair (biphoton) wavefunction in eqn (2) is a non-separable wavepacket of the one-photon frequency-domain contributions 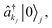 for j = 1, 2. The spectral and temporal properties of the biphoton state are determined by the joint spectral function
for j = 1, 2. The spectral and temporal properties of the biphoton state are determined by the joint spectral function
| Q(k1, k2) = l(ω1)l(ω2)sinc(ΔkL/2)eiΔkL/2αp(ω1 + ω2), | (4) |
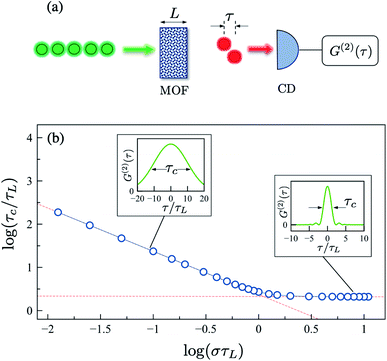
The arrival times for all the photon pairs emitted by the MOF crystal are detected in a coincidence setup, as illustrated in Fig. 4a. The probability of detecting a photon at time t1 and a second photon at time t2 is proportional to the (unnormalized) intensity correlation function G(2)(t1, t2) = |〈0|Ê(+)(t2)Ê(+)(t1)|Ψ2〉|2,58 where the far-field operators Ê(+)(tj) = ∫dωf(ω)â(ω)eiωtj take into account any spectral filtering done at the detectors through the filter function f(ω). For SPDC sources, the G(2) depends only on the relative time τ = t1 − t2.8 The actual number of entangled photon pairs produced by a MOF crystal (brightness) can be evaluated for perfect crystals from eqn (2) and (3), knowing the pump spectral profile, the transverse intensity profiles of the pump and signal fields, and the signal propagation length. For real crystals, the level of attenuation losses (in dB mm−1) due to Fresnel reflection and light scattering, at the pump and signal frequencies, should also be known.57 Technical details and crystal imperfections apart, the source brightness always scales as deff2, the intrinsic MOF property that can be evaluated from first principles.
In addition to the number photon pairs produced in SPDC, another feature that is important in applications is the pair correlation time τc, a measure of how indistinguishable (i.e., entangled) are two photons in a pair. τc can be defined as the width of the G(2) function. Pairs of distinguishable uncorrelated photons cannot be used in entanglement-based applications.21 The width of the G(2) function not only depends on the intrinsic material properties of a MOF structure, such as its Sellmeier curves along the ordinary and extraordinary axes, but also on the details of the optical pump and detection setup.8 Explicitly, for degenerate type-I phase matching, we can write the intensity correlation function as
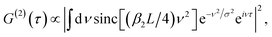 | (5) |
In Fig. 4, we plot the correlation time τc for type-I SPDC under collinear type-I phase matching as a function of the detector bandwidth σ (log–log scale). Time is in units of the characteristic crystal timescale 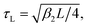 which roughly corresponds to the width of the sinc function in eqn (5). In the broadband detection limit (σ ≫ 1/τL), we have that τc ≈ 2.0τL. Therefore, given a crystal length L, we can compute τc for a given MOF crystal by evaluating β2 from the Sellmeier curve obtained from first principles. For concreteness, the GVD parameter for MIRO-101 under conditions of perfect phase matching at λ = 1064 nm is estimated to be β2 = 77.60 fs2 mm−1. For a crystal length L = 1.5 mm, the estimated correlation time is τc ≈ 10.78 fs for this MOF crystal. Fig. 4 shows that this broadband value only represents a lower bound for τc for this crystal, since the biphoton wavepacket is expected to broaden in time when a finite detector bandwidth is taken into account. For example, by using a spectral filters with a relatively broad linewidth σ = 0.2/τL ≈ 15 THz (FWHM), the coincidence correlation time now becomes τc ≈ 155 fs, for the same crystal parameters.
which roughly corresponds to the width of the sinc function in eqn (5). In the broadband detection limit (σ ≫ 1/τL), we have that τc ≈ 2.0τL. Therefore, given a crystal length L, we can compute τc for a given MOF crystal by evaluating β2 from the Sellmeier curve obtained from first principles. For concreteness, the GVD parameter for MIRO-101 under conditions of perfect phase matching at λ = 1064 nm is estimated to be β2 = 77.60 fs2 mm−1. For a crystal length L = 1.5 mm, the estimated correlation time is τc ≈ 10.78 fs for this MOF crystal. Fig. 4 shows that this broadband value only represents a lower bound for τc for this crystal, since the biphoton wavepacket is expected to broaden in time when a finite detector bandwidth is taken into account. For example, by using a spectral filters with a relatively broad linewidth σ = 0.2/τL ≈ 15 THz (FWHM), the coincidence correlation time now becomes τc ≈ 155 fs, for the same crystal parameters.
In Table 2, we summarize the results obtained for SPDC with collinear type-I phase matching for MIRO-101, MIRO-102, and MIRO-103 crystal slabs with length L = 1.5 mm. We obtain angles of perfect phase matching θm at 1064 nm, the effective nonlinearity deff at perfect phase matching, and the characteristic crystal timescales τL for ordinary and extraordinary signal field polarizations. For a given coincidence detection bandwidth σ, the photon pair correlation time τc can be estimated. As an additional validation of our DFT methods, we also compute the phase matching angle and GVD for BBO and KDP crystals, obtaining results that agree well with measurements at 1064 nm.59 For BBO, the predicted photon pair correlation time (τc ≈ 7.5 fs) for a crystal length L = 1.5 mm with λs = 1064 nm degenerate signal and idler fields, should be compared with τc ≈ 17 fs, estimated from the width of the joint spectral function for signal photons produced by a 1 mm crystal at λs = 808 nm, under degenerate collinear type-I phase matching conditions.60
| θ m (deg) | d eff (pm V−1) | ϕ (deg) | GVDo (fs2 mm−1) | GVDe (fs2 mm−1) | τ oc (fs) | τ ec (fs) | |
|---|---|---|---|---|---|---|---|
| MIRO-101 | 20.8 | −0.35 | 80° | 213.18 | 77.60 | 17.88 | 10.78 |
| +0.35 | 170° | ||||||
| MIRO-102 | 26.1 | +0.08 | 90° | 204.47 | 114.12 | 17.51 | 13.08 |
| MIRO-103 | 25.4 | +0.12 | 0° | 129.92 | 243.18 | 13.96 | 19.1 |
| −0.14 | 70° | ||||||
| BBO (calc) | 22.9 | 1.82 | 0° | 38.01 | 37.11 | 7.55 | 7.46 |
| BBO (exp) | 22.8 (ref. 59) | 2.11 (ref. 59) | |||||
| KDP (calc) | 40.4 | 0.41 | 45° | −8.04 | 19.83 | — | 5.46 |
| KDP (exp) | 41 (ref. 59) | 0.29 (ref. 59) |
In general, we expect the MOF observables in Table 2 to have a dependence with temperature, since thermal lattice distortions are known to influence the response of optical crystals.59,61,62 The ab initio analysis of the refractive index gradients dn(λ)/dT is possible,63 but falls outside the scope of this work. We can still estimate an upper bound on the expected temperature dependence of the Sellmeier curves for MIRO-101, MIRO-102 and MIRO-103, which share a dipolar push–pull organic ligand, from experiments on liquid crystals made of large dipolar aromatic molecules. Thermal molecular motions are arguably more significant in liquid crystals than in the non-porous MOFs studied here. For liquid crystals with commonly used dipolar chromophores, the index gradient at visible frequencies is on the order of 10−4 °C−1,64–66 whereas for inorganic crystals we have dn/dT ∼ 10−6 °C−1.59 Therefore, we do not expect the Sellmeier curves in Fig. 2 to vary by more than 1% over 100 °C, a variation that is smaller than systematic DFT errors.
III. Conclusions
In this work, we develop multi-scale methodology for the computational characterization of quantum light generated by nonlinear metal–organic frameworks. Specifically, we study entangled photon pair generation in the near infrared via spontaneous parametric down conversion (SPDC) in three zinc-tetrazole MOF crystals with non-centrosymmetric and non-porous unit cells: Zn(3-ptz)2 (MIRO-101), [Zn(H2O)6]NO32(3-ptz) (MIRO-102) and CdN3(3-ptz)2 (MIRO-103). Using solid-state DFT, we determine the band gaps and Sellmeier equations of these crystals. The MOFs studied are strongly birefringent, and allow conditions for type-I and type-II phase matching in SPDC. We focus on a collinear type-I scenario to illustrate the potential of our method for understanding the temporal and frequency correlations of the entangled photon pair (biphoton) wavefunction produced under strong laser pumping of the MOF crystals. Other phase matching scenarios are straightforward extensions of our type-I analysis.The similar band gaps (3.0–3.1 eV) and phase matching angles (21–26°) of the MOFs studied suggest that these properties largely depend on the molecular properties of the ligand (3-ptz). On the other hand, larger variations of the effective nonlinearities (deff) predicted under equal phase matching configuration, suggest a stronger sensibility on the crystal lattice geometry. However, only a large-scale analysis over an entire database of suitable nonlinear MOF structures would provide reliable structure–property relationships.
We have shown that MOF crystals can give entangled photon signals that are comparable with industry standards. However, the real untapped potential, thus importance, of using MOFs for quantum optical applications rests on the essentially unbounded design space for MOF self-assembly, given a library of suitable metal nodes and organic linkers.32,33 The Cambridge Structural Database currently lists over 2000 non-centrosymmetric MOF structures with closed-shell Zn nodes without structural disorder, each with a published synthetic protocol. MIRO-101, MIRO-102, and MIRO-103 are a subset of the database. Therefore, as a material class, metal–organic frameworks are promising for non-linear quantum optics because they can be computationally screened on a large scale to satisfy a set of conditions needed for a desired quantum optical technique. As a result of the screening, we can discover specific MOF crystals that significantly outperform inorganic industry standard on a given application. Our work thus paves the way for the computational discovery of novel metal–organic framework materials that are favorable for target protocols in optical quantum technology.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Gustavo Lima and Stephen Walborn for comments. RAF is supported by DICYT-USACH grant POSTDOC 041831HU. FH thanks support from CONICYT through Proyecto REDES ETAPA INICIAL, Convocatoria 2017 no. REDI 170423, FONDECYT Regular No. 1181743. This work was funded by ANID – Millennium Science Initiative Program ICN17-012. YJC thanks the University of Notre Dame for financial support through start-up funds.References
- J. L. O'Brien, A. Furusawa and J. Vučković, Nat. Photonics, 2009, 3, 687–695 CrossRef.
- H. J. Kimble, Nature, 2008, 453, 1023–1030 CrossRef CAS.
- S. Wehner, D. Elkouss and R. Hanson, Science, 2018, 362(6412), eaam9288 CrossRef.
- J. Wang, F. Sciarrino, A. Laing and M. G. Thompson, Nat. Photonics, 2020, 14, 273–284 CrossRef CAS.
- S. Pirandola, B. R. Bardhan, T. Gehring, C. Weedbrook and S. Lloyd, Nat. Photonics, 2018, 12, 724–733 CrossRef CAS.
- F. Xu, B. Qi, Z. Liao and H.-K. Lo, Appl. Phys. Lett., 2013, 103, 061101 CrossRef.
- L. Masanes, S. Pironio and A. Acín, Nat. Commun., 2011, 2, 238 CrossRef.
- Y. Shih, Rep. Prog. Phys., 2003, 66, 1009–1044 CrossRef.
- Y. Shih, IEEE J. Sel. Top. Quantum Electron., 2007, 13, 1016–1030 CAS.
- N. Gisin and R. Thew, Nat. Photonics, 2007, 1, 165–171 CrossRef CAS.
- P. Kok, W. J. Munro, K. Nemoto, T. C. Ralph, J. P. Dowling and G. J. Milburn, Rev. Mod. Phys., 2007, 79, 135–174 CrossRef CAS.
- R. Medishetty, Chem. Soc. Rev., 2017, 46, 4976–5004 RSC.
- R. W. Boyd, Nonlinear Optics, Elsevier, Burlington, MA USA, 3rd edn, 2008 Search PubMed.
- L. R. Mingabudinova, V. V. Vinogradov, V. A. Milichko, E. Hey-Hawkins and A. V. Vinogradov, Chem. Soc. Rev., 2016, 45, 5408–5431 RSC.
- R. Bedington, J. M. Arrazola and A. Ling, npj Quantum Inf., 2017, 3, 30 CrossRef.
- N. Akopian, N. H. Lindner, E. Poem, Y. Berlatzky, J. Avron, D. Gershoni, B. D. Gerardot and P. M. Petroff, Phys. Rev. Lett., 2006, 96, 130501 CrossRef CAS.
- A. Fognini, A. Ahmadi, M. Zeeshan, J. T. Fokkens, S. J. Gibson, N. Sherlekar, S. J. Daley, D. Dalacu, P. J. Poole, K. D. Jöns, V. Zwiller and M. E. Reimer, ACS Photonics, 2019, 6, 1656–1663 CrossRef CAS.
- D. S. Wang, T. Neuman and P. Narang, Dipole-Coupled Defect Pairs as Deterministic Entangled Photon Pair Sources, 2020 Search PubMed.
- A. Dousse, J. Suffczyński, A. Beveratos, O. Krebs, A. Lemaître, I. Sagnes, J. Bloch, P. Voisin and P. Senellart, Nature, 2010, 466, 217–220 CrossRef CAS.
- T. E. Kiess, Y. H. Shih, A. V. Sergienko and C. O. Alley, Phys. Rev. Lett., 1993, 71, 3893–3897 CrossRef CAS.
- L. Neves, G. Lima, J. G. Aguirre Gómez, C. H. Monken, C. Saavedra and S. Pádua, Phys. Rev. Lett., 2005, 94, 100501 CrossRef.
- V. Scarani, H. Bechmann-Pasquinucci, N. J. Cerf, M. Dusek, N. Lutkenhaus and M. Peev, Rev. Mod. Phys., 2009, 81, 1301–1350 CrossRef.
- N. Rahimi and R. Karimzadeh, Appl. Catal., A, 2011, 398, 1–17 CrossRef CAS.
- J. S. Brooks, Chem. Soc. Rev., 2010, 39, 2667–2694 CAS.
- H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 6149 CrossRef.
- C. Wang, T. Zhang and W. Lin, Chem. Rev., 2012, 112, 1084–1104 CrossRef CAS.
- X. Yang, X. Lin, Y. S. Zhao and D. Yan, Chem.–Eur. J., 2018, 24(25), 6484–6493 CrossRef CAS.
- S. Van Cleuvenbergen, I. Stassen, E. Gobechiya, Y. Zhang, K. Markey, D. E. De Vos, C. Kirschhock, B. Champagne, T. Verbiest and M. A. van der Veen, Chem. Mater., 2016, 28, 3203–3209 CrossRef CAS.
- Y.-X. Zhang, B.-X. Li, H. Lin, Z. Ma, X.-T. Wu and Q.-L. Zhu, J. Mater. Chem. C, 2019, 7, 6217–6221 RSC.
- Z. Chen, G. Gallo, V. A. Sawant, T. Zhang, M. Zhu, L. Liang, A. Chanthapally, G. Bolla, H. S. Quah, X. Liu, K. P. Loh, R. E. Dinnebier, Q.-H. Xu and J. J. Vittal, Angew. Chem., Int. Ed., 2020, 59, 833–838 CrossRef CAS.
- M. Liu, H. S. Quah, S. Wen, Z. Yu, J. J. Vittal and W. Ji, Chem. Mater., 2016, 28, 3385–3390 CrossRef CAS.
- Y. J. Colón and R. Q. Snurr, Chem. Soc. Rev., 2014, 43, 5735–5749 RSC.
- A. Sturluson, M. T. Huynh, A. R. Kaija, C. Laird, S. Yoon, F. Hou, Z. Feng, C. E. Wilmer, Y. J. Colón, Y. G. Chung, D. W. Siderius and C. M. Simon, Mol. Simul., 2019, 45, 1082–1121 CrossRef CAS.
- I. Chi-Durán, J. Enríquez, C. Manquian, K. Wrighton-Araneda, W. Cañon-Mancisidor, D. Venegas-Yazigi, F. Herrera and D. P. Singh, ACS Omega, 2018, 3, 801–807 CrossRef.
- J. Enríquez, C. Manquian, I. Chi-Duran, F. Herrera and D. P. Singh, ACS Omega, 2019, 4, 7411–7419 CrossRef.
- S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- I. Aramburu, J. Ortega, C. L. Folcia and J. Etxebarria, Appl. Phys. B: Lasers Opt., 2014, 116, 211–233 CrossRef CAS.
- T. F. Heinz, C. K. Chen, D. Ricard and Y. R. Shen, Phys. Rev. Lett., 1982, 48, 478–481 CrossRef CAS.
- L. Schneider and W. Peukert, Part. Part. Syst. Charact., 2006, 23, 351–359 CrossRef.
- M. Fiorentino, S. M. Spillane, R. G. Beausoleil, T. D. Roberts, P. Battle and M. W. Munro, Opt. Express, 2007, 15, 7479–7488 CrossRef CAS.
- S. Han, Y. Wei, C. Valente, I. Lagzi, J. J. Gassensmith, A. Coskun, J. F. Stoddart and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 16358–16361 CrossRef CAS.
- L. Li, F. Sun, J. Jia, T. Borjigin and G. Zhu, CrystEngComm, 2013, 15, 4094–4098 RSC.
- B. Seoane, S. Castellanos, A. Dikhtiarenko, F. Kapteijn and J. Gascon, Coord. Chem. Rev., 2016, 307, 147–187 CrossRef CAS.
- M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, J. Chem. Phys., 2008, 128, 014110 CrossRef.
- M. Ferrero, M. Rérat, R. Orlando and R. Dovesi, J. Comput. Chem., 2008, 29, 1450–1459 CrossRef CAS.
- M. Ferrero, M. Rérat, B. Kirtman and R. Dovesi, J. Chem. Phys., 2008, 129, 244110 CrossRef.
- A. Erba, J. Baima, I. Bush, R. Orlando and R. Dovesi, J. Chem. Theory Comput., 2017, 13, 5019–5027 CrossRef CAS.
- I. Chi-Duran, R. Fritz, V. Olaya, R. Urzua-Leiva, G. I. Cárdenas-Jirón, D. P. Singh and F. Herrera, Anisotropic Band-Edge Absorption of Millimeter-Size Zn(3-Ptz)2 Single Crystal Metal-Organic Frameworks, 2020, DOI:10.26434/chemrxiv.13370414.v1.
- S. Bordiga, C. Lamberti, G. Ricchiardi, L. Regli, F. Bonino, A. Damin, K.-P. Lillerud, M. Bjorgen and A. Zecchina, Chem. Commun., 2004, 2300–2301 RSC.
- M. Alvaro, et al. , Chem.–Eur. J., 2007, 13, 5106–5112 CrossRef CAS.
- L.-M. Yang, P. Vajeeston, P. Ravindran, H. Fjellvag and M. Tilset, Inorg. Chem., 2010, 49, 10283–10290 CrossRef CAS.
- M. R. Ryder, L. Donà, J. G. Vitillo and B. Civalleri, ChemPlusChem, 2018, 83, 308–316 CrossRef CAS.
- R. H. French, J. W. Ling, F. S. Ohuchi and C. T. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 8496–8502 CrossRef CAS.
- V. Lacivita, M. Rérat, B. Kirtman, M. Ferrero, R. Orlando and R. Dovesi, J. Chem. Phys., 2009, 131, 204509 CrossRef.
- R. E. Stoiber and S. A. Morse, in Biaxial Crystal Optics, Springer US, Boston, MA, 1994, pp. 159–171 Search PubMed.
- J. E. Midwinter and J. Warner, Br. J. Appl. Phys., 1965, 16, 1135–1142 CrossRef.
- M. G. Moebius, F. Herrera, S. Griesse-Nascimento, O. Reshef, C. C. Evans, G. G. Guerreschi, A. Aspuru-Guzik and E. Mazur, Opt. Express, 2016, 24, 9932–9954 CrossRef CAS.
- M. O. Scully and M. S. Zubairy, Quantum Optics, Cambridge University Press, 2014 Search PubMed.
- D. Nikogosyan, Appl. Phys. A: Solids Surf., 1991, 52, 359–368 CrossRef.
- J. P. Villabona-Monsalve, O. Calderón-Losada, M. Nuñez Portela and A. Valencia, J. Phys. Chem. A, 2017, 121, 7869–7875 CrossRef CAS.
- N. P. Barnes, D. J. Gettemy and R. S. Adhav, J. Opt. Soc. Am., 1982, 72, 895–898 CrossRef CAS.
- U. Schlarb and K. Betzler, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 15613–15620 CrossRef CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- J. Li, S. Gauza and S.-T. Wu, J. Appl. Phys., 2004, 96, 19–24 CrossRef CAS.
- C.-W. Chen, H.-C. Jau, C.-H. Lee, C.-C. Li, C.-T. Hou, C.-W. Wu, T.-H. Lin and I. C. Khoo, Opt. Mater. Express, 2013, 3, 527–532 CrossRef CAS.
- N. Xie, H. Zhang, B. Liu, B. Song and J. Wu, J. Lightwave Technol., 2017, 35, 2966–2972 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05572g |
| This journal is © The Royal Society of Chemistry 2021 |