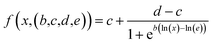Open Access Article
Open Access ArticleMolecular mechanism of inhibiting the SARS-CoV-2 cell entry facilitator TMPRSS2 with camostat and nafamostat†
Tim
Hempel
 ab,
Lluís
Raich‡
a,
Simon
Olsson‡
ab,
Lluís
Raich‡
a,
Simon
Olsson‡
 ah,
Nurit P.
Azouz
ah,
Nurit P.
Azouz
 cd,
Andrea M.
Klingler
c,
Markus
Hoffmann
cd,
Andrea M.
Klingler
c,
Markus
Hoffmann
 ef,
Stefan
Pöhlmann
ef,
Stefan
Pöhlmann
 ef,
Marc E.
Rothenberg
ef,
Marc E.
Rothenberg
 c and
Frank
Noé
c and
Frank
Noé
 *abg
*abg
aFreie Universität Berlin, Department of Mathematics and Computer Science, Berlin, Germany. E-mail: frank.noe@fu-berlin.de
bFreie Universität Berlin, Department of Physics, Berlin, Germany
cDivision of Allergy and Immunology, Cincinnati Children's Hospital Medical Center, Department of Pediatrics, University of Cincinnati College of Medicine, Cincinnati, OH, USA
dDepartment of Pediatrics, University of Cincinnati College of Medicine, Cincinnati, OH, USA
eInfection Biology Unit, German Primate Center – Leibniz Institute for Primate Research, Göttingen, Germany
fFaculty of Biology and Psychology, University Göttingen, Göttingen, Germany
gRice University, Department of Chemistry, Houston, TX, USA
hChalmers University of Technology, Department of Computer Science and Engineering, Sweden
First published on 13th November 2020
Abstract
The entry of the coronavirus SARS-CoV-2 into human lung cells can be inhibited by the approved drugs camostat and nafamostat. Here we elucidate the molecular mechanism of these drugs by combining experiments and simulations. In vitro assays confirm that both drugs inhibit the human protein TMPRSS2, a SARS-Cov-2 spike protein activator. As no experimental structure is available, we provide a model of the TMPRSS2 equilibrium structure and its fluctuations by relaxing an initial homology structure with extensive 330 microseconds of all-atom molecular dynamics (MD) and Markov modeling. Through Markov modeling, we describe the binding process of both drugs and a metabolic product of camostat (GBPA) to TMPRSS2, reaching a Michaelis complex (MC) state, which precedes the formation of a long-lived covalent inhibitory state. We find that nafamostat has a higher MC population than camostat and GBPA, suggesting that nafamostat is more readily available to form the stable covalent enzyme–substrate intermediate, effectively explaining its high potency. This model is backed by our in vitro experiments and consistent with previous virus cell entry assays. Our TMPRSS2–drug structures are made public to guide the design of more potent and specific inhibitors.
1 Introduction
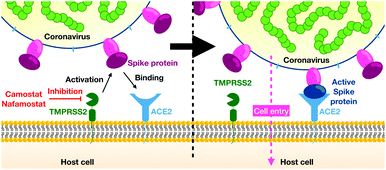
In December 2019 several cases of unusual and severe pneumonia were reported in the city of Wuhan, China. These cases were traced back to a new coronavirus, SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2); the disease is called COVID-19.1 As of October 11, 2020 there are over 37 million confirmed COVID-19 cases and more than 1 million deaths,2 with both numbers likely to be severe underestimates. Given estimates of the infection mortality rate of 0.4 to 1.4% (ref. 3–5) the virus has the potential to kill tens of millions of people unless efficient vaccines or drugs are available.As other coronaviruses,6–9 SARS-CoV-2 exploits host proteins to initiate cell-entry, in particular TMPRSS2 and ACE2, two membrane-bound proteins expressed in the upper and lower respiratory tract.10–13 TMPRSS2 contains an extracellular trypsin-like serine-protease domain that can proteolytically activate the spike (S) protein on the surface of SARS-CoV-2 viral particles14 (Fig. 1). While in certain cell lines, the S-protein can also be activated by the endo/lysosomal pH-dependent cysteine protease cathepsin L,14,15 virus entry into human airway cells14,16 seems to depend on TMPRSS2 but not cathepsin L. Consistently, epidemiological data of prostate cancer patients undergoing androgen-deprivation therapies, which lowers TMPRSS2 levels, indicate a lower risk of contracting the SARS-CoV-2 infection.17 We further note that low concentration levels of TMPRSS2 are observed in children and infants, possibly explaining lower risks of severe COVID-19 infections in younger age groups.18
TMPRSS2 is also exploited by other coronaviruses and influenza A viruses for activation of surface glycoproteins, viral spread, and pathogenesis.19–25 TMPRSS2 knock-out mice have no phenotype in the absence of infection,26 indicating that inhibiting TMPRSS2 function might not be associated with substantial unwanted side effects. As a result, TMPRSS2 is a promising therapeutic target in the context of influenza A and coronavirus infection, including SARS-CoV-2. Since TMPRSS2 is host encoded and thus genetically stable, treatment should be associated with a low risk of drug resistance.
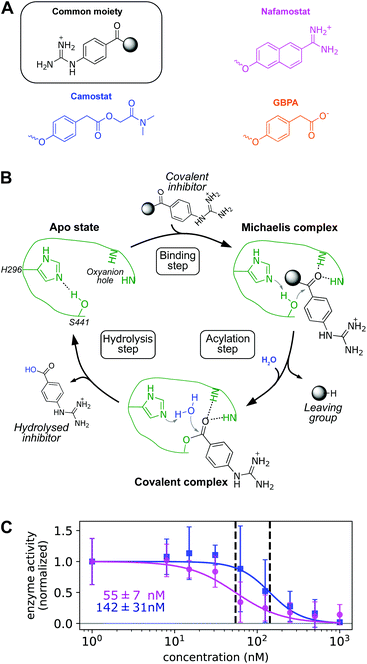
Here, we study the structural basis and molecular mechanism of TMPRSS2 inhibition by nafamostat, camostat, and its metabolic product 4-(4-guanidinobenzoyloxy)phenylacetic acid (GBPA). These guanidinobenzoyl-containing drugs are approved for human use in Japan and have been demonstrated to inhibit SARS-CoV-2 cell-entry.14,27–29 A recent survey of FDA approved drugs further found nafamostat to be an effective inhibitor of SARS-Cov-2 infection in human lung-cell cultures.30 We report experimental measurements demonstrating that nafamostat and camostat inhibit TMPRSS2 activity by using our recently established cell-based assay,31 consistent with in vitro enzymatic TMPRSS2 activity assays.32
Despite the hopes associated with TMPRSS2 inhibition, we are, as yet, lacking an experimental structure. We here go beyond the previous dependence on homology models by an extensive 330 microseconds of high-throughput all-atom molecular dynamics (MD) simulations and Markov modeling. This approach provides an ensemble of equilibrium structures of the protein–drug complex and also drug binding kinetics. We show that nafamostat, camostat, and GBPA are covalent inhibitors with an identical covalent complex, but their different inhibitory activity can be explained by different populations of their Michaelis complex preceding the covalent complex. These findings, combined with the simulation structures that we make publicly available, provide an important basis for developing more potent and specific TMPRSS2 inhibitors.
2 Results
Camostat and nafamostat inhibit the catalytic activity of TMPRSS2
First we confirm that camostat and nafamostat are TMPRSS2 inhibitors. To this end, we employ our recently reported activity assay31 of the full-length TMPRSS2 protein on the surface of live cells with both inhibitors (Fig. 2A). Briefly, we transfected the human cell-line HEK-293T with a TMPRSS2 expression vector. We then measured the protease activity of the transfected cells using the fluorogenic peptide substrate BOC-QAR-AMC, following incubation of the cell with increasing inhibitor concentrations. Peptide-digestion induced a minimal increase in fluorescent signal in control cells without exogenous TMPRSS2 expression (un-normalized mean enzyme activity = 2.4), while TMPRSS2 over-expression resulted in a much faster peptide digestion (un-normalized mean enzyme activity = 12.8). Therefore, our assay is mostly specific for TMPRSS2.31 Significantly lower enzyme activity at higher drug concentrations can thus be attributed to TMPRSS2 inhibition.For both camostat and nafamostat, we see a clear dose-dependent inhibition and estimate their respective IC50 values to 142 ± 31 nM and 55 ± 7 nM (Fig. 2C). Our results are consistent with the finding that both drugs inhibit cell entry of SARS-CoV-2 and other coronaviruses, and that nafamostat is the most potent inhibitor.27,28,32
Note that in humans, camostat is rapidly processed to 4-(4-guanidinobenzoyloxy)phenylacetic acid (GBPA) (Fig. 2A).33 It has been recently shown that GBPA also inhibits TMPRSS2 and cell entry of SARS-CoV-2 viruses, although slightly less efficiently than camostat.29 Hence, we subsequently study the molecular interactions between TMPRSS2 and all three compounds: camostat, GBPA, and nafamostat.
Equilibrium structures of TMPRSS2 in complex with camostat and nafamostat
We now set off to investigate the molecular mechanism of TMPRSS2 inhibition by nafamostat, camostat, and its metabolite GBPA. No TMPRSS2 crystal structure is available to date, however it has been shown that all-atom MD simulations can reliably model the equilibrium structures of proteins when (i) a reasonable model is available as starting structure, and (ii) simulations sample extensively, such that deficiencies of the starting structure can be overcome.35–39Here, we initialize our simulations with recent homology models of the TMPRSS2 protease domain and with camostat/nafamostat docked to them.40 Trypsins adopt a common fold and share an active-site charge relay system whose structural requirements for catalytic activity are well understood;41 we select our MD model consistent with these structural requirements. In particular, we focus on systems with Asp435 (substrate recognition) deprotonated and His296 (catalytic function) in a neutral form (Nδ protonated), as well as on the interactions of a charged lysine nearby the catalytic Asp345 (Fig. S1 and S2†).
In order to avoid artifacts of the initial structural model and to simulate the equilibrium ensemble of the TMPRSS2–drug complexes, we collected a total of 100 μs of simulation data for TMPRSS2–camostat, 50μs for TMPRSS2–GBPA, and 180 μs for TMPRSS2–nafamostat. Every drug dataset has converged RMSD distributions (Fig. S5†) and samples various drug poses and multiple association/dissociation events. Using Markov modeling42–46 we derive the structures of the long-lived (metastable) states and characterize protein–drug binding kinetics and thermodynamics.
We find TMPRSS2 has flexible loops around the binding site but maintains stable structural features shared by other trypsin-like proteases (Fig. 3A and S6†). After formation of a non-covalent substrate–enzyme complex (binding step, Fig. 2B), trypsins cleave peptide-like bonds in two catalytic steps, assisted by a conserved catalytic triad (Asp345, His296, and Ser441 in TMPRSS2). The first step involves the formation of a covalent acyl–enzyme intermediate between the substrate and Ser441.41 During this step, His296 serves as a general base to deprotonate the nucleophilic Ser441, and subsequently as a general acid to protonate the leaving group of the substrate. The second step involves the hydrolysis of the acyl–enzyme intermediate, releasing the cleaved substrate and restoring the active form of the enzyme (Fig. 2B).
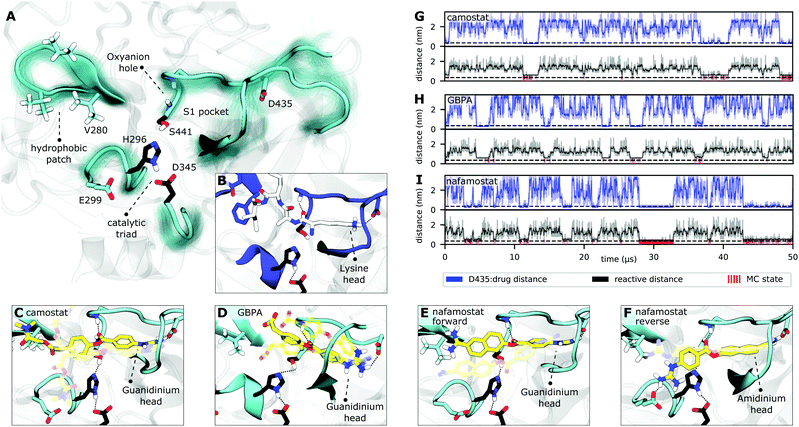 | ||
| Fig. 3 TMPRSS2 structure and Michaelis complex with camostat, its metabolic product GBPA, and nafamostat. (A) Active site overview of the catalytic domain of TMPRSS2. Protein flexibility is shown by cyan halo, catalytic triad is shown in black. (B) Pre-catalytic binding mode shown at example of trypsin peptide recognition (PDB ID 4Y0Y,34 peptide displayed in white). (C–F) Representative structures of camostat (C), GBPA (D), and nafamostat (E and F) in complex with TMPRSS2. All drugs (yellow licorice representation) bind into the S1 pocket of TMPRSS2, in (C–E) with their guanidinium heads interacting with D435, while (F) shows a reverse binding mode with nafamostat binding with its aminidinium head. (G–I) Markov model simulations of minimal distance to D435 (at the S1 pocket, blue), reactivity coordinate (black), and reactivity state (i.e. when trajectory is in MC state, red) for camostat (G), GBPA (H), and nafamostat (I). | ||
Along these two steps, the so called “oxyanion hole”, formed by the backbone NHs of Gly439 and Ser441, helps to activate and stabilize the carbonyl of the scissile bond. Another important structural feature is the S1 pocket, which contains a well conserved aspartate (Asp435) that is essential for substrate binding and recognition. At the opposite site of the S1 pocket, a loop containing a hydrophobic patch delimits the binding region of substrates within enzymatic active site. All these structural elements, known to play crucial roles in the function of serine proteases,41 are generally stable and preserved in our equilibrium structures (cf. Fig. S2 and S6†).
Structural basis of TMPRSS2 inhibition by camostat and nafamostat
Drugs with a guanidinobenzoyl moiety can inhibit trypsins by mimicking their natural substrates (Fig. 3B). Indeed, the ester group, resembling a peptide bond, can react with the catalytic serine with rates that are orders of magnitude faster,47 forming the acyl–enzyme intermediate. In contrast to peptide catalysis, the drug's guanidinobenzoyl group stays covalently linked to the catalytic serine with a small off-rate, rendering it an effective chemical inhibitor.48 Note that in its inhibited state, the TMPRSS2 active site is modified such that protease activity is disabled, preventing SARS-CoV-2 S-protein cleavage.The present MD simulations sample different conformations of the complex formed by the enzyme with each of the drugs that precede the covalent substrate–enzyme complex. We can, therefore, elucidate their binding and how specific interactions stabilize different modes. However, please note that our simulations do not simulate the covalent complex's formation. All binding modes mimic interactions made between trypsins and their natural substrates, in which lysine heads interact with a conserved aspartate in the S1 pocket (Asp435, Fig. 3B). In camostat, its metabolic product GPBA, and nafamostat, the role of the lysine heads is taken by the guanidinium heads which bind in the S1 pocket and also interact with Asp435 (Fig. 3C–E). However, the guanidinium–Asp435 salt bridge is formed and broken transiently especially for camostat and GBPA (Fig. 3G–I), indicating that these drugs are not optimized for the TMPRSS2 pocket (Fig. S4†).
Nafamostat also binds in a “reverse” orientation where the amidinium head binds into the S1 pocket and interacts with Asp435 (Fig. 3F).40 In this orientation, the guanidinium head mainly interacts with Glu299, with the drug reactive center slightly displaced from the oxyanion hole, while the “forward” orientation (Fig. 3E) keeps the amidinium head mainly nearby Val280, with the ester center well positioned for the reaction (Fig. S3†). This observation is in agreement with several crystal structures of acyl–enzyme intermediates between different trypsins and guanidinobenzoyl molecules bound to the S1 pocket (e.g. PDBs 2AH4,493DFL,50 1GBT51). There are also “inverse substrates” known to react with rates comparable to the ones of normal esters, suggesting that the inverted nafamostat orientation may also be reactive.41
A fraction of the bound-state structures resembles a reactive Michaelis complex (MC) which fulfills the necessary criteria for catalysis of the inhibitory acyl–enzyme complex: small distances of (i) the drug ester carbon to catalytic serine oxygen, and (ii) the catalytic serine hydrogen to catalytic histidine nitrogen (Methods). We observe that besides Asp435 binding to the S1 pocket, drugs in the MC state are particularly stabilized by the oxyanion hole. Our model predicts that nafamostat has the highest MC state population followed by camostat and GBPA (Fig. 4), an order that coincides with the one of experimental drug binding affinities.29 We note that the relative free energies of binding to the MC states are significantly different between nafamostat (2.1 ± 0.1 kcal mol−1) and the other drugs (2.8 ± 0.1 kcal mol−1 and 3.1 ± 0.2 kcal mol−1 for camostat and GBPA, respectively), with the bootstrap sample distributions of camostat and its metabolite displaying a partial overlap.
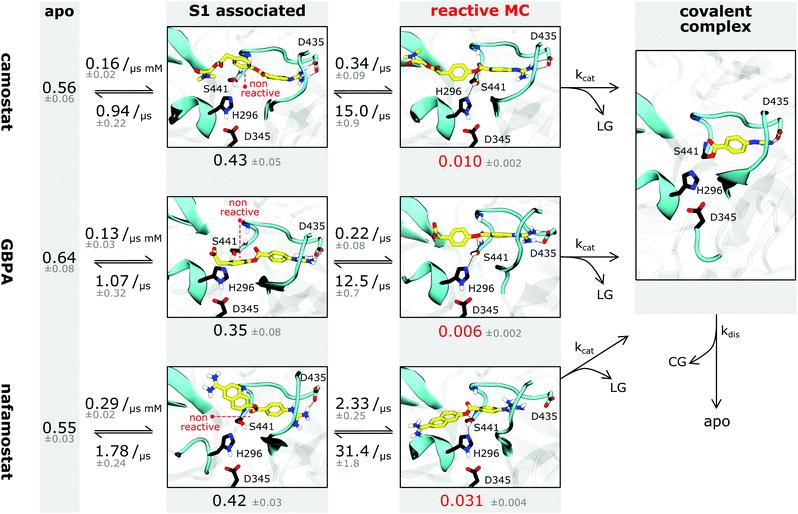 | ||
| Fig. 4 Binding kinetics model of camostat (top), camostat metabolic product GBPA (middle), and nafamostat (bottom). Inhibition process is depicted from left (apo state) to right (covalent complex). Single representative structures for each intermediate state are shown – note that all states have significant flexibility. Drugs are depicted in yellow, catalytic triad residues in black, leaving groups and covalent group are denoted by LG and CG, respectively. Rates and populations predicted by our model are annotated at reaction arrows and states, respectively. The covalent complex is illustrated using a structure with prostatin (PDB 3DFL50). | ||
Whereas the contact patterns of camostat and nafamostat associated states are similar, the leaving group in the inverted nafamostat conformation shows contacts predominantly with residues E299 and Tyr337 (Fig. S3†). GBPA, due to its shorter length, has less contacts to residues outside of the S1 pocket. In the reactive MC state, interestingly, all tested drugs display similar contact patterns overall, and their leaving groups bind in between Val280 and His296, with their ester group in contact with Ser441 (Fig. S3†).
Kinetic mechanism of TMPRSS2 inhibition by camostat, GBPA, and nafamostat
Finally, we investigate the molecular basis for the greater inhibition by nafamostat and formulate starting points for designing new and more efficient covalent TMPRSS2 inhibitors following these leads.To illustrate the reversible binding of camostat, its product GBPA, and nafamostat to TMPRSS2, we used our Markov models to simulate long time-scale trajectories of 50 μs (Fig. 3G–I). We see a clear correlation between tight inhibitor–Asp435 interactions and contact formation between catalytic serine and the inhibitor ester group, potentially forming a reactive complex. In other words, the binding of reactive drugs in the S1 pocket favors the interactions necessary for a catalytically competent MC.
We estimate the dissociation constants for the non-covalent complex, i.e. the ratio of dissociated state and non-covalent complex populations, to be between 6 and 9 mM for the three drugs. Even though our IC50-measurements include other processes and thus are not straightforward to compare, IC50-values in the 10–100s nanomolar range (i.e. 4–5 orders of magnitude smaller, Fig. 2C) are a strong indicator that the major source of inhibition cannot be the non-covalent complex, but is rather the longer-lived covalent acyl–enzyme complex. However, as all three drugs yield identical acyl–enzyme complexes, the differences in TMPRSS2 inhibition can only arise from either (1) the formation or population of their MCs, or (2) differences in the catalytic rate kcat of acylation.
Interestingly, we observe that the MSM-predicted populations of the MCs in nafamostat, camostat, and GBPA have approximate ratios of 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively, as well as a significantly higher on-rate for nafamostat (Fig. 4). A simple three-state kinetic model of dissociated state, MC and covalent complex shows that the overall association constant (Ka, ratio of inhibited versus apo protein states) directly scales with the association constant of the MC (KMa, ratio of MC versus dissociated states) by a constant factor (Methods):
1, respectively, as well as a significantly higher on-rate for nafamostat (Fig. 4). A simple three-state kinetic model of dissociated state, MC and covalent complex shows that the overall association constant (Ka, ratio of inhibited versus apo protein states) directly scales with the association constant of the MC (KMa, ratio of MC versus dissociated states) by a constant factor (Methods):
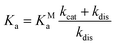 | (1) |
Simply speaking, this indicates that nafamostat is a better inhibitor because it is more often found in the reactive MC state, and is therefore more likely to be attacked by the catalytic serine oxygen and enter the long-lived acyl–enzyme inhibitor complex.
Moreover, we note that the kcat of acylation of these drugs may depend on their leaving group pKa's. Leaving groups with a low pKa will require less assistance from acid catalysis and will be easily displaced by the nucleophilic serine, favoring the formation of the acyl–enzyme intermediate. We expect the leaving group of nafamostat to have a lower pKa than the one of camostat, following the values of similar molecules such as naphthol (9.57 (ref. 52)) and 4-methylphenol (10.26 (ref. 53)), respectively. Indeed, these comparative insights are backed by computational pKa predictions for nafamostat (9.17), camostat (9.36), and GBPA (10.02) (Fig. S4†). We note that these predictions are made in aqueous solution, which could differ slightly from the estimates in the enzyme due to the different environment. Nonetheless, we expect the pKa values to be in the same relative order given that the three compounds have similar contacts with the enzyme in the reactive state (Fig. S3†). This suggests that the kcat of acylation will be slightly faster for nafamostat in particular compared to the camostat metabolic product GBPA, further contributing to nafamostat's superior inhibition of TMPRSS2.
3 Discussion
Camostat and nafamostat are promising drug candidates for a COVID-19 treatment strategy. Here we have combined cell-based assays, extensive molecular simulations, and Markov modeling to unravel the molecular action principle of these drugs and provide data that may help to improve them further.Our binding assays provide evidence that both inhibitors directly act on TMPRSS2 and that nafamostat is more potent compared to camostat, and this qualitative difference is in agreement with complementary in vitro assays on purified protein construct32 or cell-entry assays.27,28 We note that the absolute IC50 values differ between these three assay types, reflecting differences in experimental conditions and which function is being inhibited and measured.
While no crystallographic structure of TMPRSS2 is available, we provide extensive 330 microseconds of all-atom MD simulations starting from a homology model that generate stable equilibrium structure ensembles of the protein–drug complexes. These simulations sample multiple association/dissociation events and various drug poses in the protein active site. Our analyses show that the non-covalent complexes of nafamostat, camostat, and its metabolic product GBPA are relatively short-lived, suggesting that the main inhibitory effect is due to the formation of the long-lived covalent acyl–enzyme complex between the drug's guanidinobenzoyl moiety and the catalytic serine of TMPRSS2.
Although the MC state is not the main cause of inhibition, its population directly translates into the potency of the inhibitor, as higher MC population corresponds to a higher catalytic rate and therefore yields a larger population of inhibited enzyme. Consistently with the higher potency of nafamostat, it is found to have a threefold more stable MC compared to camostat, and sixfold compared to GBPA. A second contribution may be the pKa of drug leaving groups, affecting the rate of enzyme acylation.
Our detailed models of the thermodynamic and kinetics of inhibitor binding highlight the bound state's heterogeneity, with both drugs adopting multiple distinct poses. We note the importance of residue Asp435 in the conserved S1-pocket, which stabilizes the MC state and helps to orient the reactive molecules in a conformation that is suited for catalysis. Nafamostat has two groups that can potentially bind into the S1 pocket, whereas camostat has only one. However, we find that the population of S1 associated states are similar between nafamostat, camostat, and GBPA, suggesting that non-covalent inhibition is likely a minor contribution to the overall inhibition of TMPRSS2.
We conclude that the design of future TMPRSS2 inhibitors with increased potency and specificity should incorporate the following points:
First, stabilizing the non-covalent complex with the TMPRSS2 active site is beneficial for both, covalent and non-covalent inhibitors. As S1 pocket binding is a major contribution to the stability of the non-covalent complex, effective drugs may contain hydrogen bond donors and positively charged moieties that could interact principally with Asp435, but also with different backbone carbonyls of the loops that compose the cavity (e.g. from Trp461 to Gly464).
Second, for covalent inhibitors, we must consider that the catalytic serine is at a distance of around 1.3 nm from Asp435. Thus, the reactive center of an effective drug and its S1-interacting moieties should be within that distance. We note that, even though all three molecules fit well in the overall active site, the guanidinobenzoyl moiety is slightly shorter than the ideal size of the TMPRSS2 cavity (Fig. S4†). We further suggest that a drug should be size-compatible to the hydrophobic patch on the S1 distal site (Fig. 3A and S4†). We speculate that drugs with a large end to end distance and high rigidity may not fit well in the described TMPRSS2 scaffold, and in particular, might be significantly less reactive.
Third, optimizing the pKa of the drug's leaving group might be beneficial for improving covalent TMPRSS2 inhibitors. The first step of the reaction would be faster, and the acetyl–enzyme intermediate would accumulate. We note that the deacetylation off-rate must be very low, ideally on the order of magnitude of guanidinobenzoyl moiety containing drugs.
Finally, we make our simulated equilibrium structures of TMPRSS2 in complex with the simulated drugs available, hoping they will be useful to guide future drug discovery efforts.
4 Materials and methods
TMPRSS2 activity assays
The TMPRSS2 activity assay was described previously.31 Briefly, we transfected HEK-293T with a PLX304 plasmid containing the open reading frame (ORF) sequence of TMPRSS2 which encodes for the full length protein (492 amino acids). Control experiments are conducted with PLX304 plasmids.Eighteen hours later, we replaced the media to either PBS alone or PBS in the presence of varying concentrations of candidate inhibitors camostat and nafamostat. Fifteen minutes later, we added the fluorogenic substrate BOC-QAR-AMC to the wells to induce a measurable signal of enzyme activity. We measured the fluorescent signal immediately after adding the substrate, in 15 minutes intervals for a total time of 150 minutes.31 A baseline proteolytic activity of control cells was measured; we hypothesize that this is because of proteolytic cleavage of the substrate by endogenous transmembrane proteases. However, the TMPRSS2 overexpression cells have significantly increased proteolytic activity compared with control cells.31
To validate the exogenous expression of TMPRSS2, we performed western-blot analysis of cell lysates from TMPRSS2 overexpressing cells and control cells. A 60 kDa band was observed in TMPRSS2 overexpressing cells but not in control cells, which is the expected molecular weight of TMPRSS2 protein after post transcriptional modifications, indicating that the target protein has been successfully expressed.
IC50 estimation
We used a generalized log-logistic dose–response modelwith the concentration x, c and d representing the lower and upper limits, b steepness of the curve, and e to estimate IC50 values.54
Upper and lower limits were set to the means computed from control experiments with no drug (upper limit) and PLX plasmid (no TMPRSS2; background noise). We used scipy's55 curve fitting algorithms to extract the IC50 with error estimates.
Molecular dynamics simulations
MD simulations were run with OpenMM 7.4.0 (ref. 56) using the CHARMM 36 force field (2019 version).57 Camostat and nafamostat structures were taken from PubChem58 with PubChem CIDs 4413 (nafamostat) and 2536 (camostat), respectively, and modeled with the CHARMM general force field (CGenFF v. 4.3).59 We generated our MD setups with CharmmGUI.60 We initiate a simulation box of side length 7.5 nm with a NaCl ion concentration of 0.1 mol l−1 at neutral charge and the TIP3P water model.61 The setups contain 12038 (camostat), 12030 (GBPA), and 12039 (nafamostat) water molecules, respectively.We run simulations in the NPT ensemble and keep the temperature at 310 K (physiological temperature) and the pressure at 1 bar. We use a Langevin integrator with 5 fs integration step and heavy hydrogen approximation (4 amu). PME electrostatics, rigid water molecules, and a 1 nm cutoff for non-bonded interactions are used. Simulation times vary between 100 and 500 ns and accumulate to 100 μs (camostat), 50 μs (GBPA), 180 μs (nafamostat), respectively. Structures were visualized using VMD.62
Due to the lack of a crystal structure for TMPRSS2, MD simulations were seeded from a homology model. It is taken from ref. 40, model 3W94 is chosen based on precursive MD analyses that showed that 3W94 has the most stable catalytic triad configuration (Fig. S1 and S2†). The construct includes amino acids 256 to 491 of the full sequence, corresponding to the catalytic chain except for a C-terminal Glycine missing due to homology modeling against a shorter sequence. MD simulations are seeded as follows: equilibrated docking poses (highest scorers of ref. 40) of the ligand were generated in a precursive run using another homology model. We note that the used camostat docking pose resembles the one described by ref. 63. This data set was equilibrated with local energy minimization, 100 ps simulations with 2 fs time steps in NVT and NPT ensemble subsequently. Frames are selected based on a preliminary metastability analysis, protein conformation is constraint to 3W94 homology model using a constraint force minimizing minRMSD. Production run MD simulations are started from these poses, i.e. from the same protein configuration and with 77 (nafamostat) and 60 (camostat) ligand docking poses, respectively. To ensure convergence of sampling statistics, we ran multiple adaptive runs of simulations, seeding new simulations with coordinates associated with sparsely sampled states.
We later added the camostat metabolite GBPA by following the same setup procedure. Due to its similarity to camostat, we seeded production simulations from representative structures of the camostat stage 1 Markov model (described below) using 200 representative structures.
Markov modeling
We model the binding and unbinding rates in a two step procedure using Markov state type models.42–45,64–66 First, we describe drug unbound and associated states using a hidden Markov model (HMM).67 Second, we define a reactive state by using distance cutoffs.In detail, in the first stage we define distance features between drug guanidinium group and TMPRSS2 Asp435 (minimal distance), drug amidinium group and TMPRSS2 Asp435 (minimal distance, nafamostat only). We further use a binary “reactive” distance feature defined by drug ester carbon to catalytic Ser441-OG, and catalytic serine (HG) to catalytic histidine (NE2) and a threshold of 0.35 nm. If both last mentioned distances are below the threshold, both nucleophilic attack of the serine-OG to the drug ester group and proton transfer from serine to histidine are possible, thus defining the reactive state.
We discretize this space into 243 (camostat), 240 (GBPA), and 490 (nafamostat) states using regular spatial clustering and use an HMM at lag time 5 ns with 5 (camostat, GBPA) or 8 (nafamostat) hidden states. Nafamostat yields two metastable S1 associated states encoding for both binding directions, camostat/GBPA a single one, that are defined by being at salt bridge distance to Asp435. We note no significant correlation between the hidden states and the reactive state, i.e. reactivity is not metastable. Also note that in contrast to later modeling stages, reactivity according to this HMM does not necessitate S1 pocket binding. The described HMMs are used to generate the (non-equilibrium) time series presented in Fig. 3G–I. Besides distance to D435, we also show a reactivity coordinate which we define as the mean of (a) drug ester carbon to catalytic serine oxygen and (b) catalytic serine hydrogen to catalytic histidine nitrogen. Reactivity, i.e. when both reactive distances are within range, is indicated with red markers (MC state).
In the second stage, we split the HMM bound states into reactive and non-reactive by combining HMM Viterbi paths68 and the reactive state trajectories to one single discrete trajectory consisting of 3 states. We define the S1 associated states by filtering the Viterbi paths of the HMM according to S1-association. We use the reactivity trajectories to further bisect the S1 associated state into reactive and non-reactive states, yielding a three state discretization of the drug binding mode. Note that the S1-reactive state is a subset of the reactive state in the stage 1 HMM model.
We estimate a reversible maximum likelihood Markov state model (MSM) from the stage 2 trajectories as described in ref. 45. We report the stationary probability vector as well as transition rates. The latter are approximated using the matrix logarithm approximation of scipy55 to compute the transition rate matrix R from the transition probability matrix T using the definition T = exp(Rτ) with the lag time τ. We found that all reported quantities are converged with respect to the lag time above τ = 500 ns which was thus chosen as the model lag time. Errors are estimated by bootstrapping validation using a random sample (with replacement) of the stage 2 trajectory data. All MSM/HMM analyses were conducted using the PyEMMA 2 software (version 2.5.7).69
Dissociation constants Kd = punbound/pbound from the non-covalent state were estimated from this model and amount to 5.95 mM (4.60, 7.30) for camostat, 8.45 mM (5.81, 11.65) for GBPA, and 6.07 mM (5.55, 6.93) for nafamostat (68% confidence intervals).
Kinetic model
Simplifying the binding kinetics into a three-state model describing the binding to/dissociation from the Michaelis complex (ligand concentration c and rates kon, koff), catalytic rate of entering the covalent complex (kcat) and dissociation to the apo state (kdis), the kinetics are described by the rate matrix: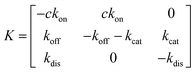 | (2) |
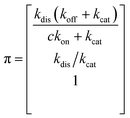 | (3) |
The overall dissociation constant is then:
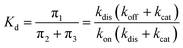 | (4) |
The non-covalent dissociation constant of the Michaelis complex:
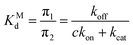 | (5) |
The dissociation constant scales as:
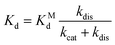 | (6) |
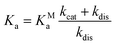 | (7) |
Software and data availability
Structural ensembles of camostat, GBPA, and nafamostat binding poses are published online at https://github.com/noegroup/tmprss2_structures.Author contributions
M. H., S. P., M. E. R., and F. N. designed the study. T. H., L. R., S. O., N. P. A., and A. M. K. performed research. T. H., L. R., S. O., and N. P. A. analyzed the data. T. H., L. R., S. O., F. N. wrote the manuscript.Conflicts of interest
M. E. R. is a consultant for Pulm One, Spoon Guru, ClostraBio, Serpin Pharm, Allakos, Celgene, Astra Zeneca, Arena Pharmaceuticals, GlaxoSmith Kline, Guidepoint and Suvretta Capital Management, and has an equity interest in the first five listed, and royalties from reslizumab (Teva Pharmaceuticals), PEESSv2 (Mapi Research Trust) and UpToDate. M. E. R. is an inventor of patents owned by Cincinnati Children's Hospital.Acknowledgements
We acknowledge financial support from Deutsche Forschungsgemeinschaft DFG (SFB/TRR 186, Project A12), the European Commission (ERC CoG 772230 “ScaleCell”), the Berlin Mathematics Center MATH+ (AA1-6) and the Federal Ministry of Education and Research BMBF (BIFOLD and RAPID Consortium, 01KI1723D). Stefan Pöhlmann was supported by DFG (PO 716/11-1) and BMBF (01K11723D). We are grateful for in-depth discussions with John D. Chodera (MSKCC New York), Matthew D. Hall (NIH), Katarina Elez, Robin Winter, Tuan Le, Moritz Hoffmann (FU Berlin), and the members of the JEDI COVID-19 grand challenge.References
- C. Sohrabi, et al., World Health Organization Declares Global Emergency: A Review of the 2019 Novel Coronavirus (COVID-19), Int. J. Surg., 2020, 76, 71–76 CrossRef.
- The World Health Organization, Weekly Epidemiological Update, Coronavirus disease 2019 (COVID-19), 12 October 2020 Search PubMed.
- T. W. Russell, et al., Estimating the Infection and Case Fatality Ratio for Coronavirus Disease (COVID-19) Using Age-Adjusted Data from the Outbreak on the Diamond Princess Cruise Ship, February 2020, Eurosurveillance, 2020, 25(12), 2000256 CrossRef.
- H. Streeck et al., Infection Fatality Rate of SARS-CoV-2 Infection in a German Community with a Super-Spreading Event, 2020, medRxiv, DOI:10.1101/2020.05.04.20090076.
- R. Verity, et al., Estimates of the Severity of Coronavirus Disease 2019: A Model-Based Analysis, Lancet Infect. Dis., 2020, 20(6), 669–677 CrossRef CAS.
- H. Hofmann and S. Pöhlmann, Cellular Entry of the SARS Coronavirus, Trends Microbiol., 2004, 12(10), 466–472 CrossRef CAS.
- W. Li, et al., Angiotensin-Converting Enzyme 2 is a Functional Receptor for the SARS Coronavirus, Nature, 2003, 426(6965), 450–454 CrossRef CAS.
- S. Matsuyama, et al., Efficient Activation of the Severe Acute Respiratory Syndrome Coronavirus Spike Protein by the Transmembrane Protease TMPRSS2, J. Virol., 2010, 84(24), 12658–12664 CrossRef CAS.
- S. Belouzard, V. C. Chu and G. R. Whittaker, Activation of the SARS Coronavirus Spike Protein via Sequential Proteolytic Cleavage at Two Distinct Sites, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(14), 5871–5876 CrossRef CAS.
- C. G. K. Ziegler, et al., SARS-CoV-2 Receptor ACE2 is an Interferon-Stimulated Gene in Human Airway Epithelial Cells and is Detected in Specific Cell Subsets across Tissues, Cell, 2020, 181(5), 1016–1035 CrossRef CAS.
- S. Lukassen, et al., SARS-CoV-2 Receptor ACE2 and TMPRSS2 are Primarily Expressed in Bronchial Transient Secretory Cells, EMBO J., 2020, 39(10), e105114 CrossRef CAS.
- K. Bilinska, P. Jakubowska, C. S. Von Bartheld and R. Butowt, Expression of the SARS-CoV-2 Entry Proteins, ACE2 and TMPRSS2, in Cells of the Olfactory Epithelium: Identification of Cell Types and Trends with Age, ACS Chem. Neurosci., 2020, 11(11), 1555–1562 CrossRef CAS.
- Y. J. Hou, et al., SARS-CoV-2 Reverse Genetics Reveals a Variable Infection Gradient in the Respiratory Tract, Cell, 2020, 182(2), 429–446 CrossRef CAS.
- M. Hoffmann, et al., SARS-CoV-2 Cell Entry Depends on ACE2 and TMPRSS2 and is Blocked by a Clinically Proven Protease Inhibitor, Cell, 2020, 181(2), 271–280 CrossRef CAS.
- T. Ou et al., Hydroxychloroquine-mediated inhibition of SARS-CoV-2 entry is attenuated by TMPRSS2, 2020, bioRxiv, DOI:10.1101/2020.07.22.216150.
- M. Hoffmann, et al., Chloroquine does not inhibit infection of human lung cells with SARS-CoV-2, Nature, 2020, 585, 588–590 CrossRef CAS.
- M. Montopoli, et al., Androgen-Deprivation Therapies for Prostate Cancer and Risk of Infection by SARS-CoV-2: A Population-Based Study (N = 4532), Ann. Oncol., 2020, 31(8), 1040–1045 CrossRef CAS.
- B. A. Schuler et al., Age-Determined Expression of Prim ing Protease TMPRSS2 and Localization of SARS-CoV-2 Infection in the Lung Epithelium, 2020, bioRxiv, DOI:10.1101/2020.05.22.111187.
- Y. Zhou, et al., Protease Inhibitors Targeting Coron avirus and Filovirus Entry, Antiviral Res., 2015, 116, 76–84 CrossRef CAS.
- N. Iwata-Yoshikawa, et al., TMPRSS2 Contributes to Virus Spread and Immunopathology in the Airways of Murine Models after Coronavirus Infection, J. Virol., 2019, 93(6), e01815-18 CrossRef.
- B. Hatesuer, et al., Tmprss2 is Essential for Influenza H1N1 Virus Pathogenesis in Mice, PLoS Pathog., 2013, 9(12), e1003774 CrossRef.
- C. Tarnow, et al., TMPRSS2 is a Host Factor that is Essential for Pneumotropism and Pathogenicity of H7N9 Influenza A Virus in Mice, J. Virol., 2014, 88(9), 4744–4751 CrossRef.
- K. Sakai, et al., The Host Protease TMPRSS2 Plays a Major Role in in Vivo Replication of Emerging H7N9 and Seasonal Influenza Viruses, J. Virol., 2014, 88(10), 5608–5616 CrossRef.
- R. L. O. Lambertz, et al., Tmprss2 Knock-out Mice are Resistant to H10 Influenza A Virus Pathogenesis, J. Gen. Virol., 2019, 100(7), 1073–1078 CrossRef CAS.
- R. L. O. Lambertz, et al., H2 Influenza A Virus is not Pathogenic in Tmprss2 Knock-out Mice, Virol. J., 2020, 17(1), 56 CrossRef CAS.
- T. S. Kim, C. Heinlein, R. C. Hackman and P. S. Nelson, Phenotypic Analysis of Mice Lacking the Tmprss2-Encoded Protease, Mol. Cell. Biol., 2006, 26(3), 965–975 CrossRef CAS.
- M. Hoffmann, et al., Nafamostat Mesylate Blocks Activation of SARS-CoV-2: New Treatment Option for COVID-19, Antimicrob. Agents Chemother., 2020, 64(6), e00754-20 CrossRef.
- M. Yamamoto, et al., The Anticoagulant Nafamostat Potently Inhibits SARS-CoV-2 S Protein-Mediated Fusion in a Cell Fusion Assay System and Viral Infection in Vitro in a Cell-Type-Dependent Manner, Viruses, 2020, 12(6), 629 CrossRef CAS.
- M. Hoffmann et al., Camostat Mesylate Inhibits SARS CoV-2 Activation by TMPRSS2-Related Proteases and Its Metabolite GBPA Exerts Antiviral Activity, 2020, bioRxiv, DOI:10.1101/2020.08.05.237651.
- M. Ko, S. Jeon, W.-S. Ryu and S. Kim, Comparative analysis of antiviral efficacy of FDA-approved drugs against SARS-CoV-2 in human lung cells, J. Med. Virol., 2020, 1–6 Search PubMed.
- N. P. Azouz, A. M. Klingler, and M. E. Rothenberg. Alpha 1 Antitrypsin Is an Inhibitor of the SARSCoV2–Priming Protease TMPRSS2, 2020, bioRxiv, DOI:10.1101/2020.05.04.077826.
- J. H. Shrimp et al., An Enzymatic TMPRSS2 Assay for Assessment of Clinical Candidates and Discovery of Inhibitors as Potential Treatment of COVID-19, 2020, bioRxiv, DOI:10.1101/2020.06.23.167544.
- I. Midgley, et al., Metabolic Fate of 14 C-Camostat Mesylate in Man, Rat and Dog after Intravenous Adminis tration, Xenobiotica, 1994, 24(1), 79–92 CrossRef CAS.
- S. Ye, et al., Fluorine Teams up with Water to Restore Inhibitor Activity to Mutant BPTI, Chem. Sci., 2015, 6(9), 5246–5254 RSC.
- N. Plattner and F. Noé, Protein Conformational Plasticity and Complex Ligand-Binding Kinetics Explored by Atomistic Simulations and Markov Models, Nat. Commun., 2015, 6, 7653 CrossRef.
- V. A. Voelz, G. R. Bowman, K. Beauchamp and V. S. Pande, Molecular Simulation of Ab Initio Protein Folding for a Millisecond Folder NTL9(1-39), J. Am. Chem. Soc., 2010, 132(5), 1526–1528 CrossRef CAS.
- N. Plattner, S. Doerr, G. D. Fabritiis and F. Noé, Complete Protein–Protein Association Kinetics in Atomic Detail Revealed by Molecular Dynamics Simulations and Markov Modelling, Nat. Chem., 2017, 9(10), 1005 CrossRef CAS.
- K. Lindorff-Larsen, et al., Systematic Validation of Protein Force Fields against Experimental Data, PLoS One, 2012, 7(2), e32131 CrossRef CAS.
- A. Raval, S. Piana, M. P. Eastwood, R. O. Dror and D. E. Shaw, Refinement of Protein Structure Homology Models via Long, All-Atom Molecular Dynamics Simulations, Proteins, 2012, 80, 2071–2079 CrossRef CAS.
- S. Rensi et al., Homology Modeling of TMPRSS2 Yields Candidate Drugs That May Inhibit Entry of SARS-CoV-2 into Human Cells, 2020, chemRxiv, DOI:10.26434/chemrxiv.12009582.
- L. Hedstrom, Serine Protease Mechanism and Specificity, Chem. Rev., 2002, 102(12), 4501–4524 CrossRef CAS.
- W. C. Swope, J. W. Pitera and F. Suits, Describing Protein Folding Kinetics by Molecular Dynamics Simulations. 1. Theory, J. Phys. Chem. B, 2004, 108(21), 6571–6581 CrossRef CAS.
- N. Singhal, C. D. Snow and V. S. Pande, Using Path Sampling to Build Better Markovian State Models: Predicting the Folding Rate and Mechanism of a Tryptophan Zipper Beta Hairpin, J. Chem. Phys., 2004, 121(1), 415–425 CrossRef CAS.
- F. Noé, C. Schütte, E. Vanden-Eijnden, L. Reich and T. R. Weikl, Constructing the Equilibrium Ensemble of Folding Pathways from Short Off-Equilibrium Simulations, Proc. Natl. Acad. Sci. U. S. A., 2009, 106(45), 19011–19016 CrossRef.
- J.-H. Prinz, et al., Markov Models of Molecular Kinetics: Generation and Validation, J. Chem. Phys., 2011, 134(17), 174105 CrossRef.
- B. E. Husic and V. S. Pande, Markov State Models: From an Art to a Science, J. Am. Chem. Soc., 2018, 140(7), 2386–2396 CrossRef CAS.
- B. Zerner, R. P. M. Bond and M. L. Bender, Kinetic Evidence for the Formation of Acyl-Enzyme Intermediates in the α-Chymotrypsin-Catalyzed Hydrolyses of Specific Substrates, J. Am. Chem. Soc., 1964, 86(18), 3674–3679 CrossRef CAS.
- M. K. Ramjee, I. M. Henderson, S. B. McLoughlin and A. Padova, The Kinetic and Structural Characterization of the Reaction of Nafamostat with Bovine Pancreatic Trypsin, Thromb. Res., 2000, 98(6), 559–569 CrossRef CAS.
- E. S. Radisky, J. M. Lee, C.-J. K. Lu and D. E. Koshland, Insights into the serine protease mechanism from atomic resolution structures of trypsin reaction intermediates, Proc. Natl. Acad. Sci. U. S. A., 2006, 103(18), 6835–6840 CrossRef CAS.
- K. W. Rickert, et al., Structure of Human Prostasin, a Target for the Regulation of Hypertension, J. Biol. Chem., 2008, 283(50), 34864–34872 CrossRef CAS.
- W. F. Mangel, et al., Structure of an acyl-enzyme intermediate during catalysis: (guanidinobenzoyl)trypsin, Biochemistry, 1990, 29(36), 8351–8357 CrossRef CAS.
- Z. Rappoport, Handbook of Tables for Organic Com pound Identification, Cleveland, Chemical Rubber Co., 1967 Search PubMed.
- P. Pearce and R. Simkins, Acid Strengths of Some Substituted Picric Acids, Can. J. Chem., 1968, 46(2), 241–248 CrossRef CAS.
- C. Ritz, F. Baty, J. C. Streibig and D. Gerhard, Dose-Response Analysis Using R, PLoS One, 2015, 10(12), e0146021 CrossRef.
- P. Virtanen, et al., SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS.
- P. Eastman, et al., OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics, PLoS Comput. Biol., 2017, 13(7), e1005659 CrossRef.
- R. B. Best, et al., Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ 1 and χ 2 Dihedral Angles, J. Chem. Theory Comput., 2012, 8(9), 3257–3273 CrossRef CAS.
- S. Kim, et al., PubChem 2019 Update: Improved Ac cess to Chemical Data, Nucleic Acids Res., 2019, 47(D1), D1102–D1109 CrossRef.
- K. Vanommeslaeghe, et al., CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields, J. Comput. Chem., 2009, 31, 671–690 Search PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, CHARMM-GUI: A Web-Based Graphical User Interface for CHARMM”, J. Comput. Chem., 2008, 29(11), 1859–1865 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of Simple Poten tial Functions for Simulating Liquid Water, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS.
- V. Kumar, et al., Withanone and Withaferin-A Are Predicted to Interact with Transmembrane Protease Ser ine 2 (TMPRSS2) and Block Entry of SARS-CoV-2 into Cells, J. Biomol. Struct. Dyn., 2020, 1–13 Search PubMed.
- C. Schütte, A. Fischer, W. Huisinga and P. Deuflhard, A Direct Approach to Conformational Dynamics Based on Hybrid Monte Carlo, J. Comput. Phys., 1999, 151(1), 146–168 CrossRef.
- F. Noé, I. Horenko, C. Schütte and J. C. Smith, Hierarchical Analysis of Conformational Dynamics in Biomolecules: Transition Networks of Metastable States, J. Chem. Phys., 2007, 126(15), 155102 CrossRef.
- F. Noé, Probability Distributions of Molecular Observables Computed from Markov Models, J. Chem. Phys., 2008, 128(24), 244103 CrossRef.
- F. Noé, H. Wu, J.-H. Prinz and N. Plattner, Projected and Hidden Markov Models for Calculating Kinetics and Metastable States of Complex Molecules, J. Chem. Phys., 2013, 139(18), 184114 CrossRef.
- L. R. Rabiner, A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition, Proc. IEEE, 1989, 77(2), 257–286 CrossRef.
- M. K. Scherer, et al., PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models, J. Chem. Theory Comput., 2015, 11(11), 5525–5542 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05064d |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2021 |