Student success and the high school-university transition: 100 years of chemistry education research

Abstract

The 100th anniversary of the first article (published in 1921) examining student success and the high school to university transition in chemistry provides an excellent opportunity to consider what has – and has not – changed in chemistry education. This review details the development and findings of chemistry education research specifically as it relates to student learning and success over this extended time period. After considering the changing educational context and definition of success, this research will be described under three main themes: different ways of knowing (learning objectives and outcomes), thinking (scientific reasoning and problem solving), and learning (preferences and approaches to studying). A key finding is that while our understanding of effective teaching and learning has advanced significantly since the early 1900s, so too have the curriculum expectations and cognitive demands placed upon students increased significantly. Thus despite the many advances and innovations in chemistry education, an achievement gap persists between high school and post-secondary education for many students to this day. A comprehensive picture of the factors influencing student success developed from the research literature not only helps understand this disconnect; it also provides an opportunity to reflect on lessons learned for teaching, learning, and directions for future research.

---

Introduction

The issue of student success is a recurring theme in chemical education research, as evidenced by the substantial number of research articles published since the appearance of the first such paper in 1921 (Powers, 1921). Although the specific questions asked – and the methods employed to answer them – have increased in sophistication and complexity over the years, the fundamental issue remains the same: why is it that students with comparable backgrounds and high school grades achieve highly variable levels of success (as measured by final course grades) in their first post-secondary chemistry course? Related questions are: can we predict which students are most at-risk of such failure; and what might we do to mitigate such undesirable outcomes? Is such failure a result, as some post-secondary instructors might claim, of students undertaught and underprepared by their high schools? Or is it, as some students and teachers might claim, a consequence of fossilized teaching and assessment practices at universities out of touch with the realities of modern education? Or is it the case, as many non-chemists seem to imply, that chemistry is an intrinsically hard subject that only a select few can – or indeed want to – master? Such questions are becoming all the more urgent as colleges and universities face increasing financial constraints and growing demands for greater accountability in the way public money is spent.

A review (constituting part of the present paper) undertaken as part of a research study to investigate the questions outlined above revealed a substantial body of work in the literature. While this clarified several issues, it was discouraging to find that a significant disconnect between performance in high school and college or university persists, despite considerable advances in understanding student learning and many reform initiatives (Stone, 2010, 2021). To illustrate, Fig. 1 shows reported high school and actual first-year chemistry grades for students participating in an annual survey from 2006–2010 (Stone, 2010, 2011). These students had all experienced the same recent high school curriculum and assessment guidelines;† yet, as will be shown, there is no better correlation between high school and university grades than was being reported in the 1920s!

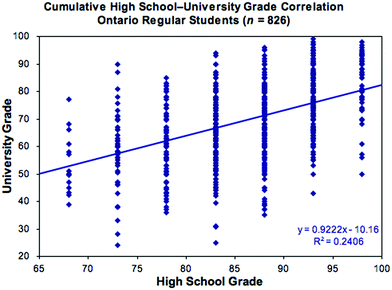Fig. 1 Representative correlation plot of first-year university versus reported high school chemistry grade. for details see: Stone (2010, 2011).

This further raises the question of whether educational research in general – and chemistry education research in particular – is of any actual benefit, either to students or instructors. The purpose of this review is therefore three-fold: to provide an extensive review of the research on the student transition from high school to post-secondary education; to relate this to relevant research on teaching and learning that can illuminate the observed data; and to discuss the lessons that can be drawn from this body of work for both chemistry teaching and education research. Finally, it should be noted that while the focus here is necessarily constrained to chemistry, an equally extensive body of work exists in the mathematics, physics, and engineering education literature, echoing the same themes, findings, and concerns.

Establishing context and defining success

Before reviewing the literature on this subject, it is essential to establish the context within which the concept of student success is being studied. The majority of the quantitative research on this subject is situated within the context of North American (and primarily US) education. This is important, as there are significant structural differences between Canada and the US on one hand, and the United Kingdom and numerous Commonwealth countries on the other (Schwartz, 2006). First, the final two years of high school in North America (grades 11 and 12) typically require students to take courses across multiple subjects rather than concentrate on just three or four as is common with A-levels. Second, North American colleges and universities operate predominantly on a liberal arts tradition, where students take a general foundation year before specializing in their degree subject from second (or third) year onwards, and must also take a certain number of additional courses drawn from the arts, humanities, and sciences as breadth requirements; this differs markedly from the traditional UK approach of studying a specific subject (with minimal required courses in cognate disciplines) from year one.

One major consequence for North American post-secondary education is that most students taking first-year undergraduate chemistry are not chemistry students; they are, by a large majority, life science or ‘pre-med’ students taking chemistry either as a breadth requirement or as a pre-requisite for their major subject or subsequent application to a professional program (medicine, nursing, dentistry, etc.; see for example George et al., 1987). For example, at the author's home institution (a large publicly funded research and teaching university), no more than 10% of the ∼2000 students taking first-year chemistry are in the course required by our chemistry degree programs, and not all of those will pursue a degree in chemistry. These numbers are comparable for peer institutions of similar size across North America, as evident from discussions with colleagues and the many research studies cited below. A firm ratio is hard to estimate due to differences between institutions – some chemistry faculty also teach engineering students, for example, while others do not – but is likely in the 5–10% range.

Another consequence is that students taking first-year undergraduate chemistry will not have studied the subject to the same breadth and depth as might be expected from a two-year A-level program and may not have taken all the mathematics courses expected of a chemistry student. Calculus, for example, is frequently taught as a separate course in high school and some students may not have taken it even though it is a common admission requirement for science programs; similarly, many life science students avoid taking pre-university physics, while there are always a small number who switched degree program and lack pre-university chemistry as well.

Finally, there are not now (generally speaking) the same regional or national examination boards in North America overseeing high school courses and final exams that there are in the UK and other countries. Curriculum content and assessment standards are usually set at the state/provincial rather than national level, although initiatives have been undertaken to define common standards for adoption by the relevant agencies, such as the Next Generation Science Standards‡ and Common Core§ initiatives. Schools may also, to varying degrees, offer courses under the aegis of the Advanced Placement (AP)¶ and International Baccalaureate (IB)|| programs; these function in much the same way by defining curriculum and assessment expectations, and providing common final exams.

In contrast to these differences, the primary measure of success has consistently been the final course grade. While less than ideal for various reasons, this single measure has the practical advantage of being both widely available and, ultimately, the arbiter of progression to the next level of education. In fact, for many early studies it was the only measure of success available. Intuitively, we might conceive of success in the high school–university transition as maintaining or improving upon prior performance. That is, successful students should exhibit some evidence of learning gain as they progress through their education. Yet the majority of students either maintain or achieve lower grades in their first post-secondary chemistry course (Stone, 2010, 2011), a consistent observation over the past 100 years and a major driver of the research reviewed here.

Surveying the literature: scope and methods

A review spanning 100 years of research is obviously an ambitious undertaking that can only hope to be extensive rather than exhaustive. As such, an initial literature survey was performed by a keyword search using the on-line database maintained by the Chemical Abstracts Service of the American Chemical Society, as well as the social sciences citation index within the Web of Science database. Further articles were identified from these by following both reverse and forward citation chains, as well as checking current publications in this journal and the Journal of Chemical Education. For the earliest literature (roughly pre-1960), this included papers concerned with the transition into general or physical science rather than just chemistry; for more recent literature, the search was increasingly restricted to chemistry or the development and application of survey instruments of use in chemistry education research.

In selecting articles for inclusion in this review, several criteria were applied. These included whether the research was original for the time, provided fresh insight or contrary evidence to existing knowledge, was associated with a major reform in curriculum or educational practice, employed a new quantitative or qualitative research methodology or instrument, or examined the effectiveness of novel pedagogical techniques for improving student learning and outcomes. Given the exponential growth of the research literature over the period in question, it was once again necessary to be increasingly selective in describing more recent research. As a result, the reader may well notice certain gaps or omissions; while inevitable given the sheer volume of relevant research, reviews and textbooks have been included where possible to provide links to this additional material.

A key aim in compiling this review was to provide a narrative account of the development of chemistry education and research at the high school and post-secondary level that would be informative to those already familiar with the field yet remain accessible for those new to such studies. The review itself is therefore presented in four main sections. First, quantitative studies of the relation between high school and first year college or university chemistry grades are described within the context of developing curriculum and pedagogical practices. Then, the factors affecting student learning and outcomes are described within the context of developments in educational and cognitive psychology under three broad and overlapping themes, being different ways of knowing, thinking, and learning. Finally, these findings are used to address the questions raised in the introduction and provide insights of relevance to teaching chemistry under the conditions resulting from the current pandemic.

High school grades and post-secondary success

Early quantitative studies (ca. 1920–1950)

The earliest published research – at least amongst North American institutions – generally employed grade range comparisons in efforts to decide whether students benefitted at all from taking chemistry in high school and, that being the case, whether post-secondary institutions should offer differentiated instruction to those entering with and without high school chemistry (Powers, 1921; Everhart and Ebaugh, 1925; Fry, 1925; Brown, 1926; Glasoe, 1929). This focus reflects the historical reality that many high schools would not have offered grade 12 or equivalent chemistry at all due to low student numbers and lack of facilities, a situation that would persist in some jurisdictions until the 1960s. For example, of students completing mandatory schooling in Ontario in 1948, only 61% continued to grade 9, 46% to grade 11, and only 4% entered university where the principal admissions requirements for science were English, Mathematics, and Latin (Gidney, 1999). These numbers increased dramatically through the 1950s onwards as socioeconomic circumstances changed and mandatory schooling was extended. Similar expansions took place across the US, for many of the same reasons (Brown and Obourn, 1956).

This period also saw the beginnings of diagnostic or placement exams (Cornog and Stoddard, 1925, 1926; Scofield, 1927; Slocombe, 1927). Most studies were purely qualitative in nature, but one (Herrmann, 1931) included a high school experience survey covering factors such as use of a text, teaching style, and the frequency of labs and demonstrations. These students were quite divided on whether their high school chemistry course was beneficial, with the author noting that “Various expletives accompanied the answers to these questions.” Such disparate and strong opinions are still voiced by students today! It should also be pointed out that the prevailing mode of education at this time was very different to today, with much more of an emphasis on the transmission of information (often by copying and memorization) by expert to novice.

Research continued along the same lines through to the late 1950s, with the focus broadening to include measures of intelligence, demographics, literacy skills, and the impact of high school math and physics courses. While methodology, rigour, and details vary, it was found that psychological test scores** and high school chemistry, math, and physics grades were each important – but insufficient – determinants of success in post-secondary chemistry. This is well-illustrated by those studies employing forms of correlation analysis (Hill, 1935; Clark, 1938; McQuary et al., 1952; Kunhart et al., 1958), the large-scale survey described by Brasted (1957), and the development of the Toledo Chemistry Placement Examination (TCPE)†† by Hovey and Krohn (1958, 1963). The many studies from this period comparing grade distributions support the same general conclusions, however the extent of the variation in individual student outcomes is effectively masked in the process.

From descriptive to conceptual chemistry (ca. 1950–1980)

Reaction to the launch of Sputnik in October 1957 combined with the radical advances in industry and technology stemming from World War 2 galvanized public opinion and government policy towards a major change in how science was viewed and taught in North America and Western Europe (Brown and Obourn, 1956; Gidney, 1999; Johnstone, 2010). In particular, there was a shift from the traditional descriptive approach to a more conceptual emphasis as exemplified by the Chemical Bond Approach (CBA) (Strong, 1962) and Chemistry Educational Materials Study (CHEM Study) (Clader, 1963; Pimentel, 1963) programs in the United States and Nuffield Chemistry in the United Kingdom, amongst others. These programs also included a strong emphasis on experimental chemistry, providing multiple laboratory experiments throughout their curricula to illustrate the concepts being taught.

In light of this unique situation, the chemistry educators at the high school and post-secondary levels developing these initiatives aimed to (in the words of Clader):

“give students a preliminary understanding of what chemistry is about, rather than simply an encyclopaedic collection of chemical reactions and laboratory techniques, or a mere overview of diverse conclusions held by chemists today” (Clader, 1963, p.126)

While enthusiastically adopted by many, and mandated in multiple jurisdictions, this shift in emphasis from factual information to conceptual understanding was not without its critics. The main criticisms were: increased cognitive demands due to the emphasis on conceptual understanding, the number of topics, and a lack of research on the best topical order for student learning (Uricheck, 1967; Davenport, 1968; Swartney, 1969; Shayer, 1970; Ingle and Shayer, 1971; Williams et al., 1979; Johnstone, 2010). The cognitive and conceptual challenges will be addressed later. Certainly, however, implementation of the new curricula was not without its challenges (Ramsey, 1970; Even, 1976). Taken against a backdrop of declining science enrolment in the face of rising student numbers associated with the ‘baby boom’ generation, these reforms could even be seen as having been over-ambitious (Davenport, 1968; Johnstone, 2010).

An open question during this period – especially when reviewing the research literature – was whether the new high school curricula contributed to both improved student outcomes and a more successful transition to post-secondary education. Certainly, the expectation was that students would be better prepared for the transition, and higher education instructors would therefore be able to spend increased time on more advanced topics. In this regard, Heath and Stickell (1963) reported that students scored better on tests designed around the curriculum they had followed; Rainey (1964), however, found no statistically significant difference between traditional versus CHEM Study students on the ACS-NSTA Cooperative Chemistry Exam. A more detailed mixed-methods study of prior knowledge on student performance within a CHEM Study program demonstrated that success in more conceptual courses required adequate preparation, especially in terms of fundamental definitions and core mathematical skills (Swartney, 1969). The most obvious conclusion to be drawn from these studies is that the planned curriculum is less important than what is actually taught, how it is taught, and – significantly – how it is assessed.

With this in mind, a broader look at the literature through the 1960s and 1970s shows very little change from earlier research (Lamb et al., 1967; Ogden, 1976). Meyer, for example, notes that some post-secondary instructors continue to doubt the relevance of high school chemistry despite a growing body of research showing that it is at least of some value (Meyer, 1962). While attention continued to be paid to high school chemistry and mathematics grades, placement exams, and Student Aptitude Test (SAT) and American College Test (ACT) scores (Hendricks et al., 1963; Schelar et al., 1963; Coley, 1973; Pedersen, 1975; Ozsogomonyan and Loftus, 1979), it was recognised that other factors were important. Coley (1973), for example, examined the predictive power of high school grades, SAT scores, and TCPE results for both first year and final college chemistry grades and concluded that:

“Based on the total variance… there is something else that contributes to success in chemistry. It may or may not be academic in nature, however, it is very significant!” (Coley, 1973, emphasis added.)

Indeed, reviewing the literature up until 1967, Ogden goes so far as to state:

“There is some indication that the taking of high school chemistry may be used as an indicator of success… There are indications that [other parameters] may be better, or at least as good, as indicators. There is also evidence that no indicator is all that good.” (Ogden, 1976, emphasis added.)

Before considering the more recent literature, it is worth pausing to consider the importance of these two statements. A number of the quantitative studies published prior to 1980 used multiple linear regression in attempts to identify factors predicting student grades in their first college or university chemistry course. The relative contributions of such different factors can be assessed from the coefficients in the resulting model equation. Similarly, the model's predictive scope is indicated by the squared product moment correlation coefficient (r²), which gives the proportion of the variance in the data explained by the model. Unfortunately, not all the published reports included such data, but Table 1 summarizes that which is available. Given that the largest multiple r² values were obtained for the smaller study cohorts, it is clear that a great deal of the variation in individual student outcomes was not explained by the factors examined in these studies.

Table 1 Summary of correlation-based studies examining the factors contributing to success as measured by first year post-secondary chemistry grade

Author(s) (year)	Parameters studied^a	r ^2 (n)
a Ranked in order of decreasing coefficient or standardized coefficient. b Multiple institutions and cohorts were involved in this study. c Denotes a single rather than multiple r^2 for the first two predictors. d Values are for male and female students, respectively. e Introductory course for students scoring <50 on the Toledo Chemistry Placement Exam (TCPE). f Results for two different chemistry courses. g Specified only as a letter grade; the model predicts course GPA, not percentage mark. h Results for two different types of post-secondary institution.
Cornog and Stoddard (1925)	Iowa Placement test	0.07–0.53, mean 0.19 (20–300^b)
Clark (1938)	Psychological exam,^c Iowa Placement test	0.49^c (49)
Kunhart et al. (1958)	HS chemistry, HS algebra, ACE scores	0.16 (111)
Hendricks et al. (1963)	HS average, SAT-math, advanced math course (AP/IB), Gender, HS size & class size, SAT-verbal	0.13, 0.10^c^d
		0.17, 0.06^c^d
Coley (1973)	Pre-requisite course,^e TCPE, HS Algebra I & II, ACT scores, HS chemistry	0.23 (108)
Mamantov and Wyatt (1978)	ACT score, other factors	0.20, 0.46^f (—)
Ozsogomonyan and Loftus (1979)	HS chemistry,^g chemistry pre-test, SAT-M	0.35 (773)
Andrews and Andrews (1979)	SAT-M, HS GPA	— (138)
Craney and Armstrong (1985)	TCPE, HS chemistry, SAT-M	0.376 (304)
Carmichael et al. (1986)	HS GPA, ACT composite	0.457, 0.460^d
Nordstrom (1990)	HS GPA, HS chemistry, SAT-M/ACT-M	0.183 (980)
Russell (1994)	California Chemistry Diagnostic Test (CCDT)	0.12, 0.14^c^h (4023)
Tai et al. (2005), Tai and Sadler (2007)	HS GPA, HS chemistry, SAT-M/ACT-M	0.183 (980)
Seery (2009)	HS GPA, with/without HS Chem	0.346 (89)

---

High school grades and post-secondary success (post 1980)

It can well be expected that any change in teaching approach for a given subject would take time to propagate: new curricula must be designed, approved and adopted, materials must be produced, teachers must be trained, and students must graduate from the revised programs. As such, it is interesting to see if the changes in chemistry teaching cited above are reflected in the quantitative research. Unfortunately, the findings are not all that positive. Thus, a review of results from the TCPE for more than 3000 students over the period 1977–1980 reports a progressive decline, both in the average test mark and the proportion of passing students (Niedzielski and Walmsley, 1982). In keeping with the importance of math skills, failing students scored poorly on the algebraic and word problem questions of the TCPE, and had a weak grasp of several basic chemical concepts; the authors also cite a parallel decline in SAT scores.

Studies employing multiple linear regression since 1980 are also included in Table 1. These include additional placement tests such as the California Chemistry Diagnostic Test (CCDT) (Russell 1994), as well as the Factors Influencing College Science Success (FICSS) study (Tai et al., 2005, 2006; Tai and Sadler, 2007).‡‡ The FICSS study was unique in that it included an extensive survey covering demographic factors and the students’ high school experiences. Notably, after weighting the model coefficients by their standard errors, the top three predictors were related to mathematical ability, the fourth was any high school science grade, and the fifth was the amount of time students recalled spending on stoichiometry. Yet despite the impressive range of factors considered, the resulting model still left over 60% of the variance in individual student outcomes unexplained. Thus, thirty years later – and after considerable reforms in high school chemistry curricula – Ogden's conclusion that “no indicator is all that good” appears to remain lamentably true.

In other words, exposure to chemistry in high school and mathematical ability are both necessary but insufficient prerequisites for success in post-secondary chemistry. Further, while the best indicators of final undergraduate success are first-year grades, and the best indicators of those are tests (such as the TCPE or CCDT) given early in that first year, even these are not particularly good predictors in terms of actual marks. This is particularly apparent from studies identifying at-risk students, either for differentiated courses or supplemental instruction (Schelar et al., 1963; Pickering, 1975, 1977; Ozsogomonyan and Loftus, 1979; Nordstrom, 1990; McFate and Olmsted, 1999; Legg et al., 2001; Wagner et al., 2002; Kennepohl et al., 2010). These papers highlight two themes present throughout the literature cited so far: firstly, that better correlations are observed for predicting letter grades – especially the highest and lowest – rather than raw scores; and secondly, that even the best pass/fail predictors misclassify a certain percentage of students.

What, then, are we to make of Coley's significant “something else”, the part that accounts for the majority of the variance in student outcomes not explained by the best quantitative model? In order to answer this question, we need to move from the primarily quantitative research cited so far to more qualitative research and – in terms of Bloom's taxonomy – from the cognitive into the affective domain (Bloom et al., 1956; Krathwohl et al., 1956; Anderson and Krathwohl, 2001). In particular, we shall see how just as advances in statistical methods provided deeper insight from quantitative studies, so developments in cognitive science, educational psychology, and – more recently – neuroscience, have provided deeper insights into student learning (Cross, 1999). In doing so, we shall identify three main themes, namely the different ways of knowing, thinking, and learning (Fig. 2).§§

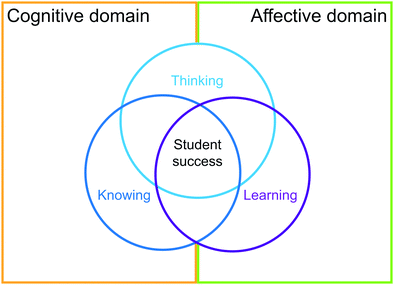Fig. 2 Theoretical framework forming the organizing basis of this review: ways of knowing, thinking and learning in relation to Bloom's affective and cognitive domains.

Ways of knowing: objectives & outcomes

Taxonomies for describing teaching and learning

We start by returning to the definition of ‘success’ raised in the introduction. As described above, many studies of necessity use a final course or cumulative exam grade as a surrogate for student success. A fair question, however, is how well these grades actually assess student performance in terms of what they know and can do (Miller et al., 2009). Specifically, any individual test indicates only what a student achieved on that specific test at that specific time; whether this truly reflects a student's abilities and content knowledge depends on the validity and reliability of the assessment (Miller et al., 2009, chapters 4 and 5). A related issue is the plasticity of language: words like ‘know’ and ‘understand’ can have multiple different (even overlapping) meanings depending on their context of use. In addressing different ways of knowing, it is therefore helpful to delineate different levels of accomplishment: in other words, we need a framework for describing learning objectives (what we want students to achieve) and outcomes (how students will demonstrate such achievement).

Amongst such frameworks, the best known is Bloom's taxonomy of cognitive learning objectives (Bloom et al., 1956) and its recent revision (Anderson and Krathwohl, 2001). The taxonomy divides aspects of student learning between three domains: the cognitive, affective, and psychomotor (although this is somewhat of an artificial separation, especially for practical subjects such as chemistry). The primary focus is on the cognitive domain, which is further divided into the knowledge and cognitive process dimensions, consisting of a hierarchy of increasingly sophisticated forms of knowledge and types of assessment or abilities (Fig. 3).

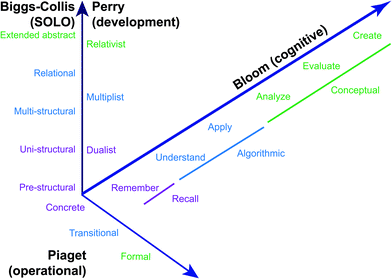Fig. 3 Stages of student development as summarized by Bloom, Perry, Biggs & Collis, and Piaget (see text for details).

Note that the first two items on the cognitive dimension underwent a name change, reflecting the different meanings of key words mentioned earlier. Thus ‘know’ is replaced with ‘remember’ or ‘recall’ (of names, definitions, etc.) (Wolfe and Heikkinen, 1978; Furst, 1981). Similarly, ‘comprehend’ is replaced by ‘understand’, although this remains somewhat ambiguous given common use of the latter. The application and analysis categories can be viewed as essential components of problem solving, while the analysis, synthesis, and evaluation categories can be considered as key components of critical thinking.

Ways of knowing: taxonomic classification schemes

Taxonomic classification of assessment items on exams or in textbooks can provide valuable insight not only for instructors and researchers (Dávila and Talanquer, 2010; Smith et al., 2010), but also students. Thus, Bloom's taxonomy can be usefully condensed into the categories of recall (or definition), algorithmic, and conceptual (Nakhleh, 1993; Nurrenbern and Robinson, 1998; Smith et al., 2010) along the cognitive process domain (Fig. 3). Here, an algorithmic process might involve following a defined set of steps to solve a problem, while a conceptual process might involve deriving such a procedure from careful analysis and reasoning from first principles (for additional definitions of conceptual understanding, see Holme et al., 2015). Of particular relevance here is the finding that, despite the earlier shift from a traditional to conceptual curriculum, a significant proportion of students taking introductory post-secondary chemistry still rely on algorithmic processes for problem-solving, and that solving problems does not – contrary to some faculty expectations – automatically develop conceptual understanding (Nurrenbern and Pickering, 1987; Nakhleh and Mitchell, 1993; Zoller et al., 1995; Phelps, 1996; Mason et al., 1997; Stamovlasis et al., 2005).

This highlights two areas touched on earlier: first, that while the intended curriculum might emphasize conceptual understanding, the curriculum as taught in high school and introductory university chemistry involves a great deal of equations and calculations (stoichiometry, gas laws, concentrations, equilibria, thermochemistry, etc. – see for example Tai and Sadler, 2007); and second, that the assessed curriculum can fail to distinguish between students who have memorized algorithmic procedures and those who have developed conceptual understanding. In this regard, it is worth noting that many of the conceptual questions used in the studies cited above have been incorporated in to end-of-chapter problems by many of the leading general chemistry textbooks.

These studies also touch on the importance of the affective domain from Bloom's taxonomy. This includes objectives commonly found in modern curricula such as valuing and appreciating, but also touches on attitude and motivation towards studying a subject (Klopfer, 1976; LaForgia, 1988; Flaherty, 2020). That is, the affective domain functions as a bridge between our ways of knowing, thinking, and learning; we will therefore return to this topic in more detail later. For now, it is sufficient to note that student attitude, engagement, and motivation contribute to metrics of success from both the student and institutional perspectives. The latter include measures such as recruitment, withdrawal and retention rates. In particular, Sheila Tobias identified that students strongly oriented towards conceptual understanding (or ‘big picture’ thinkers) found an emphasis on calculations and equations boring (Tobias, 1990). Instead, they had a strong preference for obtaining conceptual understanding first rather than repeatedly working problems to gain conceptual understanding. Such students seem to either avoid chemistry in post-secondary education (Nakhleh, 1993), or struggle in chemistry courses for non-chemistry majors unless a more concepts-first approach is adopted (Phelps, 1996).

A different taxonomic approach is represented by Perry's model of intellectual development (Perry Jr, 1970; Finster, 1989, 1991). Based on extensive student interviews, this scheme charts the development of student conceptions of the nature of knowledge and, by implication, the roles of student and instructor in learning. The nine stages or ‘positions’ within the scheme are grouped into somewhat overlapping hierarchical categories: dualism, multiplism, relativism, and commitment in relativism, with the first three being most applicable to undergraduate students. There is a certain degree of synchronicity between Bloom's and Perry's schemes (Fig. 3), although they are clearly different.

To illustrate, consider the usual progression through acid–base theories encountered in high school and introductory undergraduate chemistry. A dualist (knowledge is absolute) can easily accept that an acid is a substance that turns blue litmus red (empirical observation) and dissociates completely in water to increase the concentration of H⁺ (simple definition); they will likely do well on questions that test their recall or require rote conversions between concentration and pH. They may struggle, however, to distinguish between ionization and dissociation (strong versus weak acids and bases) and, by the time they progress through Brønsted–Lowry to Lewis theory, are likely to aver that “our teacher lied to us.”¶¶ The multiplist will not be as threatened by these concepts, though no doubt preferring fewer of them, and are more likely to be successful on application questions given appropriate cues. The relativist, accepting the provisional and contextual nature of knowledge, is the most likely to use the concepts appropriately without cuing (analysis), discern the connections between them (evaluation), and appreciate that other concepts may become necessary in the future.

Many other frameworks have been developed for describing student learning; a useful summary and comparison with Bloom's original and revised taxonomies is provided by Anderson and Krathwohl (2001, ch. 15). These can be separated into two broad categories: those – like Bloom's – that describe desired (a priori) learning outcomes, and those based on observation of actual (a posteriori) student achievement. The latter include Biggs and Collis’ Structure of the Observed Learning Outcome (SOLO) taxonomy (Biggs, 1978b, 1979; Biggs and Collis, 1982). This shares features with other developmental descriptions, although it is functionally closer to the Bloom's taxonomy (Biggs, 1979). The SOLO hierarchical categories are prestructural, unistructural, multistructural, relational, and extended abstract, referring to the ways in which students address particular learning tasks.

Ways of knowing: conceptually difficult chemistry?

Just as the post-war period saw rapid changes and an increased emphasis on concepts in science curricula from the 1950s onwards, so there was a parallel explosion in cognitive psychology and education research. Of considerable importance to understanding student success is the school of thought generally referred to as constructivism (Craig, 1972; Herron, 1975; Good et al., 1978, 1979; Bodner, 1986; Philips, 1995; Lutz and Huitt, 2004). Rather than a single, monolithic theory, this is better viewed as multiple overlapping perspectives or ‘lenses’ that each provide valuable insights into how people learn. At its simplest, constructivism can be expressed by the dictum that “knowledge is constructed in the mind of the learner” (Bodner, 1986); that is, knowledge is not simply transmitted from teacher to student ready formed but must be built up by the learner making connections – both cognitive and neurological – between new and existing information and experiences (Cross, 1999). This does not happen in isolation, however: knowledge is also constructed through interactions with others, including instructors and peers (Philips, 1995). It remains true, however, that the ability to acquire new knowledge depends on what the student already knows (Ausubel et al., 1978), but is susceptible to mislearning if what is already known is incorrect or misunderstood.

Within constructivist thought, knowledge is described in terms of a construct known as a schema (plural: schemata) consisting of “facts, ideas, and associations organized into a meaningful system of relationships” (Cross, 1999, p. 8). Schemata are sparse initially but become denser over time as their contents get added to and elaborated upon. Similarly, schemata can have few or many connections between them; the deeper a schema is, the easier it becomes to form the connections that constitute learning. When a student encounters a new idea or concept, there are several possible outcomes (Johnstone, 1997) which can either result in meaningful learning or what David Perkins refers to as “troublesome knowledge” (Perkins, 1999; Meyer and Land, 2003; Willingham, 2009). These are (Fig. 4):

Fig. 4 Possible outcomes for learning a new concept: (a) finds no connection with existing knowledge and may be forgotten; (b) is memorized within a sequence but fails to find meaningful connections; (c) is linked incorrectly to existing concepts, leading to misunderstanding and limiting further learning; (d) is linked correctly to existing concepts, leading to deep understanding and facilitating further learning.

• The new concept finds no connection with existing concepts and remains isolated; if it is remembered at all it will be inert knowledge that is not actively used. An example might be that the atomic symbol for lead comes from the Latin, plumbum.

• The new concept is learned as a minimally linked item in a sequence of concepts and is only recalled as such; it constitutes ritual knowledge that exists only as part of a memorized list or procedure but otherwise lacks meaning. An example might be the names of the elements in order of atomic number.

• The new concept is incorrectly connected with existing knowledge despite it seeming to ‘fit’; this constitutes conceptually difficult knowledge, which can lead to incorrect conclusions and actively hinder further learning (a form of misconception – see below). An example might be a failure to distinguish between the properties of a macroscopic sample of an element and an individual atom.

• The new concept is correctly connected with existing knowledge, resulting in effective connections that create a fuller understanding of the subject matter and facilitate future learning.

Perkins further defines the category of foreign knowledge as “that which comes from a [foreign] perspective”, having to do more with cultural, historical, and political contexts, beliefs, and values. While this might seem less relevant, a chemical example here might be confusion as to why radium solutions would ever be promoted as health tonics. To this can be added a final category, tacit knowledge, being that which is implicitly assumed by an instructor without being made explicit to the student (Meyer and Land, 2003).

Perkins’ conceptually difficult knowledge raises the issue of students’ actual conceptions of science. This has been a major area of research parallel to the development of conceptually based science curricula, including the work of Rosalind Driver on how school children construct their own understanding of scientific principles (Driver, 1983, 1985). Alternative conceptions – also known as misconceptions and false or naive conceptions – are beliefs, ideas, or explanations about scientific principles and phenomena that are either inaccurate, incomplete, inconsistent, or completely wrong (Mulford and Robinson, 2002). Common alternative conceptions in chemistry have been extensively documented (see for example reviews in Garnett et al., 1995; Gabel, 1999; Gilbert et al., 2002; Taber, 2002; Kind, 2004; Duit, 2009), and at least one Chemical Concepts Inventory has been developed and published (Mulford and Robinson, 2002; Barbera, 2013; Schwartz and Barbera, 2014).

A key feature common to all misconceptions is that they are resistant to change, even when new information is encountered:

“If anomalous new information is presented in a learning situation where the student is rewarded (with grades) for remembering it, the information may be memorised in order to earn the reward, but it is likely to be quickly forgotten because it does not make sense” (Mulford and Robinson, 2002, emphasis added.)

In other words, a correct answer on a test item does not necessarily imply correct understanding of a concept, hence the emphasis on more conceptual questions discussed previously. While it may seem counter-intuitive that misconceptions are not simply replaced by exposure to the ‘correct’ explanation, this itself is a common misconception: in a traditional lecture, a student may ‘tune out’ information that seems familiar since they believe they already understand it; better success can be obtained by engaging students in a discussion of different explanations for a given phenomenon, and specifically where they fail (Muller et al., 2008).

Obviously, it is better to avoid misconceptions in the first place. Fortunately, extensive research exists on how they are acquired (see for example Taber, 2002; Talanquer, 2006; Taber and Franco, 2009). At root lies the fact that “people are naturally curious, but not naturally good thinkers” (Willingham, 2009, p. 3):

“A cognitive scientist would add another observation: Humans don’t think very often because our brains are designed not for thought but for the avoidance of thought” (Willingham, 2009, p. 4)

Put another way, humans appear hard-wired to take the most efficient route to processing information. We are what has been referred to as ‘cognitive misers’ (Stanovich, 2009) making use of intuitive or ‘common sense’ reasoning based on first-hand experience and similarities with existing information, or pattern recognition (Johnstone, 1997; Cross, 1999; Talanquer, 2006; Taber and Franco, 2009). As Vicente Talanquer puts it:

“[Misconceptions] seem to result from the confident and impulsive application of a crude, incomplete, limited, and superficial explanatory framework about [scientific] phenomena. This knowledge system … creates the illusion of explanatory depth: students believe that they understand more than they actually do.” (Talanquer, 2006, emphasis added.)

Talanquer goes on to develop an explanatory conceptual framework of naïve realism which shares some features with Perry's dualism, comprising a set of empirical assumptions and reasoning heuristics.

One very common aspect of naïve realism is a failure to use, or the incorrect use of, scientific analogies. As one example, Talanquer cites the assumption of continuity in explaining atoms as the result of continuously subdividing a macroscopic sample (Fig. 5; Stone, 2017). This confusion is perhaps unsurprising given the scientific definitions of ‘atom’ and ‘element’, their inherent circularity, and their dependence on prior conceptual understanding (Taber, 2002, pp. 20–27). One consequence of this is that students may well conclude that individual copper atoms are the same colour as the bulk metal (Ben-Zvi et al., 1986). Perhaps most telling is the number of instructors who have looked at Fig. 5 and exclaimed “But that's how I was taught this concept!” This example leads to the related topic of threshold concepts.

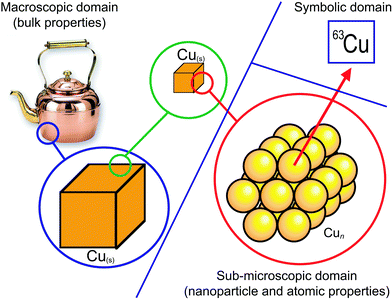Fig. 5 Misconceptions arising from the assumption of continuity applied to the terms ‘atoms’ and ‘elements’, while ignoring the difference between the macroscopic, submicroscopic, and symbolic domains (Stone, 2017).

Jan Meyer and Ray Land have defined threshold concepts as “akin to a portal, opening up a new and previously inaccessible way of thinking about something” (Meyer and Land, 2003, 2006, emphasis added). Threshold concepts are distinguished from core concepts, or ‘big ideas’, in that do not simply provide a foundation for further subject knowledge; rather, they lead to a qualitatively different view of the subject that can have cross-disciplinary impact (Talanquer, 2015; Cooper, 2020). With this in mind, both scientific representations of scale from the macroscopic to submicroscopic to symbolic (Johnstone, 1991; Gerlach et al., 2014) and the nature of scientific models (Stone, 2017) can be seen as key threshold concepts; to this can be added the nature of scientific evidence, its relevance and sufficiency (McNeill and Krajcik, 2008). If these are not taught, or not taught well, students will indeed struggle with the subject matter and master the art of ‘thinking like a chemist’. Conceptual understanding (or a lack thereof) is not, however, the only impediment to learning chemistry faced by our students.

Ways of knowing and student success

So far, we have seen that factors amenable to quantitative research, such as SAT scores and high school grades in chemistry and mathematics, can only account for a fraction of the variance in student outcome in their first post-secondary chemistry course. And this is despite curricula changes in content and an attempt to shift from rote memorization to conceptual understanding. Different ways of knowing can partly explain this in terms of the idiosyncratic way students build their understanding. Yet it also draws attention to other factors that hinder success, including the cognitive abilities needed to engage with course material. This leads us to consider different ways of thinking, or the mental toolbox of reasoning strategies essential to success. For this, we turn to constructivist theories and what they can tell us about scientific reasoning.

Ways of thinking: scientific reasoning

Building on constructivist theory

While numerous individuals contributed to the development of constructivism including John Dewey, Lev Vygotsky, and Jerome Bruner, the most influential on the field of chemistry education research has arguably been Jean Piaget (Herron, 1975, 2008; Lutz and Huitt, 2004) and his work on the intellectual development of children (Piaget and Inhelder, 1956, 1974; Inhelder and Piaget, 1958, 1964) as it relates to the different ‘ways of thinking’, or the mental strategies (Shayer and Wharry, 1974) individuals can bring to a particular problem or learning task. While Piaget's work – especially with regard to early childhood development – has not been without its critics (Lourenço and Machado, 1996) it continues to prove particularly relevant to understanding the struggles students in high school and post-secondary education have with science in general, and chemistry in particular (Herron, 1975; Bodner, 1986). Indeed, a comprehensive review of studies assessing student developmental levels conducted through the 1970s noted that there was little sustained research outside of science and mathematics (Nagy and Griffiths, 1982).

Jean Piaget and scientific reasoning

The key element of Piaget's work for chemists is the distinction between what he termed the ‘concrete operational’ and ‘formal operational’ stages of intellectual development (sometimes referred to as Piaget stage 2 and 3, respectively; different authors sub-divide these scales further) (Fig. 3). Piaget's primary interest was epistemological, that is he was concerned with how children developed their conceptual understanding and reasoning abilities. Rather than use a psychometric method, such as a norm-referenced intelligence (IQ) test, students were observed and interviewed while performing a series of experimental tasks that require specific ways of thinking in order to correctly answer predictive questions based upon their observations (Inhelder and Piaget, 1958). It is important to note here that the tasks used in identifying a student's developmental stage were mostly physics experiments (Table 2); as mentioned earlier, there is significant overlap between the thought processes described by Piaget and the physical and mathematical sciences. Even a cursory glance at the list of formal operational mental strategies suggests that chemistry, particularly when taught conceptually, requires significant formal thought in order to be understood and applied successfully (Shayer, 1970; Ingle and Shayer, 1971; Herron, 1975; Williams et al., 1979). For example, the symbolic representations used for chemical elements and compounds in reaction schemes require at least some level of formal development to handle successfully.

Table 2 Components of Piaget's stages of concrete and formal operational development and their associated diagnostic tasks

Stage	Scale component (example experimental task used in evaluation)
a Number, area, volume, etc. b Taken from Lawson et al. (1979) and used in the TOLT.
Concrete:	Classification (grouping of coloured beads; counting by sub-groups)	Conservation^a (size and shape of equal balls of clay; conservation of mass)	Decentring (comparing volume by considering both height and width of a container)	Reversibility (returning a balance arm to equilibrium by replacing a removed weight)	Seriation (ordering of objects by increasing length or weight)	Transitivity (identifying relationships between classes or groups)
Formal:	Control of variables (identifying what determines the period of a pendulum)	Combinatorial reasoning (colourless reagents that combine to form coloured or colourless solutions)	Correlational reasoning (two types of mice and tail colour; two types of fish and stripe width^b)	Hypothetical-deductive reasoning (behaviour of three pendulums with different weights & lengths)	Probabilistic reasoning (drawing coloured shapes from a bag and predicting odds)	Proportional reasoning (level of equal volume of water in different diameter cylinders)

---

Piaget initially described concrete operational thinking as developing at age 8–12, with formal operational thinking following at age 12–15. His experimental group was, however, small and from a select school and so not very representative. As larger cohorts were observed it became apparent that these ranges were not as narrow or fixed; further, a student's development stage was more accurately associated with mental age, a construct associated with IQ score (Shayer, 1970; Piaget, 1972; Shayer et al., 1976). Shayer found, for example, that less than 30% of children in England and Wales had developed formal operational thinking by the age of 15, but of the top 20% attending grammar schools (on the basis of a selection exam) that proportion rose to ∼65% (Shayer et al., 1976). More importantly, this lack of formal operational thinking was found to continue amongst students entering post-secondary education (Herron, 1975; Bird, 2010). An open question therefore became: what contribution does a student's Piagetian development level make towards a successful transition from high school to college or university?

Piagetian group assessment and student success

A significant difficulty in administering the tests developed by Piaget and colleagues is that they require time, materials, the ability to have observers work one-on-one with participants, combined with meticulous observation (what the students actually did) and interviewing (understanding their thought processes) (Shayer et al., 1981). Such tests obviously do not scale well and so are incompatible with large research studies, much less routine use. As a result, numerous groups have described scalable instruments involving either demonstrations accompanied by written answer predictive questions (Shayer and Wharry, 1974; Lawson, 1978; Martin, 1979) or strictly paper-and-pencil versions that lost both the hands-on aspect of the original task as well as the context of the student's thought process (Williams et al., 1979; for additional examples see the critiques by Lawson, 1978; Cohen, 1980; Nagy and Griffiths, 1982). There is, in fact, considerable overlap between the assessment of Piagetian formal thinking, and evaluating conceptual understanding as discussed earlier. Accordingly, test items need to distinguish between answers arrived at by the desired process (formal thinking/conceptual understanding) and those obtained by falling back on a lower-level process (concrete thinking/algorithmic problem-solving).

Such differences in instrument validity and reliability likely contribute to several of the apparently contradictory findings reported by early studies. This includes large differences in the fraction of first year undergraduate students observed to be capable of formal operational thinking (anywhere from 25% to 75%), whether or not scores on such tests could be used to predict student success, and what impact the prevailing methods of instruction might have on intellectual development (Beistel, 1975; Herron, 1975; Albanese et al., 1976; Goodstein and Howe, 1978; Kuhn, 1979; Good et al., 1979; Wiseman Jr, 1981). Despite the difficulties implicit in the different instruments used, the consensus emerging from these and related studies of the time can be summarized as:

• Not all students undergo the transition from concrete to formal operational thinking at the same time (or even at all)

• The ability to employ formal operational thinking in one subject does not automatically transfer to other subjects

• Reversion from formal to concrete operational thinking can occur, depending on familiarity the content matter

More detailed conclusions, however, awaited the development and validation of more rigorous assessment instruments.

Such instruments were not long in following. These included: The Science Reasoning Tasks (SRT) of Shayer et al. (1981); the Test of Logical Thinking (TOLT) developed by Tobin and Capie (1981) from the earlier work of Lawson (1978); and the Group Assessment of Logical Thinking (GALT) described by Roadrangka et al. (1983). Note that the GALT is an extension of the TOLT that includes two items assessing concrete operational thinking; for a detailed comparison and evaluation of the two see Jiang et al. (2010). Various studies have made use of these instruments to examine the impact of teaching strategies on student learning in high school (Tobin and Capie, 1982; Roadrangka and Yeany, 1985; Bitner, 1991; Lawson and Wollman, 2003), and as potential predictors of student success in post-secondary chemistry (Bunce and Hutchinson, 1993; Nicoll and Francisco, 2001; Lewis and Lewis, 2007; Bird, 2010; Cracolice and Busby, 2015).

Of particular relevance here is the connection between formal operational development and critical thinking skills identified by Bitner (1991). The latter were assessed under the categories of inference, recognition of assumptions, deduction, interpretation, and evaluation of arguments (Watson and Glaser, 1980). Stepwise regression analysis showed that the five formal reasoning modes included in the GALT were good (46% of variance) or strong (60–80% of variance) predictors of critical thinking skills with the exception of inference (28% of variance); similarly, they were strong predictors of grades in science but weak predictors in mathematics. Bitner notes that these also correlate well with other factors such as measures of general intelligence and ACT/SAT scores.

A similar theme emerges from the post-secondary studies cited, which combine either GALT or TOLT with SAT scores (composite, verbal, or math) and assess student achievement using the standard or special ACS general chemistry exam. Thus, Bunce and Hutchinson (1993) note that the GALT and SAT-M scores seem to be measuring a similar variable. Similarly, Lewis and Lewis’ detailed analysis shows that the TOLT and SAT scores reflect correlated but distinct variables: while both have similar predictive value in identifying at-risk students (as determined by an arbitrary cut-off score on the ACS exam) and correctly categorize a core group of under-achieving students, there are two additional groups identified by only one or another of the instruments (Lewis and Lewis, 2007). These authors conclude that mathematics achievement and reasoning ability represent different barriers to success.

A distinct possibility here is that at least some students achieve success in mathematics through the application of memorized algorithmic procedures to recognized problem types, rather than applying formal mathematical reasoning. In other words, when it comes to mathematics, they are algorithmic rather than conceptual problem solvers. Support for this comes from the observation that the math skill most indicative of success in university physical chemistry was the ability to solve word problems (Nicoll and Francisco, 2001), a statement that will likely resonate with physics instructors at all educational levels. This is paralleled by the finding that concrete operational students are primarily algorithmic problem solvers, formal operational students are conceptual problem solvers, and transitional students adopt a hybrid approach (Bird, 2010).

Concrete to formal thought: making the transition

Clearly, the development of formal operational thought is crucial to success in both high school and university chemistry. Further, this explains why the historical correlation studies highlighted in this review identified mathematics scores as strong predictors of success in chemistry. It is not just that topics such as stoichiometry, gas laws, and equilibria require basic algebra skills – although students who struggle with such calculations are very much in the at-risk group. Rather, mathematical ability is associated with the ways of thinking necessary for building a conceptual understanding of chemical principles and processes. The obvious questions then become: how does the transition from concrete to formal thinking take place; and can instructional practices facilitate that process when it is found lacking?

From the studies cited above, it is clear that concrete operational development appears to be a given. This makes sense since we use concrete thought processes to navigate daily life. These studies also show, however, that formal thinking is not developed automatically, and may remain absent even into adulthood. Deanna Kuhn, for example, points out that many of the Piagetian tasks used to assess formal operational development “are not ones that [adults] can readily relate to in terms of their everyday experience” (Kuhn, 1979). In evolutionary psychology terms, formal thinking does not develop automatically because there is no intrinsic motivation (outside of science classes) to do so – it is essentially learned behaviour brought on by extrinsic motivation such as obtaining a course grade (Genovese, 2003). Put more positively:

“[F]ormal operational reasoning strategies develop rapidly when subjects are simply given … frequent opportunities to deal with problems requiring formal reasoning for an effective solution” (Kuhn, 1979, emphasis added).

This has been confirmed by research on different teaching strategies for promoting both formal reasoning and conceptual understanding (see for example: Roadrangka and Yeany, 1985; Abraham and Renner, 1986; Adey and Shayer, 1990; Weaver, 1998; Lawson and Wollman, 2003).

Ways of thinking and ways of knowing

If different ways of knowing, as expressed in curriculum objectives and measured by learning outcomes, are what we expect students to be able to recall, understand, and apply, then ways of thinking are the cognitive toolbox that provides them the means to do so; the two are, in fact, strongly intertwined. So high level learning outcomes – such as critical thinking skills and problem-solving ability – arise from building a knowledge base and developing different reasoning skills that can be applied to a range of tasks. Thus, the observation that changes in chemistry curriculum from a factual to a conceptual basis did not result in significant improvements in achievement as measured in terms of a purely quantitative analysis of grade correlations is more understandable; cognitive factors must also be taken into account. So valid conceptual understanding can only be arrived at if a student has sufficiently developed the formal operational processes necessary to do so; fallback on more concrete processes contributes to a reliance on memorized procedures and can lead to misconceptions that hinder further learning. Yet this is not the whole picture: we have also touched on the importance of the affective domain (values and beliefs about a subject), student motivation, and the impact of teaching strategies, classroom activities, and methods of evaluation. This constitutes the third strand or theme of this review, namely different ways of learning.

Ways of learning: approaches and preferences

Student approaches, aptitudes, attitudes, and study strategies

Both Perry's model and the SOLO taxonomy of Biggs and Collis are examples of a particular approach to qualitative educational research, namely phenomenography. This involves a shift of focus from the purely cognitive to the affective domain, involving emotions, motivation, personality traits, and attitudes to learning (Krathwohl et al., 1956; Anderson and Krathwohl, 2001; Flaherty, 2020). It has led to rich descriptions – and corresponding research instruments – of the ways in which students address learning and specific learning tasks, and the influence of the academic environment and teaching practices on these processes. These are variously referred to as learning styles, approaches, aptitudes, strategies, or orchestrations.||||

Ways of learning: a question of style

Before describing in detail what these ways of learning are, however, it is important to explain that they are not what most people associate with the term ‘learning style’ – typically left brain-right brain analogies, or the visual-auditory-kinaesthetic (VAK, with or without Tactile) or multiple intelligences (MI) models. In fact, many educational researchers and cognitive psychologists, along with educational developers, state unequivocally that such learning styles either don’t exist or simply don’t work (Pashler et al., 2008; Sharp et al., 2008; Willingham, 2009; Chew, 2011, part 2; Howard-Jones, 2010; Wallace, 2011). This may come as a surprise to many, given the popularity of learning style workshops at conferences and the large industry that has grown up around some of them. To understand this discrepancy, it is helpful to realise that there are different families of such models, each of which have different conceptual bases (assumptions and theoretical frameworks), and that the associated diagnostic instruments can have very different levels of psychometric validity and reliability (Coffield et al., 2004a, 2004b).

These conceptual frameworks range from ones which posit fixed inherited personality traits that interact strongly with cognition and cannot be modified (eg. Dunn and Dunn's VAKT), to those that relate learning style to a largely stable personality type (e.g. Myers and Briggs MBPTI), express learning style as a flexibly stable preference (eg. Kolb's LSI), and end with those that combine a relatively stable cognitive style with strategies and processes that are modifiable by the educational environment (eg. Entwistle's ASSIST). Coffield et al. point out that: there is no empirical evidence for a biological basis to any learning styles, that cognitive skills are strongly influenced by the learning environment, and that no traits are so stable as to be determined solely by genetic factors (Coffield et al., 2004a). The concept of hemispherical dominance is likewise undermined by neuroscience research: while one side of the brain may show extra activity associated with a specific task, both sides are in fact active and working together in parallel during a task such as learning vocabulary (Howard-Jones, 2010, chap. 2). In general terms, these models lack substantive construct validity – they may be measuring something, but the underlying theory is flawed or incomplete; this is what is meant by claims that learning styles don’t exist.

The second claim regarding learning styles – that they don’t work – stems from examining two common assumptions about models such as VAK: first, that a person who scores highly on a questionnaire as a specific type of learner will learn best – or can only learn – that way; second, that instructors should therefore match teaching and learning to each students’ learning style. While individuals certainly have preferences for the way they interact with content, and can differ in visual and auditory abilities, we do not store information exclusively as sights and sounds, but also as meaning (Willingham, 2009). In other words, when it comes to constructing meaning it is our conscious attention to the content that matters most, not whether we engage through visual or auditory means. The second assumption – known as the meshing hypothesis – was the subject of an extensive literature review that first sought to identify what would constitute credible validation of this approach (Pashler et al., 2008). This required that students identified as possessing each learning style be taught together using methods aligned with a single style; if the meshing hypothesis was valid, only those students whose preference matched would show learning gains on the material taught. They concluded that:

“Although the literature on learning styles is enormous, very few studies have even used an experimental methodology capable of testing the validity of learning styles applied to education. Moreover, of those that did use an appropriate method, several found results that flatly contradict the popular meshing hypothesis.” (Pashler et al., 2008, emphasis added).

To summarize: while individuals may well identify with specific descriptors from certain models, this constitutes a preference and/or trait rather than a necessity for learning in a specific way. Rather than attempting to create individualized materials for each ‘type’ of student, therefore, instructors are advised to concentrate on ensuring that their activities and presentations incorporate elements that will engage all learners such as strong visuals, clear text, etc.

Ways of learning: orientations and approaches to study

With that out of the way, let us turn to more thoroughly validated descriptions of different ways of learning. These have been the subject of extensive reviews such as those of Entwistle and Ramsden (1983), Entwistle and McCune (2004) and Entwistle (2010). Here, it is sufficient to mention the pioneering work of Marton and Säljö (1976a, 1976b), Säljö (1979) and Pask (1976a, 1976b), who used quite different methods to look at the ways in which students approach specific learning and assessment tasks. The resulting outcomes were measured in terms of what and how well, rather than simply how much, students learned. Marton and Säljö in particular examined the study processes used by students on different tasks, and their subsequent learning outcomes. The latter were measured using a scale similar to the SOLO taxonomy. Thus, students who focussed on reproducing factual content were characterised as employing surface level processing, while those who paid more attention to comprehending or understanding it employed deep level processing (Marton and Säljö, 1976a). More importantly, it was found that students adopted different processes depending on what they believed would be required by subsequent assessments, and that these were not necessarily the same as those employed by the same students under open circumstances (Marton and Säljö, 1976b).

Similarly, Pask made distinctions between students’ learning preferences and adopted strategies (Pask, 1976a, 1976b). Thus, deep learning was associated with a holist strategy of finding meaning, patterns and connections amongst diverse topics; surface learning was associated with a serialist strategy in which topics were learned sequentially but in isolation (Pask, 1976b). Pask also described a third type of learner, who could move freely along the serialist–holist continuum depending on the learning context. Finally, he described specific learning pathologies related to each strategy. Thus, a holist risks globetrotting, defined by Pask in terms of misapplied or vacuous analogies, but which can be seen as reading too widely to achieve depth in the time available. In contrast, the serialist risks improvidence, a failure to use valid (or any) analogies as a consequence of not looking beyond immediate context and treating sub-topics in isolation.

Various mixed mode studies have examined the interactions between affective and cognitive domains, including the role of motivation, personality traits, and the surrounding academic environment, primarily within a post-secondary environment (Entwistle and Entwistle, 1970; Entwistle et al., 1974; Biggs, 1976, 1978a; Laurillard, 1979; Ramsden, 1979; Ramsden and Entwistle, 1981; Watkins and Hattie, 1981; Thomas and Bain, 1982, 1984; Watkins, 1983). Of particular relevance amongst the surveys used are Bigg's Study Processes Questionnaire (SPQ) (Biggs, 1976, 1978a), the Approaches and Study Skills Inventory for Students (ASSIST) of Entwistle and colleagues (Entwistle et al., 1979; Entwistle and Ramsden, 1983; Tait and Entwistle, 1996), and Ramsden's Course Experience Questionnaire (CEQ) (Ramsden, 1979, 1991; Ramsden and Entwistle, 1981; Wilson et al., 1997).*** Survey instruments specific to chemistry have also been developed, such as the ChemApproach questionnaire (Lastusaari and Murtonen, 2013; Lastusaari et al., 2016).

The picture of student learning that emerges from this body of work can be summarised as shown in Fig. 6. Here, a student's learning style includes personality type, reasons and motivation for pursuing post-secondary education, conceptions of learning, and preference for particular ways of interacting with both subject matter and instructor. Such individual learning preferences vary between meaning and reproducing orientations. A meaning orientation is associated with autonomous learning, intrinsic motivation, and a preference for developing understanding at a deep level. A reproducing orientation is associated with instructor–dependence, extrinsic motivation characterised by high anxiety and a fear of failure, and a preference for more fact-based or surface learning. This extends to the ways in which students approach problem-solving: students having a deep orientation are more likely to adopt a conceptual approach, while those having a surface orientation are more likely to use an algorithmic one (Teichert et al., 2020). A third style – the achieving orientation – characterises students who have clear goals, optimism, self-confidence, and a drive to succeed. Such students exhibit versatility in combining elements of both the meaning and reproducing styles as needed. This model also includes a student's conceptions of the nature and purpose of learning, which are subject to development in a manner similar to Perry's levels of intellectual development. As such, mature students are generally observed to adopt a deeper, meaning-orientated approach to learning (Säljö, 1979; Watkins and Hattie, 1981; Watkins, 1983).

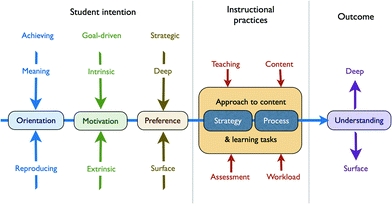Fig. 6 Student approaches to studying and learning as they intersect with instructional and assessment practices, with associated learning outcomes (after Entwistle, 2010).

Ways of learning: self, style, and substance

While individual student styles can be considered as stable to some degree, their interaction with instructional practices and the particular academic culture or environment within which learning takes place can produce situational variations in approach, influencing learning outcomes and student engagement (Biggs, 1976, 1978a; Laurillard, 1979; Ramsden, 1979; Ramsden and Entwistle, 1981; Watkins and Hattie, 1981; Thomas and Bain, 1984). This is reflected in both the strategy and resulting processes adopted for specific learning tasks (lectures, labs, assignments, etc.); these can also be described in terms of deep, surface, and strategic strategies, and may be at odds with the students’ own preferred learning style. Thus, teaching approaches, assessment practices, time pressures, and perceived workload can promote a surface over a deep approach, even if the instructor's intention was the exact opposite (Marton and Säljö, 1976b; Laurillard, 1979; Ramsden and Entwistle, 1981; Entwistle and Tait, 1990; Trigwell and Prosser, 1991; Kember et al., 1996; Kember and Leung, 1998; Trigwell et al., 1999; Kreber, 2003). Significantly, students are much more likely to employ surface strategies when preparing for multiple choice exams, especially if they perceived these as only assessing recall of information; conversely, those who perceived that such exams assessed higher order learning were more likely to employ deep strategies (Scouller and Prosser, 1994; Scouller, 1998).

A student's preferred approach to learning has a strong influence on their success. Those that adopt a deep approach favouring conceptual understanding and developing connections have been shown to attain better grades and a higher quality of learning as judged by outcomes assessment (Biggs, 1979; Entwistle et al., 1979; Watkins and Hattie, 1981; Wilson et al., 1997; Kreber, 2003). Students favouring a strategic approach show similar attainment levels, while those favouring a surface approach perform less well overall. This has led to the ASSIST instrument being used as a diagnostic tool for identifying at-risk students based on their preference for a surface over deep approach to learning, as well as identification of specific learning pathologies such as globe-trotting and improvidence (Tait and Entwisle, 1996). More recently, a modified short-form version of this instrument, the M-ASSIST has been described (Bunce et al., 2017) and similarly employed as a means of identifying at-risk students in introductory post-secondary chemistry (Atieh et al., 2021). Both studies show that surface scale scores are inversely correlated with grades and much strong predictors of success than deep scale scores.†††

There are also strong correlations between a student's learning approach and their perception of the learning environment: negative perceptions correlate with a surface approach, while positive perceptions correlate with a deep or strategic approach (Entwistle and Tait, 1990; Trigwell and Prosser, 1991; Trigwell et al., 1999; Berg, 2005). This is particularly important when it comes to laboratory courses, for which at least two survey instruments have been designed: The Science Laboratory Environment Instrument (SLEI) (Fraser et al., 1993) and the Chemistry Laboratory Anxiety Instrument (CLAI) (Bowen, 1999).

Also of relevance is a study of students in an on-line course: essentially, deep and strategic learners were found to engage more with an online environment and be more independent learners (Buckley et al., 2010). There is also a correlation with age: upper year and mature students are both more likely to adopt a deep approach to learning (Watkins and Hattie, 1981; Kreber, 2003).

One difficulty with referring to the constructs described so far as learning styles is that it tends to direct attention to the process rather than the motivation behind studying. Yet different ways of learning are very much positioned within Bloom's affective domain as described earlier. This involves not just a student's motivation and approach, but a range of related factors that have been increasingly researched over the past two decades including a student's subject-specific attitude, self-efficacy, self-concept, self-esteem, expectations, values, interest, motivation, effort beliefs, and achievement emotions (Bauer, 2005; Flaherty, 2020). A variety of survey instruments have been developed to support this research, including (amongst others): The Chemistry Self-Concept Inventory (CSCI) (Bauer, 2005); the Attitude toward the Subject of Chemistry Inventory (ASCI versions 1 and 2) (Bauer, 2008; Xu and Lewis, 2011); the Colorado Learning Attitudes about Science Survey (CLASS) (Barbera et al., 2008); and the earlier Motivated Strategies for Learning Questionnaire (MSLQ) (Pintrich and De Groot, 1990). These studies help complete the picture of the factors affecting student success in terms of course performance, completion, and continuation.

Self-concept is a robust perception of a person's ability that affects their expectations of how well or poorly they will perform in a subject: whether they perceive themselves as good or bad at the subject, their level of interest in it and confidence about their understanding of it (Bauer, 2005). While self-concept relates to how a person views themselves, attitude here refers to how they feel about the subject itself: are they predisposed to view it as interesting, useful, intellectually accessible and engaging or boring, irrelevant, inaccessible and frustrating? (Bauer, 2008; Xu and Lewis, 2011). Attitude is thus not just a significant factor in determining student success (Brandriet et al., 2011; Xu and Lewis, 2011; Xu et al., 2013; Chan and Bauer, 2014, 2016), but also in promoting high level learning outcomes such as science literacy and life-long learning. Another aspect of a student's perception of the learning environment that is attracting increasing attention is the sense of belonging, referring to a sense of connectedness or being included as part of a specific community and which has been shown to significantly affect achievement and persistence among under-represented groups (Fink et al., 2020). In summary, multiple personal factors within the affective domain contribute to both student success and persistence alongside the previously identified cognitive factors (Shedlosky-Shoemaker and Fautch, 2015; Lastusaari et al., 2019).

Ways of knowing, thinking, and learning

In looking at only the quantitative research results outlined at the start of this review, it would be tempting to conclude that plus ça change, plus c'est la même chose; this, however, would be misleading as it is more the case that advances in educational theory and practice have concurrently shifted expectations for what students can achieve and do. The findings of qualitative and mixed-methods chemistry education research on the factors contributing to student success have been described under three organizing themes: the different ways of knowing, thinking, and learning. These are clearly over-lapping and inter-dependent concepts that all contribute to how students engage with, feel about, and manage their high school and post-secondary science courses, and navigate the transition between them. This includes a wide range of cognitive and affective domain factors, along with their prior knowledge and individual approaches to studying (Fig. 7). These insights allow us to answer the first of the questions posed at the outset of this review: why do students who have similar potential (in terms of grades and curriculum studied) coming from high school experience such variability in outcomes in their first post-secondary chemistry course? The short answer is that grades do not provide the whole picture, even when obtained on standardized tests or common exams. Explaining why this is so requires us to answer the remaining questions.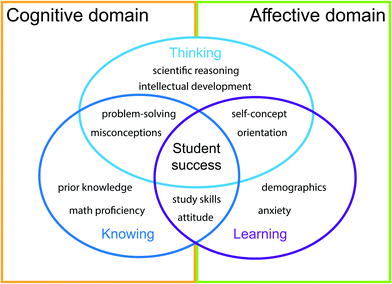

Fig. 7 Final version of the theoretical framework, showing the various factors contributing to student success within each theme.

Are students undertaught and underprepared by their high schools?

The only good answer to this question is: it depends on the student and high school in question. Both prior knowledge and prior experience are important determinants of subsequent success. It is not just what, but how curriculum content has been taught and assessed since this forms a student's attitude to chemistry, as well as defining what academic and intellectual skills or deficiencies they bring to their first – and possibly only – post-secondary chemistry course. Besides forming an attitude to the subject of chemistry (thereby affecting motivation to study it), high school also forms a student's expectations of what it takes to succeed, particularly in terms of approaches to and processes for studying.

Cognitive scientist Stephen Chew describes one essential transition facing students entering college or university as the need for “developing a more accurate sense of metacognition (awareness of level of understanding)” (Chew, 2011, part 1). Unfortunately, the need for such a recalibration is frequently realised only after the first mid-term; if this is also a high-stakes summative assessment, any unexpected lack of success can be a strongly demotivating factor. This is compounded if a student achieved success at the high school level by employing low effort surface strategies when studying for tests and exams. Anecdotally, the two biggest factors associated with at-risk science students described by colleagues at peer institutions have been a lack of mathematical proficiency and effective study skills,‡‡‡ an observation backed up by the findings outlined in the section on ways of learning above. This also relates to our next question regarding level of difficulty.

Is chemistry an intrinsically hard subject?

The answer to this question would have to be a qualified ‘yes’, although whether it is harder or easier than, say, physics or mathematics is open for debate. This stems from numerous factors including: the constant switching between macroscopic, submicroscopic, and symbolic representations inherent in describing chemical properties and processes; the highly inter-dependent nature of fundamental chemical concepts (such as the definition of atom and element); and the need for students to engage in higher level ways of thinking (whether described as formal operational thinking, scientific reasoning, or rational thought). To this we can add the laboratory component of chemistry courses, which can add significantly to a student's level of course anxiety.

As we saw earlier, formal operational thinking is required for understanding and applying many aspects of the high school chemistry curriculum; this development can be encouraged by teaching and assessment practices but is not necessarily automatic for every student. A student's intellectual development may also play a role in whether or not they are more susceptible to developing misconceptions, although this requires further research. It is worth noting here that one common area for misconceptions – particle theory – is typically introduced early in the school science curriculum (grade 7 in Ontario), very much at the lower end of the age range for the development of formal thought. In short, the ways in which a student is taught even before entering formal chemistry courses at the senior high school level can contribute to their perceptions of and attainment in chemistry.

Can we predict which students are most at-risk of failure?

To varying degrees, yes. While there are a variety of diagnostic instruments capable of identifying at-risk students (defined as those likely to score below some critical threshold on their first post-secondary chemistry course), these tend to target different causes of potential failure and, as a result, may identify different groups of students. Some, for example, focus on the level of conceptual understanding of prior knowledge, while others examine scientific reasoning skills, study approaches and orchestrations, or a student's self-concept and perception of the subject and learning environment.

While those developing the diagnostic instruments described above have endeavoured to reduce the number of test items without sacrificing validity and reliability, requiring in-coming students to take a battery of tests covering all factors would still be onerous. A single diagnostic tool combining both cognitive and affective domain factors that could more consistently identify at-risk students would therefore be a worthy research goal. That still leaves the question of what to do with the results, both those clearly at risk and those close to the critical threshold.

What might we do to mitigate such undesirable outcomes?

Clearly, simply identifying at-risk students is insufficient. But the findings outlined above also show that simply offering them a slower paced version of the same course is insufficient. Any course intended to improve a student's prospects for success must address the deficiencies identified by the diagnostic instrument, whether that be promoting a conceptual approach to understanding chemistry, developing scientific reasoning skills, addressing misconceptions, or providing supplementary instruction in effective study skills. In other words, interventions should not be limited to addressing shortcomings in prior content knowledge but should also ensure that students are equipped with both the cognitive and non-cognitive tools required for success. Further, there is considerable opportunity here for post-secondary instructors to partner with high school teachers by communicating any common issues encountered and collaborating on initiatives to proactively address these. This is particularly important since, while high school teachers often have better training in educational theory, post-secondary instructors typically have better access to current educational research tools and literature.

Are university teaching and assessment practices out of touch?

Again, the only good answer to this question is: it depends. Certainly, there has been a great deal of research on the teaching of chemistry, to the point that this really requires a separate review. The astute reader will have noticed, for example, that the topic of active learning strategies has gone largely unremarked. Active learning includes a range of teaching techniques, including classroom response systems (‘clickers’), reading circles, flipped classrooms, problem-based learning, and more. When implemented correctly, such strategies promote the deep level processing and intentional attention to subject matter required for effective learning. Conversely, poor implementation can result in opposite outcomes, leaving students feeling frustrated and instructors disillusioned.

An obvious issue here is that the majority of those teaching post-secondary chemistry are not, for obvious reasons, invested in chemistry education research, and therefore have variable awareness of current best instructional practices and how to implement them. While some jurisdictions have implemented frameworks for professional development and accreditation of teaching in higher education,§§§ in many more it is left up to non-governmental organizations¶¶¶ and individual institutions to provide voluntary certification and training. It would be wrong, however, to conclude from this that post-secondary chemistry instructors are generally uninterested in chemistry education practices: certainly, educational colloquia and workshops at the author's home department are well attended by both faculty and graduate students, especially when topics are focussed on teaching related to specific sub-disciplines.

Lessons (to be) learned

The anniversary celebrated by this review comes as we look forward to emerging from the constraints imposed by the 2020–2021 pandemic and presents an excellent opportunity for reflection on what has – and has not – worked. The abrupt switch to on-line learning certainly caused many to evaluate both what and how they were teaching, as evidenced by numerous papers in both this journal and a special edition of the Journal of Chemical Education.|||||| This review will therefore conclude by considering the current situation, and where we might go from here.

Learning outcomes and objectives

Even before the pandemic, many have been dealing with external pressures to improve and demonstrate the quality of student learning in higher education. At the author's institution, this includes not only a mandated requirement for clear learning objectives and outcomes at the institutional, divisional, program, and course levels, but also an increasing proportion of government funding becoming contingent on outcomes metrics such as student retention, graduation, and employment rates. To the extent that teaching practices affect student attitude, engagement, and success, it is therefore imperative to take this opportunity to review what we teach, as well as how we teach and assess it.

A chemistry degree has long been promoted as a means of acquiring transferrable skills desired by potential employers, such as communication skills, data analysis, information literacy, critical thinking, and problem-solving. The research cited in this review makes it clear, however, that such development is not guaranteed and can be undermined by teaching and assessment practices. Fortunately, the same literature provides the tools necessary to perform a critical evaluation of course content and effectiveness in order to identify any mismatches between intent and practice. Addressing such deficiencies becomes even more urgent as students return – or enter higher education for the first time – having been learning remotely for an extended period.

Admissions without common exams

Many institutions will be grappling with the issue of admitting students based on grades assigned exclusively by their high school teachers, without the benefit of large-scale common exams (such as A-levels). For other institutions, this will simply be ‘admissions as usual’. The province of Ontario, for example, abolished its provincial graduating exams in 1967; over succeeding decades, responsibility for approving final high school exams devolved from the school boards to individual high schools (Orpwood, 1995; Gidney, 1999). While there are differences in performance in first-year chemistry attributable to a student's high school (Browning, 2011), grade correlation studies show little difference overall between those writing a local exam and those writing either the International Baccalaureate or Advanced Placement national exams (Stone, 2011). Although taking IB or AP courses has been shown to contribute somewhat to success, single exam scores remain a poor indicator of more important factors such as level of intellectual development, conceptual understanding, and approach to learning. In other words, there is no guarantee that individual students will have the necessary academic skills to make the transitional adjustment to university chemistry regardless of the curriculum studied.

What may prove highly important is to provide these in-coming students with a more realistic evaluation of how well prepared they are for the transition to university chemistry, through the use of conceptual, cognitive, and affective diagnostic instruments such as those described above. Equally important will be to provide some level of support to under-prepared students, whether it be through existing streamed courses, supplemental instruction, or study skills workshops. It would also not be surprising if first-year students displayed greater anxiety coming to university, especially where labs are concerned. One way to address this would be to make full use of any virtual laboratory materials generated during remote learning as preparatory materials, as this has been shown to improve lab performance (Burewicz and Miranowicz, 2006).

Equity, diversity, and inclusivity

While not explicitly discussed, EDI issues feature prominently in the affective domain research cited in this review. This includes students who are first in their family to attend post-secondary education, those from under-represented groups, and non-traditional learners. Recent successful interventions employing supplemental instruction targeting mindset, self-efficacy, study skills, self-concept, and other affective factors have been shown to successfully address the achievement gap otherwise experienced by such students (see for example: Fink et al., 2018; Stanich et al., 2018). While laudable, it must be noted that many of the factors placing these students at a disadvantage in their first year play a large role in keeping more of their peers from applying to post-secondary institutions in the first place. If we are serious about addressing EDI issues in chemistry, therefore, it is essential to partner with schools and other organizations up-stream to promote the subject as a viable option and help students develop the skills needed for success.

Last thoughts

Chemistry education research has advanced considerably in the 100 years since Powers first reported on the factors affecting student success in transitioning from high school to post-secondary chemistry (Powers, 1921). We have moved from a pedagogical model based on the transmission of information to a more collaborative one focussed on the student as learner that emphasizes conceptual understanding and higher order thinking as educational outcomes. The developments and findings described throughout this review parallel those in cognitive psychology, educational and social sciences research, and statistics. The days of educational research consisting of philosophical arguments that ‘p is obviously true’, opinion surveys, and simple grade correlations are thankfully long past; a wide range of frameworks, approaches, and instruments are now available that can provide much more nuanced and informative insights into teaching and learning, allowing researchers to tackle increasingly more complex questions. It will be interesting to see what themes emerge over the next 100 years.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

I would like to thank the undergraduate research students involved in the project that formed the genesis of this review: Robin Baj, Michael Lebenbaum, Sujan Saundarakumaran, Derrick Tam, and Jakub Vodsedalek (2006–2007); Mena Gewarges, Cindy Hu, Gordon Ng, Jana Pfefferle, and Curtis Wang (2007–2008); Marlena Colasanto, Lauren Cosolo, Fei Darrin Gao, Inna Genkin, Kelly Hoang, Ju-Eun Justina Lee, Bryan Nguyen, and Emily Plobner (2008–2009); Shirin Dason, Xi Nuo Gao, James Hong, Jing Lu, He Zhen Ren, and Heba Shamsi (2010–2011); and Naushin Ali, Ada Chan, Frank Colella, Rui Hu, Sofia Patel and Bilal Suboor (2011–2012). I would also like to thank Professor Dietmar Kennephol (Athabasca University) for his helpful comments and questions on an early draft of this review.

References

1. Abraham M. R. and Renner J. W., (1986), The sequence of learning cycle activities in high school chemistry, J. Res. Sci. Teach., 23(2), 121–144.
2. Adey P. S. and Shayer M., (1990), Accelerating the development of formal thinking in middle and high school students, J. Res. Sci. Teach., 27(3), 267–285.
3. Albanese M., Brooks D. W., Day V. W., Koehler R. A., Lewis J. D., Marianelli R. S., Rack E. P. and Tomlinson-Keasey C., (1976), Piagetian criteria as predictors of success in first year courses, J. Chem. Educ., 53(9), 571–572.
4. Anderson L. W. and Krathwohl D. R., (ed.), (2001), A taxonomy for learning, teaching, and assessing: a revision of Bloom's taxonomy of educational objectives, New York: Longman.
5. Andrews M. H. and Andrews L., (1979), First-year chemistry grades and SAT math scores, J. Chem. Educ., 56(4), 231–232.
6. Atieh E. L., York D. M. and Muñiz M. N., (2021), Beneath the surface: an investigation of general chemistry students’ study skills to predict course outcomes, J. Chem. Educ., 98(2), 281–292.
7. Ausubel D. P., Novak J. D. and Hanesian H., (1978), Educational Psychology: A Cognitive View, New York NY: Holt, Rinehart and Winston.
8. Barbera J., (2013), A Psychometric Analysis of the Chemical Concepts Inventory, J. Chem. Educ., 90(5), 546–553.
9. Barbera J., Adams, W. K., Wieman C. E. and Perkins K. K., (2008), Modifying and validating the Colorado Learning Attitudes about Science Survey for use in chemistry, J. Chem. Educ., 85(10), 1435–1439.
10. Bauer C. F., (2005), Beyond “Student Attitudes”: chemistry self-concept inventory for assessment of the affective component of student learning, J. Chem. Educ., 82(12), 1864–1869.
11. Bauer C. F., (2008), Attitude towards Chemistry: A Semantic Differential Instrument for Assessing Curriculum Impacts, J. Chem. Educ., 85(10), 1440–1445.
12. Beistel D. W., (1975), A Piagetian approach to general chemistry, J. Chem. Educ., 52(3), 151–152.
13. Ben-Zvi R., Eylon B.-S. and Silberstein J., (1986), Is an atom of copper malleable? J. Chem. Educ., 63(1), 64–66.
14. Berg C. A. R., (2005), Factors related to observed attitude change toward learning chemistry among university students, Chem. Educ. Res. Pract., 6(1), 1–18.
15. Biggs J. B., (1976), Dimensions of study behaviour: another look at ATI, Brit. J. Educ. Psychol., 46(1), 68–80.
16. Biggs J. B., (1978a), Individual and group differences in study processes, Br. J. Educ. Psychol., 48(3), 266–279.
17. Biggs J. B., (1978b), The relationship between developmental level and the quality of school learning, in Mogdil S. and Mogdil C. (ed.), Towards a theory of psychological development within the Piagetian framework, Slough, Bucks: National Foundation for Educational Research.
18. Biggs J. B., (1979), Individual differences in study processes and the quality of learning outcomes, High. Educ., 8(4), 381–394.
19. Biggs J. B. and Collis K. F., (1982), Evaluating the quality of learning: the SOLO taxonomy (structure of the observed learning outcome), New York: Academic Press.
20. Bird L., (2010), Logical reasoning ability and student performance in general chemistry, J. Chem. Educ., 87(5), 541–546.
21. Bitner B. L., (1991), Formal operational reasoning modes: predictors of critical thinking abilities and grades assigned by teachers in science and mathematics for students in grades nine through twelve, J. Res. Sci. Teach., 28(3), 265–274.
22. Bloom B. S., Englehart M. D., Furst E. J., Hill W. H. and Krathwohl D., (1956), Taxonomy of educational objectives, handbook I: cognitive domain, New York: McKay.
23. Bodner G. M., (1986), Constructivism: a theory of knowledge, J. Chem. Educ., 63(10), 873–878.
24. Bowen C. W., (1999), Development and score validation of a Chemistry Laboratory Anxiety Instrument (CLAI) for college chemistry students, Educ. Psychol. Meas., 59(1), 171–185.
25. Brandriet A. R., Xu X., Bretz S. L. and Lewis J. E., (2011), Diagnosing changes in attitude in first-year college chemistry students with a shortened version of Bauer's semantic differential. Chem. Educ. Res. Pract., 12(2), 271–278.
26. Brasted R. C., (1957), Achievement in first year college chemistry related to high school preparation, J. Chem. Educ., 34(11), 562–565.
27. Brown F. E., (1926), Separate classes in freshman chemistry for pupils who present high-school credits in chemistry, J. Chem. Educ., 3(3), 301–306.
28. Brown K. E. and Obourn, E. S., (1956), Offerings and enrollments in science and mathematics in public high schools, US Department of Health, Education, and Welfare, Office of Education, Pamphlet No. 120. ERIC document ED167344.
29. Browning C. S., (2011), The elephant in the first-year science classroom I: are Ontario high schools equally and adequately preparing their students for university science, The Western Conference on Science Education 2011. Abstract available on-line: https://ir.lib.uwo.ca/wcse/WCSEEleven/Thur_July_7/15/ (accessed Mar. 16th, 2021).
30. Buckley C. A., Pitt E., Norton B. and Owens T., (2010), Students’ approaches to study, conceptions of learning and judgements about the value of networked technologies, Active Learn. High. Educ., 11(1), 55–65.
31. Bunce D. M. and Hutchinson K. D., (1993), The use of GALT (group assessment of logical thinking) as a predictor of academic success in college chemistry, J. Chem. Educ., 70(3), 183–187.
32. Bunce D. M., Komperda R., Schroeder M. J., Dillner D. K., Lin S., Teichert M. A. and Hartman J.A. R., (2017), Differential use of study approaches by students of different achievement levels, J. Chem. Educ., 94(10), 1415–1424.
33. Burewicz A. and Miranowicz N., (2006), Effectiveness of multimedia laboratory instruction, Chem. Educ. Res. Pract., 7(1), 1–12.
34. Carmichael J. W., Bauer J., Sevenair J. P., Hunter J. T. and Gambrell R. L., (1986), Predictors of first-year chemistry grades for black Americans, J. Chem. Educ., 63(4), 333–336.
35. Chan J. Y. K. and Bauer C. F., (2014), Identifying at-risk students in general chemistry via cluster analysis of affective characteristics, J. Chem. Educ., 91(9), 1417–1425.
36. Chan J. Y. K. and Bauer C. F., (2016), Learning and studying strategies used by general chemistry students with different affective characteristics, Chem. Educ. Res. Pract., 17(4), 675–684.
37. Chew S., (2011), How to get the most out of studying, Developing a Mindset for Successful Learning, part 2. On-line resource: https://www.samford.edu/departments/academic-success-center/how-to-study (Accessed: March 12th, 2021).
38. Clader C. W., (1963), Chem study – a progress report, School Sci. Math., 63(5), 377–378.
39. Clark P. E., (1938), The effect of high-school chemistry on achievement in beginning college chemistry, J. Chem. Educ., 15(6), 285–289.
40. Coffield F., Moseley. D, Hall E. and Ecclestone, K., (2004a), Learning Styles and Pedagogy in Post-16 Learning: a systematic and critical review. London: Learning and Skills Network.
41. Coffield F., Moseley. D, Hall E. and Ecclestone, K., (2004b), Should we be using learning styles? What research has to say to practice. London: Learning and Skills Network.
42. Cohen H. G., (1980), Dilemma of the objective paper-and-pencil assessment within the Piagetian framework, Sci. Educ., 64(5), 741–745.
43. Coley N. R., (1973), Prediction of success in general chemistry in a community college, J. Chem. Educ., 50(9), 613–615.
44. Cooper M. M., (2020), The cross-cutting concepts: critical component or “third wheel” of three-dimensional learning? J. Chem. Educ., 97(4), 903–909.
45. Cornog J. and Stoddard G. D., (1925), Predicting performance in chemistry, J. Chem. Educ., 2(8), 701–708.
46. Cornog J. and Stoddard G. D., (1926), Predicting performance in chemistry II, J. Chem. Educ., 3(12), 1408–1415.
47. Cracolice M. S. and Busby B. D., (2015), Preparation for college general chemistry: more than just a matter of content knowledge acquisition, J. Chem. Educ., 92(11), 1790–1797.
48. Craig B. S., (1972), The philosophy of Jean Piaget and its usefulness to teachers of chemistry, J. Chem. Educ., 49(12), 807–809.
49. Craney C. L. and Armstrong R. W., (1985), Predictors of grades in general chemistry for allied health students, J. Chem. Educ., 62(2), 127–129.
50. Cross K. P., (1999), Learning is about making connections, The Cross Papers Number 3, League for Innovation in the Community College, Laguna Hills, NJ. ERIC document ED432314.
51. Davenport D. A., (1968), Elevate them guns a little lower, J. Chem. Educ., 45(6), 419–420.
52. Dávila K. and Talanquer V., (2010), Classifying end-of-chapter questions and problems for selected general chemistry textbooks used in the United States. J. Chem. Educ., 87(1), 97–101.
53. Driver, R., (1983), The Pupil as Scientist? Milton Keynes, UK: Open University Press.
54. Driver, R., (ed.) (1985), Children's Ideas in Science, Milton Keynes, UK: Open University Press.
55. Duit R., (ed.) (2009), Bibliography STSCE: Students’ and teachers’ conceptions and science education, IPN – Leibniz Institute for Science Education at the University of Kiel. On-line database, http://www.ipn.uni-kiel.de/aktuell/stcse/ (Retrieved February 8th, 2021).
56. Entwistle N., (2010), Taking stock: an overview of key research findings, in Christensen Hughes J. and Mighty J. (ed.), Taking stock: research on teaching and learning in higher education, Montreal and Kingston: McGill-Queen's University Press, Queen's Policy Studies Series.
57. Entwistle N. and Entwistle D., (1970), The relationships between personality, study methods, and academic performance, Br. J. Educ. Pysch., 40, 132–141.
58. Entwistle N. and McCune V., (2004), The conceptual bases of study strategy inventories, Educ. Psychol. Rev., 16(4), 325–345.
59. Entwistle N. and Ramsden P., (1983), Understanding Student Learning, London/Canberra: Croom Helm.
60. Entwistle N. and Tait H., (1990), Approaches to learning, evaluations of teaching, and preferences for contrasting academic environments, High. Educ., 19(2), 169–194.
61. Entwistle N., Thompson J. and Wilson J. D., (1974), Motivation and study habits, High. Educ., 3 379–396.
62. Entwistle N., Hanley M. and Hounsell D., (1979), Identifying distinctive approaches to studying, High. Educ., 8, 365–380.
63. Even A., (1976), Changes in academic achievement patterns in grade 12 chemistry 1964–1972, Final report of the project: A study of changes in academic achievement patterns in secondary school chemistry, Toronto ON: Ontario Institute for Studies in Education.
64. Everhart W. A. and Ebaugh W. C., (1925), A comparison of grades in general chemistry earned by students who (a) have had, and (b) have not had high-school chemistry, J. Chem. Educ., 2(9), 770–774.
65. Fink A., Cahill M. J., McDaniel M. A., Hoffman, A. and Frey R. F., (2018), Improving general chemistry performance through a growth mindset intervention: selective effects on underrepresented minorities, Chem. Educ. Res. Pract., 19(3), 783–806.
66. Fink A., Frey R. F. and Solomon E. D., (2020), Belonging in general chemistry predicts first-year undergraduates’ performance and attrition, Chem. Educ. Res. Pract., 21(4), 1042–1062.
67. Finster D. C., (1989), Developmental instruction: part I. Perry's model of intellectual development, J. Chem. Educ., 66, 659–661.
68. Finster D. C., (1991), Developmental instruction: part II. Application of the Perry model to general chemistry, J. Chem. Educ., 68, 752–756.
69. Flaherty A. A., (2020), A review of affective chemistry education research and its implications for future research, Chem. Educ. Res. Pract., 21(3), 698–713.
70. Fraser B. J., McRobbie C. J. and Giddings G. J., (1993), Development and cross-national validation of a laboratory classroom environment instrument for senior high school science, Sci. Educ., 77(1), 1–24.
71. Fry H. S., (1925), Questions relative to the correlation of college and high-school chemistry courses, J. Chem. Educ., 2(4), 260–269.
72. Furst E. J., (1981), Bloom's taxonomy of educational objectives for the cognitive domain: philosophical and educational issues, Rev. Educ. Res., 51(4), 441–453.
73. Gabel D., (1999), Improving teaching and learning through chemistry education research: a look to the future, J. Chem. Educ., 76(4), 548–554.
74. Garnett P. J., Garnett P. J. and Hackling M. W., (1995), Students’ alternative conceptions in chemistry: a review of research and implications for teaching and learning, Stud. Sci. Educ., 25, 69–95.
75. George B., Wystrach V. P. and Perkins R. I., (1987), Why do high school students choose chemistry? J. Chem. Educ., 64(5), 431–432.
76. Genovese J. E. C., (2003), Piaget, pedagogy, and evolutionary biology, Evol. Psychol., 1, 127–137.
77. Gerlach K., Trate J., Blecking A., Geissinger P. and Murphy K., (2014), Valid and reliable assessments to measure scale literacy of students in introductory college chemistry courses, J. Chem. Educ., 91(10), 1538–1545.
78. Gidney R. D., (1999), From Hope to Harris: The Reshaping of Ontario's Schools, Toronto: University of Toronto Press.
79. Gilbert J. K., De Jong O., Justi R., Treagust D. F. and Van Driel J. H. (ed.), (2002), Chemical education: towards research-based practice, Dordrecht/Norwell: Kluwer Academic Publishers.
80. Glasoe P. M., (1929), The deadly parallelism between high-school and college courses in chemistry, J. Chem. Educ., 6(3), 505–509.
81. Good R., Mellon E. K. and Kromhout R. A., (1978), The work of Jean Piaget, J. Chem. Educ., 55(11), 688–693.
82. Good R., Kromhout R. A. and Mellon E. K., (1979), Piaget's work and chemical education, J. Chem. Educ., 56(7), 426–430.
83. Goodstein M. P. and Howe A. C., (1978), Application of Piagetian theory to introductory chemistry instruction, J. Chem. Educ., 55(3), 171–173.
84. Heath R. W. and Stickell D. W., (1963), CHEM and CBA effects on achievement in chemistry, Sci. Teach., 30(5), 45–46.
85. Hendricks B. O., Koelsche C. L. and Bledsoe J. C., (1963), Selected high school courses as related to first quarter chemistry marks, J. Res. Sci. Teach., 1, 81–84.
86. Herrmann G. A., (1931), An analysis of freshman college chemistry grades with reference to previous study of chemistry, J. Chem. Educ., 80(7), 1376–1385.
87. Herron J. D., (1975), Piaget for Chemists: explaining what “good” students cannot understand, J. Chem. Educ., 52(3), 146–150.
88. Herron J. D., (2008), Advice to my intellectual grandchildren, J. Chem. Educ., 85(1), 24–32.
89. Hill L. O., (1935), Results of a short first-year college course for students who have had high-school chemistry, J. Chem. Educ., 12(7), 323–324.
90. Holme T. A., Luxford C. J. and Brandiet A., (2015), Defining conceptual understanding in general chemistry, J. Chem. Educ., 92(9), 1477–1483.
91. Hovey N. W. and Krohn A., (1958), Predicting failure in general chemistry, J. Chem. Educ., 35(10), 507–509.
92. Hovey N. W. and Krohn A., (1963), An evaluation of the Toledo Chemistry Placement Examination, J. Chem. Educ., 40(7), 370–372.
93. Howard-Jones P., (2010), Introducing Neuroeducational Research: neuroscience, education and the brain from contexts to practice, ch. 2, London and New York: Routledge.
94. Ingle R. B. and Shayer M., (1971), Conceptual demands in Nuffield O-level chemistry, Educ. Chem., 8, 182–183.
95. Inhelder B. and Piaget J., (1958), The Growth of Logical Thinking, London: Routledge and Kegan Paul.
96. Inhelder B. and Piaget J., (1964), The Early Growth of Logic, London: Routledge and Kegan Paul.
97. Jiang B., Xu X., Garcia A. and Lewis J. E., (2010), Comparing two tests of formal reasoning in a college chemistry context, J. Chem. Educ., 87(12), 1430–1437.
98. Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assist. Learn., 7(2), 75–83.
99. Johnstone A. H., (1997), Chemistry teaching – science or alchemy, J. Chem. Educ., 74(3), 262–268.
100. Johnstone A. H., (2010), You can’t get there from here, J. Chem. Educ., 87(1), 22–29.
101. Kember D. and Leung D. Y. P., (1998), Influences upon students’ perception of workload, Educ. Psychol., 18(3), 293–307.
102. Kember D., Ng S., Tse H., Wong E. T. T. and Pomfret M., (1996), An examination of the interrelationships between workload, study time, learning approaches, and academic outcomes, Stud. High. Educ., 21(3), 347–358.
103. Kennepohl D., Guay M. and Thomas V., (2010), Using an Online, Self-Diagnostic Test for Introductory General Chemistry at an Open University, J. Chem. Educ., 87(11), 1273–1277.
104. Kind V., (2004), Beyond Appearances: students’ misconceptions about basic chemical ideas, 2nd edn, Royal Society of Chemistry, on-line article, https://edu.rsc.org/download?ac=15564 (Retrieved Feb. 8th, 2021).
105. Klopfer, L. E., (1976), A structure for the affective domain in relation to science education, Sci. Educ., 60(3), 299–312.
106. Krathwohl D. R., Bloom B. S. and Masia B. B., (1956), Taxonomy of Educational Objectives, Handbook II: Affective Domain, David McKay Company, Inc., New York NY.
107. Kreber C., (2003), The relationship between students’ course perception and their approaches to studying in undergraduate science courses: a Canadian experience. High. Educ. Res. Dev., 22(1), 57–75.
108. Kuhn D., (1979), The significance of Piaget's formal operational stage in education, Boston Univ. J. Educ., 161, 34–50.
109. Kunhart W. E., Olsen L. R. and Gammons R. S., (1958), Predicting success of junior college students in introductory chemistry, J. Chem. Educ., 35(8), 391–391.
110. LaForgia J., (1988), The affective domain related to science education and its evaluation, Sci. Educ., 72(4), 407–421.
111. Lamb D. P., Waggoner W. H. and Findley W. G., (1967), Student achievement in high school chemistry, School Sci. Math., 67, 221–226.
112. Lastusaari M. and Murtonen M., (2013), University chemistry students’ learning approaches and willingness to change major, Chem. Educ. Res. Pract., 14(4), 496–506.
113. Lastusaari M., Laakkonen E. and Murtonen M., (2016), ChemApproach: validation of a questionnaire to assess the learning approaches of chemistry students, Chem. Educ. Res. Pract., 17(4), 723–730.
114. Lastusaari M., Laakkonen E. and Murtonen M., (2019), Persistence in studies in relation to learning approaches and first-year grades: a study of university chemistry students in Finland, Chem. Educ. Res. Pract., 20(3), 452–467.
115. Laurillard D., (1979), The processes of student learning, High. Educ., 8(4), 395–409.
116. Lawson A. E., (1978), The development and validation of a classroom test of formal reasoning, J. Res. Sci. Teach., 15(1), 11–24.
117. Lawson A. E. and Wollman W. T., (2003), Encouraging the transition from concrete to formal cognitive functioning – an experiment, J. Res. Sci. Teach., 40(S1), 33–50.
118. Lawson A. E., Adi H. and Karplus R., (1979), Development of correlational reasoning in secondary schools: do biology courses make a difference? Am. Biol. Teach., 41(7), 420–425 + 430.
119. Legg M. J., Legg J. C. and Greenbowe T. J., (2001), Analysis of success in general chemistry based on diagnostic testing using logistic regression, J. Chem. Educ., 78(8), 1117–1121.
120. Lewis S. E. and Lewis J. E., (2007), Predicting at-risk students in general chemistry: comparing formal thought to a general achievement measure, Chem. Educ. Res. Pract., 8(1), 32–51.
121. Lourenço O. and Machado A., (1996), In defense of Piaget's theory: a reply to 10 common criticisms, Psychol. Rev., 103(1), 143–164.
122. Lutz S. T. and Huitt W. G., (2004), Connecting cognitive development and constructivism: implications from theory for instruction and assessment, Construct. Hum. Sci., 9(1), 67–90.
123. Mamantov C. B. and Wyatt W. W., (1978), A study of factors related to success in nursing chemistry, J. Chem. Educ., 55(8), 524–525.
124. Martin D. R., (1979), A group administered reasoning test for classroom use, J. Chem. Educ., 56(3), 179–180.
125. Marton F. and Säljö R., (1976a), On qualitative differences in learning: I – Outcome and process, Br. J. Educ. Psychol., 46(1), 4–11.
126. Marton F. and Säljö R., (1976b), On qualitative differences in learning: II – Outcome as a function of the learner's conception of the task, Br. J. Educ. Psychol., 46(2), 115–127.
127. Mason D. S., Shell D. F. and Crawley F. E., (1997), Differences in problem solving by nonscience majors in introductory chemistry on paired algorithmic-conceptual problems, J. Res. Sci. Teach., 34(9), 905–923.
128. Meyer H. A., (1962) What value high school chemistry to the freshman college chemistry student? School Sci. Math., 62(6), 410–414.
129. Meyer J. and Land R., (2003), Threshold concepts and troublesome knowledge: linkages to ways of thinking and practising within the disciplines, Occasional Report No. 4, Enhancing Teaching–Learning Environments in Undergraduate Courses Project, School of Education, University of Edinburgh, Edinburgh UK, on-line article, http://www.etl.tla.ed.ac.uk/docs/ETLreport4.pdf (Retrieved Feb. 8th, 2021).
130. Meyer J. and Land R., (2006), Threshold concepts and troublesome knowledge: an introduction, in Meyer J. and Land R. (ed.), Overcoming Barriers to Student Understanding: Threshold Concepts and Troublesome Knowledge, Abingdon, UK: Routledge, pp. 3–18.
131. McFate C. and Olmsted J., (1999), Assessing student preparation through placement tests, J. Chem. Educ., 76(4), 562–565.
132. McNeill K. L. and Krajcik J., (2008), Scientific explanations: characterizing and evaluating the effects of teachers’ instructional practices on student learning, J. Res. Sci. Teach., 45(1), 53–78.
133. McQuary J. P., Williams H. V. and Willard J. E., (1952), What factors determine student achievement in first-year college chemistry, J. Chem. Educ., 29(9), 460–464.
134. Miller M. D., Linn R. L. and Gronlund N. E., (2009), Measurement and assessment in teaching, 10th edn, Upper Saddle River, NJ: Merril/Pearson.
135. Mulford D. R. and Robinson W. R., (2002), J. Chem. Educ., 79(6), 739–744.
136. Muller D. A., Sharma M. D. and Reimann P., (2008), Raising cognitive load with linear multimedia to promote conceptual change, Sci. Educ., 92(2), 278–296.
137. Nagy P. and Griffiths A. K., (1982), Limitations of recent research relating to Piaget's theory to adolescent thought, Rev. Educ. Res., 52(4), 513–556.
138. Nakhleh M. B., (1993), Are our students conceptual thinkers or algorithmic problem solvers? J. Chem. Educ., 70(1), 52–55.
139. Nakhleh M. B. and Mitchell R. C., (1993), Concept learning versus problem solving: there is a difference, J. Chem. Educ., 70(3), 190–192.
140. Nicoll G. and Francisco J. S., (2001), An investigation of factors influencing performance in physical chemistry, J. Chem. Educ., 78(1), 99–102.
141. Niedzielski R. J. and Walmsley F., (1982), What do incoming freshmen remember from high school chemistry? J. Chem. Educ., 59(2), 149–151.
142. Nordstrom B. H., (1990), Predicting performance in freshman chemistry, Paper presented at the spring national meeting of the American Chemical Society, Boston MA, ERIC ED347065.
143. Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem solving: is there a difference, J. Chem. Educ., 64(6), 508–510.
144. Nurrenbern S. C. and Robinson W. R., (1998), Conceptual questions and challenge problems, J. Chem. Educ., 75(11), 1502–1503.
145. Ogden W. R., (1976), The affect of high school chemistry upon achievement in college chemistry: a summary, School Sci. Math., 76, 122–126.
146. Orpwood G., (1995), Juggling educational needs and political realities in Canada: national standards, provincial control, and teachers' professionalism, Stud. Sci. Educ., 26(1), 39–57.
147. Ozsogomonyan A. and Loftus D., (1979), Predictors of general chemistry grades, J. Chem. Educ., 56(3), 173–175.
148. Pashler H., McDaniel M., Rohrer D. and Bjork R., (2008), Learning styles: concepts and evidence. Psychol. Sci. Public Interest, 9(3), 105–119.
149. Pask G., (1976a), Conversational techniques in the study and practice of education, Br. J. Educ. Psychol., 46(1), 12–25.
150. Pask G., (1976b), Styles and strategies of learning, Br. J. Educ. Psychol., 46(2), 128–148.
151. Pedersen L. G., (1975), The correlation of partial and total scores of the scholastic aptitude test of the college entrance examination board with grades in freshman chemistry, Educ. Psychol. Meas., 35(2), 509–511.
152. Perkins D., (1999), The many faces of constructivism, Educational Leadership, 57(3), 6–11.
153. Perry Jr W. G., (1970), Forms of intellectual and ethical development in the college years: a scheme, New York, NY: Holt, Rinehart and Winston Inc.
154. Phelps A. J., (1996), Teaching to enhance problem solving: it's more than just the numbers, J. Chem. Educ., 73(4), 301–304.
155. Philips D. C., (1995), The good, the bad, and the ugly: the many faces of constructivism, Educ. Res., 24(7), 5–12.
156. Pickering M., (1975), Helping the high risk freshman chemist, J. Chem. Educ., 52(8), 512–514.
157. Pickering M., (1977), The high risk freshman chemist revisited, J. Chem. Educ., 54(7), 433–434.
158. Piaget J., (1972), Intellectual development from adolescence to adulthood, Hum Dev, 15(1), 1–12.
159. Piaget J. and Inhelder B., (1956), The Child's Conception of Space, London: Routledge and Kegan Paul.
160. Piaget J. and Inhelder B., (1974), The Child's Construction of Quantities, London: Routledge and Kegan Paul.
161. Pimentel G. C., (ed.) (1963), Chemistry: An Experimental Approach, San Francisco: W. H. Freeman.
162. Pintrich P. R. and De Groot E. V., (1990), Motivational and self-regulated learning components of classroom academic performance, J. Educ. Psychol., 82, 33–40.
163. Powers S. R., (1921), The achievement of high school and freshman college students in chemistry, School Sci. Math., 21(4), 366–377.
164. Rainey R. G., (1964), A comparison of the CHEM Study curriculum and a conventional approach in teaching high school chemistry, School Sci. Math., 64(6), 539–544.
165. Ramsden P., (1979), Student learning and perceptions of the academic environment, High. Educ., 8(4), 411–427.
166. Ramsden P., (1991), A performance indicator of teaching quality in higher education: the course experience questionnaire, Stud. High. Educ., 16(2), 129–150.
167. Ramsden P. and Entwistle N. J., (1981), Effects of academic departments on students’ approaches to studying, Br. J. Educ. Psychol., 51(3), 368–383.
168. Ramsey G. A., (1970), A review of the research and literature on the chemical education materials study project, Research Review Series – Science Paper 4, ERIC Information Analysis Center for Science Education, Columbus OH, USA. ERIC document ED037592.
169. Roadrangka, V. and Yeany, R. H., (1985), A study of the relationship among type and quality of implementation of science teaching strategy, student formal reasoning ability, and student engagement, J. Res. Sci. Teach., 22(8), 743–760.
170. Roadrangka, V., Yeany, R. H. and Padilla, M. J., (1983), The construction and validation of the Group Assessment of Logical Thinking (GALT), Paper presented at the annual meeting of the National Association for Research in Science Teaching, Dallas TX.
171. Russell A. A., (1994), A rationally designed general chemistry diagnostic test, J. Chem. Educ., 71(4), 314–317.
172. Säljö R., (1979), Learning about learning, High. Educ., 8(4), 443–451.
173. Schelar V. M., Cluff R. B. and Roth B., (1963), Placement in general chemistry, J. Chem. Educ., 40(7), 369–370.
174. Schwartz T. A., (2006), Contextualized chemistry education: the American experience, Int. J. Sci. Educ., 28(9), 977–998.
175. Schwartz P. and Barbera J., (2014), Evaluating the content and response process validity of data from the Chemical Concepts Inventory, J. Chem. Educ., 91(5), 630–640.
176. Scofield M. B., (1927), An experiment in predicting performance in general chemistry, J. Chem. Educ., 4(9), 1168–1175.
177. Scouller K., (1998), The influence of assessment method on students’ learning approaches: multiple choice question examination versus assignment essay, High. Educ., 35(4), 453–472.
178. Scouller K. M. and Prosser M., (1994), Students’ experiences in studying for multiple choice question examinations, Stud. High. Educ., 19(3), 267–279.
179. Seery M. K., (2009), The role of prior knowledge and student aptitude in undergraduate performance in chemistry: a correlation-prediction study, Chem. Educ. Res. Pract., 10(3), 227–232.
180. Sharp J. G., Bowker R. and Byrne J., (2008), VAK or VAK-uous? Towards the trivialisation of learning and the death of scholarship, Res. Pap. Educ., 23(3), 293–314.
181. Shayer M., (1970), How to assess science courses, Educ. Chem., 7(5), 182–186.
182. Shayer M. and Wharry D., (1974), Piaget in the classroom part I: testing a whole class at a time, Sch. Sci. Rev., 55, 447–458.
183. Shayer M., Küchemann D. E. and Wylam H., (1976), The distribution of Piagetian stages of thinking in British middle and secondary school children, Br. J. Educ. Psychol., 46(2), 164–173.
184. Shayer M., Adey P. and Wylam H., (1981), Group tests of cognitive development: ideals and realization, J. Res. Sci. Teach., 18(2), 157–168.
185. Shedlosky-Shoemaker R. and Fautch J. M., (2015), Who leaves, who stays? Psychological predictors of undergraduate chemistry students’ persistence, J. Chem. Educ., 92(3), 408–414.
186. Slocombe C. S., (1927), A note on the results obtained from Iowa chemistry tests, J. Chem. Educ., 4(7), 894–896.
187. Smith K. C., Nakleh M. B. and Bretz, S. L., (2010), An expanded framework for analyzing general chemistry exams. Chem. Educ. Res. Prac., 11(1), 147–153.
188. Stamovlasis D., Tsaparlis G., Kamilatos C., Papsoikonomou D. and Zarotiadou E., (2005), Conceptual understanding versus algorithmic problem solving: further evidence from a national chemistry examination, Chem. Educ. Res. Pract., 6(2), 104–118.
189. Stanich C. A., Pelch M. A., Theobald E. J. and Freeman S., (2018), A new approach to supplementary instruction narrows achievement and affect gaps for underrepresented minorities, first-generation students, and women, Chem. Educ. Res. Pract., 19(3), 846–866.
190. Stanovich K. E., (2009), Rational and irrational thought: the thinking that IQ tests miss, Scientific American Mind, November/December issue, pp. 34–39.
191. Stone D. C., (2010), High to low tide: the high school-university transition, Collected Essays Learning Teaching, 3, 133–139. On-line DOI:10.22329/celt.v3i0.3252 (Retrieved Mar. 11th, 2021).
192. Stone D. C., (2011), The high school to university transition in chemistry, On-line resource: https://sites.chem.utoronto.ca/chemistry/dstone/Research/ROP299.html (accessed March 18th, 2021).
193. Stone D. C., (2017), Know the limit and teach within it Part 1: analogies and models, CHEM13 news (University of Waterloo), 435, 22–25. https://uwaterloo.ca/chem13-news-magazine/december-2017-january-2018/feature/analogies-and-models-part-1. (Retrieved Feb. 17th, 2021).
194. Stone D. C., (2021), Chemical Education: An Annotated Reference List, Retrieved March 18th, 2021 from: https://sites.chem.utoronto.ca/chemistry/dstone/Research/bibliography.html.
195. Strong L. E., (1962), Facts, students, ideas, J. Chem. Educ., 39(3), 126–129.
196. Swartney, I. J., (1969), Learning difficulties encountered by students studying the CHEM study program, Wisconsin Research and development Center for Cognitive Learning Technical report no. TR-77, Madison WI: University of Wisconsin. ERIC document ED036445.
197. Taber K., (2002), Chemical misconceptions – prevention, diagnosis and cure; Volume 1 theoretical background, London: Royal Society of Chemistry.
198. Taber K. and Franco A. G., (2009), Intuitive thinking and learning chemistry, Educ. Chem., 46(2), on-line article, https://edu.rsc.org/feature/intuitive-thinking-and-learning-chemistry/2020171.article (Retrieved February 8th, 2021).
199. Tai R. H. and Sadler P. M., (2007), High school chemistry instructional practices and their association with college chemistry grades, J. Chem. Educ., 84(6), 1040–1046.
200. Tai R. H., Sadler P. M. and Loehr J. F., (2005), Factors influencing success in introductory college chemistry, J. Res. Sci. Teach., 42(9), 987–1012.
201. Tai R. H., Ward, R. B. and Sadler P. M., (2006), High school chemistry content background of introductory college chemistry students and its association with college chemistry grades, J. Chem. Educ., 83(11), 1703–1711.
202. Tait, H. and Entwistle, N., (1996), Identifying students at risk through ineffective study strategies, High. Educ., 31, 97–116.
203. Talanquer V., (2006), Commonsense chemistry: a model for understanding students’ alternative conceptions, J. Chem. Educ., 83(5), 811–816.
204. Talanquer V., (2015), Threshold concepts in chemistry: the critical role of implicit schemas, J. Chem. Educ., 92(1), 3–9.
205. Teichert M. A., Schroeder M. J., Lin S., Dillner D. K., Komperda R. and Bunce D. M., (2020), Problem-solving behaviors of different achievement groups on multiple-choice questions in general chemistry, J. Chem. Educ., 97(1), 3–15.
206. Thomas P. R. and Bain J. D., (1982), Consistency in learning strategies, High. Educ., 11(3), 249–259.
207. Thomas P. R. and Bain J. D., (1984), Contextual dependence of learning approaches: the effects of assessment, Hum. Learn., 3, 227–240.
208. Tobias S., (1990), They’re not dumb, they’re different: stalking the second tier, Science News Books, Public Research Corporation, Tucson AZ.
209. Tobin K. G. and Capie W., (1981), The development and validation of a group test of logical thinking, Educ. Psychol. Meas., 41(2), 413–423.
210. Tobin K. G. and Capie W., (1982), Relationships between classroom process variables and middle-school science achievement, J. Educ. Psychol., 74, 441–454.
211. Trigwell K. and Prosser M., (1991), Improving the quality of student learning: The influence of learning context and student approaches to learning on learning outcomes. High. Educ., 22(3), 251–266.
212. Trigwell K., Prosser M. and Waterhouse F., (1999), Relations between teachers’ approaches to teaching and students’ approaches to learning, High. Educ., 37(1), 57–70.
213. Uricheck M. J., (1967), Research proposal: an attempt to evaluate the success of the CBA and CHEMS chemistry courses, Sci. Educ., 51(1), 5–7.
214. Wagner E. P., Sasser H. and DiBiase W. J., (2002), J. Chem. Educ., 79(6), 749–755.
215. Wallace G. W., (2011), Why is the research on learning styles still being dismissed by some learning leaders and practitioners? eLearn Magazine, November issue, on-line article: https://elearnmag.acm.org/featured.cfm?aid=2070611 (accessed Feb. 25th, 2021).
216. Watkins D., (1983), Assessing tertiary study processes, Hum. Learn., 2, 29–37.
217. Watkins D. and Hattie J., (1981), The learning processes of Australian university students: investigation of contextual and personological factors, Br. J. Educ. Psychol., 51(3), 384–393.
218. Watson G. and Glaser E. M., (1980), Watson-Glaser Critical Thinking Appraisal and Watson-Glaser Critical Thinking Appraisal Manual, New York NY: Harcourt Brace Jovanovich.
219. Weaver G. C., (1998), Strategies in K-12 science instruction to promote conceptual change, Sci. Educ., 82(4), 455–472.
220. Williams H., Turner C. W., Debreuil L., Fast J. and Berestiansky J., (1979), Formal operational reasoning by chemistry students, J. Chem. Educ., 56(9), 599–600.
221. Willingham D. T., (2009), Why Don’t Students Like School? San Francisco, CA: Jossey–Bass.
222. Wilson K. L., Lizzio A. and Ramsden P., (1997), The development, validation and application of the course experience questionnaire, Stud. High. Educ., 22(1), 33–53.
223. Wiseman Jr L. R., (1981), The teaching of college chemistry, J. Chem. Educ., 58(6), 484–488.
224. Wolfe D. H. and Heikkinen H. W., (1978), Assessing introductory college students’ higher cognitive skills, J. Chem. Educ., 55(10), 650–651.
225. Xu X. and Lewis J. E., (2011), Refinement of a chemistry attitude measure for college students, J. Chem. Educ., 88(5), 561–568.
226. Xu, X., Villafane S. M. and Lewis J. E., (2013), College students’ attitudes toward chemistry, conceptual knowledge and achievement: structural equation model analysis, Chem. Educ. Res. Pract., 14(2), 188–200.
227. Zoller U., Lubezky A., Nakhleh M. B., Tessier B. and Dori Y. J., (1995), Success on algorithmic and LOCS vs. conceptual chemistry exam questions, J. Chem. Educ., 72(11), 987–989.

---

Footnotes

† The Ontario Science Curriculum, Grades 11 and 12, published at http://www.edu.gov.on.ca/eng/curriculum/secondary/2009science11_12.pdf (accessed February 2nd, 2021).

‡ The Next Generation Science Standards can be found at: https://www.nextgenscience.org/ (accessed February 2nd, 2021).

§ The Common Core Standards Initiative can be found at http://www.corestandards.org/about-the-standards/ (accessed February 2nd, 2021).

¶ The Advanced Placement Program is administered by The College Board https://ap.collegeboard.org/ (accessed February 2nd, 2021).

|| The parent International Baccalaureate Organization hosts pages for each national program and can be found at: https://www.ibo.org/ (accessed February 2nd, 2021).

** The nature of these tests is not clear from the original literature, but presumably included measures of IQ and general scholastic aptitude.

†† Originally called the Toledo Chemistry Achievement Test and now known as the Toledo Examination, this was published by the American Chemical Society Division of Chemical Education Examinations Institute and can be found at: https://uwm.edu/acs-exams/ (accessed February 2nd, 2021).

‡‡ The original domain for the FICSS study website is no longer controlled by the researchers. However, a complete bibliography can still be found at: http://www.cfa.harvard.edu/smg/ficss/research/publication.html (accessed February 2nd, 2021).

§§ While used in a general sense here, Canadian readers will be more familiar with the term ‘ways of knowing’ in the context of First Nations education. To the extent that the latter constitutes a specific conceptual framework for understanding, these uses are not incompatible.

¶¶ The author has had this exact same conversation numerous times!.

|||| The exact terminology varies considerably between authors.

*** Including earlier forms of these instruments by the same authors.

††† It is not clear why the deep scale has lower predictive value; this could be related to either the reduced items in the model or assessment practices. It is also possible that some students were scoring highly on both deep and surface scores.

‡‡‡ As reported by participating college and university science representatives at the Durham & Peel Catholic District School Board Round Table, Mississauga ON, March 28th, 2014.

§§§ For example, AdvanceHE in the United Kingdom: https://www.advance-he.ac.uk/ (accessed March 16th, 2021).

¶¶¶ See for example the list of initiatives posted by the Carl Wieman Science Education Initiative: https://cwsei.ubc.ca/about/related (accessed March 16th, 2021).

|||||| Journal of Chemical Education Special Issue on Insights Gained While Teaching Chemistry in the Time of COVID-19, 2020, 97(9), available on-line at: https://pubs.acs.org/toc/jceda8/97/9?ref=feature (accessed March 16th, 2021).

---