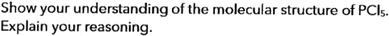The role of visuospatial thinking in students’ predictions of molecular geometry

Abstract

Visuospatial thinking is considered crucial for understanding of three-dimensional spatial concepts in STEM disciplines. Despite their importance, little is known about the underlying cognitive processing required to spatially reason and the varied strategies students may employ to solve visuospatial problems. This study seeks to identify and describe how and when students use imagistic or analytical reasoning when making pen-on-paper predictions about molecular geometry and if particular reasoning strategies are linked to greater accuracy of responses. Student reasoning was evidenced through pen-on-paper responses generated by high attaining, high school students (N = 10) studying Valence Shell Electron Pair Repulsion (VSEPR) Theory in their final year of chemistry. Through analysis and coding of students’ open-ended paper-based responses to an introductory task, results revealed that students employed multiple reasoning strategies, including analytical heuristics and the spontaneous construction of external diagrammatic representations to predict molecular geometry. Importantly, it was observed that despite being instructed on the use of VSEPR theory to find analytical solutions, some students exhibited preference for alternative reasoning strategies drawing on prior knowledge and imagistic reasoning; showing greater accuracy with 3D diagrammatic representations than students who used the algorithmic method of instruction. This has implications for both research and practice as use of specific reasoning strategies are not readily promoted as a pedagogical approach nor are they given credit for in national examinations at school level.

---

Introduction

Much attention has been given to the role of visuospatial ability for learning in science, technology, mathematics and engineering (STEM) disciplines spanning several decades (Guay and McDaniel, 1977; West, 1991; Hegarty, 2004; Lubinski, 2010; Stieff, 2011; Stieff et al., 2020). Visuospatial thinking is a fundamental component of STEM learning and problem solving, yet despite its significance, little is known about how to support students to acquire the necessary cognitive skills when employing this type of spatial reasoning and how to identify best strategies to solve spatial problems when learning in the STEM classroom.

Understanding how visuospatial thinking can enable STEM learners to construct and organise their subject knowledge through varied reasoning strategies is key to developing new and improved student learning support materials, digital teaching tools and ultimately widening access to the STEM disciplines. This study explores visuospatial thinking through students’ use of imagistic, analytical, and diagrammatic reasoning when predicting molecular geometry.

Theoretical background

Imagistic thinking

Imagistic reasoning refers specifically to the process of spatial visualisation which involves generating and manipulating perceived analog image-like mental representations and perspective taking for spatial thinking; its role is taken as self-evident to STEM problem solving (West, 1991; Hegarty, 2004; Stieff, 2011). Chemists, in particular have for some time employed imagistic reasoning when visualising and representing submicroscopic 3D structures and processes from illustrated, two-dimensional representations in textbooks (Bodner and Guay, 1997). Chemists must imagine how a structure will appear from different perspectives, visualize the effects of operations such as rotation, reflection, and inversion and mentally manipulate objects (Barnea and Dori, 1999; Wu and Shah, 2004; Vlacholia et al., 2017). For example, an organic chemist may approach drug design by first imagining how well a molecule would fit into the active site of a specific protein molecule (Stieff, 2011).

In the classroom, students learn about molecular geometry and how to predict and represent the shapes of molecules in a variety of different formats; this imagistic reasoning component of spatial thinking is key to understanding (Stieff, 2011).

In a study examining how students learn group theory, Southam and Lewis (2013) described imagistic reasoning as an instructional approach in which students must conceptualise a representation, apply an operation and produce an outcome. This study concluded that imagistic reasoning was the predominant approach used by students to manipulate representations when describing molecular symmetry and thus considered that students who were assessed as having low visuospatial skills could be disadvantaged and potentially demotivated to learn this topic.

The issue of whether the ability to imagistically reason is somehow innate or can be taught is a contentious one (Harle et al., 2010), yet these visuospatial skills are generally considered not only crucial for successful learning but important indicators of an aptitude for STEM disciplines (Lubinski et al., 2010).

Measuring visuospatial skills is not a straightforward task. Indeed, various spatial ability tests have been devised to attempt to measure these; a widely reported example being the Purdue Visualisation of Rotations Test (PVRT) which is used to assess one key aspect of spatial ability: the mental rotation of objects. The PVRT has been frequently employed over the past four decades in educational research, particularly in the STEM disciplines; for example, to probe relationships between spatial and mathematical abilities in children and preservice teachers, and to ascertain the role of spatial abilities in learning chemistry (Guay et al., 1977; Guay, 1980; Battista et al., 1982; Bodner et al., 1986; Pribyl et al., 1987; Southam et al., 2013). This type of mental rotation represents an important component of the visuospatial strategies that may be accessed during instruction in chemistry.

Previous studies have also considered the importance of external representations in providing support to STEM learners when solving problems that involve imagistic reasoning and visualisation of three-dimensional systems. Such representations include a variety of domain-specific diagrams, physical models and computer simulations that can augment and simulate spatial information relevant to the problem being solved (Stieff, 2011).

Of note is that several studies across STEM fields have reported that many learners do not use imagistic reasoning in isolation during scientific problem solving. Rather, individuals employ imagistic reasoning in tandem with alternative problem-solving strategies. Specifically, problem solvers frequently also employ strategies that involve analytical reasoning from diagrams to assist with spatial problems (Schwartz and Black, 1996; Stieff, 2007).

Analytical thinking

There are various reported instructional means with which to circumvent visuospatial imagistic reasoning; students (and experts) may use specific ‘‘rules’’ for predicting, manipulating and transforming the spatial relationships embedded in two-dimensional diagrams without necessarily employing imagistic strategies (Stieff, 2007). This analytical approach to reasoning about complex visuospatial transformations contrasts to that inherent of imagistic reasoning, thus provides an alternative strategy (Schwartz et al. 1996, Kehneer, 2004). Chemists, for example, often use analytical strategies to make spatial information explicit (Stieff, 2007).

A common analytical strategy introduced to chemistry students is Valence Shell Electron Pair Repulsion Theory. The VSEPR model essentially provides an algorithm that can predict the molecular structure and 3D shape of many chemical compounds. In VSEPR theory, pairs of negatively charged electrons that surround the central atom of a molecule are arranged as far apart as possible to minimise electron–electron repulsion. This simple idea can be used by chemists to predict the shapes of molecules by following a simple analytical stepped procedure and is the approach commonly used in textbooks (Ebbing and Gammon, 2015).

1. Firstly, decide where the central atom is in the molecule.

2. Determine the number of valence (outermost) electrons on the central atom (this information can be found from The Periodic Table of Elements).

3. Count the electrons contributed by the outer atoms to make chemical bonds (2 shared electrons) when joining with the central atom.

4. The sum of steps 2 and 3 is then divided by two to give the valence shell electron pair count.

5. Subtract the number of outer atoms attached to the central atom from the valence shell electron pair count to deduce the number of lone pairs of electrons.

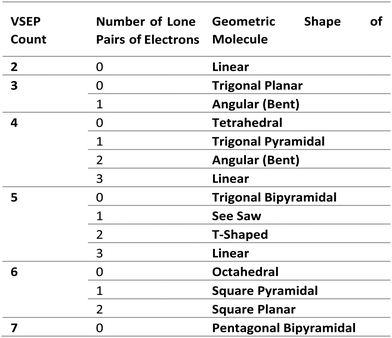
6. Finally, determine the molecular shape by referring to the known molecular geometrical shapes possible accounting for the number of lone pairs of electrons the molecule may have (see Fig. 1).

Fig. 1 Showing how valence shell electron pair (VSEP) count predicts spatial molecular geometry.

Thus, the predicted geometry of the molecule is based on the number of valence shell electrons and ultimately determined after accounting for the number of lone pairs of electrons around the central atom. For example, in the case of ammonia, with chemical formula NH₃, the molecular geometry can be predicted analytically as follows:

1. The N atom is the central atom.

2. There are 5 valence electrons (as nitrogen is in group 5 of the periodic table).

3. There are 3 electrons used by the outer H atoms to make 3 chemical bonds when joining with the central atom.

4. This gives the sum 5 + 3 = 8 which when divided by 2 gives the valence shell electron pair count of 4 and may at first glance suggest a tetrahedral geometry.

5. However, although the valence shell electron pair count is 4, the number of atoms attached to the central N atom is only 3, so subtracting 3 from 4 reveals that there must be 1 lone pair of electrons on the N atom.

6. Reference to the known molecular geometries shown in Fig. 1, would predict a trigonal pyramidal shape for an ammonia molecule (shown in Fig. 2). The wedged shaped bond represents a H atom oriented outward from the plane of the diagram (towards the reader) and the dashed bond represents a H atom pointing backwards into the plane of the diagram (away from the reader).

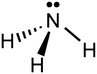Fig. 2 2D representation showing the 3D geometric shape of an ammonia molecule consisting of a central nitrogen (N) atom, 3 attached hydrogen (H) atoms and a lone pair of electrons.

Chemists often use analytical strategies like the VSEPR model to help assimilate spatial information and to predict the outcome of spatial transformations without the requirement to use imagistic mental rotation (Stieff, 2007). More recently, analytic strategies have been considered as helping to lessen the cognitive load of visuospatial thinking through the application of rules and heuristics to spatial tasks (Hegarty et al., 2013). Cognitive load theory is a concept increasingly reported in educational literature that attempts to define the relationship between the structure of information and cognitive capacity of students. According to this theory, humans are limited in the amount of information that can be processed simultaneously (Chandler and Sweller, 1991; Schnotz and Kürschner, 2007; Milenković et al., 2014). Several studies have examined the role of cognitive load on STEM learners’ ability to understand abstract concepts, use textbook representations effectively and solve problems; a few have presented findings which offer insight into how reducing cognitive load with offloading strategies may free up valuable cognitive resources and therefore improve students’ capacity for learning (Manches and O’Malley, 2012; Seery and Donnelly, 2012; Nyachwaya and Gillespie, 2016).

Tiettmeyer et al. (2017), investigated cognitive loading of chemistry students learning to use Lewis structures or electron dot structures (a key domain specific representation used to show how atoms chemically bond using their electrons). The results showed that the inclusion of nearly any structural characteristic induced a significant increase in cognitive load for novice chemistry students, but these trends were mitigated as students gained expertise. Thus, for visuospatial problem solving, employing an alternative (analytical) route may alleviate the potential cognitive load imposed by imagistic reasoning. Students’ strategy choice when solving spatial problems may therefore reveal the way they are thinking, what they have learned previously, in addition to possible cognitive load they are experiencing.

Diagrammatic thinking

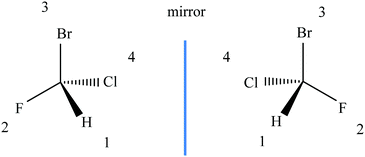
Diagrammatic reasoning is a commonly observed learning strategy central to STEM disciplines. In chemistry, students must gain competence in expressing their learning through a wide range of chemical representations of molecular structure, chemical composition, and spatial transformations of submicroscopic entities. For example, Fig. 2 shows a common diagrammatic representation of an ammonia molecule which reveals the molecular structure and connectivity of atoms, the chemical composition which comprises of 1 nitrogen atom and 3 hydrogen atoms connected via chemical bonds and the arrangement of bonds to form a 3-dimensional geometry. As students progress through their chemistry instruction they are exposed to increasing numbers of such diagrams to illustrate molecules in both two and three dimensions and to depict structures from alternative perspectives or degrees of abstraction (Stieff, 2011).

Diagrammatic reasoning has been previously defined as the application of heuristics or algorithms to domain-specific diagrams which enable students to deduce complex spatial transformations without necessarily invoking mental images (Stieff, 2011; Stieff, Hegarty and Dixon, 2010). This is to say that chemists may use domain-specific rules to reveal, manipulate and transform the spatial relationships embedded in diagrams without employing visuospatial imagistic reasoning (Hegarty, 2004). Stieff et al., reported that experts were seen to frequently make use of diagram templates that illustrated a basic set of spatial features common to many molecular structures, such as arrangement of bonds between atoms or bond angles, which they then amended without the need to necessarily invoke mental imagery. For example, experts were seen to systematically assign bonds within a given molecular structure to generate related molecules that contained structures with similar composition, but unique spatial relationships without the requirement to employ imagistic reasoning, hence the term diagrammatic reasoning. Fig. 3 shows how priority numbering of atomic groups allows for spatial manipulation and determination of molecular structure without the need to use mental visualisation or imagistic reasoning.

Fig. 3 Numbering of different types of atomic groups allows chemists to determine whether the molecule is an R type configuration where priority numbering from 1–4 is clockwise or S type where anticlockwise numbering helps to determine the structure type.

Thus, although visuospatial imagistic reasoning is intrinsic to STEM learning, it seems that training in diagrammatic reasoning strategies can offer the potential to lighten students’ visuospatial load by providing an analytical route.

Similarly common to STEM studies is the use of sketching to diagrammatically reason. Creating a sketch can make scientific modelling of a phenomenon more explicitly detailed, allowing scientists to characterise and communicate their understanding of the phenomena more effectively (Latour, 1990).

As Latour suggests, sketching is fundamental to scientific practice as it permits near instant perceptual understanding for many spatial and temporal phenomena that may otherwise go misunderstood. It was argued that the drawing of diagrams by individual scientists has been responsible for shifting a scientific community to accept new models of a phenomenon and spur entire research paradigms (Latour, 1990).

Sketching is consequently considered a powerful assessment tool that can provide detailed insight into the complexities of student understanding and mental imagery and student-generated sketches can reveal misconceptions of scientific principles that are less likely to be identified using more traditional assessment instruments that do not involve sketching (Kelly et al., 2010; Harle and Towns, 2013; Cooper et al., 2015; Cooper et al., 2017). However, recent studies have also suggested that student-generated sketches can sometimes appear conceptually accurate while still maintaining impoverished mental models of chemical phenomena and that drawing can bias learners to focus on some conceptual features at the expense of others (Cheng and Gilbert, 2017; Ploetzner and Fillisch, 2017; Cheng, 2018).

Advocates of sketching in science education have argued that sketching offers unique benefits that go beyond just assessment to directly improve science learning through increased engagement, training of observational practices, and enrichment of communication and argumentation skills (Van Meter and Garner, 2005; Chang et al., 2009; Ainsworth et al., 2011). Thus, sketching may hold the key to deeper learning among students as well as offering instructors a more nuanced and valuable insight into student visuospatial thinking through imagistic and analytical strategies evidenced within.

Research methodology and questions

Despite its importance to STEM learning, the unique ways in which novice STEM learners think spatially and the adoption of reasoning strategies when problem solving is still not well understood and leaves much to be explored. Formative studies have explored the roles that imagistic and analytical reasoning strategies can play; when examining how experts and undergraduate students employ mental rotation and diagrammatic reasoning in chemistry tasks which involve spatial information, Stieff (2007), concluded that both analytical and imagistic strategies should ultimately be used to ensure successful scientific problem solving.

Various methods have been employed to examine strategy use in chemistry including pen-on-paper written tests, think-aloud activities and pre-defined strategy selection. Stieff and Raje (2008), Hegarty et al., (2013) and Vlacholia et al. (2017) designed pen-on-paper tests to detect the use of imagistic, mental rotation and analytical strategy use. Although these methods all allow for some inferences about the reasoning strategies used during problem solving, they also have limitations. Stieff's methods to detect mental rotation could not directly assess the use of analytic strategies and required additional retrospective self-reports that were time consuming and unreliable (Stieff, 2007). Likewise, the use of think aloud protocols introduce concerns over data validity due to demands on participant and their ability to report whilst problem solving. Vlacholia et al. (2017) noted that performance in their reasoning test was not correlated to students’ base knowledge and understanding of the chemistry topic as assessed by typical examinations.

This study employed a mixed-method design to yield both quantitative and qualitative data, however is grounded in a phenomenographical framework; it attempts to address previously reported limitations by using a research instrument designed to reveal varied reasoning strategies whilst also being consistent with the typical examination style for the participants. To gain insight into student thinking, an open-ended pen-on-paper written activity designed to capture individual aspects of student reasoning in their natural classroom environment was devised; tasking participants with showing their understanding of the three-dimensional shape of molecules. Given recent research interest into the use of multimodal representations in STEM teaching resources by several authors (Meij and Jong, 2003; Ainsworth, 2006, 2011; Bodemer and Faust, 2006; Cooper et al., 2015) and how these representations assist learners to make the complex imagistic visualisations necessary for understanding, this data collection tool was deemed an appropriate way to begin investigations in this domain and was intended to be suitably open-ended to allow students to express their understanding using the typical and naturalistic modes employed to teach and assess them.

This paper will therefore seek to identify and describe how and when students use imagistic or analytical reasoning when making pen-on-paper predictions about molecular geometry and examine whether specific reasoning strategies promote greater accuracy in these predictions. Molecular geometry is a key chemistry context to investigate spatial reasoning due to it being a core skill that all chemistry students (at senior school and undergraduate levels) must acquire and understanding this abstract concept is key to comprehending a wide range of scientific topics; such as the structure and function of biomolecules, industrial catalysts, synthetic polymer engineering and quantum mechanics, spanning across several STEM disciplines (Nicoll, 2001; Erlina et al., 2018). To relate, represent and predict molecules’ submicroscopic form is difficult for learners; it requires imagining how the molecules will appear from different perspectives and as such is certainly aided by the ability to visualise and mentally manipulate (Vlacholia et al., 2017). Similarly, students have been shown to have difficulty with determination of molecular geometries using the established Valence Shell Electron Pair Repulsion Theory (VSEPR theory), commonly taught in schools and universities (Furio et al., 1996; Gillespie, 1997; Nicoll, 2001; Erlina et al., 2018).

Whether students’ written responses can reveal if they employ analytical reasoning following instruction or indeed still rely on imagistic visuospatial strategies is of interest to this study and may provide a unique, exploratory glimpse into STEM student spatial thinking which can inform novel teaching approaches, the development of teaching tools and new assessment criteria. To this end, the present research study explores the questions;

1. To what extent can the diagrammatic reasoning included in students’ pen-on-paper responses capture analytical and imagistic reasoning when predicting molecular geometry?

2. What reasoning strategies do students use when determining molecular geometry?

3. In what ways do the reasoning strategies used by students relate to the accuracy of their pen-on-paper responses to molecular geometry predictions?

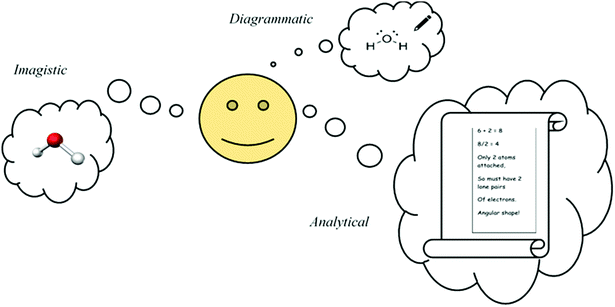
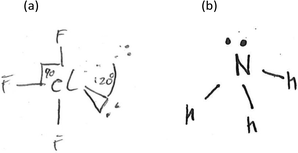
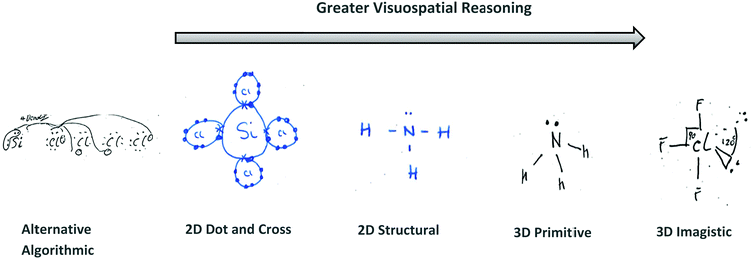
Fig. 4 depicts the key reasoning strategies reported to be intrinsic to solving visuospatial problems in chemistry, such as predicting molecular geometry (Stieff, 2007; Cooper et al., 2017). The student may rely upon imagistic reasoning to mentally visualise the molecule's geometry, they may employ an algorithmic analytical method or they may sketch a diagrammatic structure to assist with the task.

Fig. 4 Diagrammatic representation of student reasoning when predicting molecular geometry.

Study design

Research activities were conducted in a naturalistic environment and issued as part of the normal working mode of senior students in the chemistry classroom at an independent school in Scotland.

In the Scottish context, this represents the final (6th) year of secondary schooling typically completed by pupils planning to enter related undergraduate studies at University the following academic session.

The study was designed in accordance with BERA (British Ethical Research Guidelines) ethical guidelines and ethical approval from the Research and Knowledge Exchange Ethics Committee at Moray House School of Education, The University of Edinburgh was granted.

The primary researcher was also a teacher at the school, which helped provide an ecologically valid setting and analytical approach consistent with typical student assessment at this stage.

The VSEPR topic is usually taught to students over a 1 week period of 7, 40 minute lessons involving lectures and tutorial working activities.

Method

Participants

This study was conducted with a senior class of high school pupils (aged 16–17 years, N = 10) and was implemented as a typical classroom activity as part of their study towards the final year qualification (SQA Advanced Higher, 2019). All participating students were fully aware and participating in the research study having given consent.

The study centred around a single topic and core skill typically introduced during the final year chemistry course or first year of an undergraduate chemistry degree – Valence Shell Electron Pair Repulsion (VSEPR) Theory.

The students had previously received instruction on related concepts in prior courses which included theory on the molecular shape of simple molecules and covalent molecular bonding. All students (N = 10), were high attaining, having been awarded A grades in their previous national examinations at all levels.

Procedure

For this study, a double period (1 hour and 20 minutes) was used to carry out the data collection activities and served as an introduction to the topic for participants.

Initial instruction of the analytical VSEPR method consisted of a 20 minute lecture by the chemistry teacher, delivered using a slide presentation to introduce VSEPR theory in a format consistent with typical textbook learning; including text and 2D representations.

An 11 question, pen-on-paper task was then issued to allow for exploration of students’ unaided visuospatial thinking as assessed by their written responses and molecular geometry predictions. Participating students were given 30 minutes to complete the VSEPR Task, consistent with typical class assessments. Physical models (and other visualisations) were removed to encourage students to draw upon mental visualisations (as per examinations) and not supported by the tangible molecular models often available in the classroom when learning new concepts.

Materials

Data was collected from students tasked with determining the molecular geometries of selected compounds. Only the symbolic chemical formula of compounds was given, with students given space underneath to ‘show’ their understanding of the molecular shape for each compound following VSEPR theory instruction. The research task questions were purposefully open-ended to provide opportunities for students to draw supporting pictorial representations in addition to giving textual explanations if they chose to (see Fig. 5).

Fig. 5 Example open-ended question from the VSEPR task.

Data analysis

Student responses to the VSEPR task (N = 69) were analysed and coded after testing according to their use of diagrammatic sketches and/or text to reason. For each response, diagrammatic sketching and textual elements were examined for emergent similarities; allowing for inductive coding, then categorisation by the primary researcher. The data was further coded by 2 experts to reach agreement of the coding rubric's suitability to extract visuospatial reasoning elements from student responses.

A constant-comparative methodology (Strauss and Corbin, 1994) was used to devise the inductively coded scheme based upon Stieff and Raje's established scheme for capturing chemistry problem-solving strategies (Stieff and Raje, 2008). The sketched data revealed both imagistic and analytical reasoning and was categorised into 4 reasoning codes: 3D – Imagistic, 2D – Structural, 2D – Dot and Cross and Alternative Algorithmic (see Table 1).

Table 1 Coding scheme for analytical and imagistic elements of student generated sketches and representative examples

Student generated sketch coding scheme
Features	Sketch example
3D – Imagistic
	(a) Dash-wedge 3D representation with bond angles included to show spatial position of atoms and lone pairs of electrons.
	(b) Primitive 3D representation where 3D spatial form (e.g. trigonal pyramidal) is inferred through sketched position, length and orientation of N–H bonds to produce a 3D aspect drawing.
2D – Structural
	2D structural formula for the molecule showing 3 N–H bonds and 1 lone pair of electrons. This is a recognised representation showing connectivity of atoms (within plane of paper). Analytical form, with no spatial information.
2D – Dot and Cross
	2D sketch taught at previous stage (2 years previously) showing numbers of electrons from different atoms in the molecule using dots and crosses. Analytical from, with no spatial information provided.
Alternative Algorithmic
	Unique and unusual way to analytically quantify the number of bonds formed in the molecules, but no spatial information.

---

Sketched data analysis

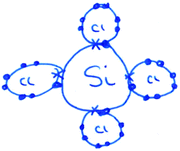
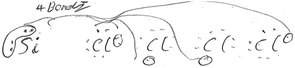
The use of 3D sketching was considered to fall under the category of ‘3D – Imagistic’ diagrammatic reasoning, where in the absence of models/diagrams, students were likely required to imagine and visualise the molecular geometry before producing the 3D aspect sketch with dash-wedge features. ‘2D – Structural’ sketches showed the bonding connectivity between different atoms in a molecule (dash) and possibly lone pairs of electrons not involved in bonding (2 dots). Although these sketches could potentially indicate the orientation of some chemical bonds and thus infer geometrical aspects, they were deemed analytical in nature as these structural formulae appear to have served as a diagrammatic way to account for the number of bonds in the molecule and no recognised 3D spatial information could be deduced. For ‘2D Dot and Cross’ type analytical sketches, the format was two dimensional where the outer shell of electrons that an atom in the molecule possesses is represented by either dots or crosses to distinguish between neighbouring atoms’ electrons. These diagrams were also considered analytical sketches as they appeared to serve only as a way of accounting for the number of outer electrons for each atom in the molecule. The 4th student sketch code was termed ‘Alternative Algorithmic’ and coded for student sketches possessing unusual or creative elements which evidenced the students’ analytical reasoning, yet not recognisable as an established chemistry representation.

Student generated sketches were graded according to the degree of three-dimensionality conveyed within the drawing (see Fig. 6). Although the absence of 3D sketching did not necessarily suggest that imagistic reasoning was not employed, 3D sketches were assessed as being ‘imagistic’ in nature given the necessity for students who used them to imagine and visualise the molecular shape in order to recreate a sketched representation of it.

Fig. 6 Student-generated sketches were graded from analytical to imagistic.

Textual data analysis

Student responses to the molecular geometry task were also assessed in a manner consistent with secondary school examinations by the primary researcher; where the correct molecular geometry is considered ‘predicted’ if shown by the use of the correct terminology to describe it. For example, inclusion of the term ‘Tetrahedral’ to describe the molecular geometry of methane, CH₄ (see Fig. 1).

Accuracy of student responses

To determine the accuracy of responses evidenced through use of different reasoning strategies, each student response was further examined for correctness (as outlined in Fig. 7).

Fig. 7 Varying accuracy of student responses as assessed by the textual diagrammatic elements within.

Diagrammatic and textual elements were marked with respect to the accuracy of the predicted molecular geometries for each question. Diagrammatic elements were deemed correct if the sketch accurately conveyed the molecular geometry using 3D – Imagistic sketches. Textual elements were marked correct if the correct geometry was predicted using the appropriate terminology (consistent with that required in examinations). See Fig. 7.

Quantitative analysis

To explore research question 3 and the ways in which student reasoning strategies related to the accuracy of their written responses to molecular geometry predictions, initial quantitative statistical analyses were performed. The accuracy of both textual and diagrammatic elements across student responses was compared to whether there was evidence of the established analytical VSEPR theory use or not.

The accuracy data of student responses was tested to verify normality and allow for further parametric analysis. A Shapiro-Wilk test yielded p values of 0.176 and 0.664 for textual correctness and diagrammatic correctness respectively, thus satisfied the non-significance required to assume normality (where p < 0.05).

A two-way repeated-measures mixed Analysis of Variance (ANOVA) was performed to compare the degree and nature of response accuracy to the use of VSEPR Theory which is the widely accepted method of instruction.

Results and discussion

Quantitative treatment of student responses to VSEPR task

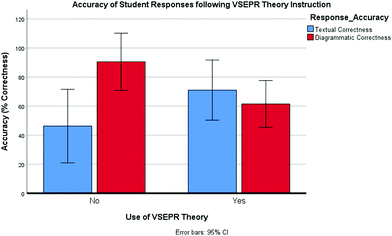
Reported statistical results for this study are presented as whole percentage values, similar to those used by Stieff and Raje (2010) and presented by Stieff (2013).

The results of a two-way mixed Analysis of Variance (ANOVA) (Fig. 8) showed that there was no significant main effect of use of VSEPR theory on percentage correctness scores overall (F(1,8) = 0.057, p = 0.82, η_p² < 0.007). Student responses which evidenced use of VSEPR theory in the molecular geometry task showed a similar overall percentage correctness score (mean = 66.25) than student responses which did not evidence use of VSEPR theory (mean = 68.34). Therefore, results suggest that use of the taught VSEPR Theory algorithm did not appear to influence the absolute accuracy as assessed by the textual and diagrammatic features within.

Fig. 8 Graphical representation of relationship between the accuracy of textual and diagrammatic features of student responses and evidence of VSEPR theory use. No overall difference in accuracy was observed depending on whether students used VSEPR theory or not, however a significant effect when examining individual features against VSEPR use was evident.

In contrast, there was a significant interaction observed between the accuracy of the individual textual and diagrammatic features of students’ responses and the use of VSEPR theory, (F(1,8) = 8.76, p = 0.018, η_p² < 0.523). Descriptive statistics showed that student responses which did not evidence use of VSEPR theory, achieved greater percentage correctness scores for diagrams generated (mean = 90.50, SD = 13.68) than for textual inclusions (mean = 46.25, SD = 25.18); moreover they also achieved greater percentage correctness scores for the diagrammatic elements of their responses than responses which did evidence use of VSEPR theory. Conversely, student responses which evidenced use of VSEPR theory showed the opposite effect where the textual elements within scored higher percentage correctness (mean = 71.00, SD = 19.78) than the diagrammatic sketched features (mean = 61.50, SD = 18.84) and showed a greater degree of textual correctness than responses which did not evidence use of VSEPR theory.

These results are significant in that despite the absolute accuracy of student responses appearing unrelated to whether there is evidence of the taught VSEPR Theory or not, there is a clear correlation between the use of VSEPR Theory and the degree of textual accuracy and vice versa. This is significant in that results might suggest that if some students prefer to rely on diagrammatic reasoning, as opposed to the taught VSEPR Theory they may also be more accurate using this preferred strategy. This could prove troublesome for such students as accurate diagrams alone are insufficient to receive credit in school examinations; the correct written terminology must also be provided. Analysis of individual student responses was carried out to further explore preferred reasoning strategies and related accuracy.

Student reasoning by sketching

The diagrammatic sketching included within the student responses to the VSEPR task appeared to be a spontaneous reasoning strategy that was used by all students (N = 10), although not in all responses, and was helpful to reveal aspects of student reasoning, evidencing both analytical and imagistic reasoning.

Fig. 9 shows that the majority (91%) of all student responses answered in the VSEPR research task (N = 69) included a diagram and a significant proportion (78%) of all student responses included a diagram showing a three-dimensional perspective or used an established 3D representation (dash/wedge).

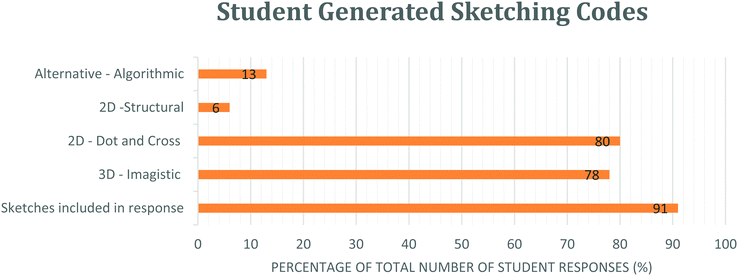Fig. 9 Graphical representation showing the variety of coded diagrammatic reasoning captured through student generated sketching.

Similarly, a high proportion (80%) of all student responses also included analytical sketches such as a ‘2D – Dot and Cross’ type sketch which is a representation taught two academic years previously. These diagrams are not a requirement to solve the molecular geometry problems and so this was a notable and unexpected diagrammatic inclusion to the cohort's reasoning strategies.

Just 13% of all student responses included ‘Alternative Algorithmic’ sketches and evidenced unusual or creative elements which similarly demonstrated students’ analytical reasoning, yet were not recognisable as an established chemistry representation. These sketches were produced by a single student.

Similarly, a small proportion (6%) of all student responses included analytical ‘2D – Structural’ sketches which also demonstrated use of prior knowledge, as this type of structural formula diagram is likewise introduced in previous schooling years and not required to predict molecular geometry.

Fig. 9 shows that through the coding and analysis of student-generated sketches, it has been possible to reveal different aspects of students’ reasoning when assigning molecular geometry.

Therefore, in response to research question 1: To what extent can the diagrammatic reasoning included in students’ pen-on-paper responses capture analytical and imagistic reasoning when predicting molecular geometry?

Table 1, Fig. 6 and 9 demonstrates the extent to which pen-on-paper student responses to molecular geometry problems can capture such reasoning strategies through sketching and as such may serve as a useful mode to do so. This is in agreement with previous studies examining other areas of chemistry (Stieff and Raje, 2008, 2010; Stieff, 2011; Hegarty et al., 2013; Vlacholia et al., 2017).

Further analysis was performed to examine individual students’ strategy use and prevalence.

Student strategy use

The results presented in Fig. 10 shows that not all student responses were comprehensive and included evidence of both analytical and imagistic reasoning across sketches and text as Stieff (2007) recommended for successful scientific problem solving. Some students evidenced reliance upon one strategy more than another but did not necessarily employ the taught analytical VSEPR theory method. This can be revealed by answering research question 2 ‘What reasoning strategies do students use when determining molecular geometry?’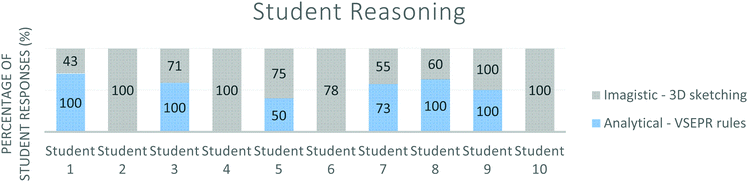

Fig. 10 Reasoning strategies used by students (N = 10) as evidenced by pen-on-paper written responses.

Fig. 10 shows the variation in the comparative prevalence of analytical reasoning evidenced (through use of taught VSEPR rules) vs imagistic reasoning (through spontaneous 3D sketching). Student 9, for example, made full use of both 3D imagistic reasoning (through 3D sketching) and analytical reasoning strategies (VSEPR rules) and evidenced comprehensive responses in 100% of questions answered of the task. 4 students (1, 3, 7 & 8) evidenced greater use of an analytical approach through the inclusion of the VSEPR rules taught and 5 students (2, 4, 5, 6 & 10) were shown to use imagistic reasoning through the 3D diagrams sketched in their responses. 4 of these 5 students did not show use of the analytical reasoning strategy taught at all, with no evidence that VSEPR rules had been employed in any of their responses. It appears, therefore that these students relied upon imagistic reasoning or alternative unmeasured strategies and for 3 out of these 4 students, used 3D sketches in 100% of their responses. Student 6 evidenced imagistic reasoning through use of 3D sketching only in 78% of completed responses to the task with no evidence for the VSEPR rules taught. The remaining 22% of responses showed no evidence of either reasoning strategy and instead evidenced alternative strategies as defined in Table 1.

Fig. 10 shows student reasoning strategy use, however this does not yield information relating to student confidence and ultimately competence with a given strategy.

Accuracy of student reasoning strategies

There was a varying degree of task completion by each student for the VSEPR task: only 2 students (2 & 7) completed all 11 questions and 2 students (5 & 10) completed just 4 out of 11 questions within the 30 minutes allocated. Therefore, a percentage accuracy across their responses (percentage correctness) was determined for ease of comparison.

Although several students showed equivalent accuracy through their use of both text and sketching (students 5, 8 & 9), for others, there was a disparity between the degree of correctness as assessed by the diagrammatic and textual elements within each response (see Fig. 7). For example, 4 students evidenced greater accuracy through their sketches than text and conversely 3 students showed greater accuracy through the written textual elements of their responses than their sketches. Thus, even across a cohort of 10, A grade students, there was variation in terms of competency and accuracy of the textual and diagrammatic elements included within their responses.

Students 2 and 4 in particular were notable examples, in that they did not evidence use of the taught VSEPR theory in any of their written responses. These students’ preference for a predominantly ‘imagistic’ strategy appeared to serve them well with 91% and 100% of respective responses showing diagrammatically correct dash-wedge sketches accurately depicting the molecular geometries. Despite their diagrammatic accuracy, only 36% and 17% of the same students’ responses also included accurate accompanying text which could receive credit in a typical chemistry examination.

Further discussion

This study sought to better understand the role of visuospatial thinking by investigating students’ choice of responses to molecular geometry prediction questions. The results have revealed that it is possible to capture high school students’ reasoning strategies through written responses to a chemistry task; with a significant proportion of the cohort relying upon imagistic strategies as predicted by Stieff et al. for novice Chemists, however a slim majority (51%) of student responses employed the algorithmic VSEPR rules taught.

Cooper et al. (2017) suggested, sketching may hold the key to deeper learning among students as well as offer instructors a more nuanced and valuable set of insight into student thinking. The widespread use and nature of sketching by participating students in this study (Table 1) in addition to text provided allowed for the coding and analysis of student reasoning strategies shown in the results section.

The much evidenced 2D ‘dot and cross’ diagrams (see Table 1) were of note as although these particular diagrams did not convey 3D imagistic reasoning or any deeper knowledge and understanding of molecular shape than that gleaned from exclusively analytical strategies (VSEPR rules), students presumably found this form of diagrammatic reasoning helpful for problem solving. Therefore, in this respect, these sketches did reveal some strategic thought processes and appeared to serve as a self-scaffolded hybridised form of both 2D diagrammatic and analytical reasoning; yielding information that may be similarly obtained from producing Lewis structures. This is particularly interesting given the reported association of increased cognitive load resulting from producing such sketches (Tiettmeyer et al. 2017). The prevalence of these 2D dot and cross type sketches would, however, suggest the contrary, that rather than increasing cognitive load, these sketches which draw on prior knowledge, actually helped to offload cognitive strain in some way as students reasoned through the problems. This would help explain their widespread use and might suggest that these ‘thinking sketches’ could prove to be an area worth examining further in future studies.

Creating a sketch, as the majority of students did in their responses, makes students’ scientific models explicit in a manner that allows them to more precisely characterise the phenomenon and to communicate their understanding of the phenomena more effectively to other scientists (Latour, 1990). Thus, the student-generated sketches may not only serve as an integral manifestation of individual reasoning strategies, but also communicates their thinking and understanding to others. However, it is pertinent to consider that despite its usefulness, sketching may also introduce additional cognitive strain to novice Chemists unfamiliar with the chemical concepts. Tiettmeyer et al. (2017), attempted to understand this by examining the structural characteristics and complexities that contributed significantly to the cognitive load of chemistry students drawing Lewis structure representations and to determine how those load-inducing characteristics changed as students gained additional chemical expertise. The results showed that the inclusion of nearly any structural characteristic induced a significant increase in cognitive load for chemistry students, but was mitigated as students gained additional chemical expertise. Given the variety of different sketches included in the students’ responses in this study, it is possible that this factor may have influenced students’ decisions to include sketches or indeed the particular type of sketches to produce.

Fig. 10 shows that even within a small cohort (N = 10), there was variation amongst the students’ initial strategy preferences despite their similar ages, stages and level of expertise (A grade students); 4 students preferred to use the taught analytical VSEPR strategy, 5 preferred imagistic sketching and 1 showed no preference, this is in some contrast to Stieff's finding that students tend to employ imagistic strategies initially whilst experts are more likely to employ analytical strategies (Stieff et al., 2012). One possibility is that 4 of these A grade students had already gained sufficient expertise through prior learning that they could confidently dispense with their more primitive imagistic tendencies from the first introduction to the task. Or perhaps the open-ended nature of the task and use of sketching throughout by the majority have revealed more subtle individual variations in student reasoning strategies that should be accounted for when considering best ways to teach and assess visuospatial concepts to more typical cohorts. The sketching may have provided a key scaffold to support analytical reasoning employed.

Students’ responses were examined to determine if VSEPR theory had been applied as taught. Students who did not evidence algorithmic working as taught were assumed to have utilised other means to predict the molecular geometry and in the case of students who included 3D sketches, were assumed to be more likely to be accessing imagistic reasoning to make their predictions.

Formative statistical analyses revealed that use of the algorithmic VSEPR theory as taught yielded more accurate textual responses to the molecular geometry problems which would likely score more highly in standardised school chemistry exams, however of note is the fact that this has not been matched by similar diagrammatic correctness. Whether this is due to students purposefully omitting 3D diagrammatic features in their responses having correctly applied the algorithmic VSEPR theory to find solutions, or these students were unable to produce accurate 3D sketches would require further investigation.

Conversely, students who did not evidence use of the algorithmic VSEPR theory in their pen-on-paper responses (e.g., student 2) showed significantly greater accuracy in their 3D sketches and appear to have relied upon imagistic reasoning to find solutions to the molecular geometry task. Although not providing the necessary terminology to be deemed textually correct and therefore receive credit in school examinations, their 3D sketching and relatively higher percentage correctness scores for the diagrammatic sketching of their responses suggests that this imagistic approach serves them well to visualise the correct molecular geometry even if they have been unable to correctly name it.

Notable is the fact that as textual responses are generally accepted as being correct as per school examinations, students showing no preference or greater preference for analytical reasoning may ensure that they are more likely to gain credit for correct solutions in examinations through accurate textual responses. Conversely, the students who showed greater preference and competence through use of 3D sketched imagistic reasoning may be at a distinct disadvantage despite this very skill being widely considered as advantageous for STEM study. This raises questions about whether the nature of typical school examinations and learning tasks are adequately suited for different learning styles to allow for true assessment of students’ knowledge, understanding and visuospatial thinking. Failure to recognise this may discourage those students who may be intrinsically suited to the STEM disciplines (and rely on imagistic reasoning strategies) from continuing their studies as a result of mediocre summative assessment scores. Likewise, promoting a learning culture whereby educators simply ‘teach to the test’, where success is guaranteed through rote memorisation and use of analytical heuristics rather than the deeper conceptual understanding that results from building a mental picture of the underlying concepts seems somewhat short-sighted. In chemistry, imagistic reasoning has been highlighted as a fundamental cognitive activity, particularly at advanced study, that is often overlooked by the teaching and learning research communities (Habraken, 1996). Visuospatial processing is considered the reasoning strategy most often employed by novices until analytical domain-specific expertise is gained (Castro-Alonso and Uttal (2019). However, this study of similarly attaining A grade high school students demonstrates that variation in the reasoning strategies employed can persist regardless of attainment and shows that some prefer to rely on imagistic and diagrammatic reasoning even after instruction on how to analytically reason.

Limitations and future studies

There are limitations to this study as research findings from this cohort sample from a single classroom of A grade students in their final school year may be unique to this context. Thus, despite this uniformity in student attainment acting as a control variable in some respects to allow the heterogeneity of reasoning strategies to be revealed, it may also limit the range that a more representative high school cohort might exhibit.

Future studies with varied and multiple measures of spatial ability may determine whether students’ use of the algorithmic VSEPR theory is a robust enough measure with which to identify whether spatial reasoning strategies are employed. Future work might use spatial aptitude tests as a diagnostic tool as well as a pre-test to provide information to students about their individual visuospatial aptitude and inform potential strategies to adopt for successful learning outcomes. Subsequent testing of student visuospatial aptitude may explore whether this ability can be developed through instructional intervention and open-ended freedom to reason and perhaps investigate if this ability is inherent to an individual and thus cannot be taught or honed. Although, the scale of this study made it possible to adopt a rich analytical approach, additional research studies in different educational authorities and regions could emulate this research to collect a greater sample of data to address the underlying lack of statistical power due to small sample size.

A further limitation of this study relates to the fact that not all students completed the research task within the timescale permitted. Although this approach was representative of typical chemistry assessments and ensured some degree of ecological validity with regards to attainment, had students been given unlimited time to complete, results may have differed. Further studies might allow more time to gather further student data or conduct follow-up interviews to assess why all questions were not attempted.

Future studies might also explore students’ textual responses in greater detail to glean richer insight into student reasoning strategies through use of language and might also examine in greater detail the relationship between student reasoning modes and the rubrics of traditional assessments used to gather evidence of students’ visuospatial understanding. Traditional assessments do not routinely recognise rough student sketching that may be used to reason through visuospatial problems, and generally a textual answer is required to be marked as correct and receive credit. Further research investigating the traditional nature of assessment and whether this adequately serves to assess true student knowledge and understanding of 3-dimensional concepts and visuospatial thinking is of importance not only to STEM instructors and students, but to assessment boards and further education providers.

Likewise, the development of new teaching resources and digital educational tools should consider individual learning styles and in particular the role of sketching to help student reasoning and support students towards ultimate visuospatial competence. Digital chemistry education tools might incorporate interfaces and activities which allow students to interact with their learning in a multimodal way which can simulate and support three-dimensional thinking. Tangible accessories and augmented reality software may be a useful way to scaffold three-dimensional manipulation of molecules to view molecular geometries from different aspects. Similarly, digital stylus tools are increasingly accessible and could serve as a crucial resource for novice chemists to benefit from the support that free-hand sketching can provide, particularly if teamed with the structure and self-assessment that digital learning platforms can offer.

Conclusion

The study reported in this paper shows that it is possible to capture high school students’ visuospatial thinking through the strategies they demonstrate in their responses to pen-on-paper tasks when predicting molecular geometry. This is in agreement with prior studies from other areas of Chemistry with older students studying undergraduate chemistry (Stieff, 2007, 2012).

This study showed that the reasoning strategies employed and evidenced following initial instruction varied in terms of preference and competence. Thus, results show some agreement with Stieff's contention (Stieff, 2011) that advanced visuospatial ability is not necessarily a requirement for ultimate success in chemistry. These findings indicate that allowing students to express their understanding of visuospatial problems through multiple pen-on-paper reasoning strategies during instruction and assessment can fulfill individual needs by promoting personalised learning that if appropriately acknowledged may ultimately lead to improved assessment criteria.

With the majority of student responses incorporating a variety of spontaneous diagrammatic sketches to the open-ended problems to be solved, findings suggest that sketching can be considered as a useful assessment tool that can reveal significant details about the quality and complexity of student understanding, with student-generated sketches revealing misconceptions of scientific phenomena that may not be detectable using traditional assessment instruments that do not include sketching (Kelly et al., 2010; Harle and Towns, 2013; Cooper et al., 2015; Cooper et al., 2017).

The widespread use of spontaneous sketching and in particular the superficially less relevant 2D ‘thinking sketches’ may have induced further cognitive load to students’ problem solving as suggested by Tiettmeyer et al. (2017) when investigating Lewis structure sketches, but given their prevalence, the student sketches may have revealed evidence of a self-scaffolded, cognitive offloading strategy that in fact aided problem solving. These sketches may be of interest for future studies.

The study findings are pertinent not only to chemistry education, but across STEM disciplines, and supported by a growing body of literature examining the role that visuospatial processing plays in science learning. Castro-Alonso and Uttal (2019) summarised approaches to science training and education and potential visuospatial activities that might be incorporated. Given the recent interest to incorporate sketching into science classrooms to aid learning (Ainsworth et al., 2011), this study's findings are relevant. However, care must be taken to ensure sketching activities are not adopted for their own sake or indeed add to cognitive load, but rather designed and implemented for best use in the classroom, otherwise they may contribute little to improving student learning or individualising assessment (Cooper et al., 2017).

Findings suggest that not only should teachers consider how to best support students’ use of multiple modalities and associated reasoning strategies in the chemistry classroom, but curriculum designers and digital learning developers should consider more valid and multimodal means of delivering and assessing student knowledge. This exploratory study on a relatively homogeneous student group suggests that although successful students will ultimately master the rote learning and heuristic rules which experts routinely employ to find STEM solutions, we are failing to recognise individual reasoning strategies of all students, some of whom may be intrinsically suited to STEM study through preference or competence with more unique, multimodal, visuospatial problem-solving strategies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by The Chemistry Department of The Edinburgh Academy. Any findings, conclusions, opinions or recommendations are those of the authors and do not necessarily reflect the views of The Edinburgh Academy.

References

1. Ainsworth S. E., (2006), DeFT: A conceptual framework for considering learning with multiple representations, Learn. Instr., 16 (3), 183–198.
2. Ainsworth S. E., Prain V. and Tytler R., (2011), Drawing to learn in science, Science, 333 (6046), 1096–1097.
3. Barnea N. and Dori Y. J., (1999), High-school chemistry students’ performance and gender differences in a computerized modelling learning environment, J. Sci. Educ. Technol., 8(4), 257–271.
4. Battista M. T., Wheatley G. H. and Talsma, G., (1982), The Importance of Spatial Visualization and Cognitive Development for Geometry Learning in Preservice Elementary Teachers, J. Res. Math. Educ., 13, 332–340.
5. Bodemar D. and Faust U., (2006), External and mental referencing of multiple representations, Comput. Hum. Behav., 22(1), 27–42.
6. Bodner G. M. and Guay R. B., (1997), Visualization of Rotations Test, Chem. Educ., 2, 1–17.
7. Bodner G. M. and McMillen, T. L. B., (1986), Cognitive Restructuring as an Early Stage in Problem Solving, J. Res. Sci. Teach.23, 727–737.
8. Castro-Alonso J. C. and Uttal D. H., (2019), Science Education and Visuospatial Processing, in J. C. Castro-Alonso (ed.), Visuospatial Processing for Education in Health and Natural Sciences, Springer International Publishing, vol. 3, pp. 53–79.
9. Chang H., Quintana C. and Krajcik J. S., (2009), The impact of designing and evaluating molecular animations on how well middle school students understand the particulate nature of matter, Sci. Educ., 94 (1), 73–94.
10. Chandler P. and Sweller J., (1991), Cognitive load theory and the format of instruction, Cognit. Instr., 8 (4), 293–332.
11. Cheng M. M. W., (2018), Students’ visualisation of chemical reactions – insights into the particle model and the atomic model, Chem. Educ. Res. Pract., 19, 227.
12. Cheng M. M. W. and Gilbert, J. K., (2017), Modelling students’ visualization of chemical reaction, Int. J. Sci. Educ.39, 1173.
13. Cooper M. M., Williams L. C. and Underwood S. M., (2015), Student Understanding of Intermolecular Forces: A Multimodal Study, J. Chem. Educ., 92, 1288–1298.
14. Cooper M. M., Stieff M. and DeSutter D., (2017), Sketching the Invisible to Predict the Visible: From Drawing to Modeling in Chemistry, Top. Cognit. Sci., 9, 902–920.
15. Ebbing D. and Gammon S. D., (2015), General Chemistry. ISBN-10: 1305580346, ISBN-13: 9781305580343.
16. Erlina, Cane C., Williams D. P., (2018), Prediction! The VSEPR Game: Using Cards and Molecular Model Building To Actively Enhance Students’ Understanding of Molecular Geometry, J. Chem. Educ., 95, 991–995.
17. Furio C., Calatayud M. L., (1996), Difficulties with the Geometry and Polarity of Molecules, J. Chem. Educ., 73 (1), 36–41.
18. Gillespie R. J., (1997), The Great Ideas of Chemistry, J. Chem. Educ., 74 (7), 862–864.
19. Guay R. B., (1980), Spatial ability measurement', a critique and an alternative. Paper presented at the A Meeting of the American Educational Research Association, Boston, MA. (ERIC Document Reproduction Service No. ED 18).
20. Guay R. B. and McDaniel E. D., (1977), The Relationship between Mathematics Achievement and Spatial Abilities among Elementary School Children, J. Res. Math. Educ., 8, 211–215.
21. Habraken C. L., (1996), Perceptions of chemistry: Why is the common perception of chemistry, the most visual of sciences, so distorted?, J. Sci. Educ. Technol., 5(3), 193 – 201.
22. Harle M. and Towns M., (2010), A Review of Spatial Ability Literature, Its Connection to Chemistry, and Implications for Instruction, J. Chem. Educ., 88, 351–360.
23. Harle M. and Towns M. H., (2013), Students’ understanding of primary and secondary protein structure: Drawing secondary protein structure reveals student understanding better than simple recognition of structures, Biochem. Mol. Biol. Educ., 41(6), 369–376.
24. Hegarty M., (2004), Diagrams in the mind and in the world: Relations between internal and external visualizations, in Blackwell A., Mariott K. and Shimojima A., (ed.), Diagrammatic representation and inference, Berlin: Springer-Verlag, pp. 1–13.
25. Hegarty M., Stieff M. and Dixon B. L., (2013), Cognitive change in mental models with experience in the domain of organic chemistry, J. Cogn. Psychol., 25(2), 220–228.
26. Keehner M., Tendick F., Meng M. V., Anwar H. P., Hegarty M., Stoller M. L., Duh Q.-Y., (2004), Spatial ability, experience and skill in laparoscopic surgery, Am. J. Surg., 188, 71.
27. Kelly R. M., Barrera J. H. and Mohamed S. C., (2010), An analysis of undergraduate general chemistry students’ explanations of the submicroscopic level of precipitation reactions, J. Chem. Educ., 87 (1), 113–118.
28. Latour B., (1990), Drawing things together, in Lynch M. and Woolgar S. (ed.), Representation in scientific practice, Cambridge, MA: MIT Press, pp. 19–68.
29. Lubinski D., (2010), Spatial Ability and STEM: A Sleeping Giant for Talent Identification and Development, Pers. Indiv. Differ., 49, 344–35.
30. Manches A. and O’Malley C., (2012), Tangibles for learning: a representational analysis of physical, Pers. Ubiquit. Comput., 16, 405–419.
31. Meij J. and Jong T., (2003), Learning with Multiple Representations: Supporting students’ translation between representations in a simulation-based learning environment, EARLI conference, Padua, Italy.
32. Milenković D., Segedinac M., Hrin T. and Cvjetićanin S., (2014), Cognitive Load at Different Levels of Chemistry Representations, Croat. J. Educ., 16 (3), p699–p722.
33. Nicoll G. A., (2001), Report of Undergraduates’ Bonding Misconceptions, Int. J. Sci. Educ.23 (7), 707–730.
34. Nyachwaya J. M. and Gillespie M., (2016), Features of representations in general chemistry textbooks: a peek through the lens of the cognitive load theory, Chem. Educ. Res. Pract., 17, 58.
35. Ploetzner R. and Fillisch B., (2017), Not the silver bullet: Learner-generated drawings make it difficult to understand broader spatiotemporal structures in complex animations, Learn. Instr.47, 13.
36. Pribyl J. R. and Bodner G. M., (1987), Spatial Ability and Its Role in Organic Chemistry: A Study of Four Organic Courses, J. Res. Sci.Teach., 24, 229–240.
37. Schnotz W. and Kürschner C., (2007), A Reconsideration of Cognitive Load Theory, Educ. Psychol. Rev., 19, 469–508.
38. Schwartz D. L. and Black J. B., (1996), Shuttling between depictive models and abstract rules: Induction and fallback, J. Cognit. Sci., 20, 4, 457.
39. Southam D. C. and Lewis J. E., (2013), Supporting Alternative Strategies for Learning Chemical Applications of Group Theory, J. Chem. Educ., 90, 1425–1432.
40. Seery M. K. and Donnelly R., (2012), The implementation of pre-lecture resources to reduce in-class cognitive load: A case study for higher education chemistry, Br. J. Educ. Technol., 43 (4), 67–677.
41. SQA, (2019), Advanced Higher Chemistry Course Specification, https://www.sqa.org.uk/files_ccc/AHChemistryCourseSpec.pdf.
42. Stieff M., (2007), Mental rotation and diagrammatic reasoning in science, Learn. Instr., 17 (2) 219–234.
43. Stieff M., (2011), When Is a Molecule Three Dimensional? A Task-Specific Role for Imagistic Reasoning in Advanced Chemistry, Sci. Educ., 95, 310–336.
44. Stieff, M., (2013), Sex Differences in the Mental Rotation of Chemistry Representations, J. Chem. Educ.90, 165–170.
45. Stieff M., Hegarty M. and Dixon B. L., (2010), Alternative strategies for spatial reasoning with diagrams, in Goel A. K., Jamnik M. and Narayanan N. H. (ed.), Diagrammatic representation and inference, Berlin: Springer, pp. 115–127.
46. Stieff M. and Raje S., (2008), Expertise & Spatial Reasoning in Advanced Problem Solving, Proceedings of the 8^th international conference on International conference for the learning sciences, vol. 2, pp. 366–373.
47. Stieff M. and Raje S., (2010), Expert algorithmic and imagistic problem solving strategies in advanced chemistry, Spat. Cognit. Comput., 10 (1), 53–81.
48. Stieff M., Ryu M., Dixon B. and Hegarty, M., (2012), The Role of Spatial Ability and Strategy Preference for Spatial Problem Solving in Organic Chemistry, J. Chem. Educ., 89, 854–859.
49. Stieff M., Werner S., DeSutter D., Franconeri S., Hegarty M., (2020), Visual Chunking as a Strategy for Spatial Thinking in STEM, Cognit. Res.: Princ. Implic., 5, 18 DOI:10.1186/s41235-020-00217-6.
50. Strauss S. and Corbin J., (1994), Grounded theory methodology: an overview, in Denzin N. and Lincoln Y. (ed.), Handbook of qualitative research, Thousand Oaks, CA: Sage, pp. 273–285.
51. Tiettmeyer J. M., Coleman A. F., Balok R. S., Gampp T. W., Duffy P. L., Mazzarone K. M. and Grove N. P., (2017), Unraveling the Complexities: An Investigation of the Factors That Induce Load in Chemistry Students Constructing Lewis Structures, J. Chem. Educ., 94 (3), p282–p288.
52. Van Meter P. and Garner J., (2005), The promise and practice of learner-generated drawing: Literature review and synthesis, Educ. Psychol. Rev., 17(4), 285–325.
53. Vlacholia M., Vosniadou S., Roussos P., Salta K., Kazi S., Sigalase M. and Tzougraki C., (2017), Changes in visual/spatial and analytic strategy use in organic chemistry with the development of expertise, Chem. Educ. Res. Pract., 18, 763–773, 763.
54. West T. G., (1991), In the mind's eye: Visual thinkers, gifted people with learning difficulties, computer images and the ironies of creativity, Buffalo, NY: Prometheus Books.
55. Wu H. K. and Shah P., (2004), Exploring visuospatial thinking in chemistry learning, Sci. Educ., 88, 465–492.

---