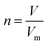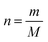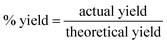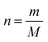View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/D0RP00291G (Paper) Chem. Educ. Res. Pract., 2021, 22, 443-456

South African physical sciences teachers’ use of formulae and proportion when answering reaction-based stoichiometry calculation questions†

Angela Elisabeth Stott
South Campus, University of the Free State, Bloemfontein, South Africa. E-mail: stottae@ufs.ac.za

Received 23rd September 2020 , Accepted 28th November 2020

First published on 28th January 2021

Abstract

Stoichiometry calculation competence tends to be particularly poor in the developing world, even among teachers. Various methods, including the unit factor method, have the potential to be effective in developing such competence. To evaluate the likelihood of such a generic proportion method, which downplays traditional formula usage, succeeding in a particular context, it is necessary first to understand teachers’ existing competence with proportion and the extent to which their calculation success relies on the explicit provision of and substitution into formulae in their written solutions. This quantitative survey study of 171 South African Physical Sciences teachers’ use of formulae and proportion found that most teachers failed to recognise the need to use proportion for some of the four reaction-based stoichiometry calculation questions used. Provision of and substitution into a formula in the written solution was found to be valuable in helping participants who underutilised proportion to obtain process marks, but to be largely irrelevant to obtaining the correct answer. The findings suggest that professional development interventions in similar contexts should focus on proportion within stoichiometry, particularly on recognition of its relevance to reaction-based questions. While a generic proportion method is well suited to this purpose, questions are raised concerning the likelihood that teachers would accept such a method in a context where process marks favour traditional formats of formula provision and substitution and where process mark attainment is highly valued. The findings also point to the need for teacher education to address competencies other than proportion.

Introduction

The fact that stoichiometry is concerned with proportional relationships contributes significantly to the difficulty which students experience with stoichiometry calculation questions (Ramful and Narod, 2014). This is particularly the case for students with low mathematics ability (Ralph and Lewis, 2019), which includes most learners (Reddy et al., 2019), and even many teachers (Taylor, 2019) in developing-world contexts such as South Africa (SA). Those stoichiometric proportional relationships which convert between variables for a single quantity have been captured in formulae, such as n = m/M (number of moles equals mass divided by molar mass). Such formulae enable employment of plug and chug methods which are cognitively less taxing (Nurrenbern and Pickering, 1987) than engagement in proportional reasoning is. Use of such formulae, which are often provided for standardized examinations, is referred to as formula usage in this article. Any use of proportion performed without a ready-made formula provided in examinations is referred to as proportion usage.

Reaction-based stoichiometry questions cannot be solved without proportion usage, whereas they could be solved without any use of formulae. Despite this, throughout the world proportion tends to be taught only implicitly in Chemistry (Wink and Ryan, 2019). In contrast, at least in the South African context, as discussed later, formula usage is given much explicit focus. It is understandable why people may choose to use formulae for conversions between variables for a single quantity, which may be called formula-accessible calculations. However, for conversions across a reaction, the solver needs to work out how to derive the proportional relationship for the given and required variables and for the relevant balanced equation, without a single ready-made formula to hand. This may be done by first converting relevant variables to moles using formulae, then by using proportion through application of the mole ratio given in the balanced equation, and finally by converting the relevant variable from moles to the required unit using a formula. Alternatively, the answer could be obtained solely through use of proportion, for example by using the unit factor method (Ramful and Narod, 2014). Proportion heuristics such as the unit factor method can be used as single generic methods to solve all stoichiometry questions, both formula-accessible calculations and applications of reaction ratios (Gabel and Sherwood, 1983).

Concentration on such a single generic proportion-based method might be desirable to simplify both teacher professional development and classroom teaching. However, for teachers to adopt such a method they need to be able to use proportion themselves (Gabel and Sherwood, 1983), and the method should be compatible with beliefs they hold regarding the purpose and nature of good science teaching (Makhechane and Qhobela, 2019). In the developing world, particularly, teachers tend to consider the purpose of science teaching to be preparation for examinations and good science teachers to be those who help their learners to garner as many marks as possible in examination questions (Okitowamba et al., 2018). These beliefs determine what teachers teach, which has been shown to delineate teachers’ own subject matter knowledge in these contexts (Brodie and Sanni, 2014). Therefore, it is valuable to determine such physical sciences’ teachers’ own abilities to use proportion, as well as the extent to which they rely on formulae for success when answering examination-style reaction-based stoichiometry questions.

Literature review

The difficulty people experience with proportion may be related to proportion requiring attainment of the formal operational stage of cognitive development (Niaz and Robinson, 1993). This is the case for only approximately 30% of high school learners in developed-world countries (Huitt and Hummel, 2003). Although all the science majors in a United States university who participated in a study by Gulacar et al. (2014) were found to have reached this stage, their sample does not seem to be representative of similar samples in developing-world countries such as SA, where Selvaratnam (2011a) found that only 52% of final year BSc students were able to solve an everyday calculation using proportion. The statistic was slightly lower (46%) for first year BSc students, and lower still (40%) for Physical Sciences (PS) teachers (Selvaratnam, 2011b). To compound the fact that proportion itself tends to be difficult, various factors make the application of proportion in stoichiometry particularly difficult (Ramful and Narod, 2014). These factors include the conceptual difficulties of the mole (Fang et al., 2014), interpretation of the sub-microscopic equivalence of chemical equations (Sanger, 2005), and the incorporation of ratio into some variables but not others (Ramful and Narod, 2014). It is therefore unsurprising that Stott (2020) found low levels of subject matter knowledge (SMK) of ratio and stoichiometric equivalence, both of which are related to proportional reasoning in stoichiometry, amongst SA physical sciences teachers. In contrast, Stott (2020) found very high levels of SMK related to formula usage, among these teachers.

Various studies regarding proportion usage when answering reaction-based calculation questions have been performed in various contexts and with various groups of subjects. Examples, in developing-world contexts, include studies which have focused on school-level learners from Lebanon (BouJaoude and Barakat, 2003), Zimbabwe (Shadreck and Enunuwe, 2018), Thailand (Dahsah and Coll, 2007), Turkey (Gultepe et al., 2013) and the United Arab Emirates (Haidar and Al Naqabi, 2008). Others have focused on pre-service teachers, e.g. from Nigeria (Danjuma, 2011), Ghana (Hanson, 2016), Turkey (Kartal and Kartal, 2019), and the Philippines (Espinosa et al., 2016). In developed world contexts, such studies include studies with grade 9 German learners (Fach et al., 2007), Hungarian learners aged 13 to 17 (Tóth and Kiss, 2005), Grade 11 German (Schmidt, 1994) and Swedish (Schmidt and Jignéus, 2003) learners, and university students in the US (Gulacar et al., 2014).

What is not clear, however, from these studies, is the extent to which practising teachers are aware of the need to apply proportion at least in the reaction-conversion step of reaction-based stoichiometry questions. This lack of clarity arises partly from a dearth of studies involving practising teachers’ abilities to answer stoichiometry calculations, with the focus tending rather to be on pre-service teachers and on conceptual knowledge (e.g.Malcolm et al., 2019) and beliefs (e.g.Makhechane and Qhobela, 2019). The lack of clarity also arises from the terminology used when classifying stoichiometry calculation answering strategies. For example, Kartal and Kartal (2019) refer to use of the chain rule for solving proportion questions as an algorithmic approach since it likely involves memorisation, whereas methods such as the cross-product or unit-factor method are classified as proportional reasoning. Similarly, the mole/proportional/logical methods classification system introduced by Schmidt (1994) and reused in various contexts (e.g.Schmidt and Jignéus, 2003; Tóth and Kiss, 2005; Espinosa et al., 2016) all make use of proportion. The focus of these studies therefore appears to be on how proportion is used, rather than whether it is used.

Further, no studies could be found which focused on: (1) the extent to which teachers explicitly provide formulae and substitutions in their written answers to stoichiometry calculation questions; (2) the value of such practises towards attaining the correct answer and towards attaining process marks; (3) how, if at all, these relationships are affected by the teachers’ competence with use of proportion. My interest in these issues arises from inconsistencies between the curriculum and examination practises in South Africa, and potential misconceptions these might be generating among teachers, as discussed below.

The SA PS curriculum stipulates that Grade 10 learners should “Reason qualitatively and proportionally the relationship between number of moles, mass and molar mass”, as well as “calculate mass, molar mass and number of moles according to the relationship n = m/M′′ (DBE, 2011). No other explicit mention of proportional reasoning is made in this document regarding stoichiometry, although this is implied for calculating the answers to various kinds of reaction-based stoichiometry questions in Grade 10 (p. 52) and Grade 11 (pp. 82–83). Further, memorandums for Grade 10, 11 and 12 Chemistry examinations assign marks to application of proportion in reaction-based stoichiometry questions. However, proportional reasoning is not given the explicit focus in examination documents as it is in the mention, given above, in the curriculum document. Two examples from SA National PS 2019 Paper 2 final examination papers and their accompanying memorandums are given to support this view. All these documents are freely available on the internet.

In the first example grade 10 learners were asked to calculate “The number of moles present in 85.5 g of Al2(SO4)3” (question 5.3., p. 9). Based on the curriculum statement, given above, it should be permissible for the answer to be obtained either by use of the formula n = m/M or by proportional reasoning, possibly aided by a generic proportional method, such as the cross-product or unit-factor method (Ramful and Narod, 2014). However, the associated memorandum assigned one mark to each of: provision of the formula n = m/M, substitution of values into the formula, and to the answer. This means that a learner would have been penalised for using a generic proportion method, which would have been evidence of a mismatch existing between the envisioned and assessed curricula.

Unlike the first example, the second example does seem to require learners to apply proportion. This is taken from question 6.2.3. (p. 11) of the grade 11 examination. Learners are given the volume of HCl produced from a given mass of impure NaCl, the applicable molar gas volume, and the balanced equation for the reaction. They are required to calculate the percentage purity of the NaCl sample. Of the six marks awarded for this question, the memorandum assigns one to provision of either of the formulae n = m/M or n = V/Vm, three to various substitutions into formulae, and one to ratio use, given in the format n(NaCl) = n(HCl). Given the 1[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio relevant here, and the placement of the tick, in the memorandum, next to the calculated value (0.0188 mol), rather than next to a display of use of proportion, it is questionable to what extent proportion use is tested at all by this question. Use of a generic proportion method, as will be illustrated later in this article, would clearly cause a learner to forfeit the first of these marks, and may even forfeit the substitution and ratio marks if the marker requires presentation in the format given in the examples. The memorandum does list proportion methods as alternatives to the formula and substitution methods. However, only a single alternative mark is indicated by the tick signs in this proportion section.

Since the assessed curriculum is a much stronger influencer of practice in South Africa (Brodie and Sanni, 2014), the examples above suggest that generic proportion methods are unlikely to be practiced in South African classrooms. Clearly this does not necessarily imply a de-emphasis of any use of proportion in South African classrooms. However, it does suggest that such a de-emphasis is possible. This suggestion is further strengthened by the exclusion of any mention of proportional reasoning in the examination guidelines document (DBE, 2015), which is a simplified version of the curriculum document. The strong emphasis on use of formulae is further illustrated by admonitions, such as “Candidates should be taught to copy formulae from the data sheet” (p. 224), in the Department of Basic Education (DBE, 2020) examiners’ report. In contrast, no mention is made of proportion in this report, although “foundational stoichiometry”, which probably includes proportion usage, is identified as being “poorly understood” (p. 21). It therefore seems that besides one overt reference to proportional reasoning in the curriculum statement, referred to above, representing the envisioned curriculum, proportion features relatively covertly in documents relevant to the enforced curriculum, whereas formulae feature overtly throughout all documents.

In South Africa, officials in the Department of Basic Education (DBE) set the final chemistry examination papers, and subject teachers mark learners’ answers. For grade 12 final examinations, selected teachers do this marking at a central marking venue under monitored conditions. For other grades and for tests and examinations other than the final examination, teachers mark their own learners’ answers at their schools, with some moderation by heads of departments and DBE subject advisors performed. In all cases, marking is done against a memorandum which is provided by the DBE, and moderation includes checking that the memorandum was strictly adhered to (van Wyk et al., 2019).

It is understandable why the mismatch between marking guidelines and the curriculum statement exists for formula-accessible calculation questions since (1) it is easier to mark formula provision and substitution than it is to mark proportional reasoning; (2) the enforcement of religious adherence to marking memoranda which prevails in developing-world contexts may be seen as necessary given the low competence of some markers (van Wyk et al., 2019); (3) even many experts may solve such questions using a formula rather than reasoning from first principles using proportion. However, these marking guidelines might be discouraging use of a generic proportion method which makes formula-use unnecessary. Further, it seems possible that the mismatch between the curriculum and the marking guidelines could create the misconception that formulae and proportion should be pitted against one another, with formulae winning. One might speculate that learners, and even teachers, may be particularly susceptible to this misconception in contexts where subject matter knowledge (SMK) is limited and therefore the potential shortcut that formulae seem to offer may be so seductive as to blind them to the fact that proportion usage cannot fully be replaced by formula usage in reaction-based stoichiometry questions.

Developing an understanding of teachers’ use of and dependence on formulae for various proportion competences in this context may contribute to determining whether such speculations are worthy of investigation. In developing world contexts assessment of teachers’ subject matter knowledge (SMK) can provide insight into what knowledge they teach, and therefore, probably also their beliefs about what knowledge is valuable. This is because the SMK of teachers in such contexts tends, largely, to be limited to, and to limit, what they teach (Brodie and Sanni, 2014) and be governed by their belief systems (Makhechane and Qhobela, 2019). Additionally, determining teachers’ SMK indicates the upper limit of SMK they are able to teach to their learners (Gess-Newsome et al., 2019). Therefore, for developing world contexts, at least, determining teachers’ practises and success regarding use of formulae and proportion in their own answers to stoichiometry calculation questions is valuable in contributing to an understanding of their belief systems, what likely happens in their classrooms and what professional development opportunities may be appropriate.

Research questions

Consequently, this research is guided by the following research questions, related to South African Physical Sciences (SA PS) teachers when answering school stoichiometry reaction-based calculation questions and for which solution success is measured as the ability to correctly show process steps and to obtain the answer, consistent with the South African practice of awarding marks to both of these:

(1) How prevalent is recognition of the need to use proportion and to what extent is this recognition coupled with obtaining the correct answer?

(2) For various extents of proportion usage, how is the extent to which relevant formulae are used related to solution success?

Method

This is a quantitative survey study which is guided by the Framework for Integrated Methodologies and set in the pragmatic paradigm (Plowright, 2011).

Sample and data collection

Although a convenience rather than representative sample was used in this study, its composition is relatively large (n = 171) and varied. Further, there were no obvious externally imposed biases in the inclusion of various types of teachers from the target population of South African Physical Sciences (SA PS) teachers from the Free State, a higher-performing province. The subject advisors of the Department of Basic Education (DBE) had extended an open invitation to the teachers in their areas to attend a two-day professional development workshop, at which data were collected. I held eight of these workshops at various locations throughout the Free State between November 2017 and March 2018. Attendance was incentivised through qualification for continuous professional development (CPD) points, as well as reception of resources for teaching stoichiometry. Although 220 teachers attended these workshops, 49 were excluded from the sample used here on the grounds of not having answered any of the questions used in this analysis at the start of each workshop, or who did not answer a biographical survey questionnaire administered at the end of each workshop.

The information given in Table 1, regarding characteristics of the sample, should aid readers’ judgement regarding the extent to which the generalisations made from this study can validly be applied to SA PS teachers and to teachers from other developing countries. As shown in this table, the sample includes teachers teaching in schools serving the full range of SA learners according to socio-economic status. SA's education system is bimodal in character (Spaull, 2013), with schools serving the richer 20% of the population (quintile 5 schools) being globally competitive, whereas those serving the poorer 80% (quintile 1–4) performing near the bottom on international benchmarking tests (Reddy et al., 2019).

Table 1 Some characteristics of the sample
Socioeconomic status of the learners taught Possess a BSc degree Stoichiometry teaching experience category N
a 3 years or less. b 3 < 10 years. c 10 years or more.
High (teach at a quintile 5 school) n = 21 (12%) No (n = 10) Inexperienceda 6
Moderately experiencedb 4
Experiencedc 0
Yes (n = 11) Inexperienced 4
Moderately experienced 2
Experienced 5
Low (teach at quintile 1–4 schools) n = 150 (88%) No (n = 96) Inexperienced 50
Moderately experienced 22
Experienced 24
Yes (n = 54) Inexperienced 27
Moderately experienced 16
Experienced 11

In South Africa physics and chemistry are combined in a single subject, physical science. Physical science teachers are generally expected to have studied either physics or chemistry at least at first year level within either of the two main routes which can be followed to qualify as a teacher in South Africa. These are: (1) the education-focused route, through obtaining a Bachelor of Education (BEd) degree; (2) the subject-specific route, e.g. through obtaining a Bachelor of Science (BSc) degree, followed by a postgraduate certificate in education (PGCE). For the SA context the sample is fairly inexperienced (6 years stoichiometry teaching experience, on average) and relatively well qualified (38% holding BSc degrees and the group averaging 2.1 years of post-matric Chemistry study). However, there is a large range present (0–30 years stoichiometry teaching experience and 0–4 years post-matric Chemistry study).

Before data collection commenced, the ethics committee for educational research at the University of the Free State evaluated the research proposal for compliance with relevant laws and institutional guidelines for ethical research and awarded ethical clearance for the study (UFS-HSD2017/1520). All teachers included in the sample gave written informed consent to anonymous inclusion of their data in this study.

The test used

See Fig. 1 for the four calculation questions used (questions 18–21), as well as a related question (question 17) which question 18 followed on from. Table 2 gives the mark allocation used and the formulae and proportion relevant to each question. The questions were designed for the purposes of the workshops and this research, namely to measure the teachers’ ability to answer minimally-word-dependent calculation questions compatible with the SA grades 10 and 11 PS curriculum (DBE, 2011) and similar to typical text-book end-of-chapter practise exercises. All the questions can be categorised as level 2 questions in Ramful and Narod's (2014) 5-level scale of difficulty for stoichiometry calculation questions since each involves only one chemical reaction equation and only extensive (non-ratio) units, with the given and required units being different to one another. This is consistent with the requirements of the curriculum document (DBE, 2011). For question 18 this conversion was necessary to determine which reagent was limiting, which was asked in the previous multiple-choice question (question 17, see Fig. 1). Question 17 was not included in this analysis since written steps had not been explicitly asked for. Provision of the questions and marking criteria, here, as well as attempts to make analysis processes transparent to the reader, are intended to enable the reader to judge the extent to which claims made are warranted, and therefore likely to be valid (Plowright, 2011).
image file: d0rp00291g-f1.tif
Fig. 1 The questions as they appeared to the teachers. Answers to questions 18–21 are analysed in this study.
Table 2 The marking and coding criteria used
No. Topic Mark allocation Formulae relevant to formula-accessible calculations Reaction ratios applicable to proportion usage
18 Yield with limiting reagent 1. Application of 2[thin space (1/6-em)]:[thin space (1/6-em)]3 ratio 3 mol H2[thin space (1/6-em)]:[thin space (1/6-em)]2 mol NH3
2. To the correctly chosen limiting reagent, i.e. 0.5 mol H2
3. Answer = 0.33 mol NH3
19 Number of atoms 1. Conversion of 17 dm3 N2 to mol (–22.4 dm3 mol−1) image file: d0rp00291g-t1.tif 3 mol H2[thin space (1/6-em)]:[thin space (1/6-em)]1 mol N2 or 3(2(6.02 × 1023)) H atoms in: 1(22.4) dm3 N2
2. Application of 3[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio
3. Conversion of mol to molecules (× 6.02 × 1023 mol−1) N = nNA
4. Conversion of molecules to atoms (× 2)
5. Answer = 2.74 × 1024 atoms H
20 Percent yield 1. Application of 3[thin space (1/6-em)]:[thin space (1/6-em)]2 ratio to mol equivalent of 7 g H2 image file: d0rp00291g-t2.tif 3 mol H2[thin space (1/6-em)]:[thin space (1/6-em)]2 mol NH3 or 3(2 g) H2[thin space (1/6-em)]:[thin space (1/6-em)]2(17 g) NH3
2. To find theoretical yield of 39.67 g or 1.65 mol NH3
3. % yield formula image file: d0rp00291g-t3.tif
4. Answer = 70.6%
21 Yield without limiting reagent 1. Balanced equation
2. MSO3 = 80 g mol−1
3. Application of 2[thin space (1/6-em)]:[thin space (1/6-em)]3 ratio 3 mol O2[thin space (1/6-em)]:[thin space (1/6-em)]2 mol SO3 or 3 mol O2[thin space (1/6-em)]:[thin space (1/6-em)]2(80) g SO3
4. Answer = 101.3 g image file: d0rp00291g-t4.tif
Total 16 Marks 5 relevant formulae to be given and substituted into 4 questions for which proportion is required

Data analysis

Marking and coding of the teachers’ solutions was done by the researcher, who is also the author of this paper, and who holds BSc(Hons), MEd and PhD (Science Education) degrees, has 15 years of high school chemistry teaching experience, and has served as a marker for grade 12 physical sciences examinations in the South African system. The marking was done twice: immediately after the teacher had written the test and later together with a more detailed coding process. The marking and coding guidelines given in Table 2 were applied. The rare discrepancies found between the marks allocated during these two processes were examined in detail to diagnose and rectify marking inconsistencies, increasing the validity of the findings. Where a participant skipped steps within their written answer, the relevant marks were assigned if a correct answer was attained at the end of the skipped steps and therefore the presence of the missing components can reasonably be assumed. The section of the coding performed during the second marking process, relevant to this article, is whether: (1) the formulae relevant to formula-accessible calculations in these questions were provided and substituted into, and (2) proportion was used to apply the reaction ratio given in the balanced equation, and (3) a correct answer was obtained.

Research question 1 relates to whether the teachers recognised that proportion needed to be applied to each of the questions, and whether those that applied proportion obtained the correct answer. In order to answer this question, counts of teachers who fell into each of the following categories were graphed for each question: (1) did not use proportion; (2) used proportion and did not obtain the correct answer; (3) used proportion and obtained the correct answer; (4) did not attempt the question.

Research question 2 relates to the relative success of strategies which differ in the extents to which formulae are explicitly given and substituted into, and proportion is used. Two measures of success are used: marks obtained (/16), according to the marking guidelines given in Table 2, and the number of questions for which a correct answer was obtained (/4). Two approaches are used to answer this question: (1) graphing other variables against one another and (2) assignment of each teacher to one of four strategy groups and performance of statistical analysis using each group's mean marks (M) out of 16 (for marks obtained) or out of 4 (for correct answers). How these two approaches were executed, is described below.

For both approaches, each teacher was assigned a formula and substitution usage code (/10) and a proportion usage code (/4) based on the extent of presence, not correctness, across the four questions, of each of these aspects visible within their written solutions. In the case of proportion usage, only two values were assigned per question: present (1) or absent (0), resulting in a total possible numerical score of 4. In the case of formula and substitution usage, a maximum total score of 2 was assigned per relevant formula. The points in these codes were assigned for provision of the relevant formula and substitution into a given or implied formula. Substitution into an implied formula was deduced when values were provided in any format in which the relevant formula from the examination data table may likely have been given in, i.e. with any of the variables being the subject of the formula and with common errors being allowed for, such as items being substituted incorrectly. Examples of how this coding was done are given in Table 3. Five formulae were relevant, as represented in Table 2, resulting in a maximum of 10 possible points for this code.

Table 3 Examples of each type of strategy used, as well as how coding was applied
Strategy Example from the number of atoms question (question 19) Codes
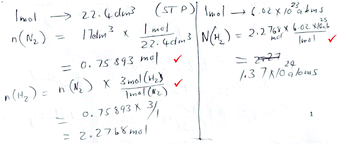
Proportion reliant image file: d0rp00291g-u1.tif Marks: 3/5
Proportion is used throughout, both for formula-accessible and reaction-based calculations. Correct answer: No
Marks 1–3 were assigned (see Table 2). Formula provision: 0/2
Substitution into a formula: 0/2
Proportion: 1/1
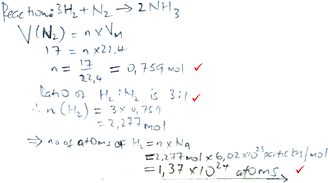
Formula and proportion image file: d0rp00291g-u2.tif Marks: 3/5
Formulae are given and values are substituted into these for formula-accessible calculations. Proportion is used for the reaction-based calculation. Correct answer: No
Marks 1–3 were assigned (see Table 2). Formula provision: 2/2
Substitution into a formula: 2/2
Proportion: 1/1
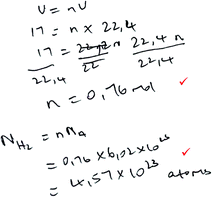
Formula reliant image file: d0rp00291g-u3.tif Marks: 2/5
Formulae are given and substituted into for formula-accessible calculations. Proportion is not used. Correct answer: No
Marks 1 and 3 were assigned (see Table 2). Formula provision: 2/2
Substitution into a formula: 2/2
Proportion: 0/1
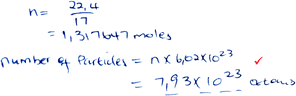
Minimal image file: d0rp00291g-u4.tif Marks: 1/5
Formulae are not given, but substitution is implied. Proportion is not used. Correct answer: No
Mark 3 was assigned (see Table 2). Formula provision: 0/2
Substitution into an implied formula: 2/2
Proportion: 0/1

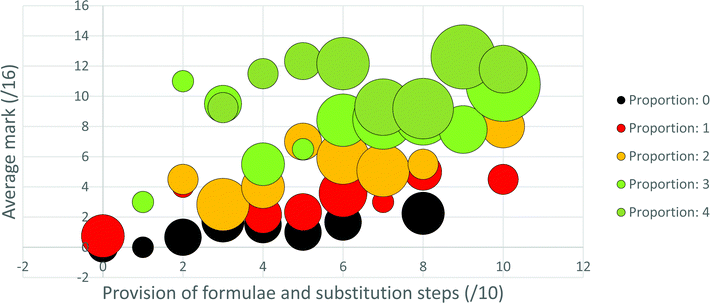
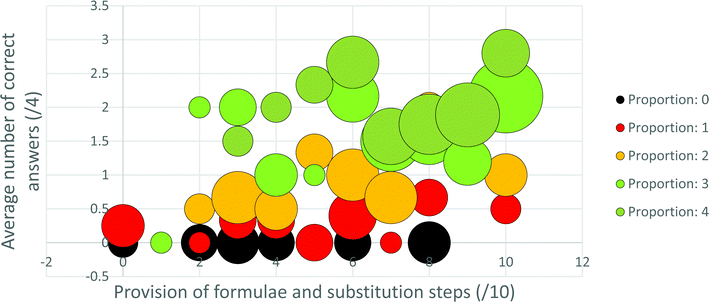
For the first approach to this data analysis, five series, corresponding to the five possible extents of proportion usage (0–4), were plotted in bubble graphs with the x-axis being formula and substitution usage (/10), the y-axis mark (/16) or correct answers (/4) obtained and the bubble sizes representing the number of teachers for each point in the graph. From these graphs trends relevant to answering the second research question can be inferred visually. However, to enable application of a statistical analysis to the data it was necessary to employ the second approach used to analyse this data.

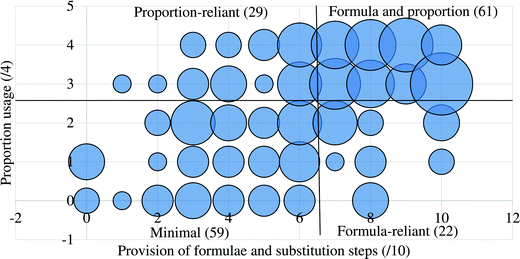
For this second approach, each teacher was assigned to one of four categories, as shown by the four labelled quadrants in Fig. 2, in which the teachers in the sample were plotted according to the extent to which they used proportion and explicitly provided formulae and substitutions. The ranges used for these categories were chosen as follows. Although proportion usage was required for a complete solution for each of the four questions, one omission was considered reasonable leeway to allow for inclusion in the high proportion usage range. Since it is possible to answer all the questions correctly without any use of formulae, the high and low categories, regarding formula usage, do not necessarily imply competence or deficiency. The threshold of 7 (/10) was arbitrarily chosen since it resulted in a roughly equal division of the number of participants in the low (Minimal and Proportion reliant, n = 88) and high (Formula reliant and Formula and proportion, n = 83) formula usage categories.


image file: d0rp00291g-f2.tif
Fig. 2 Distribution of teachers according to use of proportion and provision of formulae and substitution steps in their written solutions, showing strategy type classification groups. Bubble size represents teacher numbers.

Average scores, out of 16, per strategy, and average numbers of correct answers obtained, out of 4, were successively used as measures of the effectiveness of each strategy. These were compared, between the strategies, using a one-way ANOVA, followed by a post hoc Tukey–Kramer test, which is appropriate for unequal sample sizes. Significance was taken at an alpha level of 0.05.

Solution examples per strategy

Some examples of answers which are in some way representative of each strategy are given in Table 3. These examples were taken from question 19, which few of the teachers (13/171) answered correctly, with a quarter (n = 44) finding the number of H2 molecules, rather than H atoms, required. The first two examples (Proportion reliant and Formula and proportion strategies) shown in this table made this error. Reasons for displaying examples which made this error rather than examples of correct solutions are: (1) the error was more prevalent and (2) the Proportion reliant example given in the table was the only example in the data in which the written answer clearly makes use of a generic proportion strategy with no use of formulae. This single example is noteworthy since the feasibility of use of such a generic proportion method in this context is of interest, as has already been discussed. It should be pointed out, however, that the reduced formula usage of the other members of this strategy took the form of what may be seen as missing steps in the written solution, such as substitution into an implied, rather than explicitly given, formula. Allocation to the categories was done on the basis of the prevalence of proportion and formula provision and substitution, across all four of the questions, and therefore it is possible for a strategy to resemble one of those given in Table 3 despite the teacher having been classified differently to that in the example. Finally, although an example is given, in Table 3, of implied substitution into a formula, widely observed in the Proportion reliant and Minimal groups, an example is not given of provision of a formula without substitution, which was occasionally observed in the Minimal group.

Results

Prevalence and success of recognition of the need to use proportion

As shown in Table 4, most (87%) of the teachers recognised the need to use proportion for at least some of the questions, although relatively few (25%) recognised that all the questions required use of proportion. Alarmingly, 13% of the teachers failed to use proportion in any of the four questions.
Table 4 Categorisation of teachers according to number of questions for which they recognised that proportion should be used
Proportion usage Number of questions in which proportion was used N %
No use of proportion 0 23 13
Some use of proportion 1 25 106 62
2 33
3 48
Use of proportion in all cases measured 4 42 25

Fig. 3 shows the proportion usage, and obtainment of the correct answer, per question. For each question a few (2–7%) of the teachers did not attempt the question. For the Yield with- and -without limiting reagent questions (18 and 21) over 70% used proportion, whereas for the Number of atoms and Percent yield questions (19 and 20), fewer than 50% used proportion. Only those who used proportion could possibly obtain the correct answer. Except for question 19, roughly half of those who used proportion obtained the correct answer. The reason for the particularly poor performance in question 19 was a high prevalence of failure to distinguish between H2 molecules and H atoms, as was illustrated in Table 3.


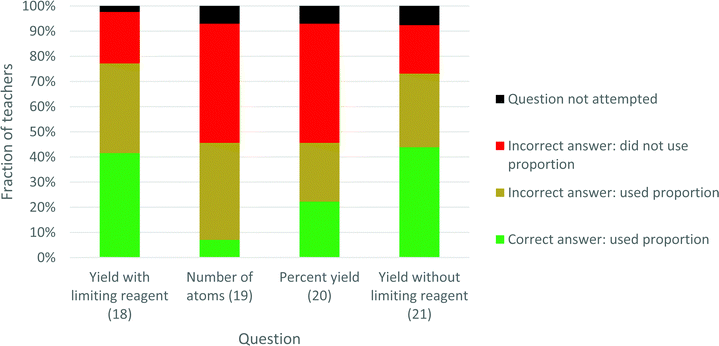image file: d0rp00291g-f3.tif
Fig. 3 Prevalence of proportion usage and success, measured as obtainment of the correct answer, for each of the four questions.

Success of strategies which vary in presence of proportion and of explicit provision of and substitution into formulae

(a) Success measured as obtaining marks. Fig. 4 shows a clear upward trend in marks with increased provision of formulae and substitution steps in the written solutions among the lower proportion-usage teachers. However, among the higher proportion-usage teachers, this trend is less clear. These visual trends are explored further in the statistical analysis reported on in Table 5.
image file: d0rp00291g-f4.tif
Fig. 4 Mark garnering success according to extent to which formulae and substitution steps are explicitly given, for each proportion usage group of teachers. Bubble sizes represent numbers of teachers.
Table 5 Comparisons of mark attainment of the four strategies
Strategy N % M (/16) SD Anova Tukey–Kramer:

image file: d0rp00291g-t5.tif

a
a Q values given here are calculated from raw values, not the rounded values given in this table. Critical q value: 3.69 for an alpha value of 0.05.
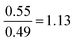
Proportion reliant 29 17 9.4 4.0 F(3.167) = 64.72, p = 8.15 × 10−28 image file: d0rp00291g-t6.tif Compared to Minimal: 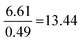image file: d0rp00291g-t7.tif
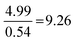
Formula and proportion 61 36 10.0 3.2 image file: d0rp00291g-t8.tif Compared to Minimal: 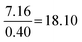image file: d0rp00291g-t9.tif
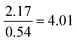
Formula reliant 22 13 5.0 3.0 image file: d0rp00291g-t10.tif Compared to Proportion reliant: 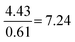image file: d0rp00291g-t11.tif
Minimal 59 35 2.8 2.4

As shown in Table 5, the ANOVA test revealed a significant difference in performance across the four strategies [F(3.167) = 64.72, p = 8.15 × 10−28]. Therefore, a post hoc Tukey–Kramer test was performed to determine to which pairs of strategies this difference applies. This yielded statistically significant differences between each possible strategy comparison, except for between the Formula and proportion and Proportion reliant strategies.

(b) Success measured as obtaining the correct answer. Fig. 5 differs from Fig. 4 in that attainment of the correct answer is used as the measure of success, rather than attainment of marks, most (12/16) of which were for process steps. The previously pointed out upward gradient for the lower proportion-usage categories in Fig. 4 is less visible in Fig. 5. This suggests that for these groups the increase in marks with increased provision of formulae and substitution, pointed out above, is not coupled with an increased likelihood of obtaining the correct answer. This conclusion is supported by the statistical analysis summarised in Table 6, which shows that the Formula reliant and Minimal strategies, in addition to the set given in Table 5 (Proportion reliant and Formula and proportion), showed no statistically significant difference in success.
image file: d0rp00291g-f5.tif
Fig. 5 Correct answer achievement according to extent to which formulae and substitution steps are explicitly given, for each proportion usage group of teachers. Bubble sizes represent numbers of teachers.
Table 6 Comparisons of correct answer achievement of the four strategies
Strategy N % M (/4) SD Anova Tukey–Kramer:

image file: d0rp00291g-t12.tif

a
a Q values given here are calculated from raw values, not the rounded values given in this table. Critical q value: 3.69 for an alpha value of 0.05.
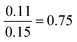
Proportion reliant 29 17 1.9 1.1 F(3.167) = 33.06, p = 7.96 × 10−17 image file: d0rp00291g-t13.tif Compared to Minimal: 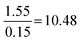image file: d0rp00291g-t14.tif
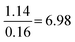
Formula and proportion 61 36 1.8 1.3 image file: d0rp00291g-t15.tif Compared to Minimal: 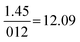image file: d0rp00291g-t16.tif
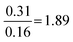
Formula reliant 22 13 0.7 0.6 image file: d0rp00291g-t17.tif Compared to Proportion reliant: 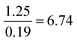image file: d0rp00291g-t18.tif
Minimal 59 35 0.4 0.4

It is evident from these analyses that the factor of high vs. low usage of proportion is significantly associated with both the number of marks garnered and the number of questions for which the correct answer was obtained. However, within each proportion usage grouping, whether formulae were provided and substituted into to a high or low extent was not significantly associated with the number of correct answers attained. As already mentioned, for the lower, but not higher, proportion usage group, this was, however, significantly associated with the number of process marks achieved.

Discussion, implications and suggestions for further investigation

The following assertions are made in response to the research questions as a summary of the findings. These assertions and suggested implications are then discussed.

• Failure to recognise the need to use proportion is a considerable, although not the only, barrier to South African Physical Sciences teachers’ ability to obtain the correct answer to equation-based stoichiometry calculations. Although most South African Physical Sciences teachers recognise the need to use proportion for some reaction-based stoichiometry calculation questions, few (25% in this sample) recognise this need consistently, and some (13% in this sample) appear to be unaware that proportion is ever relevant to such questions. Recognition of the need to use proportion is question dependent.

• When competence with proportion is low, provision of and substitution into a formula increases the number of process marks obtained although not the likelihood of obtaining the correct answer.

Underutilisation and question-dependence of proportion

An obvious implication of these findings is that PS teachers in SA and, probably, in other developing world contexts, are in need of effective professional development opportunities focused on promoting competence with proportion, particularly competence with recognition of when it is applicable to use proportion in stoichiometry calculations. Although it would seem that introducing these teachers to a generic proportion method, such as the unit factor method, may serve this purpose well, this may not be the case. The finding that failure to recognise the need to use proportion is a considerable barrier to these teachers’ success with stoichiometry reaction-based calculations is not consistent with findings in other developing world contexts. For example, Danjuma (2011) found that Nigerian pre-service science teachers were mostly able to use proportion when solving stoichiometry questions, with the limitation to their success being application of the conceptual knowledge required to obtain the correct answer. Similarly, Kartal and Kartal (2019) found that Turkish pre-service teachers generally used proportion in their stoichiometry solutions. Both Danjuma (2011) and Kartal and Kartal (2019) found high uses of memorised generic proportion methods, whereas the teacher whose work is illustrated in Table 3 as an example of the Proportion reliant strategy was the only one observed to use such a generic proportion method. This discussion is consistent with the speculation, raised earlier, that SA teachers may have an aversion to such generic proportion methods, with their strengths of guiding strategy choices, including the choice to use proportion, because of the examination practises in this context. Further, as discussed below, process marks, through use of formulae and substitution, even with a disregard for proportion, may be seen as too valuable to trade for a generic proportion method, particularly when SMK is limited. The fact that only about half of the teachers who recognised the need to use proportion managed to obtain the correct answer for three of the questions, with even fewer managing this for question 19, points to the presence of other difficulties besides recognition of the need to apply proportion. Clearly further investigation is necessary to determine what these difficulties are and how to address them.

Value of formula stress for process marks when proportion is underutilised

Provision of, and substitution into, a formula in the written solution appears to be particularly beneficial for obtaining process marks for those participants who were less competent with proportion (see Fig. 4 and 5). As alluded to above, this might be relevant to a proposed explanation for the observed underutilisation of proportion in this context. Most high school learners begin their introductory stoichiometry courses as novices to stoichiometry. Teachers may see high school stoichiometry as serving either or both of the following purposes: (1) improving the depth and breadth of learners’ knowledge and so, in Niaz's (1995) words, improving the “explanatory/heuristic power” (p. 2) of their knowledge; (2) helping learners garner as many marks as their teachers judge them as capable of attaining. In developing-world contexts, the latter tends to be the predominant focus (Makhechane and Qhobela, 2019). Further, in developing-world contexts teachers tend to perceive that their learners are unable to learn complex concepts (Hoadley, 2018), and the teachers themselves often do not possess sophisticated subject matter knowledge required to help their learners to learn complex concepts (Taylor, 2019; Stott, 2020). Additionally, intense political pressure, supported by funding incentives, is applied to SA teachers to improve pass rates (Okitowamba et al., 2018), whereas far less pressure is exerted regarding the quality of pass obtained (Stott et al., 2015). Therefore, it seems possible that teachers in the developing world might hold the perception that a focus on formulae at the expense of proportion may be efficient in helping their learners to garner process marks. Further, such a perception may be seen to be validated by the explicit focus on formulae, relative to the implicit focus on proportion, in the examination documents. Since the subject matter knowledge of teachers in developing-world contexts tends to be strongly defined by what they teach (Brodie and Sanni, 2014), it is possible that the teachers’ own ability to use proportion develops more slowly than it would have, had proportion, understanding and attainment of final answers, been more, and formulae and process marks less, explicitly focused on.

This argument seems particularly appropriate for the 13% of teachers in this sample who used the Formula reliant strategy, and it raises the question of whether educational beliefs and practises in developing world contexts are inhibiting teachers’, and possibly also learners’, development along Niaz's (1995) stages from novice to expert stoichiometry problem solving expertise. Since the ability to engage in proportional reasoning is a hallmark of operation at the formal operational stage (Ghazi et al., 2014), one could extend the question to whether such educational beliefs and practises inhibit development along Piaget's stages of mental development. It should be pointed out, however, that the argument that a focus on formulae is responsible for the underutilisation of proportion may not be valid for most teachers in this sample. The Minimal strategy, exhibited by 35% of the sample, is deficient in both use of proportion and formulae. This suggests that limited teacher subject matter knowledge, in general, including limited knowledge of both proportion and formula usage may be even more limiting than is a misconceived notion that formulae can always replace proportion.

Suggestions for practice

The findings suggest that teacher professional development opportunities which target proportion usage in stoichiometry are much needed in the studied context and, possibly, throughout the developing world. Given the difficulties associated with the formal operational reasoning which proportion requires, it may be helpful to conduct such professional development in manners which provides concrete support, for example with the use of strategy or concept maps (Gongden and Delmang, 2016), procedural steps, such as described in Fach et al. (2007), worked examples (Bentley and Yates, 2017), and structured worksheets and manipulatives (Molnar and Molnar-Hamvas, 2011). The use of structured worksheets to guide teachers to use the unit factor method, a generic proportion heuristic, is of particular interest, given such a method's potential to simplify stoichiometry calculations through application of a single heuristic. Further, such a method foregrounds proportion. This is important since proportion is the central concept in stoichiometry, and, as has been argued in this article, there appears to be a need to stress this fact among teachers in this context.

The findings suggest that every opportunity should be seized to stress the importance of use of proportion in stoichiometry. Given the power of assessment to drive practice, particularly in the developing world (Brodie and Sanni, 2014), this stress needs to be applied in particular in documents directly related to examinations. As discussed earlier, current examination marking practices in South Africa are incompatible with use of a generic proportion method. Although it is beyond the scope of this article to claim that these current examination marking practices are responsible for the observed underutilisation of proportion, the possibility of such a relationship has been suggested in the discussion section above. To illustrate the change in marking practise which may be needed to address this situation, Fig. 6's marking guidelines are proposed as an alternative to those given in the official memorandum. Note that the marking guidelines listed in Fig. 6 would assign full marks to the formula and proportion strategy solution given in the official memorandum as well as to the proportion reliant strategy solutions given in: (a) the alternative examples in the official memorandum; (b) the generic proportion method example given in Fig. 6.


image file: d0rp00291g-f6.tif
Fig. 6 Suggested marking guidelines and solution options for question 6.2.3. of the South African National Grade 11 November 2019 Paper 2 examination, which would allow for use of a generic proportion method to solve stoichiometry questions.

Limitations and suggestions for further investigation

Limitations within the data collection methods include the fact that there are a variety of ways in which marks can be assigned when marking calculation questions and fewer process marks were assigned to explicit formula provision and substitution than tends to be the case in this context. The reason for the latter is that these marks were used for multiple purposes within the broader study of which the reported research formed a part. One of these purposes was the evaluation of the intervention. The process marks assigned (Table 2) are considered to be more appropriate for this purpose than would the practise of requiring provision of formulae which a generic proportion method could render redundant. These limitations and the threat they pose to the validity of this study were reduced by transparent reporting of the marking methods used. It is expected that the value of process marks to people who have limited competence with proportion would be even greater than these findings suggest if more marks are awarded to formula-related steps. This would further strengthen, rather than invalidate, the assertion made in this regard. The finding which may be invalidated by this discrepancy is that extent of provision of and substitution into formulae was not related to mark attainment for the higher proportion usage category of teachers. For this reason, this finding was not stressed within the assertions given.

Limitations within the data analysis include the choice of arbitrary thresholds to define the strategy categories used. This includes necessarily different criteria for threshold choices for usage of formulae compared to for proportion, blurring the deduction of relative focus teachers afforded these. Again, transparent reporting of how the classification was performed enables the reader to make judgements on the warrantability, and therefore validity (Plowright, 2011), of the claims made. Further, the analysis was performed multiple times with slightly different thresholds for categorisation, and in all cases the trends asserted in the discussion were maintained, although, obviously, the relative proportions of teachers in each category varied from what has been reported here. Consequently, the relative proportions of teachers who fell into each category have not been included in the assertions made. Representation of the data in various formats has been provided to enable the reader to judge warrantability of the assertions that have been made.

Due to the great influence that context exerts on teacher subject matter knowledge (Stott, 2020), there are sure to be limitations to generalisation of the assertions made to contexts other than that investigated. Given the difficulties teachers in developing world contexts throughout the world have with subject matter knowledge (Schweisfurth, 2013), it is assumed that the assertions will have applicability to other developing countries, at least.

Conclusion

The assertions made in response to the research questions are consistent with Niaz's (1995) thesis that algorithms (which include formulae) help novices to cope with complexity but they become somewhat redundant as a person attains greater competence. Therefore, the explicit focus on formulae in examination documents in contexts where even many teachers have low stoichiometry subject matter knowledge is understandable. However, it may be wise for examination bodies to revise practises of assigning marks to formulae and substitution since this may have the unintended consequence of encouraging a superficial scramble for relatively meaningless process marks and prejudice teachers against use of generic proportion methods which may improve their competence with proportion. There is clearly a need to focus explicitly on proportion use in examination documents and professional development interventions since proportion is the central concept of stoichiometry and yet currently recognition of the relevance of proportion to stoichiometry is a considerable barrier to teachers’ stoichiometry calculation success in the context investigated.

Conflicts of interest

There are no conflicts to declare.

References

  1. Bentley B. and Yates G. C., (2017), Facilitating proportional reasoning through worked examples: two classroom-based experiments, Cogent Educ., 4, 1297213.
  2. BouJaoude S. and Barakat H., (2003), Students' problem solving strategies in stoichiometry and their relationships to conceptual understanding and learning approaches, Electron. J. Sci. Educ., 7, 1–42.
  3. Brodie K. and Sanni R., (2014), ‘We won't know it since we don't teach it’: Interactions between Teachers' Knowledge and Practice, Afr. J. Res. Math., Sci. Technol. Educ., 18, 188–197.
  4. Dahsah C. and Coll R. K., (2007), Thai Grade 10 and 11 students’ conceptual understanding and ability to solve stoichiometry problems, Res. Sci. Technol. Educ., 25, 227–241.
  5. Danjuma I. M., (2011), Methods used by pre-service Nigeria Certificate in Education teachers in solving quantitative problems in chemistry, Chem. Educ. Res. Pract., 12, 427–433.
  6. DBE, (2011), Physical Sciences curriculum and assessment policy statement, Pretoria: Department of Basic Education.
  7. DBE, (2015), Physical Sciences Examination Guidelines Grade 10, Pretoria: Department of Basic Education.
  8. DBE, (2020), Report on the 2019 National Senior Certificate Examination, Pretoria: Department of Basic Education.
  9. Espinosa A. A., España R. C. N. and Marasigan A. C., (2016), Investigating pre-service chemistry teachers’ problem solving strategies: towards developing a framework in teaching stoichiometry, J. Educ. Sci., Environ. Health, 2, 104–124.
  10. Fach M., De Boer T. and Parchmann I., (2007), Results of an interview study as basis for the development of stepped supporting tools for stoichiometric problems, Chem. Educ. Res. Pract., 8, 13–31.
  11. Fang S.-C., Hart C. and Clarke D., (2014), Unpacking the meaning of the mole concept for secondary school teachers and students, J. Chem. Educ., 91, 351–356.
  12. Gabel, D. L. and Sherwood, R. D. (1983), Facilitating problem solving in high school chemistry, J. Res. Sci. Teach., 20(2), 163–177.
  13. Gess-Newsome J., Taylor J. A., Carlson J., Gardner A. L., Wilson C. D. and Stuhlsatz M. A., (2019), Teacher pedagogical content knowledge, practice, and student achievement, Int. J. Sci. Educ., 41, 944–963.
  14. Ghazi S. R., Khan U. A., Shahzada G. and Ullah K., (2014), Formal Operational Stage of Piaget's Cognitive Development Theory: An Implication in Learning Mathematics, J. Educ. Res., 17, 71–84.
  15. Gongden E. J. and Delmang T. K., (2016), The Efficacy of Concept Mapping Instructional Strategy in Remedying Students' Problem-Solving Difficulties in Stoichiometry, Afr. Res. Rev., 10, 144–157.
  16. Gulacar O., Eilks I. and Bowman C. R., (2014), Differences in general cognitive abilities and domain-specific skills of higher-and lower-achieving students in stoichiometry, J. Chem. Educ., 91, 961–968.
  17. Gultepe N., Celik A. Y. and Kilic Z., (2013), Exploring effects of high school students' mathematical processing skills and conceptual understanding of chemical concepts on algorithmic problem solving, Aust. J. Teach. Educ. (Online), 38, 106–122.
  18. Haidar A. H. and Al Naqabi A. K., (2008), Emiratii high school students’ understandings of stoichiometry and the influence of metacognition on their understanding, Res. Sci. Technol. Educ., 26, 215–237.
  19. Hanson R., (2016), Ghanaian Teacher Trainees' Conceptual Understanding of Stoichiometry, J. Educ. e-Learn. Res., 3, 1–8.
  20. Hoadley U., (2018), Pedagogy in Poverty: Lessons from Twenty Years of Curriculum Reform in South Africa, New York: Routledge.
  21. Huitt W. and Hummel J., (2003), Piaget's theory of cognitive development, Educ. Psychol. Interact., 3, 1–5.
  22. Kartal T. and Kartal B., (2019), Examining Strategies Used by Pre-service Science Teachers in Stoichiometry Problems in Terms of Proportional Reasoning, Çukurova Üniversitesi Eğitim Fakültesi Dergisi, 48, 910–944.
  23. Makhechane M. and Qhobela M., (2019), Understanding How Chemistry Teachers Transform Stoichiometry Concepts at Secondary Level in Lesotho, S. Afr. J. Chem., 72, 59–66.
  24. Malcolm S. A., Mavhunga E. and Rollnick M., (2019), The Validity and Reliability of an Instrument to Measure Physical Science Teachers’ Topic Specific Pedagogical Content Knowledge in Stoichiometry, Afr. J. Res. Math., Sci. Technol. Educ., 22, 181–194.
  25. Molnar J. and Molnar-Hamvas L., (2011), LEGO-Method--New Strategy for Chemistry Calculation, US-China Educ. Rev. B7, 891–908.
  26. Niaz M., (1995), Progressive transitions from algorithmic to conceptual understanding in student ability to solve chemistry problems: A Lakatosian interpretation, Sci. Educ., 79, 19–36.
  27. Niaz M. and Robinson W. R., (1993), Teaching algorithmic problem solving or conceptual understanding: Role of developmental level, mental capacity, and cognitive style, J. Sci. Educ. Technol., 2, 407–416.
  28. Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem solving: Is there a difference? J. Chem. Educ., 64, 508–510.
  29. Okitowamba O., Julie C. and Mbekwa M., (2018), The effects of examination-driven teaching on mathematics achievement in Grade 10 school-based high-stakes examinations, Pythagoras, 39, 1–10.
  30. Plowright D., (2011), Using mixed methods: Frameworks for an integrated methodology, London: SAGE Publications.
  31. Ralph V. R. and Lewis S. E., (2019), An explanative basis for the differential performance of students with low math aptitude in general chemistry, Chem. Educ. Res. Pract., 20, 570–593.
  32. Ramful A. and Narod F. B., (2014), Proportional reasoning in the learning of chemistry: Levels of complexity, Math. Educ. Res. J., 26, 25–46.
  33. Reddy V., Juan A., Isdale K. and Fongwa S., (2019), Mathematics Achievement and the Inequality Gap: TIMSS 1995 to 2015, in Spaull N. and Jansen J. (ed.), South African Schooling: The Enigma of Inequality, Switzerland AG: Springer, ch. 9, pp. 169–187.
  34. Sanger M. J., (2005), Evaluating students' conceptual understanding of balanced equations and stoichiometric ratios using a particulate drawing, J. Chem. Educ., 82, 131.
  35. Schmidt H. J., (1994), Stoichiometric problem solving in high school chemistry, Int. J. Sci. Educ., 16, 191–200.
  36. Schmidt H.-J. and Jignéus C., (2003), Students strategies in solving algorithmic stoichiometry problems, Chem. Educ. Res. Pract., 4, 305–317.
  37. Schweisfurth, M., (2013), Learner-centred education in international perspective: Whose pedagogy for whose development? London: Routledge.
  38. Selvaratnam M., (2011a), Students’ Competence in some Problem Solving Skills throughout their BSc Course, S. Afr. J. Chem., 64, 185–189.
  39. Selvaratnam M., (2011b), High school Physical Sciences teachers' competence in some basic cognitive skills, S. Afr. J. Chem., 64, 231–236.
  40. Shadreck M. and Enunuwe O. C., (2018), Recurrent difficulties: Stoichiometry problem-solving, Afr. J. Educ. Stud. Math. Sci., 14, 25–31.
  41. Spaull N., (2013), Poverty & privilege: Primary school inequality in South Africa, Int. J. Educ. Dev., 33, 436–447.
  42. Stott A. E., (2020), Influence of Context on Stoichiometry Conceptual and Algorithmic Subject Matter Knowledge among South African Physical Sciences Teachers, J. Chem. Educ., 97, 1239–1246.
  43. Stott A. E., Dreyer H. and Venter P., (2015), Consequences of the progression law in the FET phase: a case study, J. Educ., 63, 89–109.
  44. Taylor N., (2019), Inequalities in teacher knowledge in South Africa, in Spaull N. and Jansen J. (ed.), South African schooling: The enigma of inequality, Cham, Switzerland: Springer, ch. 14, pp. 263–282.
  45. Tóth Z. and Kiss E., (2005), Hungarian secondary school students' strategies in solving stoichiometric problems/Estrategias de estudiantes húngaros de escuela secundaria para resolver problemas estequiométricos, J. Sci. Educ., 6, 47.
  46. van Wyk P. S., Teise K. L. and le Roux A., (2019), Threats to the quality of marking of the national senior certificate examinations in the Northern Cape, Perspect. Educ., 37, 115–129.
  47. Wink D. J. and Ryan S. A., (2019), The Logic of Proportional Reasoning and its Transfer into Chemistry, It's Just Math: Research on Students’ Understanding of Chemistry and Mathematics, ACS Publications, pp. 157–171.

Footnote

† Electronic supplementary information available: Link to video abstract of this paper. See DOI: 10.1039/d0cp00291g
This journal is © The Royal Society of Chemistry 2021