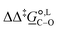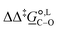Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism, kinetics and selectivity of a Williamson ether synthesis: elucidation under different reaction conditions†
Aikaterini
Diamanti
 ab,
Zara
Ganase
a,
Eliana
Grant
a,
Alan
Armstrong
ab,
Zara
Ganase
a,
Eliana
Grant
a,
Alan
Armstrong
 c,
Patrick M.
Piccione‡
d,
Anita M.
Rea
d,
Jeffery
Richardson§
e,
Amparo
Galindo
c,
Patrick M.
Piccione‡
d,
Anita M.
Rea
d,
Jeffery
Richardson§
e,
Amparo
Galindo
 a and
Claire S.
Adjiman
a and
Claire S.
Adjiman
 *a
*a
aDepartment of Chemical Engineering, Centre for Process Systems Engineering and Institute for Molecular Science and Engineering, Imperial College London, South Kensington Campus, London SW7 2AZ, UK. E-mail: c.adjiman@imperial.ac.uk
bDepartamento de Química, Centro Universitario de Ciencias Exactas e Ingenierías, Universidad de Guadalajara, Jalisco, México
cDepartment of Chemistry and Institute for Molecular Science and Engineering, Imperial College London, Molecular Sciences Research Hub White City Campus, Wood Lane, London W12 0BZ, UK
dProcess Studies Group, Process Technology AI, Syngenta, Jealott's Hill International Research Center, Bracknell, Berkshire, RG42 6EY, UK
eDiscovery Research and Technologies, Eli Lilly and Company, Erl Wood Manor, Windlesham, Surrey GU206PH, UK
First published on 28th January 2021
Abstract
The best route to uncover the mechanism of chemical reactions remains a topic of intense debate. In this work, we deploy a three-faceted approach that combines experimental probing, detailed kinetic modelling and quantum-mechanical calculations for the study of the mechanism and regioselectivity of a Williamson ether synthesis, which is of interest because of its simplicity and its broad scope in laboratory and industrial synthesis. The choice of solvent is found to have a large impact on the experimental regioselectivity, with ratios of O-alkylated to C-alkylated product at 298 K of 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in acetonitrile and of 72
3 in acetonitrile and of 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 in methanol. Through experiments and kinetic modelling, we identify reaction networks that differ significantly from solvent to solvent, providing insights into the factors (proton-exchange, solvolysis and product degradation) that impact on regioselectivity and the relative rates of O-alkylation and C-alkylation. The kinetic models yield detailed information on reaction rates and energy barriers and on the existence of an additional double alkylation pathway. We carry out quantum mechanical calculations and elucidate the transition states for the two main alkylation pathways. The quantum-mechanical calculations highlight structural differences between the transition states found for the two alkylation pathways and provide information on the effect of the solvent on the stabilisation/destabilisation of various structures and hence on reaction selectivity. The three-faceted approach provides complementary information into the elementary steps of the reaction mechanism.
28 in methanol. Through experiments and kinetic modelling, we identify reaction networks that differ significantly from solvent to solvent, providing insights into the factors (proton-exchange, solvolysis and product degradation) that impact on regioselectivity and the relative rates of O-alkylation and C-alkylation. The kinetic models yield detailed information on reaction rates and energy barriers and on the existence of an additional double alkylation pathway. We carry out quantum mechanical calculations and elucidate the transition states for the two main alkylation pathways. The quantum-mechanical calculations highlight structural differences between the transition states found for the two alkylation pathways and provide information on the effect of the solvent on the stabilisation/destabilisation of various structures and hence on reaction selectivity. The three-faceted approach provides complementary information into the elementary steps of the reaction mechanism.
1 Introduction
Understanding the mechanism of a chemical reaction and quantifying reaction progress as a function of conditions are crucial steps in numerous practical applications in organic chemistry,1 for example when optimizing reaction conditions with respect to yield and selectivity. Postulating a mechanism requires accounting for the elementary steps of the reaction, the nature of intermediates and transition states, any side reactions, the energetics of transformations and the rate laws describing each reaction step (i.e., reaction kinetics). External factors, such as temperature, pressure, solvent media and catalysts, as well as internal factors, such as reactant concentrations, physical states and surface areas, can affect the reaction mechanism, making it difficult to achieve a quantitative description of the process, especially when multiple steps and alternative pathways are present.2 In view of the complexity of reaction mechanisms, efforts have been made to combine experimental and computational tools to achieve a detailed understanding of reaction mechanisms and derive predictive results, but the role of different tools remains a subject of debate for the scientific community. Experimental techniques are most commonly employed in the study of reaction mechanisms and quantum-mechanical (QM) methods for electronic-structure calculations are often seen to be valuable in understanding of reaction mechanisms.1Several authors have questioned the value of using QM methods in isolation to investigate reaction mechanisms.2–4 Instead, the synergistic combination of experiments and QM calculations has been suggested as an effective approach to support or disprove a proposed mechanism.1,5,6 The benefits of combining experimental and QM computational approaches for the elucidation of reaction mechanisms have been illustrated in recent reviews.1,6–10 In particular, Plata and Singleton2 have shown that in the case of an alcohol-mediated Morita Baylis–Hillman reaction, QM computational studies carried out in isolation and focused on the simplest mechanism fail to capture the actual reaction mechanism. On the other hand, calculations carried out in concert with an extensive experimental study provide insights into steps that cannot be probed experimentally, e.g., the aldol step. Liu et al.11 have shown that in the case of transition-metal catalyzed Negishi coupling reaction, in situ IR experiments reveal that the reaction is promoted via a transmetalation path that occurs competitively to the reductive elimination path, which is traditionally considered as the key path leading to the cross-coupling products in the Negishi coupling reaction. Computations of energy barriers and substitution effects for the two competing paths have provided corroborating evidence in favour of the transmetalation pathway, resulting in the design of an experimental strategy to avoid the homocoupling and dehalogenation side products that hinder the scale-up of this reaction.
Singleton and Wang12 have shown that the identification of the best operative transition state (TS) for the enantioselective epoxidation of trans-β-methylstyrene is largely facilitated by the use of experimental values for the kinetic isotope effect (KIE). The initial conformational space of 66 calculated TSs was reduced to 3 TS structures through comparison of experimental and predicted KIE values. For the TS with the lowest calculated energy, the computed KIE values are in excellent agreement with the experimental values. These examples illustrate the wealth of mechanistic information that is uncovered when experiments and QM computations are employed synergistically. The combination of experimental and QM computational approaches can be particularly useful to enhance the understanding of fundamental chemical problems,1 such as the effects of additives, bases and acids on reactivity,13 the effects of solvents on reactivity and selectivity14 and the effects of ligands on bond and coordination energy.15–17
To gain a more complete understanding of a reaction, experimental and QM approaches can be complemented by a third means of analysis, namely kinetic modelling. Time-resolved experimental techniques enable the development of kinetic models that describe the observed reaction kinetics mathematically. Kinetic modelling adds a new dimension as it can be used to predict the evolution of species concentrations under conditions not assessed experimentally. Moreover, such models help to assess the validity of the mechanism postulated for a given reaction and provide a vital, quantitative link between experimental data and QM models. The role of kinetic modelling in reaction mechanism investigation has for instance been demonstrated through the use of reaction progress kinetic analysis (RPKA).18 In the study of the palladium-catalyzed Heck coupling reaction of aryl halides,18 where RPKA was applied, the combination of just three time-series experiments with different initial substrate concentrations and two graphical reaction-rate equations revealed that neither catalyst deactivation nor product inhibition influence the reaction. Such an effective analysis of the reaction mechanism was possible thanks to the abundance of experimentally measured data available to construct the graphical reaction-rate equations. Despite the usefulness of kinetic models in understanding complex reactions and in supporting subsequent process development, the derivation of such models is too often overlooked in mechanistic studies.
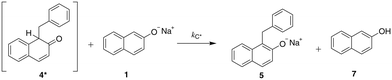
In this work, we explore the value of following a three-faceted approach that combines experiments, kinetic modelling and QM calculations by analysing the impact of reaction conditions on the mechanism of an ether synthesis reaction. We investigate how each method of analysis can inform and support the findings derived from the other two by focusing on a relatively simple and well-established ether synthesis, the Williamson reaction between sodium β-naphthoxide and benzyl bromide, shown in Scheme 1. We choose to focus on a Williamson ether synthesis due to the industrial and scientific relevance of this class of reactions. C–O bond formation is necessary for the manufacturing of important intermediates and products19 and Williamson reactions are used extensively industrially.20,21 Williamson reactions are also used routinely in pharmaceutical studies, for example in the synthesis of anti-influenza agents.22 As they involve a bimolecular nucleophilic substitution at a saturated carbon, they are representative of one of the most widely used reaction classes in synthetic organic chemistry. The particular example under study addresses the question of regioselectivity when an ambident nucleophile is used; this is a common scenario in synthetic chemistry where the effect of solvent on product ratio can be difficult to predict using standard heuristics.
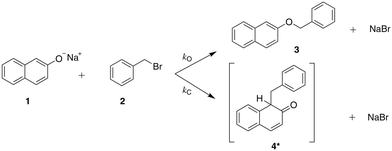 | ||
| Scheme 1 The reaction of sodium β-naphthoxide and benzyl bromide to form benzyl β-naphthyl ether (O-alkylated product) and the keto tautomer of the product 1-benzyl-2-naphthol (C-alkylated product).23 | ||
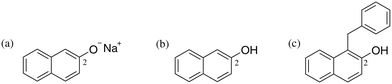
The solvent medium is known23 to impact the kinetics and the selectivity of the reaction in forming either benzyl β-naphthyl ether (O-alkylated product) or 1-benzyl-2-naphthol (C-alkylated product). The final C-alkylated product is initially formed as the keto isomer of the product which quickly tautomerizes to the more stable phenol form (Scheme 2), subsequently converting to the final C-alkylated product through a proton exchange equilibrium (Scheme 3). Product ratios in different solvents have been reported in several experimental studies.23–28 Moreover, under some circumstances,23 the formation of an additional side product, 1,1-dibenzyl-2-(1H)-naphthalenone, is observed; this is a double C-alkylated species resulting from further alkylation of the C-alkylated product with benzyl bromide, shown in Scheme 4. To the best of our knowledge, no previous computational studies on this specific Williamson reaction have been carried out and the only mechanistic postulate available is based on a pictorial description of the transition states.23
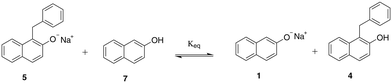 | ||
| Scheme 3 Equilibrium between protonated and deprotonated forms of sodium β-naphthoxide (7 and 1) and the C-alkylated product (4 and 5). | ||
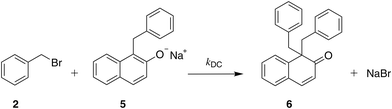 | ||
| Scheme 4 The reaction of benzyl bromide with the C-alkylated product (deprotonated) resulting in the formation of 1,1-dibenzyl-2-(1H)-naphthalenone (double C-alkylated product). | ||
We perform a detailed investigation of the mechanism of this reaction, presenting new in situ NMR data acquired over a range of temperatures and concentrations in a polar aprotic solvent (acetonitrile) and a protic solvent (methanol), as well as a mechanistic and thermodynamic analysis based on these data. We first summarize the methods used in the investigation. We then present the derivation of kinetic models for the reaction in acetonitrile and methanol, based on extensive experimental data, highlighting differences in mechanism and energetics. The observed differences are elucidated via QM calculations of the key TS structures. The suitability of QM calculations to quantify energetic differences is also assessed.
2 Methods
2.1 Experimental methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio are prepared in DMSO. We anticipate different chemical shifts for the aromatic carbon in each one of the samples tested, depending on the protonation state of the atoms attached to it. Detection of this proton-exchange phenomenon using 1H NMR would be very difficult, as the exchange happens very fast and the resulting peaks for the –OH groups in β-naphthol and the C-alkylated product are indistinguishable.
1 molar ratio are prepared in DMSO. We anticipate different chemical shifts for the aromatic carbon in each one of the samples tested, depending on the protonation state of the atoms attached to it. Detection of this proton-exchange phenomenon using 1H NMR would be very difficult, as the exchange happens very fast and the resulting peaks for the –OH groups in β-naphthol and the C-alkylated product are indistinguishable.
2.2 Computational methods
To assess the quality of the models, the mean average percentage error (MAPE) in concentration is reported. It is given by:
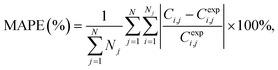 | (1) |
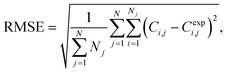 | (2) |
Additionally, we compare the calculated and experimental selectivities based on the percentage rate-constant ratio (PRCR). In the case where the only two products are the O-alkylated and C-alkylated products, PRCR is calculated as:
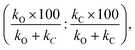 | (3) |
When the double C-alkylated product is present, PRCR is given by:
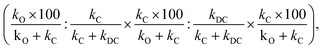 | (4) |
Furthermore, the computed PRCR is compared to an experimental PRCR obtained by using the measured (final) concentrations of the corresponding species, given by:
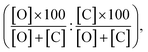 | (5) |
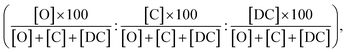 | (6) |
![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °,solv is calculated as:
°,solv is calculated as:Δ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °,solv = Δ °,solv = Δ![[E with combining low line]](https://www.rsc.org/images/entities/i_char_0045_0332.gif) el,L + el,L + ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) CDS,L = CDS,L = ![[E with combining low line]](https://www.rsc.org/images/entities/i_char_0045_0332.gif) el,L − el,L − ![[E with combining low line]](https://www.rsc.org/images/entities/i_char_0045_0332.gif) el,IG + el,IG + ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) CDS,L, CDS,L, | (7) |
![[E with combining low line]](https://www.rsc.org/images/entities/i_char_0045_0332.gif) el,L is an electrostatic term that accounts for the change in the electronic energy when transferring a solute from the gas to the liquid phase, and the term
el,L is an electrostatic term that accounts for the change in the electronic energy when transferring a solute from the gas to the liquid phase, and the term ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) CDS,L is a non-electrostatic term which accounts for free-energy changes due to short-range electrostatic effects and non-electrostatic effects, such as cavitation (C), dispersion (D) and solvent-related (S) structural changes. The SMD model is known to predict energies of solvation well, although larger deviations can occur when the level of theory or the solvent employed for the calculation were not included in the parametrization.36
CDS,L is a non-electrostatic term which accounts for free-energy changes due to short-range electrostatic effects and non-electrostatic effects, such as cavitation (C), dispersion (D) and solvent-related (S) structural changes. The SMD model is known to predict energies of solvation well, although larger deviations can occur when the level of theory or the solvent employed for the calculation were not included in the parametrization.36
| A + B ⇌ AB‡ → products, | (8) |
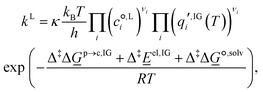 | (9) |
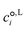 is the standard-state molar concentration for species i = A, B (reactants) and AB‡ (transition state) for eqn (8),
is the standard-state molar concentration for species i = A, B (reactants) and AB‡ (transition state) for eqn (8), 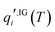 is the ideal-gas molecular partition function of species i at temperature T (excluding the electronic energy), vi is the stoichiometric coefficient of species i with a value of −1 for each of the reactants and +1 for the transition state, Δ
is the ideal-gas molecular partition function of species i at temperature T (excluding the electronic energy), vi is the stoichiometric coefficient of species i with a value of −1 for each of the reactants and +1 for the transition state, Δ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) p→c,IGi accounts for the conversion from the gas-phase standard state of T = 298.15 K and p° = 1 atm to T = 298.15 K and
p→c,IGi accounts for the conversion from the gas-phase standard state of T = 298.15 K and p° = 1 atm to T = 298.15 K and 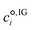 = 1 mol dm−3 as recommended by Ho et al.,41
= 1 mol dm−3 as recommended by Ho et al.,41![[E with combining low line]](https://www.rsc.org/images/entities/i_char_0045_0332.gif) el,IG is the ideal-gas electronic energy, and Δ‡ stands for the difference between the transition state and the reactants, for example
el,IG is the ideal-gas electronic energy, and Δ‡ stands for the difference between the transition state and the reactants, for example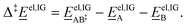 | (10) |
For competing reactions with two possible pathways, the selectivity ratio of one pathway (I) versus the other (II) may be determined by the ratio of the corresponding reaction rate constants, as
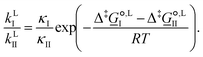 | (11) |
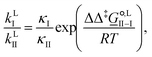 | (12) |
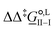 corresponds to the standard-state Gibbs free-energy difference between the transition-state structures of the two alternative pathways, given as
corresponds to the standard-state Gibbs free-energy difference between the transition-state structures of the two alternative pathways, given as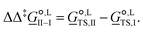 | (13) |
3 Results and discussion
3.1 Reaction networks considered
We investigate three reaction networks constructed by considering different side reactions. All the reaction networks include the two reactions between sodium β-naphthoxide and benzyl bromide towards the formation of the O- and C-alkylated products (Scheme 1), the tautomerisation reaction towards the more stable form of the C-alkylated product (Scheme 2), and the equilibrium between protonated and deprotonated forms of sodium β-naphthoxide and the C-alkylated product (Scheme 3). In addition, some networks explore the importance of two further reactions: a reaction between benzyl bromide and the C-alkylated product (Scheme 4) and a reaction between benzyl bromide and methanol-d4 (Scheme 5). The specific combinations of reactions and equilibrium we consider are presented in Table 1, with each combination corresponding to a different model. The differential equations that constitute each model are given in the ESI.† Additionally to the models presented in the main body of this study, a so-called minimal model is also developed based on the simplified Scheme shown in the ESI,† assuming that the two main O- and C-alkylated products are derived directly from the starting components while the keto isomer of the C-alkylated product is omitted. The minimal model is mentioned in the rest of the study mainly for comparison purposes. | ||
| Scheme 5 The reaction of benzyl bromide and methanol-d4 resulting in the formation of benzyl methyl ether. | ||
| Model name | Reactions modelled | # Reactions |
|---|---|---|
| Model 1 + 2 + 3 | Schemes 1–3 | 4 |
| Model 1 + 2 + 3 + 5 | Schemes 1–3 and 5 | 5 |
| Model 1 + 2 + 3 + 4 + 5 | Schemes 1–5 | 6 |
3.2 Occurrence of proton exchange
Our study commences with an experimental investigation of the occurrence of proton exchange between sodium β-naphthoxide and the C-alkylated product, a phenomenon which has not been explicitly considered in previous studies,23–27 and which we postulate on the basis of the pKa values30 of the reaction species (i.e., β-naphthol and the C-alkylated product), as well as the resulting species of Scheme 2. The chemical shifts obtained from 13C NMR are presented in Table 2. The displacement of the chemical shift of C2 (Fig. 1) in the mixture sample indicates that the magnetic shielding of the two carbon nuclei varies due to changes in the environment of the neighbouring oxygen atom in sodium β-naphthoxide and the C-alkylated product. The resulting chemical shift value for C2 in sodium β-naphthoxide in the mixture (163.6 ppm) is approximately the average of chemical shift values for C2 in the pure samples of naphthol and sodium β-naphthoxide. These findings validate the hypothesis that protonated and deprotonated forms of species 1 and 4 coexist in equilibrium, as per Scheme 3. We will evaluate the impact of this new finding on the time-evolution of species when performing kinetic analysis in different solvents.3.3 Kinetics and reaction network in acetonitrile-d3
We monitor the kinetics of the reaction in acetonitrile-d3via in situ1H NMR spectrometry; the data are reported in Zenodo (https://zenodo.org/record/3252790). To determine the reaction rate constants for Schemes 1–3 in acetonitrile-d3, we use molar concentration data to fit model 1 + 2 + 3 (see ESI†), as shown in Table 1. The estimated parameters at 298 K and their 95% confidence intervals (CI) are presented in Table 3. We specify in Table 4 the NMR peaks used for the fitting and the species associated with each peak in the model. The quality of the model is also summarized in the same table.| Model | Parameter | Value | 95% CI |
|---|---|---|---|
| k O | 1.881 × 10−2 | [1.663–2.099] × 10−2 | |
| Model 1 + 2 + 3 | k C | 6.556 × 10−4 | [3.689–9.423] × 10−4 |
| K eq | 1 | — |
| Model | NMR peak j | Species modelled | N j | RMSE | MAPE | PRCR |
|---|---|---|---|---|---|---|
| Model 1 + 2 + 3 | 6.79 | 1 + 7 | 8 | 0.0063 | 17.5 | |
| 4.54 | 2 | 20 | 0.0024 | 7.90 | ||
| 5.19 | 3 | 20 | 0.0014 | 2.64 | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
|
| 4.36 | 4 + 5 | 13 | 0.0003 | 13.8 | ||
| Overall | 1–5, 7 | 61 | 0.0028 | 8.63 | ||
| Expt. | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
|||||
At 298 K, the quality of fit for model 1 + 2 + 3 is reasonable, as shown in Fig. 2 and Table 4, and the corresponding PRCR value is in good agreement with the literature value26 of 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and our experimental value of 97
6 and our experimental value of 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. According to the RMSE and MAPE values, model 1 + 2 + 3 fits the experimental data for each monitored peak well, with slightly elevated values for the naphthol peak (see Table 4), possibly due to the small number of experimental data collected. When estimating the equilibrium constant for Scheme 1, the resulting value is very close to unity (ca. 0.97). Based on this finding and on the pKa and NMR shift values of β-naphthol and the C-alkylated product discussed above, we henceforth set the value of the equilibrium constant equal to 1. By doing so, we significantly decrease the uncertainty in the model parameters while fitting to the experimental data, thus obtaining estimated parameters with significantly narrower confidence intervals. Model 1 + 2 + 3 constitutes a complete representation of the kinetics in acetonitrile. In comparison, the minimal model performs adequately (overall MAPE value of 19%), with larger discrepancies observed for fitting the peaks of naphthol and the C-alkylated product. Based on the kinetic analysis alone, the minimal model may be judged to be sufficiently accurate to represent the kinetics of the reaction in acetonitrile. Additional information from QM calculations regarding the formation of the keto isomer as well as further experimentation to investigate side reactions based on literature and experimental evidence can provide a more accurate picture of the full reaction mechanism. Depending on the application of interest, the minimal model may be good enough for kinetic modelling despite the underlying assumptions.
3. According to the RMSE and MAPE values, model 1 + 2 + 3 fits the experimental data for each monitored peak well, with slightly elevated values for the naphthol peak (see Table 4), possibly due to the small number of experimental data collected. When estimating the equilibrium constant for Scheme 1, the resulting value is very close to unity (ca. 0.97). Based on this finding and on the pKa and NMR shift values of β-naphthol and the C-alkylated product discussed above, we henceforth set the value of the equilibrium constant equal to 1. By doing so, we significantly decrease the uncertainty in the model parameters while fitting to the experimental data, thus obtaining estimated parameters with significantly narrower confidence intervals. Model 1 + 2 + 3 constitutes a complete representation of the kinetics in acetonitrile. In comparison, the minimal model performs adequately (overall MAPE value of 19%), with larger discrepancies observed for fitting the peaks of naphthol and the C-alkylated product. Based on the kinetic analysis alone, the minimal model may be judged to be sufficiently accurate to represent the kinetics of the reaction in acetonitrile. Additional information from QM calculations regarding the formation of the keto isomer as well as further experimentation to investigate side reactions based on literature and experimental evidence can provide a more accurate picture of the full reaction mechanism. Depending on the application of interest, the minimal model may be good enough for kinetic modelling despite the underlying assumptions.
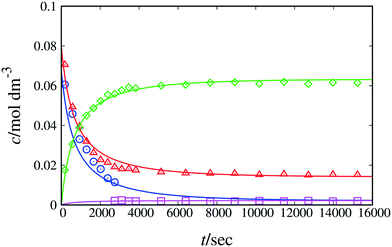 | ||
| Fig. 2 Experimental and calculated concentration as a function of time of reactants and products of Scheme 1 in acetonitrile-d3 at 298 K. The lines correspond to fitting with model 1 + 2 + 3. Symbols denote experimental data. Blue circles correspond to species 1 + 7, red triangles to species 2, green diamonds to species 3 and pink squares to species 4 + 5. | ||
3.4 Kinetics and reaction network in methanol-d4
With the knowledge obtained from studying the reaction network in acetonitrile, we proceed to study the reaction in methanol-d4. We monitor the reaction kinetics in methanol-d4via in situ1H NMR spectrometry; the data are reported in Zenodo (https://zenodo.org/record/3252790). The reaction proceeds much more slowly than in acetonitrile, so that it is challenging to estimate the kinetic parameters with precision; on the other hand, this makes data acquisition easier.In protic solvents like methanol, the selectivity of the reaction towards the O-alkylated product is reduced.23 As a result of the greater concentration of C-alkylated product, the proton exchange reaction can be expected to have a larger impact on the relative reaction rates and product distribution. The effect on reaction progress can only be quantified by the kinetic modelling. As we will show, the reaction network is more complex in methanol than in acetonitrile and kinetic modelling provides insights into the interplay between different reactions.
We begin by fitting model 1 + 2 + 3 (Fig. 3(a) and Table 6), which takes into account that sodium β-naphthoxide remains partially sequestered, and thus non-reactive, in the form of β-naphthol (7). The model results in particularly good agreement between the calculated and measured concentrations of total naphthol (1 + 7) and an overall MAPE value of 4.14% is obtained. However, despite the good performance of the model for several peaks, there is a large discrepancy between the calculated and measured amounts of benzyl bromide consumed, suggesting that there is an additional source of consumption for this reactant.
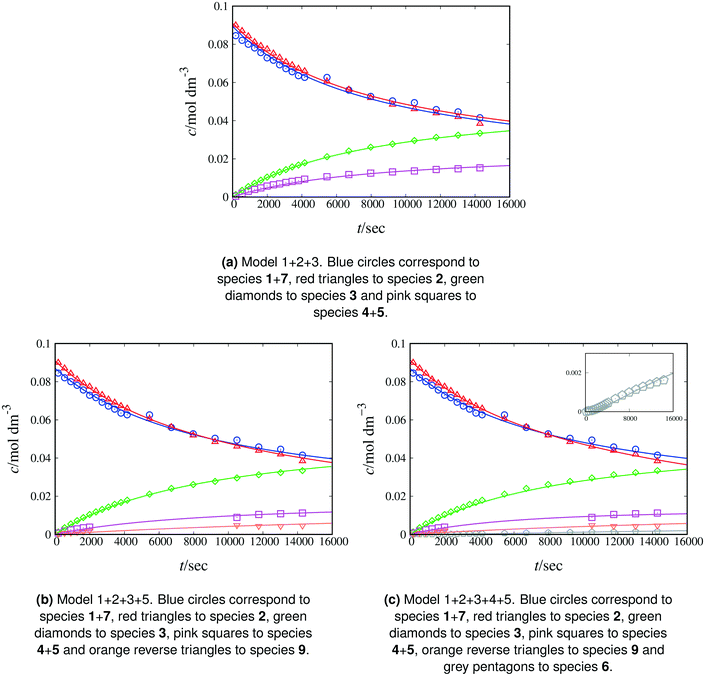 | ||
| Fig. 3 Experimental and calculated concentrations as a function of time for various species. Continuous curves correspond to calculations based on the corresponding model to capture the kinetics of Scheme 1 at 298 K in methanol-d4. Symbols denote experimental data. In panel (a), the total C-alkylated product peak sometimes includes areas of overlap with the double C-alkylated product and benzyl methyl ether peaks; these points are not taken into account in panels (b) and (c). | ||
This is confirmed by the 1H NMR spectra in methanol-d4 where we observe an unexplained peak adjacent to the peak of the C-alkylated product. The existence of a reaction between benzyl bromide and methanol yielding benzyl methyl ether has previously been reported.42 We confirm this finding by analysing a sample of benzyl bromide in methanol-d4, first through a 1H–13C HSQC experiment, where we identify the aliphatic CH2 peak of benzyl methyl ether (4.44 ppm in 1H NMR, 74.18 ppm in 13C NMR) in agreement with earlier work;43,44 and second, through a 1H–13C HMBC experiment, where we identify a cross-peak (4.44 ppm in 1H NMR, 56.09 ppm in 13C NMR) with consistent carbon chemical shift for the CD3 group of benzyl methyl ether, illustrating long-range correlations between the proton of the aliphatic CH2 group with the carbon from the CD3 group. As a result of these experiments, we include the side reaction between benzyl bromide and methanol in the postulated reaction network in methanol (see Scheme 5) and update our kinetic modelling accordingly (model 1 + 2 + 3 + 5, see ESI†). Experimental concentration data for benzyl methyl ether are derived from the NMR spectra when feasible; peak overlap often occurs due to the proximity of the aliphatic CH2 peaks monitored for benzyl methyl ether and the C-alkylated product. In some spectra the two peaks are entirely merged, thus we only integrate the spectra in which the two peaks are distinguishable. This results in a different number of fitting data for model 1 + 2 + 3 + 5 than the number of data used for model 1 + 2 + 3 and different concentrations for the C-alkylated product. The parameters of model 1 + 2 + 3 + 5 are regressed from experimental data in methanol-d4 as listed in Table 5, with concentration profiles shown in Fig. 3(b). Compared to model 1 + 2 + 3, model 1 + 2 + 3 + 5 provides a more complete description of the reaction network and the reduced RMSE and MAPE values for species 1 + 7 and 2 reported in Table 6 indicate that the rates of consumption for benzyl bromide and sodium β-naphthoxide are captured more accurately.
| Model | Parameter | Value | 95% CI |
|---|---|---|---|
| Model 1 + 2 + 3 | k O | 7.793 × 10−4 | [6.583–9.003] × 10−4 |
| k C | 3.702 × 10−4 | [2.501–4.903] × 10−4 | |
| K eq | 1 | — | |
| Model 1 + 2 + 3 + 5 | k O | 7.640 × 10−4 | [5.398–9.882] × 10−4 |
| k C | 2.515 × 10−4 | [0.941–4.089] × 10−4 | |
| K eq | 1 | — | |
| k BME·[8] | 6.531 × 10−6 | [0.248–12.81] × 10−6 | |
| Model 1 + 2 + 3 + 4 + 5 | k O | 7.371 × 10−4 | [5.520–9.222] × 10−4 |
| k C | 2.757 × 10−4 | [1.340–4.174] × 10−4 | |
| K eq | 1 | — | |
| k BME·[8] | 6.429 × 10−6 | [0.201–12.66] × 10−6 | |
| k DC | 3.506 × 10−4 | [0.000–9.752] × 10−4 | |
| Model | NMR peak j | Species modelled | # data | RMSE | MAPE | PRCR |
|---|---|---|---|---|---|---|
a This is the calculated PRCR given by eqn (4).
b This is the calculated PRCR given by eqn (6) where the calculated species concentrations are taken at the same time point (t = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281 s) as the concentrations used in calculating the experimental PRCR. 281 s) as the concentrations used in calculating the experimental PRCR.
|
||||||
| Model 1 + 2 + 3 | 6.86 | 1 + 7 | 20 | 0.0019 | 2.86 | |
| 4.51 | 2 | 20 | 0.0013 | 2.02 | ||
| 5.14 | 3 | 20 | 0.0003 | 2.48 | 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 32 32 |
|
| 4.40 | 4 + 5 | 20 | 0.0006 | 9.17 | ||
| Overall | 1–5, 7 | 80 | 0.0012 | 4.14 | ||
| Model 1 + 2 + 3 + 5 | 6.86 | 1 + 7 | 20 | 0.0012 | 1.55 | |
| 4.51 | 2 | 20 | 0.0006 | 0.84 | ||
| 5.14 | 3 | 20 | 0.0004 | 3.82 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 25 |
|
| 4.40 | 4 + 5 | 10 | 0.0006 | 19.3 | ||
| 4.41 | 9 | 10 | 0.0006 | 36.4 | ||
| Restricted average | 1–5, 7 | 70 | 0.0008 | 4.53 | ||
| Overall | 1–5, 7–9 | 80 | 0.0008 | 8.52 | ||
| Model 1 + 2 + 3 + 4 + 5 | 6.86 | 1 + 7 | 20 | 0.0011 | 1.44 | |
| 4.51 | 2 | 20 | 0.0004 | 0.53 | ||
| 5.14 | 3 | 20 | 0.0009 | 6.68 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 27 |
|
| 4.40 | 4 + 5 | 10 | 0.0005 | 17.3 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12a 12a |
|
| 4.41 | 9 | 10 | 0.0006 | 36.3 | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4b 4b |
|
| 6.61 | 6 | 20 | 0.0001 | 25.3 | ||
| Restricted average | 1–5, 7 | 70 | 0.0008 | 4.94 | ||
| Overall | 1–9 | 100 | 0.0007 | 12.1 | ||
| Expt. | 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 28 |
|||||
72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
||||||
While one might be satisfied with model 1 + 2 + 3 + 5 on the basis of the low errors obtained, analysis of the experimental evidence provides motivation to expand the reaction network further. In their study, Kornblum et al.23 mention the formation of a third by-product, 1,1-dibenzyl-2-(1H)-naphthalenone (9), a double C-alkylated product resulting from further alkylation of the C-alkylated product with benzyl bromide, as shown in Scheme 4. They report yields of the C-alkylated product and of the double C-alkylated product of 24% and of 4% respectively in ethanol, of 75% and of 10% respectively in 2,2,2-trifluoroethanol, and of 83% and 1% respectively in water. However, in aprotic solvents such as DMF and DMSO, no double C-alkylated product was observed.23 In the NMR spectra from our experiments in acetonitrile-d3, no peaks corresponding to the double C-alkylated product were observed; thus, the possibility of formation of the double C-alkylated product in acetonitrile-d3 was dismissed.
Given that in ethanol the amount of the double C-alkylated product obtained is appreciable,23 this product should also be formed in methanol. We thus conduct additional experiments, starting from the deprotonated form of the C-alkylated product reacting with benzyl bromide, to confirm the formation of the double C-alkylated product, as shown in Scheme 4. We also confirm that the protonated form of the C-alkylated product is incapable of further alkylation, as no sign of the double C-alkylated product is observed in 1H NMR spectra obtained after leaving the C-alkylated product with benzyl bromide in a vial for 24 hours (in the absence of any deprotonating agent, e.g., a base). This finding is consistent with the fact that naphthol, the protonated form of β-naphthoxide, is also incapable of reacting with benzyl bromide; the two species (naphthol and the C-alkylated product) have a very similar chemical structure, and thus similar reactivity. On the basis of these findings, we add Scheme 4 to the reaction network.
Model 1 + 2 + 3 + 4 + 5 incorporates Scheme 4 and comprises all the knowledge obtained from experimental and kinetic modelling observations. Concentration profiles for model 1 + 2 + 3 + 4 + 5 at 298 K are shown in Fig. 3(c), with the estimated parameter values listed in Table 5. As shown in Table 6, the PRCR value for model 1 + 2 + 3 + 4 + 5 of 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 is in very good agreement with our experimental value of 72
27 is in very good agreement with our experimental value of 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28, offering a significant improvement over the values found with model 1 + 2 + 3. A similarly good performance is achieved with model 1 + 2 + 3 + 5, with a PRCR of 75
28, offering a significant improvement over the values found with model 1 + 2 + 3. A similarly good performance is achieved with model 1 + 2 + 3 + 5, with a PRCR of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25, due to the slow rate of the reaction producing the double C-alkylated product. However, this model can be expected to deviate further from the experimental data as time progresses and the additional loss of C-alkylated product occurs. The same RMSE value is obtained for model 1 + 2 + 3 + 5 and model 1 + 2 + 3 + 4 + 5 (0.0008 mol dm−3) when the same data for the four main peaks are considered (“Restricted average” column in Table 6). RMSE values for each model when all data are considered (“Overall” column in the Table 6) confirm the superiority of model 1 + 2 + 3 + 4 + 5.
25, due to the slow rate of the reaction producing the double C-alkylated product. However, this model can be expected to deviate further from the experimental data as time progresses and the additional loss of C-alkylated product occurs. The same RMSE value is obtained for model 1 + 2 + 3 + 5 and model 1 + 2 + 3 + 4 + 5 (0.0008 mol dm−3) when the same data for the four main peaks are considered (“Restricted average” column in Table 6). RMSE values for each model when all data are considered (“Overall” column in the Table 6) confirm the superiority of model 1 + 2 + 3 + 4 + 5.
3.5 Comparison of kinetics in both solvents
Overall, based on the reaction-rate constants listed in Tables 3 and 5, O-alkylation proceeds faster than C-alkylation in both solvents, as indicated by the larger kO values and the resulting higher selectivities to the O-alkylated product. By comparing the values shown in Tables 3 and 5, we observe that the O-alkylation pathway proceeds much faster in the polar aprotic solvent than in the polar protic solvent. At 298 K, the estimated value of kO is nearly two orders of magnitude larger in acetonitrile than in methanol. In both solvents, the reaction-rate constants for C-alkylation, kC, are of a similar order of magnitude. The reaction constant for double C-alkylation, kDC, is found to be very similar to that of C-alkylation in methanol. The formation of benzyl methyl ether proceeds at a much slower rate than other reactions, so this only has a small impact on the observed selectivity.The measured PRCR of 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 observed in acetonitrile demonstrates a clear preference towards the O-alkylated product, in agreement with previous studies in polar aprotic solvents;23,25,26,28 in particular, the value of 97
3 observed in acetonitrile demonstrates a clear preference towards the O-alkylated product, in agreement with previous studies in polar aprotic solvents;23,25,26,28 in particular, the value of 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 at 298 K obtained here is in excellent agreement with the value of 94
3 at 298 K obtained here is in excellent agreement with the value of 94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 reported by Akabori and Tuji.26 For methanol, the measured PRCR has a value of 72
6 reported by Akabori and Tuji.26 For methanol, the measured PRCR has a value of 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 when all C-alkylated products are considered together and 72
28 when all C-alkylated products are considered together and 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 when the C-alkylated and the double C-alkylated products are considered separately. This shift towards the C-alkylated product is in line with previous studies of Scheme 1 in polar protic solvents.23,26 Kornblum et al.23 attributed higher yields of the C-alkylated product to the hydrogen bonding capability of the solvent used, which in the case of strong hydrogen bonding solvents like water or 2,2,2-trifluoroethanol can cause a change in reaction selectivity by shielding the oxygen atom, with the C-alkylated pathway becoming more favourable. They reported a percentage yield value of the O-alkylated product versus the C-alkylated product of 63
4 when the C-alkylated and the double C-alkylated products are considered separately. This shift towards the C-alkylated product is in line with previous studies of Scheme 1 in polar protic solvents.23,26 Kornblum et al.23 attributed higher yields of the C-alkylated product to the hydrogen bonding capability of the solvent used, which in the case of strong hydrogen bonding solvents like water or 2,2,2-trifluoroethanol can cause a change in reaction selectivity by shielding the oxygen atom, with the C-alkylated pathway becoming more favourable. They reported a percentage yield value of the O-alkylated product versus the C-alkylated product of 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 in methanol. The difference with our value is probably due to an underestimation of the amount of C-alkylated and double C-alkylated products in the work of Kornblum et al.23 due to loss of material during the work-up procedure, an issue we avoid by following the reaction by NMR.
37 in methanol. The difference with our value is probably due to an underestimation of the amount of C-alkylated and double C-alkylated products in the work of Kornblum et al.23 due to loss of material during the work-up procedure, an issue we avoid by following the reaction by NMR.
3.6 Temperature dependence of the reaction rate constant
We conduct further analysis using the Arrhenius equation to estimate the pre-exponential factor (A) and the activation energy (Ea), and the Eyring equation to obtain the enthalpy of activation (Δ‡![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) °) and entropy of activation (Δ‡
°) and entropy of activation (Δ‡![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) °). We use the experimental concentration profile data obtained at three temperatures in acetonitrile (at 298, 313 and 323 K) and in methanol (at 298, 313 K and 328 K) in the parameter estimation. This corresponds to 136 data points in acetonitrile and 295 data points in methanol. Due to the narrow temperature range studied, the thermodynamic quantities are assumed to be temperature-independent. Model 1 + 2 + 3 is used for acetonitrile and model 1 + 2 + 3 + 4 + 5 for methanol. The estimated thermodynamic parameters obtained are listed in Tables 7 and 8 for acetonitrile and methanol, respectively. The quality of fit across all three temperatures and both solvents is found to be highly satisfactory: the Arrhenius model gives an RMSE of 0.0030 mol dm−3 in acetonitrile and 0.0027 mol dm−3 in methanol, while the Eyring model yields RMSE values of 0.0022 mol dm−3 in acetonitrile and 0.0027 mol dm−3 in methanol. A more detailed analysis for each peak can be found in the ESI† (Fig. S1–S12 and Tables S6–S10).
°). We use the experimental concentration profile data obtained at three temperatures in acetonitrile (at 298, 313 and 323 K) and in methanol (at 298, 313 K and 328 K) in the parameter estimation. This corresponds to 136 data points in acetonitrile and 295 data points in methanol. Due to the narrow temperature range studied, the thermodynamic quantities are assumed to be temperature-independent. Model 1 + 2 + 3 is used for acetonitrile and model 1 + 2 + 3 + 4 + 5 for methanol. The estimated thermodynamic parameters obtained are listed in Tables 7 and 8 for acetonitrile and methanol, respectively. The quality of fit across all three temperatures and both solvents is found to be highly satisfactory: the Arrhenius model gives an RMSE of 0.0030 mol dm−3 in acetonitrile and 0.0027 mol dm−3 in methanol, while the Eyring model yields RMSE values of 0.0022 mol dm−3 in acetonitrile and 0.0027 mol dm−3 in methanol. A more detailed analysis for each peak can be found in the ESI† (Fig. S1–S12 and Tables S6–S10).
![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) ° and Δ‡
° and Δ‡![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) °), with their 95% confidence intervals (CI), obtained based on model 1 + 2 + 3 for acetonitrile-d3 at temperature range 298–323 K. The value of Δ‡
°), with their 95% confidence intervals (CI), obtained based on model 1 + 2 + 3 for acetonitrile-d3 at temperature range 298–323 K. The value of Δ‡![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °(298) is obtained as Δ‡
°(298) is obtained as Δ‡![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) ° = Δ‡
° = Δ‡![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) ° − TΔ‡
° − TΔ‡![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) °. The free-energy difference between the C- and O-alkylation transition states at 298 K,
°. The free-energy difference between the C- and O-alkylation transition states at 298 K, 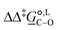 (298), is also reported
(298), is also reported
![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) ° and Δ‡
° and Δ‡![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) °), with their 95% confidence intervals (CI), obtained based on model 1 + 2 + 3 + 4 + 5 for methanol-d4 at temperature range 298–328 K. The value of Δ‡
°), with their 95% confidence intervals (CI), obtained based on model 1 + 2 + 3 + 4 + 5 for methanol-d4 at temperature range 298–328 K. The value of Δ‡![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °(298) is obtained as Δ‡
°(298) is obtained as Δ‡![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) ° = Δ‡
° = Δ‡![[H with combining low line]](https://www.rsc.org/images/entities/i_char_0048_0332.gif) ° − TΔ‡
° − TΔ‡![[S with combining low line]](https://www.rsc.org/images/entities/i_char_0053_0332.gif) °. The free-energy difference between the C- and O-alkylation transition states at 298 K,
°. The free-energy difference between the C- and O-alkylation transition states at 298 K, 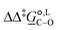 (298), is also reported
(298), is also reported
Of particular interest is the standard-state Gibbs free-energy difference between the C- and the O-alkylation transition-state structures in a given solvent, at a specific temperature (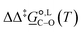 ), which can be computed as the difference in the standard-state free energies of activation of the C- and O-alkylation pathways (cf., eqn (13)). This quantity dictates the selectivity of the reaction at a specific temperature and is related to the reaction-rate constant ratio, which can be obtained from eqn (12) assuming the transmission coefficient to be unity. Based on the definition of
), which can be computed as the difference in the standard-state free energies of activation of the C- and O-alkylation pathways (cf., eqn (13)). This quantity dictates the selectivity of the reaction at a specific temperature and is related to the reaction-rate constant ratio, which can be obtained from eqn (12) assuming the transmission coefficient to be unity. Based on the definition of 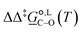 , a positive sign indicates a selectivity preference towards the O-alkylation pathway at a specific temperature, whereas a negative sign indicates a selectivity preference towards the C-alkylated product.
, a positive sign indicates a selectivity preference towards the O-alkylation pathway at a specific temperature, whereas a negative sign indicates a selectivity preference towards the C-alkylated product.
Thermodynamic analysis based on our experimental data results in 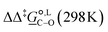 values of 7.0 kJ mol−1 in acetonitrile and of 2.8 kJ mol−1 in methanol, corresponding to PRCR values for O-alkylated product to C-alkylated product of 97
values of 7.0 kJ mol−1 in acetonitrile and of 2.8 kJ mol−1 in methanol, corresponding to PRCR values for O-alkylated product to C-alkylated product of 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 72
3 and 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28, respectively. This provides a quantification of the major impact of the solvent on the relative reaction barriers. To gain further understanding of the way in which the solvent affects the reaction, we turn to electronic-structure methods and assess the relative stabilisation of the reaction species.
28, respectively. This provides a quantification of the major impact of the solvent on the relative reaction barriers. To gain further understanding of the way in which the solvent affects the reaction, we turn to electronic-structure methods and assess the relative stabilisation of the reaction species.
3.7 Reaction analysis with quantum mechanical calculations
Density functional theory (DFT) methods have been previously employed for predicting reaction kinetics,2,45–47 with promising outcomes. In our study, we use computational chemistry methods to investigate the mechanism and kinetics of Scheme 1 for the first time, focusing particularly on the transition states and reaction energetics for Scheme 1.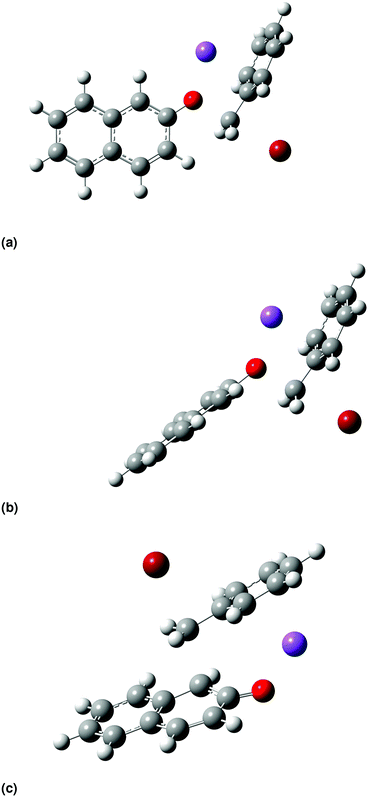 | ||
| Fig. 4 Transition-state structures optimized at the B3LYP/6-31+G(d) level of theory in vacuum for the O-alkylation pathway, (a) TSO1 and (b) TSO2, and for the C-alkylation pathway (c) TSC. | ||
For the O-alkylation pathway, two transition states are identified, TSO1 and TSO2, that differ in the orientation of the plane of the ring of the β-naphthoxide ion with respect to the plane of the ring of benzyl bromide. In TSO1 the planes of the two aromatic ring systems are perpendicular, with a dihedral angle of 88°, while in TSO2 the two planes are parallel, with a dihedral angle of 178°. TSO1 resembles closely the structure postulated by Kornblum et al.;23 however, TSO2 has a lower electronic energy by 5 kJ mol−1 (all levels of theory result in very similar geometries; the structures shown in Fig. 4 were optimized at B3LYP/6-31+G(d) followed by a single point energy calculation at MP2/cc-pVDZ). Thus, this pathway makes a much greater contribution to the reaction rate. We find that TSO2 is always of lower energy than TSO1 when the structures are optimized in acetonitrile and methanol. As a result, we assume hereafter that the O-alkylation pathway proceeds only via TSO2. In the C-alkylation transition-state structure, in line with what was suggested by Kornblum et al.,23 the carbon atom (C3) from which the bromine atom departs is above (or below) the plane of the β-naphthoxide ion, which attacks the carbon with the departing bromine atom rearward, as is consistent with an SN2 mechanism. The C-alkylation pathway thus proceeds via a quasi six-atom transition state. The main difference between the structure we find here and the one suggested by Kornblum et al.23 is that the sodium cation stabilizes the benzene ring instead of being close to the bromide ion. The stabilization occurs through cation–π interaction (non-covalent), keeping the sodium cation away from the centre of the benzene ring at a distance of 2.54 Å in vacuum and of 2.55 Å in methanol, and at a slightly longer distance in acetonitrile (2.75 Å). According to Ma and Dougherty48 and Amicangelo and Armentrout,49 the free energy of binding between benzene and sodium cation is 27 kcal mol−1 in the gas phase and decreases as we move to larger cations, e.g., K+, NH4+, etc. This trend supports the idea of coulombic forces holding the key role in the specific interaction's strength. Our study provides structural details on the transition-state structures of the two pathways that would be impossible to discern from experimental studies alone. We also gain valuable insights into mechanistic details, for example the orientation of the naphthalene ring and the involvement of the cation in the transition-state structures of the two pathways, that complement our knowledge of the mechanism of Scheme 1.
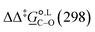 . The values computed using the different levels of theory are shown in Fig. 5. In acetonitrile, all methods predict the correct selectivity of the reaction, towards the O-alkylated product. The calculated values are in good agreement with the experimental value of 7.0 kJ mol−1. B3LYP systematically overestimates the experimental value by approximately 2.0 kJ mol−1 which is below chemical accuracy (4.18 kJ mol−1). In methanol, the predictions for
. The values computed using the different levels of theory are shown in Fig. 5. In acetonitrile, all methods predict the correct selectivity of the reaction, towards the O-alkylated product. The calculated values are in good agreement with the experimental value of 7.0 kJ mol−1. B3LYP systematically overestimates the experimental value by approximately 2.0 kJ mol−1 which is below chemical accuracy (4.18 kJ mol−1). In methanol, the predictions for 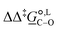 at 298 K are quite diverse including negative values, which indicate a preferred selectivity towards the C-alkylated product, contradicting the experimental evidence of the O-alkylated product being favoured in methanol. B3LYP is the only functional that consistently gives positive
at 298 K are quite diverse including negative values, which indicate a preferred selectivity towards the C-alkylated product, contradicting the experimental evidence of the O-alkylated product being favoured in methanol. B3LYP is the only functional that consistently gives positive 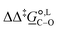 values. Among all levels of theory tested, M05-2X/6-31G(d) yields the best agreement with experiments in both solvents, predicting a
values. Among all levels of theory tested, M05-2X/6-31G(d) yields the best agreement with experiments in both solvents, predicting a 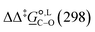 value of 6.67 kJ mol−1 in acetonitrile (expt. 7.0 kJ mol−1) and 1.93 kJ mol−1 in methanol (expt. 2.8 kJ mol−1). The free-energy of solvation difference between the C- and the O-alkylation transition-state structures is one of the two key factors for accurately predicting the value of
value of 6.67 kJ mol−1 in acetonitrile (expt. 7.0 kJ mol−1) and 1.93 kJ mol−1 in methanol (expt. 2.8 kJ mol−1). The free-energy of solvation difference between the C- and the O-alkylation transition-state structures is one of the two key factors for accurately predicting the value of 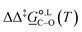 (the other being the gas-phase free-energy difference). The good performance of M05-2X/6-31G(d) in predicting
(the other being the gas-phase free-energy difference). The good performance of M05-2X/6-31G(d) in predicting 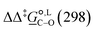 could perhaps be anticipated from its mean unsigned error (MUE) of 2.68 kJ mol−1 for non-aqueous solvation free energies (where methanol is excluded) on a test set of 2072 neutral solutes.36 Indeed, several authors have discussed the need for adhering to the computational protocol used in the parameterization of each continuum solvation model as a primary requirement in achieving quantitative results using this model.45,50,51 The accuracy of M05-2X/6-31G(d) was the highest among all the levels of theory used.
could perhaps be anticipated from its mean unsigned error (MUE) of 2.68 kJ mol−1 for non-aqueous solvation free energies (where methanol is excluded) on a test set of 2072 neutral solutes.36 Indeed, several authors have discussed the need for adhering to the computational protocol used in the parameterization of each continuum solvation model as a primary requirement in achieving quantitative results using this model.45,50,51 The accuracy of M05-2X/6-31G(d) was the highest among all the levels of theory used.
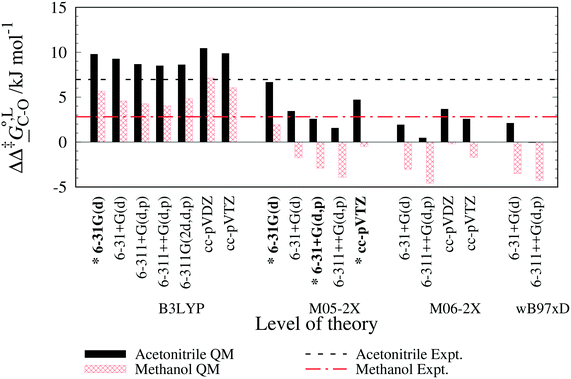 | ||
| Fig. 5 Gibbs free-energy difference between the C- and the O-alkylation transition-state structures of the reaction between sodium β-naphthoxide and benzyl bromide in acetonitrile and methanol at 298 K obtained for various levels of theory and the SMD solvation model implemented in Gaussian 09. For each QM method, the basis sets assessed are ordered from left to right in ascending order of size and complexity. The dashed lines indicate the experimental values at 298 K obtained in this work (cf.Tables 7 and 8). The 4 levels of theory in common between this study and the study of Marenich et al.36 are indicated with an asterisk. | ||
Specifically for acetonitrile, Marenich et al.36 reported that solvation free-energy calculations at the M05-2X/6-31G(d) level of theory result in a MUE of 2.64 kJ mol−1, based on a sample of 7 neutral solutes. The reported error value increased to 24.70 kJ mol−1 when a sample of 69 ionic solutes was considered. Despite the large size of the sample of ionic solutes, the error value is appreciable and gives an indication of the level of accuracy expected in the solvation free-energy calculations with the SMD model when charged species are involved. In acetonitrile, we find the MUE for 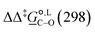 across all the methods we used to be 3.52 kJ mol−1, with the largest deviation at 7.03 kJ mol−1. When focusing only on the 4 methods that are common to our study and the parameterization of the SMD model by Marenich et al.,36 namely B3LYP/6-31G(d), M05-2X/6-31G(d), M05-2X/6-31+G(d,p) and M05-2X/cc-pVTZ, the MUE is 2.44 kJ mol−1 only, with the largest deviation at 4.38 kJ mol−1. For solvation free-energies in methanol, based on a test set of 80 ionic solutes, Marenich et al.36 reported that the MUE is lowest when using M05-2X/6-31G(d), with a value of 8.79 kJ mol−1. In calculating
across all the methods we used to be 3.52 kJ mol−1, with the largest deviation at 7.03 kJ mol−1. When focusing only on the 4 methods that are common to our study and the parameterization of the SMD model by Marenich et al.,36 namely B3LYP/6-31G(d), M05-2X/6-31G(d), M05-2X/6-31+G(d,p) and M05-2X/cc-pVTZ, the MUE is 2.44 kJ mol−1 only, with the largest deviation at 4.38 kJ mol−1. For solvation free-energies in methanol, based on a test set of 80 ionic solutes, Marenich et al.36 reported that the MUE is lowest when using M05-2X/6-31G(d), with a value of 8.79 kJ mol−1. In calculating 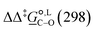 in methanol, our MUE value for all methods used here is 4.02 kJ mol−1, with the largest deviation at 7.11 kJ mol−1. For the 4 methods used in both our study and the SMD parameterization, the MUE value is 3.19 kJ mol−1, with the largest deviation equal to 5.73 kJ mol−1. The best agreement with experiments is once again achieved with M05-2X/6-31G(d), with MUE values of 0.30 kJ mol−1 in acetonitrile and 0.89 kJ mol−1 in methanol.
in methanol, our MUE value for all methods used here is 4.02 kJ mol−1, with the largest deviation at 7.11 kJ mol−1. For the 4 methods used in both our study and the SMD parameterization, the MUE value is 3.19 kJ mol−1, with the largest deviation equal to 5.73 kJ mol−1. The best agreement with experiments is once again achieved with M05-2X/6-31G(d), with MUE values of 0.30 kJ mol−1 in acetonitrile and 0.89 kJ mol−1 in methanol.
We further report QM calculations for the solvation free energy (Δ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °,solv) for the reactants and the two transition-state structures using the 4 levels of theory in common between this study and the study of Marenich et al.;36 they can be found in Table S22 and Fig. S16 in the ESI.† We focus our analysis on the M05-2X/6-31G(d) level of theory, given its good performance in calculating relative free energies. A comparison of the solvation free-energy values in the two solvents indicates that benzyl bromide and the transition-state structure for the O-alkylation pathway are destabilized in moving from acetonitrile to methanol, exhibiting a lower (more negative) free-energy of solvation in acetonitrile than in methanol, with absolute energy differences of 3.56 kJ mol−1 for benzyl bromide and 4.41 kJ mol−1 for the transition state. On the other hand, sodium β-naphthoxide and, to a smaller extent, the transition-state structure for the C-alkylation pathway are subject to a decrease in solvation free-energy from acetonitrile to methanol (i.e., stabilisation) with absolute energy differences of 4.97 kJ mol−1 and 0.33 kJ mol−1, respectively. Overall, the two reactants undergo a net stabilisation via a decrease of 1.41 kJ mol−1 in solvation free energy while the two transition states undergo a destabilisation via an increase of 4.08 kJ mol−1 in solvation free energy. The main driver for the change in selectivity from acetonitrile to methanol is due to the destabilisation of the transition-state for the O-alkylation pathway relative to the C-alkylation transition-state, which is barely affected.
°,solv) for the reactants and the two transition-state structures using the 4 levels of theory in common between this study and the study of Marenich et al.;36 they can be found in Table S22 and Fig. S16 in the ESI.† We focus our analysis on the M05-2X/6-31G(d) level of theory, given its good performance in calculating relative free energies. A comparison of the solvation free-energy values in the two solvents indicates that benzyl bromide and the transition-state structure for the O-alkylation pathway are destabilized in moving from acetonitrile to methanol, exhibiting a lower (more negative) free-energy of solvation in acetonitrile than in methanol, with absolute energy differences of 3.56 kJ mol−1 for benzyl bromide and 4.41 kJ mol−1 for the transition state. On the other hand, sodium β-naphthoxide and, to a smaller extent, the transition-state structure for the C-alkylation pathway are subject to a decrease in solvation free-energy from acetonitrile to methanol (i.e., stabilisation) with absolute energy differences of 4.97 kJ mol−1 and 0.33 kJ mol−1, respectively. Overall, the two reactants undergo a net stabilisation via a decrease of 1.41 kJ mol−1 in solvation free energy while the two transition states undergo a destabilisation via an increase of 4.08 kJ mol−1 in solvation free energy. The main driver for the change in selectivity from acetonitrile to methanol is due to the destabilisation of the transition-state for the O-alkylation pathway relative to the C-alkylation transition-state, which is barely affected.
![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) CDS term in capturing the short-range non-electrostatic interactions may be compensated by the increasingly accurate prediction of the bulk electrostatic interactions, which is again subject to the formalism and parameterization of the functional used.52 As a result, different levels of theory capture better either relative energy differences or absolute energies. For example, in our study, M05-2X/6-31G(d) has the best agreement with experiments when computing
CDS term in capturing the short-range non-electrostatic interactions may be compensated by the increasingly accurate prediction of the bulk electrostatic interactions, which is again subject to the formalism and parameterization of the functional used.52 As a result, different levels of theory capture better either relative energy differences or absolute energies. For example, in our study, M05-2X/6-31G(d) has the best agreement with experiments when computing 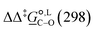 values (MAPE = 18%) but fails to capture absolute reaction rate-constant values by two orders of magnitude. There are, of course, levels of theory, such as B3LYP/6-31+G(d) and M05-2X/cc-pVTZ, that perform reasonably well for both relative and absolute reaction metrics. But generally, when computing absolute reaction rate constants for the O- and the C-alkylation pathway, we resort to functionals with more extensive basis sets, such as M05-2X/cc-pVTZ, which will provide us with more accurate estimations regarding bulk electrostatic interactions. In our study, the best agreement with experimental reaction rate constants (on average) for the two alkylation pathways is achieved in acetonitrile by M05-2X/cc-pVTZ (MAPE = 63%) and in methanol by B3LYP/6-31+G(d) (MAPE = 29%). As might be expected, augmenting the 6-31G(d) basis set with a diffuse function (+) to account for the presence of the bromide anion improves the functional's performance. As such, B3LYP/6-31+G(d) provides the best overall agreement with measured reaction rate constants for both solvents (MAPE = 47%), with a correct prediction for selectivity preference of the reaction (MAPE = 47%), also in both solvents.
values (MAPE = 18%) but fails to capture absolute reaction rate-constant values by two orders of magnitude. There are, of course, levels of theory, such as B3LYP/6-31+G(d) and M05-2X/cc-pVTZ, that perform reasonably well for both relative and absolute reaction metrics. But generally, when computing absolute reaction rate constants for the O- and the C-alkylation pathway, we resort to functionals with more extensive basis sets, such as M05-2X/cc-pVTZ, which will provide us with more accurate estimations regarding bulk electrostatic interactions. In our study, the best agreement with experimental reaction rate constants (on average) for the two alkylation pathways is achieved in acetonitrile by M05-2X/cc-pVTZ (MAPE = 63%) and in methanol by B3LYP/6-31+G(d) (MAPE = 29%). As might be expected, augmenting the 6-31G(d) basis set with a diffuse function (+) to account for the presence of the bromide anion improves the functional's performance. As such, B3LYP/6-31+G(d) provides the best overall agreement with measured reaction rate constants for both solvents (MAPE = 47%), with a correct prediction for selectivity preference of the reaction (MAPE = 47%), also in both solvents.
We use the most accurate QM-computed rate constants instead of the fitted rate constants to simulate the reaction in both solvents and to assess the impact of the errors in the QM-computed rate constants. For the side reactions, we use the experimentally-fitted reaction constants. When this is done using experimental reaction conditions, the 63% error in the kinetic constants in acetonitrile translates to a RMSE value of 0.0120 mol dm−3 and a MAPE value of 81.5%. In methanol, where there are more side reactions, the 29% error in the rate constant translates into an RMSE value of 0.0043 mol dm−1, a restricted average RMSE value of 0.0051 mol dm−3, a MAPE value of 29% and a restricted average MAPE of 17%. These findings indicate the large extent to which errors in rate constants propagate as errors in the concentrations. This, combined with the variability of the accuracy of each level of theory with solvent, highlights the need for further development of solvation models.
3.8 Complementarity of investigative methods
It is useful to reflect upon the roles played by experiments, kinetic modelling and DFT calculations in elucidating and quantifying the mechanism and kinetics of the Williamson reaction studied here. Clearly, experimental studies via quantitative 1H NMR, 1H–13C HSQC, 1H–13C HMBC, and 13C NMR all play a vital role in understanding which species are present and the evolution of the concentrations of several species as a function of time, in different solvents and at different temperatures. This is vital in guiding modelling efforts, be it kinetic or DFT modelling.The kinetic modelling plays several roles. On the one hand, it guides the interpretation of experimental data, forcing its re-evaluation when there is a mismatch between data and model predictions. For example, the deterioration in the quality of fit in benzyl bromide concentration observed from model 1 to model 1 + 3 (addition of the proton exchange reaction) in methanol helps to focus the analysis on a different reaction involving benzyl bromide, despite the small size of the peaks for benzyl methyl ether. On the other hand, the derivation of the reaction rate constant values provides a quantitative understanding of what matters for the reaction network. The proton exchange reaction is found to have similar equilibrium constants in both solvents, but only has a small impact on reaction progress in acetonitrile. The impact is much more significant in methanol, because of the smaller reaction rate of O-alkylation and the higher (detectable) reaction rate of double C-alkylated product formation. Finally, the kinetic models developed make it possible to predict reaction progress for different starting concentrations and at different temperatures than those used in the experimental studies. It is essential to capture in this way our understanding of the reaction networks so that this can be used in the design of further experiments or in reactor design calculations.
DFT calculations enable us to achieve a more detailed understanding of the reaction mechanism. Computations of structures appear reliable and help to test existing postulates on the geometries of the transition states, providing insights into the differences between the two pathways. Our experience here shows that those levels of theory that were used to parameterize the solvation model provide a good level of accuracy in terms of relative energy values, which are mostly found to be well within chemical accuracy (1 kcal mol−1 or 4.18 kJ mol−1), with the exception for M05-2X/6-31+G(d) in methanol. Such accuracy is sufficient to ascertain that the O-alkylation pathway is always more favoured over the C-alkylation pathway in acetonitrile than in methanol. This is not enough to achieve quantitative accuracy when we calculate the rate constants and relative rates; hence, the kinetic modelling and experimental data are useful in identifying the most reliable levels of theory for this reaction. The analysis nevertheless indicates that switching solvents from acetonitrile to methanol leads to the destabilisation of the transition state structure for the O-alkylation pathway and a consequent change in regioselectivity as the C-alkylation reaction becomes more competitive.
4 Conclusions
In this work, we have pursued a three-faceted approach that integrates experimental probing, kinetic modelling and quantum-mechanical calculations to provide insights into the mechanism of a Williamson ether synthesis reaction. Each methodology contributes towards the elucidation of mechanistic aspects as well as providing validation of the observations made with other approaches. Specifically for the regioselective Williamson reaction between sodium β-naphthoxide and benzyl bromide investigated here, the findings from a three-faceted analysis for solvents acetonitrile and methanol have brought to light subtle changes in product distributions and the balance between reaction pathways. Detailed experimental work in the two solvents has revealed an underlying equilibrium between two of the reaction species, one of the reactants and one of the products, taking place in both solvents, as well as two additional reactions occurring in the presence of methanol: the further reaction of the C-alkylation product to form an additional third product, and a side reaction occurring between methanol and one of the reactants.The complexity brought about by the change of solvent medium highlights the role of kinetic modelling as an integral component of the mechanistic analysis. Different kinetic models were developed to account for the species observed experimentally. The qualitative and quantitative description of the experimental concentration profiles of the reaction species as well as the statistical significance of the estimated parameters were carefully evaluated. Discrepancies between experimental data and kinetic model led to the reevaluation of experiments and incorporation of the newly obtained knowledge in the kinetic models. Model 1 + 2 + 3 for acetonitrile and model 1 + 2 + 3 + 4 + 5 for methanol were found to give the best description of reaction network and kinetics with RMSE values of 0.0028 mol dm−3 and 0.0008 mol dm−3 (for the main 4 reaction components), respectively. Estimated thermodynamic parameters were also obtained based on the corresponding model for each solvent. For the quantity 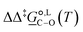 that dictates the reaction selectivity at 298 K, values of 7.0 kJ mol−1 in acetonitrile and of 2.8 kJ mol−1 in methanol were obtained, corresponding to selectivity ratio values for O-alkylated over C-alkylated product of 97
that dictates the reaction selectivity at 298 K, values of 7.0 kJ mol−1 in acetonitrile and of 2.8 kJ mol−1 in methanol were obtained, corresponding to selectivity ratio values for O-alkylated over C-alkylated product of 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 72
3 and 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28, respectively. Quantum-mechanical calculations provided mechanistic insights into the two reaction pathways such as the identification of transition-state structures for the O- and C-alkylation pathways, as well as an alternative transition-state structure for the O-alkylation pathway as opposed to the existing literature hypothesis. Further understanding of the way in which the solvent affects the reaction was obtained by assessing the relative stabilisation of the reaction species in the two solvents through calculation of the liquid free-energy and free-energy of solvation, using levels of theory consistent with the parametrization of the solvation model SMD. The solvent does not appear to alter the transition states for the two pathways, but rather acts via stabilization/destabilization of the reaction species: the O-alkylation transition-state structure and benzyl bromide are always more stable in acetonitrile than in methanol (maximum stabilization difference observed for
28, respectively. Quantum-mechanical calculations provided mechanistic insights into the two reaction pathways such as the identification of transition-state structures for the O- and C-alkylation pathways, as well as an alternative transition-state structure for the O-alkylation pathway as opposed to the existing literature hypothesis. Further understanding of the way in which the solvent affects the reaction was obtained by assessing the relative stabilisation of the reaction species in the two solvents through calculation of the liquid free-energy and free-energy of solvation, using levels of theory consistent with the parametrization of the solvation model SMD. The solvent does not appear to alter the transition states for the two pathways, but rather acts via stabilization/destabilization of the reaction species: the O-alkylation transition-state structure and benzyl bromide are always more stable in acetonitrile than in methanol (maximum stabilization difference observed for ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °,L of 6.3 kJ mol−1 at the M05-2X/6-31G(d) level of theory and 3.8 kJ mol−1 at the M05-2X/6-31G+(d,p) level of theory), whereas the C-alkylation transition-state structure and sodium β-naphthoxide are always more stable in methanol than in acetonitrile (maximum stabilization difference observed for
°,L of 6.3 kJ mol−1 at the M05-2X/6-31G(d) level of theory and 3.8 kJ mol−1 at the M05-2X/6-31G+(d,p) level of theory), whereas the C-alkylation transition-state structure and sodium β-naphthoxide are always more stable in methanol than in acetonitrile (maximum stabilization difference observed for ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °,L of 1.2 kJ mol−1 at the M05-2X/6-31+G(d,p) level of theory and for Δ
°,L of 1.2 kJ mol−1 at the M05-2X/6-31+G(d,p) level of theory and for Δ![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) °,solv of 5.5 kJ mol−1 at the same level of theory). Within the reported accuracy of the computational methods used, quantitative conclusions were also drawn that indicate that the O-alkylation pathway was always favoured in acetonitrile. No definite conclusions could be drawn in methanol due to smaller energy difference between the two pathways. The error trend was the same in both solvents, showing that the degree of overestimation or underestimation is consistent for each computational model. A range of values can be obtained for estimating
°,solv of 5.5 kJ mol−1 at the same level of theory). Within the reported accuracy of the computational methods used, quantitative conclusions were also drawn that indicate that the O-alkylation pathway was always favoured in acetonitrile. No definite conclusions could be drawn in methanol due to smaller energy difference between the two pathways. The error trend was the same in both solvents, showing that the degree of overestimation or underestimation is consistent for each computational model. A range of values can be obtained for estimating 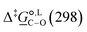 with a MUE of 3.52 kJ mol−1 in acetonitrile and 4.02 kJ mol−1 in methanol.
with a MUE of 3.52 kJ mol−1 in acetonitrile and 4.02 kJ mol−1 in methanol.
The findings in our work can be used to inform investigations of solvent effects on Williamson ether syntheses and other organic reactions. For the specific scheme considered here, it is possible to use the most accurate levels of theory identified to conduct a preliminary computational assessment of selectivity and rate in a range of other solvents, thereby guiding any experimental programme. For other substrates, similar trends can be expected for the effect of solvents on kinetics. The proposed transition state structures can be adapted for new substrates and used as a starting point to accelerate the search for a detailed mechanistic understanding. More broadly, our work provides a blueprint for the investigation of solvent effects in organic reactions, highlighting the value and complementarity of different analysis tools in such studies and demonstrating specific types of solvent effect on mechanism and kinetics (e.g., proton exchange, structural changes in transition state, reaction between reactant and solvent). Our systematic analysis of the accuracy of levels of theory shows that QM calculations can play an important role in the qualitative understanding of mechanistic impacts, but that the choice of an appropriate level of theory for quantitative analysis must be validated with experimental data.
Overall, this work highlights the value of a three-faceted approach to elucidate the impact of reaction conditions on the reaction outcome. Recognising that measurements, kinetic modelling and quantum mechanical calculations are associated with different types of uncertainty, the combination of these three methods of investigation offers a robust way to examine complex phenomena such as regioselectivity: in some cases, findings can be corroborated by two methods, providing added confidence to draw conclusions, while other aspects (e.g., the geometry of transition states) can only be probed with one of the methods. In practice, the three-faceted approach encourages the iterative improvement of the understanding of the system under study as initial hypotheses are challenged by using different types of analysis and must be revised. The principles of the three-faceted approach are generic, so that it can be applied to other reaction studies where quantitative analysis and prediction of quantitative chemical concepts are needed. The use of the proposed approach is particularly promising for the analysis of reactions that involve expensive or scarce components or that can result in toxic side products. The approach could be applied to a small number of solvents to identify a QM strategy (e.g., Struebing et al.45) to screen other solvents computationally, reducing the number of experiments required.
Data statement
Data underlying this article may be accessed on Zenodo at 10.5281/zenodo.3252790 and used under the Creative Commons Attribution licence.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge funding from Syngenta, the Pharmacat II Consortium and from the Engineering and Physical Sciences Research Council (EPSRC) (EP/M507878/1), as well as access to computational resources and support from the High Performance Computing Cluster at Imperial College London.References
- G. J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y. D. Wu, Computational Organic chemistry: Bridging Theory and Experiment in Establishing the Mechanisms of Chemical Reactions, J. Am. Chem. Soc., 2015, 137, 1706–1725 CrossRef CAS.
- R. E. Plata and D. A. Singleton, A Case Study of the Mechanism of Alcohol-Mediated Morita Baylis-Hillman Reactions. The Importance of Experimental Observations, J. Am. Chem. Soc., 2015, 137, 3811–3826 CrossRef CAS.
- J. N. Harvey, Ab Initio Transition State Theory for Polar Reactions in Solution, Faraday Discuss., 2010, 145, 9–14 RSC.
- A. Winter, Computational Chemistry: Making a Bad Calculation, Nat. Chem., 2015, 7, 473–475 CrossRef CAS.
- S. J. Klippenstein, V. S. Pande and D. G. Truhlar, Chemical Kinetics and Mechanisms of Complex Systems: A Perspective on Recent Theoretical Advances, J. Am. Chem. Soc., 2014, 136, 528–546 CrossRef CAS.
- K. N. Houk and P. H. Y. Cheong, Computational Prediction of Small-Molecule Catalysts, Nature, 2008, 455, 309–313 CrossRef CAS.
- H. Schwarz and D. Schröder, Concepts of Metal-Mediated Methane Functionalization. An Intersection of Experiment and Theory, Pure Appl. Chem., 2000, 72, 2319–2332 CAS.
- D. V. Deubel and G. Frenking, [3+2] versus [2+2] Addition of Metal Oxides across C=C Bonds. Reconciliation of Experiment and Theory, Acc. Chem. Res., 2003, 36, 645–651 CrossRef CAS.
- J. Roithová and D. Schröder, Theory Meets Experiment: Gas-Phase Chemistry of Coinage Metals, Coord. Chem. Rev., 2009, 253, 666–677 CrossRef.
- W. Thiel, Computational Catalysis - Past, Present, and Future, Angew. Chem., Int. Ed., 2014, 53, 8605–8613 CrossRef CAS.
- Q. Liu, Y. Lan, J. Liu, G. Li, Y. D. Wu and A. Lei, Revealing a Second Transmetalation Step in the Negishi Coupling and its Competition with Reductive Elimination: Improvement in the Interpretation of the Mechanism of Biaryl Syntheses, J. Am. Chem. Soc., 2009, 131, 10201–10210 CrossRef CAS.
- D. A. Singleton and Z. Wang, Isotope Effects and the Nature of Enantioselectivity in the Shi Epoxidation. The Importance of Asynchronicity, J. Am. Chem. Soc., 2005, 127, 6679–6685 CrossRef CAS.
- W. J. Xie and Y. Q. Gao, A Simple Theory for the Hofmeister Series, J. Phys. Chem. Lett., 2013, 4, 4247–4252 CrossRef CAS.
- B. Schaffner, F. Schaffner, S. Verevkin and A. Borner, Organic Carbonates as Solvents in Synthesis and Catalysis, Chem. Rev., 2010, 110, 4554–4581 CrossRef CAS.
- D. J. Henry, C. J. Parkinson, P. M. Mayer and L. Radom, Bond Dissociation Energies and Radical Stabilization Energies Associated with Substituted Methyl Radicals, J. Phys. Chem. A, 2001, 105, 6750–6756 CrossRef CAS.
- X. Solans-Monfort, E. Clot, C. Copéret and O. Eisenstein, d0 Re-Based Olefin Metathesis Catalysts, Re(=CR)(=CHR)(X)(Y): The Key Role of X and Y Ligands for Efficient Active Sites, J. Am. Chem. Soc., 2005, 127, 14015–14025 CrossRef CAS.
- E. Clot, C. Megret, O. Eisenstein, R. N. Perutz and I. C. Gerhardt, Exceptional Sensitivity of Metal-Aryl Bond Energies to ortho-Fluorine Substituents: Influence of the Metal, the Coordination Sphere, and the Spectator Ligands on M-C/H-C Bond Energy Correlations, J. Am. Chem. Soc., 2009, 7817–7827 CrossRef CAS.
- D. G. Blackmond, Reaction Progress Kinetic Analysis: A Powerful Methodology for Mechanistic Studies of Complex Catalytic Reactions, Angew. Chem., Int. Ed., 2005, 44, 4302–4320 CrossRef CAS.
- X. Wu, B. P. Fors and S. L. Buchwald, A Single Phosphine Ligand Allows Palladium-Catalyzed Intermolecular C—O Bond Formation with Secondary and Primary Alcohols, Angew. Chem., Int. Ed., 2011, 50, 9943–9947 CrossRef CAS.
- E. Fuhrmann and J. Talbiersky, Synthesis of Alkyl Aryl Ethers by Catalytic Williamson Ether Synthesis with Weak Alkylation Agents, Org. Process Res. Dev., 2005, 9, 206–211 CrossRef CAS.
- R. J. Ouellette and J. D. Rawn, Organic Chemistry: Structure, Mechanism, Synthesis, Academic Press, 2nd edn, 2018 Search PubMed.
- Y. Matsuya, N. Suzuki, S. Y. Kobayashi, T. Miyahara, H. Ochiai and H. H. Nemoto, Synthesis and Anti-Influenza Virus Activity of Dihydrofuran-Fused Perhydrophenanthrenes with a Benzyloxy-Type Side-Chain, Bioorg. Med. Chem., 2010, 18, 1477–1481 CrossRef CAS.
- N. Kornblum, R. Seltzer and P. Haberfield, Solvation as a Factor in the Alkylation of Ambident Anions: The Importance of the Dielectric Factor, J. Am. Chem. Soc., 1963, 85, 1148–1154 CrossRef.
- V. A. Zagorevskii, The Effect of the Nature of the Metal in the Metal Derivatives of a Ketoenol System on the Direction of O- and C-Substitution, Zh. Obshch. Khim., 1957, 27, 3084–3092 Search PubMed.
- V. A. Zagorevskii, A Study of the Effect of the Reagent's Character on the Direction of O- and C-Substitution of Metal Derivatives of a Keto-Enol System, Zh. Obshch. Khim., 1958, 28, 480–488 Search PubMed.
- S. Akabori and H. Tuji, The Effect of Macrocyclic Polyethers on the Alkylation of Sodium 2-Naphtholate, Bull. Chem. Soc. Jpn., 1978, 51, 1197–1199 CrossRef CAS.
- M. Badri, J. J. Brunet and R. Perron, Ionic Liquids as Solvents for the Regioselective O-Alkylation of C/O Ambident Nucleophiles, Tetrahedron Lett., 1992, 33, 4435–4438 CrossRef CAS.
- Z. Ganase, An Experimental Study on the Effects of Solvents on the Rate and Selectivity of Organic Reactions, Ph.D. thesis, Imperial College London, 2015 Search PubMed.
- Bruker, CryoProbe Prodigy, https://www.bruker.com/products/mr/nmr/probes/cryoprobes, (accessed March 23, 2020).
- Scifinder, Chemical Abstracts Service: Columbus, 2-Naphthol; pKa; RN 135–19-3; https://scifinder.cas.org, (accessed June 13, 2016); calculated using Advanced Chemistry Development (ACD/Labs) Software V11.02 (© 1994–2016 ACD/Labs).
- Scifinder, Chemical Abstracts Service: Columbus, 1-Benzyl-2-Naphthalenol; pKa; RN 36441–31-3; https://scifinder.cas.org, (accessed June 13, 2016); calculated using Advanced Chemistry Development (ACD/Labs) Software V11.02 (© 1994–2016 ACD/Labs).
- Process Systems Enterprise, gPROMS, www.psenterprise.com/gproms, 1997–2018.
- J. W. Harris and H. Stocker, Handb. Math. Comput. Sci., Springer-Verlag, New York, 1998, ch. 21, p. 824 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyora, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, Jr., F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision C.01, 2009 Search PubMed.
- A. P. Scott and L. Radom, Harmonic Vibrational Frequencies: An Evaluation of Hartree-Fock, Møller-Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- H. Eyring, The Activated Complex in Chemical Reactions, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- M. G. Evans and M. Polanyi, Some Applications of the Transition State Method to the Calculation of Reaction Velocities, Especially in Solution, Trans. Faraday Soc., 1935, 31, 875–894 RSC.
- W. F. K. Wynne-Jones and H. Eyring, The Absolute Rate of Reactions in Condensed Phases, J. Chem. Phys., 1935, 3, 492–502 CrossRef CAS.
- E. Wigner, Calculation of the Rate of Elementary Association Reactions, J. Chem. Phys., 1937, 5, 720–725 CrossRef CAS.
- J. Ho, A. Klamt and M. L. Coote, Comment on the Correct Use of Continuum Solvent Models, J. Phys. Chem. A, 2010, 114, 13442–13444 CrossRef CAS.
- G. Joshi and S. Adimurthy, New Method for the Synthesis of Benzyl Alkyl Ethers Mediated by FeSO4, Synth. Commun., 2011, 41, 720–728 CrossRef CAS.
- C. Y. Tsai, R. Sung, B. R. Zhuang and K. Sung, TiCl4-activated Selective Nucleophilic Substitutions of Tert-Butyl Alcohol and Benzyl Alcohols with π-Donating Substituents, Tetrahedron, 2010, 66, 6869–6872 CrossRef CAS.
- Scifinder, Chemical Abstracts Service: Columbus, Benzyl Methyl Ether; Experimental NMR Spectra; RN:538-86-3, https://scifinder.cas.org, (accessed June 13, 2016).
- H. Struebing, Z. Ganase, P. G. Karamertzanis, E. Siougkrou, P. Haycock, P. M. Piccione, A. Armstrong, A. Galindo and C. S. Adjiman, Computer-Aided Molecular Design of Solvents for Accelerated Reaction Kinetics, Nat. Chem., 2013, 5, 952–957 CrossRef CAS.
- A. Galano and J. R. Alvarez-Idaboy, Kinetics of Radical-Molecule Reactions in Aqueous Solution: A Benchmark Study of the Performance of Density Functional Methods, J. Comput. Chem., 2014, 35, 2019–2026 CrossRef CAS.
- A. Diamanti, C. S. Adjiman, P. M. Piccione, A. M. Rea and A. Galindo, Development of Predictive Models of the Kinetics of a Hydrogen Abstraction Reaction Combining Quantum-Mechanical Calculations and Experimental Data, Ind. Eng. Chem. Res., 2017, 56, 815–831 CrossRef CAS.
- J. C. Ma and D. A. Dougherty, The Cation-π Interaction, Chem. Rev., 1997, 97, 1303–1324 CrossRef CAS.
- J. C. Amicangelo and P. B. Armentrout, Absolute Binding Energies of Alkali-Metal Cation Complexes with Benzene Determined by Threshold Collision-Induced Dissociation Experiments and ab Initio Theory, J. Phys. Chem. A, 2000, 104, 11420–11432 CrossRef CAS.
- A. Klamt, B. Mennucci, J. Tomasi, V. Barone, C. Curutchet, M. Orozco and F. J. Luque, On the Performance of Continuum Solvation Methods. A Comment on Universal Approaches to Solvation Modeling, Acc. Chem. Res., 2009, 42, 489–492 CrossRef CAS.
- R. F. Ribeiro, A. V. Marenich, C. J. Cramer and D. G. Truhlar, Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation, J. Phys. Chem. B, 2011, 115, 14556–14562 CrossRef CAS.
- R. Peverati and D. G. Truhlar, The Quest for a Universal Density Functional: The Accuracy of Density Functionals Across a Broad Spectrum of Databases in Chemistry and Physics, Philos. Trans. R. Soc., A, 2014, 372, 20120476 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Model performance and additional computational data. See DOI: 10.1039/d0re00437e |
| ‡ Current address: F. Hoffmann-La Roche AG, Grenzacherstrasse 124, 4070 Basel, Switzerland. |
| § Current address: Sai Life Sciences Limited, Alderley Park, Macclesfield, SK10 4TG, UK. |
| This journal is © The Royal Society of Chemistry 2021 |