Open Access Article
Open Access ArticleTemperature-dependent optical properties of CuFeO2 through the structural phase transition†
Hsiao-Wen Chena,
Chu-Yun Huangc,
Guo-Jiun Shubcd and
Hsiang-Lin Liu *a
*a
aDepartment of Physics, National Taiwan Normal University, Taipei 116059, Taiwan. E-mail: hliu@ntnu.edu.tw
bDepartment of Materials and Mineral Resources Engineering, National Taipei University of Technology, Taipei 106344, Taiwan
cInstitue of Mineral Resources Engineering, National Taipei University of Technology, Taipei 106344, Taiwan
dTaiwan Consortium of Emergent Crystalline Materials, Ministry of Science and Technology, Taipei 106214, Taiwan
First published on 17th December 2021
Abstract
Delafossite CuFeO2 has recently attracted considerable attention because of its complex phase transitions and practical applications. A thorough understanding of the optical properties of CuFeO2 is essential for its further exploration. In this paper, we investigated the temperature-dependent optical properties of CuFeO2 single crystals through Raman scattering spectroscopy and spectroscopic ellipsometry. The room temperature Raman scattering spectrum exhibited six phonon modes at approximately 352, 509, 692, 1000, 1052, and 1171 cm−1. Upon cooling across 11 K, which is the rhombohedral to monoclinic structural phase transition temperature, a softening of the Eg-symmetry 352 cm−1 mode and a hardening of the A1g-symmetry 692 cm−1 mode were observed. Moreover, analysis of the temperature-dependent real part of the dielectric function and direct band gap revealed anomalies at 11 K. These results demonstrate a profound connection between the structural phase transition, lattice dynamics, and electronic structure of CuFeO2 and provide key information for CuFeO2-based device design and fabrication.
1. Introduction
In the delafossite CuMO2 (M = IIIA, transition metal elements) series, CuFeO2 is a well-known p-type semiconductor.1,2 CuFeO2 has attracted attention as a p-type transparent conducting oxide that could be used for applications of anodes in lithium ion batteries.1–3 Recent technological developments in CuFeO2 and other ferrite materials have focused on the energy conversion and storage, photocatalytic degradation of pollutants in water and air, and solar fuels production via water splitting and CO2 reduction.3–9 In addition to device applications, the special magnetic structure and structural phase transition of CuFeO2 are an attractive issue in fundamental science. CuFeO2 has two Néel temperatures. The first Néel temperature (TN1) of CuFeO2 is near 16 K, where the magnetic structure is changed from paramagnetic to collinear-incommensurate antiferromagnetic without any structural phase transition. The second Néel temperature (TN2) is near 11 K, where the magnetic structure is changed to collinear-commensurate antiferromagnetic without any structural phase transition. Further, the lattice structure is changed from the rhombohedral to monoclinic phase below TN2.10,11Numerous studies have examined the structural, magnetic, vibrational and optical properties of CuFeO2. Fig. 1 illustrates the room temperature crystal structure and structural and magnetic phase transitions of CuFeO2. Ye et al.10 and Kimura et al.11 have presented the X-ray and neutron diffraction patterns of CuFeO2 powders and single crystals. At room temperature, CuFeO2 has a rhombohedral structure with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, with lattice parameters of a = b = 3.035 Å, c = 17.163 Å, α = β = 90°, and γ = 120°.10,11 In the low temperature phase, it has a monoclinic lattice structure with the C2/m space group, with lattice parameters of a = 11.574 Å, b = 3.040 Å, c = 5.982 Å, and β = 154°.10 The c-axis compression reduced the bond length of Cu–O from 1.83805 Å (17 K) to 1.7863 Å (4 K). The structural phase transition also induced the compression of FeO6 octahedral units. The bond length of Fe–O was split from 2.024 Å (17 K) to 2.0225 and 2.0255 Å (4 K).10 Temperature-dependent magnetic susceptibility revealed that the material became antiferromagnetic below TN1 = 16 K.12 Furthermore, in neutron diffraction results, CuFeO2 displayed an incommensurate antiferromagnetic structure at approximately TN1 = 16 K.10,11 A commensurate spiral antiferromagnetic structure was exhibited at temperatures below TN2 = 11 K, and the crystal structure changed to the monoclinic phase.10–12 The unique magnetoelectric effect of this material enables functional devices to be realized.13–15
m space group, with lattice parameters of a = b = 3.035 Å, c = 17.163 Å, α = β = 90°, and γ = 120°.10,11 In the low temperature phase, it has a monoclinic lattice structure with the C2/m space group, with lattice parameters of a = 11.574 Å, b = 3.040 Å, c = 5.982 Å, and β = 154°.10 The c-axis compression reduced the bond length of Cu–O from 1.83805 Å (17 K) to 1.7863 Å (4 K). The structural phase transition also induced the compression of FeO6 octahedral units. The bond length of Fe–O was split from 2.024 Å (17 K) to 2.0225 and 2.0255 Å (4 K).10 Temperature-dependent magnetic susceptibility revealed that the material became antiferromagnetic below TN1 = 16 K.12 Furthermore, in neutron diffraction results, CuFeO2 displayed an incommensurate antiferromagnetic structure at approximately TN1 = 16 K.10,11 A commensurate spiral antiferromagnetic structure was exhibited at temperatures below TN2 = 11 K, and the crystal structure changed to the monoclinic phase.10–12 The unique magnetoelectric effect of this material enables functional devices to be realized.13–15
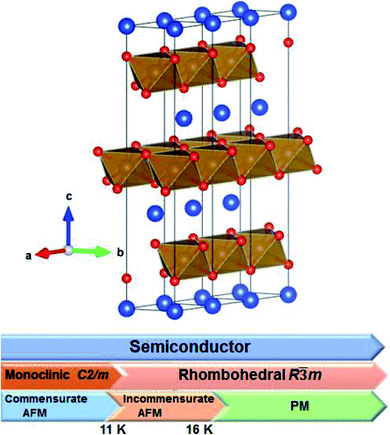 | ||
| Fig. 1 Room temperature crystal structure of CuFeO2 and a schematic depicting the electric, structural, and magnetic properties of CuFeO2 (AFM: antiferromagnetic, and PM: paramagnetic). | ||
Salke et al.16 and Pavunny et al.17 have studied the temperature-dependent Raman scattering spectra of CuFeO2 single crystals and polycrystalline pellets down to the liquid nitrogen temperature. They determined that the temperature-dependent peak positions of the in-plane Fe–O vibration Eg mode and the out-of-plane Cu–O vibration A1g mode could be predicted using theoretical anharmonic models. Salke et al.16 further investigated the pressure-dependent Raman scattering spectra of CuFeO2 single crystals up to 23 GPa. They reported that the Eg and A1g modes exhibited hardening with an increase in pressure. When the pressure was higher than 18 GPa, the Eg mode split and exhibited an obvious softening, indicating a structural phase transition. Aktas et al.18 presented the temperature-dependent Raman scattering spectra of CuFeO2 and CuCrO2 single crystals. They reported that both the Eg and A1g modes exhibited a softening within 1 cm−1 below 14 K, which was associated with a pseudo-proper ferroelastic transition occurring in multiferroic materials. Wheatley et al.19 prepared CuFeO2 thin films with thickness of 21 nm and 75 nm through pulse laser deposition. Using transmittance and diffuse reflectance spectra, they found a direct band gap of approximately 1.3 to 1.4 eV at room temperature. Roble et al.20 presented the room temperature diffuse reflectance spectroscopy of bulk 3R–CuFeO2. They found a direct band gap of approximately 1.3 eV. Eyert et al.21 reported the partial densities of states of the rhombohedral phase CuFeO2. They determined that rhombohedral CuFeO2 is a semiconductor with an optical band gap of 1.15 eV; the band gap value of the monoclinic CuFeO2 is 0.05 eV.
Most studies have focused on room temperature optical measurements and were limited to powder samples. The temperature-dependent optical properties of CuFeO2 single crystals have remained unexplored. In this study, we combined Raman scattering spectroscopy and spectroscopic ellipsometry to explore the temperature-dependent lattice dynamics and electronic structure of CuFeO2 single crystals. Furthermore, we investigated the correlation between the temperature-dependent optical response of CuFeO2 and its structural phase transition. Our results reveal the intricate relationship between charge-lattice interactions and structural phase transition in CuFeO2.
II. Experimental methods
The single-phase CuFeO2 powders were prepared by the solid-state reaction method. The starting materials used in the study were reagent-grade Cu2O (99.9%) and Fe2O3 (99.9%). The CuFeO2 was prepared directly from mixing Cu2O and Fe2O3 in stoichiometric ratio and then calcined under N2 atmosphere at 1123 K with following the formula of Cu2O + Fe2O3 = 2CuFeO2. The X-ray powder diffraction was performed to determine the phase purity of synthesized single-phase CuFeO2 powders. Furthermore, the synthesized single-phase CuFeO2 powders were pressed by isostatic compaction to form a cylindrical rod with 6–8 mm in diameter and 80 mm in length. We then sintered the rod at 900 °C in N2 atmosphere with keeping 24 hours to obtain condensed rod and increase its mechanical strength. To grow the CuFeO2 single crystal, we used the floating zone (FZ) method, which transfers this condensed rod into a furnace in FZ, and then crystal growth with the rate of 1 mm h−1 in a flow of CO/CO2 gas. As-grown CuFeO2 single crystal is opaque-black color with 5 mm in diameter and 70 mm in length. The obtained crystals in this study that formed on the (001) surface exhibited disk shapes that were 5 mm in diameter and 3 mm in thickness. The single crystals were characterized using X-ray powder diffraction and magnetization measurements.22,23 Besides the higher cost and longer growth process, the advantages of using CuFeO2 single crystal for research are high phase purity, excellent crystallinity, and easy to study the anisotropic behavior of the materials compared to CuFeO2 polycrystalline powder. Moreover, X-ray powder diffraction profile revealed that the as-grown and one year aging samples exhibited almost identical pattern, implying the good stability for CuFeO2.Micro-Raman scattering measurements were performed in a backscattering geometry using a 785 nm laser. The linearly polarized light was focused into a 3 μm-diameter spot on the sample surface. The Raman scattering signal was collected and dispersed using a SENTERRA spectrometer equipped with a 1024-pixel-wide charge-coupled detector. The spectral resolution achieved using these instruments were typically less than 0.5 cm−1. To avoid heating effects, the laser power was set to 0.1 mW. The polarized Raman scattering spectra were taken in scattering geometry of ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) (YY)Z and
(YY)Z and ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) (YX)Z. In this Porto notation, the first and the last letter represent the propagation directions of the incident and the scattered light, whereas the letters in parentheses indicate the electric field polarizations of the incident and scattered light, respectively. X, Y, Z, and
(YX)Z. In this Porto notation, the first and the last letter represent the propagation directions of the incident and the scattered light, whereas the letters in parentheses indicate the electric field polarizations of the incident and scattered light, respectively. X, Y, Z, and ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) were parallel to the [100], [010], [001], and [00
were parallel to the [100], [010], [001], and [00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] crystal directions, respectively. When the polarizations of the incident and the scattered light are carefully controlled, the selection rules for the Raman scattering from phonon modes allow accurate mode assignments.24 We placed the sample in a continuous-flow helium cryostat, which can control the temperature to be in the range of 5–300 K.25
] crystal directions, respectively. When the polarizations of the incident and the scattered light are carefully controlled, the selection rules for the Raman scattering from phonon modes allow accurate mode assignments.24 We placed the sample in a continuous-flow helium cryostat, which can control the temperature to be in the range of 5–300 K.25
Temperature-dependent spectroscopic ellipsometric spectra were obtained using a J. A. Woollam Co. M-2000U ellipsometer under a Janis ST-400 vacuum cryostat with a pressure under 10−8 torr. The data were collected in the spectra range between 0.73 and 6.42 eV with temperatures between 4.5 and 300 K25,26 The raw ellipsometry variables Ψ and Δ are related to the complex Fresnel reflection coefficients for light polarized parallel (Rp) and perpendicular (Rs) to the plane of incidence.
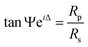 | (1) |
For isotropic bulk materials, the dielectric function can be transformed by the raw ellipsometry variables Ψ and Δ. However, the surface roughness would cause a small absorption below the absorption edge.27 The complex dielectric function was determined from fitting the ellipsometric variables by building a three medium optical model consisting of an air ambient structure/surface roughness/single crystal.25,26 The surface roughness can be described by a Bruggeman effective medium approximation by assuming 50% vacuum and 50% bulk.28 The surface roughness was approximately 1 nm in CuFeO2.
III. Results and discussion
A. Vibrational properties
The room temperature polarized Raman scattering spectra of CuFeO2 are presented in Fig. 2. Polarized Raman scattering studies allow one to obtain the symmetry properties and assignments of different Raman-active phonon modes. In the![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) (YY)Z configuration, we observed two main peaks at approximately 352 and 692 cm−1. In addition, a broad peak was observed at approximately 509 cm−1, which was attributed to the Cu vacancy induced phonon mode.16 We also observed low-intensity broad phonon modes near 1000, 1052, and 1171 cm−1, which should be ascribed to multiphonon bands.29–31 According to factor group analysis, CuFeO2 has a rhombohedral structure (space group R
(YY)Z configuration, we observed two main peaks at approximately 352 and 692 cm−1. In addition, a broad peak was observed at approximately 509 cm−1, which was attributed to the Cu vacancy induced phonon mode.16 We also observed low-intensity broad phonon modes near 1000, 1052, and 1171 cm−1, which should be ascribed to multiphonon bands.29–31 According to factor group analysis, CuFeO2 has a rhombohedral structure (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) containing one formula unit per primitive cell. The irreducible representation of the phonon modes at the center of the Brillouin zone is given by Γ = A1g + Eg + 3A2u + 3Eu.16 These modes were classified as Raman active (A1g + Eg), infrared active (2A2u + 2Eu), and acoustic (A2u + Eu). In the
m) containing one formula unit per primitive cell. The irreducible representation of the phonon modes at the center of the Brillouin zone is given by Γ = A1g + Eg + 3A2u + 3Eu.16 These modes were classified as Raman active (A1g + Eg), infrared active (2A2u + 2Eu), and acoustic (A2u + Eu). In the ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) (YX)Z configuration, the intensity of the 352 cm−1 mode became much stronger than that in the
(YX)Z configuration, the intensity of the 352 cm−1 mode became much stronger than that in the ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) (YY)Z configuration, indicating that it is of the Eg character.12–14 By contract, the 692 cm−1 and multiphonon modes almost vanished, indicating that they exhibit A1g symmetry.16–18 Our room temperature experimental results are consistent with those of previous studies.16–18
(YY)Z configuration, indicating that it is of the Eg character.12–14 By contract, the 692 cm−1 and multiphonon modes almost vanished, indicating that they exhibit A1g symmetry.16–18 Our room temperature experimental results are consistent with those of previous studies.16–18
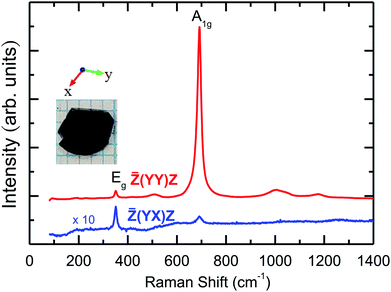 | ||
| Fig. 2 The room temperature polarized Raman scattering spectra of CuFeO2 and the optical image of CuFeO2. The notations used for the crystallographic directions are also given. | ||
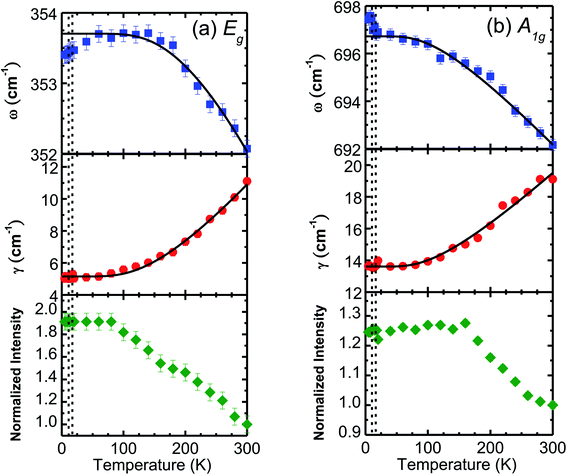
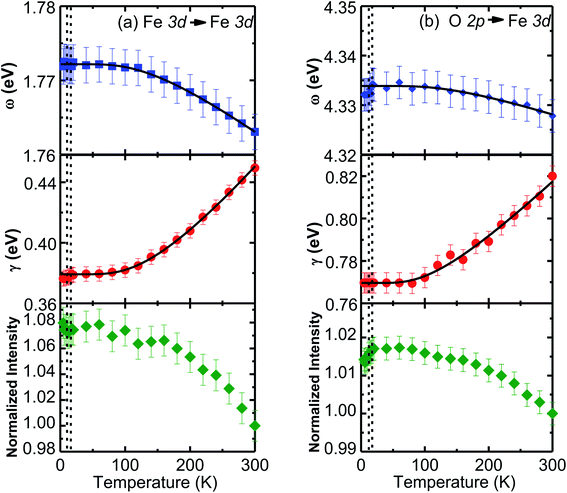
The temperature-dependent unpolarized Raman scattering spectra of CuFeO2 are depicted in Fig. 3. With a decrease in temperature, the peak positions of all phonon modes shifted to higher frequencies, their resonance linewidth narrowed, and their intensity increased. Six Lorentzian oscillators were used to fit the Raman scattering spectrum at 5 K (inset of Fig. 3). Fig. 4 illustrates the frequencies, linewidths, and normalized intensities of the Eg and A1g phonon modes as a function of temperature. The oscillation strength of the Eg and A1g phonon modes increased as temperature decreased, but remained constant when the temperature was lower than 100 K. In a normal anharmonic solid, when temperature decreases, the phonon frequency should increase and linewidth decrease. The temperature-dependent phonon frequency and linewidth can be written as32
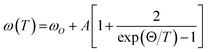 | (2) |
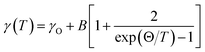 | (3) |
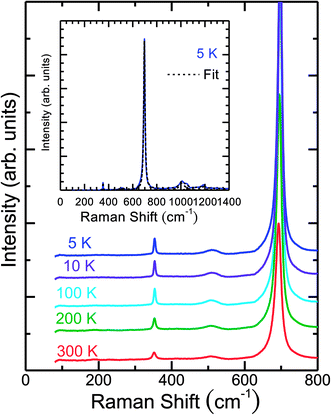 | ||
| Fig. 3 Temperature-dependent unpolarized Raman spectra of CuFeO2. The inset illustrates the fitting results of spectra obtained at 5 K using the Lorentzian model. | ||
When the temperature was below 11 K, which was denoted as structural phase transition in Fig. 1, the Eg mode exhibited a softening and the A1g mode exhibited a hardening. Our results differ from those of the previous studies, in which both the Eg and A1g modes exhibited a redshift below 14 K.18 Previous neutron diffraction studies indicated that the lattice constant a of the monoclinic phase was nearly three times larger than that of rhombohedral phase, whereas the lattice constant b remained almost the same. By contrast, the lattice constant c of the monoclinic phase was two times smaller than that of the rhombohedral phase.10 The Eg mode exhibited a softening with a 0.9 cm−1 deviation from the theoretical predictions of the anharmonic model. By contrast, the A1g mode exhibited a hardening with a 0.8 cm−1 deviation from the theoretical predictions of the anharmonic model. The effects of the structural phase transition in CuFeO2 caused in-plane vibration softening and out-of plane vibration hardening.
B. Electronic excitations
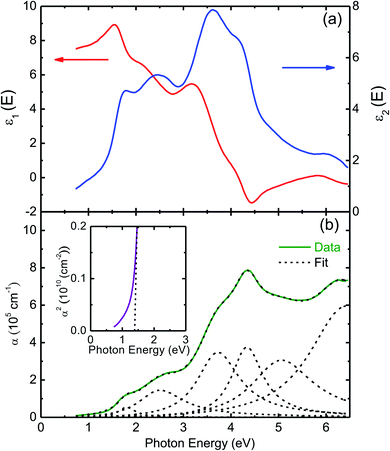
Fig. 5(a) presents the room temperature real ε1 and imaginary ε2 parts of the dielectric function ε(ω) of CuFeO2 through ellipsometric analysis. The room temperature experimental ellipsometric and best-fit calculated data of CuFeO2 are presented in Fig. S3.† The dispersion response of the frequency-dependent ε1 is typical of a semiconductor. Optical transitions are identified in the spectra according to resonance and antiresonance features that appeared at the same energy in ε1 and ε2, respectively. Specifically, the imaginary part spectrum ε2 of CuFeO2 was dominated by several optical transitions. Fig. 5(b) illustrates the room temperature optical absorption coefficient spectrum of CuFeO2. We calculated the optical absorption coefficient using the equation α =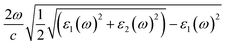 . The optical absorption spectrum was modeled reasonably well using the Lorentzian oscillator. Optical absorption started to gradually increase above 0.7 eV, reached a maximum value at approximately 4.3 eV, and then leveled off. The first absorption peak near 1.76 eV was assigned to the on-site iron ion 3d t2g to 3d eg transition. The second absorption peak near 2.51 eV was assigned to the copper 3d to iron 3d eg transition. The absorption peaks at approximately 3.70, 4.33, and 5.06 eV were associated with the charge-transfer transitions from the 2p orbital of oxygen to the 3d orbital of copper or iron.20 In a normal solid, the optical absorption coefficient α(E) includes contributions from both direct and indirect band gap transitions.34 The optical absorption coefficient is given by
. The optical absorption spectrum was modeled reasonably well using the Lorentzian oscillator. Optical absorption started to gradually increase above 0.7 eV, reached a maximum value at approximately 4.3 eV, and then leveled off. The first absorption peak near 1.76 eV was assigned to the on-site iron ion 3d t2g to 3d eg transition. The second absorption peak near 2.51 eV was assigned to the copper 3d to iron 3d eg transition. The absorption peaks at approximately 3.70, 4.33, and 5.06 eV were associated with the charge-transfer transitions from the 2p orbital of oxygen to the 3d orbital of copper or iron.20 In a normal solid, the optical absorption coefficient α(E) includes contributions from both direct and indirect band gap transitions.34 The optical absorption coefficient is given by
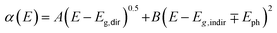 | (4) |
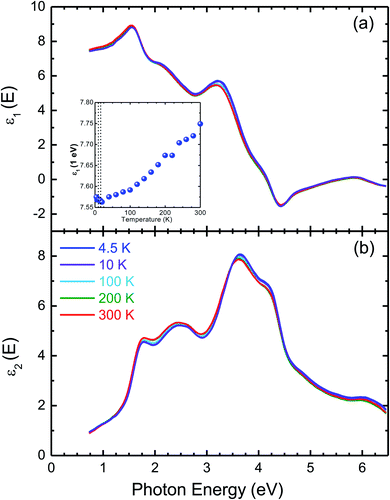
Fig. 6(a) and (b) depict the temperature-dependent complex dielectric function of CuFeO2. When temperature decreased, the real part ε1 decreased in the near-infrared region. Additionally, the real part dielectric function at 1 eV was discontinuous below 11 K. A discontinuous dielectric function due to a structural phase transition has been observed in transition metal oxides, such as BaTiO3.35 When temperature decreased, the intensity of the imaginary part ε2 slightly increased at photon energies higher than 3 eV. By contrast, the intensity slightly decreased at photon energies lower than 3 eV. The optical transition peaks at approximately 2.5 and 3.7 eV exhibited a blueshift with decreasing temperature.
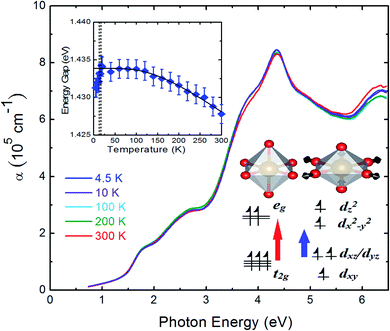
The temperature-dependent optical absorption coefficient spectra are presented in Fig. 7. The inset of Fig. 7 highlights the temperature-dependent band gap energy. The band gap became higher when temperature decreased. The band gap of typical inorganic semiconductors as a function of temperature can effectively be described in terms of the Bose–Einstein model36
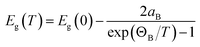 | (5) |
The inset of Fig. 7 illustrates an energy level diagram for the electronic states of Fe3+ ions. In the high temperature rhombohedral phase, non-distorted FeO6 octahedral units led to the splitting of Fe3+ d5 electronic orbitals to lower t2g energy levels and higher eg energy levels because of the crystal field effect of octahedral structure. The Fe 3d t2g, O 2p, and Cu 3d orbitals comprised the highest valence band states. The Fe 3d eg, and Cu 4s orbitals comprised the lowest conduction band states.21 For the high spin state (S = 5/2) of Fe3+ ions, all electrons occupied the Fe 3d orbital evenly. The red arrow in the inset of Fig. 7 indicates that the band gap is the electronic excitation from the Fe 3d t2g to Fe 3d eg levels. In the low temperature monoclinic phase, the compression of the c-axis lattice constant and the elongation of the ab-plane due to the structural phase transition resulted in the distortions of the FeO6 octahedral unit.10 From the rhombohedral to monoclinic phase, the bond length of Fe–O in the FeO6 octahedral unit was split into two values.10 The in-plane bond length of Fe–O increased. By contrast, the out-of-plane bond length of Fe–O decreased. This Jahn–Teller distortion of FeO6 octahedral unit occurred in other iron oxides as well.41 The compression of the FeO6 octahedral unit led to the t2g energy level splitting to a lower dxy energy level and a higher dxz/dyz energy level. The elongation of the ab-plane led to eg energy splitting to a lower dx2−y2 energy level and a higher dz2 energy level. The blue arrow in the inset of Fig. 7 indicates that the band gap is the electronic excitation from the Fe dxz/dyz to Fe dx2−y2 levels. Under the Jahn–Teller distortion, the band gap decreased, which was in good agreement with the observed band gap redshift below 11 K.
To gain further insight into the electronic structure of CuFeO2, we plotted the temperature-dependent peak position, linewidth, and normalized intensity of the optical transitions as 1.76 and 4.33 eV in Fig. 8. We also used the Bose–Einstein model to describe the temperature-dependent optical absorption peak energy and linewidth42
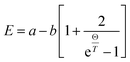 | (6) |
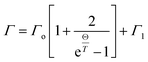 | (7) |
IV. Summary
We investigated the temperature-dependent optical properties of CuFeO2 single crystals using Raman scattering spectroscopy and spectroscopic ellipsometry. We focused on the correlation between the temperature-dependent optical response of CuFeO2 and its structural phase transition. The Eg Raman-active phonon mode exhibited a redshift whereas the A1g Raman-active phonon mode exhibited a blueshift across the structural phase transition at 11 K. The temperature-dependent real part of dielectric function and the direct band gap presented anomalies at 11 K. These results suggest that the onset of the structural phase transition alters the character of local atomic displacements and electronic states of FeO6 octahedral unit and therefore induces changes in lattice dynamics and electronic structure of CuFeO2. The results of this study provide valuable information for CuFeO2-based device design and fabrication.Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
H. L. L. and G. J. S. conceived the research and was responsible for the experimental design. H. W. C. conducted the experiments. C. Y. H. and G. J. S. were responsible for the sample preparation. H. W. C. and H. L. L. drafted the paper. All contributing authors have discussed the results and provided their comments regarding the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
H. L. L. thanks the Ministry of Science and Technology of the Republic of China for its financial support under Grants No. MOST 110-2112-M-003-017. G. J. S. thanks financial support from the Ministry of Science and Technology of Republic of China under Grants No. MOST 108-2112-M-027-002-MY3 and 110-2124-M-002-019. H. W. C. and H. L. L. specially thanks Y. T. L. and F. Y. L. for helping the photoluminescence measurements.References
- Y. Dong, C. Cao, Y. S. Chui and J. A. Zapien, Facile hydrothermal synthesis of CuFeO2 hexagonal platelets/rings and grapheme composites as anode materials for lithium ion batteries, Chem. Commun., 2014, 50, 10151 RSC.
- J. Patzsch, I. Balog, P. Krau, C. W. Lehmann and J. J. Schneider, Synthesis, characterization and p–n type gas sensing behavior of CuFeO2 delafossite type inorganic wires Fe and Cu complexes as single source molecular precursors, RSC Adv., 2014, 4, 15348 RSC.
- C. G. Read, Y. Park and K.-S. Choi, Electrochemical synthesis of p-type CuFeO2 electrodes for use in photoelectrochemical cell, J. Phys. Chem. Lett., 2012, 14, 1872 CrossRef PubMed.
- A. P. Amurte, G. O. Larrazabal, C. Mondelli and J. Perez-Ramirez, CuCrO2 delafossite: a stable copper catalyst for chlorine production, Angew. Chem., Int. Ed., 2014, 4, 15348 Search PubMed.
- C. L. Li, J. F. He, Y. Q. Xiao, Y. B. Li and J. J. Delaunary, Earth-abundant Cu-based metal oxide photocathodes for photoelectrochemical water splitting, Energy Environ. Sci., 2020, 13, 3269 RSC.
- M. H. Dhaou, S. Hcini, A. Mallah, M. L. Bouazizi and A. Jemni, Structural and complex impedance spectroscopic studies of Ni0.5Mg0.3Cu0.2Fe2O4 ferrite nanoparticle, Appl. Phys. A, 2017, 123(8), 1–9 CAS.
- P. Garcia-Munoz, F. Fresno, V. A. de la Pena O'Shea and N. Keller, Ferrite materials for photoassisted environmental and solar fuels applications, Top. Curr. Chem., 2020, 378(6), 1–43 Search PubMed.
- M. I. A. Abdel Maksoud, R. A. Fahim, A. E. Shalan, M. A. Elkodous, S. O. Olojede, A. I. Osman, C. Farrell, A. H. Al-Muhtaseb, A. S. Awed, A. H. Ashour and D. W. Rooney, Advanced materials and technologies for supercapacitors used in energy conversion and storage: a review, Environ. Chem. Lett., 2021, 19, 375 CrossRef CAS.
- R. Eivazzadeh-Keihan, S. Asgharnasl, M. S. Bani, F. Radinekiyan, A. Maleki, M. Mahdavi, P. Babaniamansour, H. Bahreinizad, A. E. Shalan and S. Lanceros-Mendez, Magnetic copper ferrite nanoparticles functionalized by aromatic polyamide chains for hyperthermia applications, Langmuir, 2021, 37, 8847 CrossRef CAS PubMed.
- F. Ye, Y. Ren, Q. Huang, J. A. Fernandez-Baca, P. C. Dai, J. W. Lynn and T. Kimura, Spontaneous spin-lattice coupling in the geometrically frustrated triangular lattice antiferromagnet CuFeO2, Phys. Rev.B: Solid State, 2006, 73(R), 220404 CrossRef.
- T. Kimura, J. C. Lashley and A. P. Ramirez, Inversion-symmetry breaking in the noncollinear magnetic phase of the triangular-lattice antiferromagnet CuFeO2, Phys. Rev.B: Solid State, 2006, 73(R), 220401 CrossRef.
- L. Zhang, B. A. Goodman, D. K. Xiong and W. Deng, Magnetic transitions in delafossite CuFeO2: a magnetocaloric effect study, Phys. Lett. A, 2019, 383, 125834 CrossRef CAS.
- H. Schmid, Multi-ferroic magnetoelectric, Ferroelectrics, 1994, 162, 317 CrossRef.
- N. A. Hill, Why are there so few magnetic ferroelectrics?, J. Phys. Chem. B, 2000, 104, 6694 CrossRef CAS.
- W. Eerenstein, N. D. Mathur and J. F. Scott, Multiferroic and magnetoelectric materials, Nature (London), 2006, 442, 759 CrossRef CAS PubMed.
- N. P. Salke, K. Kamali, T. R. Ravindran, G. Balakrishnan and R. Rao, Raman spectroscopic studies of CuFeO2 at high pressure, Vib. Spectrosc., 2015, 81, 112 CrossRef CAS.
- S. P. Pavunny, A. Kumar and R. S. Katiyar, Raman spectroscopy and field emission characterization of delafossite CuFeO2, J. Appl. Phys., 2010, 107, 013522 CrossRef.
- O. Aktas, K. D. Truong, T. Otani, G. Balakrishnan, M. J. Clouter, T. Kimura and G. Quirion, Raman scattering study of delafossite magnetoelectric multiferroic compounds: CuFeO2 and CuCrO2, J. Phys.: Condens. Matter, 2012, 24, 036003 CrossRef CAS PubMed.
- M. Roble, S. D. Rojas, R. Wheatley, S. Wallentowitz, A. L. Cabrera and D. E. Diaz-Droguett, Hydrothermal improvement for 3R-CuFeO2 delafossite growth by control of mineralizer and reaction atmosphere, J. Solid State Chem., 2019, 271, 314 CrossRef CAS.
- R. A. Wheatley, S. Rojas, C. Oppolzer, T. Joshi, P. Borisov, D. Lederman and A. L. Cabrera, Comparative study of the structural and optical properties of epitaxial CuFeO2 and CuFe1-xGaxO2 delafossite thin films grown by pulse laser deposition methods, Thin Solid Film, 2017, 626, 110 CrossRef CAS.
- V. Eyert, R. Frésard and A. Maignan, Long-range magnetic order and spin-lattice coupling in delafossite CuFeO2, Phys. Rev.B: Solid State, 2008, 78, 052402 CrossRef.
- N. Wolf, T. Schwaigert, D. Siche, D. G. Schlom and D. Klimm, Growth of CuFeO2 single crystals by the optical floating-zone technique, Appl. Phys. Lett., 2020, 535, 125426 Search PubMed.
- G. J. Shu, et al., Private communication.
- D. M. Ginsberg, Physical Properties of High Temperature Superconductors I World Scientific, Singapore, 1989, p. 409 Search PubMed.
- H. W. Chen, Y. W. Chen, J. L. Kuo, Y. C. Lai, F. C. Chou, C. H. Du and H. L. Liu, Spin-charge-lattice coupling in YBaCuFeO5: Optical properties and first-principles calculations, Sci. Rep., 2019, 9, 3223 CrossRef CAS PubMed.
- H. W. Chen, D. P. Gulo, Y. C. Chao and H. L. Liu, Characterizing temperature dependent optical properties of (MA0.13FA0.87)PbI3 single crystals using spectroscopic ellipsometry, Sci. Rep., 2019, 9, 3223 CrossRef CAS PubMed.
- C. M. Nelson, M. Spies, L. S. Abdallah, S. Zollner, Y. Xu and H. Luo, Dielectric function of LaAlO3 from 0.8 to 6 eV between 77 and 700 K, J. Vac. Sci. Technol., A, 2012, 30, 061404 CrossRef.
- D. A. G. Bruggeman, Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitatskonstanten und Leitfahigkeiten der Mischkorper aus isotropen Substanzen, Ann. Phys., 1935, 24, 636 CrossRef CAS.
- R. Kruger, B. Schulz, S. Naler, R. Rauer, D. Budelmann, J. Backstrom, K. H. Kim, S.-W. Cheong, V. Perebeinos and M. Rubhausen, Orbital ordering in LaMnO3 investigated by resonance Raman spectroscopy, Phys. Rev. Lett., 2004, 92, 0927203 CrossRef PubMed.
- L. Martin-Carron and A. de Andres, Excitations of the orbital order in RMnO3 manganites: light scattering experiments, Phys. Rev. Lett., 2004, 92, 175501 CrossRef CAS PubMed.
- J. Andreasson, J. Holmlund, R. Rauer, M. Kall, L. Borjesson, C. S. Knee, A. K. Eriksson, S.-G. Eriksson, M. Rubhausen and R. P. Chaudhury, Electron-phonon interactions in perovskites containing Fe and Cr studied by Raman scattering using oxygen-isotope and cation substitution, Phys. Rev.B: Solid State, 2008, 78, 235103 CrossRef.
- J. Menendez and M. Cardona, Temperature dependence of the first-order Raman scattering by phonons in Si, Ge, and α–Sn: Anharmonic effects, Phys. Rev.B: Solid State, 1984, 29, 2051 CrossRef CAS.
- T. Okuda, Y. Beppu, Y. Fujii, T. Onoe, N. Terada and S. Miyasaka, Specific heat of delafossite oxide CuCr1-xMgxO2, Phys. Rev.B: Solid State, 2008, 77, 134423 CrossRef.
- J. I. Pankove, Optical Processes in Semiconductors Dover, New York, 1971 Search PubMed.
- M. J. Pan and C. A. Randall, A brief introduction to ceramic capacitors, IEEE Electr. Insul. Mag., 2010, 26, 44 Search PubMed.
- K. P. O'Donnell and X. Chen, Temperature dependence of semiconductor band gaps, Appl. Phys. Lett., 1991, 58, 2924 CrossRef.
- W. W. Li, J. J. Zhu, J. D. Wu, J. Gan, Z. G. Hu, M. Zhu and J. H. Chu, Temperature dependence of electronic transitions and optical properties in multiferroic BiFeO3 nanocrystalline film determined from transmittance spectra, Appl. Phys. Lett., 2010, 97, 121102 CrossRef.
- H. L. Liu, M. K. Lin, Y. R. Cai, C. K. Tung and Y. H. Chu, Strain modulated optical properties in BiFeO3 thin films, Appl. Phys. Lett., 2013, 103, 181907 CrossRef.
- P. K. Gogi and D. Schmidt, Temperature-dependent dielectric function of bulk SrTiO3: Urbach tail, band edges, and excitonic effects, Phys. Rev.B: Solid State, 2016, 93, 075204 CrossRef.
- V. Želenzný, D. Chvostová, D. Šimek, F. Máca, J. Mašek, N. Setter and Y. H. Huang, The variation of PbTiO3 bandgap ferroelectric phase transition, J. Phys.: Condens. Matter, 2016, 28, 025501 CrossRef PubMed.
- H. Y. Huang, Z. Y. Chen, R.-P. Wang, F. M. F. de Groot, W. B. Wu, J. Okamoto, A. Singh, Z.-Y. Li, J.-S. Zhou, H.-T. Jeng, G. Y. Guo, Je-G. Park, L. H. Tjeng, C. T. Chen and D. J. Huang, Jahn-Teller distortion driven magnetic polarons in magnetite, Nat. Commun., 2017, 8, 15929 CrossRef CAS PubMed.
- L. Vina, S. Logothetidis and M. Cardona, Temperature dependence of the dielectric function of germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 1979 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra08096b |
| This journal is © The Royal Society of Chemistry 2021 |