Open Access Article
Open Access ArticleEffects of the Hubbard U correction on the electronic and magnetic properties of the tetragonal V2P2 sheet†
Yusuf Zuntu Abdullahi *a,
Sohail Ahmadb and
Abdullahi Abdu Ibrahimc
*a,
Sohail Ahmadb and
Abdullahi Abdu Ibrahimc
aDepartment of Physics, Faculty of Science, Kaduna State University, P.M.B. 2339, Kaduna State, Nigeria. E-mail: yusuf.zuntu@kasu.edu.ng
bDepartment of Physics, College of Science, King Khalid University, P O Box 9004, Abha, Saudi Arabia
cComputer Engineering Department, Altinbas University, Istanbul, Turkey
First published on 28th October 2021
Abstract
A recent theoretical work predicted the orthorhombic phase of the V2P2 sheet with the half-metallic electronic property using a linear combination of atomic orbitals (LCAO) basis set based on density functional theory (DFT). However, in the plane-wave DFT method, the tetragonal (t) V2P2 phase is the ground state structure. The total energy of the optimized tetragonal V2P2 is 0.91 eV per cell lower than that of the orthorhombic phase. Herein, we investigated the effects of Hubbard U correction onthe electronic, magnetic, and adsorption properties of the t-V2P2 sheet. The t-V2P2 sheet is found to be dynamically and mechanically stable. The t-V2P2 sheet prefers an antiferromagnetic ground state with an indirect narrowed bandgap of 0.23 eV. The estimated electron mobility in the t-V2P2 sheet at room temperature is approximately 24 times that of a hole. The t-V2P2 sheet exhibits a sizable magnetic anisotropy (MAE) of 69.63 μeV per V atom with in-plane magnetization. Mean-field approximation based on the 2D classical Heisenberg model predicts a high Néel temperature (TN) of the t-V2P2 sheet up to 1263 K. The Li atom adsorption on the t-V2P2 sheet shows a transition from semiconductor to metal. Also the Li–V2P2 system has a residual integer magnetic moment of 1 μB. Due to strong steric coulomb repulsion, the minimum diffusion energy barrier (Ea) for the Li-ion on the t-V2P2 surface is high enough to make the Li atom immobile. Our findings demonstrate the potential of the t-V2P2 sheet for antiferromagnetic spintronics and sensing applications.
1 Introduction
In recent years, basic and applied material investigations have been focused on the search for sustainable materials with revolutionary impacts on energy and related sectors. In this context, the target material should exhibit robust and controllable chemical and physical properties. Two-dimensional (2D) transition metal (TM) boride, popularly known as MBene1 may be considered as one of the ideal classes of material to meet these requirements. Typical MBene examples are TM2B2 (TM = Mn, Mo, Fe, Cr) sheets.2–5 Due to their appropriate electronic properties, they were found to be theoretically promising for spintronics, battery, and superconducting applications.2,3,5 The Cr2B2 sheet was successfully synthesized6,7 and first-principles calculations based on density functional theory (DFT) have confirmed the stability of the Cr2B2 sheet.5Motivated by the potential of MBene,2,8 it will be interesting to explore other new 2D materials with a similar MBene building block. As MBene has a dominant metal property, some questions arise: is it possible to create a new stable structure if the B atom of the MBene is replaced by another element? Would the metal property still be there? A recent report9 showed that MnX (X = As, P) sheets with half-metallic properties can be used for high Tc ferromagnetic spintronics devices. Similar to MBene, the titanium boron nitride (Ti2BN) sheet has been theoretically demonstrated for Li-ion battery (LIBs) with a capacity of about 889 mA h g−1, 24, and 165 meV diffusion barrier of Li on the Ti2BN surface and interlayer.10 Moreover, a series of TM2BC in bulk and monolayer forms have been shown to exhibit metallic properties with potential applications for superconducting, ceramic, and high Tc ferromagnetic spintronics.11–14 It should be noted that these reported MnX (X = As, P), Ti2BN and Ti2BC materials have similar MBene building blocks in 2D and bulk forms. Therefore, it will be interesting to extend the search to other new 2D materials (similar to MBene). New 2D materials are expected to show new physical properties such as their MBene counterparts.
Herein, we are interested in studying the tetragonal (t) V2P2 sheet as a potential candidate for spintronic applications using first-principles calculations based on density functional theory (DFT)15 plus Hubbard U16 (DFT+U). Spin research on 2D materials is currently one of the topics of high interest. The interest is the result of the recent experimental advancement in 2D magnetic nanostructures.17,18 However, the low Curie (TC) or Néel (TN) temperature is a fundamental limit for their practical applications in spin-related devices. To deal with this problem, alternative 2D nanostructures with isotropic symmetry are theoretically examined for high TC/TN. Recent theoretical reports have shown that the tetragonal MnX (X = S, Sb) and hexagonal Mn2C phases exhibit high Néel temperature with sizable magnetic anisotropy energy (MAE).19,20 In a similar tetragonal phase, a TC high above ambient temperature was observed with a considerable MAE for TM2BC (TM = Cr, Mn) sheets.14 These high TN and TC, potentials for 2D tetragonal structures mentioned above14,19,20 prompted us to investigate the t-V2P2 sheet through a correct choice of computational method and symmetry.
So far, the previous work on V2P2 sheet has been limited only to the orthorhombic (o) phase.21 In ref. 21 the o-V2P2 monolayer is ferromagnetic with semi-metallic electronic property using DFT21 calculations. However, previous reports have shown that most MBene and related structures prefer the tetragonal phase as the ground state.14,22 We are also aware that isotropic 2D materials which consist of TM atoms are among the most promising candidates for spintronics application.22–24
It is known that the spin-polarized DFT15 within the framework of generalized-gradient approximations (GGA) for the exchange-correlation (xc) functional fail to provide reasonable results for the transition metal (TM) systems. To correct self-interaction errors that can be seen in this kind of TM-contained system, Coulomb interactions should be included by using Hubbard + U parameters in the calculations. This DFT+U15,16 methods are commonly used to model this type of materials22–24 as it produces greater accuracy of results compared to standard DFT at a moderate computational cost. In practice, there are different types of DFT+U approaches, but the most reliable one is to use the predictive method using the ab initio method based on the linear response approach (LRA).16 The U parameter obtained using the LRA approach may not need to correspond to the experimental gap, but this approach improves the predictions of the band gap (beyond the standard DFT method) satisfactorily and is useful in cases where no previous data is available. The LRA approach has been used successfully for high-performance benchmarking of some well-known TM systems with greater accuracy that coincides with the available experimental data.25
In this study, we investigate the stability, electronic and magnetic properties of t-V2P2 sheet based on DFT+U calculations. The t-V2P2 sheet shows excellent vibrational and mechanical stabilities. We have also found that the AFM spin configuration corresponds to the ground state for the t-V2P2 sheet. The t-V2P2 exhibits a sizable magnetic anisotropy (MAE) of 69.63 μeV per V atom with an in-plane easy axis (EA). Mean-field approximation based on the 2D classical Heisenberg model predicts a high Néel temperature (TN) of the t-V2P2 sheet up to 1263 K. The Li atom adsorption on the t-V2P2 sheet shows a transition from semiconductor to metal. Also the Li–V2P2 system leaves residual integer magnetic moment of 1 μB. Due to strong steric coulomb repulsion, minimum diffusion energy barriers (Ea) for Li-ion on the t-V2P2 surface is high enough to make the Li atom immobile.
2 Method
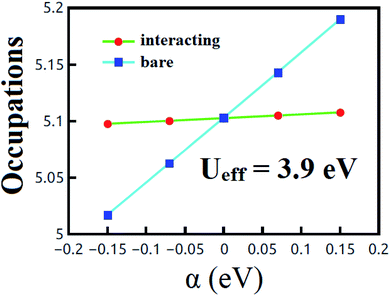
All calculations have been performed using DFT+U15,16 as implemented in the plane-wave QUANTUM ESPRESSO (QE) package.26 The generalized gradient approximation (GGA) of the Perdew–Burke–Enzerhof (PBE) functional has been used to account for the exchange-correlation potential.27 The U value for t-V2P2 sheet has been evaluated using the LRA proposed by Cococcioni et al.16 In the LRA estimations, the non-interacting (χ0) and interacting (χ) density response functions of the system for localized perturbations were first obtained (see Fig. 1). The Ueff value is then estimated from the equation: Ueff = (χ0−1 − χ−1). Based on this expression, the estimated Ueff value for t-V2P2 is Ueff = 3.9 eV. Projected augmented-wave (PAW) pseudopotentials have been used to treat the electron-ion core interaction.28 The van der Waals (vdW) correction has been included via the Grimme method of the DFT-D2 (ref. 29) using the PBE XC functional. The cut-off energies of 500 eV for the wave function and 5082 eV for the charge density have been used for all calculations. A 12 × 12 × 1 and 18 × 18 × 1 Mankhorst–Pack k-points have been used to sample the reciprocal space in the irreducible Brillouin zone (BZ) for self-consistency and total density of state computations respectively.30 A vacuum space of 20 Å was imposed in the unit cell perpendicular direction to eliminate repeated image interaction of the t-V2P2 sheet. All atom's positions were fully relaxed until the remaining force on each atom was smaller than 0.002 eV Å−1.3 Results and discussions
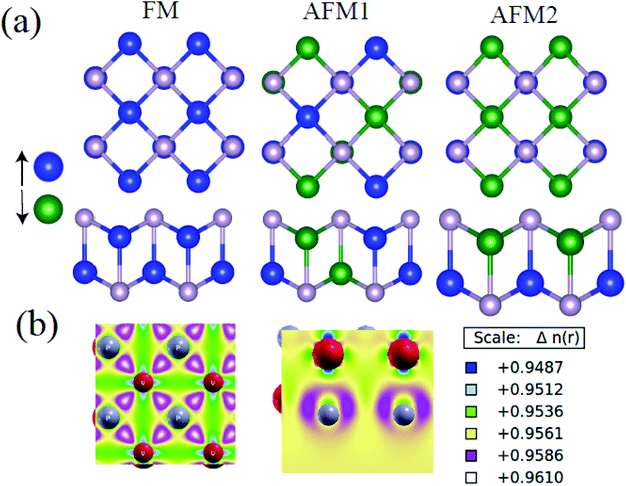
Firstly, we use PBE+D2+U to search for magnetically favorable configuration of the t-V2P2 sheet. An ferromagnetic (FM) and two antiferromagnetic states (AFM1 and AFM2) magnetic configurations in 2 × 2 supercell of t-V2P2 sheet has been considered (see Fig. 3). As listed in Table 1, the relative energy value illustrates AFM2 as the favorable magnetic ground state for t-V2P2 sheet. In AFM2, each V layer has parallel spins but opposite spins in the top and bottom V layers.| FM | AFM1 | AFM2 | |
|---|---|---|---|
| ER (eV) | 1.31 | 1.98 | 0.00 |
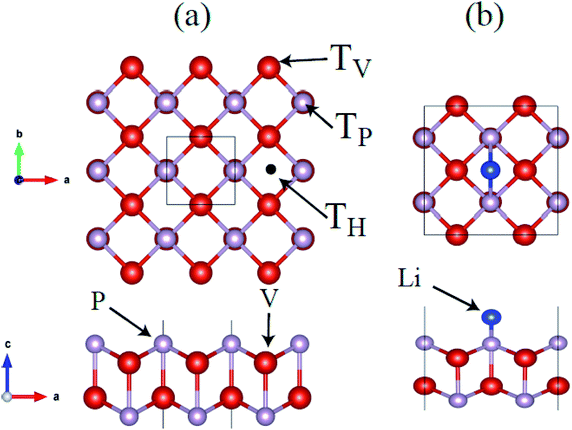
Therefore we use t-V2P2 unit cell with AFM2 configurations to compute the lattice parameters. An optimized t-V2P2 sheet is shown in Fig. 2(a). It can be viewed as a tetragonal structure with a space group of P4/mmm (no. 129). The black square line illustrates the top view of the t-V2P2 unit cell. The unit cell consists of two V and two P atoms. In the side view of Fig. 2(a), the P atom is located in the upper and lower regions of the sheet. Each atom in the sheet is chemically bonded by four neighboring atoms. The lattice constant (a = b = 3.16 Å, PBE) is found to be increased (a = b = 3.36 Å, PBE+U) when the Hubbard U correction was added. This indicates that the Hubbard U correction produces an expanded lattice constant which affects the ground state properties of t-V2P2 sheet. The optimized bond length in the x–y plane and the interlayer height (in the z-coordinate) is 2.48 Å and 2.68 Å respectively for the t-V2P2 sheet.
A recent theoretical study by Kadioglu21 predicted the orthorhombic (o) phase of the t-V2P2 sheet with half-metallic electronic property. It was shown to hold promise for optoelectronic device applications. However, since the t-V2P2 sheet has not been realized experimentally, it is theoretically important to check other stable phases of the t-V2P2 sheet. This is necessary to avoid being trapped in the local minima. We clarify here the differences between the current study and the work reported in ref. 21 The ref. 21 used a linear combination of atomic orbitals (LCAO) in their calculations whereas we used the plane-wave basis set. As regards the Wyckoff's positions of atoms, the position of V atoms is different from that reported. These newly oriented V atoms tend to energetically favor tetragonal symmetry in the t-V2P2 sheet. The atomic Wyckoff positions for considered V2P2 structure in ref. 21 are similar to those reported in ref. 9 and 31, while in this study they can be found in ref. 14 and 19. The atomic positions and lattice constant for the tetragonal and orthorhombic V2P2 sheets are listed in Tables S1 and S2,† respectively. In addition, we use PBE plus Hubbard U corrections (PBE+U) in the current study, while in ref. 21 only PBE was used. We believe that precise estimates of ground-state properties in a material involving strongly correlated electrons can only be obtained if the Hubbard U correction is taken into account. We have also considered van der Waals (vdW) interactions i.e. PBE+U+D2, whereas ref. 21 does not include the vdW interactions for the V2P2 monolayer case. In ref. 21 it was reported that the o-V2P2 monolayer becomes unstable if vdW is included. However, most of the previous reports22–24 of these kinds of 2D structures have considered vdW for the accurate estimates of ground-state properties.
To further substantiate our claims, the energy difference between orthorhombic and tetragonal V2P2 sheets have been evaluated and compared using the PBE method. We make sure that the same computational parameters are used to produce a negligible error in the results. The total energy of the optimized tetragonal V2P2 is 0.91 eV per cell more minimum than the orthorhombic phase (see Table S3†).
For comparison, the cohesive energy (Ecoh) per atom of the t-V2P2 sheet is first evaluated using the PBE method. The Ecoh is defined as follows;
| Ecoh = (nEV + 2EP − Et-V2P2)/4 | (1) |
To evaluate the possibility of experimental synthesis of the t-V2P2 sheet, we calculated the thermodynamic formation energy per atom which is expressed as
| Ef = (Et-V2P2 − 2μV − 2μP)/4 | (2) |
The strain-energy approach was used to estimate the in-plane stiffness (Y) and the Poisson's ratio (v) of the t-V2P2 sheet. The strain-energy (E) as a function of strain (β) can be expressed as a quadratic polynomial that is defined as
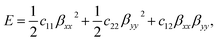 | (3) |
Uni-axial
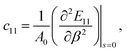 | (4) |
Bi-axial
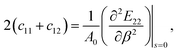 | (5) |
In-plane stiffness
| Y = c11(1 − v2), | (6) |
Poisson's ratio
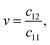 | (7) |
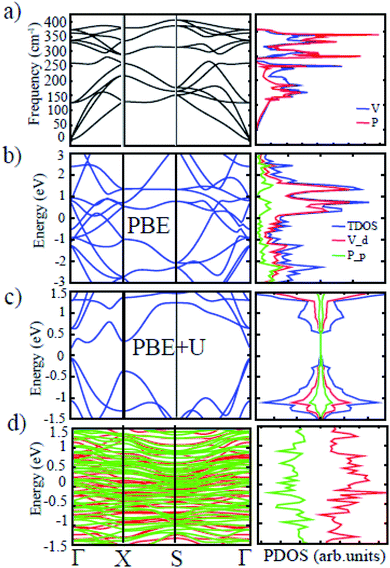
The phonon dispersion calculation has been carried out to ascertain the dynamic stability of t-V2P2 sheet. Fig. 4(a) displays the spectrum of phonons throughout the first Brillouin zone. The figure shows no imaginary frequencies for t-V2P2 sheet. The absence of imaginary frequencies confirms the dynamic stability of t-V2P2 sheet. On the right side of Fig. 4(a) is the atom projected phonon density of states (apPDOS). The apPDOS plot confirms that the lighter P atom vibrates with a frequency value greater than the heavier V atom. Overall, stability results demonstrate that the potential of the t-V2P2 sheet for real experimental synthesis.
The band structures and the corresponding atomic projected density of state (PDOS) of the t-V2P2 sheet is depicted in Fig. 3(b) and (c). The t-V2P2 sheet displays non-magnetic and metallic electronic properties using the PBE method (see Fig. 3(b)). An indirect bandgap of 0.233 eV with AFM as the preferred magnetic ground state (GS) is found when the Hubbard U (PBE+U method) correction is added. The Hubbard U correction produces a polarized spin in the 3d orbitals of the V atom after orbital reorientation. There is a magnetic moment of about 2.36 μB per V atom that is oriented in the antiparallel spins in the AFM GS. According to Hund's rules, an isolated V atom should have approximately 3 μB. However, due to bonding with neighboring P atoms in the t-V2P2 structure, the number of unpaired electrons of the 3d V orbit is reduced. This reduces the magnetic moment per V atom. Lowdin's charge analysis confirms that the magnetic moment of approximately 0.35 μB resides on each P atom in antiparallel spins. By plotting the charge density difference in Fig. 3(b), it is evident that the magnetic moment of t-V2P2 sheet is concentrated mainly in the V atoms. In AFM GS, the magnetic moment of V atoms couples in anti-parallel spins that have led to a zero magnetic moment. The metal to the semiconductor transition when U is added has been reported in a similar t-Mn2S2 structure.19 Therefore, we hope the t-V2P2 sheet to exhibit semiconducting property when synthesized experimentally, as the PBE+U method is important in defining the actual electronic property of a system involving strongly correlated electrons. From the PDOS plot of t-V2P2 sheet, the contributions of the p, and d-orbitals of the P and V atoms respectively dominate both the valence band maximum (VBM) and conduction band minimum (CBM). We further performed the HSE06 hybrid functional calculations and found not much difference with the results obtained from PBE+D2+U. The HSE06 band structure has been included in the ESI (Fig. S2†) showing a narrow band of about 0.20 eV which is comparable to PBE+D2+U. In addition, the magnetic moment of about 0.02 μB obtained from the HSE06 calculation further confirms the AFM ground state.
Based on the deformation potential (Ed) model,36 the carrier mobility of t-V2P2 sheet can be estimated using the expression defined as;
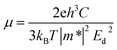 | (8) |
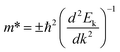 is evaluated from fitted data points on E–k curves via an automatic interpolation scheme. The data points were selected from the band portion closed to the CBM or VBM (see Fig. S2†). The slopes of each E–k curves give the coefficient for the parabolic terms which is then used to estimate the m* for holes and electrons at the VBM and CBM respectively. Our estimated results show that the holes are heavier than electrons for t-V2P2 sheet (see Table S4†). Consequently, the electron mobility in this t-V2P2 sheet at room temperature is approximately 24 times that of the hole.
is evaluated from fitted data points on E–k curves via an automatic interpolation scheme. The data points were selected from the band portion closed to the CBM or VBM (see Fig. S2†). The slopes of each E–k curves give the coefficient for the parabolic terms which is then used to estimate the m* for holes and electrons at the VBM and CBM respectively. Our estimated results show that the holes are heavier than electrons for t-V2P2 sheet (see Table S4†). Consequently, the electron mobility in this t-V2P2 sheet at room temperature is approximately 24 times that of the hole.
Magnetic anisotropy energy (MAE) calculations have been carried to determine the favorable magnetization directions on t-V2P2 sheet. It should be noted that the non-collinear spin-polarized with spin–orbit coupling (SOC) has been included in the MAE calculations. The relative energy values for the magnetization directions are summarized in Table 2, namely four in-plane ([100], [010], [110], [111]) and an out-of-plane [001] magnetization direction have been considered. A positive relative energy value shows a favorable magnetization easy axis of the system. As listed in Table 2, the t-V2P2 sheet favors in-plane [100]/[010] magnetization direction. The estimated in-plane MAE of t-V2P2 sheet is E([001]) − E[100] = 69.63 μeV per V atom. The value is almost the same as the reported Mn2C sheet20 (69 μeV per V atom) and the easy axis of the Mn2C sheets is equally in the in-plane [100] direction.
| MAE | EA |
|---|---|
| E(010) − E(100) | 0.00 |
| E(001) − E(100) | 557.00 |
| E(110) − E(100) | 1.00 |
| E(111) − E(100) | 187.50 |
Next, we investigate the magnetic properties of the t-V2P2 sheet. Looking at the obtained results, the t-V2P2 sheet can be modeled by J1 − J2 Heisenberg Hamiltonian expressed as:
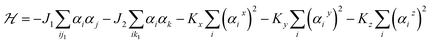 | (9) |
The first and second terms are summations over the nearest and next-nearest neighbor spin pairs, respectively. J1 and J2 denote the antiferromagnetic exchange interaction between nearest neighbors and next-nearest neighbors, respectively. Here, the exchange interaction terms of the V2P2 sheet depends on the number of J1 and J2 bond distances. αi is the magnetic moment of V atom taken from the favorable magnetic configuration (AFM2 in this case) of the V2P2 sheet. Kx, Ky and Kz represent the uniaxial magnetic anisotropy constants in x, y and z directions, respectively. The Kz factor is neglected since the preferred magnetization direction is along [100]/[010] for the V2P2 sheet.
Based on the (2 × 2) V2P2 unit cell, the analysis of the three magnetic states, FM, AFM1 and AFM2 in terms of their energies E(FM), E(AFM1) and E(AFM2), respectively can be derived as follows:
| E(FM) = E0 − 9J1α2 − 8J2α2 | (10) |
| E(AFM1) = E0 + J1α2 + 8J2α2 | (11) |
| E(AFM2) = E0 + 9J1α2 − 8J2α2. | (12) |
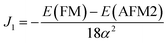 | (13) |
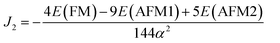 | (14) |
Using eqn (11) and (12) given above, the exchange parameters J1 and J2 were estimated to be −16.86 meV/αB2 and −20.37 meV/αB2 respectively. These J1 and J2 values can be used to estimate the TN of t-V2P2 sheet using Monte Carlo simulations based on the Heisenberg model.
However, within the mean-filed approximation, the Néel temperature for an AFM state can be estimated as
| TN = 2ER/3kBN | (15) |
We further explore the Li atom adsorption and diffusion properties on t-V2P2 sheet. We begin with the search for the single Li atom favorable high-symmetric adsorption site (Ads. site) on the V2P2 sheet. Based on the tetragonal symmetry of t-V2P2 sheet, three Ads. site has been considered on (2 × 2) supercell of t-V2P2 sheet, i.e. for the Li atom at the top of the V (TV), P (TH), atoms and hollow (TH) sites (see Fig. 4). All atoms in the t-V2P2 with adsorbed Li (Li–V2P2) are fully relaxed without any geometry constraint. There is no sign of reconstruction (see Fig. 2) after full structural optimization and top of the V (TV) is energetically favorable Ads. site for Li atom on t-V2P2. To estimate the favorable magnetic ground state, ferromagnetic (FM) and antiferromagnetic (AFM) calculations have been performed for Li–V2P2 system. The AFM configuration has parallel spins within each layer of V, but opposite spins in the upper and lower layer of V. Our PBE+D2+U calculation favors antiferromagnetic configuration with an energy difference of about 1.14 eV as compared with ferromagnetic calculation. Moreover, both PBE+D2 and PBE+D2+U have been considered for the Li–V2P2 with adsorbed Li system phonon calculations. The plot shows no imaginary modes for PBE+D2 and a negligible numerical noise for the PBE+D2+U case. The results confirm the dynamic stability of Li–V2P2 system (see Fig. S4†).
The adsorption energy (Eads) of Li–V2P2 system can be calculated as,
| Eads = (EV2P2 + ELi) − ELi–V2P2, | (16) |
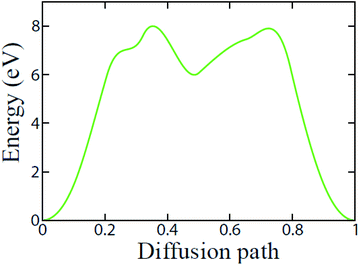
We further investigate the diffusion pathway and energy barrier of Li-ion on the t-V2P2 surface. The calculation in this section has been performed using the CI-NEB approach. Only one minimum pathway has been considered for Li-ion diffusion on the t-V2P2 surface. The pathway is chosen according to the preferred above-mentioned high-symmetric adsorption site for Li. As illustrated in Fig. 5, the deduced minimum diffusion energy barriers (Ea) for Li-ion on t-V2P2 the sheet is approximately 8 eV. The estimated Ea for Li on t-V2P2 surface indicate a strong interaction between Li and the surrounding atoms in the t-V2P2 sheet. This steric coulomb effect provided by the t-V2P2 surface atoms impact the Li diffusion on the t-V2P2 surface and hence the higher Ea is needed for the Li diffusion. The high value of Ea for Li on t-V2P2 indicates that Li–V2P2 may not be a suitable candidate for Li-ion battery (LIBs) anode electrode. However, t-V2P2 can be proposed as a good candidate for sensing application.
4 Conclusions
In conclusion, we presented theoretical results on the electronic, magnetic, and adsorption properties of new t-V2P2 sheet using a DFT+U. The t-V2P2 sheet is found to be dynamically and mechanically stable. The t-V2P2 sheet prefers an antiferromagnetic ground state with an indirect narrowed bandgap of 0.23 eV. The estimated electron mobility in the t-V2P2 sheet at room temperature is approximately 24 times that of a hole. The t-V2P2 sheet exhibits a sizable magnetic anisotropy (MAE) of 69 μeV per V atom with in-plane magnetization. Mean-field approximation based on the 2D classical Heisenberg model predicts a high Néel temperature (TN) of the t-V2P2 sheet up to 1263 K. The Li atom adsorption on the t-V2P2 sheet shows a transition from semiconductor to metal. Also the Li–V2P2 system leaves residual integer magnetic moment of 1 μB. Due to strong steric coulomb repulsion, minimum diffusion energy barriers (Ea) for Li-ion on the t-V2P2 surface is high enough to make the Li atom immobile. Finally, our theoretical results indicate the potential of the t-V2P2 sheet for antiferromagnetic spintronics and sensing applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Sohail Ahmad extends his appreciation to the Deanship of Scientific Research at King Khalid University for financial support through the research groups program under grant number (R. G. P. 2/188/42). We would like to acknowledge Prof. Dr Ethem Akturk and Prof. Dr Olcay Üzengi Aktürka from the Department of Physics and Department of Electrical and Electronic Engineering, Adnan Menderes University, Aydın, Turkey for providing the computing resources to carry out part of the calculations done in this paper.References
- M. Khazaei, J. Wang, M. Estili, A. Ranjbar, S. Suehara, M. Arai, K. Esfarjani and S. Yunoki, Nanoscale, 2019, 11, 11305–11314 RSC.
- Y. Zuntu Abdullahi, Z. Demir Vatansever, E. Aktürk, Ü. Akıncı and O. Üzengi Aktürk, Phys. Chem. Chem. Phys., 2020, 22, 10893–10899 RSC.
- T. Bo, P.-F. Liu, J. Zhang, F. Wang and B.-T. Wang, Phys. Chem. Chem. Phys., 2019, 21, 5178–5188 RSC.
- Z. Guo, J. Zhou and Z. Sun, J. Mater. Chem. A, 2017, 5, 23530–23535 RSC.
- T. Bo, P.-F. Liu, J. Xu, J. Zhang, Y. Chen, O. Eriksson, F. Wang and B.-T. Wang, Phys. Chem. Chem. Phys., 2018, 20, 22168–22178 RSC.
- H. Zhang, H. Xiang, F.-z. Dai, Z. Zhang and Y. Zhou, J. Mater. Sci. Technol., 2018, 34, 2022–2026 CrossRef.
- H. Zhang, F.-Z. Dai, H. Xiang, X. Wang, Z. Zhang and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 1593–1600 CrossRef.
- G. Yuan, T. Bo, X. Qi, P.-F. Liu, Z. Huang and B.-T. Wang, Appl. Surf. Sci., 2019, 480, 448–453 CrossRef CAS.
- B. Wang, Y. Zhang, L. Ma, Q. Wu, Y. Guo, X. Zhang and J. Wang, Nanoscale, 2019, 11, 4204–4209 RSC.
- Y.-Y. Wu, T. Bo, X. Zhu, Z. Wang, J. Wu, Y. Li and B.-T. Wang, Appl. Surf. Sci., 2020, 513, 145821 CrossRef CAS.
- R. Escamilla, E. Carvajal, M. Cruz-Irisson, F. Morales, L. Huerta and E. Verdin, J. Mater. Sci., 2016, 51, 6411–6418 CrossRef CAS.
- H. Bolvardi, J. Emmerlich, D. Music, J. von Appen, R. Dronskowski and J. Schneider, J. Phys.: Condens. Matter, 2012, 25, 045501 CrossRef PubMed.
- P. Barua, M. Hossain, M. Ali, M. Uddin, S. Naqib and A. Islam, J. Alloys Compd., 2019, 770, 523–534 CrossRef CAS.
- Y. Z. Abdullahi, Z. D. Vatansever, F. Ersan, U. Akinci, O. U. Akturk and E. Akturk, Phys. Chem. Chem. Phys., 2021, 23, 6107–6115 RSC.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864 CrossRef.
- M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire and D. H. Cobden, Nature, 2017, 546, 270 CrossRef CAS PubMed.
- Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu and A. F. May, Nat. Mater., 2018, 17, 778 CrossRef CAS PubMed.
- Y. Z. Abdullahi, F. Ersan, Z. D. Vatansever, E. Aktürk and O. Ü. Aktürk, J. Appl. Phys., 2020, 128, 113903 CrossRef CAS.
- L. Hu, X. Wu and J. Yang, Nanoscale, 2016, 8, 12939–12945 RSC.
- Y. Kadioglu, Mater. Sci. Eng., B, 2021, 268, 115111 CrossRef CAS.
- T. Bo, P. F. Liu, J. Zhang, F. Wang and B. T. Wang, Phys. Chem. Chem. Phys., 2019, 21, 5178–5188 RSC.
- Y. Z. Abdullahi and S. Ahmad, Phys. Chem. Chem. Phys., 2021, 23, 16316–16323 RSC.
- T. Gorkan, E. Vatansever, Ü. Akıncı, G. Gökoğlu, E. Aktürk and S. Ciraci, J. Phys. Chem. C, 2020, 124, 12816–12823 CrossRef CAS.
- N. E. Kirchner-Hall, W. Zhao, Y. Xiong, L. Timrov and I. Dabo, Appl. Sci., 2021, 11, 2395 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- A. V. Kuklin, S. A. Shostak and A. A. Kuzubov, J. Phys. Chem. Lett., 2018, 9, 1422–1428 CrossRef CAS PubMed.
- Y. Z. Abdullahi, Z. D. Vatansever, E. Aktürk, Ü. Akıncı and O. Ü. Aktürk, Phys. Status Solidi B, 2020, 2000396 Search PubMed.
- Y. Z. Abdullahi, T. L. Yoon and A. A. Kassimu, Mater. Chem. Phys., 2020, 254, 123470 CrossRef CAS.
- M. Yagmurcukardes, Turk. J. Phys., 2020, 44, 450–457, DOI:10.3906/fiz-2004-17.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72 CrossRef CAS.
- N. D. Mermin and H. Wagner, Phys. Rev. Lett., 1966, 17, 1133–1136 CrossRef CAS.
- J. M. Kosterlit and D. J. Thouless, J. Phys. C: Solid State Phys., 1973, 6, 1181–1203 CrossRef.
- S. Tiwari, M. L. Van de Put, B. Sorée and W. G. Vandenberghe, npj 2D Mater. Appl., 2021, 5, 1–7 CrossRef.
- Y.-D. Hsieh, Y.-J. Kao and A. W. Sandvik, J. Stat. Mech.: Theory Exp., 2013, P09001 CrossRef.
- J. M. Kosterlitz, Rep. Prog. Phys., 2016, 79, 026001 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra07558f |
| This journal is © The Royal Society of Chemistry 2021 |