DOI:
10.1039/D1RA07324A
(Paper)
RSC Adv., 2021,
11, 37612-37623
Effect of irradiation-induced cascade mixing on spinodal decomposition in U–Nb and U–Zr alloys: a phase field study
Received
1st October 2021
, Accepted 29th October 2021
First published on 23rd November 2021
Abstract
The spinodal decomposition of the γ-phase in U–Nb and U–Zr alloys under irradiation was investigated using the phase-field method coupled with micro-elasticity theory and rate dependent cascade mixing model. Microstructure evolutions of spinodal decomposition in U–Nb and U–Zr alloys were simulated by considering different initial compositions and dose rates. The volume fraction and composition distribution under different cascade mixing were presented. The simulation results show that the volume fractions and equilibrium composition of the (Nb,Zr)-rich γ2-phase and the rate of spinodal decomposition are influenced by the dose rate and initial alloy composition. The cascade mixing can drive Nb or Zr atoms back into solution until a new equilibrium state between local cascade mixing and spinodal decomposition is reached. The evolution analysis indicated that irradiation-induced cascade mixing acts in opposition to thermodynamically driven spontaneous spinodal decomposition, which can not only slow down the spinodal decomposition but also reduces the composition range of the miscibility gap.
1. Introduction
Recently, uranium based metallic nuclear fuels have attracted more and more attention due to their advantages in mechanical properties, thermal conductivity and irradiation performance.1,2 The body centered cubic (bcc) γ-phase in metallic uranium alloys is more resistant to swelling than the orthorhombic α-phase under irradiation conditions. Uranium alloys with the addition of Nb greatly improves the melting point, heat transfer and swelling resistance,3,4 while the addition of Zr increases the solidus temperature and stabilizes the isotropic γ-phase over a wider temperature range.5,6 According to thermodynamic equilibrium phase diagram,7,8 both of U–Nb and U–Zr alloys have continuous solid solution of γ-phase and miscibility gap in the high temperature region, which make it possible for the alloys to be used steadily at high temperatures. The addition of Nb and Zr can prevent oxidation of uranium9 and reduce the chemical interaction of fuel-cladding.10 Therefore, U–Nb and U–Zr alloys are considered the candidates of metallic nuclear fuels for next generation fast reactors.3,11
There are many efforts made to develop the U–Nb and U–Zr alloys, such as the studies of mechanical properties,12,13 creep behavior,4,14 and phase transformation.3 Many researches have focused on spinodal decomposition in U–Nb and U–Zr alloys, which could bring miscibility gaps and heterogeneous microstructure in a large temperature region. According to Hsiung et al.'s15 study and Clarke et al.'s16 experimental results, the nanoscale modulation caused by the spinodal decomposition can lead to the age hardening and make good stability at low temperatures in U–Nb alloys. Studying the microstructure of irradiated annular U–Zr fuel by microscopic multi-scale characterization, Yao et al.17,18 found that the alloy formed nanoscale spinodal decomposition microstructure after irradiation, which could effectively prevent radiation swelling of fuel slug. Thus, it is essential to study the spinodal decomposition in metallic nuclear fuels under irradiation.
As good candidates for nuclear fuels, U–Nb and U–Zr alloys are exposed to the extreme environment of intense irradiation and high temperature inevitably. Previous studies have showed that irradiation impact microstructure changes of alloys through two main mechanisms: irradiation-induced mixing and irradiation-enhanced diffusion,19,20 both of which could be investigated by phase-field method. There are plenty of researchers have studied the microstructure evolution under irradiation by using the phase-field method and achieved successful applications, such as gas bubble growth,21–24 composition segregation,25–28 grain growth29–31 and so on. A phase-field model with irradiation effect proposed by Dilles et al.32 and successfully predicted the formation of various microstructures related to spinodal hardening in Ag–Cu alloy, which provided a new perspective for the improvement of mechanical properties of alloys. Ke et al.33 established a phase-field model for the microstructure evolution of Fe–Cr coupling with the cascade mixing model, which verified the consistency between the simulation and experimental results. The phase-field model with micro-elastic theory has also achieved success due to the application of the Khachaturyan–Shatalov theory,34,35 which fully describes the inhomogeneity of structure and its spatial distribution in the mesoscopic scale. Recently, Yan et al.36 have successfully carried out a phase-field model coupling with micro-elastic theory to study the interstitial atom and vacancy evolution in Fe–Cr alloys. Therefore, it is feasible and necessary to investigate the spinodal decomposition behavior of U–Nb and U–Zr systems under irradiation based on the phase-field method.
In the present study, based on the thermodynamic database, we have employed Cahn–Hilliard-type phase-field simulations combined with cascade mixing model to investigate the spinodal decomposition of γ-phase in U–Nb and U–Zr alloys under irradiation. Since the spinodal decomposition is a form of solid phase transition, we also consider the elastic energy in the phase-field model. In an attempt to find out the influence of irradiation on spinodal decomposition, different composition of U–Nb and U–Zr alloys have been studied.
2. Simulation methods
2.1 Phase-field model
To study the evolution of spinodal decomposition in U–Nb and U–Zr alloys, we have employed the phase-field model developed originally by Cahn and Hilliard.37 The total free energy F of the U–Nb and U–Zr alloys includes the chemical free energy, the interfacial gradient energy and the elastic strain energy. The total free energy can be expressed as:38| |
 | (1) |
where, c is the molar fraction of species Nb or Zr, κ is the gradient energy coefficient and Eel is the elastic strain energy of U–Nb or U–Zr alloy. The chemical free energy of γ-phase in U–Nb and U–Zr alloys can be obtained by Gchem = Gm/Vm, in which Vm is the molar volume, Gm is the molar Gibbs free energy and can be expressed with the regular solution model:| |
 | (2) |
where 0Gγi is the molar Gibbs free energy of pure i constituent element in the γ-phase, which is taken from the SGTE database compiled by Dinsdale.39 The ci is the atomic fraction of species i and jLγA,B is the temperature-dependent interaction parameters in the binary system which can be described as:Here aj and bj are optimized parameters. The thermodynamic data in eqn (3) are obtained from the U–Nb and U–Zr thermodynamic assessment.7,40 The governing equations describing the spatial and temporal evolutions of composition is determined by the Cahn–Hilliard-type equation with a forced mixing term:33| |
 | (4) |
where the first term at the right side in the equation accounts for thermal diffusion driven by the gradient of diffusion potential and the second term corresponds to the cascade mixing contribution of damage cascades. The chemical mobility M is defined by Darken's equation:41| | |
M = c(1 − c)[cMU + (1 − c)Mi], (i = Nb or Zr)
| (5) |
where MU, MNb and MZr are the atomic mobilities of U, Nb and Zr, respectively. They are related to the diffusivity through Einstein's relation Mi = Di/RT, where i denotes the elements of U, Nb or Zr. R is the gas constant, T is the absolute temperature, and Di is the intrinsic diffusion coefficient which can be seen in the Table 1.42,43
Table 1 Parameters for the simulations
| Parameters |
Symbols |
Values |
Ref. |
| Gradient energy coefficient |
κ |
1.8 × 10−14 (mol m2) J−1 (In U–Nb) |
55 |
| 0.5 × 10−15 (mol m2) J−1 (In U–Zr) |
| Intrinsic diffusion coefficient of U |
DU |
 |
42 |
| Intrinsic diffusion coefficient of Nb |
DNb |
 |
42 |
| Intrinsic diffusion coefficient of Zr |
DZr |
 |
43 |
| Lattice parameters of U |
aU |
0.343 nm |
52 |
| Lattice parameters of Nb |
aNb |
0.330 nm |
54 |
| Lattice parameters of Zr |
aZr |
0.357 nm |
53 |
| Gas constant |
R |
8.314 J mol−1 K−1 |
This work |
| Grid length |
l |
3.37 × 10−10 m (in U–Nb) |
52–54 |
| 3.50 × 10−10 m (in U–Zr) |
| Elastic constant of γ-U |
Cij |
C11 = 111.0 GPa, C12 = 117.0 GPa, C44 = 15.0 GPa |
52 |
| Elastic constant of pure Nb |
Cij |
C11 = 246.5 GPa, C12 = 134.5 GPa, C44 = 28.7 GPa |
54 |
| Elastic constant of β-Zr |
Cij |
C11 = 86.6 GPa, C12 = 92.3 GPa, C44 = 26.6 GPa |
53 |
| Replacements per displacement |
b |
50 |
33 and 56 |
| Average relocation distance |
RL |
3.37 × 10−10 m (In U–Nb) |
52–54 |
| 3.50 × 10−10 m (In U–Zr) |
| Time steps |
Δt* |
0.005 s |
This work |
The continuum atom relocation model which is used in our simulation was developed by Enrique and Bellon to treat cascade mixing, in which the finite-range atomic replacements in displacement cascades is considered,44 and the model was proved to be feasible by Ke et al.33 Changes of the local component which is caused by the forced cascade mixing can be expressed as:
| |
 | (6) |
Here
Γ is the reorientation frequency which has a relationship to the irradiation displacement rate by
bΦ, where
b is the parameter that represents the number of substitutions per atomic displacement,
Φ is the irradiation displacement rate,
44,45 and 〈
c〉
RL is the non-local mean value of concentration which is weighted by the normalized function:
| | |
〈c〉RL = ∫ωRL(r − r′)c(r′)dr′
| (7) |
and
ωRL is the normalized function, which can be expressed by a Gaussian distribution, describing the distribution of atomic reorientations.
46 It can be characterized as:
| |
 | (8) |
Here,
r represents the spatial location and
RL corresponds to the average jump distance during repositioning. In the model, the characteristics of cascades and the types of high-energy particles decide the value of
RL and
b. The value of
RL is typically approximated as the average interatomic distance in bcc-lattice.
47 In consideration of atomic displacement without creating Frenkel pairs during the cool-down of cascades, the number of substitutions is expected to be larger than the estimated value in the model proposed by Norgett
et al.48 The value of
b ranges from ∼1 for electrons to ∼30–100 for neutrons and heavy ions.
49,50 The results of this study are not highly sensitive to the specific value of
b and the effect of changing the primary dose rate is less than an order of magnitude. In the simulation, the values of
RL and
b for neutron/heavy-ion irradiations are chosen in
Table 1.
2.2 Elastic energy model
The elastic strain induced by composition inhomogeneity and lattice mismatch in U–Nb and U–Zr alloys can be written as:and the stress free strain ε0ij can be expressed as:where δij is the Kronecker–Delta function, ε0 = 1/a0(da/dc) is the lattice expansion coefficient, in which a0 and a are the average lattice constant and the lattice constant of the alloy with composition c. The total strain εij can be expressed as:| |
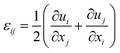 | (11) |
Here ui and uj is the ith and jth composition of the displacement, respectively. According to the Hook's law, the stress σij can be written as a function of elastic strain: σij = Cijklεelkl, where Cijkl is the elastic modulus tensor. The elastic strain energy related to the configuration can be described in the reciprocal space:51| |
 | (12) |
where k denotes the Fourier wave vector, c~(k) is the Fourier transform of composition c, and the integral  in the infinite reciprocal space is evaluated as a principal value excluding a volume (2π)3/V around the point n = 0. And B(n) is the elastic interaction energy which can be described as:
in the infinite reciprocal space is evaluated as a principal value excluding a volume (2π)3/V around the point n = 0. And B(n) is the elastic interaction energy which can be described as:| | |
B(n) = Cijklε0ijε0kl − niσ0ijΩjk(n)σ0klnl
| (13) |
in the expression, 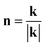 represents a unit vector in reciprocal space, Ωjk(n) is the Green tensor which is inverse to the tensor Cijklnknl.
represents a unit vector in reciprocal space, Ωjk(n) is the Green tensor which is inverse to the tensor Cijklnknl.
2.3 Numerical method
In the simulation, the composition evolution equation can be obtained by substituting eqn (6) into eqn (4). For the convenience of numerical calculation, the composition evolution equation can be converted to a dimensionless form which can be expressed as:| |
 | (14) |
where  , ∇* = l∇,
, ∇* = l∇, 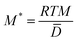 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = cUDU + ciDi, (i = Nb or Zr). l is the grid length which is chosen as the average lattice parameter of U and Nb, or U and Zr for c = 0.5, and the dimensionless grid size is Δx* = Δy* = 1.0. The simulation cell is 256Δx* × 256Δy* and Δt* is the dimensionless time steps. NA is the Avogadro constant, and
= cUDU + ciDi, (i = Nb or Zr). l is the grid length which is chosen as the average lattice parameter of U and Nb, or U and Zr for c = 0.5, and the dimensionless grid size is Δx* = Δy* = 1.0. The simulation cell is 256Δx* × 256Δy* and Δt* is the dimensionless time steps. NA is the Avogadro constant, and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) represents the average inter-diffusion coefficient of U–Nb or U–Zr alloy which depends on the temperature T and the concentration of Nb or Zr, and can be calculated with the intrinsic diffusion coefficients in the Table 1. At 973 K, the calculated values of
represents the average inter-diffusion coefficient of U–Nb or U–Zr alloy which depends on the temperature T and the concentration of Nb or Zr, and can be calculated with the intrinsic diffusion coefficients in the Table 1. At 973 K, the calculated values of ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) are 1.96 × 10−15 m2 s−1 in U-45 at% Nb alloy and 2.04 × 10−15 m2 s−1 in U-25 at% Zr alloy. The lattice parameters ai (i = U, Nb or Zr) and anisotropy elastic constants Cij of γ-U, pure Nb and β-Zr are shown in the Table 1.52–54 Eqn (14) is discretized in 2-D space with a uniform grid and solved by using an explicit finite difference scheme with forward Euler time-stepping under periodic boundary conditions. The crystallographic orientation of the simulated region was determined to be [10] in horizontal direction and [01] in vertical direction.
are 1.96 × 10−15 m2 s−1 in U-45 at% Nb alloy and 2.04 × 10−15 m2 s−1 in U-25 at% Zr alloy. The lattice parameters ai (i = U, Nb or Zr) and anisotropy elastic constants Cij of γ-U, pure Nb and β-Zr are shown in the Table 1.52–54 Eqn (14) is discretized in 2-D space with a uniform grid and solved by using an explicit finite difference scheme with forward Euler time-stepping under periodic boundary conditions. The crystallographic orientation of the simulated region was determined to be [10] in horizontal direction and [01] in vertical direction.
3. Results
3.1 Effect of irradiation on spinodal decomposition of γ-phase
In present work, the spinodal decomposition of U–Nb and U–Zr alloys located in relative high temperature regions (>900 K) and we incorporated the continuum treatment of ballistic events by Enrique and Bellon44,57 into our model, which was previously used to study compositional patterning and phase stability under irradiation. According to the phase diagram of U–Nb and U–Zr alloys,7,8 the miscibility gaps of Nb component in U–Nb alloys and Zr component U–Zr alloys range from 0.14 to 0.7 and 0.13 to 0.42, respectively. The spinodal decomposition behavior in the composition range is mainly studied in this work. In our simulation, the effect of irradiation dose rate on the spinodal decomposition and microstructure evolution of different Nb or Zr component in U–Nb and U–Zr alloys at 973 K have been studied.
In order to study the effect of irradiation on the microstructure evolution, the spinodal decomposition of γ-phase in U-45 at% Nb alloy at 973 K with 0 dpa s−1, 3 × 10−4 dpa s−1 and 6 × 10−4 dpa s−1 were simulated. As shown in Fig. 1, the temporal simulation results for 56, 142, 284 and 568 s were labeled by (a) to (d). The dark red regions are the Nb or Zr enriched γ2-phase, and the dark blue regions denote the U enriched γ1-phase. It can be seen that two-phase microstructure gradually appears as the simulation time increases. The size of γ2-phase decreases and the microstructure evolution in U–Nb alloy slows down with the increase of dose rates. Fig. 2 shows the time evolution of spinodal decomposition of γ-phase in U-25 at% Zr alloy with 0 dpa s−1, 5 × 10−5 dpa s−1 and 1 × 10−4 dpa s−1, and the columns of (a) to (d) indicate simulation results of 327, 3272, 8180 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 s, respectively. The spinodal decomposition evolves along the vertical and horizontal directions and the phase fraction of Zr enriched γ2-phase increases with the increase of dose rates in the Fig. 2. The simulation results indicate that the elastic energy could have great influence on the anisotropy of the microstructure morphology.
270 s, respectively. The spinodal decomposition evolves along the vertical and horizontal directions and the phase fraction of Zr enriched γ2-phase increases with the increase of dose rates in the Fig. 2. The simulation results indicate that the elastic energy could have great influence on the anisotropy of the microstructure morphology.
 |
| | Fig. 1 Phase-field simulations of the spinodal decomposition of the γ-phase in U-45 at% Nb alloy at 973 K under different dpa rates: (a) t = 56 s; (b) t = 142 s; (c) t = 284 s; (d) t = 568 s. | |
 |
| | Fig. 2 Phase-field simulations of the spinodal decomposition of the γ-phase in U-25 at% Zr alloy at 973 K under different dpa rates: (a) t = 327 s; (b) t = 3272 s; (c) t = 8180 s; (d) t = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 s. 270 s. | |
The compositions–distance curves of γ1 and γ2-phase under different dpa rate in U-45 at% Nb alloy and U-25 at% Zr alloy were plotted in Fig. 3(a) and (b), respectively. One can easily find that the γ1 and γ2-phase in U-45 at% Nb alloy can reach equilibrium compositions of 0.19 and 0.68 without irradiation, while reducing to equilibrium compositions of 0.36 and 0.57 under the dpa rate of 6 × 10−4 dpa s−1. The γ1-phase and γ2-phase in U-25 at% Zr alloy can reach equilibrium compositions of 0.13 and 0.41 without irradiation, while reducing to equilibrium compositions of 0.20 and 0.29 under the dpa rate of 1 × 10−4 dpa s−1. In the simulation, Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = |
eq = |![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq1 −
eq1 − ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq2| indicates the width of the miscibility gap in the equilibrium phase diagram, where
eq2| indicates the width of the miscibility gap in the equilibrium phase diagram, where ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq1 and
eq1 and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq2 are the average equilibrium compositions of Nb or Zr-lean and Nb or Zr-rich phases, respectively. The width of the miscibility gap Δ
eq2 are the average equilibrium compositions of Nb or Zr-lean and Nb or Zr-rich phases, respectively. The width of the miscibility gap Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq in U-45 at% Nb alloy is 0.49 without irradiation, while Δ
eq in U-45 at% Nb alloy is 0.49 without irradiation, while Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = 0.21 under the dpa rate of 6 × 10−4 dpa s−1. In U-25 at% Zr alloy, Δ
eq = 0.21 under the dpa rate of 6 × 10−4 dpa s−1. In U-25 at% Zr alloy, Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = 0.28 without irradiation, while Δ
eq = 0.28 without irradiation, while Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = 0.09 under the dpa rate of 1 × 10−4 dpa s−1. As can be seen from the figures, the width of miscibility gap for both of the U–Nb and U–Zr shrink with the increase of dose rates.
eq = 0.09 under the dpa rate of 1 × 10−4 dpa s−1. As can be seen from the figures, the width of miscibility gap for both of the U–Nb and U–Zr shrink with the increase of dose rates.
 |
| | Fig. 3 Profile of solute compositions at 973 K under different dpa rates: (a) U-45 at% Nb and (b) U-25 at% Zr. | |
As referred above, the irradiation-induced cascade mixing can influence the equilibrium composition of two phases after spinodal decomposition. Furthermore, in order to clarify the effects of irradiation on the speed of spinodal decomposition, the variations of γ2-phase volume fractions as a function of time under different dose rates in U-45 at% Nb and U-25 at% Zr alloys were plotted in Fig. 4(a) and (b), respectively. It is seen that, without irradiation, the volume fractions of γ2-phase are able to reach the equilibrium values of 0.50 and 0.42 for U-45 at% Nb and U-25 at% Zr alloys, respectively. As the dose rate increases, it takes longer time for the γ2-phase to reach the equilibrium volume fractions. In addition, the increase of dose rates results in a decrease of volume fraction of the γ2-phase in U-45 at% Nb alloy (e.g. from 0.50 to 0.40) and an increase of volume fraction of the γ2-phase in U-25 at% Zr alloy (e.g. from 0.42 to 0.52).
 |
| | Fig. 4 The volume fraction variation of γ2-phase as a function of time under different dpa rates: (a) U-45 at% Nb and (b) U-25 at% Zr. | |
 |
| | Fig. 5 Morphology of U–Nb alloy at 973 K under different dpa rates and initial compositions. | |
3.2 Effect of initial alloy composition on spinodal decomposition of U–Nb and U–Zr under irradiation
To investigate the influences of initial composition on spinodal decomposition under irradiation, the U–Nb and U–Zr alloys with different initial composition were simulated by phase-field method, and the results were shown in Fig. 5 and 6. Fig. 5 shows the morphologies of spinodal decomposition of U-40 at% Nb, U-45 at% Nb and U-50 at% Nb alloys under different dpa rates of 0 dpa s−1, 2 × 10−4 dpa s−1 and 4 × 10−4 dpa s−1. The simulation temperature is 973 K and the time t = 1000 s. Fig. 6 shows the spinodal decomposition morphology of U-20 at% Zr, U-25 at% Zr and U-30 at% Zr alloys under different dpa rates of 0 dpa s−1, 3 × 10−5 dpa s−1 and 6 × 10−5 dpa s−1, the simulation temperature is 973 K and the time t = 10000 s. It can be seen that, without irradiation, the phase fraction of in U–Nb and U–Zr alloys increases with the increase of Nb or Zr initial composition. The matrix phase is U enriched γ1-phase and the isolated phase is Nb or Zr enriched γ2-phase in U-40 at% Nb and U-20 at% Zr alloy. When the initial alloy composition increase to 45 at% Nb and 25 at% Zr, the U enriched γ1-phase and the Nb or Zr enriched γ2-phase are interconnected. For U-50 at% Nb and U-30 at% Zr, the matrix phase is γ2-phase and the isolated phase is U enriched γ1-phase. It can be noticed that the favorite growth direction in the two alloys remain unchanged during spinodal decomposition with the increase of dose rates.
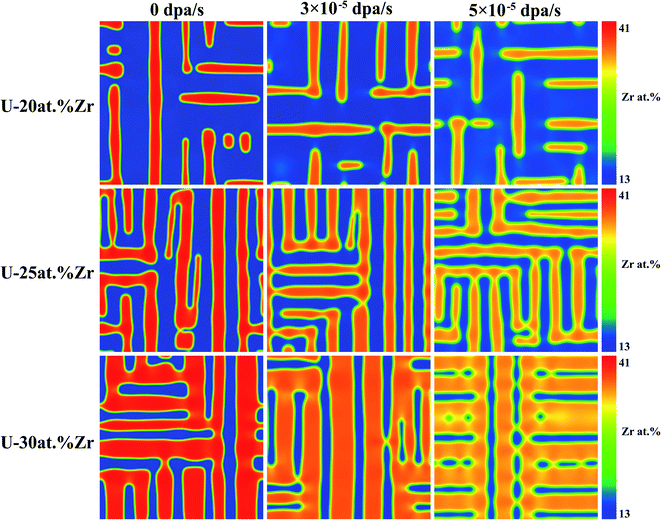 |
| | Fig. 6 Morphology of U–Zr alloy at 973 K under different dpa rates and initial compositions. | |
 |
| | Fig. 7 The volume fraction variation of γ2-phase as a function of time for different dpa rates and compositions. (a) U–Nb, (b) U–Zr. | |
Fig. 7(a) and (b) show the change of γ2-phase volume fraction as a function of simulation time under different initial composition and dose rates for U–Nb and U–Zr alloys, respectively. The red, blue, and black color of lines represent different initial compositions and the types of lines represent different dose rates. As can be seen in Fig. 7, the volume fraction of the γ2-phase quickly increases to its equilibrium value for all initial compositions without irradiation and the final volume fraction of the γ2-phase increases with the increase of the initial Nb or Zr concentration. As the dose rate increases, the speed of spinodal decomposition decreases due to the atomic cascade mixing effect.
3.3 Effect of irradiation on the two-phase microstructure in U–Nb and U–Zr alloys
To study the effect of irradiation on the evolution of two-phase microstructure after spinodal decomposition, the two-phase microstructures of U–Nb and U–Zr alloys after spinodal decomposition for 1 h were applied as the initial state, and the simulated microstructure evolution of U-45 at% Nb and U-25 at% Zr alloys under irradiation were shown in Fig. 8 and 9, respectively. As can be seen from the figures, although the morphological orientation of two-phase structure does not change with time under irradiation, the equilibrium compositions of two phases are affected by the irradiation-induced cascade mixing. With the increase of irradiation time, the microstructure after spinodal decomposition gradually disappeared in U-45 at% Nb alloy under dpa rate of 6 × 10−4 dpa s−1 and U-25 at% Zr alloy under dpa rate of 1 × 10−4 dpa s−1. The variations of compositions of two phases with time under irradiation in U-45 at% Nb and U-25 at% Zr alloys are shown in Fig. 10(a) and (b), respectively. It can be seen that the composition of the two phases gradually shift to the initial composition and then reach equilibrium values, leading to the decrease of miscibility gap width.
 |
| | Fig. 8 Effect of irradiation on the evolution of two-phase microstructure for U-45 at% Nb alloys at 973 K: (a) t = 0 s; (b) t = 5 s; (c) t = 28 s; (d) t = 284 s. | |
 |
| | Fig. 9 Effect of irradiation on the evolution of two-phase microstructure for U-25 at% Zr alloys at 973 K: (a) t = 0 s; (b) t = 32 s; (c) t = 163 s; (d) t = 1636 s. | |
 |
| | Fig. 10 Composition evolution of γ1-phase and γ2-phase as a function of time at 973 K under different dpa rates: (a) U-45 at% Nb and (b) U-25 at% Zr. | |
4. Discussion
In this work, a phase-field model coupled with cascade mixing and micro-elastic theory has been used to investigate the spinodal decomposition in U–Nb and U–Zr alloys. The results show that the elastic energy has an important influence on the orientation of the microstructure during the spinodal decomposition, and the irradiation-induced cascading mixing can affect the velocity of the spinodal decomposition and the composition of the equilibrium state after decomposition. The microstructures and equilibrium compositions vary with the change of initial components in U–Nb and U–Zr.
In the above simulation, the elastic energy induced by the lattice misfit of the two phases was calculated during the spinodal decomposition. The isolated domains prefer to align in vertical and horizontal directions, which can be explained with the elastic anisotropy of the two alloy systems. It is well known that the elastic modulus can be defined as,58
| |
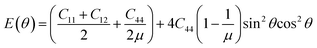 | (15) |
where
μ = 2
C44/(
C11 −
C12) is orientation factor. The curves of the variation of
E as a function of the orientation in the U-45 at% Nb and U-25 at% Zr alloys are shown in
Fig. 11(a) and (b). In the simulation, the stress free strain
ε0ij of U-45 at% Nb and U-25 at% Zr alloys are chosen as 0.038 and 0.040.
59 It can be obviously seen from
Fig. 1 and
2 that the overall spatial distribution of the isolated domains is interconnected rectangular stripes aligned in the 〈10〉 crystallographic direction in order to reduce the elastic energy, which is in good agreement with the calculated results of elastic modulus shown in
Fig. 11. The influence of elastic energy on the microstructure anisotropy of U–Nb alloy is greater than that of U–Zr alloy. With the increase of aging time, the microstructure after spinodal decomposition in U–Nb or U–Zr alloy gradually coarsens because of the Ostwald ripening. According to the simulation results of spinodal decomposition with different alloy composition under different irradiation intensities, it is obviously that the irradiation-induced cascade mixing has little effect on the morphology orientation of the separated two phases, but shows great influence on the equilibrium composition and volume fraction of the separated two phases.
 |
| | Fig. 11 Diagram of Young's modulus: (a) U-45 at% Nb and (b) U-25 at% Zr. | |
According to the Fig. 2 and 6, the simulated microstructure morphology of U–Zr alloy after spinodal decomposition without irradiation is consistent of the experiment results studied by Yao et al. who investigated the U-50 wt% Zr spinodal microstructure and element distribution by in situ TEM annealing at 873 K for 30 min.60 In Fig. 3 and 4, with the increase of dpa rate from 0 to 6 × 10−4 dpa s−1, equilibrium composition of γ2-phase in U-45 at% Nb alloy decreases from 0.68 to 0.57 and the volume fraction of γ2-phase decreases from 0.50 to 0.40. As the dpa rate increases from 0 to 1 × 10−4 dpa s−1, γ2-phase of Zr equilibrium composition in U-25 at% Zr alloy decreases from 0.41 to 0.29 and the volume fraction of γ2-phase increases from 0.42 to 0.52. The irradiation slows down the speed of the spinodal decomposition and reduces the amplitude of composition fluctuation. The increase of dose rates leads to the variation of equilibria composition in U-45 at% Nb and U-25 at% Zr alloys. In the U–Nb and U–Zr alloys, the volume fraction of γ2-phase changes differently with the increase of dose rates. Under different irradiation conditions, the equilibria compositions of U-45 at% Nb are changed and the increase of dose rate inhibits solute enrichment, which leads to the decrease of the volume fraction of γ2-phase in U–Nb alloy. The volume fraction of γ2-phase in U-25 at% Zr alloy increases with the increase of dose rate, which indicate that the cascade mixing is able to strongly affect the process of spinodal decomposition.
With the increase of dose rates, the difference of the two equilibrium compositions (Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq) of spinodal decomposition in U–Nb and U–Zr alloys decreases dramatically. Without considering the irradiation, the metastable supersaturated solid solution will spontaneously decompose into two-phase mixtures with the same crystal structure by spinodal decomposition to reduce the free energy of the system. According to the simulation results, it can be seen that U–Nb alloy does not have the spinodal decomposition when the dpa rate reaches 1.87 × 10−3 dpa s−1, while the maximum dpa rate of U–Zr alloy which can undergo the spinodal decomposition is 2.40 × 10−4 dpa s−1. The ballistic effects oppose spinodal ordering according to Martin's results,61 and the alloy does not undergo spinodal decomposition when the dose rate is large enough. Through the analysis of the above results, the time required for the alloy to decompose to the equilibrium state gradually increases with the increase of the dose rates. The irradiation-induced ballistic mixing causes a number of exchanges of atomic positions occur within a finite average relocation distance (RL = 3.37 × 10−10 m in U–Nb and RL = 3.50 × 10−10 m in U–Zr), which “re-mix” the local atom and makes the average composition of local atoms to a certain extent. In other words, irradiation-induced ballistic mixing acts in opposition to spinodal decomposition or demixing mechanism. Therefore, the spinodal decomposition of U-45 at% Nb and U-25 at% Zr alloys under irradiation is the competitive result of demixing and irradiation-induced ballistic mixing. Through the irradiation experiment on as-cast austenitic stainless steel, Fujii et al.62 found that irradiation can reduce the fluctuation of solute composition and the degree of spinodal decomposition, which is consistent with our simulation results. The change of the equilibrium composition in γ1 and γ2-phase at increasing dose rates is caused by more frequent cascade mixing replacement events, forcing the exchange of atoms from the matrix to precipitates and vice versa.33 The simulation results of spinodal decomposition under irradiation in U–Nb and U–Zr alloys are consistent with the different effect of cascade mixing in mesoscale phase field models by Schwen et al.63 Their study demonstrated that the alloys exhibit obvious phase separation under low irradiation rates, and the degree of phase separation decreases with increasing irradiation rates. At sufficiently large irradiation rates, the alloys don't show phase separation and remain mixed. Thus, the irradiation-induced cascade mixing can slow the speed of spinodal decomposition and influences the equilibrium composition and volume fraction of the separated two phases in U-based alloys.
eq) of spinodal decomposition in U–Nb and U–Zr alloys decreases dramatically. Without considering the irradiation, the metastable supersaturated solid solution will spontaneously decompose into two-phase mixtures with the same crystal structure by spinodal decomposition to reduce the free energy of the system. According to the simulation results, it can be seen that U–Nb alloy does not have the spinodal decomposition when the dpa rate reaches 1.87 × 10−3 dpa s−1, while the maximum dpa rate of U–Zr alloy which can undergo the spinodal decomposition is 2.40 × 10−4 dpa s−1. The ballistic effects oppose spinodal ordering according to Martin's results,61 and the alloy does not undergo spinodal decomposition when the dose rate is large enough. Through the analysis of the above results, the time required for the alloy to decompose to the equilibrium state gradually increases with the increase of the dose rates. The irradiation-induced ballistic mixing causes a number of exchanges of atomic positions occur within a finite average relocation distance (RL = 3.37 × 10−10 m in U–Nb and RL = 3.50 × 10−10 m in U–Zr), which “re-mix” the local atom and makes the average composition of local atoms to a certain extent. In other words, irradiation-induced ballistic mixing acts in opposition to spinodal decomposition or demixing mechanism. Therefore, the spinodal decomposition of U-45 at% Nb and U-25 at% Zr alloys under irradiation is the competitive result of demixing and irradiation-induced ballistic mixing. Through the irradiation experiment on as-cast austenitic stainless steel, Fujii et al.62 found that irradiation can reduce the fluctuation of solute composition and the degree of spinodal decomposition, which is consistent with our simulation results. The change of the equilibrium composition in γ1 and γ2-phase at increasing dose rates is caused by more frequent cascade mixing replacement events, forcing the exchange of atoms from the matrix to precipitates and vice versa.33 The simulation results of spinodal decomposition under irradiation in U–Nb and U–Zr alloys are consistent with the different effect of cascade mixing in mesoscale phase field models by Schwen et al.63 Their study demonstrated that the alloys exhibit obvious phase separation under low irradiation rates, and the degree of phase separation decreases with increasing irradiation rates. At sufficiently large irradiation rates, the alloys don't show phase separation and remain mixed. Thus, the irradiation-induced cascade mixing can slow the speed of spinodal decomposition and influences the equilibrium composition and volume fraction of the separated two phases in U-based alloys.
As can be seen from the Fig. 5–7, the U-50 at% Nb reaches the equilibrium composition much quicker than other U–Nb alloys, and the time to reach the equilibrium composition for the U-25 at% Zr is less than other U–Zr alloys. According to the thermodynamic database,7,8 the U-50 at% Nb has the largest chemical driving force compared with other alloy components in U–Nb, while the chemical driving of U-25 at% Zr is stronger than other U–Zr alloys. At the temperature of 973 K, the diffusivity of U-50 at% Nb is 1.51 × 10−15 m2 s−1 and the initial composition of alloys changes so little that the diffusivity of U–Nb alloys does not change much. The diffusivity at 973 K of U-25 at% Zr is 2.04 × 10−15 m2 s−1, and the change of composition in U–Zr alloys has little effect on the diffusivity under the same temperature. The influence of driving force during the spinodal decomposition is stronger than the effect of diffusivity, which leads to the less time to reach the equilibrium state for U-50 at% Nb and U-25 at% Zr alloys. The influence of irradiation on spinodal decomposition of different alloy composition shows that the greater driving force, the smaller effect of irradiation on the spinodal decomposition. Furthermore, the driving force of spinodal decomposition at 973 K for U-50 at% Nb alloy is larger than that of U-25 at% Zr alloy and irradiation has less effect on the spinodal decomposition of U–Nb alloy. The change of free energy with concentration was calculated based on the thermodynamic database,7,8 the value of free energy decreases significantly with the increase of Nb concentration from 0.2 to 0.7, while the value of free energy increases gently with the increase of Zr concentration from 0.1 to 0.4. Under irradiation, due to the breaking of the original degree of order, the entropy of γ-phase can be increased, which leads to the decrease of the effective free energy in U–Nb and U–Zr alloys.64,65 Under the influence of local cascade mixing, the effective free energy of Nb-lean phase decreases more than that of Nb-rich phase in U–Nb alloy, which leads to the volume fraction of Nb enriched phase decreases with the increase of dose rate. While the volume fraction of Zr enriched phase increases with the increase of dose rate because the effective free energy of Zr-rich phase decreases more than that of Zr-lean phase in U–Zr alloy. The volume fraction of Nb enriched phase decreasing in U–Nb alloy and the volume fraction of Zr enriched phase increasing in U–Zr alloy could be the various effect of driving force of spinodal decomposition and the decrease of effective free energy. Thus, the speed of spinodal decomposition and the equilibrium volume fraction of the γ2-phase are influenced by the irradiation and the initial composition.
From Fig. 8–10, the forced cascade mixing can destabilize the γ1 and γ2-phase precipitates by driving the Nb or Zr atoms back into solution. With the increase of the irradiation time, the microstructure of the alloys after the spinodal decomposition gradually disappeared until a new equilibrium state was reached. The largest composition difference appears at the interface of γ1 and γ2-phase after spinodal decomposition. According to the equilibrium phase diagram,64 the equilibrium concentration of Nb enriched phase after spinodal decomposition is 67.5% in U–Nb alloy. After long time aging, the concentration of Nb enriched phase decreases to 63.6% under the dpa rate of 3.0 × 10−4 dpa s−1, and the equilibrium concentration of Nb enriched phase decreases to 57.6% under the dpa rate of 6.0 × 10−4 dpa s−1. In the U–Zr alloy, the equilibrium concentration of Zr enriched phase after spinodal decomposition is 40.5% without irradiation,65 while the equilibrium concentration of Zr enriched phase decreases to 35.9% under the dpa rate of 5.0 × 10−5 dpa s−1, and the equilibrium concentration of Zr enriched phase decreases to 29.2% under the dpa rate of 1.0 × 10−4 dpa s−1. According to Fig. 10, at 973 K, the width of the miscibility gap (Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq) is 0.36 under the dpa rate of 3.0 × 10−4 dpa s−1 in U–Nb alloy, while the width of the miscibility gap decreases to 0.21 at the dpa rate of 6.0 × 10−4 dpa s−1. In U–Zr alloy, the width of the miscibility gap decreases from 0.21 to 0.09 with the increase of dpa rate from 5.0 × 10−5 dpa s−1 to 1.0 × 10−4 dpa s−1. According to the simulated results of spinodal decomposition, the tendency of composition region to shrink in the present work coincides well with the previous thermodynamic calculation,64–66 which shows that the miscibility gap shrinks with the effect of irradiation. Therefore, the atom mixing effect is most obvious at the interface at early stage and then causes the change of composition inside γ1 and γ2-phase under irradiation. When the effect of irradiation-induced ballistic mixing and spinodal decomposition reaches an equilibrium state, and the compositions of the two phases no longer change.
eq) is 0.36 under the dpa rate of 3.0 × 10−4 dpa s−1 in U–Nb alloy, while the width of the miscibility gap decreases to 0.21 at the dpa rate of 6.0 × 10−4 dpa s−1. In U–Zr alloy, the width of the miscibility gap decreases from 0.21 to 0.09 with the increase of dpa rate from 5.0 × 10−5 dpa s−1 to 1.0 × 10−4 dpa s−1. According to the simulated results of spinodal decomposition, the tendency of composition region to shrink in the present work coincides well with the previous thermodynamic calculation,64–66 which shows that the miscibility gap shrinks with the effect of irradiation. Therefore, the atom mixing effect is most obvious at the interface at early stage and then causes the change of composition inside γ1 and γ2-phase under irradiation. When the effect of irradiation-induced ballistic mixing and spinodal decomposition reaches an equilibrium state, and the compositions of the two phases no longer change.
5. Conclusion
In summary, the phase field method coupled with CALPHAD database and cascade mixing model have been employed to study the spinodal decomposition of U–Nb and U–Zr alloys under irradiation. The simulation results are helpful for understanding the spinodal decomposition in U–Nb and U–Zr alloys and the designing of metallic fuels working at high temperature and irradiation. It provides a new study on the behavior of U–Nb and U–Zr metallic nuclear fuels under neutron irradiation conditions with following results:
(1) The spinodal decomposition in U–Nb and U–Zr alloys could be inhibited with the increase of dose rates. The irradiation slows down the speed of the spinodal decomposition and reduces miscibility gap, which leads to the shrink of equilibria composition in U-45 at% Nb and U-25 at% Zr alloys.
(2) The volume fraction of γ2-phase increases with increasing initial composition of Nb or Zr in U–Nb and U–Zr alloys under the same conditions. The dose rate shows great influence in the equilibria composition in U–Nb and U–Zr. With the increase of dose rates, the volume fraction of Nb enriched phase in U–Nb alloy decreases after spinodal decomposition, while the volume fraction of Zr enriched phase in U–Zr alloy increases.
(3) When applying irradiation effect on the equilibrium two-phase microstructure of spinodal decomposition, the cascade mixing can destabilize the γ1 and γ2-phase by driving the Nb or Zr atoms back into solution till the effect local cascade mixing and spinodal decomposition reach to a new equilibrium state.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors would like to thank the financial support for this research by Natural Science Foundation of Fujian Province (2019J01033), National Key Research and Development Program of China (2017YFB0702401) and Fundamental Research Funds for the Central Universities (20720170038).
References
- D. E. Burkes, R. S. Fielding, D. L. Porter, D. C. Crawford and M. K. Meyer, J. Nucl. Mater., 2009, 389, 458–469 CrossRef CAS.
- B. S. Chandrasekhar and J. K. Hulm, J. Phys. Chem. Solids, 1958, 7, 259–267 CrossRef CAS.
- T. C. Duong, R. E. Hackenberg, V. Attari, A. Landa, P. E. A. Turchi and R. Arróyave, Comput. Mater. Sci., 2020, 175, 109573 CrossRef CAS.
- K. Ghoshal, T. R. G. Kutty, S. Mishra and A. Kumar, J. Nucl. Mater., 2013, 432, 20–22 CrossRef CAS.
- L. C. Walters, J. Nucl. Mater., 1999, 270, 39–48 CrossRef CAS.
- G. L. Hofman, L. C. Walters and T. H. Bauer, Prog. Nucl. Energy, 1997, 31, 83–110 CrossRef CAS.
- X. J. Liu, Z. S. Li, J. Wang and C. P. Wang, J. Nucl. Mater., 2008, 380, 99–104 CrossRef CAS.
- W. Xiong, W. Xie, C. Shen and D. Morgan, J. Nucl. Mater., 2013, 443, 331–341 CrossRef CAS.
- M. Paukov, I. Tkach, F. Huber, T. Gouder, M. Cieslar, D. Drozdenko, P. Minarik and L. Havela, Appl. Surf. Sci., 2018, 441, 113–119 CrossRef CAS.
- S. Kaity, J. Banerjee, S. C. Parida, P. G. Behere and V. Bhasin, J. Nucl. Mater., 2020, 541, 152427 CrossRef CAS.
- W. Chen and X.-M. Bai, J. Nucl. Mater., 2018, 507, 360–370 CrossRef CAS.
- A. J. Clarke, R. D. Field, R. E. Hackenberg, D. J. Thoma, D. W. Brown, D. F. Teter, M. K. Miller, K. F. Russell, D. V. Edmonds and G. Beverini, J. Nucl. Mater., 2009, 393, 282–291 CrossRef CAS.
- D. W. Brown, M. A. M. Bourke, A. J. Clarke, R. D. Field, R. E. Hackenberg, W. L. Hults and D. J. Thoma, J. Nucl. Mater., 2016, 481, 164–175 CrossRef CAS.
- G. Bozzolo, H. O. Mosca, A. M. Yacout, G. L. Hofman and Y. S. Kim, Comput. Mater. Sci., 2010, 50, 447–453 CrossRef CAS.
- L. Hsiung and J. Zhou, MRS Online Proceedings Library Archive, 2005 Search PubMed.
- A. J. Clarke, R. D. Field, R. E. Hackenberg, D. J. Thoma, D. W. Brown, D. F. Teter, M. K. Miller, K. F. Russell, D. V. Edmonds and G. Beverini, J. Nucl. Mater., 2009, 393, 282–291 CrossRef CAS.
- T. Yao, A. R. Wagner, X. Liu, A. EI-Azab, J. M. Harp, J. Gan, D. H. Hurley, M. T. Benson and L. He, Materialia, 2020, 9, 100592 CrossRef CAS.
- T. Yao, L. Capriotti, J. M. Harp, X. Liu, Y. Wang, F. Teng, D. J. Murray, A. J. Winston, J. Gan, M. T. Benson and L. He, J. Nucl. Mater., 2020, 542, 152536 CrossRef CAS.
- G. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 1424 CrossRef CAS.
- P. Wilkes, J. Nucl. Mater., 1979, 83, 166–175 CrossRef CAS.
- S. Hu, C. H. Henager, H. L. Heinisch, M. Stan, M. I. Baskes and S. M. Valone, J. Nucl. Mater., 2009, 392, 292–300 CrossRef CAS.
- S. Hu, D. E. Burkes, C. A. Lavender, D. J. Senor, W. Setyawan and Z. Xu, J. Nucl. Mater., 2016, 479, 202–216 CrossRef CAS.
- Y. Li, S. Hu, R. Montgomery, F. Gao and X. Sun, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 303, 62–67 CrossRef CAS.
- S. Y. Hu and C. H. Henager, Acta Mater., 2010, 58, 3230–3237 CrossRef CAS.
- X. Q. Ma, S. Q. Shi, C. H. Woo and L. Q. Chen, Scr. Mater., 2002, 47, 237–241 CrossRef CAS.
- X. Q. Ma, S. Q. Shi, C. H. Woo and L. Q. Chen, Mech. Mater., 2005, 38, 3–10 CrossRef.
- X. H. Guo, S. Q. Shi, Q. M. Zhang and X. Q. Ma, J. Nucl. Mater., 2008, 378, 110–119 CrossRef CAS.
- X. H. Guo, S. Q. Shi, Q. M. Zhang and X. Q. Ma, J. Nucl. Mater., 2008, 378, 120–125 CrossRef CAS.
- K. Ahmed, J. Pakarinen, T. Allen and A. El-Azab, J. Nucl. Mater., 2014, 446, 90–99 CrossRef CAS.
- M. R. Tonks, Y. Zhang, X. Bai and P. C. Millett, Mater. Res. Lett., 2014, 2, 23–28 CrossRef CAS.
- Z. G. Mei, L. Y. Liang, Y. S. Kim, T. Wiencek, E. O'Hare, A. M. Yacout, G. Hofman and M. Anitescu, J. Nucl. Mater., 2016, 473, 300–308 CrossRef CAS.
- D. Gilles, D. Sylvain, L. Laurence, S. David and P. Vassilis, Sci. Rep., 2018, 8, 1–12 Search PubMed.
- J. Ke, E. R. Reese, E. A. Marquis, G. R. Odette and D. Morgan, Acta Mater., 2019, 164, 586–601 CrossRef CAS.
- A. G. Khachaturyan, Theory of structural transformations in solids, Courier Corporation, 2013 Search PubMed.
- Y. U. Wang, Y. M. Jin and A. G. Khachaturyan, J. Appl. Phys., 2002, 92, 1351–1360 CrossRef CAS.
- Z. W. Yan, S. J. Shi, Y. S. Li, J. Chen and M. Shahid, Phys. Chem. Chem. Phys., 2020, 22, 3611–3619 RSC.
- J. W. Cahn, J. Chem. Phys., 1965, 42, 93–99 CrossRef CAS.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- A. T. Dinsdale, Calphad, 1991, 15, 317–425 CrossRef CAS.
- Y. Lu, Q. Q. Tang, C. P. Wang, Z. S. Li, Y. H. Guo and X. J. Liu, J. Phase Equilib. Diffus., 2018, 39, 714–723 CrossRef CAS.
- J. O. Andersson and J. Ågren, J. Appl. Phys., 1992, 72, 1350–1355 CrossRef CAS.
- B. Bian, P. Zhou, S. Wen and Y. Du, Calphad, 2018, 61, 85–91 CrossRef CAS.
- Y. Park, R. Newell, A. Mehta, D. D. Keiser and Y. H. Sohn, J. Nucl. Mater., 2018, 502, 42–50 CrossRef CAS.
- R. A. Enrique and P. Bellon, Phys. Rev. Lett., 2000, 84, 2885 CrossRef CAS.
- P. E. L'vov and V. V. Svetukhin, Modell. Simul. Mater. Sci. Eng., 2021, 29, 035013 CrossRef.
- R. A. Enrique and P. Bellon, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 134111 CrossRef.
- P. Bellon, Materials Science with Ion Beams, 2009, pp. 29–52 Search PubMed.
- M. J. Norgett, M. T. Robinson and I. M. Torrens, Nucl. Eng. Des., 1975, 33, 50–54 CrossRef.
- G. Martin and P. Bellon, Solid State Phys., 1996, 50, 189–331 Search PubMed.
- R. S. Averback and T. D. D. L. Rubia, Solid State Phys., 1997, 51, 281–402 Search PubMed.
- Y. H. Wen, J. P. Simmons, C. Shen, C. Woodward and Y. Wang, Acta Mater., 2003, 51, 1123–1132 CrossRef CAS.
- B. Beeler, C. Deo, M. Baskes and M. Okuniewski, J. Nucl. Mater., 2013, 433, 143–151 CrossRef CAS.
- B. T. Wang, P. Zhang, H. Y. Liu, W. D. Li and P. Zhang, J. Appl. Phys., 2011, 109, 063514 CrossRef.
- Z. H. Liu and J. X. Shang, Chin. Phys. B, 2012, 21, 357–362 Search PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1959, 31, 688–699 CrossRef CAS.
- K. Nordlund, S. J. Zinkle, A. E. Sand, F. Granberg, R. S. Averback, R. E. Stoller, T. Suzudo, L. Malerba, F. Banhart, W. J. Weber, F. Willaime, S. L. Dudarev and D. Simeone, J. Nucl. Mater., 2018, 512, 450–479 CrossRef CAS.
- R. A. Enrique, K. Nordlund, R. S. Averback and P. Bellon, J. Appl. Phys., 2003, 93, 2917–2923 CrossRef CAS.
- Y. H. Wang, D. C. Zhang, Z. P. Pi, J. G. Lin and C. Wen, J. Appl. Phys., 2019, 126, 085102 CrossRef.
- Y. S. Li, Y. Z. Yu, X. L. Cheng and G. Chen, Mater. Sci. Eng., A, 2011, 528, 8628–8634 CrossRef CAS.
- T. Yao, A. Sen, A. Wagner, F. Teng, M. Bachhav, A. EI-Azab, D. Murray, J. Gan, D. H. Hurley, J. P. Wharry, M. T. Benson and L. He, Materialia, 2021, 16, 101092 CrossRef CAS.
- G. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 1424 CrossRef CAS.
- K. Fujii and K. Fukuya, J. Nucl. Mater., 2013, 440, 612–616 CrossRef CAS.
- D. Schwen, S. Schunert and A. Jokisaari, Comput. Mater. Sci., 2021, 192, 110321 CrossRef CAS.
- X. J. Liu, Y. L. Zhao, Y. Lu, W. W. Xu, J. P. Jia and C. P. Wang, J. Nucl. Mater., 2014, 451, 366–371 CrossRef CAS.
- Y. Lu, Z. Jiang, L. Y. Li, C. P. Wang, Y. H. Guo, J. J. Han and X. J. Liu, J. Nucl. Eng. Radiat. Sci., 2021, 7, 011605 CrossRef CAS.
- C. Abromeit, H. Wollenberger, S. Matsumura and C. Kinoshita, J. Nucl. Mater., 2000, 276, 104–113 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Honghao Guoa,
Hengfeng Gongc,
Zheng Jianga,
Xiaoyi Huanga,
Xingjun Liuab and
Cuiping Wang*ab
*a,
Honghao Guoa,
Hengfeng Gongc,
Zheng Jianga,
Xiaoyi Huanga,
Xingjun Liuab and
Cuiping Wang*ab








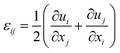

 in the infinite reciprocal space is evaluated as a principal value excluding a volume (2π)3/V around the point n = 0. And B(n) is the elastic interaction energy which can be described as:
in the infinite reciprocal space is evaluated as a principal value excluding a volume (2π)3/V around the point n = 0. And B(n) is the elastic interaction energy which can be described as: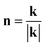 represents a unit vector in reciprocal space, Ωjk(n) is the Green tensor which is inverse to the tensor Cijklnknl.
represents a unit vector in reciprocal space, Ωjk(n) is the Green tensor which is inverse to the tensor Cijklnknl.

 , ∇* = l∇,
, ∇* = l∇, 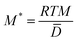 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) = cUDU + ciDi, (i = Nb or Zr). l is the grid length which is chosen as the average lattice parameter of U and Nb, or U and Zr for c = 0.5, and the dimensionless grid size is Δx* = Δy* = 1.0. The simulation cell is 256Δx* × 256Δy* and Δt* is the dimensionless time steps. NA is the Avogadro constant, and
= cUDU + ciDi, (i = Nb or Zr). l is the grid length which is chosen as the average lattice parameter of U and Nb, or U and Zr for c = 0.5, and the dimensionless grid size is Δx* = Δy* = 1.0. The simulation cell is 256Δx* × 256Δy* and Δt* is the dimensionless time steps. NA is the Avogadro constant, and ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) represents the average inter-diffusion coefficient of U–Nb or U–Zr alloy which depends on the temperature T and the concentration of Nb or Zr, and can be calculated with the intrinsic diffusion coefficients in the Table 1. At 973 K, the calculated values of
represents the average inter-diffusion coefficient of U–Nb or U–Zr alloy which depends on the temperature T and the concentration of Nb or Zr, and can be calculated with the intrinsic diffusion coefficients in the Table 1. At 973 K, the calculated values of ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) are 1.96 × 10−15 m2 s−1 in U-45 at% Nb alloy and 2.04 × 10−15 m2 s−1 in U-25 at% Zr alloy. The lattice parameters ai (i = U, Nb or Zr) and anisotropy elastic constants Cij of γ-U, pure Nb and β-Zr are shown in the Table 1.52–54 Eqn (14) is discretized in 2-D space with a uniform grid and solved by using an explicit finite difference scheme with forward Euler time-stepping under periodic boundary conditions. The crystallographic orientation of the simulated region was determined to be [10] in horizontal direction and [01] in vertical direction.
are 1.96 × 10−15 m2 s−1 in U-45 at% Nb alloy and 2.04 × 10−15 m2 s−1 in U-25 at% Zr alloy. The lattice parameters ai (i = U, Nb or Zr) and anisotropy elastic constants Cij of γ-U, pure Nb and β-Zr are shown in the Table 1.52–54 Eqn (14) is discretized in 2-D space with a uniform grid and solved by using an explicit finite difference scheme with forward Euler time-stepping under periodic boundary conditions. The crystallographic orientation of the simulated region was determined to be [10] in horizontal direction and [01] in vertical direction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 s, respectively. The spinodal decomposition evolves along the vertical and horizontal directions and the phase fraction of Zr enriched γ2-phase increases with the increase of dose rates in the Fig. 2. The simulation results indicate that the elastic energy could have great influence on the anisotropy of the microstructure morphology.
270 s, respectively. The spinodal decomposition evolves along the vertical and horizontal directions and the phase fraction of Zr enriched γ2-phase increases with the increase of dose rates in the Fig. 2. The simulation results indicate that the elastic energy could have great influence on the anisotropy of the microstructure morphology.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 s.
270 s.![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = |
eq = |![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq1 −
eq1 − ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq2| indicates the width of the miscibility gap in the equilibrium phase diagram, where
eq2| indicates the width of the miscibility gap in the equilibrium phase diagram, where ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq1 and
eq1 and ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq2 are the average equilibrium compositions of Nb or Zr-lean and Nb or Zr-rich phases, respectively. The width of the miscibility gap Δ
eq2 are the average equilibrium compositions of Nb or Zr-lean and Nb or Zr-rich phases, respectively. The width of the miscibility gap Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq in U-45 at% Nb alloy is 0.49 without irradiation, while Δ
eq in U-45 at% Nb alloy is 0.49 without irradiation, while Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = 0.21 under the dpa rate of 6 × 10−4 dpa s−1. In U-25 at% Zr alloy, Δ
eq = 0.21 under the dpa rate of 6 × 10−4 dpa s−1. In U-25 at% Zr alloy, Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = 0.28 without irradiation, while Δ
eq = 0.28 without irradiation, while Δ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq = 0.09 under the dpa rate of 1 × 10−4 dpa s−1. As can be seen from the figures, the width of miscibility gap for both of the U–Nb and U–Zr shrink with the increase of dose rates.
eq = 0.09 under the dpa rate of 1 × 10−4 dpa s−1. As can be seen from the figures, the width of miscibility gap for both of the U–Nb and U–Zr shrink with the increase of dose rates.





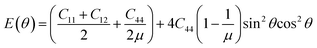
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq) of spinodal decomposition in U–Nb and U–Zr alloys decreases dramatically. Without considering the irradiation, the metastable supersaturated solid solution will spontaneously decompose into two-phase mixtures with the same crystal structure by spinodal decomposition to reduce the free energy of the system. According to the simulation results, it can be seen that U–Nb alloy does not have the spinodal decomposition when the dpa rate reaches 1.87 × 10−3 dpa s−1, while the maximum dpa rate of U–Zr alloy which can undergo the spinodal decomposition is 2.40 × 10−4 dpa s−1. The ballistic effects oppose spinodal ordering according to Martin's results,61 and the alloy does not undergo spinodal decomposition when the dose rate is large enough. Through the analysis of the above results, the time required for the alloy to decompose to the equilibrium state gradually increases with the increase of the dose rates. The irradiation-induced ballistic mixing causes a number of exchanges of atomic positions occur within a finite average relocation distance (RL = 3.37 × 10−10 m in U–Nb and RL = 3.50 × 10−10 m in U–Zr), which “re-mix” the local atom and makes the average composition of local atoms to a certain extent. In other words, irradiation-induced ballistic mixing acts in opposition to spinodal decomposition or demixing mechanism. Therefore, the spinodal decomposition of U-45 at% Nb and U-25 at% Zr alloys under irradiation is the competitive result of demixing and irradiation-induced ballistic mixing. Through the irradiation experiment on as-cast austenitic stainless steel, Fujii et al.62 found that irradiation can reduce the fluctuation of solute composition and the degree of spinodal decomposition, which is consistent with our simulation results. The change of the equilibrium composition in γ1 and γ2-phase at increasing dose rates is caused by more frequent cascade mixing replacement events, forcing the exchange of atoms from the matrix to precipitates and vice versa.33 The simulation results of spinodal decomposition under irradiation in U–Nb and U–Zr alloys are consistent with the different effect of cascade mixing in mesoscale phase field models by Schwen et al.63 Their study demonstrated that the alloys exhibit obvious phase separation under low irradiation rates, and the degree of phase separation decreases with increasing irradiation rates. At sufficiently large irradiation rates, the alloys don't show phase separation and remain mixed. Thus, the irradiation-induced cascade mixing can slow the speed of spinodal decomposition and influences the equilibrium composition and volume fraction of the separated two phases in U-based alloys.
eq) of spinodal decomposition in U–Nb and U–Zr alloys decreases dramatically. Without considering the irradiation, the metastable supersaturated solid solution will spontaneously decompose into two-phase mixtures with the same crystal structure by spinodal decomposition to reduce the free energy of the system. According to the simulation results, it can be seen that U–Nb alloy does not have the spinodal decomposition when the dpa rate reaches 1.87 × 10−3 dpa s−1, while the maximum dpa rate of U–Zr alloy which can undergo the spinodal decomposition is 2.40 × 10−4 dpa s−1. The ballistic effects oppose spinodal ordering according to Martin's results,61 and the alloy does not undergo spinodal decomposition when the dose rate is large enough. Through the analysis of the above results, the time required for the alloy to decompose to the equilibrium state gradually increases with the increase of the dose rates. The irradiation-induced ballistic mixing causes a number of exchanges of atomic positions occur within a finite average relocation distance (RL = 3.37 × 10−10 m in U–Nb and RL = 3.50 × 10−10 m in U–Zr), which “re-mix” the local atom and makes the average composition of local atoms to a certain extent. In other words, irradiation-induced ballistic mixing acts in opposition to spinodal decomposition or demixing mechanism. Therefore, the spinodal decomposition of U-45 at% Nb and U-25 at% Zr alloys under irradiation is the competitive result of demixing and irradiation-induced ballistic mixing. Through the irradiation experiment on as-cast austenitic stainless steel, Fujii et al.62 found that irradiation can reduce the fluctuation of solute composition and the degree of spinodal decomposition, which is consistent with our simulation results. The change of the equilibrium composition in γ1 and γ2-phase at increasing dose rates is caused by more frequent cascade mixing replacement events, forcing the exchange of atoms from the matrix to precipitates and vice versa.33 The simulation results of spinodal decomposition under irradiation in U–Nb and U–Zr alloys are consistent with the different effect of cascade mixing in mesoscale phase field models by Schwen et al.63 Their study demonstrated that the alloys exhibit obvious phase separation under low irradiation rates, and the degree of phase separation decreases with increasing irradiation rates. At sufficiently large irradiation rates, the alloys don't show phase separation and remain mixed. Thus, the irradiation-induced cascade mixing can slow the speed of spinodal decomposition and influences the equilibrium composition and volume fraction of the separated two phases in U-based alloys.![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) eq) is 0.36 under the dpa rate of 3.0 × 10−4 dpa s−1 in U–Nb alloy, while the width of the miscibility gap decreases to 0.21 at the dpa rate of 6.0 × 10−4 dpa s−1. In U–Zr alloy, the width of the miscibility gap decreases from 0.21 to 0.09 with the increase of dpa rate from 5.0 × 10−5 dpa s−1 to 1.0 × 10−4 dpa s−1. According to the simulated results of spinodal decomposition, the tendency of composition region to shrink in the present work coincides well with the previous thermodynamic calculation,64–66 which shows that the miscibility gap shrinks with the effect of irradiation. Therefore, the atom mixing effect is most obvious at the interface at early stage and then causes the change of composition inside γ1 and γ2-phase under irradiation. When the effect of irradiation-induced ballistic mixing and spinodal decomposition reaches an equilibrium state, and the compositions of the two phases no longer change.
eq) is 0.36 under the dpa rate of 3.0 × 10−4 dpa s−1 in U–Nb alloy, while the width of the miscibility gap decreases to 0.21 at the dpa rate of 6.0 × 10−4 dpa s−1. In U–Zr alloy, the width of the miscibility gap decreases from 0.21 to 0.09 with the increase of dpa rate from 5.0 × 10−5 dpa s−1 to 1.0 × 10−4 dpa s−1. According to the simulated results of spinodal decomposition, the tendency of composition region to shrink in the present work coincides well with the previous thermodynamic calculation,64–66 which shows that the miscibility gap shrinks with the effect of irradiation. Therefore, the atom mixing effect is most obvious at the interface at early stage and then causes the change of composition inside γ1 and γ2-phase under irradiation. When the effect of irradiation-induced ballistic mixing and spinodal decomposition reaches an equilibrium state, and the compositions of the two phases no longer change.


