Phase relations, and mechanical and electronic properties of nickel borides, carbides, and nitrides from ab initio calculations

Abstract

Based on density functional theory and the crystal structure prediction methods, USPEX and AIRSS, stable intermediate compounds in the Ni–X (X = B, C, and N) systems and their structures were determined in the pressure range of 0–400 GPa. It was found that in the Ni–B system, in addition to the known ambient-pressure phases, the new nickel boride, Ni₂B₃-Immm, stabilizes above 202 GPa. In the Ni–C system, Ni₃C-Pnma was shown to be the only stable nickel carbide which stabilizes above 53 GPa. In the Ni–N system, four new phases, Ni₆N-R3̄, Ni₃N-Cmcm, Ni₇N₃-Pbca, and NiN₂-Pa3̄, were predicted. For the new predicted phases enriched by a light-element, Ni₂B₃-Immm and NiN₂-Pa3̄, mechanical and electronic properties have been studied.

---

Introduction

Transition metal borides, carbides, and nitrides are of interest in terms of materials science due to the relatively high bulk moduli, ultra-high melting points, and high chemical stabilities. This combination of properties makes these materials highly desirable for a number of industrial applications. Specifically, TMX, TMX₂, and TMX₄ (X = B, C, and N; TM-transition metal) possess comparable bulk moduli to that of superhard cubic-BN (400 GPa), such as ReB₂, WB, OsC, RuC, WC, OsN₂, PtN₂, and WN,^1–3 and some of them have been put to the test and proved to be superhard materials, such as MoN, WB₄, and FeB₄.^4–6 High pressure enables not just the production of new polymorphic modifications of known borides, carbides, and nitrides but also the synthesis of new compounds having stoichiometries not accessible at ambient pressure.⁷ Therefore, recently, the number of theoretical and experimental studies devoted to the search for stable TM–X (X = B, C, and N) compounds has increased. The study of borides, carbides, and nitrides has been carried out practically for all IV group transition metals, with the exception of nickel and copper. For instance, there are many works devoted to the crystal structure predictions and high pressure syntheses of Fe–B,^6,8,9 Fe–C,^10–12 and Fe–N^13–16 compounds.

In the present paper, we investigate nickel borides, carbides, and nitrides under high pressure using modern ab initio crystal structure prediction methods. The Ni–B system comprises several stable (NiB, Ni₄B₃, Ni₂B, and Ni₃B) and metastable (Ni₂₃B₆ and Ni₇B₃) crystalline compounds.^17–19 Recently, Wang et al.²⁰ estimated the stability of ambient-pressure phases up to 100 GPa. They showed that Ni₃B and Ni₄B₃ are unstable at pressures of 80–100 GPa, while Ni₂B and NiB remains stable relative to the decomposition into isochemical mixture. In the Ni–C system, there is no stable intermediate compounds at ambient pressure. Recently, first stable nickel carbide, Ni₃C with cementite-type structure, was synthesized in a diamond anvil cell (DAC) with laser heating through a direct reaction of a nickel powder with carbon at 184 GPa.²¹ In the Ni–N system, there is one known stable intermediate compound, Ni₃N, at ambient pressure. Guillaume et al.²² show that the ambient-pressure structure of Ni₃N remains stable at 20 GPa. Recently, nickel pernitride (NiN₂) with marcasite-type structure was synthesized at 40 GPa using a laser-heated DAC.²³ It should be noted that no crystal structure prediction calculations were performed for these systems.

In our work, we search for new stable structures and study the phase stability, electronic and mechanical properties of the structures in the Ni–B, Ni–C, and Ni–N systems within first-principles calculations.

Computational methods

The search for new stable crystal structures of nickel borides, carbides, and nitrides were performed using evolutionary algorithms implemented in the USPEX package^24–26 and the random sampling method implemented in the AIRSS software^27,28 at 50, 100, 200, 300, and 400 GPa.

The search with USPEX was performed in variable composition mode with 6–36 atoms per unit cell. The size of the first generation in the calculations was equal to 65 structures. 60% of the structures with the lowest enthalpy were selected after the optimization and then used to produce the next generation. A new generation was produced as follow: 35% of all structures were generated by heredity, 20% – by atomic mutation, 10%—by lattice permutation, and 35%—randomly. In average, 36–40 generations have been produced and relaxed at each pressure. Using AIRSS, about 3500–4000 structures were randomly generated and optimized for compounds with fixed stoichiometries (NiX_n; X = B, C, and N; n = 1–4) at each pressure, and those with the lowest enthalpy were selected.

The total energies and forces were calculated by solving the Schrödinger equation based on projector augmented plane-wave implementation of density functional theory (DFT) using the VASP package.^29,30 Exchange correlation effects were treated in the generalized gradient approximation (GGA) with Perdew–Bürke–Ernzerhof scheme.³¹

In all crystal structure prediction calculations, medium-quality optimization was performed using the conjugate gradient. The medium quality settings were as follows: plane-wave cutoff energy—420 eV; Monkhorst–Pack k-point sampling grid of spacing—0.5 Å⁻¹; Gaussian smearing with parameter σ = 0.15 eV. The most promising predicted structures were then optimized at various pressures with higher accuracy: the cutoff energy—700 eV, k-point sampling grid of spacing—0.2 Å⁻¹, and σ = 0.05 eV.

To investigate mechanical properties, static elastic stiffness tensor (C_ij) was calculated from the stress (σ) – strain (ε) relation σ_i = C_ijε_j.

To investigate electronic properties, in addition to the standard PBE, Dudarev's GGA + U (ref. 32) and hybrid functional Heyd–Scuseria–Ernzerhof (HSE06)³³ methods were used.

Structures were visualized in the VESTA package,³⁴ and symmetries of the predicted structures were analyzed using the FindSym program.³⁵

Results and discussion

Crystal structure prediction

The thermodynamic stability of the most favorable structures among the predicted ones was estimated using the convex hull diagrams, which give the convenient graphical representation of the thermodynamic stability of the predicted structures.

Crystal structure prediction calculations have been performed only for the intermediate compounds in the Ni–X (X = B, C, and N) systems. Crystal structure prediction calculations of pure Ni performed earlier by similar procedure showed its stability in Fm3̄m (fcc) structure up to 400 GPa.^36,37 For pure boron, carbon, and nitrogen the following data have been used: B-R3̄m, -Pnnm, -Cmca, and -P6₃/mcm;³⁸ C-P6₃mc (graphite) and -Fd3̄m (diamond); N-Pa3̄, -I2₁3,³⁹, -Pba2,⁴⁰ and -I4̄3m.⁴¹ The pressures of phase transition between listed polymorphic modifications are shown in Fig. 1b–3b.

Fig. 1 Thermodynamic convex hulls of Ni–B system at various pressures and zero temperature (a). Filled symbols denote stable structures, open symbols—metastable structures. Predicted pressure–composition phase diagram for the Ni–B system (b).

Fig. 2 Stability convex hulls of the Ni–C system at various pressures and zero temperature (a). Filled symbols denote stable structures, open symbols—metastable structures. Predicted pressure–composition phase diagram for the Ni–C system (b).

Fig. 3 Stability convex hulls of the Ni–N system at various pressures and zero temperature (a). Filled symbols denote stable structures, open symbols—metastable structures. Predicted pressure–composition phase diagram for the Ni–N system (b).

The Ni–B system. The Ni–B system is most rich in intermediate compounds with representatives in both Ni-rich and B-rich parts. In the Ni-rich part of the system four intermediate compounds, Ni₃B, Ni₂B, Ni₄B₃, and NiB, were revealed (Fig. 1a and S1†).

The Ni₃B-Pnma phase was predicted at 50 GPa and it is stable from ambient pressure to 80 GPa. Above 80 GPa, Ni₃B-Pnma decomposes into solid Ni and Ni₂B (Fig. 1a and Table S1†). For Ni₂B, the structure with the I4/mcm symmetry was predicted at 50, 100, 200, 300, and 400 GPa as the lowest-enthalpy one. This structure is stable in the entire considered pressure range without any phase transitions (Fig. 1b). The Ni₄B₃-Pnma was predicted at 50 GPa as the most energetically favorable. It is stable from 0 to 86 GPa, and above this pressure decomposes into the mixture of (Ni₂B + NiB). The NiB was predicted in the Cmcm structure, which stabilizes at a pressure of 2 GPa and remains stable up to 400 GPa.

In the B-rich part of the Ni–B system, we predicted a new compound that was not previously known, namely Ni₂B₃ (Fig. 1 and Table S1†). This compound was found at 200, 300, and 400 GPa with Immm symmetry. Above 202 GPa, the enthalpy of Ni₂B₃-Immm becomes lower than that of mechanical mixture of (2NiB + B), indicating that the Ni₂B₃-Immm structure stabilizes relative to the decomposition reaction Ni₂B₃ ↔ 2NiB + B (Fig. S2a†).

All these Ni–B structures are dynamically stable, which were confirmed by the calculated phonon spectra (Fig. S3†).

Although the search of the structures stable at ambient pressure has not been performed, the comparison of the found structures with the known ones show, that all the structures stable at ambient pressure, which were observed in experiments, were revealed in our calculations at 50 GPa.^42,43 In addition, we have considered Ni₂₃B₆,¹⁸ observed in experiments, and Ni₇B₃ (ref. 19) suggested theoretically. According to our calculations, Ni₂₃B₆ is metastable at 0 GPa. This is in agreement with experimental results.¹⁸ For Ni₇B₃, we considered two structures: Ni₇B₃-P6₃mc suggested in ref. 19 and Ni₇B₃-Pbca constructed from Fe₇C₃-Pbca,⁴⁴ replacing Fe by Ni and C by B atoms. These structures are very similar and their distinguishing by X-ray powder diffraction technique is problematic. Our calculation showed that Ni₇B₃-Pbca has lower enthalpy than Ni₇B₃-P6₃mc in the pressure range of 0–155 GPa (Fig. S4a†). Based on this, we suggest that most likely the Pbca phase was formed in experiments of Hofmann et al.,¹⁹ than hexagonal phase suggested in that work. With pressure increase, Ni₂₃B₆ and Ni₇B₃ becomes even less favorable (Fig. 1).

The Ni–C system. Crystal structure prediction calculations have revealed one stable compound in the Ni–C system, Ni₃C (Fig. 2 and Table S2†). It stabilizes in cementite-type orthorhombic structure Pnma, which is in agreement with recent experimental results,²¹ where Ni₃C-Pnma was synthesized at 184 GPa using DAC technique. According to the obtained results, Ni₃C-Pnma becomes energetically more favorable than (3Ni + C) above 53 GPa (Fig. 2b). There are no imaginary modes in the phonon spectra of Ni₃C-Pnma (Fig. S5†), indicating that it is dynamically stable.

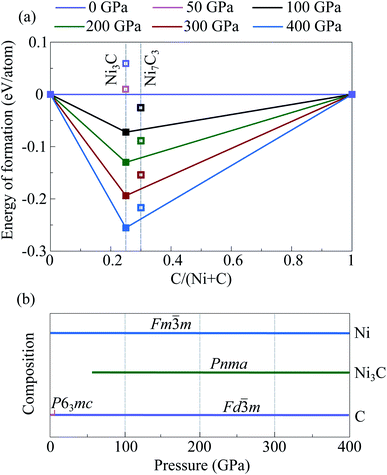
In addition, we constructed Ni-analogs of stable iron carbide structures Fe₇C₃-P6₃mc,⁴⁵ Fe₇C₃-Pbca,⁴⁴ and Fe₂C-Pnma,¹² by replacing all iron atoms by nickel ones. According to the obtained results, constructed Ni₇C₃-Pbca is more favorable than constructed Ni₇C₃-P6₃mc (Fig. S4b†). Nevertheless, Ni₇C₃-Pbca is unstable relative to the mechanical mixtures of (Ni + C) or (Ni₃C + C) in the entire considered pressure range (Fig. 2). Similar calculations for Ni₂C-Pnma showed that this compound is not stable, and the energy difference reaches 0.4 eV f.u⁻¹.

Crystal structure predictions in C-rich part of the Ni–C system were performed for fixed stoichiometries, namely NiC₄, NiC₃, NiC₂, and NiC. For all these compounds the lowest-enthalpy structures are unstable and decompose into isochemical mixture in the entire considered pressure range.

The Ni–N system. The preliminary results of crystal structure prediction calculations in the Ni–N system in the pressure range of 0–300 GPa were reported as the conference proceedings.⁴⁶ Here, we extended the studied pressure range up to 400 GPa, found new structures based on the analogy with carbides and reanalyze obtained phase relations.⁴⁶ In addition to crystal structure predictions, we constructed two structural models, Ni₇N₃-Pbca and Ni₇N₃-P6₃mc, from known iron carbides Fe₇C₃-Pbca and Fe₇N₃-P6₃mc by replacing all Fe by Ni atoms. The volume, lattice parameters, and atomic coordinates were optimized at various pressures for the resulting models.

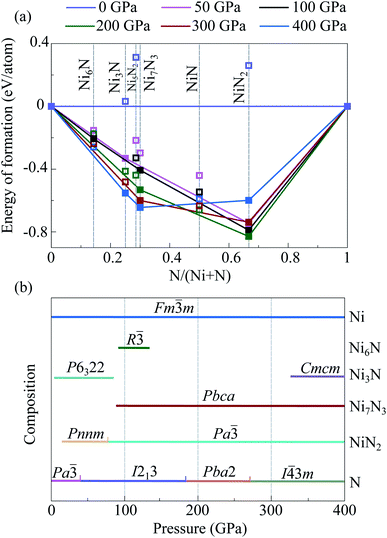
Performed crystal structure prediction calculations show that there are two stable intermediate compounds in the Ni–N system at 50 GPa, Ni₃N and NiN₂ (Fig. 3 and Table S3†). Both predicted Ni₃N-P6₃22 and NiN₂-Pnnm were observed earlier in high-pressure experiments.^22,23 According to obtained results, Ni₃N-P6₃22 is stable in the pressure range of 4–96 GPa. Below 4 GPa, Ni₃N-P6₃22 is unstable relative to mechanical mixture of (3Ni + N), and above 96 GPa it is unstable relative to mechanical mixture of (Ni₇B₃ + Ni). NiN₂-Pnnm stabilizes above 14 GPa. At 100 GPa, there are three stable nickel nitrides, predicted Ni₆N-R3̄ and NiN₂-Pa3̄, and constructed Ni₇N₃-Pbca. Ni₆N-R3̄ stabilizes at 98 GPa, and above 114 GPa decomposes into solid Ni and Ni₇N₃. Constructed Ni₇N₃-Pbca is more favorable than constructed Ni₇N₃-P6₃mc in the entire pressure range (Fig. S2†). Ni₇N₃-Pbca become stable relative to Ni₃N + NiN₂ above 93 GPa and stable at least up to 400 GPa. NiN₂ undergoes a phase transition from known NiN₂-Pnnm to the new predicted NiN₂-Pa3̄ at 96 GPa. NiN₂-Pa3̄ is stable at least up to 400 GPa. At 400 GPa, in addition to Ni₇N₃-Pbca and NiN₂-Pa3̄, one new nitride Ni₃N-Cmcm was predicted. It stabilizes relative to the mechanical mixture of (Ni₇N₃ + Ni) above 331 GPa. Phonon calculations show that the predicted nickel nitrides are dynamically stable; i.e., they have no imaginary modes in the phonon spectra (Fig. S6†).

Crystal chemistry of the predicted structures

Structural data of the new predicted compounds are given in Table 1.

Table 1 Structural data of structures introduced in the present work

Compound	P (GPa)	Space group	Lattice parameters (Å, deg)			Atom	Coordinates
							x	y	z
Ni2B3	250	Immm (#71)	a = 2.695	b = 3.357	c = 5.622	Ni1	0.000	0.000	0.804
			α = 90.00	β = 90.00	γ = 90.00	B1	0.500	0.000	0.500
						B2	0.000	0.251	0.500
Ni6N	100	R3̄ (#148)	a = 4.058	b = 4.058	c = 11.653	Ni1	0.316	0.331	0.246
			α = 90.00	β = 90.00	γ = 120.00	N1	0.000	0.000	0.000
Ni7N3	100	Pbca (#61)	a = 4.131	b = 12.671	c = 10.978	Ni1	−0.080	0.534	0.686
			α = 90.00	β = 90.00	γ = 90.00	Ni2	0.744	0.878	0.585
						Ni3	0.411	0.622	0.626
						Ni4	0.204	0.779	0.522
						Ni5	0.251	0.873	0.702
						Ni6	−0.092	0.718	0.693
						Ni7	0.249	−0.037	0.521
						N1	−0.004	−0.017	0.656
						N2	−0.004	0.632	0.561
						N3	0.499	0.765	0.648
Ni3N	300	Cmcm (#63)	a = 2.295	b = 7.492	c = 5.541	Ni1	0.000	0.060	0.250
			α = 90.00	β = 90.00	γ = 90.00	Ni2	0.000	0.637	−0.059
						N1	0.000	0.741	0.250
NiN2	200	Pa3̄ (#205)	a = 4.054	b = 4.054	c = 4.054	Ni1	0.000	0.000	0.000
			α = 90.00	β = 90.00	γ = 90.00	N1	0.592	0.592	0.592

---

The most crystallochemically interesting structures are the structures of compounds enriched by the light element. We have revealed two such compounds, NiN₂ and Ni₂B₃. Two found structures of NiN₂, NiN₂-Pa3̄, corresponds to the well-known structural type of pyrite with N–N molecular units.

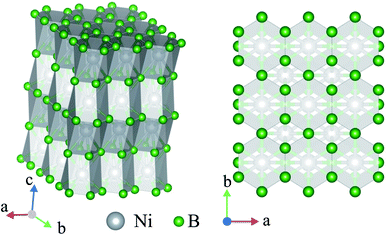
The crystal structure of Ni₂B₃ is also characterised by the covalently bonded units. In this case, these are infinite (001) layers of boron atoms. In the layer each B atom is connected to four other B atoms forming the net with hexagonal and rhombic loops (Fig. 4a). The B–B bond distance within the layer is 1.67 Å at 250 GPa. The elemental boron is characterised by nearly the same B–B distance, 1.7 Å. The covalent nature of B–B bond in Ni₂B₃ structure is also confirmed by the electronic density distribution (Fig. S8†). Boron layers alternates with layers of Ni atoms, forming rectangular centered network (Fig. 4b). Each Ni is coordinated by 10 boron atoms, the six of which are from the top, and four are from the bottom layer. The performed analysis of the structures with the similar stoichiometry has revealed another structure, W₂CoB₂, belonging to the described structural type.^47,48

Fig. 4 Crystal structure of Ni₂B₃-Immm in two projections.

Graphical representation of the Ni₆N-R3̄, Ni₃N-Cmcm, Ni₇N₃-Pbca, and NiN₂-Pa3̄ crystal structures are shown in Fig. S7.†

Elastic properties

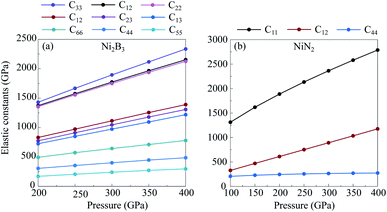
Transition metal borides, carbides, and nitrides often exhibit extraordinary mechanical properties. Elastic constants are helpful to understand the mechanical properties and provide useful information to estimate the hardness of a structure. To that end, we investigate the elastic properties of new predicted compounds enriched by a light-element, NiN₂-Pa3̄ and Ni₂B₃-Immm, within the strain–stress method in combination with the DFT. Calculated elastic constants of NiN₂-Pa3̄ and Ni₂B₃-Immm are listed in Table 2. From Table 2 and Fig. 5, it could be seen that the elastic constants C_ij for these structures are all positive, increase monotonically with increasing pressure, and the whole set of the elastic constants of the structures satisfy the mechanical stability criteria.⁴⁹ This means that NiN₂-Pa3̄ and Ni₂B₃-Immm are mechanically stable in the considered pressure range.

Table 2 Calculated elastic constants C_ij (GPa) of NiN₂-Pa3̄ and Ni₂B₃-Immm at different pressures

Phase	P (GPa)	C11	C12	C13	C22	C23	C33	C44	C55	C66
NiN2-Pa3̄	100	1311.6	326.4	326.2	1311.5	326.5	1311.6	204.8	204.8	204.8
	200	1887.7	609.7	609.5	1887.7	609.7	1887.7	243.5	243.5	243.5
	300	2363.3	891.5	891.3	2363.3	891.5	2363.3	263.1	263.1	263.1
	400	2787.9	1175.5	1175.2	2787.9	1175.5	2787.9	272.8	272.8	272.8
Ni2B3-Immm	200	1372.3	831.2	724.6	1354.5	774.6	1429.9	305.3	169.8	493.4
	300	1773.5	1114.3	973.2	1750.0	1045.2	1895.3	400.4	239.6	643.6
	400	2153.0	1389.9	1218.3	2126.0	1307.1	2336.1	486.2	297.1	780.4

---

Fig. 5 Calculated elastic constants of Ni₂B₃-Immm (a) and NiN₂-Pa3̄ (b) as functions of pressure.

Calculated bulk modulus B of NiN₂-Pa3̄ and Ni₂B₃-Immm are ∼87% and ∼82% of that estimated for diamond, respectively, while shear modulus G of NiN₂-Pa3̄ and Ni₂B₃-Immm are ∼35% and ∼38% of that estimated for diamond, respectively (Table 3). Predicted NiN₂-Pa3̄ and Ni₂B₃-Immm are ductile materials since their B/G values (Table 3) are greater than 1.75.⁵⁰

Table 3 Calculated bulk modulus B (GPa), shear modulus G (GPa), the B/G ratio and Vickers hardness (GPa) of NiN₂-Pa3̄ and Ni₂B₃-Immm at different pressures. For comparison, the data⁵³ on diamond are presented

Phase	P (GPa)	B	G	B/G	H^ChenV	H^TianV
NiN2-Pa3̄	100	654.8	293.6	2.23	18.7	20.6
	200	1035.7	362.7	2.86	15.4	18.1
	300	1382.1	403.2	3.43	12.8	15.8
	400	1712.9	428.6	4.00	10.7	13.9
Ni2B3-Immm	200	979.7	297.5	3.29	10.9	13.4
	300	1298.1	388.1	3.34	12.9	15.9
	400	1604.8	467.7	3.43	14.2	17.6
Diamond^53	100	838	848	—	—	—
	200	1188	1023	—	—	—
	300	1521	1168	—	—	—
	400	1839	1295	—	—	—

---

In order to investigate the hardness of NiN₂-Pa3̄ and Ni₂B₃-Immm at various pressures we employ empirical Chen⁵¹ and Tian et al.⁵² models. The Vickers hardness of NiN₂-Pa3̄ and Ni₂B₃-Immm are estimated to be 19 GPa and 12 GPa, respectively. The hardness of NiN₂-Pa3̄ decreases with increasing pressure, while that of Ni₂B₃-Immm increases with increasing pressure. The estimated H_V of both predicted structures are below minimal criteria of 20 GPa of hardness. Therefore, NiN₂-Pa3̄ and Ni₂B₃-Immm are not classified as a hard materials.

Electronic structure

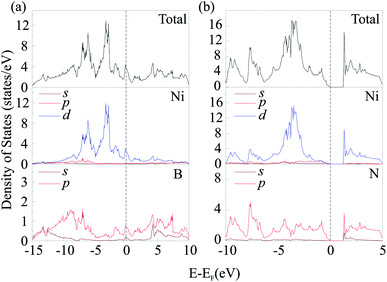
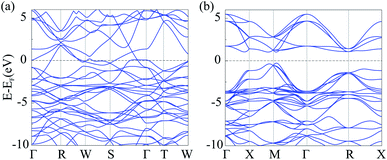
To investigate electronic characteristics of NiN₂-Pa3̄ and Ni₂B₃-Immm, we calculate their total/partial electronic density of states (DOS) (Fig. 6) and band structures (Fig. 7).

Fig. 6 Total and partial DOS calculated for Ni₂B₃-Immm (a) and NiN₂-Pa3̄ (b).

Fig. 7 Calculated band structures of Ni₂B₃-Immm (a) and NiN₂-Pa3̄ (b).

The Fermi level of the considered phases is set to zero. The result shows that Ni₂B₃-Immm exhibit metallic features. From calculated partial DOS (Fig. 6a), we noticed that Ni d orbital has hybridization with B p orbital. The lower bands in the valence band region are mainly contributed by B 2p states, while near the top of valence bands main contributors are Fe 3d states. The Fermi level are mostly occupied by the Fe 3d electrons, with some contribution of B 2p electrons. On the other hand, NiN₂-Pa3̄ is found to be a semiconductor with the indirect band gap of 1.297 eV. The electronic states at the lower energy range of the valence bands are mainly contributed by N 2p orbitals, while Ni 3d orbitals dominate at the top of valence bands. The main contributors in the conduction band region are unoccupied Fe 3d states, with some contribution of N 2p states.

It is well-known that GGA often underestimates the width of band gap. For this reason, and also to avoid misleading, we performed GGA + U (with U = 2, 4 eV) and hybrid (HSE06) calculations. The obtained results showed that PBE, GGA + U, and HSE06 give qualitatively the same DOS and band structures (Fig. S9 and S10†). This fact indicates that the results obtained by standard PBE calculations are valid. For NiN₂-Pa3̄, the band gap obtained by GGA + U with U = 2 eV was equal to 1.524 eV, by GGA + U with U = 4 – 1.001 eV, by HSE06 − 2.237 eV (Fig. S10b†).

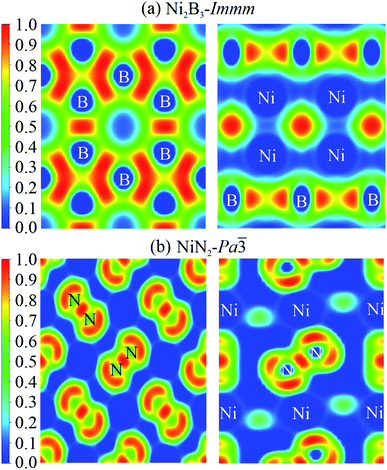
To elucidate chemical bond properties of Ni₂B₃-Immm and NiN₂-Pa3̄, electron localization function (ELF) diagrams were constructed (Fig. 8). The ELFs of the structures are derived from various planes and different colours indicate diverse degrees of electron localization: the red means that the electron is totally localized at the realm and blue means the opposite situation, namely, the electron is not localized at all. According to the obtained result, in Ni₂B₃-Immm, we could observe that the boron atoms form a mesh structure. In NiN₂-Pa3̄, the nitrogen atoms form N₂ dimers. In both structures, valence electrons are not localized around the Ni atoms. These data suggest that the chemical bonds among nickel mainly exhibit ionic characteristics and boron/nitrogen atoms form covalent chemical bonds, which seemingly do not strongly interact with nickel atoms.

Fig. 8 Electron localization functions of Ni₂B₃-Immm (a) and NiN₂-Pa3̄ (b).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was funded by the Ministry of Education and Science of the Republic of Kazakhstan under research project AP09562464 “Search for functional (superhard) materials in Ni–B, Ni–C, and Ni–N systems” and the state-assigned project of the IGM SB RAS. The computations were performed using resources provided by the Novosibirsk State University Supercomputer Center.

Notes and references

1. J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Science, 2006, 311, 1275–1278.
2. Z. Zhao, L. Xu, L.-M. Wang, B. Xu, M. Wang, Z. Liu and J. He, Comput. Mater. Sci., 2011, 50, 1592–1596.
3. Y. Zhang, Z.-R. Liu, D.-W. Yuan, Q. Shao, J.-H. Chen, C.-L. Wu and Z.-L. Zhang, Acta Metall. Sin., 2019, 32, 1099–1110.
4. M. Ürgen, O. Eryilmaz, A. Çakir, E. Kayali, B. Nilüfer and Y. Işik, Surf. Coat. Technol., 1997, 94–95, 501–506.
5. R. Mohammadi, A. T. Lech, M. Xie, B. E. Weaver, M. T. Yeung, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10958–10962.
6. H. Gou, N. Dubrovinskaia, E. Bykova, A. A. Tsirlin, D. Kasinathan, W. Schnelle, A. Richter, M. Merlini, M. Hanfland, A. M. Abakumov, D. Batuk, G. Van Tendeloo, Y. Nakajima, A. N. Kolmogorov and L. Dubrovinsky, Phys. Rev. Lett., 2013, 111, 157002.
7. A. Zerr, R. Riedel, T. Sekine, J. E. Lowther, W.-Y. Ching and I. Tanaka, Adv. Mater., 2006, 18, 2933–2948.
8. I. Harran, H. Wang, Y. Chen, M. Jia and N. Wu, J. Alloys Compd., 2016, 678, 109–112.
9. A. N. Kolmogorov, S. Shah, E. R. Margine, A. F. Bialon, T. Hammerschmidt and R. Drautz, Phys. Rev. Lett., 2010, 105, 217003.
10. Z. G. Bazhanova, A. R. Oganov and O. Gianola, Phys.-Usp., 2012, 55, 489.
11. G. L. Weerasinghe, R. J. Needs and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 174110.
12. N. Sagatov, P. Gavryushkin, I. Medrish, T. Inerbaev and K. Litasov, Russ. Geol. Geophys., 2020, 61, 1345–1353.
13. L. Wu, R. Tian, B. Wan, H. Liu, N. Gong, P. Chen, T. Shen, Y. Yao, H. Gou and F. Gao, Chem. Mater., 2018, 30, 8476–8485.
14. Y. Chen, X. Cai, H. Wang, H. Wang and H. Wang, Sci. Rep., 2018, 8, 10670.
15. Z. Wang, Y. Li, H. Li, I. Harran, M. Jia, H. Wang, Y. Chen, H. Wang and N. Wu, J. Alloys Compd., 2017, 702, 132–137.
16. M. Bykov, E. Bykova, G. Aprilis, K. Glazyrin, E. Koemets, I. Chuvashova, I. Kupenko, C. McCammon, M. Mezouar and V. Prakapenka, et al., Nat. Commun., 2018, 9, 2756.
17. V. Raghavan, J. Phase Equilib. Diffus., 2007, 28, 377–379.
18. M. Baricco, E. Ferrari and L. Battezzati, MRS Proceedings, 1995, 398, 81.
19. K. Hofmann, N. Kalyon, C. Kapfenberger, L. Lamontagne, S. Zarrini, R. Berger, R. Seshadri and B. Albert, Inorg. Chem., 2015, 54, 10873–10877.
20. M. Wang, J. Xie, K. Xue and L. Li, Comput. Mater. Sci., 2021, 194, 110465.
21. T. Fedotenko, S. Khandarkhaeva, L. Dubrovinsky, K. Glazyrin, P. Sedmak and N. Dubrovinskaia, Minerals, 2021, 11, 516.
22. C. Guillaume, J. P. Morniroli, D. J. Frost and G. Serghiou, J. Phys.: Condens. Matter, 2006, 18, 8651–8660.
23. K. Niwa, R. Fukui, T. Terabe, T. Kawada, D. Kato, T. Sasaki, K. Soda and M. Hasegawa, Eur. J. Inorg. Chem., 2019, 2019, 3753–3757.
24. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
25. A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237.
26. A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182.
27. C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2006, 97, 045504.
28. C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201.
29. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
30. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
32. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
33. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
34. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
35. H. T. Stokes and D. M. Hatch, J. Appl. Crystallogr., 2005, 38, 237–238.
36. T. M. Inerbaev, N. Sagatov, D. Sagatova, P. N. Gavryushkin, A. T. Akilbekov and K. D. Litasov, ACS Earth Space Chem., 2020, 4, 1978–1984.
37. N. E. Sagatov, A.-D. B. Bazarbek, T. M. Inerbaev, P. N. Gavryushkin, A. T. Akilbekov and K. D. Litasov, ACS Earth Space Chem., 2021, 5, 596–603.
38. H. Dong, A. R. Oganov, V. V. Brazhkin, Q. Wang, J. Zhang, M. M. D. Esfahani, X.-F. Zhou, F. Wu and Q. Zhu, Phys. Rev. B, 2018, 98, 174109.
39. M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Nat. Mater., 2004, 3, 558–563.
40. Y. Ma, A. R. Oganov, Z. Li, Y. Xie and J. Kotakoski, Phys. Rev. Lett., 2009, 102, 065501.
41. C. J. Pickard and R. Needs, Phys. Rev. Lett., 2009, 102, 125702.
42. R. Gumeniuk, H. Borrmann and A. Leithe-Jasper, Z. Kristallogr. - New Cryst. Struct., 2006, 221, 425–426.
43. E. Havinga, H. Damsma and P. Hokkeling, J. Less-Common Met., 1972, 27, 169–186.
44. C. Prescher, L. Dubrovinsky, E. Bykova, I. Kupenko, K. Glazyrin, A. Kantor, C. McCammon, M. Mookherjee, Y. Nakajima and N. Miyajima, et al., Nat. Geosci., 2015, 8, 220–223.
45. N. Sagatov, P. N. Gavryushkin, T. M. Inerbaev and K. D. Litasov, RSC Adv., 2019, 9, 3577–3581.
46. P. N. Gavryushkin, N. Sagatov, D. Sagatova, M. V. Banaev, K. G. Donskikh and K. D. Litasov, J. Phys.: Conf. Ser., 2020, 1590, 012010.
47. E. Partee and B. Chabot, Handb. Phys. Chem. Rare Earths, 1984, 6, 113–334.
48. M. Pani, F. Merlo and M. L. Fornasini, Z. Kristallogr. - Cryst. Mater., 2002, 217, 415–419.
49. Z. Wu, E. Zhao, H. Xiang, X. Hao, X. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
50. S. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843.
51. X.-Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281.
52. Y. Tian, B. Xu and Z. Zhao, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106.
53. E. Güler and M. Güler, Chin. J. Phys., 2015, 53, 195–205.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra06160g

---