Reactive force fields for modeling oxidative degradation of organic matter in geological formations

Abstract

In an attempt to better explore organic matter reaction and properties, at depth, to oxidative fluid additives, we have developed a new ReaxFF potential to model and describe the oxidative decompositions of aliphatic and aromatic hydrocarbons in the presence of the oxychlorine ClO_n⁻ oxidizers. By carefully adjusting the new H/C/O/Cl parameters, we show that the potential energies in both training and validation sets correlate well with calculated density functional theory (DFT) energies. Our parametrization yields a reliable empirical reactive force field with an RMS error of ∼1.57 eV, corresponding to a 1.70% average error. At this accuracy level, the reactive force field provides a reliable atomic-level picture of thermodynamically favorable reaction pathways governing oxidative degradation of H/C/O/Cl compounds. We demonstrate this capability by studying the structural degradation of small aromatic and aliphatic hydrocarbons in the presence of oxychlorine oxidizers in aqueous environments. We envision that such reactive force fields will be critical in understanding the oxidation processes of organic matter in geological reservoirs and the design of the next generation of reactive fluids for enhanced shale gas recovery and improved carbon dioxide adsorption and sequestration.

---

Introduction

Oxidation of natural organic matter (OM), whether in soil or geological formations, leads to changes in the chemical and physical properties of OM. Soil OM, when oxidized, undergoes changes in nutrient bioavailability, pollutant retention and its effects upon water quality, and soil productivity. Given that soils participate in half of the carbon that is recycled in the atmosphere,¹ understanding the chemical redox processes that control CO₂ release are of paramount concern for global climate initiatives. While soils contain more organic carbon than the combined totals of Earth's vegetation and atmosphere, the majority of organic carbon on earth is held in geological formations.² Kerogen as the source of petroleum hydrocarbons³ is a crosslinked polymeric material with a disordered molecular structure intertwined with a nanogranular mineral matrix.^4,5 It has the mechanical and physical characteristic signatures of polymers,⁶ though its chemical structure is not as readily oxidizable as synthetic polymers due to its compaction and thermal alteration over geological time. Since the 1950's, attempts to unravel the chemical structure of kerogen have utilized oxidation chemistry as a means of breaking the polymer structure into smaller fragments for analysis.⁷

In unconventional source rock reservoirs, the hydrocarbon reserves are predominantly trapped in the pore space of the organic matter.⁸ Traditional hydraulic fracturing methods designed to fracture conventional reservoirs may not effectively crack and stimulate the ductile, polymeric kerogen. Chemical treatment of the polymeric properties of kerogen while taking into account its nanoscale porosities and ultra-low permeability, will introduce open flow channels, increase its permeability and eventually optimize recovery purposes. Recently, in an attempt to address the challenges associated with the kerogen's low permeability, Hull et al.⁹ designed fluid oxidizers as additives to the slick water in hydraulically fracking source rocks. The designed fluid additive has strong oxidizers with very high concentrations, and was successfully used recently. Oxidizing agents composed of oxyhalides such as bromate BrO₃⁻ and chlorate ClO₃⁻ are effective in breaking down shale's organic matter under reservoir temperatures.⁹

To further identify and develop oxidizers for various organic matter treatment, at depth, the earlier studies had to be generalized and optimized. In this work, we concentrate on oxychlorine ClO_n⁻ oxidizers as a class of effective oxidizing reagents to elucidate the oxidative degradation pathways likely to lead to organic matter cleavage, porosity enhancement, and increase in organic surface area. ClO_n⁻ oxidizers (n = 1–4), typically as alkali or alkaline earth metal salts, are stable, commercially available compounds with wide applicability. Hypochlorite ClO⁻ is ubiquitously used for disinfection and water treatment, while chlorite ClO₂⁻ is one of the common oilfield oxidizers used in reservoir stimulation. Perchlorate ClO₄⁻, though thermodynamically is a strong oxidant, is kinetically inert except under acidic conditions or in the presence of metal activator. ClO₄⁻ and chlorate ClO₃⁻ are also naturally occurring, coexisting on earth and on the Mars surface.¹⁰

The atomistic simulations of complex reactive processes at the organic matter–oxidizer interface require a numerically efficient framework to describe interatomic and intermolecular forces while faithfully describing the formation and breakage of covalent bonds. Although the first principle quantum chemistry approaches provide such information, their exorbitant computational cost still limits their application to short time and small length scales that render them unamenable to simulating multi-stage oxidative decomposition processes. Alternatively, adequately calibrated ReaxFF potentials can describe the formation, transition, and dissociation of chemical bonds with the density functional theory (DFT)-level accuracy at a reasonable computational cost.^11,12 A well-calibrated ReaxFF can also simulate chemical reactions at the solid, liquid, and gas interfaces. This transferability gives ReaxFF a unique capability to simulate complex reactive processes involving multiple phases.^13–16 These attributes make the ReaxFF potential an ideal simulation framework to unravel the mechanistic picture of oxidative reaction pathways at the kerogen-reactive fluid interface.

In this paper, we summarize ReaxFF's functional form and describe the new H/C/O/Cl ReaxFF parameterizations while comparing the calibrated ReaxFF's performance against DFT energetics. By performing ab initio molecular dynamics (MD) simulations, we propose the energetically-favorable oxidative decomposition pathways (reactant, transition, and product states) of small aromatic and aliphatic hydrocarbons in the presence of oxychlorine oxidizers (ClO_n⁻: n = 1–4). Subsequently, we demonstrate that ReaxFF can quantitatively capture the energetics of proposed oxidation pathways. Finally, with the new ReaxFF parameterization at hand, we study the mechanistic picture of the oxidative degradations of small organic molecules with aromatic and aliphatic moieties representing the small unit of polymer-like kerogen frameworks with ClO_n⁻ in aqueous environments.

Model and methods

Density functional theory (DFT) calculations

We have systematically conducted a series of nonperiodic DFT energy calculations in establishing parameter optimization data sets used for the new ReaxFF parameterizations. The DFT calculations of the target molecules use B3LYP functional^17,18 with different basis sets, as implemented in Gaussian16,¹⁹ such as 6-31G* (ref. 20) for minimum energy/single-point energy calculations, 6-31G** (ref. 21 and 22) for charge distribution calculations, 6-31G*(D3)/6-31++G**(D3)²³ for van der Waals interatomic interaction energy calculations, and PBE functional²⁴ for further charge evaluations by Bader analysis as considering adequate accuracy and computational time expense. For potential energy surfaces (PES) calculations, we employ the reliable B3LYP functional that has been extensively used and proven to fit the potential energies of various conformational H/C/O molecules.^25–31 We performed the DFT (with B3LYP) calculations for closed-shell systems using the spin-restricted DFT (RDFT) approach to be consistent with the classical mechanics' concept employed in the ReaxFF parameterization procedure when reproducing the minimum and single-point energies. We note that it is essential to use a consistent DFT energy level across fitting and validation data sets to ensure that the newly calibrated ReaxFF properly represents the PES.

Reactive force field (ReaxFF) parameterizations

In ReaxFF, the bond energy calculations are derived from a general energy expression like below;

E^TOT = E^intra + E^inter (1)

E^intra: this term represents all intramolecular interactions for bond order and bond energy estimations. It describes bond dissociations and formations based on bond distance, bond angle, and torsion angle-dependent terms. The parameters in these terms are adjusted to fit the minimized DFT energy curves for a predefined set of target molecules. The short-ranged bond order and bond energy result from the directional bonding environment surrounding atoms. The ReaxFF should be parameterized such that it reproduces a local bonding environment's energy and should be able to characterize the energy difference between conformational molecular structures. ReaxFF uses over- and under-coordination terms to penalize unphysical valence configurations that might occur during dynamic simulations in the cases of highly compressed and expanded systems. These terms ensure proper valency and allow a smooth transition from bonded to non-bonded configurations. Such transitions are usually defined by a cut-off tapering function as implemented in Tersoff-like bond order potentials such as REBO and AIREBO.^32–34 It is noteworthy that the ReaxFF's short-ranged bond order ideas are inspired by the work of Pauling,³⁵ Johnston,³⁶ and others on chemical reactions.

E^inter: this term can be decomposed to E_Coulomb and E_vdW. The electrostatic interactions between pairs of atoms are based on the charge populations reflected from charge transfer by electronegativity and polarization effects. The E_Coulomb term uses a geometry-based charge calculation scheme³⁷ similar to charge equilibration with the feature that Coulomb effects between bonded atoms are shielded to saturate for short distances. One of the most widely used methods for calculating atomic charges in DFT is the Mulliken charge population method. Mulliken charges do not fit the dipole and higher charge moments but do reasonably well in describing the local electronegativity and provide a self-consistent scheme to partition atomic charges. In other words, Mulliken is well suited to fit electronegativity and hardness parameters in the EEM³⁷, similar to QEq³⁸ schemes, employed in ReaxFF. The E_vdW term includes all non-bonding interactions, which indicate short-ranged Pauli repulsion and long-ranged dispersion interactions.

We used the general H/C/O parameters³¹ and H/O parameters³⁹ as initial parameter sets to optimize H/C/O/Cl parameters that are fully transferable with various conformational H/C/O/Cl molecules and aqueous environment described in this study. The optimized parameters for the new ReaxFF implemented in large-scale atomic/molecular massively parallel simulator (LAMMPS) code⁴⁰ were determined by using continuous single-parameter search trial and error with in-house codes and fitting the minimum energies to the DFT energetics to minimize the root mean squared error (RMSE) expressed as below;

where x_i,DFT is the ith molecule's DFT energy value, x_i,ReaxFF is the ith molecule's ReaxFF energy estimate, and n is the number of molecules used in non-periodic boundary condition simulations for the fitting and validation data sets.

Transition state (TS) optimizations

To understand the local reaction mechanism of a small hydrocarbon oxidized by ClO_n⁻, a transition state search is necessary to find a saddle-point of the potential energy landscape. This is a critical step in defining the minimum reaction path between the reactant and product states. To locate the transition state with one negative eigenvalue, we used the quadratic synchronous transit approach technique to get closer to the quadratic region of the transition state. We also used the eigenvector-following algorithm to complete the search and converge to the saddle point. These transition state optimizations can be readily performed using the Gaussian16 program.¹⁹ In this work, we employed ab initio molecular dynamics (MD) to determine a suitable initial geometry for the constrained transition state calculations. For these MD simulations, we used the generalized gradient approximation and Perdew–Burke–Ernzerhof functional (GGA–PBE²⁴), implemented in the Vienna Ab Initio Simulation Package (VASP).^41–43 We used the projector-augmented wave (PAW) method with a plane-wave basis set to describe the interaction between the core and valence electrons. We performed single point ReaxFF energy calculations with the DFT-optimized geometries to check whether the ReaxFF's TS energy profile matches that of DFT.

Molecular dynamics (MD) simulations

The system configurations for the new ReaxFF MD simulations are composed of the following components: (a) 23 perchlorate (ClO₄⁻) oxidizers as benchmarking the same concentration (0.013 M) of bromate BrO₃⁻ oxidizer used in experiments to break down the polymeric structure of organic matter,⁹ (b) 23 hydronium ions (H₃⁺O) which are added to ensure charge-neutrality in the model for each simulation box, and (c) relaxed water box at ∼1.0 g cm⁻³ density placed in a periodic box. The MD simulations of the new ReaxFF implemented in the LAMMPS code⁴⁰ are performed in the NVT ensemble for 100 ps. The equations of motion are integrated via the velocity Verlet algorithm with a time step of 0.25 fs at 450 K using a thermostat with a 100 fs of temperature rescaling constant. We used DFT-optimized geometry for all molecules, including the relaxed aliphatic and aromatic molecules. To initialize MD configurations, we placed the DFT-relaxed molecules randomly in the simulation box.

Results and discussion

Potential energy surface (PES) of the new ReaxFF parameterization

Since the new ReaxFF parameterization is to provide a chemical and physical means of describing the oxidative decompositions of the small aromatic and aliphatic hydrocarbons with chlorate oxidizers (ClO_n⁻: n = 1–4), the reliable DFT training and testing data sets should include a wide range of reactive and non-reactive H/C/O/Cl bonding environments. The extensive DFT data set is needed to ensure accurate PES descriptions. The H/C/O/Cl compound data sets used herein are as follows: (a) thirty-five small molecules that have mostly aliphatic-like structures as the PES fitting data set and (b) thirty-five larger molecules that are predominantly aromatic-like structures as the PES validation data set.

Fig. 1 shows bond formation energies that are evaluated at energy-minimized geometries for seventy different molecules in the training and validation data sets. We compare the new ReaxFF energies against the DFT energies at B3LYP/6-31G* level of theory. The bond formation energies were calculated by

E_f = E_complex − n_HE_H − n_CE_C − n_OE_O − n_ClE_Cl (3)

where E_f is defined as the formation energy, E_complex is the total energy per each complex, n_x (x = H, C, O, and Cl) is the number of atoms, and E_x is atomic energy for each element. With the new parameterization, the linear regression plot (correlation coefficient, R² = 0.997) exhibits a strong correlation between the bond formation energies calculated by the new ReaxFF and the DFT bond formation energies. With this slope, an average percent error of the bonding configurations of the total seventy molecules is only 1.70%, indicating that the root mean square (RMS) average difference between the new ReaxFF parametrization and DFT energies is ∼1.57 eV (RMS average error per atom of ∼0.10 eV). The bond formation energy values calculated with the energy-minimized geometries for all H/C/O/Cl compounds are summarized in Table S1 presented in ESI.†

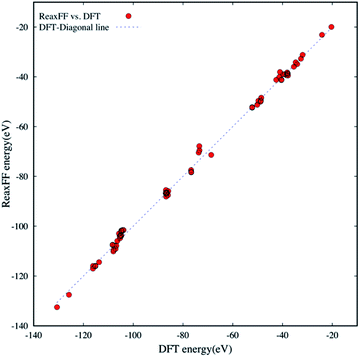Fig. 1 The comparison of DFT and ReaxFF bond formation energies for seventy H/C/O/Cl compounds in the fitting and validation data sets. The dashed diagonal line serves as a guide for eyes.

PES using the new ReaxFF for reactive bonding interactions

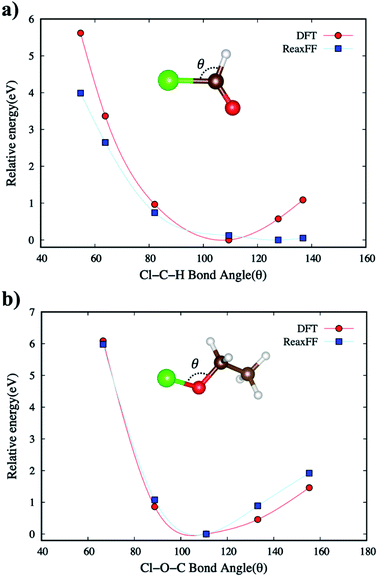
As explained earlier for E^intra term, all the directional bonding interactions for empirical bond order estimations in describing the bond environment are based on bond distance, bond angle, and torsion angle. We calibrated the ReaxFF to fit the energy-minimized curves for the target molecular systems when compared to DFT (B3LYP/6-31G*) energies.

Distance dependence. We first calculated single point DFT energies for the bond dissociation energies for Cl–H, Cl–C, Cl–O, and Cl–Cl bonds and compared the DFT data with ReaxFF predictions. We obtained the dissociation energy curves for two-body interactions by constraining interatomic bond distance on a 1-D direction of interest. The equilibrium bond distances corresponding to minimum energies calculated by the new ReaxFF are 1.29 Å and 1.73 Å for Cl–H and Cl–O atom pairs, respectively, which are the same as those of the DFT results. The dissociation energy patterns are nearly consistent with those of the DFT calculations within cut-off bond lengths (i.e., ≤2.6 Å), shown in Fig. 2a and c. In the case of Cl–C and Cl–Cl bonds, the difference of ∼0.2 Å and ∼0.1 Å in the equilibrium bond distance between the new ReaxFF and DFT calculations can be acceptable. There is also a very similar dissociation energy trend up to 4.0 Å, although that is at much longer distance than the cut-off bond length of the Cl–C atom pair displayed in Fig. 2b. Although the dissociation energy curves obtained from the new ReaxFF parameter set are broader than those of DFT calculations, the equilibrium distances (1.73 Å and 2.04 Å) of Cl–O and Cl–Cl bonds are both equal or very similar to those predicted by DFT. Also, the curvature of the parabolic region in both DFT and ReaxFF dissociation energy curves are mostly similar. Therefore, the energy deviations are tolerable in most cases within the presumable cut-off distances. We also emphasize that our energetic deviations are lower than the RMS error of bond formation energies obtained for the seventy H/C/O/Cl compounds in our fitting and validation data sets.

Fig. 2 The comparison of DFT and ReaxFF bond dissociation energies by changing interatomic bond distances for (a) Cl–H bond in HCl, (b) Cl–C bond in CH₃Cl, (c) Cl–O bond in ClOH, and (d) Cl–Cl bond in Cl₂. The brown, red, white, and green-colored balls indicate C, O, H, and Cl atoms, respectively.

Bond angle dependence. We estimated bond energies resulting from bond angle variations in the three-body bonding environment with DFT and the new ReaxFF using single-point energy calculations. We constrained bond angles on the only 2-D plane of interest. As shown in Fig. 3a and b, Cl–C–H and Cl–O–C bond angle energies of the new ReaxFF are generally consistent with those calculated via the DFT method. Additional bond bending energetics for different three-body interactions are provided in ESI.†

Fig. 3 The comparison of relative energies of DFT and ReaxFF for (a) Cl–C–H bond angle in CHClO and (b) Cl–O–C bond angle in C₂H₅ClO. The brown, red, white, and green-colored balls indicate C, O, H, and Cl atoms, respectively.

Torsional angle dependence. We calculated the single point DFT and ReaxFF torsional angle energies resulting from torsional angle distortion in the four-body connected bonds. Bond energies of the new ReaxFF calculations in Cl–C–C–H and H–C–C–O torsional angles composed of the sp³–sp³ hybridized configurations are suitably comparable in the energy trend to those of the DFT calculations, shown in Fig. 4. The constraints applied to the torsional angle rotations are based on a bond torsion of interest located at the center of the four-body bond backbone. We provide more comparisons between ReaxFF and DFT energetics for the four-body torsional angle variations, such as the sp–sp³, sp–sp², and sp²–sp³ hybridized configurations in ESI.†

PES of the new ReaxFF for non-bonded interactions

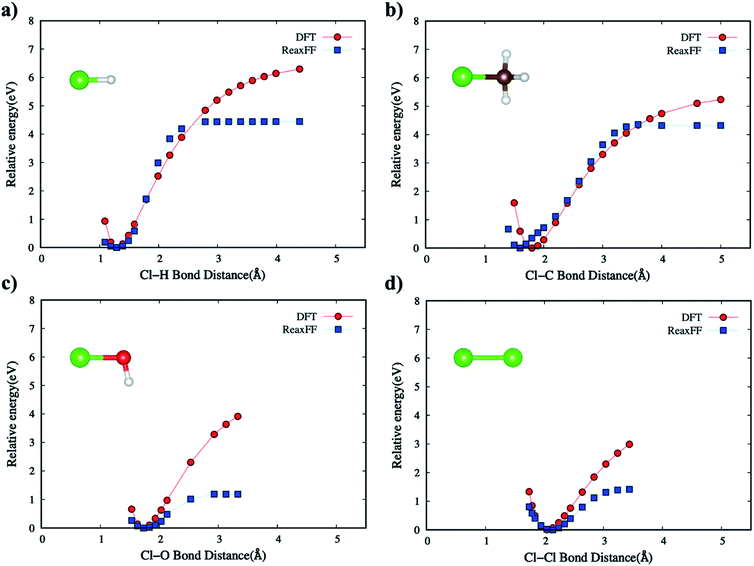
We have also parametrized the non-bonded terms in the new ReaxFF force field. This parameterization includes fitting both charge distribution parameters, also known as the EEM method,³⁷ and dispersion interaction coefficients. Following electronegativity rules, the new ReaxFF includes parameters that allow charge distributions, correlated with charge transfers, which are dependent on the local bonding environment of a particular atom.

Fig. 4 The comparison of relative energies of DFT and ReaxFF for (a) Cl–C–C–H torsional angle in C₂H₃Cl₃ and (b) H–C–C–O torsional angle in C₂H₃Cl₃O. The brown, red, white, and green-colored balls indicate C, O, H, and Cl atoms, respectively.

Charge distributions. We have parameterized the new ReaxFF parameter set to reproduce charge distributions similar to the DFT-Mulliken charge population scheme. Fig. 5 shows the comparison of DFT and the new ReaxFF charge distributions in four different aliphatic and aromatic molecules. In ESI,† we provide a full list of charge distribution comparisons between DFT and the new ReaxFF potential in eight other molecules. In the case of acetyl chloride (C₂H₃ClO), the new ReaxFF predicts charges close to those of DFT (at the level of theory, B3LYP/6-31G**) calculations. However, in the cases of formic acid, dichloromethyl ester (C₂H₂Cl₂O₂) and methyltrichloromethyl ether (C₂H₃Cl₃O) summarized in ESI,† the charges of the chlorine atom and its immediate carbon atom in the new ReaxFF differ from those of the DFT method. This discrepancy can be justified on the basis of electronegativity, χ_O = 3.44 > χ_Cl = 3.16 > χ_C = 2.55 > χ_H = 2.20. This means that since chlorine is more electronegative than carbon, it should be more negatively charged compared to its immediate carbon atom. We also confirm that the charge predictions by the new ReaxFF are consistent with Bader charge values calculated with PBE functional.²⁴ We also must note that the Mulliken charge population method is strongly dependent on the dividing surface, i.e., the surface dividing electronic charge density between atoms. Since the designation of the dividing surface can be arbitrary, the partial charges vary in different charge population schemes. This has encouraged us to place more emphasis and confidence in the basic notion of electronegativity in interpreting charge distributions.

Fig. 5 The comparison of charge distributions of DFT and ReaxFF in (a) C₂H₃ClO, (b) C₆H₅ClO, (c) C₄H₅ClO₃, and (d) C₂H₅ClO. The red-colored values are for DFT-calculated Mulliken charges and the blue-colored values are for the ReaxFF-calculated EEM charges based on electronegativity. The brown, red, white, and green-colored balls indicate C, O, H, and Cl atoms, respectively.

Non-bonded dispersion interactions. From the electronic structure calculations viewpoint, non-bonded energies are the sum of electrostatic and dispersion (van der Waals) interactions. Hence, separating the hydrogen-binding effect from a specific term is not straightforward. To show the quality of the new ReaxFF parametrization for dispersion interactions, we compared the non-bonded energies for Cl–C in between CH₃Cl and CH₄, Cl–H in between H₂O and H-terminated ClO₄⁻ (perchloric acid), and Cl–Cl in between two CCl₄ molecules, as calculated against the DFT energies, shown in Fig. 6.

Fig. 6 The comparison of (a) DFT and (b) the new ReaxFF non-bonded energies for Cl–C in between CH₃Cl and CH₄, Cl–H in between H₂O and H-terminated ClO₄⁻ (perchloric acid), and Cl–Cl in between two CCl₄ molecules. The inset in part (b) shows the non-bonded interactions of Cl–Cl atom pair in CCl₄–CCl₄.

The non-bonded energies of the Cl–Cl and Cl–H calculated by the DFT and new ReaxFF are consistent with regard to the position of energy minimum (equilibrium distance) and the energy curve pattern. The equilibrium Cl–C distance predicted by the new ReaxFF is slightly longer (∼0.2 Å) than that calculated by DFT. However, the non-bonded energy pattern for the Cl–Cl and Cl–H cases remain consistent between the new ReaxFF potential and DFT calculations. We also note that the depth of the non-bonded attractive energy well is less than 0.55 eV, especially for the Cl–H pair interaction, Fig. 6b. The majority of this attractive interaction might arise from coulombic interactions, as shown in the inset of Fig. S5b provided in ESI.† The aforementioned discrepancy in the magnitude of potential well depth might be due in part to the previous H/C/O parameterizations with regard to hydrocarbon oxidation³¹ on which we based our H/C/O/Cl parameter set. Having shown such slight differences between DFT and the new ReaxFF results, we note that the attractive energy well's depth is still smaller than the 1.57 eV threshold satisfied in the parametrization of the new ReaxFF to formation energy of the H/C/O/Cl compound data set.

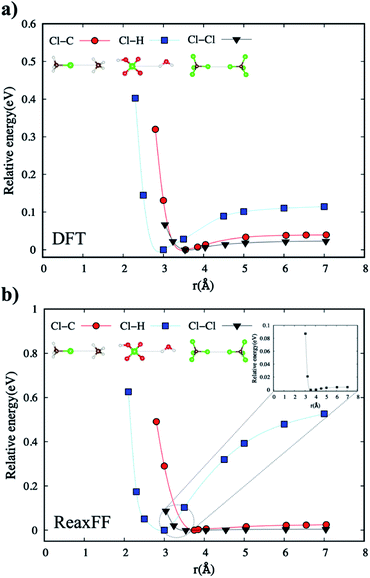
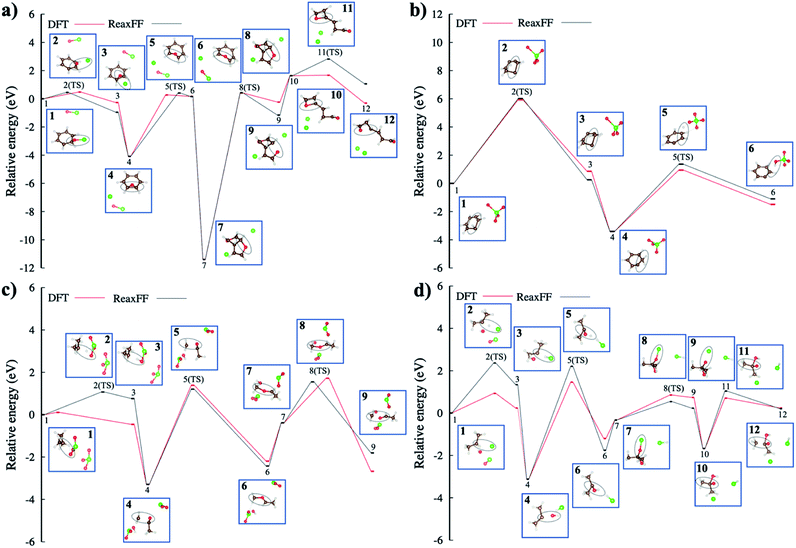
Transition state (TS) simulations of hydrocarbon oxidation

Oxidative degradation of aromatic hydrocarbon. We first study the oxidation of small aromatic hydrocarbon, namely a benzene molecule, with oxychlorine oxidizers (ClO_n⁻; 1 ≤ n ≤ 4) using ab initio MD simulations. We used the ab initio MD trajectories to propose reaction pathways, estimate transition states, and ultimately validate the new ReaxFF potential with the proposed oxidation paths. Fig. 7a illustrates a process in which a small hydrocarbon (i.e., benzene) is oxidized by ClO⁻, to form trans, trans-muconaldehyde,⁴⁴ which includes CHO hydrophilic polar parts at the end of the backbone as a function of reaction coordinates. In this reaction pathway, benzene oxygenation begins with the direct interaction of reactive states of oxygen (χ_O = 3.44) from the ClO⁻ oxidizer with the C–C bond. The benzene's C–C bond with an energy barrier of ∼0.5 eV is likely epoxidized before going through reversible valence tautomerism.⁴⁵ We also illustrate this reaction in Scheme 1 that can be found in ESI.† Oxidative ring-opening of benzene through C–C bond cleavage from the epoxy configuration creates a seven-membered ring. The ring is oxidized by a second ClO⁻, which brings the internal C–C bond formation to allow a C–O bond breaking with ∼1.6 eV energy differences from the TS saddle points, by which the linear-like hydrocarbon configuration is partially produced. The reaction product contains CHO hydrophilic end.

Fig. 7 The proposed reaction pathways and potential energy surfaces in the oxidative decompositions of small aromatic and aliphatic hydrocarbons with oxychlorine oxidizers (ClO_n⁻; 1 ≤ n ≤ 4), as compared between the DFT and ReaxFF energetics; (a) oxygen transfer to the benzene forms a seven-membered benzene oxide ring and C–O bond breakings with the addition of ClO⁻ produces a linear molecules, (b) proton transfers in the internal benzene and to the oxygen of ClO₄⁻, (c) proton transfer to the oxygen of ClO₃⁻, bond transition from a C–C bond of the oxygen-combined isopropyl backbone to a C–O bond with the ˙CH₃ radical, and the C–O bond breaking to take apart the ˙CH₃ radical that produce an acetaldehyde, (d) proton transfer to ˙Cl radical to produce HCl and oxygen transfer with the addition of ClO⁻ that generates acetic acid. The brown, red, white, and green-colored balls indicate C, O, H, and Cl atoms, respectively.

Fig. 7b shows a proton transfer within the benzene itself and then, its transfer to the oxygen of ClO₄⁻. This reaction coordinate shows how the presence of ClO₄⁻ affects the structural deformation of the benzene, induced by strong vibrations. The proton transfer energy barrier is shown to be ∼6.0 eV, which is well correlated to DFT energy. In the meantime, the energy barrier of the other proton transfer to the oxygen of ClO₄⁻ molecule is ∼2.5 eV indicating that the unsaturated benzene configuration with a carbon radical requires less energy to be endothermic for the proton hopping. The proposed proton transfer reaction steps are detailed in Scheme 1 presented in ESI.†

Oxidative degradation of aliphatic hydrocarbon. Oxidative dehydrogenation (considered proton transfer) of propane by ClO₃⁻ oxidizer is observed in the TS reaction paths, shown in Fig. 7c. The proton transfers from the propane backbone to the ClO₃⁻ producing an isopropyl radical similar to the previously reported oxidative dehydrogenation of propane on the cubic V₄O₁₀ catalyst.^46,47 The activation energy barrier calculated for this reaction by the new ReaxFF (E_a = 25.3 kcal mol⁻¹ ≈ 1.1 eV) is in good agreement with an experimental energy barrier of the proton transfer from propane using the vanadium oxide (E_a = 27.0 kcal mol⁻¹ ≈ 1.17 eV). In the second stage of the reaction path, ClO₃⁻ addition leads to C–O bond formation at the carbon radical of the isopropyl backbone and ˙CH₃ radical formation at one of the methyls. The transition from a C–C bond in the oxygen-derived isopropyl backbone to a C–O bond with the ˙CH₃ radical is exothermic, as observed in the TS profile of the new ReaxFF. The C–O bond-breaking step releases the ˙CH₃ radical, and thus, acetaldehyde containing a CHO hydrophilic polar end is generated in the last stage of the reaction paths, described in Scheme 1 of ESI.†

In Fig. 7d, the radical–radical combination, i.e., the combination of ˙H and ˙Cl radicals to form hydrochloric acid, gives rise to an energy barrier of ∼2.36 eV. We also note that Cl's strong electronegativity (χ_Cl = 3.16) may play a role in the proton transfer process. In the meantime, hydroxyl radical approaches the unsaturated isopropyl configuration to form a 2-propanol radical. Finally, an additional ClO⁻ oxygenates the 2-propanol radical site, with an energy barrier of ∼0.87 eV, forming a carboxyl functional group. At the end, the released ˙CH₃ radical yields acetic acid in this reaction profile.

Fig. 8 Trajectory snapshots of the new ReaxFF-MD simulations: (a) coronene (C₂₄H₁₂) as an aromatic hydrocarbon and (b) two relaxed polyethylenes (–(CH₂–CH₂)_n–, one for n = 9 and the other for n = 6) as aliphatic hydrocarbons with ClO₄⁻ oxidizers and H₃⁺O ions dissolved in water. The brown, red, white, and green-colored balls indicate C, O, H, and Cl atoms, respectively. In time (i)–(iv) snapshots, water molecules are not displayed to clearly show the oxidative fragmentation process.

Molecular dynamics (MD) simulations of oxidative decomposition

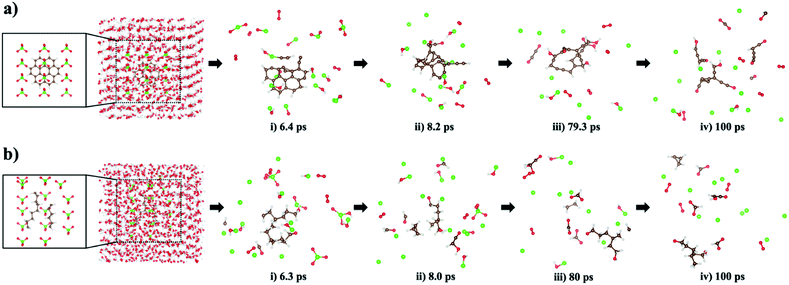
Using this newly parameterized ReaxFF, we carried out MD simulations to observe the mechanistic picture of oxidative decomposition of small hydrocarbon molecules at 450 K using ClO₄⁻ oxidizers, shown in Fig. 8. For these MD simulations, we selected coronene (C₂₄H₁₂) as an aromatic hydrocarbon, and two relaxed polyethylenes (–(CH₂–CH₂)_n–, where n = 9 and n = 6) as aliphatic hydrocarbons. During MD simulations, the decompositions of ClO₄⁻, which were experimentally confirmed,¹⁵ produce O₂ and ˙Cl radical, which are the main source for generating the H/C/O/Cl compounds, whenever H and C atoms detach from the deformed hydrocarbon structures. As seen in the stage (i) snapshot taken from the MD trajectory at 6.4 ps, the coronene structure degrades to produce a small H/C/O/Cl compound and O₂/ClOH/ClO_n⁻ (n: 1–3). In stage (ii) at 8.2 ps, all but one of the remaining aromatic rings in the parent structure are broken to form a hydrocarbon chain terminated with a hydrophilic H/C/O. Complete degradation of the fused ring matrix takes place at stage (iii) of the 79.3 ps snapshot while a small H/C/O molecule is separated. A new H/C/O/Cl compound and other H/C/O species appear at 100 ps stage (iv) verifying the irreversible nature of the ring breaking.

Oxidative degradation of the two aliphatic polyethylenes occurs in stage (i) at 6.3 ps where small molecules containing H/C/O elements are formed. In stage (ii), the curved –(CH₂–CH₂)_n– domain found in the snapshot at 6.3 ps predominantly loses its chain characteristics while gaining a terminal H/O. Also, more C₁ and H atoms released from the curved –(CH₂–CH₂)_n– domain combine with H/O/Cl elements to form H/C/O and H/C/O/Cl compounds. In stage (iii) and (iv) snapshots, short hydrocarbon fragments (i.e., H_nC_n: n = 1–3) and small H/C/O compounds are observed. The time period of 100 ps is enough to see a variety of H/C/O/Cl compounds derived from aliphatic hydrocarbon fragmentation, though no chlorocarbons are observed at the end of the simulations.

Conclusions

In this paper, we developed a new ReaxFF parameter set to model the oxidative degradation of small aromatic and aliphatic hydrocarbons in response to oxychlorine oxidizers (ClO_n⁻: n = 1–4). The potential energy surface in the calibrated ReaxFF correlates well with that of DFT (R² = 0.997). The new H/C/O/Cl parameterization shows the RMS error of only ∼1.57 eV, corresponding to the average percent error of 1.70%. The energy patterns estimated by the new ReaxFF for covalent bonding interactions provide a good description of the DFT energies with regards to the bond distance, bond angle, and torsional angle changes. Furthermore, the new ReaxFF adequately reproduces the non-bonding interactions such as coulombic, and intermolecular dispersions as well as H-bonding interactions. Through ab initio MD simulations, we benchmarked thermodynamically-favorable oxidation paths for small hydrocarbon molecules by ClO_n⁻. We showed that the ReaxFF potential could quantitatively reproduce the energetics of proposed reaction paths. We subsequently performed MD simulations to study the effect of perchlorate on the degradation of small aromatic and aliphatic hydrocarbons. The MD trajectories describe the unfolding of hydrocarbon fragmentation, delineating how H/C/O/Cl species are formed and broken during complex oxidative processes.

This reactive force field serves only as a proof of concept that the properly parameterized ReaxFF potentials can be employed to obtain the atomic-level understanding of the oxidative degradation processes at the kerogen-oxidizing fluid interface. We have already geared our parameterization efforts toward developing Na/H/C/O/Cl and Na/H/C/O/Br parameter sets to resolve the oxidative reaction pathways responsible for kerogen fragmentation and degradation reported in benchtop experiments.⁹ We envision that such transferable reactive force fields will pave the path for designing the next generation of reactive oxidizing fluids for improving the efficiency of stimulation operations in unconventional reservoirs and pretreatment of geological reservoirs for enhanced carbon dioxide sequestration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge computational support by the UCI HPC staff.

References

1. J. Lehmann and M. Kleber, Nature, 2015, 528, 60–68.
2. M. Vandenbroucke and C. Largeau, Org. Geochem., 2007, 38, 719–833.
3. H. Sanei, Sci. Rep., 2020, 10, 15595.
4. F.-J. Ulm and Y. Abousleiman, Acta Geotechnica, 2006, 2, 77–88.
5. K. L. Hull, Y. N. Abousleiman, Y. Han, G. A. Al-Muntasheri, P. Hosemann, S. S. Parker and C. B. Howard, SPE J., 2017, 22, 1024–1033.
6. Y. N. Abousleiman, K. L. Hull, Y. Han, G. Al-Muntasheri, P. Hosemann, S. Parker and C. B. Howard, Acta Geotechnica, 2016, 11, 573–594.
7. W. E. Robinson, H. H. Heady and A. B. Hubbard, Ind. Eng. Chem., 1953, 45, 788–791.
8. B. J. Katz and I. Arango, Org. Geochem., 2018, 123, 1–16.
9. K. L. Hull, D. Jacobi and Y. N. Abousleiman, Energy Fuels, 2019, 33, 4758–4766.
10. K. Mitra and J. G. Catalano, J. Geophys. Res.: Planets, 2019, 124, 2893–2916.
11. M. Zheng, X. Li, J. Liu, Z. Wang, X. Gong, L. Guo and W. Song, Energy Fuels, 2014, 28, 522–534.
12. K. Nomura, R. K. Kalia, A. Nakano and P. Vashishta, Comput. Phys. Commun., 2008, 178, 73–87.
13. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409.
14. T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2, 15011.
15. S. Masoumi, S. Zare, H. Valipour and M. J. Abdolhosseini Qomi, J. Phys. Chem. C, 2019, 123, 4755–4766.
16. M. J. A. Qomi, M. Bauchy, F.-J. Ulm and R. J.-M. Pellenq, J. Chem. Phys., 2014, 140, 054515.
17. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
18. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016.
20. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
21. P. C. Hariharan and J. A. Pople, Chem. Phys. Lett., 1972, 16, 217.
22. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
23. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. M. L. Coote, J. Phys. Chem. A, 2004, 108, 3865–3872.
26. D. Chakraborty, R. P. Muller, S. Dasgupta and W. A. Goddard, J. Phys. Chem. A, 2000, 104, 2261–2272.
27. K. N. Rogstad, Y. H. Jang, L. C. Sowers and W. A. Goddard, Chem. Res. Toxicol., 2003, 16, 1455–1462.
28. X. Xu, R. P. Muller and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 3376–3381.
29. M. T. Feldmann, S. L. Widicus, G. A. Blake, D. R. Kent and W. A. Goddard, J. Chem. Phys., 2005, 123, 034034.
30. M. S. Rudner, D. R. Kent, W. A. Goddard and J. D. Roberts, J. Phys. Chem. A, 2005, 109, 9083–9088.
31. K. Chenoweth, A. C. T. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053.
32. J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6991–7000.
33. D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783–802.
34. S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486.
35. L. Pauling, The nature of the chemical bond, Cornell University Press, Ithaca, NY, 3rd edn, 1960.
36. H. S. Johnston and C. Parr, J. Am. Chem. Soc., 1963, 85, 2544–2551.
37. W. J. Mortier, S. K. Ghosh and S. Shankar, J. Am. Chem. Soc., 1986, 108, 4315–4320.
38. A. K. Rappe and W. A. Goddard, J. Phys. Chem., 1991, 95, 3358–3363.
39. W. Zhang and A. C. T. van Duin, J. Phys. Chem. B, 2017, 121, 6021–6032.
40. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 http://lammps.sandia.gov.
41. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
42. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
43. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
44. L. Latriano, B. D. Goldstein and G. Witz, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 8356–8360.
45. A. Karich, M. Kluge, R. Ullrich and M. Hofrichter, AMB Express, 2013, 3, 5.
46. M.-J. Cheng, K. Chenoweth, J. Oxgaard, A. van Duin and W. A. Goddard, J. Phys. Chem. C, 2007, 111, 5115–5127.
47. M. D. Argyle, K. Chen, A. T. Bell and E. Iglesia, J. Phys. Chem. B, 2002, 106, 5421–5427.

---

Footnote

† Electronic supplementary information (ESI) available: Bond formation energies, PES data for reactive and non-reactive bonding, atomic charges, TS schemes, the new ReaxFF parameters, and parameterization flow chart. See DOI: 10.1039/d1ra04397h

---