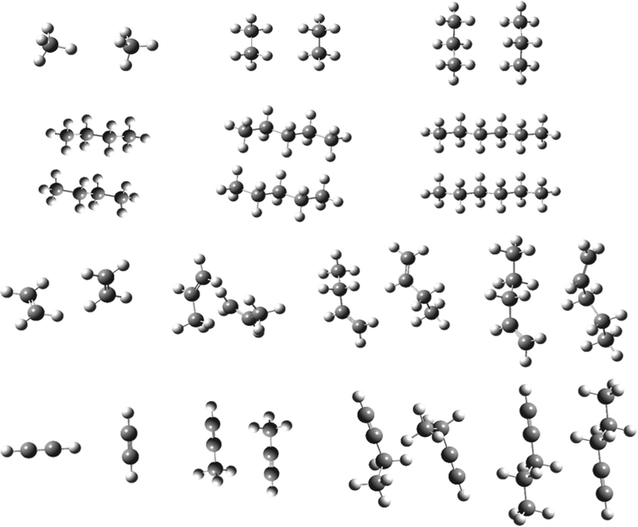Pairing double hybrid functionals with a tailored basis set for an accurate thermochemistry of hydrocarbons

Abstract

A collection of five challenging datasets, including noncovalent interactions, reaction barriers and electronic rearrangements of medium-sized hydrocarbons, has been selected to verify the robustness of double-hybrid functionals used in conjunction with the small DH-SVPD basis set, especially developed for noncovalent interactions. The analysis is completed by other, more standard functionals, for a total of 17 models, including also empirical corrections for dispersion. The obtained results show that the chemical accuracy threshold, that is an error lower than 1.0 kcal mol⁻¹, can be obtained by pairing the nonempirical PBE-QIDH functional with the DH-SVPD basis set, as well as by other semi-empirical functionals, such as DSD-PBEP86, using larger basis sets and empirical corrections. More in general, a significant improvement can be obtained using the DH-SVPD basis set with DHs, without resorting to any empirical corrections. This choice leads to a fast computational protocol that, avoiding any empirical potential, remains on a fully quantum ground.

---

1. Introduction

The constant development of robust and versatile quantum chemical approaches is allowing the accurate evaluation of an increasing number of physico-chemical properties. Reaching the so-called “chemical” accuracy for these properties, that is an accuracy roughly matching that of experiment measurements (when available) has been the ultimate objective in computational chemistry for many years.^1,2 It was reached at the end of '90 for thermochemistry, but only for small molecular systems, due to computer and methodological restrictions of the pioneering ab initio methods.³ Later developments of composite protocols or extrapolation schemes allowed the extension of this accuracy target to larger molecules (see for instance ref. 4–8). Indeed, this threshold, conventionally fixed at 1 kcal mol⁻¹,⁹ can be nowadays routinely reached by a few robust and validated approaches suited for thermochemistry. Consequently, the bar has been raised (or better said lowered) to a sub-chemical level, that is an accuracy lower than 1 kcal mol⁻¹.¹⁰ Other properties, such as vertical excitation energies or ionization potentials, are following a similar evolution, albeit with a temporal delay mainly dictated by methodological or numerical issues.^11,12

These valuable computational methods operate with “costly” engines derived from refined post-Hartree–Fock (HF) methods. It is then natural that the efforts for extension to larger molecular systems have been done by considering lower-level approaches, further extrapolation schemes or even the inclusion of statistical models.^13–18 However, the drawback of introducing some approximations in electronic-structure models could be the negligible risk of introducing errors in energy evaluations of the same magnitude of the chased accuracy.^19,20

In this context, it should not be forgotten that the most recent developments in Density Functional Theory (DFT) have conducted to the definition of exchange–correlation functionals with improved performances, even for large (that is more than fifty atoms) systems at a fraction of the computational cost.²¹ In particular, the so-called double hybrid functionals, models including a fraction of HF exchange and a second-order Moller–Plesset (MP2) correlation contribution, present several advantages with respect to their Global Hybrids (GH) predecessors, including improved performances on larger domain of chemical applicability.^22–25 This is true, for instance, for thermochemistry, where some DHs rival in accuracy with some composite ab initio models.²⁶ Thanks to a balanced description of both covalent and non-covalent interactions, it is not rare that a DH model provides errors in the range of 1.0 to 1.5 kcal mol⁻¹ on thermochemistry.²⁷ Even lower errors can be then reached upon the inclusion of an empirical potential, such as those proposed by Grimme,²⁸ to better couple with dispersion interactions.^{26,27,29–31}

Among others, we have recently found that DHs coupled to a small basis set,^32,33 tailored for noncovalent interactions, reach, or even exceed, the chemical accuracy threshold for the Bond Separation Reactions (BSR), an elegant way to investigate the greater stability of branched alkanes with respect to their linear forms using the isodesmic principle.³⁴

Here we want to further extend our investigation to other medium-sized hydrocarbons included in selected datasets, for which accurate reference values are available. These sets (vide infra) have been chosen to show a larger diversity of chemical situations, including multiple carbon–carbon bonds, large electronic delocalization and, of course, weak noncovalent interactions. The aim is to verify the limits of modern DHs methods in modelling the thermochemistry of hydrocarbons, that plays a central role in both experimental and theoretical chemistry.

2. Computational details

2.1 Methods

In the following, a particular attention will be devoted to the results obtained with the DH-SVPD basis set. This basis set has been developed starting from the small Def2-SVPD basis³⁵ and optimizing the most diffuse functions (one p-function and one d-function for C atom and one s-function and one p-function for H atom) so to minimize the following expression for the benzene dimer:³⁶where E is the total energy of the dimer, J and K are the corresponding Coulomb and exchange energies and E⁰ is the total energy of the isolated benzene. This procedure leads to the optimization of the interaction energy of a dimer as expressed at a zero-order perturbation theory,³⁶ without the necessity of external reference data from, for instance, experiments or accurate post-HF methods, a common practice in computational chemistry. In practice, this procedure is based on an error compensation between Basis Set Superposition Error (BSSE) and Basis Set Incompleteness Error (BSIE). These errors are not only strictly entangled, but act in an opposite way, the former leading to an overestimation of the interaction energies in weakly bonded systems, whereas the latter leads to an underestimation.³⁷

It is worth to mention that the DH-SVPD basis is significantly smaller than standard basis sets used in accurate energy evaluation. For instance, it has 10 and 30 primitive functions for H and C, respectively, while the Def2-TZVPP³⁵ basis foreseen 16 and 46 primitives which rise to 18 and 58 for the cc-PVTZ,³⁸ just to mention two other bases considered in the following. The gain in computer resources is then evident.

Concerning DH functionals we have considered 5 models among those which can be easily find in the most-common quantum-chemistry packages, namely B2-PLYP,³⁹ DSD-PBEP86,⁴⁰ revDSD-PBEP86-D3(BJ),⁴¹ PBE0-DH⁴² and PBE-QIDH.⁴³ These functionals have been developed following different criteria, including a fitting procedure to external reference data for the first three and theoretical “educated” guesses (aka ansatz) for the others.⁴⁴ These criteria classified B2-PLYP, DSD-PBEP86, revDSD-PBEP86-D3(BJ) as semi-empirical functionals, while PBE0-DH and PBE-QIDH are nonempirical. In such a way the main trends in functional developments are covered.

To complete our analysis, we have also considered M06-L,⁴⁵ a local approach particularly performant on weak interactions, 4 global hybrids, namely M06,⁴⁶ TPSSh,⁴⁷ PBE0,⁴⁸ B3LYP,⁴⁹ and two range-separated hybrids, that is CAM-B3LYP,⁵⁰ ωB97XD.⁵¹ In such a way, albeit considering a limited number of models, the most representative functional families are represented. In some cases, all these functionals have been paired with the D3 and/or D3(BJ) dispersion potentials, with the appropriate parametrization.^28,52–54

All DFT calculations have been performed with the Gaussian 16 program.⁵⁵

2.2 Chemical space

Five different sets have been considered as benchmarks, including saturate, unsaturated and aromatic hydrocarbons. They are listed in Table 1, together with their main characteristics.

Table 1 Chemical space considered in the present work

Set	Type	Energy^a	Relative energies	Single-point calculations	Geom. opt.	Reference data	Reference
a ΔEint = dimerization energy; ΔE = reaction energy; ΔE^≠ = reaction barrier height.
ADIM6	Hydrocarbon dimers	ΔEint	6	12	No	CCSD(T)/CBS	56
AAA	Hydrocarbon dimers	ΔEint	7	21	Yes	CCSD(T)/CBS	58
IDHC5	Isomerization and folding reactions	ΔE	5	10	No	CCSD(T)/CBS	This work
PAH5	PAH isomers	ΔE	5	10	No	CCSD(T)/CBS	65
Cope	Cope rearrangements	ΔE, ΔE^≠	25	50	No	CCSD(T)/CBS	66

---

The first set is the so-called ADIM6,⁵⁶ part of the very large GMTKN55 database (and its predecessors),²⁷ that is considered as a reference for benchmarking functionals. Indeed, structures and references energies are those reported in the original paper and retrieved from the Grimme's website.⁵⁷ It is composed by 6 six alkane dimers obtained from ethane to n-heptane.

The second set, called AAA (see Fig. 1), has been recently introduced by Chao and collaborators⁵⁸ and it is composed by 6 dimers of n-alkanes (from methane to hexane) in all-trans conformation, 4 alkenes (ethene, propene, 1-butene and 1-pentene) and 4 alkynes (ethyne, propyne, 1-butyne and 1-pentyne). The interactions energies discussed in the following were computed for the optimized structures of the dimers, using the same functional for structural and energetic evaluation. The comparison is done with the CCSD(T)/CBS values reported in the original paper. These two sets, ADIM6 and AAA, have been created to probe weak dispersive interactions.

Fig. 1 The optimized structures of the dimers in the AAA groups at PBE-QIDH/DH-SVPD level.

The third set, IDHC5, concerns intramolecular dispersion interactions in hydrocarbons and it extracted by that originally proposed by Grimme.⁵⁹ It is composed by the energies of the following reactions:

(1) N-Octane → tetramethylbutane

(2) N-Undecane → hexamethylpentane

(3) C₁₄H₃₀ (linear) → C₁₄H₃₀ (folded)

(4) C₂₂H₄₆ (linear) → C₂₂H₄₆ (folded)

(5) C₃₀H₆₂ (linear) → C₃₀H₆₂ (folded)

As it can be seen, this set is nonuniform containing two isomerization reactions (1) and (2) and three folding reactions (3)–(5). The original reference data, QCISD(T) for 1, experimental for 2, and MP2 for the others, have been replaced by CCSD(T)/CBS values in order to keep consistency with the other datasets. For the sake of homogeneity, all structures were first fully optimized at the PBE0-D3(BJ) level of theory using the def2-TZVPP basis set. Then, DLPNO-CCSD(T)⁶⁰ single point energy computations were performed with the release 4.1.2 of the Orca program package⁶¹ making use of a TightPNO convergence criteria as recommended in ref. 62. The complete basis set limit is finally obtained from a triple- to quadruple-ζ extrapolation based on the aug-cc-pVTZ and aug-cc-pVQZ and corresponding auxiliary basis set⁶³ following the scheme developed in ref. 64.

The PAH5 set has been proposed by Karton some years ago.⁶⁵ It is composed by the following isomerization reactions involving medium-sized polycyclic aromatic hydrocarbons (PAHs, see Fig. 2):

Fig. 2 Sketches of the molecules composing the PAH5 set. Only one of the possible resonance structures is reported.

(6) Phenanthrene → anthracene

(7) Triphenylene → chrysene

(8) Triphenylene → benz[a]anthracene

(9) Triphenylene → benz[a]phenanthrene

(10) Triphenylene → naphthacene.

The difficulty in these large molecules is represented by the π-conjugated pattern which significantly changes in going from one isomer to the other. Also in this case, reliable CCSD(T)/CBS values are taken as references.

Finally, the last set (Cope) recently proposed by Karton, is composed by reaction energies and barrier heights for the Cope rearrangement of substituted bullvalene.⁶⁶ The reactions, sketched in Fig. 3, are sigmatropic rearrangement involving a large reorganization of the electronic structure along the reaction path, even if the number and type of bond is unaffected from reactants to products. We have discarded 3 molecules from the original set, since they contain atoms (S, F and Cl) not included in the currently available DH-SVPD basis set. Also in this case, the reference values are computed at the CCSD(T)/CBS level of theory.

Fig. 3 Schematic representation of the unimolecular rearrangements in the Cope database (R = NH₃, OH, CH₃ and CN).

Even if it can be argued that these systems are medium-sized ones, they, except for the recent AAA set, are currently used in literature as representative benchmarks for DFT approaches. At the same, it should be stressed that the outcomes of any benchmark analysis, in term of accuracy and domain of applicability of tested functionals, depends on the quality of the reference values. Indeed, in validating theory against theory we face to the above-mentioned problems related to the size/computational cost ratio derived from the consideration of post-HF methods as reference. Reference values obtained at the CCSD(T)/CBS level, which is considered as the gold standard in thermochemistry,⁶⁷ are already available or have been obtained at a reasonable computational cost for all the considered datasets. This is not always the case for larger systems, but this choice does not affect the legitimacy of our tests, in terms of numerical accuracy for thermochemistry, domain of applicability of the protocol and chemical analysis.

3. Results

3.1 The ADIM6 and AAA sets

As above mentioned, these first two sets, having some overlap, have been developed for benchmarking weak interactions in terms of interaction energy (ΔE_int) between dimers and separated monomers. The Mean Absolute Deviations (MAD) of the selected functional obtained for the first test are reported in Table 2. Since ADMI6 is part of the larger GMTKN55, that have been widely applied to any class of known functionals (or almost), no unexpected behavior can be evidenced in the results obtained with the larger Def2-QZVP basis set. Indeed, sub-chemical accuracies can be obtained with DHs casting empirical potentials, with deviations as low as 0.1 kcal mol⁻¹ (B2-PLYP-D3 and DSD-PBEP86). It should be also noticed that the PBE-QIDH prefers, on this set, to be coupled with the D3 potential rather than the D3(BJ) one (MAD of 0.4 vs. 0.8 kcal mol⁻¹). More interesting are, however, the low MADs showed by the hybrid M06 functionals (0.3 kcal mol⁻¹) and its local counterpart, M06-L (0.2 kcal mol⁻¹), obtained without any specific corrections. The B3LYP-D3 model is also very competitive (0.5 kcal mol⁻¹). In order to give a flavor of the reached accuracies, it can be mentioned that the DLPNO-CCSD(T) approach provides on this set a MAD of 0.4 kcal mol⁻¹ with respect to the same reference values.¹⁹

Table 2 Computed mean absolute deviations (MAD, kcal mol⁻¹) for interaction energies of the ADIM6 dataset

	DH-SVPD	Def2-QZVP
M06-L	1.95	0.22
TPSSh	3.07	4.64
B3LYP	2.98	4.99
PBE0	1.74	3.43
M06	1.86	0.28
CAM-B3LYP	1.51	3.55
ωB97X-D	2.80	1.03
B3LYP-D3	2.47	0.46
B2-PLYP	0.70	2.90
PBE0-DH	0.95	2.76
PBE-QIDH	0.15	1.86
B2-PLYP-D3	2.06	0.14
DSD-PBEP86	2.42	0.10
revDSD-PBEP86-D3(BJ)	2.07	0.32
PBE0-DH-D3(BJ)	1.57	0.23
PBE-QIDH-D3(BJ)	1.24	0.77
PBE-QIDH-D3	1.64	0.37

---

By moving to the DH-SVPD basis set, a deterioration of the performances of all the DHs coupled to empirical potential can be observed, as already remarked for other systems ruled by pure dispersive interactions. This is true for both PBE- and BLYP-based functional as well as DSD-PBEP86 functionals. In contrast, the three pure DHs, B2-PLYP, PBE0-DH and PBE-QIDH, are all below the chemical-accuracy threshold, with the last functional showing a MAD value of 0.2 kcal mol⁻¹. This last value is lower than that obtained by the same functional corrected with the empirical potential and the large basis set, thus showing that one of the primary objectives in the development of the DH-SVPD basis set was reached.

All the other functionals show similar behaviors: those already providing good performances with the larger basis set are worsening (e.g. M06 or ωB97X-D), while those with more moderate performances improves their MADs up to about 50%.

The AAA set can be considered an enlargement of the previous one, containing both alkenes and alkynes, with the structures of the 14 noncovalently bounded dimers depicted in Fig. 1, while the MADs for the interaction energies are reported in Table 3. In this case the structures of the dimers have been fully optimized with each single functional, so to verify the coherence between energy and structure evaluation. The trends observed for the ADIM6 dataset are globally preserved, with minor modifications, and most of the deviations are even lower than before. Indeed, all the DHs give very low MADs, between 0.1 kcal mol⁻¹ (B2-PLYP-D3) and 0.4 kcal mol⁻¹ (PBE0-DH-D3(BJ) and PBE-QIDH-D3(BJ)) when coupled with an empirical potential and a larger basis set. Few hybrid functionals also provide very respectable performances with deviations under the 1 kcal mol⁻¹ threshold. They include ωB97X-D (0.7 kcal mol⁻¹), B3LYP-D3 (0.4 kcal mol⁻¹) and, as before, M06 (0.4 kcal mol⁻¹). The local M06-L gives also a remarkable accuracy (0.3 kcal mol⁻¹). The D3 correction seems to be more suitable for the PBE-QIDH functional than D3(BJ), since it significantly halves the error, as for the ADIM6 set.

Table 3 Computed mean absolute deviations (MAD, kcal mol⁻¹) for the interaction energies of the AAA set. In parenthesis are reported the values obtained at with cc-pVQZ basis set

	DH-SVPD	cc-pVTZ
M06-L	1.12	0.30
TPSSh	1.40	2.04
B3LYP	1.53	2.30
PBE0	0.91	1.75
M06	1.23	0.41
CAM-B3LYP	0.95	2.04
ωB97X-D	1.91	0.66
B3LYP-D3	1.57	0.43
B2-PLYP	0.49	1.69
PBE0-DH	0.56	1.53 (1.52)
PBE-QIDH	0.18	1.07 (1.05)
B2-PLYP-D3	1.32	0.09
DSD-PBEP86	0.44	0.23
revDSDPBEP86-D3(BJ)	1.35	0.13
PBE0-DH-D3(BJ)	1.11	0.39
PBE-QIDH-D3(BJ)	0.80	0.39
PBE-QIDH-D3	1.08	0.16

---

The performances of these dispersion-corrected functionals significantly deteriorate with the small DH-SVPD basis set, while those not including an empirical potential become competitive. Among the latter, it should be emphasized B2-PLYP (0.5 kcal mol⁻¹) and PBE-QIDH, whose value is very close to that obtained with an empirical potential and larger basis (0.2 kcal mol⁻¹, see Table 3).

In Fig. 4 are reported the intermolecular distance for three selected cases of the AAA set, namely methane, propane and ethyne dimers. There is a general agreement on the computed distances for all the considered methods, independently from the basis set and the inclusion of an empirical potential. This is particularly evident for the ethyne dimers, where all the methods predict the distance between a hydrogen atom and the mid-point of the CC bond to be about 2.8 Å. Larger variations, as a function of the DFT approach used, are observed for the larger CC distances in the two other dimers, albeit for a given functionals, the two basis sets provide very close results. Two notable exceptions are evident from the figure: B3LYP and the related CAM-B3LYP functional. In both cases, the two dimers of methane and ethane are not bound (intermolecular distance >7 Å in the plot) when the cc-pVTZ basis is considered. Of course, the two interactions energies are significantly underestimated at both the B3LYP and CAM-B3LYP levels (between −20% and −50% of the references values), but the statistical weight of these deviations on the MAD is small due to the low interaction energies (see Table S4†). The DH-SVPD leads to shorter distances for both functionals, even if B3LYP also provides the largest distance for these two dimers, thus confirming its large underestimation of the dispersion interactions. Of course, the addition of an empirical potential to B3LYP gives a better description, both in term for energy and distances. However, B3LYP distances are among the most overestimated and the related energies are significantly underestimated, thus confirming a significantly overbonding character of the empirical correction.^68–70

Fig. 4 Values of the reported intermolecular distances (Å) for the indicated dimers, computed with the small (DH-SVPD) and larger (cc-pVTZ) basis set.

3.2 IDHC5

The second set, IDHC5, it has been scarcely considered in previous benchmarks, due probably to the absence of updated reference data. To resolve this omission, the reaction energies of the reactions (1) to (5) have been computed at the DPNLO-CCSD(T)/CBS level. The MADs for the selected functionals are, instead, gathered in Table 4. The most striking feature among the results obtained with the larger Def2-TZVPP basis is the very good performances obtained by M06 and M06-L functionals, which complete the very good performances already observed for the ADIM6 and AAA sets. Indeed, these two models, with a MAD around 1.9 kcal mol⁻¹ are the best performers among the local, GH and RSH approaches. Even the introduction of empirical potential into B3LYP, the worst performer, does not allow to reach of the chemical accuracy threshold, even if the error is reduced by an order of magnitude (from 14.9 to 2.7 kcal mol⁻¹). Pure DHs do not behave as expected, albeit significantly better that their GH counterparts, since their deviations range between 7.7 kcal mol⁻¹ (B2-PLYP) and 3.7 kcal mol⁻¹ (PBE-QIDH). However, the coupling with an empirical dispersion correction, either D3 or D3(BJ), leads to the overcoming of the 1 kcal mol⁻¹ threshold for four functionals (DSD-PBEP86, revDSDPBEP86-D3(BJ), PBE0-DH-D3(BJ) and PBE-QIDH-D3(BJ)), the lowest value being 0.4 kcal mol⁻¹, obtained with the DSD-PBEP86 model.

Table 4 Computed mean absolute deviations (MAD, kcal mol⁻¹) for the reaction energies of the IDHC5 set

	DH-SVPD	Def2-TZVPP
M06-L	4.04	1.90
TPSSh	10.17	12.32
B3LYP	11.49	14.86
PBE0	7.64	10.06
M06	4.21	1.94
CAM-B3LYP	7.31	10.55
ωB97X-D	4.26	3.11
B3LYP-D3	3.13	2.66
B2-PLYP	4.75	7.72
PBE0-DH	4.62	7.05
PBE-QIDH	1.07	3.65
B2-PLYP-D3	1.87	1.34
DSD-PBEP86	3.39	0.41
revDSDPBEP86-D3(BJ)	2.19	0.88
PBE0-DH-D3(BJ)	1.71	0.72
PBE-QIDH-D3(BJ)	1.21	1.37
PBE-QIDH-D3	1.62	0.96

---

When the smaller DH-SVPD basis set is considered, the trend already discussed for ADIM6 and AAA is also now observed, that is an increasing of the MADs for all the methods, and in particular DHs, casting an empirical potential. Indeed, the reaction energies are in these cases all overestimated, since the attractive potential alters the balance between BSSE and BSIE at the base of our approach.

This is no longer the case when the empirical correction is not considered. Indeed, a significant improvement is found for the PBE-QIDH that, as before, shows with the small DH-SVPD basis set an error comparable to that obtained with the larger basis set and empirical potential (1.1 vs. 1.0 kcal mol⁻¹). However, in this case the chemical accuracy is just marginally reached. Also, the other two pure DHs provide significantly lower (about −40%) deviations the DH-SVPD basis. However, as pointed out by one of the referees, the DPNLO-CCSD(T) could be affected by a not negligible error, as for the case of the ADIM6 set,¹⁹ so that PBE-QIDH/DH-SVPD could be more accurate on this set than it appears. This point requires a deeper analysis based on very expensive full CCSD(T) calculations, that, at the moment, are not affordable on our local computer infrastructure.

3.3 PAH5

The PAH5 set is composed by 7 molecules, two of them are C₁₄H₁₀ isomers and five are C₁₈H₁₂ isomers. Their structures are sketched in Fig. 2.

As already highlighted by Karton,⁶⁵ GGA functionals underestimate the relative energies of the reactions (6) to (10) and only GHs including either a high percent of HF exchange or a low percent and a dispersion potential significantly reduce the deviations with respect to the reference data. DHs follow the same trends, so that the MADs are bracketed between 0.7 kcal mol⁻¹ (B2-PLYP) and 0.1 kcal mol⁻¹ (B2GP-PLYP-D3). In all cases, the DHs provide an accuracy lower than 1 kcal mol⁻¹ and, in particular, indicate triphenylene as the most stable isomer of C₁₈H₁₂ and anthracene as the most stable C₁₄H₁₀ molecule.

The data reported in Table 5 follows this trend. In particular, two DHs, PBE0-DH and PBE-QIDH, provide very low deviations in conjunction with the cc-pVQZ basis set (0.2 and 0.3 kcal mol⁻¹). These functionals are among the better performing functionals of their class not corrected for dispersion. The inclusion of empirical potential has a beneficial effect for B2-PLYP whose error is significantly reduced (from 0.7 to 0.2 kcal mol⁻¹), while a negative impact is obtained for the DHs casting the PBE functional. Indeed, the empirical potential, further strengthening the weak interactions, leads to an overestimation of the reaction energies with a consequent increase of the MADs. The PBE0-DH functional represents the worst case, since its error grows from 0.2 kcal mol⁻¹ to 1.5 kcal mol⁻¹, if the D3(BJ) correction is added. This behavior is not surprising since empirical potentials work at their best with functional (like B3LYP) significantly underestimating weak interactions. In contrast, functionals which already somehow give an energy minimum, even if small (such as PBE0), lead to an overestimation of the interactions upon addition of classical potentials.

Table 5 Computed mean absolute deviations (MAD, kcal mol⁻¹) for reaction energies of the PAH5 set

	DH-SVPD	cc-pVQZ
a Data from ref. 65.
M06-L	0.71	0.74^a
TPSSh	1.10	1.20^a
B3LYP	1.38	1.48^a
PBE0	0.68	0.79^a
M06	0.49	0.53^a
CAM-B3LYP	0.40	0.38^a
ωB97X-D	0.79	0.69^a
B3LYP-D3	1.11	0.69^a
B2-PLYP	0.69	0.74^a
PBE0-DH	0.21	0.24
PBE-QIDH	0.34	0.31
B2-PLYP-D3	0.57	0.22^a
DSD-PBEP86	0.10	0.36^a
revDSDPBEP86-D3(BJ)	0.32	0.36
PBE0-DH-D3(BJ)	0.41	1.46
PBE-QIDH-D3(BJ)	0.50	0.45
PBE-QIDH-D3	0.42	0.36

---

In going from the larger to the smaller basis set, the MADs decrease or are unchanged (±0.05 kcal mol⁻¹). The exceptions are represented by ωB97X-D (+0.1 kcal mol⁻¹), B3LYP-D3 (+0.4 kcal mol⁻¹) and B2-PLYP-D3 (+0.4 kcal mol⁻¹).

In conclusion, all DHs give deviation below the chemical accuracy thresholds with both large (cc-pVQZ) and small (DH-SVPD) basis set. In most cases, the two bases provide very close deviations. However, while the DSD-PBEP86 provides the lowest MADs when coupled to the DH-SVPD basis (0.1 kcal mol⁻¹), PBE0-DH and PBE-QIDH are not far (0.2 and 0.3 kcal mol⁻¹, respectively) without further introduction of an empirical correction.

3.4 Cope set

The last set, Cope, collects 25 reactions and transition-state energies derived from the structural reorganization of the 5 bullvalene derivatives depicted in Fig. 3. These two sets of data span different energy intervals, from −22 kcal mol⁻¹ to 6 kcal mol⁻¹ for the reaction energies and from 42 to 66 kcal mol⁻¹ for the barrier heights. More interesting, they collect molecules different in nature, minima and transition states, so that they represent a very difficult play ground for most of the DFT approaches. Indeed, few DFT methods provide a balanced description of both sets.⁶⁷ In particular, some of the functionals, such as PBE-QIDH or ωB97X-2 provides sub-chemical accuracy on both barriers and reaction energies, whereas other functionals are good only on one of these properties.

The obtained results are collected in Table 6. The first feature to be commented is that the MADs obtained for the barrier heights are larger than those calculated for the reaction energies. Indeed, several functionals are lower than the 1 kcal mol⁻¹ threshold when coupled to the larger Def2-TZVPP basis set. In particular, DH performances for reaction energies range between 0.7 kcal mol⁻¹ (B2-PLYP) and 0.2 kcal mol⁻¹ (rev-DSDPBEP86-D3(BJ)), the only exception in this family being PBE0-DH (1.0 kcal mol⁻¹). In contrast, the range is between 0.4 kcal mol⁻¹ (PBE-QIDH-D3 and PBE-QIDH) and 0.9 kcal mol⁻¹ (PBE0-DH) for energy barriers, with three functionals, B2-PLYP(D3), B2-PLYP and DSD-PBEP86 providing large errors (between 3.7 and 1.7 kcal mol⁻¹). The other non-DH functionals provide correct (around 1 kcal mol⁻¹) deviations for reactions barrier, while only PBE0 is close to the chemical accuracy (1.0 kcal mol⁻¹, see Table 6).

Table 6 Computed mean absolute deviations (MAD, kcal mol⁻¹) for energies of the Cope set

	Barrier heights		Reaction energies
	DH-SVPD	Def2-TZVPP	DH-SVPD	Def2-TZVPP
M06-L	1.26	1.35	1.88	1.83
TPSSh	2.54	3.24	1.81	1.64
B3LYP	2.70	3.33	1.56	1.40
PBE0	0.97	1.03	1.64	1.45
M06	2.22	1.95	0.91	0.89
CAM-B3LYP	2.57	1.91	1.00	0.84
ωB97X-D	2.18	1.52	1.09	0.93
B3LYP-D3	2.88	3.52	1.13	0.98
B2-PLYP	3.05	3.56	0.9	0.74
PBE0-DH	1.41	0.86	1.22	1.04
PBE-QIDH	0.63	0.37	0.85	0.68
B2-PLYP-D3	3.14	3.65	0.66	0.50
DSD-PBEP86	1.26	1.65	0.43	0.26
revDSDPBEP86-D3(BJ)	0.46	0.83	0.41	0.24
PBE0-DH-D3(BJ)	1.25	0.70	1.01	0.83
PBE-QIDH-D3(BJ)	0.59	0.36	0.81	0.65
PBE-QIDH-D3	0.60	0.36	0.80	0.63

---

More interesting, only few functionals provide a balanced description of reaction and barrier energies, in terms of comparable deviations. They include all those casting the PBE functionals, either GH or DH, M06-L and revDSDPBEP86-D3(BJ). For the other ones, the difference can be as high as some kcal mol⁻¹, as in the case of B2-PLYP(D3) (0.5 and 3.7 kcal mol⁻¹ for the two sets, respectively) and DSD-PBEP86 (0.3 and 1.7 kcal mol⁻¹). It is also remarkable the small effect of dispersion on the computed energies, as showed by the small or even negligible variations of the MADs observed upon addition to empirical corrections. For the reaction energies there is a variation of −0.2 kcal mol⁻¹ in going from B2-PLYP to B2-PLYP-D3 and a negligible difference (<0.1 kcal mol⁻¹) for PBE-QIDH and PBE-QIDH-D3(BJ). Even smaller differences are found for barrier heights.

In going from the larger to the small basis set a significant increase of the MADs is observed. This variation is smaller and constant for the reaction energies of all DHs (around + 0.2 kcal mol⁻¹), while larger values are observed for barrier heights (between 0.2 and 0.6 kcal mol⁻¹). A similar behavior is also observed for the other classes of functionals, even if with some small variation for some functional and energies (see Table 6 for details).

Overall, two functionals provide a subchemical accuracy with the DH-SVPD basis set on both reaction energies and barrier heights, namely PBE-QIDH, with and without corrections, and revDSDPBEP86-D3(BJ).

4. An overview and discussion

As mentioned above, the selected datasets constitute a quite heterogeneous ensemble, where dispersion interactions are, in some cases, combined with subtle modifications of the electronic structures in such a way that they cannot be disentangled. At the same time, this difficulty concomitantly increases the interest of the selected datasets, which represent reasonably well “real-world” chemical problems where several factors rule the overall behavior. Some trends can be however evidenced from the obtained results.

In the first two sets, ADIM6 and AAA, dominated by intermolecular dispersion interactions, the combination of PBE-QIDH functionals with the DH-SVPD basis set, provides basically the same deviations obtained with larger basis sets and empirical potentials. The remaining pure DHs behaves in a similar way. This trend is also observed for the IDHC5 dataset which also contains some isomerization reactions with moderate modifications of the electronic structures. For all these three datasets, the small basis cannot be used in conjunction with an empirical potential, since this latter adds an extra-attractive energy leading to a consequent overestimation of the reaction energies.

Moving to the PAH5 dataset, the obtained results show that the small basis is able to capture the modifications in the electronic structure observed in going from one isomer to another one.

The last set, Cope, reveals a different behavior with the DH-SVPD basis giving higher deviations that the triple-ζ basis, more evident in some cases. This could be related to the peculiar features of the reaction intermediates, which have not the same number and type (double, triple) of bonds. Indeed, the DH-SVPD basis set provides very accurate results for the so-called bond separation reactions, where the thermochemistry of selected reactions is evaluated with an isodesmic principle which leads to the preservation of the number and type of intramolecular bonds.³⁴ The situation is even more complex due to the absence of dispersion effects for these reactions. This makes the Cope set very peculiar in the context of this study, well representing the limits of the pairing a DH with the tailored DH-SVPD. However, it should be also remarked that the computational time of a DHs paired with this small basis is in practice equivalent to that of a GH with a large triple-ζ basis set, since the use of the smaller basis set largely compensates for the more computer-demanding time of the perturbative part in PBE-QIDH.

The overall trends can be better observed from the plots in Fig. 5 and 6. In the first one, are reported the MADs for all the considered DHs functionals and datasets, obtained with the DH-SVPD and reference basis sets. From these data it clearly appears that the small basis provides error smaller, or at least close, to that systematically provided with the larger basis set, in absence of empirical corrections for all the datasets. The advantages in term of computational speed-up are evident. For instance, the whole computational time for the ADIM6 with the DH-SVPD basis set is only 3% of that needed for the Def2-QZVP basis (about 5 minutes of wall-clock time against 188 minutes, respectively). When the empirical corrections are added, larger bases of triple-ζ or quadruple-ζ quality are mandatory for obtaining a small deviation with respect to reference data. It should be outlined, however, that sub-chemical accuracy can be obtained with the two approaches, DH and DH-SVPD or DH + D together with a large basis set, for most of the considered sets, with the few exceptions already discussed. For these exceptions, the small basis provides a smaller deviation than the larger basis sets, even if the 1 kcal mol⁻¹ threshold cannot be reached.

Fig. 5 Mean absolute deviations (MAD, kcal mol⁻¹) obtained with the larger and DH-SVPD basis set for pure and dispersion-corrected double hybrids. The shadow areas correspond to values lower than the chemical accuracy (1 kcal mol⁻¹).

Fig. 6 Average of the mean absolute deviations (〈MAD〉, kcal mol⁻¹) computed for the considered benchmarks and double hybrid functionals. The shadow area corresponds to values lower than the chemical accuracy (1 kcal mol⁻¹).

Finally, in Fig. 6 are reported the MADs for all the DHs considered. To avoid any bias coming from the different nature and number of data the different considered set, these MADs are simply the mathematical average of those computed for the different set, that is their sum divide by 6 (counting reaction and barriers for the Cope in a different way). The first striking feature of the plot concerns two functionals, namely PBE0-DH and B2-PLYP, which do not reach the threshold of 1 kcal mol⁻¹, even if a significant improvement is found in going for the larger basis set to DH-SVPD. As already discussed, all DHs including an empirical dispersion prefer the larger basis set which lead to sub-chemical accuracies. In contrast, the PBE-QIDH/DH-SVPD combinations is competitive with these latter. In short, the lowest values are obtained with PBE-QIDH/DH-SVPD or by combining PBE-QIDH-D3(BJ), DSD-PBEP86 and rev-DSDPBEP86-D3(BJ) with a larger basis, all these models providing a mean MAD around 0.5 kcal mol⁻¹. It is reassuring than on such global performance indicator, the PBE-QIDH-D3(BJ)/DH-SVPD model, which is our DHthermo model for the thermochemistry of alkanes,³⁶ is among the best performers, thus extending its applicability beyond isodesmic reactions.

5. Conclusions

A detailed analysis of the performances of DHs coupled with the small DH-SVPD basis set, especially developed for weak noncovalent interactions, have been carried out on a series of difficult datasets. The aim is to extend the applicability domain of this computational protocol (DH + DH-SVPD basis set) while showing its reliability with respect to data obtained with larger basis sets of triple-ζ or quadruple-ζ quality and empirical pairwise potentials for modeling noncovalent interactions. The data sets were chosen so to include, beyond the mentioned noncovalent interactions, others subtle electronic effects and simple, yet challenging, reactions. The obtained results suggest that the chemical accuracy, that is deviations of less than 1 kcal mol⁻¹ with respect to reference values, can be obtained with the nonempirical PBE-QIDH functionals for the 5 considered datasets, when it is coupled with the tailored DH-SVPD basis set. Globally speaking, this pairing is competitive with respect to modern semiempirical DHs, such as rev-DSD-PBEP86, coupled to empirical potential and large basis set. A similar positive behavior is found for all the other pure DHs functionals, where the DH-SVPD basis set leads to a significant improvement toward the chemical accuracy threshold.

Albeit this newly developed basis set is based on a compensation between two errors, that is BSSE and BSIE, the results clearly show that it is transferable to both nonempirical and empirical DH, when an empirical potential is not further added. The resulting protocol is robust, fast, and simple to use, as showed by the Gaussian input example reported in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Bernardino Tirri (Chimie ParisTech) for fruitful discussions. E. B. thanks ANR (Agence Nationale de la Recherche) and CGI (Commissariat à l'Investissement d'Avenir) for their financial support to this work through Labex SEAM (Science and Engineering for Advanced Materials and devices), Grant No. ANR-10-LABX-096 and ANR-18-IDEX-0001. H. L. acknowledges the financial support from the China Scholarship Council (grant no. 201908310062).

References

1. C. W. Bauschlicher and S. R. Langhoff, Science, 1991, 254, 394–398.
2. T. Helgaker, T. A. Ruden, P. Jørgensen, J. Olsen and W. Klopper, J. Phys. Org. Chem., 2004, 17, 913–933.
3. J. A. Pople, M. Head-Gordon, D. J. Fox, K. Raghavachari and L. A. Curtiss, J. Chem. Phys., 1989, 90, 5622–5629.
4. J. M. L. Martin, Annu. Rep. Comput. Chem., 2005, 1, 31–43.
5. A. Karton, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2016, 6, 292–310.
6. A. Tajti, P. G. Szalay, A. G. Csaszar, M. Kallay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613.
7. A. Tajti, P. G. Szalay, A. G. Csaszar, M. Kallay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, J. Chem. Phys., 2004, 121, 11599–11613.
8. A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108–144117.
9. J. A. Pople, Rev. Mod. Phys., 1999, 71, 1267–1274.
10. A. Karton, E. Rabinovich, J. M. L. Martin and B. Ruscic, J. Chem. Phys., 2006, 125, 144108–144117.
11. P.-F. Loos, N. Galland and D. J. Jacquemin, J. Phys. Chem. Lett., 2018, 9, 4646–4651.
12. C. Puzzarini and V. Barone, Phys. Chem. Chem. Phys., 2008, 10, 6991–6997.
13. J. H. Thorpe, C. A. Lopez, T. L. Nguyen, J. H. Baraban, D. H. Bross, B. Ruscic and J. F. Stanton, J. Chem. Phys., 2019, 150, 224102–224116.
14. A. Ganyecz, M. Kállay and J. Csontos, J. Chem. Theory Comput, 2017, 13, 4193–4204.
15. B. Chan and L. Radom, J. Chem. Theory Comput, 2013, 9, 4769–4778.
16. Y. Zhao, L. Xia, X. Liao, Q. He, M. X. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2018, 20, 27375–27384.
17. M. Bogojeski, L. Vogt-Maranto, M. E. Tuckerman, K.-R. Müller and K. Burke, Nat. Commun., 2020, 11, 5223–5233.
18. E. M. Collins and K. Raghavachari, J. Chem. Theory Comput, 2020, 16, 4938–4950.
19. G. L. Dimitrios, G. Yang and N. Frank, J. Phys. Chem. A, 2020, 124, 90–100.
20. F. Ballesteros, S. Dunivan and K. U. Lao, J. Chem. Phys., 2021, 154, 154104–154114.
21. R. Peverati and D. G. Truhlar, Philos. Trans. R. Soc. A., 2014, 372, 1–52.
22. J. C. Sancho-García and C. Adamo, Phys. Chem. Chem. Phys., 2013, 15, 14581–14594.
23. L. Goerigk and S. Grimme, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2014, 4, 576–600.
24. N. Q. Su, Z. Zhu and X. Xu, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2287–2292.
25. J. M. L. Martin and G. Santra, Isr. J. Chem., 2020, 60, 1–19.
26. E. Semidalas and J. M. L. Martin, J. Chem. Theory Comput, 2020, 16, 4238–4255.
27. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
28. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
29. N. Mehta, M. Casanova-Páez and L. Goerigk, Phys. Chem. Chem. Phys., 2018, 20, 1463–9076.
30. D. Bakowies, J. Phys. Chem. A, 2013, 117, 228–243.
31. D. Bousquet, E. Brémond, J. C. Sancho-García, I. Ciofini and C. Adamo, Theor. Chem. Acc., 2015, 134, 1602–1613.
32. J. C. Sancho-García, E. Brémond, M. Campetella, I. Ciofini and C. Adamo, J. Chem. Theory Comput, 2019, 15, 2944–2953.
33. H. Li, B. Tirri, E. Brémond, J. C. Sancho-García and C. Adamo, J. Org. Chem., 2021, 86, 5538–5545.
34. W. C. McKee and P. v. R. Schleyer, J. Am. Chem. Soc., 2013, 135, 13008–13014.
35. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
36. A. J. C. Varandas, Chem. Phys. Lett., 1980, 69, 222–224.
37. É. Brémond, I. Ciofini, J. C. Sancho-García and C. Adamo, J. Phys. Chem. A, 2019, 123, 10040–10046.
38. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
39. S. Grimme, J. Chem. Phys., 2006, 124, 034108–034116.
40. S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 1463–9076.
41. G. Santra, N. Sylvetsky and J. M. L. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143.
42. E. Brémond and C. Adamo, J. Chem. Phys., 2011, 135, 024106.
43. E. Brémond, J. C. Sancho-García, A. J. Pérez-Jiménez and C. Adamo, J. Chem. Phys., 2014, 141, 031101–031104.
44. E. Brémond, I. Ciofini, J. C. Sancho-García and C. Adamo, Acc. Chem. Res., 2016, 49, 1503–1513.
45. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101–194118.
46. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
47. J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401–146404.
48. C. Adamo, J. Chem. Phys., 1999, 110, 6158–6169.
49. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
50. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
51. J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
52. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108.
53. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
54. J. C. Sancho-García, É. Brémond, M. Savarese, A. J. Pérez-Jiménez and C. Adamo, Phys. Chem. Chem. Phys., 2017, 19, 13481–13487.
55. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
56. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119.
57. https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/GMTKN, retrieved 1/04/2020.
58. Y.-M. Chang, Y.-S. Wang and S. D. Chao, J. Chem. Phys., 2020, 153, 154301–154313.
59. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406.
60. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106–034118.
61. F. Neese, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2017, 8, e1327.
62. D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539.
63. R. A. Kendall, T. H. Dunning, Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
64. T. Helgaker, W. Klopper, H. Koch and J. Noga, J. Chem. Phys., 1997, 106, 9639–9646.
65. A. Karton, J. Comput. Chem., 2017, 38, 370–382.
66. A. Karton, Chem. Phys., 2021, 540, 111013–111031.
67. J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151–2155.
68. M. Savarese, É. Brémond and C. Adamo, Theor. Chem. Acc., 2016, 135, 99.
69. K. Tonigold and A. Groß, J. Comput. Chem., 2012, 33, 695–701.
70. F. Di Meo, I. Bayach, P. Trouillas and J. C. Sancho-García, J. Mol. Model., 2015, 21, 291.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra04108h

---