The mechanism of enhanced photocatalytic activity for water-splitting of ReS₂ by strain and electric field engineering

Abstract

To enhance the photocatalytic water splitting performance of 2D ReS₂, we theoretically propose a feasible strategy to engineer its band structure by applying strain or an electric field. Our calculated results show that the strains greatly tune the electronic structure of ReS₂ especially band gap and band edge positions, because the strains significantly alter the crystal structure and then cause rearrangement of the surface charge. However, electric fields have little influence on band gap but obviously affect the band edge positions. This is because the electric fields have little effect on the crystal structure of ReS₂ but easily produce an in-plane electric dipole moment. The shifts in band edge position mainly arise from competition between the surface charge and the in-plane electric dipole. For an applied strain, the shifts are dominated by rearrangement of surface charge; for an applied electric field, the shifts are determined by an induced electric dipole moment. Importantly, functionalized ReS₂ with a bi-axial strain of −4% or an electronic field of −0.1 V Å⁻¹ may be good candidates for water-splitting photocatalysts owing to their suitable band edge positions for water splitting, ideal band gaps, good stability, reduced electron–hole recombination and high carrier mobility. We hope our findings will stimulate experimental efforts to develop new photocatalysts based on functionalized ReS₂.

---

1. Introduction

Photocatalytic water splitting using solar energy for hydrogen generation is a clean and “green” approach to solving environmental and energy problems.^1–12 Efficient semiconductor photocatalysts for water splitting should satisfy the following requirements: (1) an ideal band gap for wide visible-light adsorption; (2) suitable band edge positions which should straddle water redox potentials; (3) fewer electron–hole pair recombination; (4) high carrier mobility; and (5) good stability.^13–16 Traditional photocatalysts such as TiO₂,^17,18 ZnO,^19,20 and KNbO₃ have been reported to be promising photocatalysts.^21,22 Nevertheless, their large band gaps greatly limit their visible-light absorption and result in poor photo-to-hydrogen conversion efficiency.

Since graphene was first prepared, two-dimensional (2D) transition-metal materials have shown efficient photocatalytic properties because of their good surface to volume ratio, abundant chemically active sites, and low charge carrier diffusion distance.^23–28 2D transition-metal dichalcogenides (TMDs),^29–32 as represented by MoS₂, have a direct band gap, strong visible-light absorption, excellent stability, and high electrocatalytic activity, so they are potential candidates for electronic, optoelectronic, and photovoltaic applications.^33–35 Different from the traditional TMDs (e.g., MoS₂ and WS₂), ReS₂ has a triclinic symmetry and displays a distorted 1T (1T′) octahedral crystal structure, showing a particular electronic and optical anisotropy with a high experimental anisotropic mobility ratio of 3.1.^36–40 The electronic and dynamic decoupling in the interface with weak van der Waals forces enable it to retain a direct band gap (∼1.5 eV) almost independent of thickness.⁴¹ The weak coupling enables ReS₂ to be easily prepared as nanosheets, exhibiting excellent Raman active modes and catalytic activity in the hydrogen evolution reaction.⁴² These advantages make ReS₂ a potential candidate for photocatalytic water splitting.¹³ However, the conduction band minimum (CBM) of ReS₂ is below the hydrogen redox potential of water, hindering its application in photocatalytic hydrogen generation.^43,44 Therefore, it is necessary to tune the band energy alignment of ReS₂ to enhance its photocatalytic activity for water splitting. In particular, mechanical strain or an external electric field are effective and practical ways to adjust the electronic properties of a 2D semiconductor.^45–52 For example, Bai et al. have shown that single-layer ZnGeN₂ could be effectively tuned to provide a better match with the redox potentials of water and to enhance light absorption in the visible-light region at a tensile strain of 5%.⁴⁹ Edalati et al. suggested that CsTaO₃ and LiTaO₃ exhibited optical bandgap narrowing and ∼2.5 times enhancement of photocatalytic hydrogen generation by straining.⁵⁰ Wang et al. reported that the biaxial strain tuned the bandgap and band alignment of a 2D CdS/g-C₃N₄ heterostructure for visible-light photocatalytic water splitting and accelerated the separation of photogenerated carriers and improved the photocatalytic activity.⁵¹ Dai et al. have described the ferroelectric photocatalysts could be greatly improved because the intrinsic internal electric field was beneficial for separation and migration of photogenerated carriers.⁵²

In this work, we investigate the potential of 2D ReS₂ for photocatalytic water splitting by strain and electric field functionalization. The first-principles calculations show that the strains greatly engineer the band gap and band alignment of ReS₂. A progressive shrinking in the band gap can be observed upon increasing the applied strain for both tensile and compressive strain, and for both axial and bi-axial strain. This is because the strains induce significant geometric distortion and lead to charge rearrangement. Although the band gap of ReS₂ is insensitive to an electric field, the band alignment depends greatly on an electric field because the electric field has little influence on the crystal structure but can produce an in-plane dipole moment. As a result, functionalized ReS₂ with a bi-axial strain of −4% or an electronic field of −0.1 V Å⁻¹ are considered good candidates for water-splitting photocatalysts.

2. Computational model and methods

In our calculations, density functional theory (DFT) were adopted with the Vienna ab initio simulation package (VASP).⁵³ The exchange correlation potential was the generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE).^54,55 The frozen core projector augmented wave method was employed to describe the electron–ion interaction. The plane wave cutoff energy was 400 eV, the total change in energy for geometrical optimization was 1.0 × 10⁻⁵ eV, the atomic forces were less than 0.01 eV Å⁻¹. 7 × 7 × 1 and 11 × 11 × 1 Monkhorst–Pack k-point mesh were respectively used for geometric optimization and the electronic structure calculations.

As we know, monolayer ReS₂ has almost the same electronic structure as multilayer ReS₂.⁴¹ Thus, a 2 × 2 supercell of free-standing monolayer ReS₂ was used as our model by cleaving the bulk ReS₂ along (0001) direction. A vacuum space along the y-direction was 15 Å to separate the interactions between the neighbouring slabs. As shown in Fig. 1, uniaxial lattice strain (x-axial or z-axial) was imposed by changing the dimension of the supercell in the x- or z-directions. Bi-axial lattice strain was imposed by changing the dimension of the supercell in the x- and z-directions simultaneously. We calculated the percentage applied strain according to % strain = (a − a₀)/a × 100%, where a and a₀ are the lattice constants of the ReS₂ monolayer before and after the application of strain. The strains were varied from −10% to 10% in steps of 2%, where the positive numbers represent tensile strains, and the negative numbers represent compressive strains. The positions of all the atoms in the supercell were fully relaxed but the lattice vectors were constrained. An external electric field intensity E_⊥ was applied along the y-direction with a net electric-dipole moment, from −0.2 V Å⁻¹ to 0.2 V Å⁻¹ in steps of 0.05 V Å⁻¹. Dipole corrections were applied to remove spurious dipole interactions between periodic images.^56,57

Fig. 1 (a) Top and (b) side views of ML-ReS₂; the blue and red arrows represent the directions of applied strain and the green arrows represent the direction of the electric field. (c) Band structure and atom-PDOS of ML-ReS₂. (d) Work-function of ML-ReS₂ (red line) and band alignments (denoting by the red solid lines) relative to the water redox potential positions (denoting by the black lines).

3. Results and discussion

3.1 Pristine ReS₂ monolayer

As shown in Fig. 1(a), the monolayer ReS₂ retains a triclinic structure. The bond distances d_Re–Re, d_Re2–S2, d_Re2–S3, and d_S–S are 2.717 Å, 2.359 Å, 2.432 Å, and 3.807 Å, respectively. The bond angles of Re₁–S₂–Re₂, S₂–Re₂–S₂, and S₁–Re₂–S₃ are defined as θ₁, θ₂, and θ₃ with values 70.2°, 105.2°, and 80.9°, which are consistent with the experimental values (d_Re–Re = 2.722 Å, d_Re2–S2 = 2.360 Å, d_Re2–S3 = 2.434 Å, d_S–S = 3.806 Å, θ₁ = 70.3°, θ₂ = 105.1°, and θ₃ = 81.1°).

The band structure of ReS₂ was reported in our previous calculation.²⁹ ML-ReS₂ is a direct-band-gap semiconductor, both the valence band maximum (VBM) and the conduction band minimum (CBM) are located at the Γ point, with a calculated band gap of 1.431 eV. Analysis of the partial density of states (PDOS) shows that the VBM originates mainly from hybridization among S-3p_x, Re-5d_yz, and Re-5d_xz orbitals; the CBM consists mainly of S-3p_z and Re-5d_xz and Re-5d_z² [see PDOS in Fig. 1(c)]. Though the VBM is below the water oxidation level, the CBM is located below the hydrogen redox potential [see Fig. 1(d)], the photocatalytic activity of hydrogen production in ReS₂ is inhibited. These calculated results are in good agreement with the experimental results.⁴⁴

3.2 Tuning band edge positions to improve the photocatalytic performance of ReS₂ through applying uniaxial or bi-axial strain

3.2.1 Stability. It is found that the in-plane strains greatly influence not only the in-plane Re–S (d_Re–S) and Re–Re bond (d_Re–Re) lengths but also the vertical distance between the S atoms d_S–S (within an S–Re–S sheet) and S–Re–S bond angle.

As shown in Fig. 2, tensile strains, whether uniaxial or bi-axial, elongate the in-plane bond lengths, but slightly shorten the vertical S–S distance because the lattice vectors in the plane are fixed in the process of atomic relaxation. Compressive strains produce the opposite effect. Here d_Re2–S3 increases with an increase in x-axial strain, while it is almost unchanged with an increase in z-axial strain because there are no components of d_Re2–S3 in the z-direction. Similarly, d_Re2–S3 and d_Re–Re increase with an increase in z-axial strain, while they are almost unchanged with an increase in x-axial strain because there are no components of d_Re–Re in the z-direction. As far as bond angle is concerned, the opposite sides of θ₁ and θ₃ are Re₁–Re₂ and S₁–S₃, respectively, which being parallel to z-axial and x-axial strains, will be elongated by tensile strains. Thus, θ₁ increases with an increase in z-axial strain and θ₃ increases with an increase in x-axial strain. The influence of bi-axial strain is found to be more pronounced than that of uniaxial strains because it comes from the common effect of x-axial and z-axial strains.

Fig. 2 The calculated structural parameters and formation energies of ReS₂ as a function of (a) x-axial, (b) z-axial and (c) bi-axial strain.

To further investigate the stability of ReS₂, we calculated its formation energy, which is defined as:⁴⁶ E_f = E_2D/N_2D − E_3D/N_3D, where E_2D and E_3D are the total energy of monolayer and bulk ReS₂, and N_2D and N_3D are the number of atoms in monolayer and bulk ReS₂. The formation energies of x-axial-strained ReS₂ decrease with an increase in the strains and the decrease is sharper under compressive strains than under tensile strains. Additionally, all the formation energies have negative values and are smaller than that of pristine ReS₂, indicating that monolayer ReS₂ is stable. For z-axial and bi-axial strains, the formation energies decrease with an increase in the compressive strains but increase with an increase in the tensile strains, indicating that the systems are more stable under compressive strains than under tensile strains.

3.2.2 Electronic structures. The structural change has a significant impact on the electronic structure of strained ReS₂. Under compressive strain, localized states appear at the bottom of the valence band, originating from Re-5d_xz and S-3p_x states, and the energy of the CBM decreases. Meanwhile, the CBM changes from the Γ point to the K point, the VBM transfers from the Γ point to the M point then to the K point, and as a result ReS₂ becomes an indirect-band-gap semiconductor and the band gap decreases with the increase in compressive strain [see Fig. 3(a)–(d)]. Under x-axial tensile strains, the systems still display direct-band-gap semiconductor properties, as shown in Fig. 3(f)–(i). More particularly, the tensile strain little affects the CBM, while it causes a decrease in the energy at the VBM, induced by a reduction in the distance between the S atoms (d_S–S) and an increase in the distance between the Re and S atoms (d_Re–S). The 5d_x²−y² of the Re atoms gradually has a great effect on the CBM; therefore the band gap decreases from 1.431 to 0.540 eV when the applied tensile strain changes from 0 to 10%.

Fig. 3 Band structure and PDOS of ML-ReS₂ at x-axial strains of (a) −10%, (b) −6%, (c) −4%, (d) −2%, (e) 0%, (f) 2%, (g) 4%, (h) 6% and (i) 10%.

For z-axial compressive strained ReS₂, the energy of the CBM decreases with an increase in the compressive strain, thus, the band gap decreases from 1.431 to 0.688 eV when the compressive strain varies from 0 to −10% [see Fig. S1(a)–(d) in the ESI†].⁴² Under z-axial tensile strain, ReS₂ changes to indirect-band-gap semiconductor, the VBM locates at the Γ point but its energy decreases, while the CBM relocates from the Γ point to the M point and then to the K point. The PDOS in Fig. S1(f)–(i)† indicates that the Re-5d_xz states and S-3p_y states play important roles in the process. This is mainly induced by the changes in d_S–S and d_Re–Re. Thus, the band gap decreases from 1.431 eV to 0.783 eV as the tensile strains vary from 0 to 10%.

The effect of the bi-axial strain on ReS₂ is the result of the common effect of x-axial and z-axial strain on ReS₂. Thus, bi-axial-strained ReS₂ is an indirect-band-gap semiconductor and the band gap decreases (from 1.431 eV to 0.452 eV) with an increase in the strains, whether compressive or tensile. ReS₂ displays metallic properties at 10% bi-axial compressive strain as there are a few bands across the Fermi level which mainly originate from hybridization of Re-5d_x²−y², 5d_xz, and S-3p_x. Clearly, for the bi-axial compressive strain, Re-5d_xz and S-3p_x play a leading role near the Fermi level. While for the bi-axial tensile strain, Re-5d_x²−y² and S-3p_y play important roles near the Fermi level [see Fig. S2†].

3.2.3 The band edge positions of strained ReS₂ for photocatalytic water splitting. The redox potentials at pH = 7, which is the solution condition for VASP calculation, are −5.26 eV for water-oxidation potential (O₂/H₂O) and −4.03 eV for the hydrogen reduction (H⁺/H₂).⁵⁸ Fig. 4 shows the band alignment of strained-ReS₂ related to water redox potentials at pH = 7. For x-axial strain, the CBM of ReS₂ moves upward by 0.049–0.210 eV for compressive strain but downshifts by 0.076–0.701 eV for tensile strain compared to pristine ReS₂. A similar phenomenon occur under z-axial and bi-axial strains. According to Bader charge analysis, we find there is charge transfer inside the strained ReS₂.⁵⁹ For the compressive strains, ReS₂ gains electrons (for example, ReS₂ gains 0.022e with a compressive x-axial strain of −2%), the Fermi energy level increases, and the band edge positions upshifts. This is because the crystal structure becomes compact under compressive strain, and the surface charge distribution is relatively concentrated. Conversely, for tensile strains, ReS₂ loses electrons (for example, ReS₂ loses 0.005e with a tensile x-axial strain of 2%), the Fermi energy reduces, the band edge position downshifts, because the crystal structure becomes looser under tensile strain, and the surface charge distribution is relatively scattered.

Fig. 4 Calculated band alignments and band gaps of ReS₂ at different (a) x-axial, (b) z-axial and (c) bi-axial strains in comparison with water redox potentials.

As we know, the work function is greatly determined by the crystal structure which is related to the surface charge distribution and the electron surface barrier caused by an internal electron field related to the surface electric dipole distribution. There is competition between the surface charge and the surface electric dipole. The in-plane strains cause severe distortion of the crystal structure, then influence the surface charge distribution, and thus decisively affect the work function. However, the in-plane strain induces little geometric distortion in the vertical direction, therefore inducing a very small dipole moment perpendicular to the surface component μ_⊥,⁶⁰ and then slightly affecting the work function. For example, for ReS₂ with a bi-axial strain of −4%, the induced dipole density μ_⊥ is only −0.006 D nm⁻² [see the Table S1 in the ESI†],⁴² little affecting the work function. Thus, the strain-induced rearrangement of surface charge plays an important role, leading to a great change in the work function of −0.382 eV. According to ΔV_⊥ = −ΔW_⊥, where ΔV_⊥and ΔW_⊥ respectively refer to the band edge shifts and the opposite direction. The band edge position upshifts by 0.382 eV [see the Table in the ESI†].⁴² As a result, the CBM of ReS₂ straddles the water reduction potential, and ReS₂ satisfies the demands of water splitting.

3.3 Tuning band edge positions to improve the photocatalytic performance of ReS₂ through applying an electric field

We further attempted to tune the band structure of ReS₂ by applying an electric field. The vertical electric fields are applied with different intensities along the y-direction. Fig. 5(a) shows that the formation energies of ReS₂, defined as E_f = E_2D/N_2D − E_3D/N_3D,⁴⁶ have negative values, indicating that the systems have good stability under different vertical electric fields.

Fig. 5 (a) Formation energy, (b) average electrostatic potential and (c) work function of ReS₂ under different electric fields.

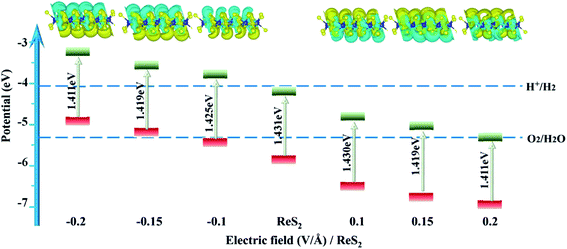
Fig. 6 displays the electronic structures of ReS₂ under different external electric fields. ReS₂ maintaining direct-band-gap semiconductor properties. For a positive electric field, the Re-5d and S-3p components of the CBM are slightly enlarged [see Fig. 6(d)–(f)], for a negative electric field, the Re-5d component of the VBM is slightly enlarged [see Fig. 6(a)–(c)]. Thus the band gap decreases slightly with an increase in the electric fields, changing from 1.431 to 1.411 eV, and the minimum value of 1.411 eV is found under electric fields of −0.2 V Å⁻¹ and 0.2 V Å⁻¹.

Fig. 6 Band structure and PDOS of ML-ReS₂ under vertical electric fields of (a) −0.2 V Å⁻¹, (b) −0.15 V Å⁻¹, (c) −0.1 V Å⁻¹, (d) 0.1 V Å⁻¹, (e) 0.15 V Å⁻¹ and (f) 0.2 V Å⁻¹.

Though the electric field has little influence on the band gap, it produces an in-plane dipole moment and then greatly affects the average electrostatic potential of ReS₂. As shown in the charge difference density in the inset of Fig. 7, surface charge transfer depends on the direction of E_⊥: for a negative electric field, the charge transfers from the upper side to the lower side, whereas, for a positive electric field, the charge transfers from the lower side to the upper side. The Bader charge analysis also quantitatively shows that there are 0.036e charges transferred from the upper side to the lower side for E_⊥ = −0.1 V Å,⁵⁹ there are 0.143e charges transfer from the lower side to the upper side for E_⊥ = 0.1 V Å⁻¹. Simultaneously, a vertical electric field alters the surface charge concentration of ReS₂. Fig. 5(b) shows the electrostatic potential V̄(y) under different electric fields, which displays a sawtooth behavior. For a negative electric field, V̄(y) increases linearly with an increasing vacuum layer, while the opposite is true for a positive field. Thus, the work function on both sides can be defined as W = mE_⊥ + Φ_w,^61,62 where Φ_w is the work function of ReS₂ without the external electric field, and m is the slope of the line relating to vacuum lengths. Fig. 5(c) shows that the work function varies linearly with the electric field, and the change in work function (ΔW_⊥ arises from the electric-field-induced dipole density, expressed as ΔW_⊥ = μ_⊥/Aε₀, where A is the surface area per molecule, ε₀ is the dielectric constant of the vacuum). As shown in Table 1, when E_⊥ is −0.1 V Å⁻¹, the induced dipole density is −1.382 D nm⁻², and the resultant change in work function is 0.521 eV, which is in agreement with the energy shift calculated from the average electrostatic potential.

Fig. 7 The band alignments and band gaps of ReS₂ at different external electric fields. The inset shows the charge density difference of ReS₂; yellow and green colors represent charge accumulation and charge depletion, respectively. The isovalue is 0.003 e Å⁻³.

Table 1 Vertical electric field E_⊥ (in eV), electric-field-induced dipole density μ_⊥/A (in D nm⁻²), change in work function ΔW_⊥ (in eV) of functionalized ReS₂ relative to pure ReS₂, band gap E_g (in eV), VBM and CBM positions E_VBM and E_CBM (in eV), and the formation energy E_f (in meV) of ReS₂ under different vertical electric fields

E⊥	μ⊥/A	ΔW⊥	Eg	EVBM	ECBM	Ef
−0.2	−2.767	−1.043	1.411	−4.743	−3.332	−0.8
−0.15	−2.074	−0.782	1.419	−5.012	−3.593	−0.9
−0.1	−1.382	−0.521	1.425	−5.279	−3.854	−0.6
0	0	0	1.431	−5.807	−4.376	−1.1
0.1	1.389	0.523	1.430	−6.330	−4.900	−1.2
0.15	2.081	0.784	1.419	−6.580	−5.161	−0.9
0.2	2.777	1.047	1.411	−6.835	−5.424	−1.7

---

Fig. 7 shows the band edges of ReS₂ with different electric fields. ReS₂ obviously upshifts with increasing negative electric fields, and the reduction capacity increases, while it downshifts with increasing positive electric fields, and the oxidation capacity increases. It is worth mentioning that the applied electric field can not only tune the band edge but also accelerate electron–hole separation and enhance activity carrier mobility. For ReS₂ with an applied electric field of −0.1 V Å⁻¹, the band edge upshifts by 0.521 eV and straddles the water redox potential.

4. Conclusions

To summarize, based on DFT calculations, we applied an external strain or an electric field to engineer the electronic structure of ReS₂ to meet the requirements of hydrogen production through photocatalytic water splitting. The in-plane strains have a great influence on the band gap and band alignment originating from great changes in the crystal structure. An increase in the strain decreases the band gap of ReS₂, and the band edge positions downshift with an increase in the tensile strains and upshift with an increase in compressive strains, where the shifts come mainly from rearrangement of surface charge. While the external electronic fields slightly influence the band gap of ReS₂ but greatly affect its band alignment. The band edge position shifts come from an external-electronic-field-induced dipole moment. Importantly, ReS₂ with a bi-axial strain of −4% or an electric field of −0.1 V Å⁻¹ can be considered strong candidates for photocatalytic water splitting because they possess suitable band edge positions for water splitting, ideal band gaps for visible-light absorption, good stability, reduced electron–hole recombination, and high carrier mobility. Notably, applying strain or an electric field is a feasible means of functionalization of single-layered and multilayered nanostructures for better photocatalytic water splitting.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the NSFC (11774302, 21903014 and 12074332) and the Qinglan Project of Jiangsu Province of Yangzhou University. The authors are grateful for access to the computational resources at YZU.

References

1. R. Schloegl, Nat. Mater., 2008, 7, 772.
2. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
3. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
4. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
5. T. Su, Q. Shao, Z. Qin, Z. Guo and Z. Wu, ACS Catal., 2018, 8, 2253–2276.
6. W. W. Zhong, Z. P. Wang, N. Gao, L. A. Huang, Z. P. Lin, Y. P. Liu, F. Q. Meng, J. Deng, S. F. Jin, Q. H. Zhang and L. Gu, Angew. Chem., Int. Ed., 2020, 59, 22743–22748.
7. S. J. Shen, Z. P. Lin, K. Song, Z. P. Wang, L. G. Huang, L. H. Yan, F. Q. Meng, Q. H. Zhang, L. Gu and W. W. Zhong, Angew. Chem., Int. Ed., 2021, 60, 12360–12365.
8. Z. Lin, S. Shen, Z. Wang and W. Zhong, iScience, 2021, 24, 102469.
9. B. Fang, J. H. Kim, M.-S. Kim and J.-S. Yu, Acc. Chem. Res., 2013, 46, 1397–1406.
10. S. Yu, S. Song, R. Li and B. Fang, Nanoscale, 2020, 12, 19536–19556.
11. B. Z. Fang, M. Kim, J. H. Kim and J. S. Yu, Langmuir, 2008, 24, 12068–12072.
12. Y. Xing, B. Fang, A. Bonakdarpour, S. Zhang and D. P. Wilkinson, Int. J. Hydrogen Energy, 2014, 39, 7859–7867.
13. M. Faraji, M. Yousefi, S. Yousefzadeh, M. Zirak, N. Naseri, T. H. Jeon, W. Choi and A. Z. Moshfegh, Energy Environ. Sci., 2019, 12, 59–95.
14. G. Liao, J. Fang, Q. Li, S. Li, Z. Xu and B. Fang, Nanoscale, 2019, 11, 7062–7096.
15. G. Liao, C. Li, X. Li and B. Fang, Cell Rep. Phys. Sci., 2021, 2, 100355.
16. Y. Liu, S. Shen, Z. Li, D. Ma, G. Xu and B. Fang, Mater. Charact., 2021, 174, 111031.
17. M. Ni, M. K. H. Leung, D. Y. C. Leung and K. Sumathy, Renewable Sustainable Energy Rev., 2007, 11, 401–425.
18. S. U. Khan, M. Al-Shahry and W. B. Ingler Jr, Science, 2002, 297, 2243–2245.
19. J. Liqiang, Q. Yichun, W. Baiqi, L. Shudan, J. Baojiang, Y. Libin, F. Wei, F. Honggang and S. Jiazhong, Sol. Energy Mater. Sol. Cells, 2006, 90, 1773–1787.
20. T. Xu, L. Zhang, H. Cheng and Y. Zhu, Appl. Catal., B, 2011, 101, 382–387.
21. Y. Huan, X. Wang, W. Hao and L. Li, RSC Adv., 2015, 5, 72410–72415.
22. G. Liao, Y. Gong, L. Zhang, H. Gao, G.-J. Yang and B. Fang, Energy Environ. Sci., 2019, 12, 2080–2147.
23. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
24. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
25. S. Stankovich, D. A. Dikin, G. H. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286.
26. Z. P. Wang, Z. P. Lin, J. Deng, S. J. Shen, F. Q. Meng, J. T. Zhang, Q. H. Zhang, W. W. Zhong and L. Gu, Adv. Energy Mater., 2021, 11, 7.
27. L. Lu, S. Zou and B. Fang, ACS Catal., 2021, 11, 6020–6058.
28. C. Wang, M. Zhu, Z. Cao, P. Zhu, Y. Cao, X. Xu, C. Xu and Z. Yin, Appl. Catal., B, 2021, 291, 120071.
29. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712.
30. M. Chhowalla, H. S. Shin, G. Eda, L. J. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263–275.
31. Z. Lin, B. Xiao, Z. Wang, W. Tao, S. Shen, L. Huang, J. Zhang, F. Meng, Q. Zhang, L. Gu and W. Zhong, Adv. Funct. Mater., 2021, 2102321.
32. C. Z. Wang, X. D. Shao, J. Pan, J. G. Hu and X. Y. Xu, Appl. Catal., B, 2020, 268, 7.
33. D. Voiry, J. Yang and M. Chhowalla, Adv. Mater., 2016, 28, 6197–6206.
34. Q. Lu, Y. Yu, Q. Ma, B. Chen and H. Zhang, Adv. Mater., 2016, 28, 1917–1933.
35. D. Wang, Y. Liu, X. Meng, Y. Wei, Y. Zhao, Q. Pang and G. Chen, J. Mater. Chem. A, 2017, 5, 21370–21377.
36. D. A. Chenet, O. B. Aslan, P. Y. Huang, C. Fan, A. M. van der Zande, T. F. Heinz and J. C. Hone, Nano Lett., 2015, 15, 5667–5672.
37. E. Liu, Y. Fu, Y. Wang, Y. Feng, H. Liu, X. Wan, W. Zhou, B. Wang, L. Shao, C. H. Ho, Y. S. Huang, Z. Cao, L. Wang, A. Li, J. Zeng, F. Song, X. Wang, Y. Shi, H. Yuan, H. Y. Hwang, Y. Cui, F. Miao and D. Xing, Nat. Commun., 2015, 6, 6991.
38. J. Hamalainen, M. Mattinen, K. Mizohata, K. Meinander, M. Vehkamaki, J. Raisanen, M. Ritala and M. Leskela, Adv. Mater., 2018, 30, e1703622.
39. L. Hart, S. Dale, S. Hoye, J. L. Webb and D. Wolverson, Nano Lett., 2016, 16, 1381–1386.
40. W. W. Zhong, B. B. Xiao, Z. P. Lin, Z. P. Wang, L. G. Huang, S. J. Shen, Q. H. Zhang and L. Gu, Adv. Mater., 2021, 33, 7.
41. S. Tongay, H. Sahin, C. Ko, A. Luce, W. Fan, K. Liu, J. Zhou, Y. S. Huang, C. H. Ho, J. Yan, D. F. Ogletree, S. Aloni, J. Ji, S. Li, J. Li, F. M. Peeters and J. Wu, Nat. Commun., 2014, 5, 3252.
42. M. Rahman, K. Davey and S.-Z. Qiao, Adv. Funct. Mater., 2017, 27, 1606129.
43. Y. Li, Y.-L. Li, B. Sa and R. Ahuja, Catal. Sci. Technol., 2017, 7, 545–559.
44. X. Xu, H. Zhao, R. Wang, Z. Zhang, X. Dong, J. Pan, J. Hu and H. Zeng, Nano Energy, 2018, 48, 337–344.
45. X. Liu and Z. Li, J. Phys. Chem. Lett., 2015, 6, 3269–3275.
46. H. Chen, C. Tan, K. Zhang, W. Zhao, X. Tian and Y. Huang, Appl. Surf. Sci., 2019, 481, 1064–1071.
47. B. You, M. T. Tang, C. Tsai, F. Abild-Pedersen, X. Zheng and H. Li, Adv. Mater., 2019, 31, e1807001.
48. J. Qi, X. Li, X. Qian and J. Feng, Appl. Phys. Lett., 2013, 102, 173112.
49. Y. Bai, G. Luo, L. Meng, Q. Zhang, N. Xu, H. Zhang, X. Wu, F. Kong and B. Wang, Phys. Chem. Chem. Phys., 2018, 20, 14619–14626.
50. K. Edalati, K. Fujiwara, S. Takechi, Q. Wang, M. Arita, M. Watanabe, X. Sauvage, T. Ishihara and Z. Horita, ACS Appl. Energy Mater., 2020, 3, 1710–1718.
51. G. Wang, F. Zhou, B. Yuan, S. Xiao, A. Kuang, M. Zhong, S. Dang, X. Long and W. Zhang, Nanomaterials, 2019, 9, 244.
52. B. Dai, Y. CHen, S. M. Hao, H. Huang, J. Kou, C. Lu, Z. Lin and Z. Xu, J. Phys. Chem. Lett., 2020, 11, 7407–7416.
53. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
54. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
55. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
56. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
57. L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301.
58. S. Yang, D. Prendergast and J. B. Neaton, Nano Lett., 2012, 12, 383–388.
59. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
60. J. Pan, Z. Wang, Q. Chen, J. Hu and J. Wang, Nanoscale, 2014, 6, 13565–13571.
61. M. Topsakal, H. H. Gürel and S. Ciraci, J. Phys. Chem. C, 2013, 117, 5943–5952.
62. R. Gholizadeh and Y.-X. Yu, J. Phys. Chem. C, 2014, 118, 28274–28282.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03821d

‡ These authors contributed equally.

---