A GGA + U investigation into the effects of cations on the electromagnetic properties of transition metal spinels

Abstract

Spinel oxides are promising low-cost catalysts with manifold and controllable physicochemical properties. Trial and error strategies cannot achieve the effective screening of high-performance spinel catalysts. Therefore, unraveling the structure–performance relationship is the foundation for their rational design. Herein, the effects of cations in tetrahedral and octahedral sites on the electronic structures of spinels were systematically investigated using GGA + U calculations based on ACr₂O₄ (A = Mn, Fe, Co, Ni, and Zn) and Zn/LiB₂O₄ (B = Cr, Mn, Fe, Co and Ni). The results indicate that the octahedrally coordinated B cations have notable influence on the electronic structures of spinels. The Jahn–Teller active ions Fe²⁺, Ni²⁺, Mn³⁺, Ni³⁺, Cr⁴⁺ and Fe⁴⁺ can remarkably reduce the band gaps of spinels and even change their electroconductibilities. These results will provide theoretical insights into the electronic properties of 3d transition metal spinels.

---

Introduction

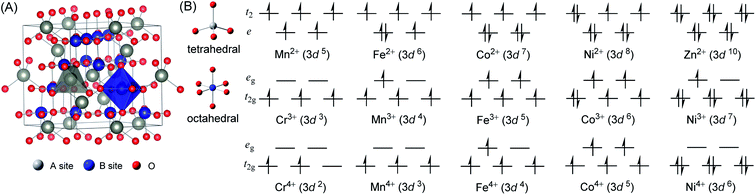
Spinels were initially regarded as precious stones such as the famous Black Prince's Ruby and Timur Ruby. In 1915, the first report of the crystal structure of a spinel lifted the veil of gems.¹ The spinel structure is formulated AB₂X₄, where A and B are tetrahedrally and octahedrally coordinated metal cations, respectively, and X is an anion (typically O or F). Fig. 1A presents the structural model of normal AB₂O₄, where O²⁻ has a close-packed array and A²⁺ and B³⁺ ions are in tetrahedral and octahedral cages formed by the oxygens, respectively. Each unit cell contains eight formula units and has a composition of A₈B₁₆O₃₂.

Fig. 1 (A) The geometric structure of AB₂O₄ spinel. The A²⁺ ions (grey spheres) and the B³⁺ ions (light blue spheres) are in tetrahedral and octahedral cages formed by the oxygen atoms (red spheres). (B) Electron configurations of A²⁺ and B³⁺ ions with increasing 3d electron.

Spinels contain a large number of species and embody almost all main group metals and transition metals.^2,3 The benefits of spinels, such as tunable composition, electron configurations, valence and magnetic states as well as low cost, make them increasingly attractive in optical, electromagnetic, information technology, environmental science, energy storage and conversion fields.^4–6 Recently, their intrinsic enzyme-mimicking activities, such as peroxidase-, oxidase-, superoxide dismutase- and catalase-like activities, cast light on broad biomedical applications.^7–19

However, trial and error strategies cannot achieve the effective screening of high-performance spinels, which hinder the rational design spinel catalysts. Recently, Xu et al. developed cations in octahedral sites as an effective descriptor to predict spinel catalysts with high oxygen-reduction reaction (ORR) and oxygen-evolution reaction (OER) performance.²⁰ Although progresses have been achieved,^21–25 efforts are still needed to reveal the unambiguous structure–function relationship. The rational design roots in the physicochemical properties. According to previous reports, the electronic configuration of metal cations,²⁶ the occupation of tetrahedral and octahedral sites²⁰ and the spin orders^22,23,27 are key factors affecting the geometric and electronic properties of spinels.

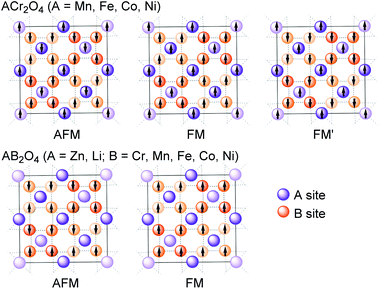
Herein, to investigate the effects of cations in tetrahedral and octahedral sites on the electronic structures of spinels, three series of spinels (Fig. 1B), where the metals on A and B sites have continuously varying electronic conformations, namely ACr₂O₄ (A = Mn, Fe, Co, Ni, and Zn) and Zn/LiB₂O₄ (B = Cr, Mn, Fe, Co and Ni), were investigated as the model system. The B cations in the LiB₂O₄ series have two valence states, particularly half B³⁺ and half B⁴⁺. The results indicate that the magnetism of spinels depends on the indirect exchange of cations (J_MM). The configuration of octahedrally coordinated B cations has notable influence on the electronic structures of spinels. The results presented here provide insights into the physicochemical properties of spinels.

Methods

Calculations were performed under periodic boundary conditions employing the Vienna Ab initio Simulation Package (VASP).²⁸ Projector-augmented wave (PAW)²⁹ pseudopotentials and Perdew–Burke–Ernzerhof (PBE)³⁰ exchange-correlation functional of generalized gradient approximation (GGA) were used to describe the interactions between core electrons. Both geometric optimizations and density of states (DOS) analysis were performed using a standard Monkhorst–Pack grid³¹ sampling at 7 × 7 × 7. An energy cut-off was set to 450 eV and the convergence thresholds for the electronic structure and forces were set to 10⁻⁵ eV and 0.02 eV Å⁻¹, respectively. The Hubbard U correction^32,33 was used to make the strong coulomb interactions of d electrons more accurate. Following a literature survey,^25,34–36 the U_eff values used for 3d metals are shown in Table S1.†

Results and discussion

To verify the ground states for spinels, initial magnetic states illustrated in Fig. 2 with different spin orders were set for geometric optimizations. All initial structures with eight formula units in one unit cell are crystallized in the Fd3̄m space group (No. 227). The calculated energies for all magnetic states are listed in Table S1,† and the geometric structures of the ground states are illustrated in Figure S1.† The optimized physicochemical characteristics including the ground state (GS), lattice parameters, band gap (E_g) and magnetic moments on tetrahedral and octahedral metal atoms (MO and MT) are listed in Table 1.

Fig. 2 Magnetic states initially set for optimizations. There are three initial states, namely AFM, FM and FM′, for ACr₂O₄ (A = Mn, Fe, Co, and Ni). The net magnetic moments for A, B and the whole bulk are zero in the AFM state. In the FM state, the magnetic moments of A and B are in the same direction, while in the opposite directions in the FM′ state. There are two magnetic states for Zn/LiB₂O₄ (B = Cr, Mn, Fe, Co, and Ni) since Zn²⁺ and Li⁺ have no unpaired 3d electron.

Table 1 Summary of the calculated ground states (GS), lattice parameters, band gaps (E_g, in eV) and the magnetic moments (μ) on the metal atoms in tetrahedral (MT) and octahedral (MO) environments^a

Spinel	GS	Lattice parameters			Eg		Magnetic moment (μ)
		Cal.	Exp.	δ (%)	Theor.	Exp.	μMT	n3d_MT	μMO	n3d_MO
a The number of unpaired 3d electrons (n3d) of the metals are derived from μ 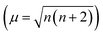. The lattice parameters measured by experiments are also listed for comparison.
MnCr2O4	AFM	8.46	8.44^45	0.237	2.91	2.50^46	4.56	3.67	2.95	2.11
FeCr2O4	FM′^47	a = c = 8.41, b = 8.39	8.38^48	0.239	2.15	1.95^49	3.69	2.82	2.95	2.11
						2.90^49
CoCr2O4	FM′^50	8.36	8.33^50	0.360	2.87	2.77^51	2.70	1.88	2.95	2.11
NiCr2O4	FM′^35	a = 8.30, b = c = 8.36	a = 8.18, b = 8.17, c = 8.57^27	—	2.39	1.70^52	1.75	1.42	2.96	2.12
ZnCr2O4	AFM^53	8.34	8.31^53	0.361	3.30	1.66^54	0.0	0.00	2.95	2.11
						3.61^55
ZnMn2O4	AFM^53	a = b = 8.63, c = 8.0	a = b = 8.10, c = 9.24^53	—	0.22	1.28^56	0.00	0.00	3.79	2.92
ZnFe2O4	AFM^53	8.39	8.46^57	0.827	1.60	1.78^58	0.00	0.00	4.25	3.37
ZnCo2O4	AFM	a = c = 8.38, b = 8.08	8.05^53	—	1.11	1.71^59	0.00	0.00	3.25	2.40
						2.77^59
ZnNi2O4	FM	8.17	—	—	—		0.00	0.00	1.39	0.71
LiCr2O4	AFM	a = c = 8.16, b = 8.24	8.11^60	—	1.03		0.00	0.00	2.90/2.03	2.07/1.26
LiMn2O4	AFM^61	a = c = 8.32, b = 8.00	8.25^62,63	—	0.69	0.58^64	0.00	0.00	3.77/2.96	2.90/2.12
LiFe2O4	AFM	a = b = 8.32, c = 8.05	—	—	—		0.00	0.00	4.20/3.61	3.32/2.75
LiCo2O4	AFM^26	a = 8.06, b = c = 8.19	7.99,^26 8.153^65	—	0.24		0.00	0.00	3.45/2.78	2.59/1.95
LiNi2O4	FM	a = 8.06, b = c = 7.80	8.04^66	—	0.44		0.00	0.00	1.05/0.01	0.45/0.00

---

Ferrite spinels are of technological interest because of their magnetic ordering. How the unpaired spins of metal ions are coupled determines the magnetism of spinels. The 2nd column of Table 1 lists the magnetic orders for the ground states of the spinels. The Goodenough–Kanamori rules^37–44 predict the local magnetism, which results from the superexchange coupling of the electron spins of transition metal ions. The O²⁻ ions shared by two metal ions can mediate the coupling of spins by superexchange, as shown in Fig. 3.

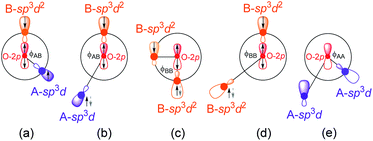Fig. 3 Five cases of indirect exchange interactions between A–B (a and b), B–B (c and d) and A–A (e).

In spinel, each magnetic ion at site A has 12 magnetic ions at site B to undergo A–B exchanges and each B site ion has 6 A site ions undergo A–B exchanges. Moreover, the angles between A and B (ϕ_AB) are close to 180° and the distances between A and B are the shortest. Therefore, the A–B exchanges (Fig. 3a and b) are the strongest, followed by B–B exchanges (Fig. 3c and d) and A–A (Fig. 3e) exchanges are the weakest. The above rules can profoundly explain the magnetic ground states of spinels listed in Table 1. For ACr₂O₄ (A = Mn, Fe, Co, and Ni), the exchange between A and its nearest B are the strongest leading to opposite spin orders on A and B. If the A–B and B–B exchanges (Fig. 3b–d) are strong enough to oppositely arrange the spin orders of A–B and B–B, the final magnetism of the spinel will be AFM like MnCr₂O₄, where the Mn²⁺ has the largest net spins, as shown in Fig. 1b. Spinels ACr₂O₄ (A = Fe, Co, and Ni) have strong A–B but weak B–B exchanges, which finally leads to the FM′ magnetic states. For Zn/LiB₂O₄ (A = Zn and Li; B = Cr, Mn, Fe, Co, and Ni), the B–B exchanges are the dominating interactions because Zn²⁺ and Li⁺ have fully and empty occupied 3d orbitals.

The B–B exchanges in Zn/LiB₂O₄ (B = Cr, Mn, Fe, and Co) are stronger than those in Zn/LiNi₂O₄, which leads to their AFM and FM states.

The 3–4 columns of Table 1 list the lattice parameters for the spinels calculated in present work and as reported by previous experiments. The relative errors (δ) between them are less than 1.00%. In ACr₂O₄ (A = Fe, Co, and Ni), A = Fe and Ni are Jahn–Teller active ions²³ with orbital degeneracy and slightly collective distortion are observed in the relaxed unit cell. For spinels with nonmagnetic A site ions, namely Zn/LiB₂O₄ (B = Cr, Mn, Fe, and Co), the antiferromagnetic J_B–B exchange interactions lead to highly frustrated ground states on the pyrochlore sublattice. This frustration can be released by the spin-Jahn–Teller effect^67,68 and lead to lattice distortions. The calculated magnetic moments (μ) on MO and MT are also listed in Table 1. The number of unpaired 3d electrons (n_3d) can be derived from 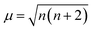. Although the calculated n_3d are smaller than the theoretical values illustrated in Fig. 1B, it does not affect the reliability of the calculations since the rational tendency is predicted.

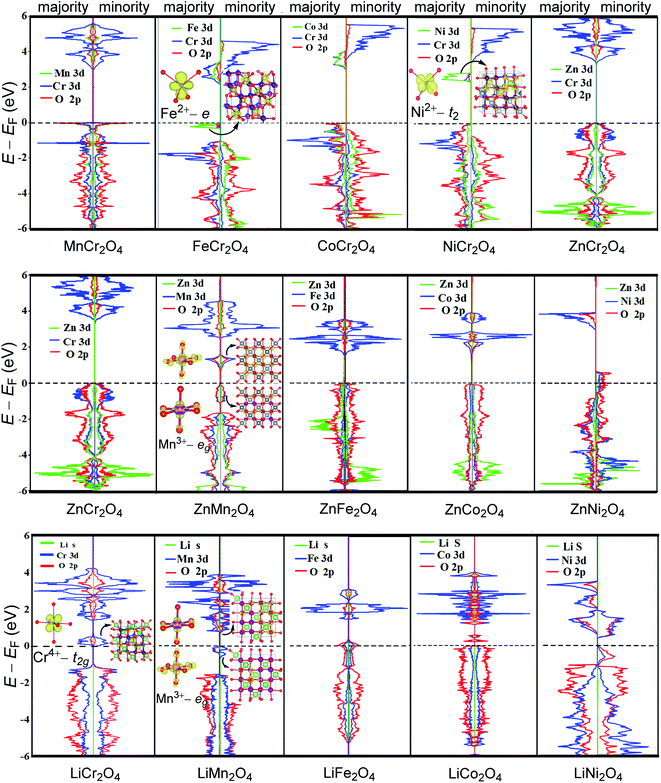
To investigate the influences induced by cation A and B on the electronic structures of spinels, we calculated the projected density of states (PDOS) of ACr₂O₄ (A = Mn, Fe, Co, Ni, Zn) and Zn/LiB₂O₄ (B = Cr, Mn, Fe, Co and Ni). The band gaps were also calculated and are listed in Table 1. Fig. 4A presents the PDOS for ACr₂O₄ (A = Mn, Fe, Co, Ni, and Zn), which indicate that cation A has limited impact on the electronic structures of spinels. The E_g of ACr₂O₄ differs in a narrow range from 2.30 to 3.30 eV. Mn/Co/ZnCr₂O₄ has Jahn–Teller inactive A ions and thus have similar electronic structures. The Jahn–Teller active Fe²⁺ and Ni²⁺ can reduce E_g because the e³ configuration of Fe²⁺ raises the valence-band maximum (VBM) and the t_2g⁴ configuration of Ni²⁺ lowers the conduction band minimum (CBM). The above-mentioned results can be verified by the fact that the partial charge populations, corresponding to the VBM of FeCr₂O₄ and the CBM of NiCr₂O₄ are mainly contributed by the e orbital of Fe²⁺ and the t₂ orbital of Ni²⁺.

Fig. 4 The spin-resolved PDOS of ACr₂O₄ (A = Mn, Fe, Co, Ni, and Zn) and Zn/LiB₂O₄ (B = Cr, Mn, Fe, Co and Ni). The partial charge density populations corresponding to some specific states are also illustrated.

Fig. 4B and C indicate that the electronic configuration of cation B has notable influence on the electronic structure of spinel. The Jahn–Teller active Mn³⁺, Ni³⁺, Cr⁴⁺ and Fe⁴⁺ can remarkably reduce the E_g of spinels and even change the semiconductor to metal and half-metal. The notable differences between ZnCr₂O₄ and LiCr₂O₄ indicate that the Jahn–Teller active Cr⁴⁺in LiCr₂O₄ lowers the CBM to the Fermi level and notably narrows the band gap of LiCr₂O₄. The reason is that CBM in ZnCr₂O₄ is contributed by the e_g orbital but by the t_2g orbital with a lower energy level in LiCr₂O₄. In ZnMn₂O₄, VBM and CBM are contributed by the two e_g orbitals, namely d_z² and d_x²−y², of Mn³⁺. The introduction of Mn⁴⁺ in LiMn₂O₄ does not change the contributions of e_g orbitals to VBM and CBM, and thus, LiMn₂O₄ has similar E_g with ZnMn₂O₄. Compared with ZnFe₂O₄, the extra electron on the e_g orbital of Fe⁴⁺ raises the VBM to the Fermi level and makes LiFe₂O₄ a metal. Analogously, the single e_g electron of Ni³⁺ makes ZnNi₂O₄ a half-metal, while LiNi₂O₄ is a semiconductor because Ni⁴⁺ is a Jahn–Teller inactive ion with fully occupied t_2g orbitals but empty e_g orbitals. To evaluate the quality of the above-mentioned quantum chemical calculations, we compared the present results with experimental data and listed the theoretically calculated and experimentally measured band gaps in Table 1. The scatter of the band gap values is associated with different determining methods. Most of the Exp. E_g values listed in Table 1 are optical band gaps obtained by UV-Vis absorption^{49,51,54–56,58,59,64} or diffuse reflectance spectroscopy.^46,52 The values indicate that the calculated band gaps of FeCr₂O₄, CoCr₂O₄, ZnCr₂O₄, ZnFe₂O₄, ZnCo₂O₄ and LiMn₂O₄ accord well with the experimental measured values with errors within 0.5 eV.

In summary, the configuration of cation B has notable influence on the electronic structure of spinels. The Jahn–Teller active ions Fe²⁺, Ni²⁺, Mn³⁺, Ni³⁺, Cr⁴⁺ and Fe⁴⁺ can remarkably regulate the E_g of spinels and even change the electroconductibility.

Conclusions

The spinels are promising low-cost catalysts. Unravelling the structure–performance relationship is the foundation to realize the rational design of spinel-based catalysts. Herein, the effects of cations in tetrahedral and octahedral sites on the electronic structures of spinels were systematically investigated via GGA + U calculations. Three series of spinels with varying A and B, namely ACr₂O₄ (A = Mn, Fe, Co, Ni, and Zn) and Zn/LiB₂O₄ (B = Cr, Mn, Fe, Co and Ni), were elected as the model system. The results indicate that the magnetism of spinels depends on the indirect exchanges of cations (J_MM). The configurations of B cations in an octahedral O environment, rather than the A in tetrahedral ones have notable influence on the electronic structures of spinels. The Jahn–Teller active ions Fe²⁺, Ni²⁺, Mn³⁺, Ni³⁺, Cr⁴⁺ and Fe⁴⁺ can remarkably regulate the band gaps of spinels and even change their electroconductibilities. The results will provide theoretical insights into the electronic properties of 3d transition metal spinels.

Author contributions

Chunyu Li: data curation, investigation, writing – original draft. Peng Li: investigation. Leyun Li: investigation. Dingjia Wang: investigation. Xingfa Gao: supervision. Xuejiao J. Gao: project administration, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (NSFC) Project (21907043 and 21773095), the Natural Science Foundation of Jiangxi, China (20202BABL213013).

Notes and references

1. W. H. Bragg, Philos. Mag., 1915, 30, 305–315.
2. M. G. Brik, A. Suchocki and A. Kamińska, Inorg. Chem., 2014, 53, 5088–5099.
3. Q. Zhao, Z. Yan, C. Chen and J. Chen, Chem. Rev., 2017, 117, 10121–10211.
4. N. R. D. Fino, G. Saracco and V. Specchia, J. Catal., 2006, 242, 38–47.
5. Q. Chen, Z. Tang, H. Lia, Q. Zhao and B. Pana, Chem. Eng. J., 2020, 381, 122656.
6. G. S. H. Michael Woodhouse and B. A. Parkinson, Chem. Mater., 2005, 17, 4318–4324.
7. D. Bhattacharya, A. Baksi, I. Banerjee, R. Ananthakrishnan, T. K. Maiti and P. Pramanik, Talanta, 2011, 86, 337–348.
8. N. Dhandapani, A. Rebekah, C. Viswanathan and P. Nagamony, Mater. Res. Bull., 2017, 95, 1–8.
9. V. Figueroa-Espí, A. Alvarez-Paneque, M. Torrens, A. J. Otero-González and E. Reguera, Colloids Surf., A, 2011, 387, 118–124.
10. C. M. Hussain and B. Kharisov, Advanced Environmental Analysis. Applications of Nanomaterials, 2016.
11. S. Mumtaz, L.-S. Wang, M. Abdullah, S. Z. Hussain, Z. Iqbal, V. M. Rotello and I. Hussain, J. Phys. D: Appl. Phys., 2017, 50, 11LT02.
12. X. Niu, Y. Xu, Y. Dong, L. Qi, S. Qi, H. Chen and X. Chen, J. Alloy. Compd., 2014, 587, 74–81.
13. Y. Peng, Z. Wang, W. Liu, H. Zhang, W. Zuo, H. Tang, F. Chen and B. Wang, Dalton Trans., 2015, 44, 12871–12877.
14. R. Sahoo, S. Santra, C. Ray, A. Pal, Y. Negishi, S. K. Ray and T. Pal, New J. Chem., 2016, 40, 1861–1871.
15. W. Shi, X. Zhang, S. He and Y. Huang, Chem. Commun., 2011, 47, 10785–10787.
16. L. Su, W. Qin, H. Zhang, Z. U. Rahman, C. Ren, S. Ma and X. Chen, Biosens. Bioelectron., 2015, 63, 384–391.
17. A. A. Vernekar, T. Das, S. Ghosh and G. Mugesh, Chem.–Asian J., 2016, 11, 72–76.
18. Z. Yang, F. Ma, Y. Zhu, S. Chen, C. Wang and X. Lu, Dalton Trans., 2017, 46, 11171–11179.
19. K. Zhang, W. Zuo, Z. Wang, J. Liu, T. Li, B. Wang and Z. Yang, RSC Adv., 2015, 5, 10632–10640.
20. C. Wei, Z. Feng, G. G. Scherer, J. Barber, Y. Shao-Horn and Z. J. Xu, Adv. Mater., 2017, 29, 1606800.
21. S. H. Lee, C. Broholm, T. H. Kim, W. Ratcliff and S. W. Cheong, Phys. Rev. Lett., 2000, 84, 3718–3721.
22. A. B. Sushkov, O. Tchernyshyov, W. R. Ii, S. W. Cheong and H. D. Drew, Phys. Rev. Lett., 2005, 94, 137202.
23. V. Kocsis, S. Bordács, D. Varjas, K. Penc, A. Abouelsayed, C. A. Kuntscher, K. Ohgushi, Y. Tokura and I. Kézsmárki, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 064416.
24. F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121.
25. F. Zasada, J. Grybos, P. Indyka, W. Piskorz, J. Kaczmarczyk and Z. Sojka, J. Phys. Chem. C, 2014, 118, 19085–19097.
26. V. B. O. Peña, T. Guizouarn, E. Meza and J. L. Gautier, Bol. Soc. Esp., 2004, 43, 736–739.
27. M. R. Suchomel, D. P. Shoemaker, L. Ribaud, M. C. Kemei and R. Seshadri, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 054406.
28. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
29. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3968.
31. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
32. V. V. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
33. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
34. D. Debashish and S. Ghosh, J. Phys. D: Appl. Phys., 2015, 48, 425001.
35. D. Andersson and C. Stanek, Phys. Chem. Chem. Phys., 2013, 15, 15550–15564.
36. D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195106.
37. J. S. Zhou and J. B. Goodenough, Phys. Rev. Lett., 2006, 96, 247202.
38. K. Ueda, H. Tabata and T. Kawai, Science, 1998, 280, 1064.
39. J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23.
40. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
41. J. Kanamori, Prog. Theor. Phys., 1957, 17, 177–196.
42. J. B. Goodenough and J. S. Zhou, in Localized to Itinerant Electronic Transition in Perovskite Oxides, Springer Berlin Heidelberg, Berlin, Heidelberg, 2001.
43. J. B. Goodenough, J. Phys. Chem. Solids, 1958, 6, 287–297.
44. J. B. Goodenough, Phys. Rev., 1955, 100, 564–573.
45. N. Mufti, A. A. Nugroho, G. R. Blake and T. T. M. Palstra, J. Phys.: Condens. Matter, 2010, 22, 075902.
46. V. Kocsis, S. Bordács, D. Varjas, K. Penc, A. Abouelsayed, C. A. Kuntscher, K. Ohgushi, Y. Tokura and I. Kézsmárki, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 064416.
47. C. Benhalima, S. Amari, L. Beldi and B. Bouhafs, Spin, 2019, 09, 1950014.
48. D. E. C. G. Shirane and S. J. Pickart, J. Appl. Phys., 1964, 35, 954.
49. T. L. S. L. Wijesighe and D. J. Blackwood, J. Phys.: Conf. Ser., 2006, 28, 74–78.
50. M. Akyol, İ. Adanur, A. O. Ayaş and A. Ekicibil, Phys. B, 2017, 525, 144–148.
51. I. Efthimiopoulos, Z. T. Y. Liu, S. V. Khare, P. Sarin, T. Lochbiler, V. Tsurkan, A. Loidl, D. Popov and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 064108.
52. M. Enhessari, A. Salehabadi, S. Khanahmadzadeh, K. Arkat and J. Nouri, High Temp. Mater. Processes, 2017, 36, 121–125.
53. H. J. Kim, I. C. Song, J. H. Sim, H. Kim, D. Kim, Y. E. Ihm and W. K. Choo, Solid State Commun., 2004, 129, 627–630.
54. Y. Benrighi, N. Nasrallah, T. Chaabane, V. Sivasankar, A. Darchen and O. Baaloudj, Opt. Mater., 2021, 115, 111035.
55. Q. Wang, J. Chen, H. Lu, P. Huang, J. Wang, M. Li, Y. Lu, G. Chang, Z. C. Feng and Y. He, Appl. Surf. Sci., 2019, 475, 820–827.
56. R. Gherbi, Y. Bessekhouad and M. Trari, J. Phys. Chem. Solids, 2016, 89, 69–77.
57. W. P. W. Schiessl, H. Karzel, M. Steiner and G. M. Kalvius, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 9143–9152.
58. N. Kislov, S. S. Srinivasan, Y. Emirov and E. K. Stefanakos, Mater. Sci. Eng., B, 2008, 153, 70–77.
59. H. Guo, J. Chen, W. Weng, Q. Wang and S. Li, Chem. Eng. J., 2014, 239, 192–199.
60. M. Lauer, R. Valenti, H. Kandpal and R. Seshadri, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 75117.
61. C. Y. Ouyanga, S. Q. Shib and M. S. Leid, J. Alloys Compd., 2009, 474, 370–374.
62. D. Santos-Carballal, P. Ngoepe and N. Leeuw, Phys. Rev. B, 2018, 97, 085126.
63. G. R. J. Rodríguez-Carvajal, Masquelier and M. Hervieu, Phys. Rev. Lett., 1998, 81, 4660–4663.
64. V. Paulraj, B. Swami and K. Kamala Bharathi, Appl. Phys. Lett., 2019, 115, 093901.
65. Y. Mouhib, M. Belaiche, C. A. Ferdi, M. Lacham and A. Elacham, New J. Chem., 2020, 44, 2538–2546.
66. M. G. S. R. Thomas, W. I. F. David and J. B. Goodenough, Mater. Res. Bull., 1985, 93, 473–476.
67. O. Tchernyshyov, R. Moessner and S. L. Sondhi, Phys. Rev. Lett., 2002, 88, 067203.
68. Y. Yamashita and K. Ueda, Phys. Rev. Lett., 2000, 85, 4960–4963.

---

Footnote

† Electronic supplementary information (ESI) available: The Hubbard U_eff (eV) values employed for metal ions, the calculated energies for spinels with different magnetic states and the optimized structures for the spinels. See DOI: 10.1039/d1ra03621a

---