Open Access Article
Open Access ArticleEstimation of total energy requirement for sewage treatment by a microbial fuel cell with a one-meter air-cathode assuming Michaelis–Menten COD degradation†
Taiki Yamane‡
,
Naoko Yoshida‡ * and
Mari Sugioka
* and
Mari Sugioka
Department of Civil and Environmental Engineering, Nagoya Institute of Technology (Nitech), Gokiso-Cho, Showa-Ku, Nagoya, Aichi, Japan. E-mail: yoshida.naoko@nitech.ac.jp
First published on 4th June 2021
Abstract
Calculations of chemical oxygen demand (COD) degradation in sewage by a microbial fuel cell (MFC) were used to estimate the total energy required for treatment of the sewage. Mono-exponential regression (MER) and the Michaelis–Menten equation (MME) were used to describe the MFC's COD removal rate (CRR). The tubular MFC used in this study (ϕ 5.0 × 100 cm) consisted of an air core surrounding a carbon-based cathode, an anion exchange membrane, and graphite non-woven fabric immersed in sewage. The MFC generated 0.26 A m−2 of the electrode area and 0.32 W m−3 of the sewage water, and 3.9 W h m−3 in a chemostat reactor supplemented continuously with sewage containing 180 mg L−1 of COD with a hydraulic retention time (HRT) of 12 h. The COD removal and coulombic efficiency (CE) were 46% and 19%, respectively, and the energy generation efficiency (EGE) was 0.054 kW h kg−1-COD. The CRR and current in the MFC were strongly dependent on the COD, which could be controlled by varying the HRT. The MER model predicted first-order rate constants of 0.054 and 0.034 for reactors with and without MFC, respectively. The difference in these values indicated that using MFC significantly increased the COD removal. The results of fitting the experimental data to the MME suggested that the total COD can be separated into nondegradable CODs (Cn) and degradable CODs (Cd) via MFC. The values of CRR for Cd and CE suggest that MFC pretreatment for 12 hours prior to aeration results in a 75% decrease in net energy consumption while reducing sewage COD from 180 to 20 mg L−1.
1. Introduction
The recovery of current by electrodes from wastewater has received great attention as a novel treatment used in microbial fuel cells (MFC)1 and microbial electrochemical systems (MES).2 Extensive studies on MFCs have demonstrated the considerable potential of these devices, as well as the difficulties involved in upscaling them for practical application.3–5 Studies on the direct recovery of electricity from sanitary wastewater6,7 and urine8 have also shown the efficient removal of organic matter, and have proven that the recovered electricity can be used to power lighting devices.9 Onsite installation of floating MFC vessels in sewage wastewater treatment plants can enable current recovery at relatively low concentrations of chemical oxygen demand (COD), i.e., 400–20 mg L−1.10–12 These results suggest that MFCs can be employed in municipal wastewater treatment for a wide range of COD values.Large-scale MFCs are effective in removing organic compounds from real wastewater with relatively low energy consumption,13–15 or even net production of energy in some cases.16,17 Studies on sewage treatment using MFCs with capacities greater than five liters and hydraulic retention times (HRTs) between 12 hours and six days have observed 54–79% COD removal efficiency (COD-RE) with 70–210 mg L−1 of effluent COD (CODEF).12,15,17,18 In Japan, the standard for sewage treatment plant effluent is less than 15 mg L−1 of BOD, which corresponds to a COD range of 20–35 mg L−1.19 The difference between the CODEF and the discharge standards demonstrates the need for improvements in MFC design or the integration of MFCs with post-treatment processes such as aeration,15 anaerobic membrane filtration,20 and flocculation.21
Conventionally, the performance of an MFC is characterized in terms of output variable values such as COD-RE, electric power density, and coulombic efficiency (CE).1 Recently, parameters such as current density,16 electrical energy,22 normalized energy recovery,23 and energy generation efficiency (EGE)12,15 have been used to shift the focus towards practical application. In most cases, these values are independently determined by averaging measurements under different operational conditions despite reports that the operational parameters themselves affect the performance. Specifically, influents with higher COD resulted in higher COD-RE24,25 and power density25,26 but lower CE.15,27 Increasing the HRT caused further reductions in the COD and current and power densities.15,17 The mutual interactions between operational and output parameters make the evaluation of MFC performance difficult. A judicious combination of these parameters based on analysis of the governing equations and experimental data may provide a more concise and comprehensive basis for evaluating MFC performance.
To determine the optimal operation, it is crucial to consider the balance between energy production and consumption for the wastewater treatment process as a whole.15–17 In some cases, a trade-off is required between power production and COD-RE. Power production can be increased at higher cell voltages by lowering the anode potential and oppositely recovering current from anode to cathode. Reducing the anode potential theoretically decreases the generation of Gibbs free energy, which decreases COD-RE.28 This increases the energy requirement for the post-treatment of the remaining COD. The total energy (TE), rather than its inversely related individual components of COD-RE and electricity production, should therefore be optimized. During the sewage treatment process, the COD removed by the MFC is converted to electricity while that remaining in the effluent is assumed to be removed to meet a given discharge standard by a standard activated sludge process at an energy cost of 0.6 kW h kg−1-COD.29
In this study, the rate of COD degradation in an MFC was calculated using two equations: the mono-exponential regression equation (MER) and the Michaelis–Menten equation (MME). The Michaelis–Menten equation is originally a concept whereby the number of complexes of a single substrate and single catalyst determine the reaction rate. Consequently, the use of this model in wastewater treatment is logically incorrect because wastewater includes a variety of redox reactions, and cannot be modeled by a defined calculation method. However, only MME can integrate the MFC performance for different influents and HRTs in a single line, which has been applied to the COD as a bundle of organic matter and complex microbial communities.30–32 The CE was used as a constant and was calculated by fitting the experimentally observed COD degradation and current. This result was then used to calculate the TE for a combined MFC and post-aeration process that met the discharge standard. A tubular33 and air-core MFC unit34 with a depth of 1.0 m was evaluated for sewage wastewater treatment.15 To the best of our knowledge, this unit is comparable to the previously studied deepest air-cathode MFCs.35
2. Experimental
2.1 MFC
The MFC used in this study was tubular and had an air-chamber core, as previously described,15 although the size of the MFC unit increased from ϕ 4.0 × 33 cm to ϕ 5.0 × 100 cm (Fig. 1A). The air core was composed of stainless-steel mesh surrounded by a cathode, separator, and anode without spacing. The latter components included a carbon cloth painted with a mixture of activated carbon, carbon black,36 and anion exchange polymer,15 an anion exchange membrane, and graphite non-woven fabric. The graphite anode was inoculated with activated sludge taken from an aeration tank in a sewage wastewater treatment plant in Nagoya City prior to the operation. | ||
| Fig. 1 Appearance of one-meter air-cathode MFC (A) and chemostat reactor without MFC (NON-reactor) and with MFC (MFC-reactor) (B). | ||
The MFC was first polarized using external resistances of 27, 3, and 1 Ω in an acclimation reactor with a continuous supply of influent from the effluent channel of the primary sedimentation tank (PST). The acclimation process lasted 17 days, during which time the influent flow rate was such that the HRT was between 9 and 12 h. The external resistances were selected to have maximum current at that time, although the current data were not recorded. The polarization curve was obtained in another MFC with the same configuration floating in the effluent channel of the PST for 40 days, and the MFC voltage was recorded at external resistances of 100, 88, 60, 22, 10, 8, 6, 3, and 1 Ω.
2.2 MFC operation in chemostat reactors
The acclimated MFC was moved into a cylindrical chemostat reactor (ϕ 12.5 × 150 cm) (Fig. 1B). The reactor was constructed from polyvinylchloride (PVC) plastic pipe connected to an outlet pipe. The MFC was polarized using external resistances of 1 Ω. The voltage in the MFCs was recorded every 60 min using a data logger (T&D Corporation, Nagano, Japan) connected in parallel to the external resistance and current. The current was calculated based on Ohm's law. The volume ratio of the MFC and reactor was approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (v/v). A similar cylindrical reactor without the MFC (NON, ϕ 10.0 × 130 cm) (Fig. 1A) was also constructed from a PVC pipe (ϕ 10.0 × 130 cm) and was operated in parallel as a control. The outlet was placed at a height of 110 cm, and the inlet tube was placed on the bottom in the both reactors.
5 (v/v). A similar cylindrical reactor without the MFC (NON, ϕ 10.0 × 130 cm) (Fig. 1A) was also constructed from a PVC pipe (ϕ 10.0 × 130 cm) and was operated in parallel as a control. The outlet was placed at a height of 110 cm, and the inlet tube was placed on the bottom in the both reactors.
The wastewater volumes in the MFC and NON reactors were 9.7 L and 8.6 L, respectively. The reactors were maintained under chemostat conditions by a continuous supply of influent from an effluent water channel of the PST. The HRTs were set at 3, 6, 12, and 18 hours using a tubing pump (TP-1973, AS ONE Co., Osaka, Japan). The reactor's wastewater was circulated to the reactor using the tubing pump at a circulation rate of 1.5 h of HRT for 10 days after the reactor's installation. From the eleventh day onwards, a submersible water pump (LEDGLE, Shenzhen, China) was used for circulation at a rate of 0.2 h of HRT on and after 11 days. The electrodes were polarized with an external resistance of 2 Ω, and the voltage was recorded every hour using a data logger (T&D Co., Nagano, Japan). The influent was common to both the MFC and NON reactors, and the effluents were taken from the two reactors independently but simultaneously, and stored at −20 °C before the analysis. At least four samples were collected for each HRT. The CODs of the influent (CODIN) and effluent (CODEF) from the two reactors were analyzed as previously described.17
2.3 Calculation of COD removal
The MFC was operated in chemostat mode in this study, and the current production under these conditions became stable between 30 and 40 days of operation. The biomass on the anode and in the anolyte was therefore assumed to be constant in the MFC. The CRR depends on the COD concentration and can be calculated using eqn (1):
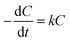 | (1) |
C = C0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−kt e−kt
| (2) |
In this study, the CODEF [mg L−1] is the concentration C that is obtained when using the values of CODIN [mg L−1] as C0, and HRT [h] as t in eqn (2). The reaction rate constant k was determined by the least-squares fitting of the measured and calculated values of the CODEF with different HRTs using the solver function of Microsoft Excel and the curve-fitting module of MATLAB R2020a (MathWorks Inc., Natick, MA, USA).
The CRR can also be calculated using the MME for the stable biofilm on the anode assuming constant active biomass30 via eqn (3):
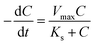 | (3) |
| C = Cd + Cn | (4) |
The CRR can then be expressed as follows:
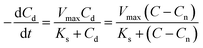 | (5) |
The parameters of Vmax, Ks, and Cn were determined by the least-squares fitting of the measured and calculated values of the CRR with different HRTs, as described above. The C at HRT = t [h] is given by eqn (6):
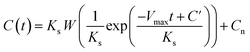 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(w)) and C′ is the integration constant calculated from eqn (7) with an initial COD concentration of C0.
exp(w)) and C′ is the integration constant calculated from eqn (7) with an initial COD concentration of C0.
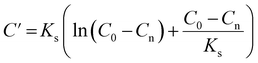 | (7) |
2.4 Determination of coulombic efficiency
Based on the strong dependence of current on lower COD concentrations, the current recovery by the MFC is assumed as an anode-limiting but not cathode-limiting reaction. In the MFC, the electrons are emitted from the COD degradation and then recovered as current at a specific ratio, CE. The current density I [A m−3] can thus be calculated as follows (eqn (8)):
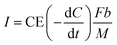 | (8) |
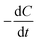 [g m−3 h−1] is the CRR; F is Faraday's constant, 96
[g m−3 h−1] is the CRR; F is Faraday's constant, 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1; b is the number of electrons produced per molecule of oxygen, 4; and M is the molar mass of oxygen, 32 g mol−1.
485 C mol−1; b is the number of electrons produced per molecule of oxygen, 4; and M is the molar mass of oxygen, 32 g mol−1.
The current when the concentration reaches Cn is assumed to be generated from the endogenous substrate in the biofilm (IE), hence I can be expressed as follows:
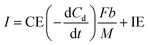 | (9) |
CE can be calculated based on electricity production and COD-RE during the given HRT, and is described by eqn (10):
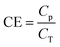 | (10) |
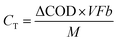 | (11) |
2.5 Calculation of total energy
The total energy (TE) for the combined MFC and post-aeration wastewater treatment was calculated for different MFC HRTs. The energy generated by the MFC is represented by energy generation efficiency (EGE) [W h g−1-COD], which was calculated using eqn (12):
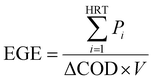 | (12) |
The energy consumption efficiency for COD removal by the aeration was found to be 0.6 [W h g−1-COD].29 Therefore, TE [W h m−3] for the treatment of 1 m3 of the wastewater is the sum of the energy generated by the MFC, i.e., the product of EGE and the COD removed by the MFC (ΔCODMFC) [g m−3], and the energy consumption for aeration, i.e., the product of −0.6 and the COD removed by aeration [g m−3].
| TE = EGE × ΔCODMFC − 0.6(CODEF − CODSTD) | (13) |
3. Results
3.1 Current production
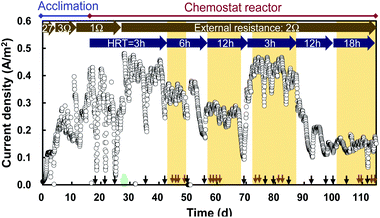
The MFC increased current production within a few days and the current stabilized between 0.3 and 0.4 A m−2 within 17 days in an acclimation reactor (Fig. 2). The MFC had a stable current of 0.40 A m−2 between days 28 and 43 in the chemostat reactor with continuous inflow at HRT = 3 h, while the current was occasionally unstable in the reactor that had trouble, for example clogging of the tube or pump. The current decreased with increasing HRT, and became 0.14 A m−2 at an HRT of 18 h (Table 1). This decline is attributed to the decrease of COD in the reactor.| HRT [h] | Current density [A m−2] | Electric power density [W m−3] | Electric energy density [W h m−3] |
|---|---|---|---|
| 3 | 0.41 ± 0.04 | 0.76 ± 0.14 | 2.3 ± 0.41 |
| 6 | 0.32 ± 0.03 | 0.48 ± 0.09 | 2.9 ± 0.46 |
| 12 | 0.26 ± 0.02 | 0.32 ± 0.05 | 3.9 ± 0.54 |
| 18 | 0.14 ± 0.06 | 0.10 ± 0.02 | 1.8 ± 0.32 |
The trend in electric power was similar: from a value of 0.76 W m−3 at HRT = 3 h, the electric power decreased to 0.10 W m−3 when the HRT was increased to 18 h (Table 1). The electric energy increased with the HRT in the range of 3–12 h, but a marked decrease was observed for 18 h of HRT (Table 1). The electric energy increased because more time was available for recovering energy at HRTs up to 12 h, but the value decreased at 18 h of HRT owing to low current production. In addition to the MFC in the reactor, an MFC with the same configuration was operated in the waster channel of the effluent from the PST, and its polarization curve was obtained (ESI Fig. 1†). The MFC in the water channel displayed a maximum power density of 0.12 W m−2 and a maximum current of 0.5 A m−2.
3.2 COD removal in the chemostat reactor
The COD-RE efficiency of the MFC increased with the HRT, and the averages were 28, 30, 46, and 59% at 3, 6, 12, and 18 h of HRT, respectively (Table 2). The NON reactor also had a gradual decrease in COD with increasing HRT. The COD-RE values of the MFC and NON reactors differed significantly at HRTs of 12 and 18 h (p < 0.05) but were similar for shorter HRTs. Moreover, the actual COD removal by the MFC was estimated to be 16% of the total COD removal.| HRT [h] | CODIN [mg L−1] | CODEF [mg L−1] | COD-RE [%] | ||
|---|---|---|---|---|---|
| MFC | NON | MFC | NON | ||
| 3 | 150 ± 11 | 110 ± 10 | 110 ± 11 | 28 ± 3.6 | 29 ± 5.4 |
| 6 | 210 ± 13 | 150 ± 6.3 | 160 ± 13 | 30 ± 4.2 | 21 ± 10 |
| 12 | 180 ± 21 | 99 ± 21 | 130 ± 8.9 | 46 ± 6.4* | 31 ± 4.0 |
| 18 | 180 ± 30 | 73 ± 6.4 | 100 ± 12 | 59 ± 3.9* | 43 ± 4.0 |
3.3 COD removal calculation
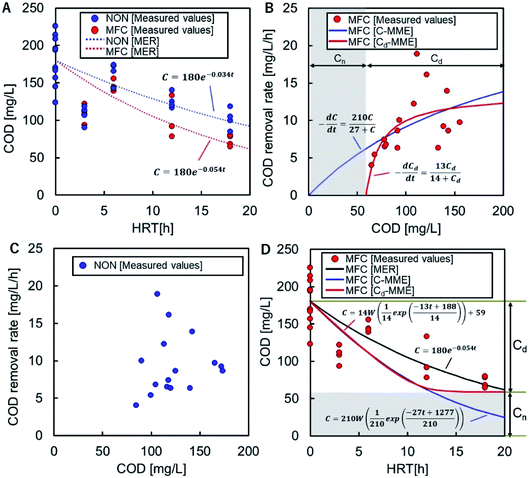
The COD-RE based on the MER in the MFC and NON reactors were C = 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−0.054t and C = 180
e−0.054t and C = 180![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−0.034t, respectively (Fig. 3A). The overall trends in COD degradation by MFC and NON indicated that the MFC significantly enhanced COD-RE.
e−0.034t, respectively (Fig. 3A). The overall trends in COD degradation by MFC and NON indicated that the MFC significantly enhanced COD-RE.
The CRR in the MFC reactor fitted the standard MME (C-MME), (eqn (3)), with values of Vmax and Ks of 27 mg L−1 h−1 and 210 mg L−1, respectively (Fig. 3B). The parameter could not be fitted to the experimental data for the NON reactor (Fig. 3C). The COD reductions at each HRT calculated using the C-MME were greater than those calculated using the MER (Fig. 3D). In the MME calculation of the CRR using Cd (Cd-MME), eqn (5), the value of Cn was 59 mg L−1, which was close to the lowest CODEF (65 mg L−1) observed in the MFC at HRT = 18 h (Fig. 3D).
The value of Vmax for Cd was found to be 13 mg L−1 h−1 and was approximately half the Vmax calculated using C. The Ks value for Cd was 14 mg L−1, corresponding to 73 mg L−1 of C, which was approximately one-third of the value determined by C-MME. The HRT-dependent COD decline showed a similar trend to using C-MME until HRT = 12 h, but had a constant lower limit, Cn, unlike the continuous decline in the C-MME calculation (Fig. 3D).
3.4 Coulombic efficiency and calculation of current
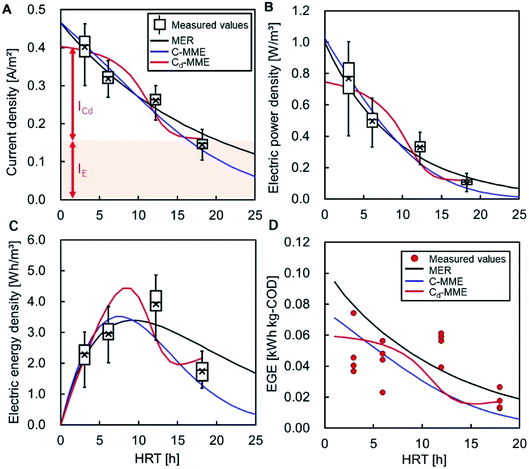
The measured CE of the MFC at each HRT is shown in Table 3. No dependence of CE on the HRT was observed. Longer HRTs appear to have more CEs, although the low COD given by a longer HRT limited current production, and CEs did not increase with longer HRTs. The balance of increasing HRT and decreasing current resulted in no dependency of CE on HRTs. The average CE in all of the MFCs with different HRTs was 15 ± 4.2%, which is consistent with the actual COD-RE of the MFC. Assuming that CE is constant and independent of HRT, CE was determined by fitting the current data and the calculated CODEF to eqn (8) and (9). The CEs were 22, 16, and 9.8% for MER, C-MME, and Cd-MME, respectively, and the calculated currents were similar to those observed experimentally (Fig. 4A). In the Cd-MME calculation, the current was taken as the sum of ICd and IE, and the ICd-based calculation resulted in a lower CE and a reverse sigmoid curve. The value of IE was calculated to be 0.16 A m−2, which was close to the average current of 0.14 A m−2 observed in the reactor at HRT = 18 h. The calculated currents reflected the electric power density effectively for all calculations (Fig. 4B).| HRT [h] | CE [%] | EGE [kW h kg−1-COD] |
|---|---|---|
| 3 | 13 ± 3.3 | 0.049 ± 0.015 |
| 6 | 14 ± 3.2 | 0.043 ± 0.012 |
| 12 | 19 ± 2.7 | 0.054 ± 0.009 |
| 18 | 12 ± 3.4 | 0.017 ± 0.006 |
3.5 Calculation of electric energy and energy recovery efficiency
Electric energy calculations using three different methods gave a range of 3.4 to 4.5 W h m−3 of the maximum at HRT values between 7 and 10 h. This reflects the balance between increasing HRT and the HRT-dependent reduction in the current (Fig. 4C). The values were highly consistent with the maximum electric energy observed at HRT = 12 h (3.9 W h m−3) (Table 1).In the Cd-MME calculation, the electric energy increased again at HRT = 16 h because IE was set to a constant value. Logically, IE should gradually decline over time because of the reduction of the substrate in the biofilm. However, we could not conduct experiments at HRTs longer than 18 h to find a decline in IE. Therefore, a constant value of IE can be used for calculations for HRTs shorter than 18 h.
The energy generation efficiency (EGE) was within the range of 0.043–0.054 W h g−1-COD for HRTs between 3 and 12 h (Table 3). No significant difference was observed at these HRTs, and the drop in the EGE value at 6 h caused by unknown reasons includes variance of influent water quality. The value decreased to 0.017 when the HRT was 18 h owing to the lower COD availability and lower production of electricity. The calculated EGE values were within the range of 0.0086–0.079 W h g−1-COD at HRT = 3–18 h and were similar to the experimental values (Fig. 4D). The MER and C-MME calculations suggest gradual declines in EGE as HRT increased, while the Cd-MME calculation predicted a reverse sigmoid trend, both resulted in the division of electric energy density (Fig. 4C) and accumulative removed-COD.
3.6 Total energy requirement for the MFC-integrated wastewater treatment
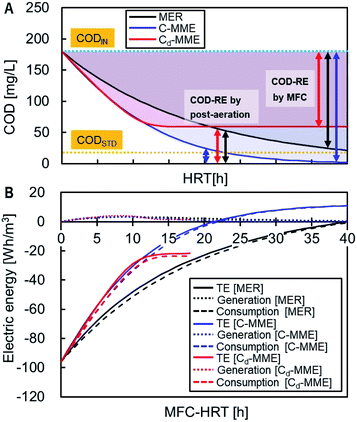
The TE, i.e., the sum of the electric energy generated by the MFC and consumed for the aeration, was calculated for the treatment of 1 m3 sewage to reduce the COD from CODIN, 180 mg L−1, to CODSTD, 20 mg L−1 (Fig. 5). Energy generation contributed little to TE and the energy reduction was attributed to COD-RE by the MFC determined TE. The C-MME and Cd-MME calculations predicted similar TE until HRT = 12 h, with more energy reduction compared with the MER calculation. When MFC was performed with HRT = 18 h before the aeration, C-MME and Cd-MME showed 94% and 78% reductions in TE compared with COD removal by the aeration alone, while MER estimated a 72% reduction in TE. The difference among the three TE-values becomes greater with longer HRTs. The Cd-MME estimated −23 W h m−3 of the maximum energy, while the C-MME and MER suggested that the energy becomes positive at >21 h and >41 h of HRT, respectively.3.7 Comparison of performance in MFC treating municipal wastewater
ESI Table 1† compares the performance of the MFC used in this study (air–AEM–MFC) with that of other MFCs in terms of treating municipal wastewater, especially for upscaling to 85–100 L of wastewater volume: biocathode-MES,13 biocathode-IEM-MFC,37 air-cathode-MFC with non-ionic exchange separator (air-NIE-MFC),15,18,38 and air-cathode-MFC with ion exchange separator (air-IEM-MFC).16,17,39 One exception is a scalable MFC unit treating 4.0 L of wastewater,40 which was upscaled by other studies.16,41 The current density of the MFC with 12 h of HRT and 100 mg L−1 of COD was 4.1 A m−3 of wastewater, which was higher than all of the other MFCs, except one with no available data for current density.37 In contrast, the power density, 0.32 W m−3-wastewater, was as low as the lowest value recorded in an air-NIE-MFC.15 This trend was observed as the operating conditions were set to ensure recovery of current rather than electric power. The COD-RE in the proposed MFC was lower than in the other MFCs, although the COD-RE depends on the COD concentration. Because of the higher current but lower COD-RE, the proposed MFC had a higher CE than the majority of other MFCs. The highest CE was obtained in the biocathode-IEM-MFC, possibly owing to the ionic strength of the synthetic catholyte in the stacked MFCs.37 However, the use of a synthetic medium poses another problem—the requirement for addition of large quantities of the medium in practical use.4. Discussion
We estimated COD consumption using the MER and MME equations. Both calculations reproduced COD-RE and current effectively for the air-cathode-AEM-MFC treating sewage wastewater. The calculations include uncertainty owing to the lack of replicates running for multiple MFCs, although the equivalent current and COD reductions were confirmed by using MFCs with the same configurations but with a length of 30 cm.15 The consistency between the results of these independently performed evaluations involving similar MFCs indicates the reproducibility of the performance of the proposed type of MFC. The goodness-of-fit suggests a strong dependence of CRR and current on COD in a steady-state MFC reactor, with HRT as the only variable parameter and a relatively low COD, and was polarized using a low external resistance. The operating conditions were such that the MFC was less affected by external factors such as cathode potential, inhibition of substrates in the influent,42 and electron mediators.43 Comparing the MER and MME, the former provides a convenient and straightforward rough estimate of the MFC performance. The latter requires improvement, but is advantageous for integrating all data of COD degradation and electricity with influent at different CODs as a single line, and to determine two critical factors, Vmax and Ks, that are important for further improvement of MFC performance.In the MME calculation, two different COD parameters were used: C and Cd. These resulted in different values for Vmax and Ks. The C-MME overestimated COD consumption in the MFC, especially at lower COD. This difference is likely caused by the heterogeneity of organic matter in the MFC44 and the overestimation of Vmax as a result of using the data at COD including abundant readily biodegradable matter. This value could not be used in calculations for the low COD dominated by unfavorable residues of organic matter.45 The Cd-MME calculation yielded more realistic performance predictions for our MFC. Evaluations with longer HRT are required to validate the underlying assumption, but tube clogging prevented these experiments. The Cd-MME calculation is contradictory; the current production at time Cd equals zero. We believe that the current was produced from endogenous substrates in the anode biofilm46 and estimated current as the sum of the current from Cd (ICd) and a constant current from the endogenous substrate (IE) for HRTs until 18 h. Strictly, the value of IE can vary depending on the balance of CODs inside and outside the biofilm. The HRT in this case determines these CODs in the MFC. Treating a mixture of organic matter as a unit is a limitation of the approximation that also occurs in other calculations of sewage treatment by MFCs, for example, the Monod equation47 which is an empirical equation of biomass growth rate.48 Notwithstanding the limitation, approximations of COD-RE and current still provide useful insights into the applicability and limitations of MFCs, and these insights can be used to improve MFC performance.
The Cd-MME calculation predicted 13 mg L−1 h−1 of Vmax and 14 mg L−1 of Ks for Cd, corresponding to 73 mg L−1 as C. According to the predicted values, our MFC maintains CRR at more than 80% Vmax until HRT = 6 h, but the CRR decreases to half at HRT = 11 h, and approximates zero at HRT = 18 h. The CRR is the overall consumption, including fermentation in the liquid phase and current recovery at the anode. Minor contribution of current recovery in COD-RE and low CE in MFC was noticeably observed in the MFC when treating municipal wastewater, whereas the MFC with the same configuration showed high COD-RE and CE for synthetic wastewater.49 The other electron scavengers in the MFC treating municipal wastewater have been reported as sulfate in wastewater and oxygen derived from IEM,40 although the sulfate-reduction products, H2S and HS−, can also act as electron donors in MFCs.50
As the COD-RE in the liquid are virtually uncontrollable, current recovery must be increased for further COD-RE. The observed COD-RE was lower than the values reported in studies on other MFCs (ESI Table 1†). The comparison with other MFCs suggests two possible methods to improve the performance—increasing the specific surface area of the separator (SSSA) and anode (ASSA). The former is ideal but not practical when scaling up because the percentage of IEM in the initial cost of an air-IEM-MFC is the highest among all parts of the MFC.16 The use of a cost-effective separator such as a ceramic separator6–8 is a promising approach to increase SSSA; however, wastewater treatment performance at a range similar to COD was not reported in previous studies. The latter is more effective for the proposed MFC by eliminating the rate-determination on anodes due to the lowest ASSA, 16 m2 m−3, compared to the other large MFCs. To employ an anode with a high ASSA, carbon brush51 or other three-dimensional anodes52,53 would be effective. In addition to increasing ASSA, designing fluid to enhance the COD supplement to anodes is also effective to eliminate the rate-determination on anodes at low COD.54
In this present study, the COD-RE and current parameters were combined as the energy requirement per volume of wastewater to achieve a specified effluent COD. For the calculation, a value of 0.6 W h g−1-COD was taken as the energy cost to remove COD by aeration.29 In this study, the COD-RE and current parameters were combined as the energy requirement per volume of wastewater to achieve a specified effluent COD. For the calculation, a value of 0.6 W h g−1-COD was taken as the energy cost to remove the COD via aeration.29 The value is an indicator to determine whether the MFC's operational mode should be focused on power generation or COD removal, but it varies depending on the installation process and post-COD-removal treatments such as intermittent aeration55 and usage of anaerobic membrane bioreactors.20 Specifically, if the energy requirement is less than the EGE of the MFC, the MFC can be optimized for power generation. Although the value is greater than the EGE of the MFC, the operation focusing on COD removal is preferable considering overall energy requirement.
A voltage booster has been used to boost the MFC power, although the EGE value has rarely been calculated and an MFC treating sewage wastewater was calculated to have 0.146 of EGE56 in an MFC. Surpassing the value by system control is extremely challenging, the organic loading rate and a long HRT would likely become key parameters, as well as biogas production.57 The use of MFC as power for some electric devices has been demonstrated. MFCs have been fed with human urine to power a mobile phone58 and a microcomputer.59 MFCs treating municipal wastewater have also been used to power an intermittent pump16 and an aerator.60
For the practical application of MFC in treating wastewater, thorough feasibility studies are still required to match the advantage of MFC and the social demand. However, in all matters, further improvement of the MFC unit is most important. Carbon brush is an excellent anode51 but is expensive to process from fiber to anode; carbonization, forming brush, and surface oxidization for the hydrophilizing.61 Reducing the steps is required for mass production to decrease the processing cost. The AEM rather than CEM has become a good ion-selective separator for MFC.12,62–64 However, all membrane needing to separate liquid and gas have the problem to be scaled-up to several meters in depth and the ceramic separator is promising in terms of strength.6–8 The air-cathode also needs improvement to maintain a high potential for the removal of nitrogenous compounds from wastewater.65 We believe that solving these individual problems will enable the realization of practical use of MFC in wastewater treatment.
5. Conclusion
Both the mono-exponential regression and the Michaelis–Menten calculations of COD removal indicated a strong dependence on COD in an MFC fed with sewage wastewater. The data suggest that increasing the anode-specific surface area will yield improvements in MFC performance. The experimental data and calculations both demonstrate that coulombic efficiency is almost constant. When this MFC was combined with post-aeration for COD reduction to meet discharge standards, a 75% reduction of total energy could be anticipated by feeding the MFC at an HRT of 12 h.Author contributions
TY performed MFC experiments, analyzed the data, and described the draft manuscript. NY designed the experiments and described and revised the draft. MS performed MFC experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study received funding from MEXT/JSPS KAKENHI (grant number: 18K18876) and JSPS Joint Research Program with NSFC. This study was supported by Nippon Koei Co., Ltd., Tamano Consultants Co., Ltd, TOYOBO Co., Ltd., and Nagoya City Waterworks and Sewerage Bureau. We thank Kazuki Iida of Nippon Koei Co., Ltd. for coordinating research collaboration, Mitsuhiro Sakoda and Akihiro Iwata of Tamano Consultants Co., Ltd. for their technical support during reactor construction, and Takahiro Matsumura of TOYOBO Co., Ltd. for the production of the MFC unit.References
- B. E. Logan, B. Hamelers, R. Rozendal, U. Schröder, J. Keller, S. Freguia, P. Aelterman, W. Verstraete and K. Rabaey, Environ. Sci. Technol., 2006, 40, 5181–5192 CrossRef CAS PubMed.
- H. Wang and Z. J. Ren, Biotechnol. Adv., 2013, 31, 1796–1807 CrossRef CAS PubMed.
- B. E. Logan, Appl. Microbiol. Biotechnol., 2010, 85, 1665–1671 CrossRef CAS PubMed.
- C. Munoz-Cupa, Y. Hu, C. Xu and A. Bassi, Sci. Total Environ., 2021, 754, 142429 CrossRef CAS PubMed.
- A. AlSayed, M. Soliman and A. Eldyasti, Renewable Sustainable Energy Rev., 2020, 134, 110367 CrossRef CAS.
- I. Das, M. M. Ghangrekar, R. Satyakam, P. Srivastava, S. Khan and H. N. Pandey, J. Hazard., Toxic Radioact. Waste, 2020, 24, 04020025 CrossRef CAS.
- D. A. Jadhav, I. Das, M. M. Ghangrekar and D. Pant, J. Water Process. Eng., 2020, 38, 101566 CrossRef.
- I. Gajda, O. Obata, M. Jose Salar-Garcia, J. Greenman and I. A. Ieropoulos, Bioelectrochemistry, 2020, 133, 107459 CrossRef CAS PubMed.
- X. A. Walter, J. You, J. Winfield, U. Bajarunas, J. Greenman and I. A. Ieropoulos, Appl. Energy, 2020, 277(1), 115514, DOI:10.1016/j.apenergy.2020.115514.
- P. Cristiani, I. Gajda, J. Greenman, F. Pizza, P. Bonelli and I. Ieropoulos, Front. Energy Res., 2019, 7, 1–11 CrossRef.
- E. Martinucci, F. Pizza, D. Perrino, A. Colombo, S. P. M. Trasatti, A. Lazzarini Barnabei, A. Liberale and P. Cristiani, Int. J. Hydrogen Energy, 2015, 40, 14683–14689 CrossRef CAS.
- M. Sugioka, N. Yoshida and K. Iida, Front. Energy Res., 2019, 7, 91 CrossRef.
- W. He, Y. Dong, C. Li, X. Han, G. Liu, J. Liu and Y. Feng, Water Res., 2019, 155, 372–380 CrossRef CAS PubMed.
- Y. Dong, W. He, D. Liang, C. Li, G. Liu, J. Liu, N. Ren and Y. Feng, J. Power Sources, 2019, 441, 227124 CrossRef CAS.
- H. Hiegemann, D. Herzer, E. Nettmann, M. Lübken, P. Schulte, K. G. Schmelz, S. Gredigk-Hoffmann and M. Wichern, Bioresour. Technol., 2016, 218, 115–122 CrossRef CAS PubMed.
- Z. Ge and Z. He, Environ. Sci.: Water Res. Technol., 2016, 2, 274–281 RSC.
- N. Yoshida, Y. Miyata and K. Iida, RSC Adv., 2019, 9, 39348–39354 RSC.
- Y. Feng, W. He, J. Liu, X. Wang, Y. Qu and N. Ren, Bioresour. Technol., 2014, 156, 132–138 CrossRef CAS PubMed.
- S. H. Lin and K. W. Cheng, Desalination, 2001, 133, 41–51 CrossRef CAS.
- L. Ren, Y. Ahn and B. E. Logan, Environ. Sci. Technol., 2014, 48, 4199–4206 CrossRef CAS PubMed.
- W. Ding, S. Cheng, L. Yu and H. Huang, Chemosphere, 2017, 182, 567–573 CrossRef CAS PubMed.
- Z. He, Environ. Sci. Technol., 2013, 47, 332–333 CrossRef CAS PubMed.
- Z. He, ACS Energy Lett., 2017, 2, 700–702 CrossRef CAS.
- Y. Goto and N. Yoshida, AIP Conf. Proc., 2016, 1709, 020007 CrossRef.
- A. Mahmoudi, S. A. Mousavi and P. Darvishi, Int. J. Hydrogen Energy, 2020, 45, 4887–4896 CrossRef CAS.
- U. Abbasi, W. Jin, A. Pervez, Z. A. Bhatti, M. Tariq, S. Shaheen, A. Iqbal and Q. Mahmood, Bioresour. Technol., 2016, 200, 1–7 CrossRef CAS PubMed.
- Y. Goto and N. Yoshida, Water, 2019, 11, 1803 CrossRef CAS.
- M. Cao, Y. Feng, N. Wang, Y. Li, N. Li, J. Liu and W. He, Electrochim. Acta, 2020, 340, 135922 CrossRef CAS.
- M. Maktabifard, E. Zaborowska and J. Makinia, Rev. Environ. Sci. Biotechnol., 2018, 17, 655–689 CrossRef.
- B. E. Logan, C. Murano, K. Scott, N. D. Gray and I. M. Head, Water Res., 2005, 39, 942–952 CrossRef CAS PubMed.
- Y. Sharma and B. Li, Int. J. Hydrogen Energy, 2010, 35, 3789–3797 CrossRef CAS.
- F. Meng, A. Yang, G. Zhang, P. Zhang and J. Ye, Bioresour. Technol. Rep., 2018, 1, 31–38 CrossRef.
- J. R. Kim, G. C. Premier, F. R. Hawkes, R. M. Dinsdale and A. J. Guwy, J. Power Sources, 2009, 187, 393–399 CrossRef CAS.
- H. Liu, R. Ramnarayanan and B. E. Logan, Environ. Sci. Technol., 2004, 38, 2281–2285 CrossRef CAS PubMed.
- F. Zhang, Z. Ge, J. Grimaud, J. Hurst and Z. He, Bioresour. Technol., 2013, 136, 316–321 CrossRef CAS PubMed.
- X. Zhang, X. Xia, I. Ivanov, X. Huang and B. E. Logan, Environ. Sci. Technol., 2014, 48, 2075–2081 CrossRef CAS PubMed.
- P. Liang, R. Duan, Y. Jiang, X. Zhang, Y. Qiu and X. Huang, Water Res., 2018, 141, 1–8 CrossRef CAS PubMed.
- R. Rossi, D. Jones, J. Myung, E. Zikmund, W. Yang, Y. A. Gallego, D. Pant, P. J. Evans, M. A. Page, D. M. Cropek and B. E. Logan, Water Res., 2019, 148, 51–59 CrossRef CAS PubMed.
- Z. Ge, L. Wu, F. Zhang and Z. He, J. Power Sources, 2019, 297, 260–264 CrossRef.
- F. Zhang, Z. Ge, J. Grimaud, J. Hurst and Z. He, Environ. Sci. Technol., 2013, 47, 4941–4948 CrossRef CAS PubMed.
- Z. Ge, L. Wu, F. Zhang and Z. He, J. Power Sources, 2015, 297, 260–264 CrossRef CAS.
- T. Jafary, A. A. Ghoreyshi, G. D. Najafpour, S. Fatemi and M. Rahimnejad, Int. J. Energy Res., 2013, 37, 1539–1549 CrossRef CAS.
- C. Picioreanu, I. M. Head, K. P. Katuri, M. C. M. van Loosdrecht and K. Scott, Water Res., 2007, 41, 2921–2940 CrossRef CAS PubMed.
- H. Kim, B. Kim and J. Yu, Bioresour. Technol., 2015, 186, 136–140 CrossRef CAS PubMed.
- M. A. Rodrigo, P. Cañizares, J. Lobato, R. Paz, C. Sáez and J. J. Linares, J. Power Sources, 2007, 169, 198–204 CrossRef CAS.
- J. An and H. S. Lee, RSC Adv., 2013, 3, 14021–14028 RSC.
- C. Xia, D. Zhang, W. Pedrycz, Y. Zhu and Y. Guo, J. Power Sources, 2018, 373, 119–131 CrossRef CAS.
- J. Monod, Annu. Rev. Microbiol., 1949, 3, 371–394 CrossRef CAS.
- X. Zhang, W. He, L. Ren, J. Stager, P. J. Evans and B. E. Logan, Bioresour. Technol., 2015, 176, 23–31 CrossRef CAS PubMed.
- I. C. B. Rodrigues and V. A. Leão, Environ. Sci. Pollut. Res., 2020, 27, 36075–36084 CrossRef CAS PubMed.
- B. Logan, S. Cheng, V. Watson and G. Estadt, Environ. Sci. Technol., 2007, 41, 3341–3346 CrossRef CAS PubMed.
- A. A. Yaqoob, M. N. M. Ibrahim and S. Rodríguez-Couto, Biochem. Eng. J., 2020, 164, 107779 CrossRef CAS.
- N. Yoshida, Y. Miyata, A. Mugita and K. Iida, Materials, 2016, 9, 742 CrossRef PubMed.
- K. Fujii, N. Yoshida and K. Miyazaki, Bioelectrochemistry, 2021, 140, 107821 CrossRef CAS PubMed.
- G. Zhang, D. J. Lee and F. Cheng, Bioresour. Technol., 2016, 218, 680–686 CrossRef CAS PubMed.
- N. J. Koffi and S. Okabe, Chem. Eng. J., 2021, 15, 122443 Search PubMed.
- Yadvika, Santosh, T. R. Sreekrishnan, S. Kohli and V. Rana, Bioresour. Technol., 2004, 95, 1–10 CrossRef CAS PubMed.
- I. A. Ieropoulos, P. Ledezma, A. Stinchcombe, G. Papaharalabos, C. Melhuish and J. Greenman, Phys. Chem. Chem. Phys., 2013, 15, 15312–15316 RSC.
- X. A. Walter, J. Greenman and I. A. Ieropoulos, J. Power Sources, 2020, 446, 227328 CrossRef CAS PubMed.
- Y. Dong, Y. Feng, Y. Qu, Y. Du, X. Zhou and J. Liu, Sci. Rep., 2015, 5, 1–8 CAS.
- Y. Feng, Q. Yang, X. Wang and B. E. Logan, J. Power Sources, 2010, 195, 1841–1844 CrossRef CAS.
- R. Rossi, X. Wang and B. E. Logan, J. Power Sources, 2020, 475, 228633 CrossRef CAS.
- R. Rossi, G. Baek, P. E. Saikaly and B. E. Logan, ACS Sustainable Chem. Eng., 2021, 9, 2946–2954 CrossRef CAS.
- R. Rossi and B. E. Logan, Chem. Eng. J., 2021, 422, 130150 CrossRef CAS.
- N. J. Koffi and S. Okabe, Chemosphere, 2021, 274, 129715 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra03061b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |