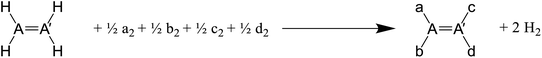Open Access Article
Open Access ArticleSteric effects vs. electron delocalization: a new look into the stability of diastereomers, conformers and constitutional isomers†
Sopanant Datta and
Taweetham Limpanuparb
and
Taweetham Limpanuparb *
*
Science Division, Mahidol University International College, Mahidol University, Salaya, Nakhon Pathom 73170, Thailand. E-mail: taweetham.lim@mahidol.edu
First published on 10th June 2021
Abstract
A quantum chemical investigation of the stability of compounds with identical formulas was carried out on 23 classes of compounds made of C, N, P, O and S atoms as core structures and halogens H, F, Cl, Br and I as substituents. All possible structures were generated and investigated by quantum mechanical methods. The prevalence of a formula in which its Z configuration, gauche conformation or meta isomer is the most stable form is calculated and discussed. Quantitative and qualitative models to explain the stability of the 23 classes of halogenated compounds were also proposed.
1. Introduction
Steric effects, non-bonded interactions leading to avoidance of spatial congestion of atoms or groups, are often the central theme in the discussion of stability of diastereomers, conformers and constitutional isomers. Reasoning based on steric effects is relatively intuitive and gives rise to a generally accepted rule of thumb that an E configuration, anti conformer and para isomer in diastereomers, conformational and constitutional isomers, respectively, should be the most stable forms.Many findings in contrast to steric predictions exist in the literature. Table 1 shows experimental and theoretical investigations of the Z configuration, gauche conformer and meta isomer being the most stable forms in carbon-backbone compounds. The experiments include heat of combustion or hydrogenation and spectroscopic measurement while the theoretical studies are mainly quantum mechanical methods.
| Case | Exceptions to steric prediction and reasonings |
|---|---|
| Z configuration18,31,60–72 | • Early experimenters such as Demiel conjectured that more electronegative atoms are on the same side in the most stable isomers.11,13 |
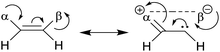
• Representative examples compiled by Eliel et al.73 include CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHF, CHF CHF, CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCl, CHF CHCl, CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHBr, CHF CHBr, CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHI, CHCl CHI, CHCl![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCl, CHBr CHCl, CHBr![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHBr. Halogens can be both donors and acceptors of electronic charges. When the donor and acceptor are on the same side, the structure is more stable due to the interaction of α and β substituents in the scheme.73 CHBr. Halogens can be both donors and acceptors of electronic charges. When the donor and acceptor are on the same side, the structure is more stable due to the interaction of α and β substituents in the scheme.73 |
|
 |
|
• Yamamoto et al. proposed four delocalization effects, σ-LP (nσ → 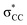 ), π-LP (nπ → ), π-LP (nπ → 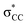 ), AP (σCX → ), AP (σCX → 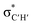 ) and SP (σCX → ) and SP (σCX → 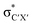 ), in C2H2X2 compounds where X = F, Cl, Br and found that π-LP effect is the major origin of cis effect in the three compounds.18–20 ), in C2H2X2 compounds where X = F, Cl, Br and found that π-LP effect is the major origin of cis effect in the three compounds.18–20 |
|
| Gauche conformation16,17,74–84 | • For CH2F–CH2F, the gauche form is preferred73 due to hyperconjugative interactions. The dominant one is the antiperiplanar σCH to 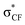 delocalization17 described in the scheme. delocalization17 described in the scheme. |
 |
|
| • Potential energy surfaces of rotamers have been thoroughly investigated. For CH2F–CH2F, the twofold (V2) potential actually has an energy minimum when the F–C–C–F torsional angle is ±90°.79 Rotational barriers can be small such that the shift in equilibrium can be easily observed when polar solvents promote the interconversion of anti to gauche conformers. | |
| • “Bent bond” may offer an explanation for the destabilization of the anti conformer.17,80,81 | |
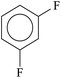
| Meta isomer85–87 | • For difluorobenzene, heat of combustion results clearly showed that the meta isomer is the most stable.87 |
 |
|
| • Computational studies showed that meta isomers are the most stable forms in most cases of dihalobenzenes. Taskinen attributed this to the absence of electronic interactions (shown below) between the two halogen substituents when they are at 1,3-positions.86 | |
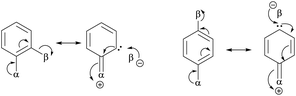 |
Even when steric effect reasoning correctly predicts the result, controversy ensues. For example, a number of organic chemistry textbooks attributed the relative stability of the staggered conformation of ethane to steric factor alone. This has led to controversy discussed at length across the scientific community for over eight years.1–8
Electron delocalization effects, on the other hand, are relatively more complicated. The reasoning for energy prediction often involves resonance structures9–15 (formerly called mesomeric effect) or hyperconjugation16–20 (delocalization) of orbitals. Specific reasonings for each case of exception to steric prediction are shown in Table 1. The preference for Z configuration and gauche conformation are primarily due to hyperconjugation in a similar vein to the ethane case,17,18 but the reasoning underlying the preference for meta isomer is still lacking.
In addition to carbon-backbone compounds in Table 1, there are many experimental and theoretical studies for other backbones discussed in this paper, namely, C3,21 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N,22,23 C
N,22,23 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P,24 N
P,24 N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N,25–31 N
N,25–31 N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P,32 P
P,32 P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P,33,34 C–N,35 C–P,36,37 C–O,38–40 C–S,41 N–N,38,42–44 N–P,38,43 P–P,38,43,45,46 N–O,38,42,47 N–S,47 P–O,48,49 P–S,50 O–O,38,42,51,52 O–S,53,54 and S–S.38,55
P,33,34 C–N,35 C–P,36,37 C–O,38–40 C–S,41 N–N,38,42–44 N–P,38,43 P–P,38,43,45,46 N–O,38,42,47 N–S,47 P–O,48,49 P–S,50 O–O,38,42,51,52 O–S,53,54 and S–S.38,55
Inspired by Bent's rule,21,56 which states how orbital hybridizations can explain trends of bond lengths and bond angles in a series of compounds correctly while the steric argument fails, in this paper, we want to advance the understanding of energy prediction of chemical structures that are derived from the same molecular formula.
Non-superimposable structures of the same molecular formula can be enantiomers, diastereomers, conformers and constitutional isomers (structural isomers). As energies of enantiomers are identical, they are excluded from our investigation. For the other three types of isomerism, E and Z configurations in A![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) A′ compounds and halocyclopropanes represent diastereomerism, gauche and anti conformers in A–A′ compounds represent conformational isomerism and ortho, meta and para structures in halobenzenes represent constitutional isomerism.
A′ compounds and halocyclopropanes represent diastereomerism, gauche and anti conformers in A–A′ compounds represent conformational isomerism and ortho, meta and para structures in halobenzenes represent constitutional isomerism.
2. Materials and methods
2.1 Quantum chemical calculations and datasets
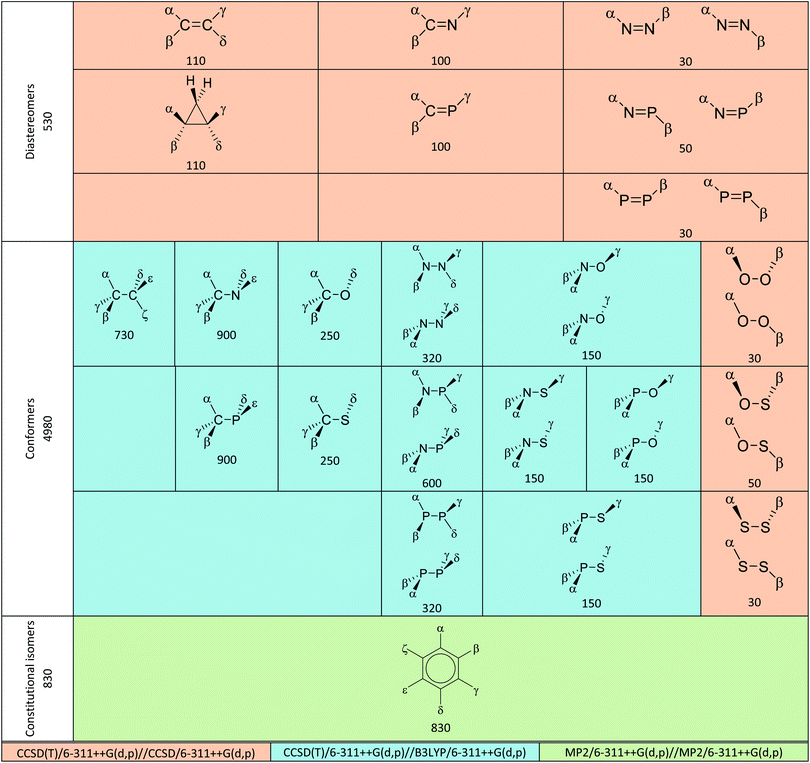
All possible structures made of two atoms A![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) A′ and A–A′ where A, A′ ∈ {C, N, P, O, S} or C3 or C6 as the core structure and combinations of halogen (H, F, Cl, Br, I) as substituents were previously generated by our group.57–59 Up to four levels of theory (HF, B3LYP, MP2 and CCSD) were used in these studies and B3LYP frequency calculations were completed for all structures. As shown in Table 2, we improved upon existing results by performing single-point electronic energy calculation at CCSD(T)/6-311++G(d,p) on diastereomer and conformer groups. For the constitutional isomer group, original MP2/6-311++G(d,p) energies were used due to prohibitive computational cost of CCSD(T) in benzene class of compounds. Our choice of methodology was inspired by observations in three dihaloethenes that HF is not good enough for geometries and MP2 is better than DFT for energy calculation.18 HF and B3LYP results are available in the supporting information† for comparison. We used them for diagnostic purpose in some difficult cases of rotamers.
A′ and A–A′ where A, A′ ∈ {C, N, P, O, S} or C3 or C6 as the core structure and combinations of halogen (H, F, Cl, Br, I) as substituents were previously generated by our group.57–59 Up to four levels of theory (HF, B3LYP, MP2 and CCSD) were used in these studies and B3LYP frequency calculations were completed for all structures. As shown in Table 2, we improved upon existing results by performing single-point electronic energy calculation at CCSD(T)/6-311++G(d,p) on diastereomer and conformer groups. For the constitutional isomer group, original MP2/6-311++G(d,p) energies were used due to prohibitive computational cost of CCSD(T) in benzene class of compounds. Our choice of methodology was inspired by observations in three dihaloethenes that HF is not good enough for geometries and MP2 is better than DFT for energy calculation.18 HF and B3LYP results are available in the supporting information† for comparison. We used them for diagnostic purpose in some difficult cases of rotamers.
Pople's basis set of 6-311++G(d,p) was used due to the availability of iodine atom and its reasonable computational cost. However, Pople's basis sets are well-known to produce imaginary frequency under certain conditions.88 Therefore, sample frequency calculations at MP2/6-311++G(d,p) were performed on all classes and only the benzene class was found to have imaginary frequencies. In agreement with the previous study,88 we found that imaginary frequencies disappear at MP2/6-311G(d,p) and the electronic energies are very close to MP2/6-311++G(d,p). While mean absolute deviation is 12.4 kcal mol−1 from 1505 structures, R2 and slope for the energies from the two basis sets are virtually unity. In other words, energies of all structures are shifted by similar magnitudes in the same direction. As a result, we use the basis 6-311++G(d,p) consistently for all classes of compounds in this study.
Optimized geometries of selected A![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) A′, A–A′ and halobenzene compounds were compared to gas-phase experimental data in previous studies.18,89,90,101 The current level of theory and/or basis set yields acceptable results. Additional confirmation with solid-phase X-ray structures from the Cambridge Structural Database (CSD)91 shows good agreement between calculated geometries from the current work and experimental results from the database for dichlorobenzenes (see the supporting information† for the results).
A′, A–A′ and halobenzene compounds were compared to gas-phase experimental data in previous studies.18,89,90,101 The current level of theory and/or basis set yields acceptable results. Additional confirmation with solid-phase X-ray structures from the Cambridge Structural Database (CSD)91 shows good agreement between calculated geometries from the current work and experimental results from the database for dichlorobenzenes (see the supporting information† for the results).
Revised dataset of all classes of compounds in the previous studies together with additions from this work are available online in Open Science Framework. This new data repository is intended to supersede the three separate datasets.57–59 Raw output files from Q-Chem,92 lists of structures, energies, PubChem CIDs, detailed methodology, source codes, scripts and templates are included. Unless specified differently, default settings of Q-Chem were used for the calculations. For some difficult cases of rotamers, different convergence criteria for energies and forces were applied. These attempts can be clearly seen in datasets in the supporting information.†
2.2 Definitions of convention and labels
We followed the standard definitions as per the Cahn–Ingold–Prelog (CIP) sequence rules and the International Union of Pure and Applied Chemistry (IUPAC)'s definitions. The relative bulkiness of all substituents (by covalent or van der Waals radii) in this study also follows the priority rule by chance.For E and Z configuration of diastereomers, if all four substituents are different, there are six possible isomers of a halo-substituted C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C. To differentiate them, labels of Ea, Eb, E1, E2, E3, Za, Zb, Z1, Z2, Z3, G0, G1, G3 (G stands for geminal) were used for C
C. To differentiate them, labels of Ea, Eb, E1, E2, E3, Za, Zb, Z1, Z2, Z3, G0, G1, G3 (G stands for geminal) were used for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and six other classes of compounds in accordance with the previous study.57 Therefore, energy comparison can be made within a diastereomeric pair (same label such as E1 vs. Z1) and geminal compounds were excluded from the current investigation.
C and six other classes of compounds in accordance with the previous study.57 Therefore, energy comparison can be made within a diastereomeric pair (same label such as E1 vs. Z1) and geminal compounds were excluded from the current investigation.
In a similar manner, for gauche and anti conformers, the torsional angle between the highest-priority substituents per CIP rule from the two ends of the molecule are considered. The angles within the interval (−120°, 120°) are treated as gauche and the angles within the interval [−180°, −120°) or (120°, 180°] are counted as anti. Unlike the previous definition of gauche effect,38 for simplicity, ambiguous cases (compounds with at least one conformer having ambiguity in labelling) are not considered. For example, all conformers of CBr2Cl–CF2Cl are not considered since the presence of the two Br atoms as the highest priority atoms on the left leads to an ambiguity in labelling the conformers as gauche or anti. However, compounds with more than one gauche conformer are considered normally in this paper.
For constitutional isomers of halobenzenes, we extended the standard nomenclature ortho, meta, para in disubstituted benzenes to highly substituted benzenes if it can be done by using the two highest priority substituents without ambiguity for all isomers in an empirical formula. For example, C6F4Cl2 isomers can be considered but C6Cl4F2 isomers are not included in our analysis.
As per the definition above, steric effects therefore predict that the E configuration, the anti conformer and the para isomer for compounds in this study are the most stable structures. Herein, deviations from these expectations are called Z configuration effect, gauche conformation effect and meta isomer effect respectively. Preliminary exclusion of irrelevant structures mentioned above reduced the total number of structures for the three groups from 710, 8365 and 1505 in previous studies57–59 to 530, 4980 and 830, respectively. Table 2 shows breakdowns of these numbers for each class.
The numbers of structures shown in Table 2 may differ from those in the results and analysis due to the following reasons.
• In the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N class, NBr
N class, NBr![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NI and NI
NI and NI![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NI disintegrated during the CCSD optimization process and are therefore excluded.
NI disintegrated during the CCSD optimization process and are therefore excluded.
• Some conformers interconverted during the geometry optimization process and are excluded from the analysis.
• Enantiomeric structures exist in many conformer classes. Only one from the pair was chosen for quantum chemical calculation. The excluded structures are still included in the analysis using energetic data from their enantiomers.
3. Results and discussion
3.1 Prevalence rates of steric prediction failure
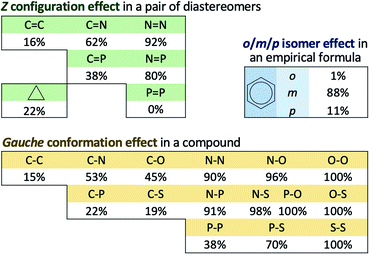
The main results are shown in Fig. 1 as the percentage of cases for the three groups, the first made of 7 classes of E/Z diastereomers, the second made of 15 classes of anti/gauche conformers and the third made of one class of ortho/meta/para isomers. These prevalence rates can be simply interpreted as how often the steric reasoning fails to identify the most stable structure in these classes of compounds. For the three large classes of carbon compounds (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C3 and C–C), the rates between 15% to 22% are not negligible. There are relatively small classes where the rates are as extreme as 0% (P
C, C3 and C–C), the rates between 15% to 22% are not negligible. There are relatively small classes where the rates are as extreme as 0% (P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P only) and 100% (O–O, P–O, O–S and S–S). The increasing trend toward the upper right side of periodic table can be seen from the figure. For the purpose of this paper, prevalence rates can be regarded as cases in which electron delocalization effects are in the counteracting direction and are stronger than steric effects.
P only) and 100% (O–O, P–O, O–S and S–S). The increasing trend toward the upper right side of periodic table can be seen from the figure. For the purpose of this paper, prevalence rates can be regarded as cases in which electron delocalization effects are in the counteracting direction and are stronger than steric effects.
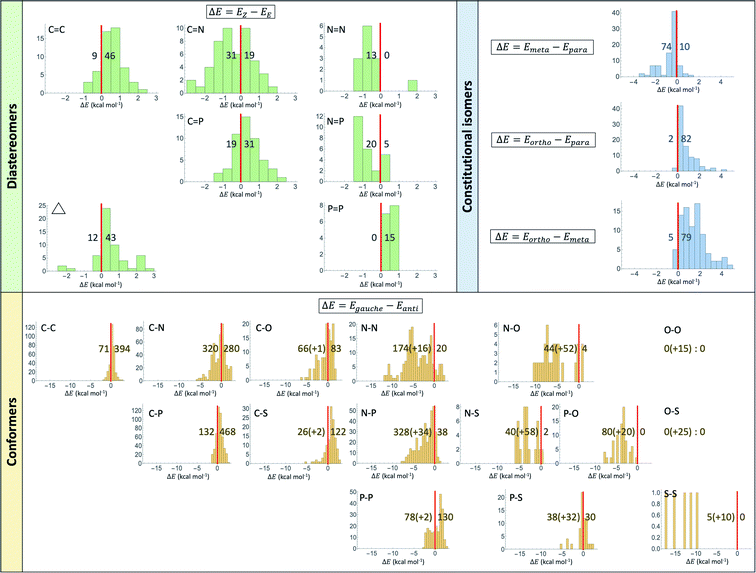
The uncertainty in computational results can be quantified in several ways. The change in level of theory from MP2 in previous studies57–59 to CCSD(T) in the present study leads to a change in prevalence rate in Fig. 1 of at most 7% (C–N). The prevalence rates at various other levels of theory (HF, B3LYP, MP2) with codes that generate them are available in the supporting information.† The basis set change from 6-311++G(d,p) to 6-311G(d,p) in MP2 optimization jobs of halobenzene compounds has no effect on the distribution of prevalence rates. Fig. 2 shows detailed distributions of energy differences as an extension to Fig. 1. Most of the distributions appear to be approximately bell-shaped if not uniformly distributed. The range of difference can be very small (e.g. 0.3 to 0.8 kcal mol−1 for P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P) and considerably large (e.g. −11.6 to 2.1 kcal mol−1 for N–N).
P) and considerably large (e.g. −11.6 to 2.1 kcal mol−1 for N–N).
There are borderline cases in both experimental and computational results as the difference in energy can be extremely small. For the example of CHBr![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHBr in Table 1, the gas-phase experimental value for a configuration conversion from E to Z is −100 ± 160 cal mol−1 in one source60 and revised to 90 ± 240 cal mol−1 in another.66 The present CCSD(T) electronic energy agrees with the latter source that the E configuration is more stable. However, in a similar vein to conformers discussed in Table 1, the Z structure is preferred in the liquid phase.66
CHBr in Table 1, the gas-phase experimental value for a configuration conversion from E to Z is −100 ± 160 cal mol−1 in one source60 and revised to 90 ± 240 cal mol−1 in another.66 The present CCSD(T) electronic energy agrees with the latter source that the E configuration is more stable. However, in a similar vein to conformers discussed in Table 1, the Z structure is preferred in the liquid phase.66
The main results of prevalence rates here agree with experimental and computational studies previously mentioned in the introduction. The well-known cases in carbon compounds in Table 1 summarized in the infamous book by Eliel, Wilen and Mander73 were reproduced in the current work with only one exception mentioned above. Moreover, the extreme cases of 0% (P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P) and 92% (N
P) and 92% (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) are also in line with previous work by others.28,30,33,34 For the majority of halobenzenes, in contrast to steric prediction, meta isomers are the most stable forms. This is confirmed by previous computational results for dihalobenzenes.86 Similar observations in polychlorinated compounds also confirm this meta preference e.g. for the first few chlorine substitutions to biphenyls (PCB), dibenzo-p-dioxins (PCDD) and dibenzofurans (PCDF), the most stable chlorination occurs at meta positions with respect to the other ring.93
N) are also in line with previous work by others.28,30,33,34 For the majority of halobenzenes, in contrast to steric prediction, meta isomers are the most stable forms. This is confirmed by previous computational results for dihalobenzenes.86 Similar observations in polychlorinated compounds also confirm this meta preference e.g. for the first few chlorine substitutions to biphenyls (PCB), dibenzo-p-dioxins (PCDD) and dibenzofurans (PCDF), the most stable chlorination occurs at meta positions with respect to the other ring.93
3.2 Quantitative and qualitative models for relative stability
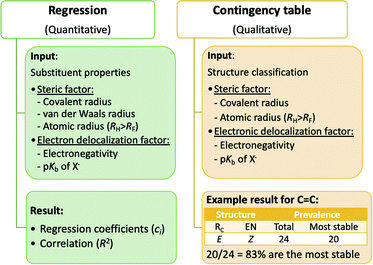
To gain insights into stability of Z configuration, gauche conformation and meta isomer, previous studies have focused on a small number of representative compounds. The total energy of these chemical structures can be partitioned by quantum mechanical methods, for example, exchange repulsion for steric effect and four different types of electron delocalization.18 Our approach in this paper is different in two ways. First, all possible permutations in a class of compounds were used in the study. Second, the energies were partitioned by statistical methods. The roles of steric and electron delocalization factors in determining the stability of structures were explored using quantitative and qualitative models as shown in Fig. 3.Simple predictors in which their periodic trends are obvious were selected for our preliminary analysis here. To represent steric bulk, one from three measures of atomic size, covalent radius (RC), van der Waals radius (RV) and atomic radius (RA), was used; the first two exhibit the typical trend of R(H) < R(F) < R(Cl) < R(Br) < R(I) whereas the last leads to the trend of R(F) < R(H) < R(Cl) < R(Br) < R(I). To represent electron delocalization, one from two measures, electronegativity (Pauling's scale, EN(H) < EN(I) < EN(Br) < EN(Cl) < EN(F)) and pKb of the conjugate base X− (pKb(H−) < pKb(F−) < pKb(Cl−) < pKb(Br−) < pKb(I−)), was used.
The models for all classes of compounds with all combinations of steric and electron delocalization factors, together with detailed descriptions can be found in the supporting information.† This analysis can be conducted on a class of compounds or a larger group of classes. In the latter case, additional term(s) are required to represent the class a compound belongs to (mean Ef within a class or central atom properties). An RV vs. pKb model created for the diastereomers group is shown in Table 3 as an example. In this model, the additional predictor A is the mean Ef of a class of compounds. The expectation for coefficient trends of cr2 > cr3 and ce2 < ce3 would represent the aforementioned counteracting effects in diastereomers. The resulting coefficients are as expected. As shown in the table, CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHI is predicted to be more stable in its Z configuration whereas CHI
CHI is predicted to be more stable in its Z configuration whereas CHI![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHI is predicted to be more stable in its E configuration. Cases whereby the final prediction indicates a more stable E configuration can be regarded as those having the more prominent steric effects overpowering electron delocalization effects. The vice versa is applied if Z configuration turns out to be more stable. The RV (or RC) vs. pKb models resulted in expected coefficient trends for conformers (all classes of compounds in one model) and constitutional isomers as well.
CHI is predicted to be more stable in its E configuration. Cases whereby the final prediction indicates a more stable E configuration can be regarded as those having the more prominent steric effects overpowering electron delocalization effects. The vice versa is applied if Z configuration turns out to be more stable. The RV (or RC) vs. pKb models resulted in expected coefficient trends for conformers (all classes of compounds in one model) and constitutional isomers as well.
| Regression model for the group of diastereomers (R2 = 0.8537, adjusted R2 = 0.8531, RMSE = 11.85). All coefficients are significant at p < 0.01 with four exceptions of cr2, cr3, ce2 and ce3 | ||||||
|---|---|---|---|---|---|---|
| Type of interaction | Predictora | Coefficient | Standard error | |||
| a ri and ei are values of the steric factor r (RV in Å) and the electron delocalization factor e (pKb – unitless), respectively, of substituent i (i ∈ {a, b, c, d}). The unit of coefficients can be inferred from this information and the nature of one and two-body terms. | ||||||
| 1 | c0 = | −968.1540 | 17.5752 | |||
| A | c1 = | 1.0242 | 0.0270 | |||
| ERV | 1-body | ra + rb + rc + rd | cr0 = | 150.7690 | 6.0272 | |
| 2-body | Geminal | rarb + rcrd | cr1 = | 23.2610 | 2.2489 | |
| Vicinal – Z | rarc + rbrd | cr2 = | −2.0951 | 2.4623 | ||
| Vicinal – E | rard + rbrc | cr3 = | −3.7969 | 2.4623 | ||
| EpKb | 1-body | ea + eb + ec + ed | ce1 = | −2.5909 | 0.0296 | |
| 2-body | Geminal | eaeb + eced | ce1 = | −0.0047 | 0.0005 | |
| Vicinal – Z | eaec + ebed | ce2 = | 0.0006 | 0.0005 | ||
| Vicinal – E | eaed + ebec | ce3 = | 0.0011 | 0.0005 | ||
| Example of prediction | |||||
|---|---|---|---|---|---|
| Structure | CCSD(T) Ef | Predicted Ef | ERV | EpKb | |
CHF![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHI CHI |
Z | −37.6837 | −27.4818 | 953.467 | 21.6087 |
| E | −37.1600 | −27.1276 | 953.108 | 22.3213 | |
CHI![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHI CHI |
Z | 19.6092 | 26.2601 | 1040.1556 | −11.3382 |
| E | 18.2007 | 26.2321 | 1039.1202 | −10.3308 | |
However, regression models using other combinations of steric and electron delocalization factors, especially with EN as the electron delocalization factor, often did not result in expected coefficient trends.
For each class of compounds, four contingency tables from four different combinations of steric and electron delocalization factors were constructed and can be found in the supporting information.† The RC vs. pKb model provides results that can be considered the same as those in Fig. 1, as the two factors give identical substituent rankings. The prevalence rates are obtained from the counts of structures classified as Z configuration, gauche conformer or meta isomer by both factors.
An example of a contingency table is shown in Fig. 3 for the class of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C compounds under the RC vs. EN model. For this model, the assumption is that the steric factor favours the E configuration (ERC) whereas the electron delocalization factor favours the Z configuration (ZEN).11,13 Therefore, a final 100% is expected from an ERC and ZEN structure and a 0% from its isomeric counterpart (ZRC and EEN). There are 24 C
C compounds under the RC vs. EN model. For this model, the assumption is that the steric factor favours the E configuration (ERC) whereas the electron delocalization factor favours the Z configuration (ZEN).11,13 Therefore, a final 100% is expected from an ERC and ZEN structure and a 0% from its isomeric counterpart (ZRC and EEN). There are 24 C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C structures of this classification, of which 20 structures are the most stable in their diastereomeric pairs. This shows that 20/24 = 83% of ERC and ZEN structures are the most stable compared to their diastereomers. Neither a 100% nor a 0% were attained from the other two classifications (ZRC and ZEN, and ERC and EEN) in this class of compounds. Expected results (0% and 100%) were achieved for C
C structures of this classification, of which 20 structures are the most stable in their diastereomeric pairs. This shows that 20/24 = 83% of ERC and ZEN structures are the most stable compared to their diastereomers. Neither a 100% nor a 0% were attained from the other two classifications (ZRC and ZEN, and ERC and EEN) in this class of compounds. Expected results (0% and 100%) were achieved for C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, C
N, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P and cyclopropane as described in the supporting information.† However, this is relatively small compared to the number of classes of compounds in which expected results were not achieved. Thus, this qualitative model was not able to illustrate conclusive results across all classes of compounds of diastereomers, conformers and constitutional isomers.
P and cyclopropane as described in the supporting information.† However, this is relatively small compared to the number of classes of compounds in which expected results were not achieved. Thus, this qualitative model was not able to illustrate conclusive results across all classes of compounds of diastereomers, conformers and constitutional isomers.
3.3 Improvement on the two models
Deviations from expected results in both quantitative and qualitative models above could be explained or addressed in three ways.Firstly, there could be a third factor affecting the results. For example, the deviation from idealized geometry was considered by performing both quantitative and qualitative analyses on the unoptimized structures, using standard bond lengths and bond/torsional angles. Improved trends were observed as described in the supporting information.†
Secondly, steric and electron delocalization predictors are highly correlated as per the periodic trend. A more appropriate electronic predictor may help improve the model. Steric factors may, in fact, be negligible when compared to electron delocalization factors for the studied classes of compounds after appropriate treatment of electron delocalization terms are employed.
Lastly, in cases of qualitative models for conformers and constitutional isomers, only considering the pair of highest priority substituents has an inherent flaw and may not reflect the summative effect of all substituents.
4. Conclusions, implications and future work
Most previous studies focused on a few model compounds and orbital-based energy partition schemes. To the best of our knowledge, our work is the first attempt to use combinatorics to enumerate94 all possible compounds and to employ statistical methods for energy partition schemes. The prevalence rates strongly support that the phenomenon8 of Z configuration effect, gauche conformation effect and meta isomer effect are real and not negligible.The implications for teaching are manifold. Many general, organic and biochemistry (GOB) textbooks95–97 mention the relative stability of E/Z (cis–trans or geometric) isomers but neglect to mention these phenomena probably for simplicity or because the phenomena were thought to be rare. There are two possible changes. First, one must be apprehensive when the steric reasoning is used to make stability predictions of compounds based on the size of halogen substituents. Second, for reasoning of these phenomena, there should be a more balanced view or a shift from teaching of VSEPR (steric-driven reasoning) to Bent's rule98 and hyperconjugation (electron delocalization-driven reasoning). The call to move away from VSEPR99,100 has been discussed elsewhere and this work only provides an additional piece of supporting evidence. It is important to note that even in the case that the steric prediction is right, the hyperconjugation energy can still be dominant as in the controversial case of ethane rotational barrier.1–8
The data presented should lead to a renewed interest in finding a new approach to describe stability of chemical compounds. The dataset is open for further analysis and utilization in many ways. For example, the models can be applied in molecular mechanics force field construction. Further analysis of bond length and bond angles for different structural classifications may reveal important insights into the three phenomena. Also, we are aware that constitutional isomers exist within the group of diastereomers (only C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, and C
N, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P). There is currently no specific naming convention for the relationship. Preliminary analysis shows that the failure rate of steric prediction from 1,2-interchange of substituents is 22/55, 20/50 and 17/50, respectively for the three classes. For example, in C2F2I2, the geminal structure is more stable than the E structure (see the supporting information† for the complete list). Similarly, constitutional isomers do exist within the group of conformers too but an exchange of two substituents will have the constitutional isomer effect intertwined with conformational isomer effect.
P). There is currently no specific naming convention for the relationship. Preliminary analysis shows that the failure rate of steric prediction from 1,2-interchange of substituents is 22/55, 20/50 and 17/50, respectively for the three classes. For example, in C2F2I2, the geminal structure is more stable than the E structure (see the supporting information† for the complete list). Similarly, constitutional isomers do exist within the group of conformers too but an exchange of two substituents will have the constitutional isomer effect intertwined with conformational isomer effect.
It is possible to further improve upon the levels of theory and basis used in this study. Specifically, Pople's basis sets are known for issues with post-HF calculations. A well-balanced approach should be developed for this particular area of study. Application of machine learning techniques may also help make a better sense of the data set and reduce the number of structures required to undergo expensive quantum mechanical calculations.
Author contributions
S. D. and T. L. contributed equally. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by mid-career researcher development grant (NRCT5-RSA63015-22) jointly funded by the National Research Council of Thailand (NRCT) and Mahidol University. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. We are grateful to Kridtin Chinsukserm, Peter Gill, Junming Ho, Wanutcha Lorpaiboon and Pierre Priest for analysis, ideas and suggestions in the early phase of this project. We thank the organizing committee of the 24th international annual symposium on computational science and engineering (ANSCSE24) for invitation to give a talk on 29 April 2021.Notes and references
- V. Pophristic and L. Goodman, Nature, 2001, 411, 565–568 CrossRef CAS PubMed
.
- F. Weinhold, Nature, 2001, 411, 539–541 CrossRef CAS PubMed
.
- P. R. Schreiner, Angew. Chem., Int. Ed., 2002, 41, 3579–3582 CrossRef CAS PubMed
.
- F. M. Bickelhaupt and E. J. Baerends, Angew. Chem., Int. Ed., 2003, 42, 4183–4188 CrossRef CAS PubMed
.
- F. Weinhold, Angew. Chem., Int. Ed., 2003, 42, 4188–4194 CrossRef CAS
.
- Y. Mo, W. Wu, L. Song, M. Lin, Q. Zhang and J. Gao, Angew. Chem., Int. Ed., 2004, 43, 1986–1990 CrossRef CAS PubMed
.
- Y. Mo and J. Gao, Acc. Chem. Res., 2007, 40, 113–119 CrossRef CAS PubMed
.
- S. Liu, N. Govind and L. G. Pedersen, J. Chem. Phys., 2008, 129, 094104 CrossRef PubMed
.
- L. Pauling, L. O. Brockway and J. Y. Beach, J. Am. Chem. Soc., 1935, 57, 2705–2709 CrossRef CAS
.
- K. S. Pitzer and J. L. Hollenberg, J. Am. Chem. Soc., 1954, 76, 1493–1496 CrossRef CAS
.
- A. Demiel, J. Org. Chem., 1962, 27, 3500–3504 CrossRef CAS
.
- G. B. Savitsky and K. Namikawa, J. Phys. Chem., 1963, 67, 2754–2756 CrossRef CAS
.
- A. Demiel, J. Org. Chem., 1965, 30, 2121–2126 CrossRef CAS
.
- J. Reuben and A. Demiel, J. Chem. Phys., 1966, 44, 2216–2217 CrossRef CAS
.
- J. T. Waldron and W. H. Snyder, J. Am. Chem. Soc., 1973, 95, 5491–5495 CrossRef CAS
.
- N. C. Craig, A. Chen, K. H. Suh, S. Klee, G. C. Mellau, B. P. Winnewisser and M. Winnewisser, J. Am. Chem. Soc., 1997, 119, 4789–4790 CrossRef CAS
.
- L. Goodman, H. Gu and V. Pophristic, J. Phys. Chem. A, 2005, 109, 1223–1229 CrossRef CAS PubMed
.
- T. Yamamoto, D. Kaneno and S. Tomoda, Bull. Chem. Soc. Jpn., 2008, 81, 1415–1422 CrossRef CAS
.
- I. V. Alabugin, K. M. Gilmore and P. W. Peterson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 109–141 CAS
.
- I. V. Alabugin, G. dos Passos Gomes and M. A. Abdo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1389 Search PubMed
.
- I. V. Alabugin, S. Bresch and M. Manoharan, J. Phys. Chem. A, 2014, 118, 3663–3677 CrossRef CAS PubMed
.
- J. M. Howell, J. Am. Chem. Soc., 1976, 98, 886–887 CrossRef CAS
.
- H. G. Li, C. K. Kim, B. S. Lee, C. K. Kim, S. K. Rhee and I. Lee, J. Am. Chem. Soc., 2001, 123, 2326–2333 CrossRef CAS PubMed
.
- M. T. Nguyen, A. Van Keer and L. G. Vanquickenborne, J. Organomet. Chem., 1997, 529, 3–14 CrossRef CAS
.
- G. T. Armstrong and S. Marantz, J. Chem. Phys., 1963, 38, 169–172 CrossRef CAS
.
- N. Wiberg, G. Fischer and H. Bachhuber, Angew. Chem., Int. Ed., 1977, 16, 780–781 CrossRef
.
- K. Nordhoff and E. Anders, J. Org. Chem., 1999, 64, 7485–7491 CrossRef CAS
.
- G. S. Tschumper, M. C. Heaven and K. Morokuma, Chem. Phys. Lett., 2003, 370, 418–424 CrossRef CAS
.
- P. R. P. Barreto, A. F. A. Vilela and R. Gargano, Int. J. Quantum Chem., 2005, 103, 659–684 CrossRef CAS
.
- T. Yamamoto, D. Kaneno and S. Tomoda, J. Org. Chem., 2008, 73, 5429–5435 CrossRef CAS PubMed
.
- D. Banerjee, A. Ghosh, S. Chattopadhyay, P. Ghosh and R. K. Chaudhuri, Mol. Phys., 2014, 112, 3206–3224 CrossRef CAS
.
- X. Zeng, H. Beckers and H. Willner, Angew. Chem., Int. Ed., 2009, 48, 4828–4831 CrossRef CAS PubMed
.
- T. Lu, A. C. Simmonett, F. A. Evangelista, Y. Yamaguchi and H. F. Schaefer, J. Phys. Chem. A, 2009, 113, 13227–13236 CrossRef CAS PubMed
.
- S. Vogt-Geisse and H. F. Schaefer, J. Chem. Theory Comput., 2012, 8, 1663–1670 CrossRef CAS PubMed
.
- J. J. Irwin, T. K. Ha and J. D. Dunitz, Helv. Chim. Acta, 1990, 73, 1805–1817 CrossRef CAS
.
- P. Coppens, B. J. van der Veken and J. R. Durig, J. Mol. Struct., 1986, 142, 367–370 CrossRef CAS
.
- E. C. Wang, Y. S. Li and R. A. Beaudet, J. Mol. Struct., 1990, 223, 15–32 CrossRef CAS
.
- S. Wolfe, Acc. Chem. Res., 1972, 5, 102–111 CrossRef CAS
.
- S. Wolfe, L. M. Tel, W. J. Haines, M. A. Robb and I. G. Csizmadia, J. Am. Chem. Soc., 1973, 95, 4863–4870 CrossRef CAS
.
- K. Omoto, K. Marusaki, H. Hirao, M. Imade and H. Fujimoto, J. Phys. Chem. A, 2000, 104, 6499–6504 CrossRef CAS
.
- C. F. Su and C. R. Quade, J. Chem. Phys., 1983, 79, 5828–5834 CrossRef CAS
.
- F. A. Van-Catledge, J. Am. Chem. Soc., 1974, 96, 5693–5701 CrossRef CAS
.
- A. H. Cowley, D. J. Mitchell, M.-H. Whangbo and S. Wolfe, J. Am. Chem. Soc., 1979, 101, 5224–5231 CrossRef CAS
.
- H. B. Schlegel and A. Skancke, J. Am. Chem. Soc., 1993, 115, 7465–7471 CrossRef CAS
.
- J. Odom, C. Wurrey, L. Carreira and J. Durig, Inorg. Chem., 1975, 14, 2849–2853 CrossRef CAS
.
- K. D. Sen, K. Ohta and K. Morokuma, J. Mol. Struct.: THEOCHEM, 1984, 109, 287–292 CrossRef
.
- M. D. Burtzoff, L. Peter, P. A. Lepse and D. Y. Zhang, J. Mol. Struct.: THEOCHEM, 2002, 619, 229–239 CrossRef CAS
.
- W. B. Person, J. S. Kwiatkowski and R. J. Bartlett, J. Mol. Struct., 1987, 157, 237–254 CrossRef CAS
.
- R. Withnall and L. Andrews, J. Phys. Chem., 1987, 91, 784–797 CrossRef CAS
.
- M. Korn, H. Oberhammer and R. Minkwitz, J. Mol. Struct., 1993, 300, 61–72 CrossRef CAS
.
- A. Veillard, Chem. Phys. Lett., 1969, 4, 51–52 CrossRef CAS
.
- D. C. Ghosh, Int. J. Mol. Sci., 2006, 7, 289–319 CrossRef CAS
.
- G. I. Cárdenas-Jirón, J. R. Letelier and A. Toro-Labbé, J. Phys. Chem. A, 1998, 102, 7864–7871 CrossRef
.
- O. Baum, HSOH - An elusive species with many different traits, Cuvillier Verlag, Göttingen, Germany, 2008 Search PubMed
.
- B. P. Prascher and A. K. Wilson, J. Mol. Struct.: THEOCHEM, 2007, 814, 1–10 CrossRef CAS
.
- H. A. Bent, Chem. Rev., 1961, 61, 275–311 CrossRef CAS
.
- K. Chinsukserm, W. Lorpaiboon, P. Teeraniramitr and T. Limpanuparb, Data Brief, 2019, 27, 104738 CrossRef PubMed
.
- T. Limpanuparb, S. Datta, K. Chinsukserm and P. Teeraniramitr, Data Brief, 2020, 30, 105442 CrossRef PubMed
.
- S. Datta and T. Limpanuparb, Data Brief, 2020, 30, 105386 CrossRef PubMed
.
- J. M. Dowling, P. G. Puranik, A. G. Meister and S. I. Miller, J. Chem. Phys., 1957, 26, 233–240 CrossRef CAS
.
- H. G. Viehe, Chem. Ber., 1960, 93, 1697–1709 CrossRef CAS
.
- N. C. Craig and E. A. Entemann, J. Am. Chem. Soc., 1961, 83, 3047–3050 CrossRef CAS
.
- H. G. Viehe and E. Franchimont, Chem. Ber., 1963, 96, 3153–3158 CrossRef CAS
.
- N. Craig, Y. S. Lo, L. Piper and J. C. Wheeler, J. Phys. Chem., 1970, 74, 1712–1727 CrossRef CAS
.
- N. C. Craig, D. A. Evans, L. G. Piper and V. L. Wheeler, J. Phys. Chem., 1970, 74, 4520–4527 CrossRef CAS
.
- N. C. Craig, L. G. Piper and V. L. Wheeler, J. Phys. Chem., 1971, 75, 1453–1460 CrossRef CAS
.
- D. Dixon, T. Fukunaga and B. E. Smart, J. Am. Chem. Soc., 1986, 108, 1585–1588 CrossRef CAS
.
- J. B. P. da Silva, J. Braz. Chem. Soc., 2000, 11, 219–223 CrossRef CAS
.
- R. Kanakaraju, K. Senthilkumar and P. Kolandaivel, J. Mol. Struct.: THEOCHEM, 2002, 589–590, 95–102 CrossRef CAS
.
- N. A. Pradie and H. V. Linnert, J. Phys. Chem. A, 2007, 111, 4836–4848 CrossRef CAS PubMed
.
- D. Feller, K. A. Peterson and D. A. Dixon, J. Phys. Chem. A, 2011, 115, 1440–1451 CrossRef CAS
.
- S. Jenkins, S. R. Kirk, C. Rong and D. Yin, Mol. Phys., 2013, 111, 793–805 CrossRef CAS
.
- E. L. Eliel, S. H. Wilen and L. N. Mander, Stereochemistry of Organic Compounds, Wiley, New York, USA, 1994 Search PubMed
.
- P. R. Rablen, R. W. Hoffmann, D. A. Hrovat and W. T. Borden, J. Chem. Soc., Perkin Trans. 2, 1999, 1719–1726 RSC
.
- F. R. Souza, M. P. Freitas and R. Rittner, J. Mol. Struct.: THEOCHEM, 2008, 863, 137–140 CrossRef CAS
.
- D. Y. Buissonneaud, T. van Mourik and D. O'Hagan, Tetrahedron, 2010, 66, 2196–2202 CrossRef CAS
.
- J. C. R. Thacker and P. L. A. Popelier, J. Phys. Chem. A, 2018, 122, 1439–1450 CrossRef CAS PubMed
.
- F. A. Martins and M. P. Freitas, Eur. J. Org. Chem., 2019, 2019, 6401–6406 CrossRef CAS
.
- L. Radom, W. A. Lathan, W. J. Hehre and J. A. Pople, J. Am. Chem. Soc., 1973, 95, 693–698 CrossRef CAS
.
- R. C. Bingham, J. Am. Chem. Soc., 1976, 98, 535–540 CrossRef CAS
.
- K. B. Wiberg, M. A. Murcko, K. E. Laidig and P. J. MacDougall, J. Phys. Chem., 1990, 94, 6956–6959 CrossRef CAS
.
- C. Thiehoff, Y. P. Rey and R. Gilmour, Isr. J. Chem., 2017, 57, 92–100 CrossRef CAS
.
- D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308–319 RSC
.
- D. R. Silva, L. de Azevedo Santos, T. A. Hamlin, C. Fonseca Guerra, M. P. Freitas and F. M. Bickelhaupt, ChemPhysChem, 2021, 22, 641–648 CrossRef PubMed
.
- J. Cioslowski, G. Liu and D. Moncrieff, J. Phys. Chem. A, 1997, 101, 957–960 CrossRef CAS
.
- E. Taskinen, Struct. Chem., 2000, 11, 293–301 CrossRef CAS
.
- W. D. Good, J. L. Lacina, D. W. Scott and J. P. McCullough, J. Phys. Chem., 1962, 66, 1529–1532 CrossRef CAS
.
- D. Moran, A. C. Simmonett, F. E. Leach, W. D. Allen, P. v. R. Schleyer and H. F. Schaefer, J. Am. Chem. Soc., 2006, 128, 9342–9343 CrossRef CAS PubMed
.
- M. Baranac-Stojanović, RSC Adv., 2014, 4, 43834–43838 RSC
.
- E. Cané, A. Miani and A. Trombetti, Chem. Phys. Lett., 2001, 340, 356–361 CrossRef
.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed
.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, Mol. Phys., 2015, 113, 184–215 CrossRef CAS
.
- S. Datta and T. Limpanuparb, Molecules, 2020, 25, 5697 CrossRef CAS PubMed
.
- W. Lorpaiboon and T. Limpanuparb, ChemRxiv, 2021 DOI:10.26434/chemrxiv.14571546
.
- R. H. Petrucci, F. G. Herring, J. D. Madura and C. Bissonnette, General chemistry: principles and modern applications, Pearson, New Jersey, USA, 2017 Search PubMed
.
- T. W. G. Solomons, C. B. Fryhle and S. A. Snyder, Organic Chemistry, John Wiley & Sons, Inc., New Jersey, USA, 2016 Search PubMed
.
- P. Vollhardt and N. Schore, Organic Chemistry: Structure and Function, W. H. Freeman and Company, New York, USA, 2018 Search PubMed
.
- S. Phankingthongkum and T. Limpanuparb, BMC Res. Notes, 2021, 14, 66 CrossRef PubMed
.
- I. V. Alabugin, S. Bresch and G. dos Passos Gomes, J. Phys. Org. Chem., 2015, 28, 147–162 CrossRef CAS
.
- F. Weinhold and C. R. Landis, Discovering Chemistry With Natural Bond Orbitals, Wiley, Hoboken, NJ, 2012 Search PubMed
.
- M Baranac-Stojanović, J Aleksić and M Stojanović, RSC Adv., 2015, 5, 22980–22995 RSC
.
Footnote |
| † The data presented in this study are openly available in Open Science Framework with the reference number 6ECP4. See DOI: 10.17605/OSF.IO/6ECP4. |
| This journal is © The Royal Society of Chemistry 2021 |