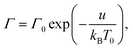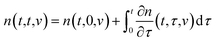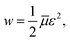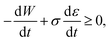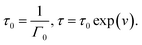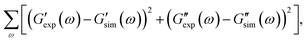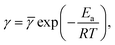Open Access Article
Open Access ArticleStructure–property relations in linear viscoelasticity of supramolecular hydrogels†
Aleksey D. Drozdov * and
Jesper deClaville Christiansen
* and
Jesper deClaville Christiansen
Department of Materials and Production Aalborg University Fibigerstraede 16, Aalborg 9220, Denmark. E-mail: aleksey@m-tech.aau.dk
First published on 13th May 2021
Abstract
Extraordinary mechanical properties of supramolecular gels (fracture toughness, fatigue resistance, injectability and self-healing ability) are strongly affected by their viscoelastic response driven by rearrangement (association and dissociation) of physical bonds. The kinetics of rearrangement is traditionally studied in small-amplitude shear oscillatory tests by analyzing the effect of the frequency of oscillations ω on the storage G′ and loss G′′ moduli. Conventional Maxwell-type models describe observations rather poorly when the gels reveal a pronounced flattening of the graphs G′′(ω) at high frequencies. A simple model is derived in linear viscoelasticity of supramolecular gels. Its advantage is that the model reproduces experimental data correctly, on the one hand, and involves only four material constants, on the other. Based on the analysis of experimental data on gels cross-linked by coiled-coil complexes, covalent and ionic bonds, phenylboronic acid-diol complexes and metal–ligand coordination bonds, the model is applied to develop structure–property relations that describe the influence of chemical structure of supramolecular gels (concentration of polymer chains and type and molar fraction of temporary bonds) and environmental conditions (temperature, pH and ionic strength of buffer solutions) on their viscoelastic response.
1 Introduction
Supramolecular hydrogels with polymer chains bridged by non-covalent bonds have recently become a focus of attention due to their extraordinary mechanical and physical properties and numerous applications in biomedicine, biotechnology and soft electronics.1–3 Owing to the transient nature of physical bonds between chains (that associate and dissociate being driven by external stimuli), these gels demonstrate high strength,4 exceptional stretchability,5 high fracture toughness6 and fatigue resistance,7 and rapid self-recovery.8 Among other important features of supramolecular gels, it is worth mentioning (i) their self-healing ability,9,10 (ii) shape memory property,11,12 (iii) self-assembling (the ability to undergo sol–gel–sol transitions driven by mechanical and chemical triggers),13,14 and (iv) the ability to secure strong and robust adhesion to a variety of surfaces.15–17As the mechanical behavior of supramolecular gels is strongly affected by rearrangement (dissociation and re-association) of temporary bonds between chains, a number of studies analyzed the kinetics of this process by means of the standard rheological tests (shear oscillations in the frequency sweep mode).18–20 Due to a variety of supramolecular motifs (hydrogen bonding, hydrophobic interaction, multivalent electrostatic interaction, metal–ligand coordination, host–guest recognition, dipole–dipole interaction, π–π stacking, charge transfer (donor–acceptor) interaction21,22), direct comparison of observations in these tests is difficult, and more sophisticated treatment of the experimental data is required.23
Breakage and reformation of supramolecular bonds is conventionally evaluated by matching the experimental dependencies of the storage, G′, and loss, G′′, moduli on the angular frequency of oscillations ω with the help of constitutive equations in linear viscoelasticity.24 The most popular approach is grounded on the generalized Maxwell model
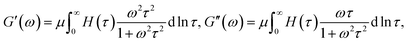 | (1) |
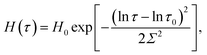 | (2) |
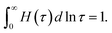 | (3) |
An advantage of eqn (1)–(3) is that they involve only three adjustable parameters, μ, τ0 and Σ, which implies that these relations can be applied for comparison of viscoelastic properties of hydrogels with various chemical structures and compositions. A shortcoming of these equations is that they do not ensure good agreement with experimental data on all supramolecular gels. In particular, eqn (1)–(3) fail to describe an upturn in the graph G′′(ω) observed at relatively large frequencies.25
Several modifications of eqn (2) were proposed to improve the quality of matching observations. Grindy et al.25 suggested to replace eqn (2) with the relation
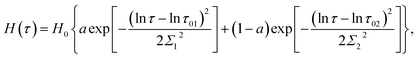 | (4) |
To avoid the growth in the number of parameters to be found by matching observations, the Gaussian function (2) is replaced with non-Gaussian semi-empirical expressions for the relaxation spectrum. Ahmadi and Seiffert29 suggested to use a particular form of the gamma distribution function
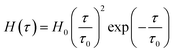 | (5) |
Another technique was proposed by Tang et al.30,31 based on the assertion that the dependence of the relaxation modulus Gr on relaxation time t was described by the same relaxation spectrum H(τ) that was included in eqn (1). Presuming the decay in Gr to be governed by the Kohlrausch stretched exponential function
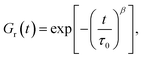 | (6) |
An analogous method was developed by Zheng et al.,32 who presumed the relaxation modulus to decay with t following the algebraic dependence
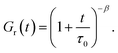 | (7) |
As the gamma distribution function in eqn (5) and the stretched exponential function in eqn (6) are closely connected with the fractional derivatives,33 a similar (in some sense) approach was suggested by Holten-Andersen et al.,34 who proposed to replace the conventional derivatives in the governing equations for the Maxwell medium with their fractional analogs.
An alternative description of the function H(τ) consists in treatment of a supramolecular gel as a viscoelastic medium with a discrete spectrum characterized by a prescribed distribution of relaxation times τm (m = 1, 2,…). Fitting experimental data by means of this approach with the Rouse model and the pom–pom model for τm was performed by Zhang et al.35 and Boothroyd et al.,36 respectively. Although this method describes observations in oscillatory tests adequately, it requires a large number of coefficients in the expansion of H(τ) to be found numerically.
The objective of this study is threefold: (i) to develop a simple model in linear viscoelasticity of supramolecular gels (with only four material parameters), (ii) to demonstrate the ability of this model to describe experimental data in shear oscillatory tests on supramolecular gels with various compositions, types and concentrations of supramolecules bonds between chains, and (iii) to formulate structure–property relations characterizing the influence of external factors (temperature, pH and molar fraction of salts in buffer solutions) on the kinetics of association and dissociation of physical bonds.
The model is based on the following scenario.37 The polymer network in a gel consists of entangled chains bridged by supramolecular bonds. Thermal fluctuations induce rearrangement (dissociation and association) of temporary junctions. When one of the junctions merging a chain with the network breaks, reptative diffusion of the chain starts. It induces its partial disentanglement and development of new entanglements. This process is terminated when the broken junction rearrange (form a new bond with the network).
According to this picture (a similar scenario was suggested by Jangizehi et al.38), the time-dependent behavior of a gel reflects two kinetics processes at the micro-level: (i) rearrangement of supramolecular bonds and (ii) disentanglement and re-entanglement of polymer chains. The former process is typical of supramolecular gels, while the latter is characteristic for all polymer melts.
In a dense system (a polymer melt), the rates of disentanglement and re-entanglement of chains are relatively low, and the dynamics of this process can be studied by means of conventional oscillatory tests (with the angular frequency ω ranging from 0.01 to 100 rad s−1). In a loose system (a swollen gel with a large volume fraction of water molecules), these rates are high, and rearrangement of entanglements becomes practically “invisible,” as its characteristic rate exceeds strongly the frequency of oscillations. As a result, only the influence of disentanglement and re-entanglement of chains on the kinetics of rearrangement of supramolecular bonds can be observed in rheological tests.
When the effect of disentanglement and re-entanglement of chains on association and dissociation of supramolecular bonds is negligible, changes in the storage and loss moduli with frequency are correctly described by eqn (1) and (2) (see Fig. 5 below). When this effect is pronounced (it is observed as flattening of the graphs G′′(ω) and, in some cases, as the growth of the loss modulus at high frequencies ω), eqn (1) and (2) fail to reproduce these “tails” (see Fig. 1 and 2 below), and more sophisticated models are required for their description.
 | ||
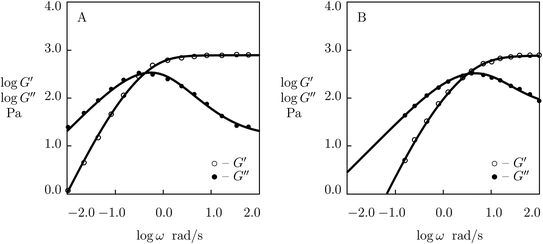
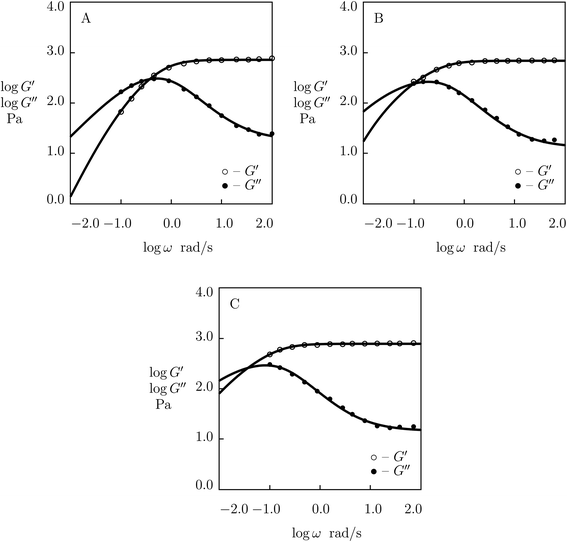
| Fig. 1 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data27 on protein gels with equal molar ratios of CKK and CCE polypeptides and various mass fractions of proteins ϕ (A – ϕ = 0.04, B – ϕ = 0.10, C – ϕ = 0.13, D – ϕ = 0.16) at temperature T = 20 °C. Solid lines: results of simulation. | ||
 | ||
| Fig. 2 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data27 on protein gels with total concentration of proteins ϕ = 0.07 and various molar fractions of CCK r (A – r = 0.75, B – r = 0.67, C – r = 0.33, D – r = 0.25) at temperature T = 20 °C. Solid lines: results of simulation. | ||
As the interval of frequencies in shear oscillatory tests is limited by the abilities of testing devices, it seems natural to “enlarge” this interval by constructing master-curves for the storage and loss moduli with the help of the time–temperature superposition principle. This method was applied to examine the influence of the disentanglement and re-entanglement processes on the kinetics of rearrangement of supramolecular bonds in ref. 20, 29, 35, 36 and 39, to mention a few. Although smooth master-curves for G′(ω) and G′′(ω) can be constructed by vertical and horizontal shifts of experimental data obtained at various temperatures, a shortcoming of this approach is that it presumes the effect of temperature on two processes (disentanglement of chains and disassociation of supramolecular bonds) to be governed by the same activation energy. The activation energies calculated from the horizontal shifts of experimental diagrams accept different values that are strongly affected by the algorithm of shifting (according to Han et al.,40 for poly(acrylic acid) gel cross-linked with Fe3+ ions, these values lie in the interval between 45 and 298 kJ mol−1).
To develop a model in linear viscoelasticity of supramolecular gels with the minimum number of adjustable parameters, we describe the kinetics of rearrangement of physical bonds only and disregard the dynamics of disentanglement of re-entanglement of chains. The latter process is accounted for in a phenomenological way by presuming the rate of dissociation of physical bonds to depend on frequency of oscillations. Constitutive models where the rate of breakage of physical bonds between chains depends on the amplitude of external load are widely used in the analysis of the nonlinear viscoelastic response of solid polymers41,42 and polymer melts.43,44 Application of a similar approach to describe the effect of frequency of oscillations on the viscoelastic behavior of supramolecular gels was recently proposed by Yu et al.45
The exposition is organized as follows. A model for the linear viscoelastic response of supramolecular gels is reported in Section 2. This model is applied to describe observations in shear oscillatory tests on gels with various types of supramolecular bonds in Section 3. Some concluding remarks are formulated in Section 4.
2 Model
A supramolecular gel is modeled as a two-phase medium composed of an equivalent polymer network and water molecules. Adopting the affinity hypothesis, we suppose that deformation of the network coincides with macro-deformation of the gel. The polymer network is treated as transient, where two types of chains are distinguished: (i) active (both ends of a chain are connected to separate junctions) and (ii) dangling (an end of a chain detaches from the network due to dissociation of an appropriate bond).46,47 When an end of an active chain separates from the network at some instant τ1, the chain is transformed into the dangling state. When the free end of a dangling chain merges with the network at instant τ2 > τ1, the chain returns into the active state. Attachment and detachment events occur at random times being driven by thermal fluctuations.The polymer network is presumed to be inhomogeneous. It consists of meso-regions with various activation energies for rearrangement of bonds. The rate of dissociation of bonds (separation of active chains from their junctions) in a meso-domain with activation energy u is governed by the Eyring equation
Γ(v) = Γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−v). exp(−v).
| (8) |
The inhomogeneity of the network is characterized by the probability density f(v) to find a meso-region with dimensionless activation energy v ≥ 0. For definiteness, we adopt the quasi-Gaussian formula for this function (the random energy model48),
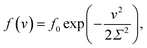 | (9) |
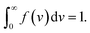 | (10) |
An advantage of eqn (9) is that the function f(v) is characterized by the only parameter Σ > 0.
The state of a transient network is characterized by the function n(t, τ, v) that equals the number (per unit volume) of chains at time t ≥ 0 that have returned into the active state before instant τ ≤ t and belong to a meso-domain with activation energy v. In particular, n(t, t, v) is the number of active chains in meso-domains with activation energy v at time t. The number of chains that were active at the initial instant t = 0 and have not separated from their junctions until time t reads n(t, 0, v). The number of chains that were active at t = 0 and detach from their junctions within the interval [t, t + dt] is given by − ∂n/∂t(t, 0, v) dt. The number of dangling chains that return into the active state within the interval [τ, τ + dτ] reads P(τ, v)dτ with
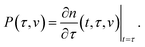 | (11) |
The number of chains (per unit volume) that merged (for the last time) with the network within the interval [τ, τ + dτ] and detach from their junctions within the interval [t, t + dt] equals − ∂2n/∂t∂τ(t, τ, v) dtdτ.
We suppose that the number of active chains (per unit volume) in meso-domains with various activation energies v remain constant,
| n(t, t, v) = Nf(v), | (12) |
Separation of active chains from their junctions is described by the kinetic equations
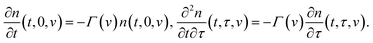 | (13) |
Eqn (13) imply that the rate of transformation of active chains into the dangling state (the rate of dissociation of supramolecular bonds) is proportional to the number of active chains in an appropriate meso-region. These relations differ from appropriate equations in ref. 32 and 49, where the rate of breakage of temporary bonds was calculated by using another assumption.
Integration of eqn (13) with the initial conditions (11) and (12) implies that
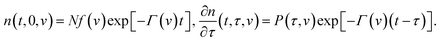 | (14) |
Inserting eqn (14) into the equality
| P(t, v) = NΓ(v)f(v). | (15) |
Eqn (15) differs from the corresponding equation for the rate of association of supramolecular bonds proposed in ref. 50. Combination of eqn (14) and (15) implies that
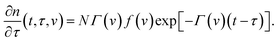 | (16) |
Adopting the conventional formula for the mechanical energy stored in an active chain under shear deformation with small strains,
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) is the rigidity of a chain, and ε stands for shear strain, we calculate the strain energy density (per unit volume) of the network as the sum of mechanical energies of active chains,
is the rigidity of a chain, and ε stands for shear strain, we calculate the strain energy density (per unit volume) of the network as the sum of mechanical energies of active chains,
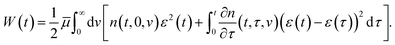 | (17) |
The first term in eqn (17) equals the strain energy of chains that have not been rearranged within the interval [0, t]. The other term expresses the strain energy of active chains that have last merged with the network at various instants τ ∈ [0, t]. Eqn (17) presumes stresses in dangling chains to relax entirely before these chains merge with the network, which implies that the mechanical energy (at time t) stored in a chain transformed into the active state at time τ depends on the relative strain ε*(t, τ) = ε(t) −ε(τ).
Inserting expression (17) into the Clausius–Duhem inequality
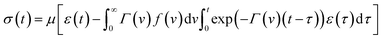 | (18) |
![[small mu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cd.gif) N.
N.
According to eqn (18), in a relaxation test with the program
| ε(t) = 0 (t < 0), ε(t) = ε0 (t ≥ 0), |
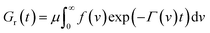 | (19) |
It follows from eqn (18) that in a shear oscillatory test with amplitude ε0 and angular frequency ω,
ε(t) = ε0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(lwt), exp(lwt), |
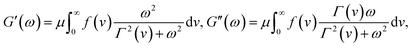 | (20) |
When the rate of breakage of physical bonds Γ0 in eqn (8) is constant, we substitute eqn (8) and (9) into eqn (20), and introduce the notation
Under this transformation, eqn (20) accept the form
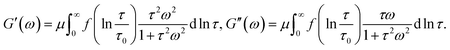 | (21) |
Eqn (21) coincide with eqn (1) and (2) under condition (9). This means that the proposed model for rearrangement of physical bonds in a polymer network is equivalent to the generalized Maxwell model under two conditions: (i) the inhomogeneity of the network is described by eqn (9), and (ii) the rate of dissociation of bonds is governed by the Eyring eqn (8) with a constant pre-factor Γ0.
As it is mentioned in Introduction, eqn (1) and (2) describe poorly experimental data on hydrogels for which the characteristic rates of rearrangement of supramolecular bonds and disentanglement and re-entanglement of chains are sufficiently close to each other, and these two processes are mutually dependent. To improve the quality of matching observations, we presume Γ0 to be affected by the strain rate. Adopting the linear dependence of Γ0 on ω, we set
| Γ0 = γ(1 + Kω), | (22) |
Eqn (22) allows flattening of the experimental dependencies G′′(ω) to be described adequately, but does not predict the growth of G′′(ω) at large ω. The latter can be described by setting
| Γ0 = γ(1 + Kωa) | (23) |
3 Fitting of experimental data
The aim of the analysis of experimental data is twofold: (i) to demonstrate the ability of the model to describe observations in shear oscillatory tests on supramolecular gels, and (ii) to develop structure–property relations for these gels that describe evolution of material parameters driven by (a) changes in the chemical structure, type and concentration of physical bonds and (b) the influence of external factors (temperature, pH and molar fraction of salt in buffer solutions).3.1 Protein gels cross-linked by coiled-coil complexes
We begin with the study of observations on protein gels consisting of two proteins, CCE-(GB1)4-CCE and CCK-(GB1)5-CCK-(GB1)5-CCK (designated as CCE and CCK), physically cross-linked by hetero-coiled-coil complexes formed by CCK and CCE blocks (Sun et al.27). The gels were prepared by mixing solutions of CCE and CCK proteins in phosphate buffered saline (PBS with pH = 7.4) at room temperature. The chemical structure of the globular protein GB1 and the CCE and CCK polypeptides is reported in ref. 27.Experimental data in shear oscillatory tests on these gels are chosen as the benchmark for comparison with observations on other supramolecular gels because these tests were performed on gels with various (i) mass fractions of proteins in solutions ϕ (at a fixed molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of CCE and CCK polypeptides), (ii) molar ratios of CCK blocks r (at a fixed mass fraction of proteins ϕ = 0.07), and (iii) various environmental conditions (temperature T and molar fraction of NaCl in buffer solutions).
1 of CCE and CCK polypeptides), (ii) molar ratios of CCK blocks r (at a fixed mass fraction of proteins ϕ = 0.07), and (iii) various environmental conditions (temperature T and molar fraction of NaCl in buffer solutions).
Observations on protein gels27 are depicted in Fig. 1–4 together with results of simulation with the material parameters reported in Fig. S-1 to S-3 and Table S-1.† Each set of data, G′(ω) and G′′(ω), is fitted separately. The coefficients γ, Σ and K are determined by the method of nonlinear regression to minimize the difference
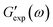 and
and 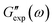 are the storage and loss moduli measured in a test,
are the storage and loss moduli measured in a test, 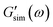 and
and 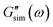 are predictions of the model, and summation is performed over all frequencies ω for which observations are provided.
are predictions of the model, and summation is performed over all frequencies ω for which observations are provided.
 | ||
| Fig. 3 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data27 on protein gel with mass fraction of proteins ϕ = 0.07 and equal molar fractions of CCK and CCE at various temperatures T (A – T = 20, B – T = 37 °C). Solid lines: results of simulation. | ||
 | ||
| Fig. 4 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data27 on protein gel with mass fraction of proteins ϕ = 0.07 and equal molar fractions of CCK and CCE in PBS solution with various molar fractions θ of NaCl (A – θ = 0.137, B – θ = 0.5, C – θ = 1.0 M) at temperature T = 20 °C. Solid lines: results of simulation. | ||
Fig. 1 shows that an increase in concentration of proteins in pre-gel solutions ϕ results in the growth of the elastic modulus μ (observed as an increase in G′ at high frequencies ω), a slight decrease in the rate of rearrangement of bonds γ (observed as a shift of the point of maximum on the diagram G′′(ω) to lower frequencies), and an increase in the measure of inhomogeneity of the network Σ (reflected by widening of the experimental curves G′′(ω)). All experimental data are fitted with the fixed coefficient K = 0.051.
The effect of concentration of proteins on parameters μ, γ and Σ is illustrated in Fig. S-1,† where the data are approximated by the equations
μ = μ0ϕm, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ = γ0 + γ1ϕ, Σ = Σ0 + Σ1ϕ γ = γ0 + γ1ϕ, Σ = Σ0 + Σ1ϕ
| (24) |
The effect of molar fraction of CKK blocks r on the viscoelastic behavior of protein gels is illustrated in Fig. 2. This figure reveals that an increase in the molar ratio of CKK peptides r induces a substantial decrease in the elastic modulus μ, the growth of the rate of dissociation of supramolecular bonds γ, and a strong reduction in the coefficient K (reflecting deviations of the graphs G′′(ω) from predictions of the model (1) and (2)), but does not affect the measure of heterogeneity of the polymer network Σ (matching observations is conducted with a constant value Σ = 0.8). Evolution of parameters μ, γ and K with r is illustrated in Fig. S-2.† The data are approximated by the equations
μ = μ0 + μ1r, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ = γ0 + γ1r, K = K0 + K1r, γ = γ0 + γ1r, K = K0 + K1r,
| (25) |
The influence of temperature T on the storage and loss moduli of the gel with ϕ = 0.07 and r = 0.5 is demonstrated in Fig. 3, where observations at T = 20 and 37 °C are reported together with results of numerical simulation with the material parameters collected in Table S-1.† This table shows that the elastic modulus μ is weakly affected by temperature. The growth of temperature leads to a slight increase in Σ and results in (i) a strong (by an order of magnitude) growth of the rate of dissociation of supramolecular bonds γ and (ii) a substantial (by twice) decrease in the coefficient K.
The effect of ionic strength of phosphate buffer solution (PBS) (caused by dissolution of various molar fractions θ = 0.137, 0.5 and 1.0 M of NaCl) on the viscoelastic response of the protein gel with ϕ = 0.07 and r = 0.5 is demonstrated in Fig. 4, where experimental data are presented together with results of simulation with the adjustable parameters reported in Fig. S-3.† Fig. S-3† shows that the elastic modulus μ remains independent of molar fraction of monovalent salt θ (the value μ = 0.78 kPa is used to fit all experimental data), whereas the coefficients γ, Σ and K are affected by concentration of NaCl. An increase in θ induces (i) a strong (by a factor of 5) decrease in the rate of dissociation of supramolecular bonds γ, (ii) a slight increase in the measure of inhomogeneity of the network Σ, and (iii) a pronounced (by a factor of 6) growth of the coefficient K characterizing interactions between physical bonds and entanglements between chains. The effect of θ on these quantities is described by the equations
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ = γ0, + γ1θ, Σ = Σ0 + Σ1θ, K = K0 + K1θ γ = γ0, + γ1θ, Σ = Σ0 + Σ1θ, K = K0 + K1θ
| (26) |
3.2 The effects of chemical structure
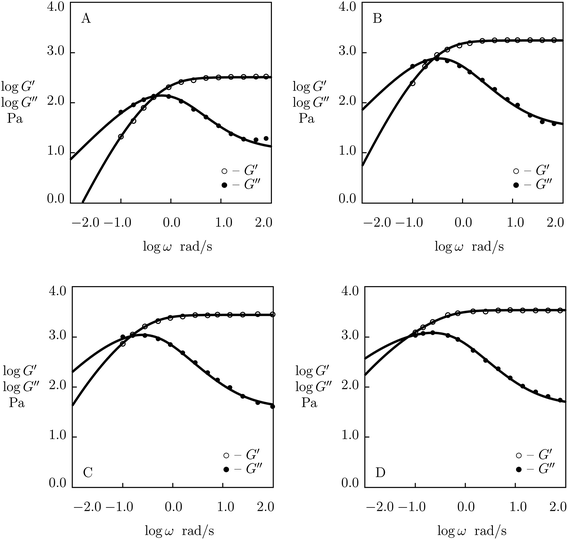
Although the data reported in Fig. S-1 and S-2† describe how the viscoelastic response of protein gels is affected by the structure of their polymer networks, a shortcoming of these data is that they account for two phenomena (the effect of concentration of polymer chains and the influence of concentration of temporary junctions between them) simultaneously. To examine these effects separately, we fit observations in shear oscillatory tests on several gels where concentrations of polymer chains and supramolecular bonds are varied independently.Experimental data on PEG gels cross-linked by Ni2+-histidine coordination bonds51 are depicted in Fig. 5 together with results of simulation with the material constants reported in Fig. S-4† (all experimental data are fitted with the same parameter K = 1.5 × 10−3). Fig. 5 shows that an increase in concentration of PEG chains ϕ results in a pronounced increase in the elastic modulus μ (observed as the growth of G′ at high frequencies of oscillations) and a weak reduction in the rate of dissociation of supramolecular bonds (reflected by a shift of maxima on the G′′(ω) diagrams to lower frequencies), but it does not affect inhomogeneity of the polymer network. Changes in μ, γ and Σ with ϕ are demonstrated in Fig. S-4,† where the data are approximated by eqn (24) with m = 1.7.
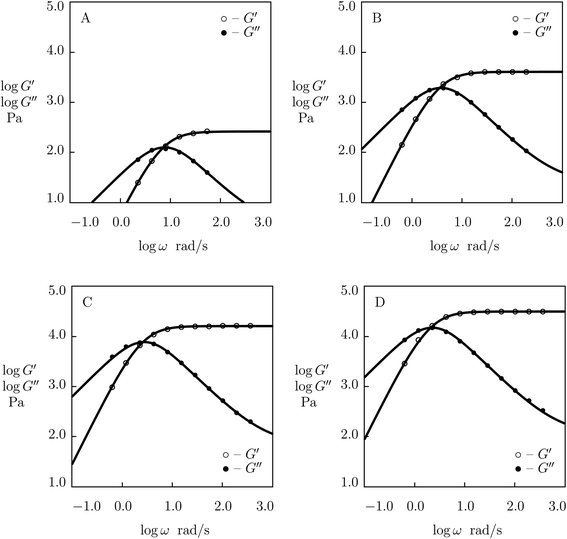 | ||
| Fig. 5 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data51 on histidine-functionalized PEG gels cross-linked with Ni2+ ions with various concentrations ϕ of PEG chains (A – ϕ = 25, B – ϕ = 50, C – ϕ = 100, D – ϕ = 150 g L−1) in buffer solution with pH = 8 at room temperature. Solid lines: results of simulation. | ||
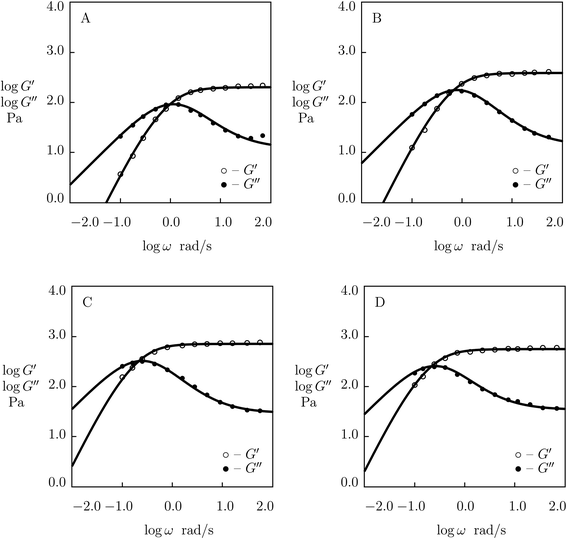
To examine the applicability of eqn (24) to other types of supramolecular gels, we fit experimental data in shear oscillatory tests on phenanthroline-functionalized PEG gels cross-linked with Co2+ ions. The gels were synthesized by means of a two-stage process (Ahmadi and Seiffert28). At the first step, tetra-arm amine-functionalized PEG chains (molar mass 20 kg mol−1) were grafted with 5,6-epoxy-5,6-dihydro-[1,10]phenanthroline. At the other step, phenanthroline-grafted PEG chains were dissolved (with various concentrations ϕ ranging from 15 to 60 g L−1) in a buffered solution of CoNO3 (molar fraction of Co2+ ions equaled 1/3 of molar fraction of phenanthroline groups). Gelation was performed due to formation of metal–ligand complexes between Co2+ ions and phenanthroline groups.
Experimental data on PEG gels cross-linked by Co2+-phenanthroline supramolecular bonds28 are plotted in Fig. 6 together with results of numerical analysis with the material constants reported in Fig. S-5† (all sets of data are fitted with the coefficient K = 0.01). The effect of ϕ on parameters μ, γ and Σ is illustrated in Fig. S-5,† where the data are approximated by eqn (24) with m = 2.5.
 | ||
| Fig. 6 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data28 on phenanthroline-functionalized PEG gels cross-linked with Co2+ ions with various concentrations ϕ of PEG chains (A – ϕ = 15, B – ϕ = 30, C – ϕ = 45, D – ϕ = 60 g L−1) in pre-gel solutions at temperature T = 25 °C. Solid lines: results of simulation. | ||
Finally, observations are matched on 2-methacryloyloxyethyl phosphorylcholine (MPC) gels whose chains were functionalized with benzoxaborole-containing monomer 5-methacrylamido-1,2-benzoxaborole (MAABO) and catechol-containing monomer dopamine methacrylamide (DMA) (Chen et al.52). The gels were prepared by mixing solutions of poly(MPC-MAABO) and poly(MPC-DMA) chains (with equimolar amounts of MAABO and DMA functional groups and molar masses 44.2 and 54.7 kg mol−1, respectively) in phosphate buffer saline (PBS) with pH = 7.4. Gelation was driven by formation of benzoxaborole-catechol supramolecular complexes.
Observations in oscillatory shear tests on MPC gels with various concentrations of polymer chains ϕ (ranging from 75 to 125 g L−1)52 are presented in Fig. 7 together with results of simulation with the material constants reported in Fig. S-6† (all experimental data are fitted with K = 0.03). Changes in parameters μ, γ and Σ with ϕ are illustrated in Fig. S-6,† where the data are approximated by eqn (24) with m = 5.4.
 | ||
| Fig. 7 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data52 on MPC gels cross-linked by benzoxaborole-catechol complexes with various concentrations ϕ of MPS chains (A – ϕ = 75, B – ϕ = 100, C – ϕ = 125 g L−1) in PBS solutions with pH = 7.4 at temperature T = 25 °C. Solid lines: results of simulation. | ||
The following conclusions are driven from Fig. S-1 and S-4 to S-6:†
(I) Unlike hydrogels with covalent bonds, whose elastic modulus is weakly affected by concentration of polymer chains in pre-gel solutions, the elastic modulus μ of supramolecular gels grows strongly with ϕ following the pattern (24) with m ranging from 1.5 to 5.4 (depending on the type of supramolecular bonds).
(II) The rate of dissociation of bonds in supramolecular gels γ decreases exponentially with concentration of polymer chains ϕ (due to interactions between neighboring junctions that slow down the rearrangement process).
(III) The parameter K characterizing the influence of disentanglement and re-entanglement of chains on breakage and reformation of supramolecular bonds is independent of ϕ.
(IV) Depending on the type of supramolecular bonds between chains, the coefficient Σ (treated as a measure of inhomogeneity of the polymer network) increases with ϕ (Fig. S-1†), decreases with ϕ (Fig. S-6†), or remains unaffected by this parameter (Fig. S-4 and S-5†).
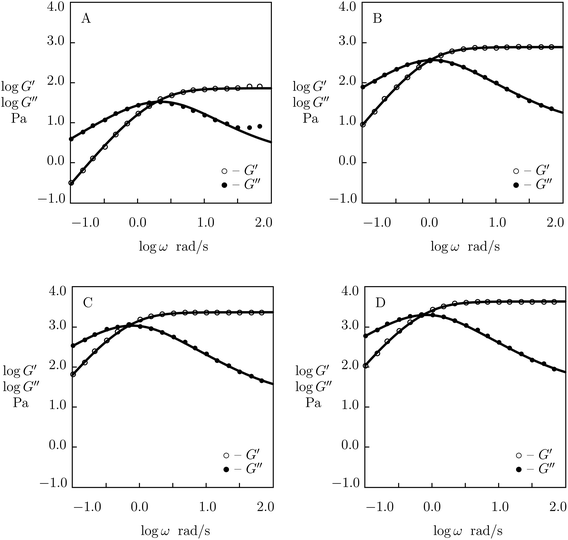
Experimental data in shear oscillatory tests on P(AAm-AAc) gels53 are presented in Fig. 8 together with results of simulation with the material parameters reported in Fig. S-7.† Each set of observations is matched separately by means of three parameters: μ, γ and Σ. The value K = 0.61 is found by fitting data on the gel with r = 0.1 and used in approximation of observations on the other gels without changes.
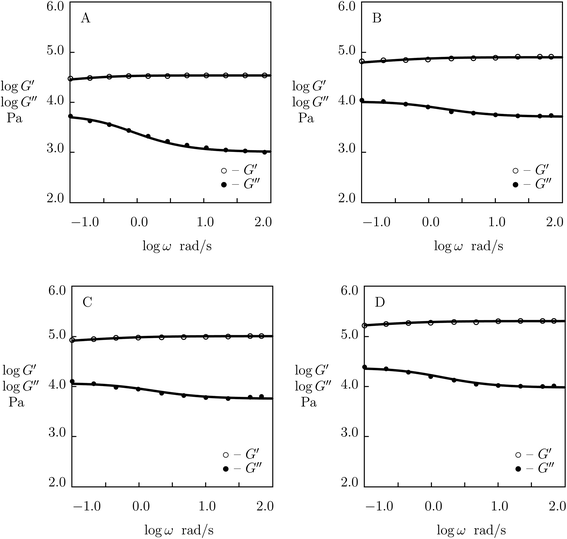 | ||
| Fig. 8 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data53 on P(AAm-AAc) gels with various molar ratios r of AAc and AAm monomers (A – r = 0.1, B – r = 0.15, C – r = 0.2, D – r = 0.25) cross-linked with Fe3+ ions. Solid lines: results of simulation. | ||
Fig. S-7† shows that μ and Σ grow strongly (by several times) with parameter r (which characterizes concentration of ionic bonds between chains), whereas γ increases rather weakly. Changes in these parameters with r are described by the equations
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μ = μ0 + μ1r, log μ = μ0 + μ1r, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ = γ0 + γ1r, Σ = Σ0 + Σ1r, γ = γ0 + γ1r, Σ = Σ0 + Σ1r,
| (27) |
Although the model is developed for hydrogels with physical bonds between chains, Fig. 8 demonstrates its ability to describe observations on gels with covalent (permanent) and supramolecular (temporary) junctions when concentration of permanent cross-links is relatively low.
Two features of doubly cross-linked P(AAm-AAc) gels are to be mentioned: (i) a high value of the coefficient K reflecting the strong effect of disentanglement and re-entanglement of chains on rearrangement of supramolecular bonds, and (ii) high value of the parameter Σ that characterizes inhomogeneity of the polymer network.
We proceed with fitting experimental data on tetra-arm poly(ethylene glycol) (PEG) gels cross-linked with two types of dynamic covalent bonds based on phenylboronic acid–diol complexation (Yesilyurt et al.54). Macromers PEG-PBA and PEG-APBA (end-functionalized with phenylboronic acid derivatives; PBA stands for phenylboronic acid, and APBA denotes o-aminomethylphenylboronic acid) were synthesized by reaction of tetra-arm poly(ethylene glycol) NH2HCl salt (Mw = 5 kg mol−1) with 4-carboxyphenylboronic acid and by reductive amination of this salt with 2-formylphenylboronic acid, respectively. Macromers PEG-GL (end-functionalized with diol) were synthesized by reaction of tetra-arm poly(ethylene glycol) NH2HCl salt with D-gluconolactone. Hydrogels were prepared by mixing equimolar amounts of PEG-GL macromers with a mixture of PEG-PBA and PEG-APBA macromers (with mass fractions of PEG-APBA macromers in the mixture r = 0.0, 0.25, 0.50, 0.75 and 1.0) in buffered aqueous solutions (mass fraction of macromers in solution 0.1).
Observations in shear oscillatory tests on PEG gels with two types of temporary bonds (between PEG-PBA and PEG-GL and between PEG-APBA and PEG-GL macromers)54 are presented in Fig. 9 and S-8.† In these figures, the experimental dependencies G′(ω) and G′′(ω) are depicted together with results of numerical analysis with the material parameters μ, γ and Σ reported in Fig. S-9† (calculations are conducted with K = 0). Fig. 9 and S-8† demonstrate good agreement between the data and results of simulation. The same quality of fitting was reached in ref. 54 by approximation of the data with the help of eqn (1) with the relaxation spectrum H(τ) treated as an adjustable function.
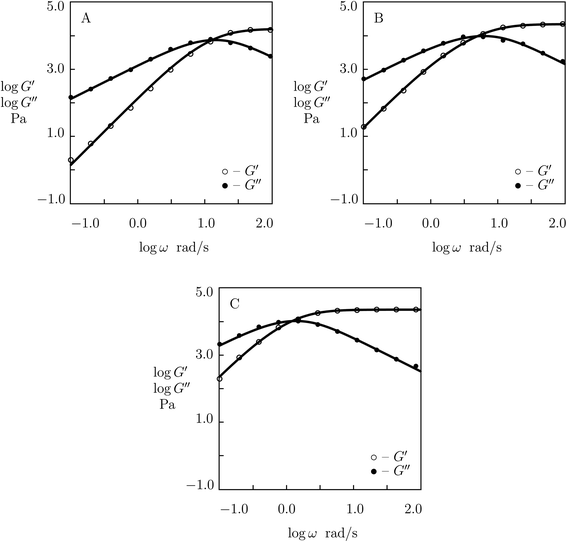 | ||
| Fig. 9 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data54 on PEG gels cross-linked by phenylboronic acid-diol (PBA-GL and APBA-GL) complexation with various mass fraction r of PEG-APBA macromers (A – r = 0.0, B – r = 0.5, C – r = 1.0) in buffered solution with pH = 7.4 at room temperature. Solid lines: results of simulation. | ||
Fig. S-9† describes “competition” between two types of dynamic covalent bonds. One of them, between PEG-PBA and PEG-GL macromers, is relatively weak, and its rate of rearrangement is high, while the other, between PEG-APBA and PEG-GL macromers, is stronger, and its rate of dissociation is lower. It is shown in this figure that (i) the elastic modulus μ grows linearly with parameter r describing concentration of strong bonds, (ii) the rate of breakage of temporary bonds γ reduces monotonically with r, whereas (iii) the coefficient Σ reflecting inhomogeneity of the polymer network behaves non-monotonically: it adopts similar values for gels with r = 0 and r = 1, but reaches its maximum when concentrations of PEG-PBA and PEG-APBA coincide. The data in Fig. S-9† are approximated by the equations
μ = μ0 + μ1r, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ = γ0 + γ1r, Σ = Σ0 + Σ1(r − r0)2 γ = γ0 + γ1r, Σ = Σ0 + Σ1(r − r0)2
| (28) |
3.3 The effect of temperature
The influence of temperature T on rearrangement of supramolecular bonds between chains in protein gels was studied in ref. 27 at two temperatures (T = 20 and 37 °C) only (Fig. 3). To examine this phenomenon in more detail, observations in shear oscillatory tests are studied on three supramolecular gels with various types of physical cross-links.We begin with fitting experimental data on histidine-modified tetra-arm PEG gel cross-linked by metal coordination bonds with Ni2+ ions (Fullenkamp et al.51). The gels were prepared by dissolution of PEG chains end-functionalized with histidine in water (concentration of polymer chains 150 g L−1), addition of an aqueous solution of NiCl2 (molar ratio of Ni2+ ions equaled 0.5 of molar ratio of histidine end-groups) and control of pH of the buffer by addition of NaOH solution.
Experimental data in rheological tests at temperatures T = 10, 25 and 37 °C are presented in Fig. 10 together with results of simulation with the material parameters reported in Fig. S-10.† Each set of observations in Fig. 10 is matched separately with the help of four adjustable parameters: μ, Σ, γ and K. Fig. S-10A† shows that μ and Σ decrease linearly with temperature T, and their evolution is described by the equations
| μ = μ0 + μ1T, Σ = Σ0 + Σ1T | (29) |
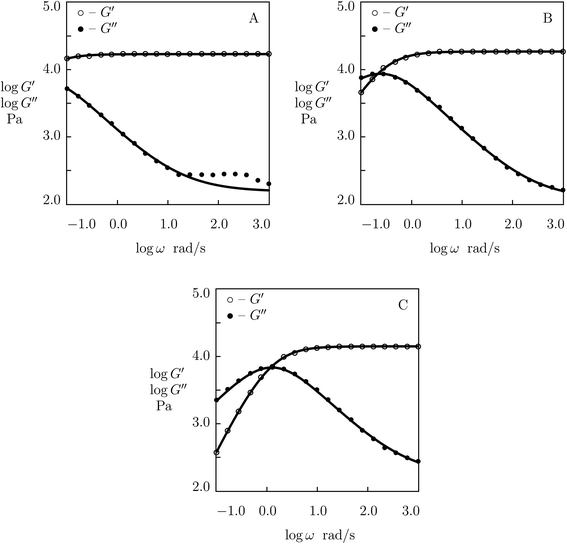 | ||
| Fig. 10 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data51 on histidine-functionalized PEG gels cross-linked with Ni2+ ions at various temperatures T (A – T = 10, B – T = 25, C – T = 37 °C) in buffer solution with pH = 7. Solid lines: results of simulation. | ||
According to the Arrhenius law, temperature-induced growth of the rate of dissociation of supramolecular bonds γ is governed by the relation
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) stands for a pre-factor, R is the universal gas constant, T is the absolute temperature, and Ea is an activation energy. It follows from this equation that
stands for a pre-factor, R is the universal gas constant, T is the absolute temperature, and Ea is an activation energy. It follows from this equation that
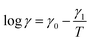 | (30) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) and γ1 = Ea/(R
and γ1 = Ea/(R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10). An analogous formula is accepted to predict the influence of temperature on parameter K,
10). An analogous formula is accepted to predict the influence of temperature on parameter K,
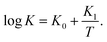 | (31) |
It is shown in Fig. S10B† that eqn (30) and (31) with similar activation energies (Ea = 68.5 and 71.5 kJ mol−1 for γ and K, respectively) describe adequately the effect of temperature on these parameters.
Keeping in mind that K is introduced as a measure of interaction between the processes of rearrangement of supramolecular bonds and disentanglement and re-entanglement of chains, the closeness of activation energies for γ and K may be interpreted as follows. An increase in temperature T induces an increase in the rate of dissociation of physical bonds between chains, while its effect on the rate of disentanglement of chains may be disregarded (when T changes in rather narrow intervals under consideration). At low temperatures T, when γ is low, changes in the structure of a polymer network driven by disentanglement and re-entanglement of chains have sufficient time to accumulate between subsequent dissociation events and to affect the rearrangement process. At relatively high temperatures T, these changes in the network structure become negligible as the duration between subsequent dissociation events is small (γ is high), and their influence of the rearrangement of supramolecular bonds weakens.
To confirm these conclusions, we fit experimental data (Zou et al.53) in shear oscillatory tests on double-network P(AAm-AAc) gel (with molar fraction of AAm monomers in a pre-gel solution 3 M and molar ratio of AAc and AAm monomers 0.25) at temperatures T = 25, 40, 50, 60, 70 and 80 °C. Observations at the lowest and highest temperatures (25 and 80 °C) are depicted in Fig. 11 and those at intermediate temperatures (40, 50, 60 and 70 °C) are reported in Fig. S-11.† Each set of data is matched by the model with four adjustable parameters, μ, Σ, γ and K. Their best-fit values are reported in Fig. S-12† together with their approximations by eqn (29)–(31). This figure demonstrates good agreement between the data and results of numerical analysis with similar activation energies for γ and K (Ea = 71.6 and 73.9 kJ mol−1, respectively).
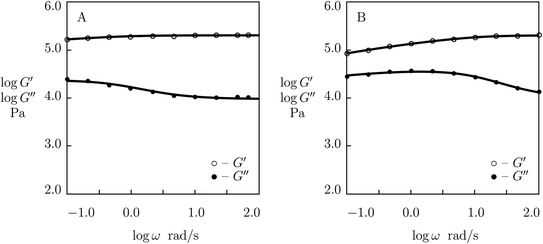 | ||
| Fig. 11 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data53 on P(AAm-AAc) gel cross-linked with Fe3+ ions at various temperatures T (A – T = 25, B – T = 80 °C). Solid lines: results of simulation. | ||
Finally, experimental data are matched in shear oscillatory tests on PEG gels cross-linked by phenylboronic acid–diol complexation between tetra-arm PEG chains end-functionalized with 3-fluorophenylboronic acid (FPBA) and D-gluconolactone (GL) (Parada and Zhao50). The gels were prepared by mixing equimolar amounts of PEG-FPBA and PEG-GL macromers (molar mass of PEG chains 5 kg mol−1, molar fractions of macromers 25 mM) in PBS buffered solutions with pH = 7.2. Rheological tests were conducted at temperatures T = 5, 10, 15, 25, 35 and 45 °C. Observations in experiments at the lowest and highest temperatures are depicted in Fig. 12, and those at intermediate temperatures are presented in Fig. S-13† together with results of numerical analysis. Each set of data is fitted separately with four adjustable parameters, μ, Σ, γ and K. The effect of temperature on these quantities is illustrated in Fig. S-14.† This figure shows that the effect of temperature on the material parameters is adequately described by eqn (29)–(31), and the activation energies for γ and K adopt similar values (Ea = 39.2 and 44.3 kJ mol−1, respectively).
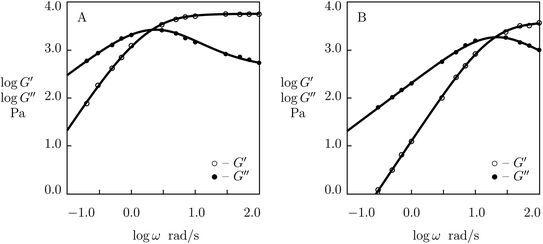 | ||
| Fig. 12 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data50 on PEG gel cross-linked by phenylboronic acid–diol (FPBA-GL) complexation in buffer solution with pH = 7.2 at various temperatures T (A – T = 5, B – T = 45 °C). Solid lines: results of simulation. | ||
The following conclusions are drawn from Fig. S-10, S-12 and S-14:†
(I) An increase in temperature T results in a decrease in the elastic modulus μ of supramolecular gels (which is tantamount for a decay in the number of supramolecular bonds between chains). In the intervals of temperature under consideration, this decrease is correctly described by eqn (29).
(II) Temperature-induced reduction in concentration of supramolecular bonds is accompanied by a decay in the measure of inhomogeneity of the polymer network Σ determined by eqn (29). This decrease reflects destruction of “weak” bonds between chains which leads to a more homogeneous structure of the network.
(III) The effect of temperature T on the rate of dissociation of supramolecular bonds γ is adequately predicted by eqn (30). The accuracy of calculation of the activation energies in the Arrhenius law is confirmed by closeness of Ea values found by fitting observations on temperature-induced changes in parameters γ and K.
(IV) Analysis of observations in oscillatory tests on supramolecular gels is conventionally conducted by means of the time–temperature superposition principle and construction of master-curves for the dependencies G′(ω) and G′′(ω). Predictions grounded on this approach may be questioned as this method presumes thermo-rheological simplicity of the materials under investigation, whereas changes in Σ and K with T indicate that this condition is not satisfied.
3.4 The effect of pH
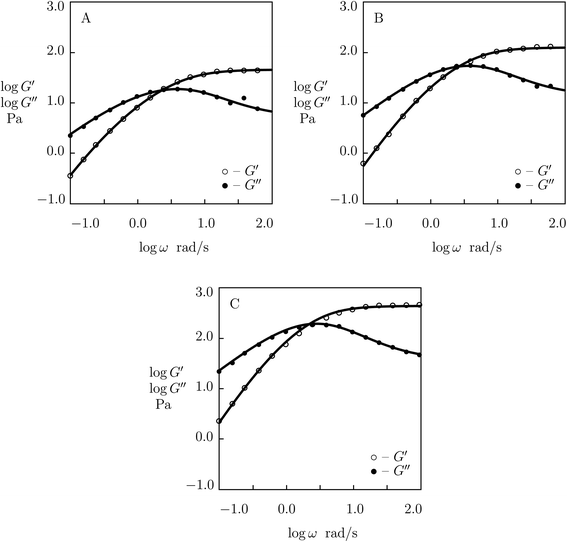
To examine the influence of pH of buffered solutions on the viscoelastic response of supramolecular gels, we analyze 5 sets of experimental data in shear oscillatory tests.We begin with fitting observations on PEG gel prepared by phenylboronic acid-diol complexation of tetra-arm PEG chains end-functionalized with FPBA and GL (concentration of macromers in buffer solutions 15 mM). Shear oscillatory tests were conducted at room temperature in PBS with pH = 6.9, 7.2, 7.4, 7.7, 8.1 (Parada and Zhao50). Experimental data are depicted in Fig. 13 (pH = 6.9, 7.4 and 8.1) and S-15† (pH = 7.2 and 7.7) together with results of simulation with the material parameters reported in Fig. S-16.† Each set of observations is matched separately with four adjustable parameters, μ, Σ, γ and K.
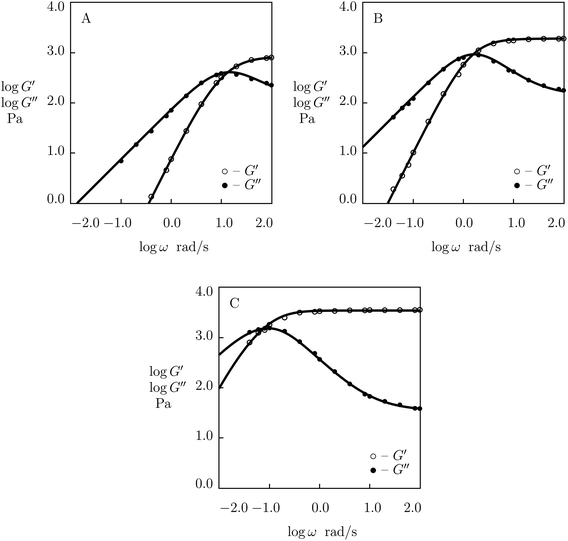 | ||
| Fig. 13 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data50 on PEG gel cross-linked by phenylboronic acid–diol (FPBA-GL) complexation in buffer solutions with various pH (A – pH = 6.9, B – pH = 7.4, C – pH = 8.1) at room temperature. Solid lines: results of simulation. | ||
Fig. S-16A† shows that the elastic modulus μ and the coefficient Σ (charactering inhomogeneity of the polymer network) increase with pH. Changes in these parameters are described by the equations
μ = μ0 + μ1 pH, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Σ = Σ0 + Σ1 pH Σ = Σ0 + Σ1 pH
| (32) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ = γ0 − γ1 pH, log γ = γ0 − γ1 pH, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = K0 + K1 pH, K = K0 + K1 pH,
| (33) |
Comparison of Fig. S-16 with Fig. S-10, S-12 and S-14† demonstrates an analogy between the effects of pH and temperature T on the viscoelastic response of supramolecular gels (all material parameters evolve in the same way when pH increases and T decreases).
To confirm that this analogy is typical of other supramolecular gels, three sets of experimental data are analyzed.
First, observations are matched on PEG gels prepared by mixing equimolar amounts of tetra-arm macromers (molar mass 10 kg mol−1) end-functionalized with phenylboronic acid (PEG-PBA) and cis-1,2-diol (PEG-GL) in buffer solutions (mass fraction of macromers 0.1) at room temperature (Marco-Dufort et al.55). Experimental data in shear oscillatory tests on the gels prepared in buffer solutions with pH = 7, 8 and 9 are depicted in Fig. 14 together with results of numerical simulation. Each set of data is fitted separately with four parameters, μ, Σ, γ and K. The effect of pH on these quantities is illustrated in Fig. S-17,† where the data are approximated by eqn (32) and (33).
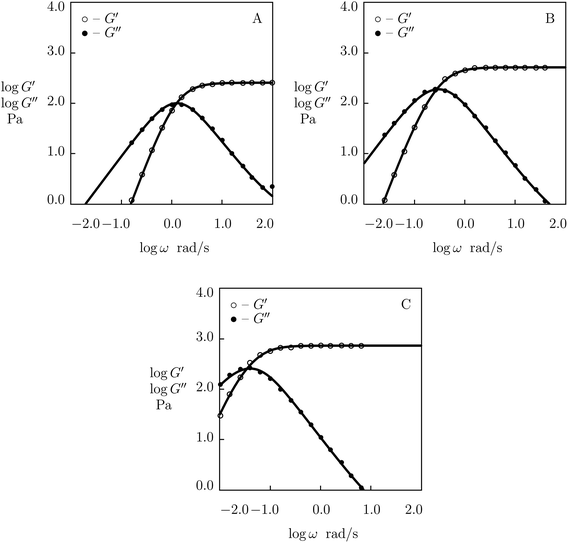 | ||
| Fig. 14 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data55 on PEG gels cross-linked by phenylboronic acid-diol (PBA-GL) complexation in buffer solutions with various pH (A – pH = 7, B – pH = 8, C – pH = 9) at room temperature. Solid lines: results of simulation. | ||
We proceed with matching experimental data on PEG gels cross-linked by phenylboronic acid-diol complexation of tetra-arm PEG chains (molar mass 5 kg mol−1) functionalized with APBA and GL functional groups (Yesilyurt et al.56). The gels were prepared by mixing equimolar solutions of PEG-APBA and PEG-GL macromers (total molar fraction of macromers 0.1 M) in phosphate buffers with various pH. Experimental data in shear oscillatory tests (at temperature T = 37 °C) on gels synthesized in solutions with pH = 6, 7 and 8 are depicted in Fig. 15 together with results of numerical analysis. Each set of data is fitted by means of four material parameters, μ, Σ, γ and K. The effect of pH on these quantities is demonstrated in Fig. S-18,† where the data are approximated by eqn (32) and (33).
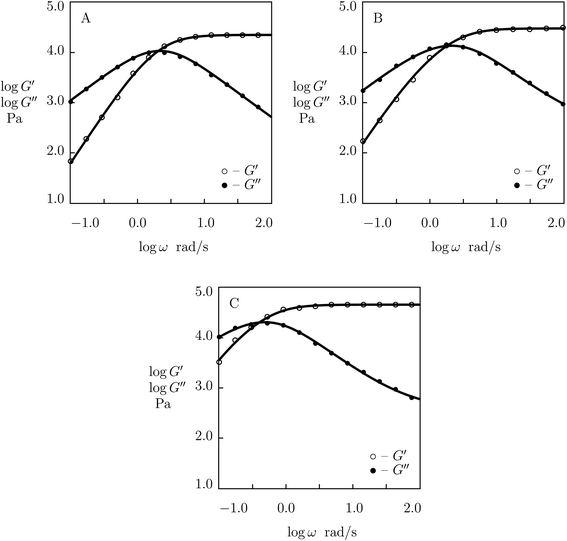 | ||
| Fig. 15 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data56 on PEG gel cross-linked by phenylboronic acid-diol (APBA-GL) complexation in buffered solutions with various pH (A – pH = 6, B – pH = 7, C – pH = 8) at temperature T = 37 °C. Solid lines: results of simulation. | ||
Finally, we approximate observations on PEG gel cross-linked with Fe3+ ions. The gel was prepared by means of the following procedure (Menyo et al.57). First, tetra-arm PEG-OH chains (molar mass 10 kg mol−1) were transformed into PEG-COOH chains by reaction of terminal hydroxyl groups with ethyl bromoacetate followed by hydrolysis of the ester groups. These chains were functionalized with 3-hydroxy-4-pyridinone (HOPO) through an amide coupling reaction. The macromers were dissolved in deionized water (mass fraction 0.1), to which an aqueous solution of FeCl3 was added to achieve a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio between HOPO functional groups and metal ions, and an appropriate buffer solution was immersed to control pH in the gels.
1 molar ratio between HOPO functional groups and metal ions, and an appropriate buffer solution was immersed to control pH in the gels.
Experimental data in shear oscillatory tests in solutions with various pH (ranging from 4.5 to 9.0)57 are depicted in Fig. 16 together with results of simulation. Each set of data is fitted separately. The effect of pH on adjustable parameters μ, Σ, γ and K is demonstrated in Fig. S-19,† where the data are approximated by eqn (32) and (33).
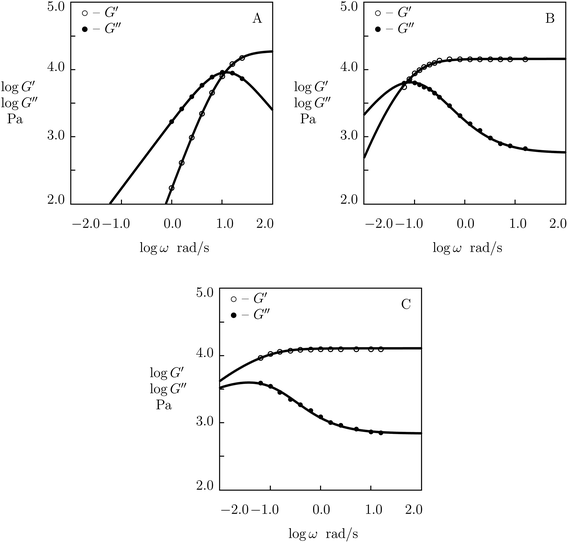 | ||
| Fig. 16 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data57 on HOPO-functionalized PEG gel cross-linked with Fe3+ ions in buffer solutions with various pH (A – pH = 4.5, B – pH = 7.4, C – pH = 9.0) at room temperature. Solid lines: results of simulation. | ||
The following conclusions are drawn from Fig. S-16 to S-19:†
(I) For most supramolecular gels under consideration, the elastic modulus μ grows linearly with pH. HOPO-functionalized PEG gels cross-linked with Fe3+ ions provide an exception from this rule as their modulus decreases weakly with pH.
(II) Inhomogeneity of the polymer network (characterized by the coefficient Σ) increases with pH in all gels. For supramolecular gels cross-linked by phenylboronic acid-diol complexation, this growth is rather modest, but it becomes more pronounced for the gels cross-linked by metal–ligand coordination bonds.
(III) The rate of dissociation of supramolecular bonds γ decreases with pH, while the parameter K (reflecting the effect of disentanglenent and re-entanglement of chains on rearrangement of supramolecular bonds) increases with pH. Unlike the corresponding graphs depicted in Fig. S-10, S-12 and S-14† (where the slopes of the curves γ(T) and K(T) coincide practically), the effects of pH on the coefficients γ and K differ noticeably.
The difference between the dependence μ(pH) for HOPO-functionalized PEG gels cross-linked by Fe3+ ions and the corresponding dependencies for the other gels under consideration is conventionally explained by pH-induced changes in the molar fractions of metal–ligand complexes with various structures (mono-, bis-, and tris-).58 In supramolecular gels prepared in aqueous solutions with pH slightly exceeding 7, the appearance of tris-complexes as temporary bonds between chains should result in a strong increase in their elastic moduli as these complexes are more strong and stable than their bis-counterparts.
On the other hand, the presence of two types of physical cross-links (formed by bis- and tris-complexes) simultaneously should lead to a pronounced growth of the network inhomogeneity observed as a non-monotonic dependence of Σ on concentration of cross-linkers (see Fig. S-9†).
To examine this conclusion, observations are fitted in shear oscillatory tests on PEG gels cross-linked by metal–ligand coordination bonds between Fe3+ ions and catechol-modified PEG chains. The gels were prepared by means of the two-stage procedure (Barrett et al.59). At the first stage, 8-arm amine-terminated PEG chains (molar mass 20 kg mol−1) were functionalized with catechol. At the other stage, catechol-modified PEG chains were dissolved in buffer solutions with given pH (mass fraction of macromers 0.3), to which appropriate amounts of FeCl3 were added (to reach molar ratio of Fe3+ ions and catechol-functionalized groups 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3).
3).
Experimental data (Barrett et al.59) in rheological tests at room temperature on PEG gels prepared in buffer solutions with pH = 5, 7 and 9 are depicted in Fig. 17 together with results of numerical analysis. Each set of data is matched separately. The effect of pH on the adjustable parameters μ, Σ, γ and K is demonstrated in Fig. S-20.† The data for γ and K are fitted by eqn (33), whereas those for μ and Σ are approximated by the equations
μ = μ0 − μ1 (pH − pH0)2, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Σ = Σ0 + Σ1 (pH − pH0)2 Σ = Σ0 + Σ1 (pH − pH0)2
| (34) |
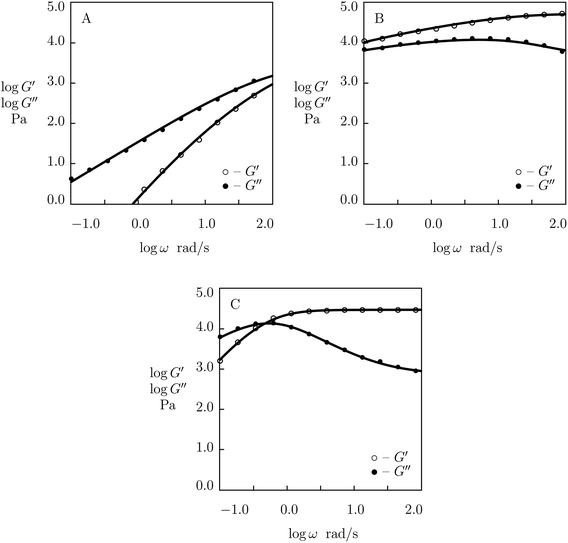 | ||
| Fig. 17 Storage modulus G′ and loss modulus G′′ versus frequency ω. Symbols: experimental data59 on catechol-functionalized PEG gel cross-linked by Fe3+ ions in buffer solutions with various pH (A – pH = 5, B – pH = 7, C – pH = 9) at room temperature. Solid lines: results of simulation. | ||
The decay in γ (and an appropriate increase in K) in Fig. S-20B† is explained by pH-induced “replacement” of Fe-catechol bis-complexes with more stable tris-complexes. A noticeable increase in μ below pH0 is attributed to formation of strong tris-complexes, whereas the reduction of μ above the critical pH is driven by transformation of bis-complexes into mono-complexes that do not form cross-links between chains. The non-monotonic effect of pH on the parameter Σ (similar to that observed in Fig. S-9†) reflects an increase in the non-homogeneity of the polymer network (due to the presence of two types of physical bonds with different rates of rearrangement) below pH0 and its decrease driven by disappearance of bis-complexes (transformed into mono- and tris-complexes) above pH0.
3.5 Validation of the model
As the model involves an extra material parameter K (whose presence affects the values of other parameters found by fitting experimental data in shear oscillatory tests), its validity requires confirmation.For this purpose, we determine material constants by matching observations in shear oscillatory tests on PEG gels cross-linked by metal–ligand coordination bonds between Fe3+ ions and catechol-modified 8-arm PEG chains,59 calculate the relaxation modulus Gr as a function of relaxation time t by means of eqn (19) with parameters reported in Fig. S-20,† and compare results of numerical analysis with experimental data in shear relaxation tests (Barrett et al.59). Fig. 18 demonstrates good agreement between the observations on gels prepared in buffer solutions with pH = 7 and 9 and predictions of the model, which confirms the ability of the model to describe the linear viscoelastic response of supramolecular gels.
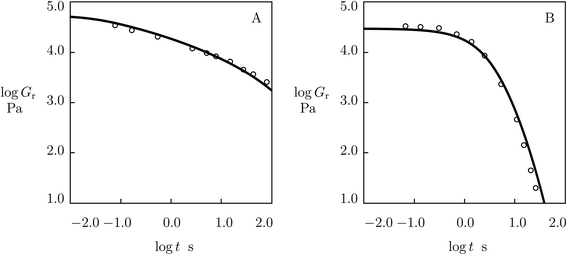 | ||
| Fig. 18 Relaxation modulus Gr versus relaxation time t. Circles: experimental data59 in relaxation tests on catechol-functionalized PEG gel cross-linked by Fe3+ ions in buffer solutions with pH = 7 (A) and pH = 9 (B) at room temperature. Solid lines: predictions of the model. | ||
4 Conclusions
A simple model is developed for the linear viscoelastic behavior of supramolecular gels. An advantage of the model is that it describes adequately the experimental dependencies G′(ω) and G′′(ω) in shear oscillatory tests on gels with various types of physical bonds, on the one hand, and involves only four material parameters with transparent physical meaning, on the other. The latter allows structure–property relations to be formulated that characterize the effects of chemical composition, temperature, pH and ionic strength of buffer solutions on the viscoelastic response of supramolecular gels.Three parameters in the model are conventional: the elastic modulus of the polymer network μ, the rate of dissociation of temporary cross-links γ (an analog of the characteristic time for rearrangement of physical bonds τ0), and the measure of inhomogeneity of the network Σ. The coefficient K (reflecting the influence of disentanglement and re-entanglement of chains on the rate of dissociation of supramolecular bonds) appears to be new. It is introduced in eqn (22) to account for flattening of the experimental curves G′′(ω) at high frequencies ω.
The model is applied to fit observations in shear oscillatory tests on (i) protein gels cross-linked by coiled-coil complexes, (ii) poly(acrylamide-acrylic acid) P(AAm-AAc) gels cross-linked with covalent and ionic bonds, (iii) poly(2-methacryloyloxyethyl phosphorylcholine) (P(MPC)) gels copolymerized with benzoxaborole-containing monomers (MAABO) and catechol-containing monomers (DMA) and cross-linked by benzoxaborole-catechol complexes, (iv) poly(ethylene glycol) PEG gels prepared by functionalization of tetra-arm PEG chains with various phenylboronic acid (PBA, APBA, FPBA) and diol (GL) moieties and cross-linked by phenylboronic acid-diol complexation, and (v) PEG gels synthesized by modification of multi-arm PEG chains with histidine, 3-hydroxy-4-pyridinonone (HOPO), and catechol and cross-linked by metal–ligand coordination bonds with Ni2+, Co2+ and Fe3+ ions. Fig. 1–17 show good agreement between experimental data in shear oscillatory tests and results of simulation. The ability of the model to predict the viscoelastic response of supramolecular gels is demonstrated in Fig. 18, where results of numerical analysis are depicted together with observations in shear relaxation tests.
Analysis of the structure–property relations for supramolecular gels leads to the following conclusions:
(I) The growth of concentration of polymer chains in a buffer solution induces a pronounced increase in the elastic modulus μ (described by the power law (24)) and accompanying by a reduction in the rate of dissociation of physical bonds γ (Fig. S-1, S-4 to S-6†).
(II) The presence of two types of “competing” bonds (characterizes by molar fraction r of some bonds in the mixture) in a supramolecular gel causes a non-monotonic dependence of the measure of inhomogeneity of the polymer network Σ on r (Fig. S-9 and S-20†) that may be accompanied by an appropriate non-monotonic dependency of the elastic modulus μ(r) (Fig. S-20†).
(III) An increase in temperature T results a decrease in the elastic modulus μ and coefficient Σ (described by eqn (29)) and causes a strong growth of the rate of dissociation of supramolecular bonds γ and pronounced decay in the coefficient K predicted by the Arrhenius laws (30) and (31) (Fig. S-10, S-12 and S-14†).
(IV) When changes in pH of buffer solutions do not induce changes in the structure of supramolecular bonds between chains, the growth of pH is equivalent (in some sense) to a reduction in temperature T, and evolution of material parameters with pH is described by eqn (32) and (33) (Fig. S-16–S-19†). The same conclusion can be drawn regarding the influence of ionic strength θ of buffer solutions (Fig. S-3†).
(V) When the structure of supramolecular bonds changes with pH (due to formation of mono-, bis- and tris-metal–ligand coordination complexes), the dependencies of μ and Σ on pH become non-monotonic (Fig. S-20†). This non-monotonicity is driven by “competition” between various types of supramolecular bonds, and it is described by eqn (34).
Author contributions
ADD: conceptualization, methodology, software, formal analysis, writing – original draft, writing – review and editing. JdC: conceptualization, methodology, funding acquisition, writing – review and editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support by Innovationsfonden (Innovation Fund Denmark, project 9091-00010B) is gratefully acknowledged.References
- X. Yan, F. Wang, B. Zheng and F. Huang, Chem. Soc. Rev., 2012, 41, 6042–6065 RSC.
- R. Dong, Y. Pang, Y. Su and X. Zhu, Biomater. Sci., 2015, 3, 937–954 RSC.
- J. Y. C. Lim, Q. Lin, K. Xue and X. J. Loh, Mater. Today Adv., 2019, 3, 100021 CrossRef.
- W. Wang, Y. Zhang and W. Liu, Prog. Polym. Sci., 2017, 71, 1–25 CrossRef.
- J.-Y. Sun, X. Zhao, W. R. K. Illeperuma, O. Chaudhuri, K. H. Oh, D. J. Mooney, J. J. Vlassak and Z. Suo, Nature, 2012, 489, 133–136 CrossRef CAS PubMed.
- T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. A. Haque, T. Nakajima and J. P. Gong, Nat. Mater., 2013, 12, 932–937 CrossRef CAS PubMed.
- Q. Chen, X. Yan, L. Zhu, H. Chen, B. Jiang, D. Wei, L. Huang, J. Yang, B. Liu and J. Zheng, Chem. Mater., 2016, 28, 5710–5720 CrossRef CAS.
- A. D. Drozdov, J. deClaville Christiansen, N. Dusunceli and C.-G. Sanporean, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 438–453 CrossRef CAS.
- D. L. Taylor and M. in het Panhuis, Adv. Mater., 2016, 28, 9060–9093 CrossRef CAS PubMed.
- S. Wang and M. W. Urban, Nat. Rev. Mater., 2020, 5, 562–583 CrossRef CAS.
- Z.-C. Jiang, Y.-Y. Xiao, Y. Kang, M. Pan, B.-J. Li and S. Zhang, ACS Appl. Mater. Interfaces, 2017, 9, 20276–20293 CrossRef CAS PubMed.
- W. Lu, X. Le, J. Zhang, Y. Huang and T. Chen, Chem. Soc. Rev., 2017, 46, 1284–1294 RSC.
- J. Hoque, N. Sangaj and S. Varghese, Macromol. Biosci., 2019, 19, 1800259 CrossRef PubMed.
- M. G. Raucci, U. D'Amora, A. Ronca and L. Ambrosio, Adv. Healthcare Mater., 2020, 9, 2000349 CrossRef CAS PubMed.
- C. Heinzmann, C. Weder and L. M. de Espinosa, Chem. Soc. Rev., 2016, 45, 342–358 RSC.
- A. H. Hofman, I. A. van Hees, J. Yang and M. Kamperman, Adv. Mater., 2018, 30, 1704640 CrossRef PubMed.
- J. Yang, R. Bai, B. Chen and Z. Suo, Adv. Funct. Mater., 2020, 30, 1901693 CrossRef CAS.
- D. Mozhdehi, J. A. Neal, S. C. Grindy, Y. Cordeau, S. Ayala, N. Holten-Andersen and Z. Guan, Macromolecules, 2016, 49, 6310–6321 CrossRef CAS.
- A. Dawn and H. Kumari, Chem.–Eur. J., 2018, 24, 762–776 CrossRef CAS PubMed.
- M. Golkaram and K. Loos, Macromolecules, 2019, 52, 9427–9444 CrossRef CAS PubMed.
- Z. Song, Z. Han, S. Lv, C. Chen, L. Chen, L. Yin and J. Cheng, Chem. Soc. Rev., 2017, 46, 6570–6599 RSC.
- J. L. Mann, A. C. Yu, G. Agmon and E. A. Appel, Biomater. Sci., 2018, 6, 10–37 RSC.
- M. Vazquez-Gonzalez and I. Willner, Angew. Chem., Int. Ed., 2020, 59, 15342–15377 CrossRef CAS PubMed.
- V. Montano, S. J. Picken, S. van der Zwaag and S. J. Garcia, Phys. Chem. Chem. Phys., 2019, 21, 10171–10184 RSC.
- S. C. Grindy, R. Learsch, D. Mozhdehi, J. Cheng, D. G. Barrett, Z. Guan, P. B. Messersmith and N. Holten-Andersen, Nat. Mater., 2015, 14, 1210–1216 CrossRef CAS PubMed.
- C. S. Y. Tan, G. Agmon, J. Liu, D. Hoogland, E.-R. Janecek, E. A. Appel and O. A. Scherman, Polym. Chem., 2017, 8, 5336–5343 RSC.
- W. Sun, T. Duan, Y. Cao and H. Li, Biomacromolecules, 2019, 20, 4199–4207 CrossRef CAS PubMed.
- M. Ahmadi and S. Seiffert, Macromolecules, 2021, 54, 1388–1400 CrossRef CAS.
- M. Ahmadi and S. Seiffert, Soft Matter, 2020, 16, 2332–2341 RSC.
- S. Tang, M. Wang and B. D. Olsen, J. Am. Chem. Soc., 2015, 137, 3946–3957 CrossRef CAS PubMed.
- S. Tang, H. Ma, H.-C. Tu, H.-R. Wang, P.-C. Lin and K. S. Anseth, Adv. Sci., 2018, 5, 1800638 CrossRef PubMed.
- S. Y. Zheng, C. Liu, L. Jiang, J. Lin, J. Qian, K. Mayumi, Z. L. Wu, K. Ito and Q. Zheng, Macromolecules, 2019, 52, 6748–6755 CrossRef CAS.
- A. D. Drozdov, Acta Mech., 1997, 124, 155–180 CrossRef.
- N. Holten-Andersen, A. Jaishankar, M. J. Harrington, D. E. Fullenkamp, G. DiMarco, L. He, G. H. McKinley, P. B. Messersmith and K. Y. C. Lee, J. Mater. Chem. B, 2014, 2, 2467–2472 RSC.
- X. Zhang, Y. Vidavsky, S. Aharonovich, S. J. Yang, M. R. Buche, C. E. Diesendruck and M. N. Silberstein, Soft Matter, 2020, 16, 8591–8601 RSC.
- S. C. Boothroyd, D. M. Hoyle, T. C. B. McLeish, E. Munch, R. Schach, A. J. Smith and R. L. Thompson, Soft Matter, 2019, 15, 5296–5307 RSC.
- A. D. Drozdov and J. deClaville Christiansen, Macromolecules, 2018, 51, 1462–1473 CrossRef CAS.
- A. Jangizehi, S. Reza Ghaffarian, W. Schmolke and S. Seiffert, Macromolecules, 2018, 51, 2859–2871 CrossRef CAS.
- B. J. Gold, C. H. Hovelmann, N. Luhmann, W. Pyckhout-Hintzen, A. Wischnewski and D. Richter, J. Rheol., 2017, 61, 1211–1226 CrossRef CAS.
- Y. Han, J. Li, Z. Zhang, Y. Liu, Y. Li and Q. Chen, Rheol. Acta, 2019, 58, 513–523 CrossRef CAS.
- A. D. Drozdov and A. L. Kalamkarov, Polym. Eng. Sci., 1996, 36, 1907–1919 CrossRef CAS.
- A. D. Drozdov, Int. J. Solids Struct., 1998, 35, 2315–2347 CrossRef.
- H. G. Sim, K. H. Ahn and S. J. Lee, J. Non-Newtonian Fluid Mech., 2003, 112, 237–250 CrossRef CAS.
- A. Tripathi, K. C. Tam and G. H. McKinley, Macromolecules, 2006, 39, 1981–1999 CrossRef CAS.
- W. Yu, W. Sun, Q. Fan, B. Xue, Y. Li, M. Qin, Y. Li, B. Chen, W. Wang and Y. Cao, Soft Matter, 2019, 15, 4423–4427 RSC.
- M. S. Green and A. V. Tobolsky, J. Chem. Phys., 1946, 14, 80–92 CrossRef CAS.
- F. Tanaka and S. F. Edwards, Macromolecules, 1992, 25, 1516–1523 CrossRef CAS.
- B. Derrida, Phys. Rev. Lett., 1980, 45, 79–92 CrossRef.
- J. Guo, P. Long, K. Mayumi and C.-Y. Hui, Macromolecules, 2016, 49, 3497–3507 CrossRef CAS.
- G. A. Parada and X. Zhao, Soft Matter, 2018, 14, 5186–5196 RSC.
- D. E. Fullenkamp, L. He, D. G. Barrett, W. R. Burghardt and P. B. Messersmith, Macromolecules, 2013, 46, 1167–1174 CrossRef CAS PubMed.
- Y. Chen, D. Diaz-Dussan, D. Wu, W. Wang, Y.-Y. Peng, A. B. Asha, D. G. Hall, K. Ishihara and R. Narain, ACS Macro Lett., 2018, 7, 904–908 CrossRef CAS.
- X. Zou, X. Kui, R. Zhang, Y. Zhang, X. Wang, Q. Wu, T. Chen and P. Sun, Macromolecules, 2017, 50, 9340–9352 CrossRef CAS.
- V. Yesilyurt, A. M. Ayoob, E. A. Appel, J. T. Borenstein, R. Langer and D. G. Anderson, Adv. Mater., 2017, 29, 1605947 CrossRef PubMed.
- B. Marco-Dufort, R. Iten and M. W. Tibbitt, J. Am. Chem. Soc., 2020, 142, 15371–15385 CrossRef CAS PubMed.
- V. Yesilyurt, M. J. Webber, E. A. Appel, C. Godwin, R. Langer and D. G. Anderson, Adv. Mater., 2016, 28, 86–91 CrossRef CAS PubMed.
- M. S. Menyo, C. J. Hawker and J. H. Waite, Soft Matter, 2013, 9, 10314–10323 RSC.
- N. Holten-Andersen, M. J. Harrington, H. Birkedal, B. P. Lee, P. B. Messersmith, K. Y. C. Lee and J. H. Waite, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2651–2655 CrossRef CAS PubMed.
- D. G. Barrett, D. E. Fullenkamp, L. He, N. Holten-Andersen, K. Y. C. Lee and P. B. Messersmith, Adv. Funct. Mater., 2013, 23, 1111–1119 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra02749b |
| This journal is © The Royal Society of Chemistry 2021 |