Adsorption of toxic gases on borophene: surface deformation links to chemisorptions

Abstract

β₁₂ borophene has received great attention because of its intriguing mechanical and electronic properties. One of the possible applications of borophene is gas sensing. However, the interaction between common gases and β₁₂ borophene remains to be clarified. In this work, we study the interactions of β₁₂ borophene towards five hazardous gases, namely, CO, NO, NH₃, NO₂, and CO₂ using various non-empirical van der Waals density functionals and provide an insight into the adsorption behavior of borophene. The adsorption mechanism and molecular vibrations are discussed in great detail. Among the gases considered, CO₂ is physisorbed while other gases are chemically bonded to β₁₂ borophene. We also demonstrate that the deformation at the ridge of borophene enables its active p_z orbital to strongly hybridize with frontier orbitals of the studied polar gases. Consequently, borophene is predicted to interact strongly with CO, NO, NH₃, and especially NO₂, making it a sensitive sensing material for toxic gases.

---

1. Introduction

The emission of hazardous industrial gases (CO_x, NO_x, NH₃, SO₂, etc.) driven by economic growth not only threatens human wellbeing but also damages the environment. These gases may contribute to the worsening of cardiovascular and respiratory diseases, the greenhouse effect, and ozone depletion.^1–3 The severe impacts of these gases have raised the need for efficient toxic-gas sensing technology to monitor and remove the harmful culprits.

In the trend of constant attempts at sensor minimization, the two-dimensional polymorph of boron β₁₂ (also known as ν_1/6) is a promising candidate for an efficient sensing material.⁴ β₁₂ borophene is the line-defective phase of borophene^5–7 and can be stably synthesized by various bottom-up^6–9 and top-down¹⁰ methods. This material was found to have intriguing electronic properties such as spin gapless Dirac cone, rich band structure, and extraordinary mechanical and optical behavior,^11–15 which account for its potential in many practical applications. However, there has been a limited number of theoretical work on β₁₂ borophene for sensing applications, compared to the theoretically proposed buckled borophene, which received more attention^15–19 despite the lack of its empirical realization. Thus, to accurately explain or predict the sensing performance of borophene, it is essential to understand the adsorption behaviors of β₁₂ borophene.

The study of gas adsorptions on β₁₂ borophene is still in its infancy.^10,20,21 Tan et al. theoretically studied the CO₂ adsorption on β₁₂ borophene under an electric field and found that CO₂ moderately adsorbed on this material.²⁰ Huang and co-workers analyzed how four inorganic gases (NH₃, NO, NO₂, and CO) interact with both buckled and β₁₂ borophene by employing density functional theory (DFT) calculations with semiempirical dispersion correction.²¹ They found that β₁₂ borophene chemically interacts with these gases and is significantly distorted upon adsorption. Experimentally, the realization of borophene as a gas sensor has been ignited. Ranjan and co-workers demonstrated that borophene-based sensor exhibited high sensitivity to NH₃.¹⁰ Nevertheless, in these works, the gas adsorption mechanism of borophene remains unclear and the dependence of the predicted adsorption performance on exchange–correlation functionals is not considered.

In this work, we investigate the adsorption of five main hazardous industrial gases, namely CO, NO, NH₃, NO₂, and CO₂, on β₁₂ borophene by using van der Waals (vdW) density functionals (vdW-DFs).^22–24 These functionals allow us to consider the contributions of non-local vdW interaction to the different toxic gas–β₁₂ borophene systems in a non-empirical fashion, which is lacking in the literature to date. Furthermore, we discuss the bonding nature of these molecules with β₁₂ borophene via electronic structure and vibrational analyses.

2. Computational details

All of the periodic DFT^25,26 calculations were performed using the projector augmented wave method^27,28 as implemented in the Vienna Ab initio Simulation Package (VASP).²⁹ The vdW-DFs are shown to accurately describe molecular adsorption, but for the current system, there are no benchmark calculations obtained from using highly accurate methods (see for example ref. 30 and 31). We used four vdW-DFs, namely revPBE-vdW (referred to as vdW-DF1 hereafter),³² vdW-DF2,³³ optPBE-vdW,³⁴ and rev-vdW-DF2,³⁵ to provide the range of adsorption geometries and energies. In addition, an attempt to apply a recently developed vdW-DF3 functional³⁶ for comparison was made. The generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof functional (PBE)³⁷ was also used for comparison. The convergence threshold for the self-consistent field calculations was set to 10⁻⁵ eV per cell, and the geometrical structures were fully optimized until the Hellmann–Feynman forces acting on atoms were less than 0.01 eV Å⁻¹. To eliminate spurious interactions with image borophene sheets, a vacuum of 20 Å thickness was inserted between the neighboring borophene sheets. The wave functions were expanded using a plane-wave basis set with the kinetic energy cutoff of 500 eV. An 11 × 11 k-point mesh of the first Brillouin zone was used in optimizing the geometrical structure of the β₁₂ borophene conventional unit cell. For the adsorption systems, a (4 × 3) borophene supercell was employed and a 3 × 3 k-point mesh was used. The spin polarization was properly taken into account for the systems with molecules having unpaired electrons (i.e., NO and NO₂).

To seek the most stable geometries of the adsorption systems (gas–borophene), structural optimization was carefully carried out by climbing up the ladder of accuracy. The borophene layer was restricted along the z-direction and the structural optimization was performed first by using the universal force field,³⁸ which was further optimized by DFT. Then, the stable gas–borophene configuration was explored by calculating the interaction energy as a function of spatial coordinate using the computational DFT-based Nanoscope tool^39,40 (see ESI S1†), and subsequently, full geometry optimization was performed. Finally, the adsorption energy, amount of charge transfer, and the change of work function were computed for the most favorable configurations.

We define the adsorption energy as

E_ad = E_gas+boro − (E_gas + E_boro) (1)

where E_gas+boro, E_gas, and E_boro are the total energies of the adsorption system, isolated gas molecule, and isolated borophene, respectively. We calculated the amount of charge transfer from borophene to molecules by using the Bader charge analysis code.⁴¹ The work function is defined as ϕ = E_vac − E_F and was calculated with dipole correction,^42,43 where E_vac and E_F are the vacuum level and the Fermi energy, respectively.

To understand the hybridization between the gas molecule and borophene orbitals, we performed the crystal orbital overlap population (COOP)^44–46 and the projected density of states (PDOS) analyses as implemented in the STATE (Simulation Tool for Atom Technology) code.^47,48 The change in molecular internal bonds of the adsorbed state is understood by using COOP analysis among atomic orbitals (AOs) implemented in the LOBSTER package.⁴⁹ The vibrational modes of molecules were obtained using finite-difference harmonic approximation by diagonalizing the mass-weighted Hessian matrix.

3. Results and discussion

3.1. Geometric and electronic structures of pristine borophene

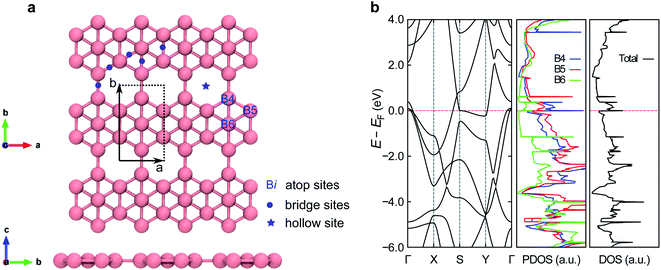
To investigate the impacts of non-empirical vdW functionals on the adsorption systems, we first employed five different functionals to calculate the lattice constants of pristine borophene (Table 1). These optimized lattice constants converge to the order of pm and agree well with published experimental^6–8 and other theoretical works.^50–52 Our results suggest that any of the four investigated vdW-DFs can properly describe the pristine borophene.

Table 1 Optimized lattice constants of β₁₂ borophene by employing different functionals, along with the experimental values

	a (Å)	b (Å)
a Ref. 6.b Ref. 7. Lattice parameters are indicated in Fig. 1.
PBE	2.921	5.083
vdW-DF1	2.928	5.106
optPBE-vdW	2.931	5.075
vdW-DF2	2.915	5.078
rev-vdW-DF2	2.917	5.078
Experiment	2.9 ± 0.2^a, 3.0^b	5.1 ± 0.2^a, 5.0^b

---

As a sensing material, β₁₂-borophene possesses various high symmetry adsorption sites. This property arises from the presence of hollow hexagons (Fig. 1a) which leads to site-discrimination in the electronic state (Fig. 1b). As in the middle panel of Fig. 1b, the B4 site has more unoccupied p_z states compared with the other atop sites. Furthermore, with less spatial and coordinated constraint, B4 is the most likely adsorption site for a compact adsorbate, which agrees with our findings in the optimized gas–borophene configurations as discussed below.

Fig. 1 Geometric and electronic structures of β₁₂ borophene. (a) The (4 × 3) supercell used in the calculation and its high symmetry adsorption sites. (b) Electronic band structure (left), site-projected density of states (middle) and total density of states of β₁₂ borophene (right). In (a) the primitive cell is marked by the dotted line. Bi denotes the i-coordinated boron atom site.

3.2. Adsorption geometries

We investigated the adsorption state of different molecules on β₁₂-borophene. For the four out of five gases (CO, NO, NH₃, and NO₂) studied, the most favorable adsorption site is B4 (Fig. 2a–d). These four cases are well categorized as chemisorption since their adsorption distances are in the range of chemical interaction (Table 2). Additionally, in these cases, the deformation of β₁₂-borophene is substantial. This flat-to-wrinkled deformation of borophene is consistent with its highly anisotropic mechanical properties⁵³ and its undulation observed when it is supported on a silver substrate.^14,54 The underlying mechanism of this deformation is discussed in detail later in the electronic structure analysis.

Fig. 2 Equilibrium geometries of (a) CO, (b) NO, (c) NH₃, (d) NO₂, and (e) CO₂ on β₁₂ borophene.

Table 2 Adsorption energies (E_ad), adsorption distances (d), charge transfers based on the Bader charge analysis (Δq), and work function changes (Δϕ) of the systems of a single gas molecule on β₁₂ borophene obtained using the non-empirical vdW-DFs, along with E_ad obtained using the empirical vdW dispersion correction PBE-D2. The work function (ϕ) of pristine β₁₂ borophene is also shown. The positive (negative) sign of Δq indicates that the gas molecule accepts (donates) electrons. The positive (negative) sign of Δϕ indicates that the work function increases (decreases) upon the adsorptions

Molecules	Adsorption properties	vdW-DF2	vdW-DF1	optPBE-vdW	rev-vdW-DF2	PBE-D2
CO2	Ead (eV)	−0.19	−0.21	−0.27	−0.32	−0.18 (ref. 20)
	d (Å)	3.36	3.41	3.30	3.30
	Δq (e)	+0.05	+0.05	+0.03	+0.05
	Δϕ (eV)	+0.03	+0.05	+0.05	+0.05
CO	Ead (eV)	−0.49	−0.64	−0.86	−1.18	−1.19 (ref. 21)
	d (Å)	1.49	1.49	1.49	1.49
	Δq (e)	+0.37	+0.38	+0.40	+0.35
	Δϕ (eV)	−0.03	−0.01	−0.02	−0.04
NH3	Ead (eV)	−0.41	−0.52	−0.83	−1.15	−1.11 (ref. 21)
	d (Å)	1.68	1.66	1.64	1.63
	Δq (e)	−0.09	−0.11	−0.15	−0.10
	Δϕ (eV)	−0.03	−0.01	−0.03	0.01
NO	Ead (eV)	−0.38	−0.39	−0.72	−1.05	−0.95 (ref. 21)
	d (Å)	1.38	1.38	1.38	1.38
	Δq (e)	+0.52	+0.70	+0.63	+0.65
	Δϕ (eV)	+0.03	0.00	−0.02	−0.02
NO2	Ead (eV)	−1.28	−1.56	−1.67	−1.91	−1.80 (ref. 21)
	d (Å)	1.59	1.59	1.58	1.57
	Δq (e)	+0.82	+0.83	+0.80	+0.83
	Δϕ (eV)	+0.30	+0.28	+0.26	+0.23
Borophene	ϕ (eV)	5.01	4.95	5.02	5.09

---

In contrast to the other molecules, CO₂ is physisorbed at the hollow site with its molecular axis parallel to borophene surface, as shown in Fig. 2e. This configuration offers optimal interaction between the frontier orbitals of CO₂ (i.e., 2π and 3π*) and the p_z orbital of borophene (see Fig. S3 of ESI†).

3.3. Impacts of vdW functionals on adsorption properties

The adsorption properties obtained using the four non-empirical vdW-DFs are summarized in Table 2, along with those obtained using the semiempirical PBE-D2 dispersion correction. We found that the adsorption energies strongly depend on the vdW-DF used, especially for chemisorption cases (i.e., CO, NO, NH₃ and NO₂). The magnitude of the energies is sorted in a certain order as vdW-DF2 < vdW-DF1 < optPBE-vdW < rev-vdW-DF2. This consistent prediction trend is in line with the performance of vdW-DFs in literature.^55,56 Therein, the vdW-DF1 and vdW-DF2 systematically predict comparatively smaller adsorption energies due to their overestimation of Pauli repulsion.²⁴ Among four functionals, the rev-vdW-DF2 predicts the largest adsorption energies. Interestingly, these values resemble those predicted by the semiempirical PBE-D2 in ref. 21. We further confirm the prediction by using a recent generation of non-local vdW functionals vdW-DF3 (ref. 36) implemented in Quantum ESPRESSO code^57–59 (see ESI Table S2†). Notably, comparable predictions of adsorption characteristics obtained by rev-vdW-DF2 and vdW-DF3-opt1 are recorded in the chemisorption cases, whereas the similar values of adsorption energy to those obtained by vdW-DF1 and vdW-DF2 are given by both versions of vdW-DF3 for the physisorption case of CO₂.

The calculated adsorption energies indicate that borophene interacts more strongly with CO, NH₃, NO, and NO₂ compared with other 2D materials such as MoS₂,⁶⁰ germanene,⁶¹ WS₂,⁶² phosphorene,⁶³ or graphene⁶⁴ (see Table S3 in ESI for detailed comparison†). Therefore, we expect borophene to be a good toxic-gas sensing material.

In the realization of borophene as a chemiresistive gas sensor, the amount of charge transferred between the adsorbate and borophene is an indicator to predict the sensitivity and selectivity of the sensor. As shown in Table 2, the Bader charge analysis indicates that borophene is impressively sensitive to NO₂, NO, and CO due to the remarkably large amount of charge transferred. The results show that NH₃ is an electron donor while other gases are electron acceptors. The accepted or donated charge is expected to cause the change in resistivity of the substrate material. Thus, NH₃ might be recognized among these gases due to the opposite trend of resistivity change.

Upon adsorption, the amount of either lost or gained charge is expected to influence the work function of borophene. While most gases induce an insignificant change in the work function, NO₂ causes a remarkable increase (+0.23 to +0.30 eV depending on the functional). This increase is not surprising since it is consistent with the Bader charge analysis, where borophene donates a great amount of charge to NO₂ so that the valence electron has to overcome a greater total potential barrier to escape to the vacuum level. Given the fact that the calculated work function of pristine borophene is quite high (∼5.0 eV), which is consistent with the experiment value of ∼4.9 eV,⁶⁵ the significant enhancement of work function induced by the NO₂ adsorption is interesting.

3.4. Analyses of the adsorption systems

Despite the great effects of vdW functionals on the adsorption energies, the electronic structure and properties are barely affected by the functionals if the geometric structures remain similar.^66,67 Since the geometry of each gas–borophene system are analogous among the functionals, we used the optimized geometries obtained using optPBE-vdW for further analyses. In the following subsections, we discuss the vibrational properties and the adsorption mechanisms based on the electronic structures.

3.4.1. Vibrational analysis. We computed the vibrational frequencies of the molecules in both the gas phase and the adsorption state and summarized them in Table 3 and ESI S5.† The DFT-calculated frequencies of molecules in the gas phase are also compared with the experimental values.^68–70 The DFT calculations reliably reproduce the vibrational frequencies of all the molecules with a small deviation (less than 8%). More importantly, we found that the molecular vibrations are sensitive to the adsorbate–substrate interactions. Upon adsorption, the vibrational frequencies tend to become lower (softened) for most of the molecules.

Table 3 Calculated vibrational-frequencies ν (cm⁻¹) and the shifts (cm⁻¹) induced by the adsorptions on β₁₂ borophene, along with the vibrational frequencies for the gas-phase molecule^a

	CO	NO	NH3				NO2			CO2
	νS	νS	νSS	νDS	νDD	νSD	νAS	νSS	νB	νAS	νSS	νIPB	νOPB
a S: stretching, SS: symmetrical stretching, DS: degenerate stretching, DD: degenerate deformation, SD: symmetrical deformation, AS: asymmetrical stretching, B: bending, IPB: in-plane bending, OPB: out-of-plane bending.
Gas phase (Exp.)^68–70	2149	1875	3337	3444	1627	950	1618	1318	750	2349	1333	667	667
Gas phase (DFT) calculation	2115	1894	3379	3494	1639	1022	1624	1316	722	2335	1306	625	625
Adsorption state (DFT)	2030	1717	3282	3372, 3378	1611, 1608	1338	1558	1002	696	2325	1304	617	608
Frequency shifts (DFT)	−85	−177	−97	−122, −116	−28, −31	+316	−66	−314	−26	−10	−2	−8	−17

---

It is noteworthy to elaborate the origin of the frequency shifts of NH₃ because of its interesting vibrational behavior (for other molecules, see ESI S6†). Upon the strong interaction with borophene, the normal modes of NH₃ are red-shifted, except for the symmetric deformation mode. Counterintuitively, the decreases in the frequencies for the N–H stretching modes are significant although N–H bonds point toward vacuum in the adsorption configuration (Fig. 2c). These shifts can be understood as follows: the lowest unoccupied molecular orbital (LUMO) 3a₁ of NH₃ has an antibonding character with respect to the N–H bond and is spatially distributed over the hydrogen atoms (inset in Fig. 3). Upon adsorption, this orbital hybridizes with the borophene states and become partially occupied as indicated by COOP between atomic orbitals of N and H atoms in Fig. 3. This occupation results in elongating N–H bonds (ESI Table S1†) and softening the stretching modes.

Fig. 3 Crystal orbital overlap population between atomic orbitals of N and H atoms for NH₃ chemisorbed on β₁₂ borophene.

A similar red-shift was observed in the C–H stretching modes of n-alkane molecules adsorbed on metal surfaces⁴⁸ and cyclohexane molecule on Rh(111)⁷¹ and was attributed to the interaction between LUMO and metal substrate states.⁴⁸ There, the softening is considerable when C–H bonds point to the surface, opposite to our case with NH₃ where none of the N–H bonds point to the surface. However, this softening can be understood rather straightforwardly by considering the orbital interactions.

3.4.2. Electronic structure analysis. Projected density of states (PDOS) and COOP analyses are two essential tools frequently used in analyzing the interaction between the adsorbates and the surface. In this section, we present in detail the adsorption behaviors of CO, NH₃, and NO₂ on borophene as representative cases. These three cases represent the typical chemical adsorption of simple gases on borophene. For each gas, we present the analyses of PDOS, COOP, and the charge density difference to get an insight into the orbital-interaction origin in these systems. The detailed interpretations of NO and CO₂ adsorptions are also given in ESI S7.†
CO. Fig. 4a shows PDOS onto the molecular orbitals (MOs) of CO (details of MOs of isolated CO and other molecules are provided in ESI Fig. S3†), while Fig. 4b shows COOP between MOs of CO and borophene states, in which positive peaks indicate bonding states, while negative ones, antibonding.⁴⁴ The interaction between CO and borophene substrate can be understood by Blyholder's 5σ donation and 2π* backdonation model.⁷² By comparing COOP and PDOS of CO (Fig. 4a and b) to PDOS of B atom (Fig. 4c) between E_F −9.5 eV and E_F −7 eV, we can see positive peaks on both 5σ (1π) orbital of CO and 2s & 2p_z (2p_x,y) orbitals of B in the corresponding energy range. The positive peaks demonstrate bonding states established by the hybridizations of 5σ and 2s & 2p_z and of 1π and 2p_x,y due to the similar symmetries. The bonding states are far below E_F and are closer to core states. From E_F −6 eV to E_F, an important bonding contribution results from the interaction between the filled CO 2π* and B 2p_x & 2p_y orbitals, which can be understood by COOP in this energy range. As for the antibonding states, we found that 5σ is present as a delocalized negative peak as seen at wide energy range from E_F −8 eV to E_F. Above E_F, the unoccupied 2π* is dominant, an unoccupied part of 5σ is also significant.

Fig. 4 Electronic structure of CO adsorbed on β₁₂ borophene. (a) Molecular-orbital projected density of states of CO on borophene. (b) Crystal orbital overlap population between CO and borophene. (c) Atomic-orbital projected density of states of the nearest neighbor B atom to CO. (d) Charge density difference induced by the adsorption of CO on β₁₂ borophene.

In Fig. 4d, we plot the charge density difference defined by Δρ = ρ_gas+boro − ρ_gas − ρ_boro, where ρ_gas+boro, ρ_gas, and ρ_boro are the charge densities of the adsorption system, isolated molecule, and isolated borophene, respectively. There is the charge accumulation due to the backdonation to 2π* orbital of CO, as well as the depletion due to the donation from 5σ orbital. More importantly, charge accumulates between CO and B underneath, implying the chemical bond formation between the C and B atoms.

NH₃. Fig. 5 shows COOP and PDOS for the doubly degenerate 1e orbitals (HOMO−1 and HOMO−2), lone pair 2a₁ orbital (highest occupied molecular orbital (HOMO)), orbital (LUMO), and 2e orbital (LUMO+1) of NH₃. We found that both bonding and antibonding components of 2a₁ orbital are occupied, indicating a repulsive interaction of this orbital with the substrate state. On the other hand, there is a noticeable contribution to the bonding from the 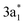orbital, as indicated by the positive peaks in COOP and PDOS at E_F −5 eV. By comparing PDOS onto AOs of the B atom underneath the N atom of NH₃, we concluded that the bonding between NH₃ and borophene is mainly attributed to the hybridization of the NH₃ lone pair 2a₁ orbital with B 2p_z and 2s orbitals. Therein, the 2a₁ orbital donates electrons to the empty p_z states of B, leading to the increase in electrons in the substrate. The instant increase in electron as charge carriers in borophene might explain the significant increase in electric current of borophene sensor upon NH₃ exposure as observed in the experiment in ref. 10.

Fig. 5 Electronic structure of NH₃ adsorbed on β₁₂ borophene. (a) Molecular-orbital projected density of states of NH₃ on borophene. (b) Crystal orbital overlap population between NH₃ and borophene. (c) Atomic-orbital projected density of states of the nearest neighbor B atom to NH₃. (d) Charge density difference induced by the adsorption of NH₃ on β₁₂ borophene.

The charge density difference plot (Fig. 5d) shows that in addition to the charge depletion around the molecule due to the Pauli repulsion of the occupied MOs, the charge accumulation between B and N as well as those in N–H bonds were found, indicating the chemical bond formation between NH₃ and borophene.

NO₂. The gas-phase NO₂ molecule has an unpaired electron (i.e., spin-polarized) (Fig. S3†). Upon adsorption, NO₂ turns to be spin-unpolarized. It results from great hybridizations among MOs of NO₂ and between them and borophene as shown in PDOS and COOP analyses (Fig. 6). The 5a₁ orbital of NO₂ strongly hybridizes with B 2s states, distributes over a wide energy range. Both the bonding and antibonding states are occupied, indicating that interaction between NO₂ 5a₁ and B 2s is repulsive. Likewise, the 1a₂ orbital (HOMO−1) is lifted and interacts repulsively with the B 2p_y states. The split 6a₁ orbitals, which form singly occupied and unoccupied MOs in the gas phase, are fully occupied upon adsorption. This orbital forms bonding states with B 2p_z and the antibonding counterpart is partially occupied, contributing to the repulsive interaction. On the other hand, the attraction between the molecule and the surface arises from the filled 5b₁ of NO₂ (LUMO), which is indicated by the partially occupied positive COOP ranging from ∼E_F −5.0 eV to E_F.

Fig. 6 Electronic structure of NO₂ adsorbed onβ₁₂ borophene. (a) Molecular-orbital projected density of states of NO₂ on borophene. (b) Crystal orbital overlap population between NO₂ and borophene. (c) Atomic-orbital projected density of states of nearest neighbor B atom of NO₂. (d) Charge density difference induced by the adsorption of NO₂ on β₁₂ borophene.

The PDOS and COOP analyses are consistent with the charge density difference plotted in Fig. 6d. It is found that NO₂ gain electrons from borophene through the 6a₁ orbital, as indicated by the charge accumulation. The electron filling of the antibonding-type orbital weakens the N–O bond, leading to the considerable elongation of this bond (from 1.21 to 1.36 Å), narrowing of the O–N–O angle (from 133° to 120°), and red-shifts of the vibrational frequencies of NO₂.

3.5. Role of the borophene deformation

Finally, we discuss the deformation of the substrate borophene. To clarify the electronic origin of the protrusion of the B4 atom in borophene, we calculated the projected density of states onto atomic orbitals of this atom in both wrinkled and flat borophene structures. Fig. 7a shows that B4 p_z electron in the wrinkled borophene is likely to be more localized around E_F. In the flat borophene, on the other hand, B orbitals form π band, and therefore its density of states is broadly distributed (Fig. 7b). By wrinkling from the surface, B atomic orbitals tend to form sp³ hybridization rather than the sp² ones in the flat borophene. Having an sp³-like hybridized state, p_z orbital is relatively localized and therefore, it forms a peak at around the Fermi level, leading to a strong bonding with adsorbates.

Fig. 7 Projected density of states on atomic orbitals of B4 in cases of (a) wrinkled and (b) flat β₁₂ borophene.

We have clarified the important role of the deformation. In particular, we compared the adsorption performance of borophene on the two systems so-called: (i) z-restricted system and (ii) unrestricted system. In (i), we constrained the movement of boron atoms along z axis (i.e., flat borophene). In (ii), there is no constraint in any degree of freedom (i.e., fully relaxed borophene). The adsorption energies of the two systems are compared in Fig. 8. In the z-restricted systems, most of the adsorptions are physisorptions, which are in contrast to the strong chemisorptions in the unrestricted ones. Thus, the deformation is responsible for the great interactions between borophene and the molecules, especially in the cases of CO and NH₃ adsorption.

Fig. 8 Adsorption energies of the molecules on the (i) z-restricted and (ii) unrestricted borophene.

4. Conclusions

We presented a systematic study on the interactions of β₁₂ borophene with five hazardous gas molecules, namely CO, NO, NH₃, NO₂, and CO₂ using four different vdW-DFs (vdW-DF1, optPBE-vdW, vdW-DF2, and rev-vdW-DF2). We found that the magnitude of the adsorption energies increases in the sequence vdW-DF2 < vdW-DF1 < optPBE-vdW < rev-vdW-DF2, regardless of the nature of the gas-phase molecules while the adsorption geometries are essentially the same. We also clarified the important role played by the deformation of β₁₂ borophene, especially in the cases of CO and NH₃ adsorption. The deformation can strengthen the interaction of molecules and the surface. The results of adsorption energies and charge transfers imply that borophene is most sensitive to NO₂ gas and most inert to CO₂. Analyzing the electronic structure, we have gained an insight into the adsorption mechanisms of the gas molecules on borophene. Furthermore, our vibrational analyses show the vibrational modes of chemisorbed molecules are significantly softened. Our study consolidates the theoretical²¹ and experimental¹⁰ works on sensing application of β₁₂ borophene and is useful to interpret the results obtained by further experiments in this field.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant Number 103.01-2018.315, and also partly by Grant-in-Aid for Scientific Research (B) (Grant No. JP20H02569 and JP18H01829) and for Transformative Research Areas “Hyperordered Science” (Grant No. JP20H05883) from the Japan Society for the Promotion of Science. The authors also acknowledge the project on the establishment of Master Program of Nanotechnology, Vietnam Japan University, under the contract between Japan Cooperation International Agency (JICA) and Osaka University. L. T. T. acknowledges the Ministry of Education, Culture, Sport, Science and Technology, Japan (MEXT) and the Innovative Asia Program from JICA for financial supports.

References

1. H. Ritchie, M. Roser, CO₂ and Greenhouse Gas Emissions, Our World in Data, 2020, (August), pp. 1–52, Available from: https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions [Online Resource].
2. B. Zhao, S. X. Wang, H. Liu, J. Y. Xu, K. Fu, Z. Klimont, J. M. Hao, K. B. He, J. Cofala and M. Amann, Atmos. Chem. Phys., 2013, 13, 9869–9897.
3. H. Wang, W. P. Lustig and J. Li, Chem. Soc. Rev., 2018, 47, 4729–4756.
4. Z. Xie, X. Meng, X. Li, W. Liang, W. Huang, K. Chen, J. Chen, C. Xing, M. Qiu, B. Zhang, G. Nie, N. Xie, X. Yan and H. Zhang, Research, 2020, 2020, 1–23.
5. Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 1–6.
6. A. J. Mannix, X.-F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516.
7. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568.
8. G. P. Campbell, A. J. Mannix, J. D. Emery, T.-L. Lee, N. P. Guisinger, M. C. Hersam and M. J. Bedzyk, Nano Lett., 2018, 18, 2816–2821.
9. Q. Li, V. S. C. Kolluru, M. S. Rahn, E. Schwenker, S. Li, R. G. Hennig, P. Darancet, M. K. Y. Chan and M. C. Hersam, Science, 2021, 371, 1143–1148.
10. P. Ranjan, T. K. Sahu, R. Bhushan, S. S. Yamijala, D. J. Late, P. Kumar and A. Vinu, Adv. Mater., 2019, 31, 1900353.
11. B. Feng, O. Sugino, R.-Y. Liu, J. Zhang, R. Yukawa, M. Kawamura, T. Iimori, H. Kim, Y. Hasegawa, H. Li, L. Chen, K. Wu, H. Kumigashira, F. Komori, T.-C. Chiang, S. Meng and I. Matsuda, Phys. Rev. Lett., 2017, 118, 096401.
12. N. Gao, X. Wu, X. Jiang, Y. Bai and J. Zhao, FlatChem, 2018, 7, 48–54.
13. Y. Huang, S. N. Shirodkar and B. I. Yakobson, J. Am. Chem. Soc., 2017, 139, 17181–17185.
14. A. Brotchie, Nat. Rev. Mater., 2016, 1, 16083.
15. H. Cui, X. Zhang and D. Chen, Appl. Phys. A, 2018, 124, 636.
16. V. Shukla, J. Wärnå, N. K. Jena, A. Grigoriev and R. Ahuja, J. Phys. Chem. C, 2017, 121, 26869–26876.
17. Y. Valadbeigi, H. Farrokhpour and M. Tabrizchi, J. Chem. Sci., 2015, 127, 2029–2038.
18. T. Liu, Y. Chen, M. Zhang, L. Yuan, C. Zhang, J. Wang and J. Fan, AIP Adv., 2017, 7, 125007.
19. V. Nagarajan and R. Chandiramouli, J. Inorg. Organomet. Polym. Mater., 2018, 28, 920–931.
20. X. Tan, H. A. Tahini and S. C. Smith, ACS Appl. Mater. Interfaces, 2017, 9, 19825–19830.
21. C. S. Huang, A. Murat, V. Babar, E. Montes and U. Schwingenschlögl, J. Phys. Chem. C, 2018, 122, 14665–14670.
22. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
23. D. C. Langreth, B. I. Lundqvist, S. D. Chakarova-Käck, V. R. Cooper, M. Dion, P. Hyldgaard, A. Kelkkanen, J. Kleis, L. Kong, S. Li, P. G. Moses, E. Murray, A. Puzder, H. Rydberg, E. Schröder and T. Thonhauser, J. Phys.: Condens. Matter, 2009, 21, 084203.
24. K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 6.
25. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
26. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
27. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
29. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
30. J. G. Brandenburg, A. Zen, D. Alfè and A. Michaelides, J. Chem. Phys., 2019, 151, 164702.
31. J. A. Garrido Torres, B. Ramberger, H. A. Früchtl, R. Schaub and G. Kresse, Phys. Rev. Mater., 2017, 1, 060803.
32. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
33. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
34. J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201.
35. I. Hamada, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103.
36. D. Chakraborty, K. Berland and T. Thonhauser, J. Chem. Theory Comput., 2020, 16, 5893–5911.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
39. V. O. Vo, T. L. Pham and V. A. Dinh, Mater. Trans., 2020, 61, 1449–1454.
40. T. L. Pham, T. L. Ta, V. O. Vo and V. A. Dinh, VNU J. Sci. Math. - Phys., 2020, 36, 95–102.
41. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
42. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
43. L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304.
44. R. Hoffmann, Rev. Mod. Phys., 1988, 60, 601–628.
45. H. Aizawa and S. Tsuneyuki, Surf. Sci., 1998, 399, L364–L370.
46. Y. Hamamoto, S. A. Wella, K. Inagaki, F. Abild-Pedersen, T. Bligaard, I. Hamada and Y. Morikawa, Phys. Rev. B, 2020, 102, 75408.
47. T. N. Pham, Y. Hamamoto, K. Inagaki, D. N. Son, I. Hamada and Y. Morikawa, J. Phys. Chem. C, 2020, 124, 2968–2977.
48. Y. Morikawa, H. Ishii and K. Seki, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 041403.
49. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
50. B. Peng, H. Zhang, H. Shao, Z. Ning, Y. Xu, G. Ni, H. Lu, D. W. Zhang and H. Zhu, Mater. Res. Lett., 2017, 5, 399–407.
51. B. Mortazavi, O. Rahaman, A. Dianat and T. Rabczuk, Phys. Chem. Chem. Phys., 2016, 18, 27405–27413.
52. H. Xiao, W. Cao, T. Ouyang, S. Guo, C. He and J. Zhong, Sci. Rep., 2017, 7, 45986.
53. Z. Zhang, Y. Yang, E. S. Penev and B. I. Yakobson, Adv. Funct. Mater., 2017, 27, 9.
54. Z. Zhang, A. J. Mannix, Z. Hu, B. Kiraly, N. P. Guisinger, M. C. Hersam and B. I. Yakobson, Nano Lett., 2016, 16, 6622–6627.
55. L. Spanu, S. Sorella and G. Galli, Phys. Rev. Lett., 2009, 103, 196401.
56. S. Lebègue, J. Harl, T. Gould, J. G. Ángyán, G. Kresse and J. F. Dobson, Phys. Rev. Lett., 2010, 105, 196401.
57. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
58. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. De Gironcoli, P. Delugas, R. A. Distasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-De-La-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
59. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. De Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105.
60. S. Zhao, J. Xue and W. Kang, Chem. Phys. Lett., 2014, 595–596, 35–42.
61. W. Xia, W. Hu, Z. Li and J. Yang, Phys. Chem. Chem. Phys., 2014, 16, 22495–22498.
62. V. Q. Bui, T.-T. Pham, D. A. Le, C. M. Thi and H. M. Le, J. Phys.: Condens. Matter, 2015, 27, 305005.
63. Y. Cai, Q. Ke, G. Zhang and Y.-W. Zhang, J. Phys. Chem. C, 2015, 119, 3102–3110.
64. K. Takeuchi, S. Yamamoto, Y. Hamamoto, Y. Shiozawa, K. Tashima, H. Fukidome, T. Koitaya, K. Mukai, S. Yoshimoto, M. Suemitsu, Y. Morikawa, J. Yoshinobu and I. Matsuda, J. Phys. Chem. C, 2017, 121, 2807–2814.
65. X. Liu, L. Wang, B. I. Yakobson and M. C. Hersam, Nano Lett., 2021, 21, 1169–1174.
66. I. Hamada and S. Yanagisawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 153104.
67. S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921–28930.
68. G. E. Leroi, G. E. Ewing and G. C. Pimentel, J. Chem. Phys., 1964, 40, 2298–2303.
69. E. P. J. Linstrom and W. G. Mallard, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, Coblentz Society, Inc., 2017, p. 20899.
70. T. Shimanouchi, J. Phys. Chem. Ref. Data, 1977, 6, 993–1102.
71. K. Fidanyan, I. Hamada and M. Rossi, Adv. Theory Simul., 2021, 2000241.
72. G. Blyholder, J. Phys. Chem., 1964, 68, 2772–2777.

---

Footnote

† Electronic supplementary information (ESI) available: The details of electronic structure, geometrical profiles, and vibrational modes of molecules in the gas phase; the 2D potential energy surfaces of gases on z-restricted borophene; vdW-DF3 calculations; and analyses of chemical interactions of NO and CO₂ with borophene. See DOI: 10.1039/d1ra02738g

---