Mechanistic insights into dioxygen activation by a manganese corrole complex: a broken-symmetry DFT study

Abstract

The Mn–oxygen species have been implicated as key intermediates in various Mn-mediated oxidation reactions. However, artificial oxidants were often used for the synthesis of the Mn–oxygen intermediates. Remarkably, the Mn(V)–oxo and Mn(IV)–peroxo species have been observed in the activation of O₂ by Mn(III) corroles in the presence of base (OH⁻) and hydrogen donors. In this work, density functional theory methods were used to get insight into the mechanism of dioxygen activation and formation of Mn(V)–oxo. The results demonstrated that the dioxygen cannot bind to Mn without the axial OH⁻ ligand. Upon the addition of the axial OH⁻ ligand, the dioxygen can bind to Mn in an end-on fashion to give the Mn(IV)–superoxo species. The hydrogen atom transfer from the hydrogen donor (substrate) to the Mn(IV)–superoxo species is the rate-limiting step, having a high reaction barrier and a large endothermicity. Subsequently, the O–C bond formation is concerted with an electron transfer from the substrate radical to the Mn and a proton transfer from the hydroperoxo moiety to the nearby N atom of the corrole ring, generating an alkylperoxo Mn(III) complex. The alkylperoxo O–O bond cleavage affords a Mn(V)–oxo complex and a hydroxylated substrate. This novel mechanism for the Mn(V)–oxo formation via an alkylperoxo Mn(III) intermediate gives insight into the O–O bond activation by manganese complexes.

---

1. Introduction

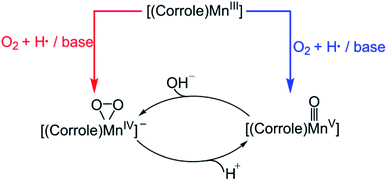
Molecular oxygen (O₂), the most sustainable oxidant, is crucial for important chemical reactions in living cells. However, the direct reaction between triplet O₂ and singlet substrate is spin-forbidden and therefore kinetically unfavoured. In nature, many metalloenzymes utilize their transition metal centres (e.g. iron, copper and manganese) to activate dioxygen for various oxidative transformations.^1,2 Numerous studies have been undertaken to understand the underlying mechanism of metal-mediated dioxygen activation and substrate oxidation. The metal–oxygen species, such as metal–superoxo, –peroxo, –hydroperoxo, and –oxo species, are proposed to be key intermediates that can act as reactive species.^3–6 Notably, iron–oxygen species have been trapped and characterized spectroscopically in some dioxygen-activating heme and nonheme enzymes.^7–10 Although, various metal–oxygen intermediates have been successfully synthesized in biomimetic studies,¹¹ these synthetic metal–oxygen complexes were usually generated using artificial oxidants, such as iodosylbenzene (PhIO), NaOCl, peracids, and H₂O₂.^12–14 As such, significant efforts have been made to use O₂ as the source of oxidant in biomimetic oxidation reaction over the last few decades.^15–18

Recently, Mn–oxygen intermediates have attracted extensive research interest since they are invoked as the key reactive intermediates in O₂ activation,^19–21 C–H bond oxidation,^4,5,22,23 oxygen atom transfer,²⁴ and water oxidation by the oxygen-evolving complex in photosystem II.^25–28 Specially, the reactivity of the high-valent Mn–oxo complexes has been extensively studied. In contrast to porphyrin-based systems, the corrole macrocycle can effectively stabilize the transition metal ions in higher oxidation states. PhIO has been offen used as an oxidant for the synthesis of the Mn(V)–oxo corroles.^29–32 Goldberg and co-workers reported the first example of a direct transformation of a Mn(III)–corrolazine to a high-valent Mn(V)–oxo complex with O₂ under the visible-light irradiation.³³ Later, Nam et al. have shown that the Mn(III) corroles are capable of activing dioxygen in the present of base and H atom donor, thereby forming Mn(V)–oxo and Mn(IV)–peroxo species, that can be used directly in the O–O bond cleavage and formation reactions.³⁴ As already demonstrated before, the Mn(V)–oxo corrole can be formed upon addition of proton to Mn(IV)–peroxo, while addition of base to the Mn(V)–oxo corrole results in the formation of Mn(IV)–peroxo (Scheme 1).³²

Scheme 1 Formation of Mn(IV)–peroxo and Mn(V)–oxo corrole complexes.

A possible mechanism for the formation of Mn(V)–oxo and Mn(IV)–peroxo species in the dioxygen activation reaction by (TPFC)Mn(III) (TPFC = 5, 10, 15-tris-(pentafluorophenyl) corrolato trianion) was proposed.³⁴ As shown in Scheme 2, the addition of base to Mn(III)–superoxo generates [(TPFC)Mn(III)(OH)]⁻, which can bind dioxygen to form a putative Mn(IV)–superoxo species. The Mn(IV)–superoxo species was then proposed as the active species to abstract a hydrogen atom from H atom donor to form the Mn(IV)–hydropeoroxo species. The subsequent O–O bond cleavage affords the Mn(V)–oxo species. Addition of base to Mn(V)–oxo species results in the formation of Mn(IV)–peroxo via O–O bond formation. The H-abstraction by the Mn(IV)–superoxo was found to be the rate-determining step for the formation of Mn(V)–oxo species. It is well-known that the high-valent Mn(V)–oxo can acts as the reactive intermediate in substrate oxidation. The reactivity of Mn(V)–oxo has been widely studied, especially for H-abstraction reaction. However, the reactivity of Mn(IV)–superoxo and the formation of Mn(V)–oxo in the dioxygen-activing reaction are so far unclear.

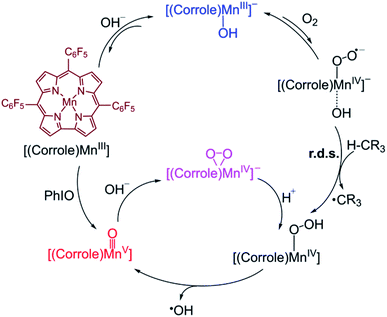Scheme 2 Proposed mechanisms for formation of Mn(V)–Oxo and Mn(IV)–peroxo species in dioxygen activation by a Mn(III) corrole complex.³⁴

Herein, we present a detailed density functional theory (DFT) on the mechanism of dioxygen activation by Mn(III)–corrole. Our results indicated that the formation of Mn(V)–oxo in the dioxygen activation reaction involves the initially hydrogen abstraction from the hydrogen donor (substrate), the O–C formation to give an alkylperoxo Mn(IV) complex which undergoes O–O cleavage to generate the MnO and hydroxylated substrate. These findings provide important insights into the dioxygen O–O activation by manganese complexes.

2. Methods

All calculations were performed using density functional theory (DFT). It should be pointed out that in the transition metal systems prediction of the correct spin-state ordering is a still challenging subject.³⁵ The reliability of the DFT methods in describing the relative energies could be sensitive to the amount of exact Hartree–Fock (HF) exchange included.^36–39 The hybrid B3LYP functional (20% HF exchange)^40–42 has been widely used to investigate the reactivity of Mn^V–oxo complexes.^39,43–45 However, a recent study of the electron structure of Mn^V–oxo suggested that a range of HF exchange from ∼10–14% was necessary for broken-symmetry DFT to produce acceptable agreement with the multi-configurational self-consistent field (MCSCF) calculations.⁴⁶ The hybrid meta-GGA functional TPSSh⁴⁷ with 10% HF exchange has been shown to correctly predict the ground state of transitional metal complexes.^48,49 In this work, geometry optimization was carried out using the TPSSh since it gives the best match for bond lengths in our primary calculations for the Mn^IV–peroxo complex. To examine the impact of the DFT functional, test calculations were also performed using both the B3LYP, BP86,⁵⁰ and PBE0,^51,52 which are typical examples for pure and hybrid functionals. Geometry optimizations were done with def2-SVP⁵³ basis set (basis set B1). Since the experimental work used acetonitrile as a solvent, the solvent effects were considered in all cases of the calculations using conductor-like polarizable continuum model (CPCM)⁵⁴ with a dielectric constant of ε = 35.688 as implemented in Gaussian16 (ref. 55) mimicking the acetonitrile solvent. Frequency calculations were carried out at the same level of theory to verify the optimized structures as either minima (no imaginary frequency) or transition states (only one imaginary frequency) and to obtain the thermodynamic data (zero-point energy, enthalpy, and entropy) at T = 298.15 K and 1 atm in acetonitrile solution. The electronic energies were obtained by single-point calculations on the optimized geometry using a larger all-electron basis set (basis set B2), which is def2-TZVP⁵³ for all atoms. Dispersion correction was computed with Grimme's D3 method.^56–58 Scalar relativistic effects were incorporated by applying the second-order Douglas–Kroll–Hess (DKH2) approach^59,60 and full-electron DKH-def2-TZVP⁶¹ basis set as implemented in the ORCA software.⁶²

The oxidation potential of the Mn(III) complex 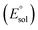was calculated from the free energy change associated with the redox couple in the solvent using the Nernst equation 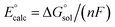(F is Faraday constant, n is the number of electrons transferred) and the value shifted relative to the standard calomel electrode (SCE) in order to compare with experimental values. The absolute potential of normal hydrogen electrode (NHE) is −4.48 V ⁶³ and the formal potential of SCE is at 0.24 V versus NHE, then the redox potential of Mn^IV/III can be calculated directly from DFT results calibrated with SCE with a value of −4.72 V, i.e., .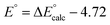

3. Results and discussion

Benchmark studies of DFT methods

In transition metal complexes, the choice of the density functional is important for an accurate description of spin-state orderings and relative energies. Although the experimental data on dioxygen bound intermediate is lack, the Mn–O and Mn–N bond lengths for the Mn(IV)–peroxo complex [(TPFC)Mn^IV(O₂)]⁻ were assessed based on curve-fitting analysis of the extended X-ray absorption fine structure (EXAFS) data.³⁴ Therefore, we started our work with the DFT calculations on [(TPFC)Mn^IV(O₂)]⁻, which has a quartet (S = 3/2) ground state. As shown in Table 1, The Mn–N bond is well modelled with all the functionals used here. PBE0 overestimates the Mn–O bond length (with an error of 0.16 Å), thus was not considered to be used for the geometry optimization in the further study. The average Mn–O and Mn–N bond lengths predicted by TPSSh are in excellent agreement with the EXAFS fitting results.³⁴

Table 1 Optimized average Mn–O and Mn–N bond Lengths (Å) of the triplet [(TPFC)Mn^IV(O₂)]⁻ using different DFT functionals

Bond length	BP86	TPSSh	B3LYP	PBE0	Expt. (ref. 34)
d(Mn–O)	1.87	1.85	1.89	1.98	1.83
d(Mn–N)	1.98	1.97	1.98	1.96	1.96

---

It has been demonstrated that the dioxygen activation by Mn(III) corroles occurs only in the presence of base.³⁴ The electrochemical experiments showed that the oxidation potential of [(TPFC)Mn^III] is shifted negatively by 0.56 V in the present of OH⁻. Then, the role of OH⁻ is thought to lower the oxidation potential of Mn(III) corrole, which is then oxidized easily to form Mn(IV)–superoxo. To validate the used DFT methods, we calculated the oxidation potential of [(TPFC)Mn^III] with and without the OH⁻ ligand using different DFT functionals. The results showed that the binding of the axial OH⁻ ligand shifts the oxidation potential of [(TPFC)Mn^III] toward a more negative potential, in consistent with the experiment (Table 2). The DFT functionals has only minor effects on the structural parameters of the Mn–corrole complexes. The calculated oxidation potentials at PBE0(B2)//TPSSh(B1) and PBE0(B2)//PBE0(B1) are very close, both are in reasonable agreement with the experimental values. To examine the solvent effect, we also calculated the oxidation potential of [(TPFC)Mn^III(OH)(CH₃CN)]⁻, in which a solvent molecule, acetonitrile forms a hydrogen binding interaction with the axial OH⁻ ligand (Fig. S2 in ESI†). Our calculations suggest such H-binding interaction has only minor effect on the oxidation potential (−0.35 V vs. −0.31 V).

Table 2 Comparison of calculated and experimental E°(V/SCE) for [(TPFC)Mn^IVL]/[(TPFC)Mn^IIIL] in acetonitrile

E°(Mn^IV/III)	TPSSh-D3(B2)//TPSSh(B1)	PBE0-D3(B2)//PBE0(B1)	PBE0-D3(B2)//TPSSh(B1)	Expt.
a The calculated oxidation potential of [(TPFC)Mn^III(OH)(CH3CN)]^−.
L = none	0.56	0.63	0.65	0.74
L = OH^−	−0.31 (−0.35)^a	−0.11	−0.06	0.18

---

Dioxygen binding

To further investigate the role of base in the dioxygen activation by [(TPFC)Mn^III], we study the reaction of [(TPFC)Mn^III] with O₂ in the absence and presence of base (OH⁻). [(TPFC)Mn^III] has a high-spin quintet (S = 2) ground state.⁶⁴ The coupling of triplet dioxygen with quintet Mn^III gives rise to three possible spin states, triplet, quintet, and septet. Whereas the Mn^V–oxo species has a singlet ground state. We therefore optimized the geometries of [(TPFC)Mn^III(O₂)] in the four spin states (S = 0, 1, 2, 3).

Table 3 summarizes the calculated Mn–O and O–O bond lengths of [(TPFC)Mn^III(O₂)], as well as the energies relative to the separated [(TPFC)Mn^III] and O₂. The spin-state energetics was found to be sensitive to the DFT functional, as has been demonstrated before in transition-metal complexes. All three functionals give similar geometries with a very long Mn–O distance (>3.6 Å) in the septet state, which contains a high-spin Mn(III) ferromagnetically with a triplet O₂ (Fig. 1). BP86-D3 predicts the triplet as the lowest one, while the unbound septet state is 8.8 kcal mol⁻¹ higher in energy. In the triplet ground state, the calculated Mn–O and O–O bond length is 1.88 Å and 1.26 Å, respectively. The spin densities on Mn and dioxygen is 3.09 and −1.13, suggesting a Mn^IV–superoxo character. As such, BP86-D3 results show that the dioxygen can bind to [(TPFC)Mn^III] through the single electron transfer from Mn to dioxygen.

Table 3 Key geometrical parameters (Å) for the various spin states of [(TPFC)Mn(O₂)] complex and energies (kcal mol⁻¹) relative to the separated [(TPFC)Mn] (S = 2) and O₂ (S = 1)

	d(Mn–O)			d(O–O)			ΔG (ΔH)
	BP86	TPSSh	B3LYP	BP86	TPSSh	B3LYP	BP86-D3	TPSSh-D3	B3LYP-D3
Septet	3.63	3.64	3.64	1.22	1.20	1.20	−0.5 (−7.2)	3.8 (−1.7)	5.7 (−1.8)
Quintet	2.01	2.16	2.12	1.27	1.24	1.21	−2.3 (−11.4)	12.6 (5.1)	16.9 (9.5)
Triplet	1.88	2.27	2.77	1.26	1.22	1.20	−9.3 (−20.0)	7.5 (−1.2)	7.2 (0.2)
Singlet	1.64	1.80	1.81	1.25	1.25	1.27	−1.9 (−13.4)	26.8 (16.9)	33.7 (22.6)

---

Fig. 1 Singly occupied orbitals of the septet [(TPFC)Mn^III(O₂)].

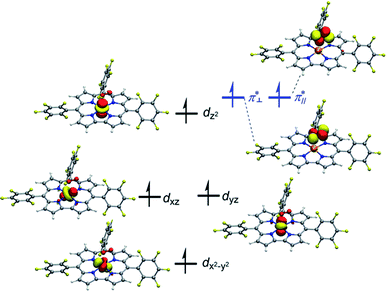
Both TPSSh and B3LYP predict the unbound septet to be the ground state. All attempt to locate the Mn^IV–superoxo species failed when TPSSh and B3LYP were used. Starting from the BP86-optimized structures (Mn^IV–superoxo), O₂ dissociated after TPSSh/B3LYP geometry optimization for both triplet and quintet states. At the TPSSh level of theory, the triplet state has a Mn–O distance of 2.27 Å with an energy of 3.7 kcal mol⁻¹ higher than the corresponding ferromagnetically coupled septet state. The B3LYP gives a longer Mn–O distance of 2.77 Å in the triplet state and a smaller energy-gap of 1.5 kcal mol⁻¹ relative to the septet. In both cases (B3LYP and TPSSh), the spin population suggested that the triplet spin state is a Mn^III–O₂⁰ species with a high-spin Mn(III) antiferromagnetically coupled to a triplet dioxygen (Table S3 in ESI†). The quintet state is a hexaradicaloid Mn^III (S = 2)–O₂⁰ (S = 0), having a configuration 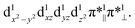The Fe–O₂ bonding involves a σ-bond pair between singly occupied d_z²(↑) orbital of Mn^III and singly occupied in-plane π*(↓) orbital of O₂ (Fig. S1 in the ESI†). The quintet state is 8.8/11.2 kcal mol⁻¹ higher than the unbound septet state at the TPSSh-D3/B3LYP-D3 level. The singlet state containing an intermediate-spin (S = 1) Mn^III antiferromagnetically coupled to a superoxo and a corrole radical, is much higher in energy (>23 kcal mol⁻¹).

Clearly, our calculations showed that the choice of the density functional can dramatically influence the electronic and spatial structures of the [(TPFC)Mn^III(O₂)] in different spin states. The pure BP86 functional tend to exaggerate the stability of Mn^IV–superoxo, showing that the dioxygen can bind to [(TPFC)Mn^III] even without the axial OH⁻ ligand. In contrast, the B3LYP and TPSSh results suggested that the dioxygen binding to [(TPFC)Mn^III] is energetically unfavourable.

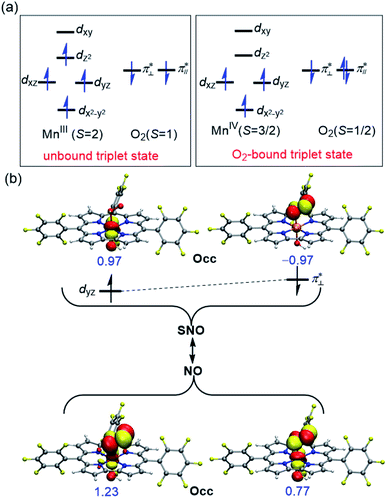
Table 4 summarizes the calculated Mn–O and O–O bond lengths of different spin state of [(TPFC)Mn^III(OH)(O₂)]⁻, as well as the energies relative to the separated [(TPFC)Mn^III(OH)]⁻ and O₂. Similar to the case of [(TPFC)Mn^III(O₂)], BP86-D3 predicts the triplet ground state, which has a Mn^IV–superoxo character. The singlet, quintet, and septet states are 12.6, 3.4, and 10.0 kcal mol⁻¹ higher than the triplet. The calculated binding free energy is −16.9 kcal mol⁻¹. TPSSh-D3 predicts the septet ground state. The quintet state contains ferromagnetically coupling of the S = 3/2 Mn(IV) and the superoxo radical anion, laying 1.1 kcal mol⁻¹ higher than the septet. Interestingly, two triplet states, the dioxygen-bound and unbound states, were located. Their electronic configurations were shown in Fig. 2a. The unbound triplet state has a long Mn–O distance of 3.47 Å, composed of a triplet ground state O₂ coupled antiferromagnetically with the high-spin S = 2 (TPFC)Mn(III) complex. The O₂-bound triplet having a short Mn–O distance of 2.03 Å, is 2.0 kcal mol⁻¹ lower in free energy than the unbound triplet state. As shown in Fig. 2a, the O₂-bound triplet has the orbital occupation 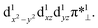Clearly, one electron is shifted from the d_z² orbital to the in-plane π* orbital of O₂ upon the dioxygen binding. The singlet coupling between π*_⊥ and the d_yz electron pair is strong enough to lead to a Mn–O bonding (see natural orbitals in Fig. 2b). This π-type Mn–O₂ bonding is similar to the Weiss structure of oxy-heme (the binding of O₂ by myoglobin).⁶⁵ The open-shell singlet state containing a S = 1 Mn(III) antiferromagnetically coupled with the S = 1 dioxygen, lies 8.9 kcal mol⁻¹ above the septet state. When B3LYP was used, attempts to obtain the triplet Mn^IV–superoxo failed, even starting from the BP86-optimized geometry and wave function. The calculated Mn–O distance is very long (>3.6 Å) in both triplet and septet states, which correspond to antiferromagnetic and ferromagnetic coupling of a Mn(III) and a triplet dioxygen. These two states are very close in energy, with septet only 0.2 kcal mol⁻¹ higher than the triple ground state. The quintet/singlet state has a shorter Mn–O distance of 2.08/2.06 Å, their energies are around 10 higher than the unbound triplet state. As such, B3LYP-D3 predict that the dioxygen binding is energetically unfavourable, even with the axial OH⁻ ligand.

Table 4 Key geometrical parameters (Å) for the various spin states of [(TPFC)Mn(OH)(O₂)]⁻ complex and the energies (in kcal mol⁻¹) relative to the separated [(TPFC)Mn(OH)]⁻ (S = 2) and O₂ (S = 1)

	d(Mn–O) (Å)			d(O–O) (Å)			ΔG (ΔH)
	BP86	TPSSh	B3LYP	BP86	TPSSh	B3LYP	BP86-D3	TPSSh-D3	B3LYP-D3
a The dioxygen-bound triplet state were located when TPSSh was used.
Septet	4.22	3.96	3.92	1.22	1.20	1.20	−6.9 (−12.7)	2.7 (−3.4)	0.8 (−5.6)
Quintet	2.10	2.06	2.08	1.29	1.29	1.28	−13.5 (−24.0)	3.9 (−7.4)	11.3 (−0.4)
Triplet	2.00	3.47	3.61	1.29	1.21	1.21	−16.9 (−28.2)	3.5 (−3.8)	0.6 (−5.6)
Triplet^a	—	2.03	—	—	1.28	—	—	1.5 (−10.1)	—
Singlet	1.88	2.87	2.06	1.27	1.21	1.25	−4.3 (−17.2)	12.0 (2.9)	13.6 (4.4)

---

Fig. 2 (a) Electronic structure of the two located triplet states of [(TPFC)Mn^III(OH)(O₂)]⁻ using TPSSh function. (b) Spin natural orbitals (SNO) and natural orbitals (NO) describing the symmetry broken phenomenon in the O₂-bound triplet state. Occupancy numbers (Occ) are marked in blue.

As demonstrated above, the spin state ordering and electronic structure of the studied Mn–O₂ complexes are very sensitive to the DFT functionals. In brief, the hybrid B3LYP-D3 functional predicts that dioxygen binding to [(TPFC)Mn^III] is unfavourable in both absence and presence of OH⁻, whereas the BP86-D3 seems overestimate the stability of the dioxygen adduct of Mn corrole complex. The TPSSh-D3 results demonstrated that the presence of axial OH⁻ ligand can help in the dioxygen binding, as suggested by the experiment. Without the axial OH⁻ ligand, dioxygen is unbound in the triplet and septet state of [(TPFC)Mn(O₂)], while the dioxygen-bound quintet (Mn^III–O₂⁰) has a binding free energy of 6.9 kcal mol⁻¹, suggested the dioxygen binding is unfavorable. As shown in Scheme 3, the binding of dioxygen to form Mn^IV–superoxo in the presence of the axial OH⁻ ligand is slightly uphill in free energy (ΔG = 1.5 kcal mol⁻¹), due to entropic contributions (ΔH = −10.1 kcal mol⁻¹, −TΔS = 12.6 kcal mol⁻¹). Note that the bound state is 2.0 kcal mol⁻¹ lower in energy than the unbound state. The small energy difference between these two states suggests the binding is in equilibrium. The small positive binding free energy calculated at the TPSSh level suggests the binding equilibrium is toward the dissociation of dioxygen, and the further reaction with H donor should both thermodynamically favoured and kinetically feasible to drive the reaction forward. These results support the experimental finding that [(TPFC)Mn(OH)]⁻ is the only detectable species in the reaction solution in the absence of H atom donor.³⁴ We also did single point calculations using the PBE0 functional on the TPSSh-optimized geometries, which give accurate oxidation potential of Mn(III) corrole complexes. However, PBE0 gives a larger energy gap between the O₂-bound and unbound triplet states, with the former being 9.9 kcal mol⁻¹ higher than the latter one, suggesting the dioxygen binding is energetically unfavourable. As such, the TPSSh-D3 description of the dioxygen binding process is consistent with experiment. Considering also that the TPSSh give more accurate bond lengths for Mn(IV)–peroxo species, we therefore use the TPSSh functional to study the further reactions.

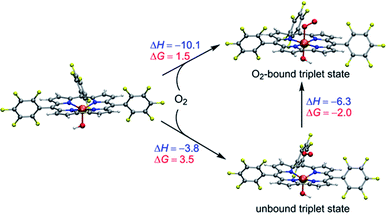Scheme 3 Energetics (kcal mol⁻¹) of dioxygen binding into [(TPFC)Mn^III(OH)] at the TPSSh-D3 level of theory.

Reactivity studies of Mn(IV)–superxo

The reactivity of high-valent metal–oxo complexes toward C–H bond activation have been extensively investigated due to the important roles in both biological and synthetic systems. In contrast, the C–H bond activation by the metal–superoxo complex is less understood. Although several iron and copper-containing enzymes were found to use metal–superoxo to cleave C–H bond in the past few years, the targeted C–H bonds in the enzymatic reactions are activated by adjacent heteroatom or a π-system.⁶⁶ For better understanding the reactivity of the Mn–superoxo, we performed DFT calculations using TPSSh functional to study the mechanism of tetrahydrofuran (THF) C–H bond activation and the formation of Mn(V)–oxo by a Mn(IV)–superoxo corrole complex, [(TPFC)Mn(OH)(O₂)]⁻.

As already mentioned above, the septet Mn–O₂ is an unbound state with all the unpaired electrons having parallel spins, hence is unreactive toward C–H bond activation. The unbound singlet state, lying 10.0 kcal mol⁻¹ higher in energy than the triplet state, was found to unable to active C–H bond due to a much high barrier (>30 kcal mol⁻¹, Fig. S3 in ESI†). The triplet and quintet states having a Mn(IV)–superoxo character are very close in energy. We therefore focus here on the reaction pathways on the triplet and quintet states. The free energy profiles are shown in Fig. 3. The optimized structures for key intermediates and transition states (TSs) are displayed in Fig. 4.

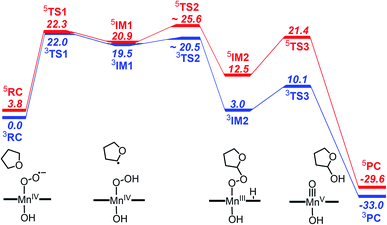Fig. 3 Gibbs free energy profile (kcal mol⁻¹) for reaction of C–H bond activation and the formation of [(TPFC) Mn^III(OH)(O₂)]⁻ with THF at the TPSSh-D3 level of theory.

Fig. 4 TPSSh/def2-SVP optimized structures of critical species along the reaction pathways on the triplet and quintet surface. Bond lengths and distances are given in angstroms. The imaginary frequency of the transition states is also given.

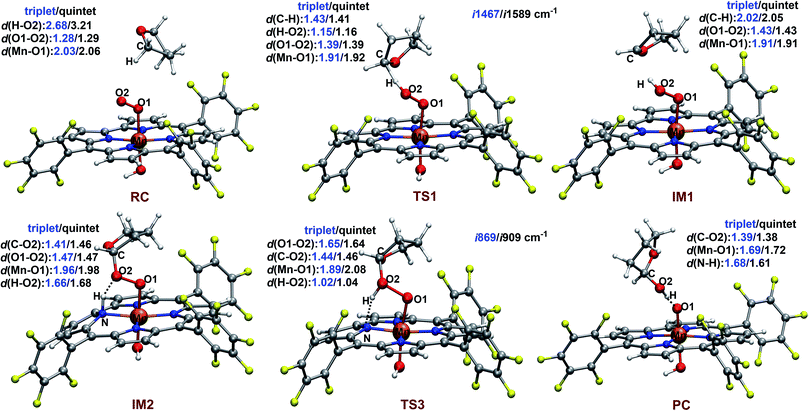
The reaction starts with the C–H bond activation via hydrogen atom abstraction by Mn(IV)–superoxo. For both triplet and quintet states, the C–H bond activation is attended by an electron shift from the corresponding σ_CH orbital to the singly occupied π*_⊥ of the superoxo moiety, generating a Mn(IV)–hydroperoxo with a radical at the 2-position of THF (IM1). As shown in Fig. 4, the transition states for this step (³TS1/⁵TS1) are late with long C–H (1.43/1.41 Å) and short O–H distances (1.15/1.16 Å). The unique imaginary frequency is i1467 cm⁻¹ for ³TS1 and i1589 cm⁻¹ for ⁵TS1, which is associated with hydrogen atom swaying motion between the C atom at 2-position of THF and the distal oxygen (O₂).

Energetically, ³TS1 and ⁵TS1 are very close, lying 22.0 and 22.3 kcal mol⁻¹ above the triplet reactant ³RC. This hydrogen atom transfer (HAT) process is highly endothermic. The energy of ³IM1/⁵IM1 is 19.5/20.9 kcal mol⁻¹ (relative to ³RC). For better understanding the H-abstraction by the Mn(IV)–superoxo complex, we analysed its thermodynamic driving force (ΔG_rp), which can be written as the difference between two bond dissociation free energies (BDFEs) of the broken C–H bond and the formed O–H bond, as defined in eqn (1)–(3).

Sub–H → Sub˙ + H˙, BDFE(Sub–H) (1)

[(TPFC)Mn(OH)(OOH)]⁻ → [(TPFC)Mn(OH)(O₂)]⁻ + H˙, BDFE(O–H) (2)

ΔG_rp = BDFE(Sub–H) − BDFE(O–H) (3)

The calculated C–H BDFE value of THF is 82.1 kcal mol⁻¹, while BDFE(O–H) value of 62.1 kcal mol⁻¹ was obtained for [(TPFC)Mn(OH)(OOH)]⁻. As such, the driving forces for H-abstraction of THF by [(TPFC)Mn(OH)(O₂)]⁻ is 20.0 kcal mol⁻¹, in agreement with the calculated reaction free energy from ³RC to ³IM1 (19.5 kcal mol⁻¹, see Fig. 3). The high reaction barrier and large endothermicity suggested that the Mn(IV)–hydropeoxo species is less potential to active the C–H bond. Therefore, the further reaction from the Mn(IV)–hydroperoxo species is fundamental important to drive the reaction forward.

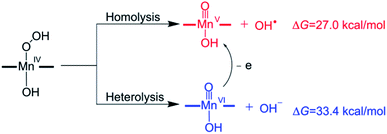
The mechanism of the O–O bond cleavage of Mn(IV)–hydroperoxo complexes has been extensively investigated in biomimetic studies.^67–74 Two possible pathways for the conversion of the Mn(IV)–hydroperoxo species to Mn(V)–oxo were proposed (Scheme 4): the homolytic O–O bond cleavage (generating Mn(V)–oxo and OH˙) and the heterolytic cleavage followed by a fast one-electron reduction.³² However, both homolysis and heterolysis of O–O bond for the isolated Mn(IV)–hydroperoxo complex were found to be energetically unfavourable due to high reaction free energies (27.0 kcal mol⁻¹ for the O–O bond homolysis and 33.4 kcal mol⁻¹ for the O–O bond heterolysis). A previous study for the Mn(III) complex with bispidine ligands reported that the OH transfer from Mn(III)–hydroperoxo complex to the substrate radical occurs with simultaneous O–O bond cleavage and C–O bond formation to give Mn(III)–oxo.⁷⁵ It is expected that the Mn(IV)–hydroperoxo can react with the substrate radical to give a Mn(V)–oxo complex and a hydroxylation product.

Scheme 4 Two proposed mechanisms for the conversion of Mn(IV)–hydroperoxo to Mn(V)–oxo.

Here, we identify a two-step pathway for the formation of Mn(V)–oxo from the Mn(IV)–hydroperoxo with a substrate radical (IM1 → PC, Fig. 3). Firstly, the O–C bond formation is concerted with a proton transfer from the hydroperoxo moiety to a nearby N atom of corrole ring, generating an alkylperoxo Mn(III) complex (IM2). Then, the alkylperoxo O–O bond cleavage affords a Mn(V)–oxo complex and a 2-hydroxy-tetrahydrofuran. The lowest-energy pathway is on the triplet potential energy surface (PES). Details of the C–O bond formation on the triplet surface are given in the geometry scan displayed in Fig. 5. During this process, the Mn center “gains” one electron from the substrate. This electron flow was found to occur in an early stage when the C–O distance is around 2.6 Å. When the C–O distance is further shortened to 1.7 Å, the proton transfer from hydroperoxo to the nearby N atom of corrole happens. The TS2 structure could not be properly characterized since the electronic structure changes abruptly. An estimate from the geometry scan predicts it to be less than 1.5 kcal mol⁻¹ on the triplet PES. The alkylperoxo intermediate IM2 has a triplet ground state with the quintet state being 9.5 kcal mol⁻¹ higher. The closed-shell singlet state ¹IM2 is 25.1 kcal mol⁻¹ higher than the triplet (see Fig. S3 in ESI†). Interesting to note that the manganese–alkylperoxo species have been proposed as key intermediates in manganese containing enzymes and are presumed to play an important role in catalytic substrate oxidation.^76–78 Although the Mn–alkylperoxo complexes have been generated and characterized in some biomimetic studies,^79,80 their reactivity is not well understood. It can be seen from Fig. 4 that the alkylperoxo intermediate IM2 has an O–O bond distance of 1.47 Å, which is close to the synthetic Mn–alkylperoxo complexes (1.46–1.51 Å).^79,80

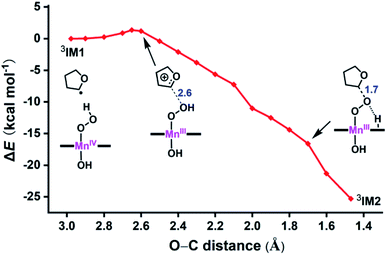Fig. 5 Geometry scan for the O–C bond formation from ³IM1 to ³IM2. Energetics (kcal mol⁻¹) taken relative to ³IM1 at TPSSh/def2-SVP. The bond lengths (Å) are marked in blue.

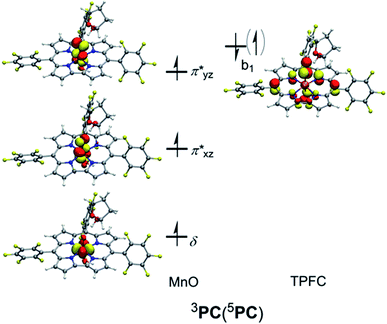
The subsequent alkylperoxo O–O bond cleavage occurs on the triplet state, yielding a Mn(V)–oxo complex and a 2-hydroxy-tetrahydrofuran (2OH-THF). The transition state ³TS3 has an imaginary frequency of i869 cm⁻¹, whose normal mode corresponded to the simultaneous O–O bond breaking and proton transfer from the corrole N atom to distal oxygen (O₂). The structure of ³TS3 in Fig. 4 has an O–O bond distance of 1.65 Å and a H–O₂ bond distance of 1.02 Å. In this transition state, the spin density on Mn and dioxygen is 2.05 and −0.06, suggesting a biradical property. During this process, the Mn–O bond length is decreased from 1.96/1.98 Å in ³IM2 to 1.69/1.72 Å in ³PC/⁵PC (Fig. 4). In the triplet product ³PC, the spin density on the Mn, O1, and corrole is 2.52, 0.18, and −0.61, respectively. While in ⁵PC, the spin density on the Mn, O1, and corrole is 2.59, 0.49, and 0.81, respectively. Clearly, both ³PC and ⁵PC are Mn(IV)–oxo corrole π–radical–cation complexes (Fig. 6). On the triplet surface, this step has a free energy barrier of 7.1 kcal mol⁻¹ and a large exothermicity of 30 kcal mol⁻¹. The transition state on quintet surface ⁵TS3 is 11.3 kcal mol⁻¹ higher than the triplet ³TS. The final product PC has a triplet ground state, with ⁵PC/¹PC being 3.4/4.7 kcal mol⁻¹ higher than the triplet. This is in contrast with the experimentally determined singlet ground state of the Mn(V)–oxo complex (without an axial OH⁻ ligand).³⁴ Interesting to note that for the iron–oxo porphyrin (P) complex, the Fe(IV)–oxo porphyrin radical electromer is the ground state with an axial Cl⁻ ligand, while the five-coordinate FeO(P)⁺ complex has a stronger preference for the Fe(V)–oxo state.⁸¹ In addition, it has been reported that the Lewis acid induces the interconversion of Mn(V)–oxo with a valence tautomer, in which an electron from the corrole ring is transferred to Mn to give the electronic isomer Mn^IV(O)(π–radical–cation) porphyrinoid complex.^82,83 For the presently studied system, the product PC has an axial OH⁻ ligand and has a hydrogen bonding interaction between the hydroxyl group of 2OH-THF and the oxo group, which may affect the spin state orderings. To test this hypothesis, we calculated the relative energies for the different spin states of the MnO species with and without an axial OH⁻ ligand, i.e., [(TPFC)Mn(OH)(O)]⁻ and [(TPFC)Mn(O)]. Our calculations showed that the [(TPFC)Mn(OH)(O)]⁻ has a triplet ground state, while the [(TPFC)Mn(O)], which is devoid of the axial ligand, has a closed-shell ground state. These results confirmed that the spin-state ordering is dependent on the local environmental conditions.

Fig. 6 Singly occupied orbitals for the generated MnO complexes (PC).

4. Conclusions

The reaction mechanism of the formation of Mn(V)–oxo complex via dioxygen activation by a Mn(III) complex bearing the TPFC ligand in the present of base and hydrogen donor THF were explored by using DFT methods. Our results indicated that with the axial OH⁻ ligand the dioxygen can bind to Mn in an end-on fashion to generate the Mn(IV)–superoxo species (albeit endothermically). The Mn(IV)–superoxo can abstract a hydrogen atom from THF with a high reaction barrier and a large endothermicity. This step was found to be the rate-limiting step in the formation of Mn(V)–oxo. Subsequently, the O–C bond formation is concerted with an electron transfer from the C2 radical of THF to the Mn(IV)–hydroperoxo and proton transfer from the hydroperoxo moiety to a nearby N atom of corrole ring, generating an alkylperoxo Mn(III) complex. Finally, the alkylperoxo O–O bond cleavage affords a Mn^IV(O)(π–radical–cation) porphyrinoid complex, a valence tautomer of Mn(V)–oxo. To the best of our knowledge, the conversion of Mn–hydroperoxo to MnO via a Mn–alkylperoxo species has never been reported. Thus, the present study broaden the landscape of dioxygen activation by the Mn complexes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work is supported by the grants from National Natural Science Foundation of China (No. 21673286). The computer resources were provided by High-performance Computing Platform of Renmin University of China.

References

1. W. Nam, Acc. Chem. Res., 2007, 40, 465.
2. Y. F. Wang, J. S. Li and A. M. Liu, J. Biol. Inorg Chem., 2017, 22, 395–405.
3. S. Fukuzumi, K. B. Cho, Y. M. Lee, S. Hong and W. Nam, Chem. Soc. Rev., 2020, 49, 8988–9027.
4. W. Nam, Y. M. Lee and S. Fukuzumi, Acc. Chem. Res., 2018, 51, 2014–2022.
5. J. J. D. Sacramento and D. P. Goldberg, Acc. Chem. Res., 2018, 51, 2641–2652.
6. C. E. Elwell, N. L. Gagnon, B. D. Neisen, D. Dhar, A. D. Spaeth, G. M. Yee and W. B. Tolman, Chem. Rev., 2017, 117, 2059–2107.
7. E. G. Kovaleva and J. D. Lipscomb, Science, 2007, 316, 453–457.
8. J. H. Jeoung, M. Bommer, T. Y. Lin and H. Dobbek, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12625–12630.
9. R. P. McAndrew, N. Sathitsuksanoh, M. M. Mbughuni, R. A. Heins, J. H. Pereira, A. George, K. L. Sale, B. G. Fox, B. A. Simmons and P. D. Adams, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6029–6030.
10. Y. F. Wang, K. F. Liu, Y. Yang, I. Davis and A. M. Liu, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 19720–19730.
11. I. Ghosh and T. K. Paine, in Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2020, DOI:  DOI:10.1016/B978-0-08-102688-5.00019-2.
12. K. Ray, F. F. Pfaff, B. Wang and W. Nam, J. Am. Chem. Soc., 2014, 136, 13942–13958.
13. S. A. Cook and A. S. Borovik, Acc. Chem. Res., 2015, 48, 2407–2414.
14. X. Engelmann, I. Monte-Perez and K. Ray, Angew. Chem., Int. Ed., 2016, 55, 7632–7649.
15. S. Sahu and D. P. Goldberg, J. Am. Chem. Soc., 2016, 138, 11410–11428.
16. S. Caron, R. W. Dugger, S. G. Ruggeri, J. A. Ragan and D. H. B. Ripin, Chem. Rev., 2006, 106, 2943–2989.
17. M. Costas, M. P. Mehn, M. P. Jensen and L. Que, Chem. Rev., 2004, 104, 939–986.
18. V. V. Smirnov, D. W. Brinkley, M. P. Lanci, K. D. Karlin and J. P. Roth, J. Mol. Catal. A: Chem., 2006, 251, 100–107.
19. R. L. Shook, S. M. Peterson, J. Greaves, C. Moore, A. L. Rheingold and A. S. Borovik, J. Am. Chem. Soc., 2011, 133, 5810–5817.
20. C. M. Lee, C. H. Chuo, C. H. Chen, C. C. Hu, M. H. Chiang, Y. J. Tseng, C. H. Hu and G. H. Lee, Angew. Chem., Int. Ed., 2012, 51, 5427–5430.
21. J. D. Parham, G. B. Wijeratne, J. R. Mayfield and T. A. Jackson, Dalton Trans., 2019, 48, 13034–13045.
22. D. B. Rice, A. A. Massie and T. A. Jackson, Acc. Chem. Res., 2017, 50, 2706–2717.
23. K. A. Prokop, S. P. de Visser and D. P. Goldberg, Angew. Chem., Int. Ed., 2010, 49, 5091–5095.
24. N. Sharma, H. B. Zou, Y. M. Lee, S. Fukuzumi and W. Nam, J. Am. Chem. Soc., 2021, 143, 1521–1528.
25. Y. Gao, T. Akermark, J. Liu, L. Sun and B. Akermark, J. Am. Chem. Soc., 2009, 131, 8726–8727.
26. Z. Codola, L. Gomez, S. T. Kleespies, L. Que Jr, M. Costas and J. Lloret-Fillol, Nat. Commun., 2015, 6, 6405.
27. B. Gerey, E. Gouré, J. Fortage, J. Pécaut and M.-N. Collomb, Coord. Chem. Rev., 2016, 319, 1–24.
28. B. K Semin, L. N. Davletshina, M. Seibert and A. B. Rubin, J. Photochem. Photobiol., B, 2018, 178, 192–200.
29. Z. Gross, G. Golubkov and L. Simkhovich, Angew. Chem., Int. Ed., 2000, 39, 4045–4047.
30. H. Y. Liu, T. S. Lai, L. L. Yeung and C. K. Chang, Org. Lett., 2003, 5, 617–620.
31. H. Y. Liu, F. Yam, Y. T. Xie, X. Y. Li and C. K. Chang, J. Am. Chem. Soc., 2009, 131, 12890–12891.
32. S. H. Kim, H. Park, M. S. Seo, M. Kubo, T. Ogura, J. Klajn, D. T. Gryko, J. S. Valentine and W. Nam, J. Am. Chem. Soc., 2010, 132, 14030–14032.
33. K. A. Prokop and D. P. Goldberg, J. Am. Chem. Soc., 2012, 134, 8014–8017.
34. M. Guo, Y. M. Lee, R. Gupta, M. S. Seo, T. Ohta, H. H. Wang, H. Y. Liu, S. N. Dhuri, R. Sarangi, S. Fukuzumi and W. Nam, J. Am. Chem. Soc., 2017, 139, 15858–15867.
35. A. Ghosh and P. R. Taylor, Curr. Opin. Chem. Biol., 2003, 7, 113–124.
36. M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55.
37. T. Z. H. Gani and H. J. Kulik, J. Chem. Theory Comput., 2017, 13, 5443–5457.
38. A. A. Tsaturyan, A. P. Budnyk and C. Ramalingan, ACS Omega, 2019, 4, 10991–11003.
39. D. Janardanan, D. Usharani and S. Shaik, Angew. Chem., Int. Ed., 2012, 51, 4421–4425.
40. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
41. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
42. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
43. T. Yang, M. G. Quesne, H. M. Neu, F. G. Cantu Reinhard, D. P. Goldberg and S. P. de Visser, J. Am. Chem. Soc., 2016, 138, 12375–12386.
44. H. M. Neu, T. Yang, R. A. Baglia, T. H. Yosca, M. T. Green, M. G. Quesne, S. P. de Visser and D. P. Goldberg, J. Am. Chem. Soc., 2014, 136, 13845–13852.
45. Y. Xu, Z. G. Xu, X. H. Zhang, H. B. Chen, X. Xu and H. Y. Liu, Chin. J. Struct. Chem., 2019, 38, 1857–1866.
46. D. C. Ashley and M.-H. Baik, ACS Catal., 2016, 6, 7202–7216.
47. J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401–146404.
48. K. P. Jensen, Inorg. Chem., 2008, 47, 10357–10365.
49. J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097–14105.
50. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822–8824.
51. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
52. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
53. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
54. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
55. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016.
56. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
57. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 19.
58. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
59. B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748.
60. G. Jansen and B. A. Hess, Phys. Rev. A, 1989, 39, 6016–6017.
61. J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305.
62. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
63. C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2007, 111, 408–422.
64. J. Krzystek, A. Schnegg, A. Aliabadi, K. Holldack, S. A. Stoian, A. Ozarowski, S. D. Hicks, M. M. Abu-Omar, K. E. Thomas, A. Ghosh, K. P. Caulfield, Z. J. Tonzetich and J. Telser, Inorg. Chem., 2020, 59, 1075–1090.
65. S. Shaik and H. Chen, JBIC, J. Biol. Inorg. Chem., 2011, 16, 841–855.
66. J. M. Bollinger Jr and C. Krebs, Curr. Opin. Chem. Biol., 2007, 11, 151–158.
67. B. Meunier, S. P. de Visser and S. Shaik, Chem. Rev., 2004, 104, 3947–3980.
68. R. van Eldik and C. D. Hubbard, Coord. Chem. Rev., 2010, 254, 297–308.
69. J. Cho, S. Jeon, S. A. Wilson, L. V. Liu, E. A. Kang, J. J. Braymer, M. H. Lim, B. Hedman, K. O. Hodgson, J. S. Valentine, E. I. Solomon and W. Nam, Nature, 2011, 478, 502–505.
70. L. V. Liu, S. Hong, J. Cho, W. Nam and E. I. Solomon, J. Am. Chem. Soc., 2013, 135, 3286–3299.
71. S. Bang, S. Park, Y. M. Lee, S. Hong, K. B. Cho and W. Nam, Angew. Chem., Int. Ed. Engl., 2014, 53, 7843–7847.
72. M. Oszajca, A. Drzewiecka-Matuszek, A. Franke, D. Rutkowska-Zbik, M. Brindell, M. Witko, G. Stochel and R. van Eldik, Chemistry, 2014, 20, 2328–2343.
73. M. Oszajca, A. Franke, M. Brindell, G. Stochel and R. van Eldik, Coord. Chem. Rev., 2016, 306, 483–509.
74. I. Gamba, Z. Codola, J. Lloret-Fillol and M. Costas, Coord. Chem. Rev., 2017, 334, 2–24.
75. F. G. Cantu Reinhard, P. Barman, G. Mukherjee, J. Kumar, D. Kumar, D. Kumar, C. V. Sastri and S. P. de Visser, J. Am. Chem. Soc., 2017, 139, 18328–18338.
76. W. A. Gunderson, A. I. Zatsman, J. P. Emerson, E. R. Farquhar, L. Que, J. D. Lipscomb and M. P. Hendrich, J. Am. Chem. Soc., 2008, 130, 14465–14467.
77. A. Company, J. Lloret-Fillol and M. Costas, in Comprehensive Inorganic Chemistry II, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Amsterdam, 2nd edn, 2013, pp. 487–564, DOI:  DOI:10.1016/B978-0-08-097774-4.00323-5.
78. E. Skrzypczak-Jankun, R. A. Bross, R. T. Carroll, W. R. Dunham and M. O. Funk, J. Am. Chem. Soc., 2001, 123, 10814–10820.
79. M. K. Coggins, V. Martin-Diaconescu, S. DeBeer and J. A. Kovacs, J. Am. Chem. Soc., 2013, 135, 4260–4272.
80. M. K. Coggins and J. A. Kovacs, J. Am. Chem. Soc., 2011, 133, 12470–12473.
81. M. Radoń, E. Broclawik and K. Pierloot, J. Chem. Theory Comput., 2011, 7, 898–908.
82. J. P. T. Zaragoza, R. A. Baglia, M. A. Siegler and D. P. Goldberg, J. Am. Chem. Soc., 2015, 137, 6531–6540.
83. P. Leeladee, R. A. Baglia, K. A. Prokop, R. Latifi, S. P. de Visser and D. P. Goldberg, J. Am. Chem. Soc., 2012, 134, 10397–10400.

---

Footnote

† Electronic supplementary information (ESI) available: Energies, spin densities, and Cartesian coordinates of all computed species. See DOI: 10.1039/d1ra02722k

---