 Open Access Article
Open Access ArticleElectroactive macromolecular motors as model materials of ectotherm muscles
Toribio Fernández Otero†

Technical University of Cartagena, Laboratory of Electrochemistry, Intelligent Materials and Devices, Department of Chemical and Environmental Engineering, Campus Alfonso XIII, 30203, Cartagena, Spain. E-mail: toribio.fotero@upct.es
First published on 17th June 2021
Abstract
The electrochemical reaction in liquid electrolytes of conducting polymers, carbon nanotubes, graphenes, among other materials, replicates the active components (macromolecular electro-chemical motors, ions and solvent) and volume variation of the sarcomere in any natural muscles during actuation, allowing the development of electro-chemo-mechanical artificial muscles. Materials, reactions and artificial muscles have been used as model materials, model reactions and model devices of the muscles from ectotherm animals. We present in this perspective the experimental results and a quantitative description of the thermal influence on the reaction extension and energetic achievements of those muscular models using different experimental methodologies. By raising the temperature for 40 °C keeping the extension of the muscular movement the cooperative actuation of the macromolecular motors harvest, saving chemical energy, up to 60% of the reaction energy from the thermal environment. The synergic thermal influence on either, the reaction rate (Arrhenius), the conformational movement rates of the motors (ESCR model) and the diffusion coefficients of ions across polymer matrix (WLF equation) can support the physical chemical foundations for the selection by nature of ectotherm muscles. Macromolecular motors act, simultaneously, as electro-chemo-mechanical and thermo-mechanical transducers. Technological and biological perspectives are presented.
Introduction
During the last decades model materials replicating the dense gel environment and the reactive functional elements of the intracellular matrix (ICM) from the muscle cell sarcomere (macromolecular or polymeric motors, ions and solvent) have been described.1–3 Driven by electrochemical reactions films of conducting polymers (CP), carbon nanotubes (CNT), graphenes (G) and other electroactive (understood in the sense that they follow oxidation/reduction reactions) materials react in liquid electrolytes exchanging counterions and solvent with the electrolyte becoming dense reactive gels.1,3 Each film element (polymer chain, nanotube or nanosheet) acts during the reaction as a multi-step (exchanging, one by one, up to n electrons) polymeric motor (see reaction (2) below). The cooperative actuation of the film chains (macromolecular motors) during the reaction promotes the film swelling/contraction to lodge/expel, respectively, balancing counterions and solvent (Fig. 1). The reaction-driven changes of the material volume have been used to produce electrochemical artificial muscles working, as they do natural muscles, by cooperative actuation of the constitutive macromolecular motors.2,4–10 | ||
| Fig. 1 The cooperative actuation of the macromolecular electrochemical motors (the chains of the conducting polymer) during the film oxidation (reaction (2) forwards) incorporates counterions (yellow circles) and solvent (blue circles) from the solution for charge and osmotic balance originating the film swelling going from the upper left to the bottom right figure. During the film reduction the macromolecular motor's actuation originates reverse processes and the film contraction coming back from the bottom right figure to the upper left one. This figure has been reproduced from ref. 11 with permission from Springer Nature, copyright 1999. | ||
In this context, during the last years either, films of conducting polymers, carbon nanotubes or graphenes and artificial muscles made with those films have been used as model materials and model devices in order to characterize the energetic changes during electrochemical reactions involving macromolecular machines under different temperatures. This thermal influence has been exploited to initiate a quantitative description of the behavior of natural ectotherm muscles (coldblooded animals) from the parallel study and quantitative energetic descriptions attained by the physical chemical characterization of model materials and model devices.
Basic chemical aspects from natural muscles to be replicated
Animal muscles (skeletal, cardiac or smooth) are biological macroscopic motors which basic actuating element is the cell sarcomere. Despite the complex biological reactions taking place in a muscle cell three are the basic chemical and electrical elements originating the sarcomere actuation: macromolecular chemical motors (actin, myosin, kinesin, tropomyosin, or troponin) driven by ATP reactions, triggered by a brain order (a nervous pulse) liberating Ca2+ ions (electrical and chemical pulse) inside the sarcomere changing the Ca2+ concentration there for several orders of magnitude.12,13 As final result the cooperative conformational movements (cooperative actuation) of the macromolecular motors constituting the sarcomere unit fueled by the ATP reaction under an electro-chemical order originates the muscle contraction. Thus, natural muscles are electro-chemo-mechanical transducers: under an electric order they transform chemical energy stored by ATP into mechanical energy (muscle contraction), heat and, probably, nervous pulses sent back through the sensory neuron to inform the brain about the muscle working physical and chemical conditions.12–14The basic simplified reaction driving every mono-step actuation of the macromolecular motors can be written as:
| (MM)ext + ATP4− → (MM)contr + ADP3− + P2− + H+ | (1) |
Moreover we know that muscles from ectotherm animals work faster and easier after the animal heating under the sun light or from a thermal source.15,16 As chemists or biochemists our interpretation, in an initial approach, is that the driven reaction rate, involving the macromolecular motors and ATP, increases when the body temperature (Tb) rises following the Arrhenius description. This explanation does not provide any quantitative relationship between the consumed reaction energy and the temperature of the animal body and cannot define the percentage of chemical energy saved under a constant muscular performance when the muscle temperature rises. In fact all aspects of the behavior and physiology of ectotherms are sensitive to Tb. The relationship between Tb and a specific type of performance is described by an empirical asymmetric function: from a minimum critical thermal limit (CTmin) the performance increases passes through the thermal maximum (T0) and then decreases very fast up to the maximum critical thermal limit (CTmax).15–17 Temperatures outside the critical thermal limits are not compatible with life functions. The empirical asymmetric function Tb/performance is a result of the temperature influence on a plethora of biological reactions, including reactants degradation or denaturation. As a partial conclusion we don't have quantitative descriptions clear enough to reveal the physical chemical foundations behind the selection by nature of coldblooded animal muscles by evolution, which performance increases with the body temperature from the CTmin to the thermal maximum, T0.
At present our limited control of the reactions involving the above mentioned biological macromolecular motors (after its isolation from the muscle), if rising quite fast,14,18–28 does not allow a deep physical-chemical characterization of the muscle driven reactions under different thermal conditions. In fact, most of the literature present responses to thermal variations from the full muscle,15,29(and references therein) which means involving many reactions in addition to that of the macromolecular motors.
In this work advances attained from the study of model materials and model devices, as well as the future technological and biological perspectives are presented and discussed. We hope that some aspects of the applied methodologies and procedures here used could help in the future to attain a full theoretical description of any biological function originated by the actuation of electro-chemo-mechanical macromolecular machines (protein motors).
Driving electro-chemical reaction
By electrochemical oxidation/reduction every chain, tube or nano-sheet from films of any conducting polymer, carbon nanotube or graphene, respectively, used as the working electrode in a liquid electrolyte behaves as a multi-step (n steps) macromolecular motor.2 Using films of conducting polymers exchanging anions (the most studied in nowadays literature) during its reversible oxidation/reduction (p-doping/p-de-doping) in liquid electrolytes the material reactions can be written, in its simplest expression (not including ion trapping effects), as:30–33
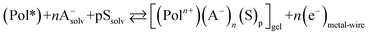 | (2) |
The reaction (2) indicates that the extraction/injection of every electron from/towards each polymeric chain of the conducting polymer film must occur simultaneously to the entrance/expulsion of one monovalent anion from/towards, respectively, the solution. As a consequence of this required simultaneity the reaction is inhibited in presence of large counterions: by structural restrictions large counterions, as macroanions or polymeric anions, cannot penetrate through the narrow interchain ionic channels open by actuation of the macromolecular motors.34
Descriptions, equations and conclusions here attained will be also valid for those materials exchanging cations during electrochemical oxidation (p-doping), i.e. reaction (3) below, or during electrochemical reduction (n-doping) starting from the neutral state of the chain.31,35 The only macroscopic difference is that for those materials exchanging cations the oxidation reaction drives the expulsion of cations and the material macroscopic contraction (versus macroscopic swelling in material exchanging anions) and its reduction drives the material macroscopic swelling (versus contraction in materials exchanging anions).31,35
Multi-step electro-chemical polymeric motors
Thus, the extraction/injection of one electron from/to, respectively, a polymeric chain drives the change of the double bonds distribution along 3 to 5 monomeric units (Fig. 2).2 In the reduced state of the chain σ bonds are present between those monomeric units (Fig. 2 left reaction side) allowing its relative free rotation getting, above the glass transition temperature of the polymer, different conformational states. The π conjugated flat polaronic structure (Fig. 2 right reaction side), generated by the electronic extraction,36–39 means that the reaction drives conformational (mechanical) movements of the chain: whatever the initial reduced conformational state was becomes by oxidation a flat π conjugated conformation. By reduction the σ bonds between monomeric units are restored and one of the initial conformations is recovered. This is a mono-step reversible electrochemical motor: the reversible formation/destruction of a polaronic structure in the chain drives reversible conformational movements of the consecutive monomeric units. Professors Sauvage, Feringa and Stoddart received the 2016 Nobel prize in Chemistry for the design and synthesis of molecular (mono-step) machines.40 That means that this is a quite recent research field trying to replicate biological chemical and electro-chemical macromolecular (protein) machines.41–48During the reversible oxidation/reduction of a polymeric chain (reaction (2)) consecutive electrons are extracted from the chain one by one at increasing oxidation potentials related to the first, second…, nth ionization potentials of the chain.3,11,35 Each new electronic extraction generates a new π conjugated flat polaronic structure originating a small conformational movement of the chain. The formation of consecutive polaronic structures during the reaction gives large conformational movements (large mechanical changes) of the chain helped by the strong polaron–polaron repulsions and the polaron–counterion and polaron–water attractive forces. During reduction consecutive electrons are injected to the oxidized chain at increasing cathodic potentials recovering both, the σ bonds between consecutive monomeric units and one of the initial conformations related to the strong polymer–polymer interactions in neutral chains. Each chain is a multi-step macromolecular polymeric motor.2,11,35
Muscular model materials
As a result of the facts described in the two previous sections the reactive material becomes a dense gel constituted by macromolecular electro-chemical motors, ions and solvent (Fig. 1). This can be the model material replicating the active functional elements and reactions of the muscle sarcomere that we were looking for in order to perform a physical and chemical characterization of the muscle temperature influence on the muscle energetic achievements.Let see if they cover three of the basic events taking place during any muscular actuation.
Large ionic concentration variations
The actuation of natural muscles requires the Ca2+ concentration variation for several orders of magnitude inside the dense sarcomere gel.12 Reaction (2) drives the variation of the counterion concentration, [A−], inside the conducting polymer gel for several orders of magnitude, mimicking biological cell processes.49 Following reaction (2) the charge consumed to oxidize the material from the same initial state every time controls the final concentration of counterions in the material: giant non-stoichiometric material.50,51Cooperative actuation of macromolecular machines
The muscle sarcomere works under cooperative actuation of the electro-chemical macromolecular proteins constituting the sarcomere, e.g. actin-myosin.12 In our model materials the reaction (2) only occurs if the cooperative actuation of the macromolecular machines constituting the film, the polymer chains, generates/destroys the required free volume to lodge/expel, respectively, balancing counterions and solvent.52Reaction-driven volume variations
As a consequence of the cooperative actuation of the polymeric chains driven by the material reversible oxidation/reduction (reaction (2)) the material volume swells/contracts, respectively, in a reverse way (Fig. 1) replicating the reaction-driven volume contraction occurring during actuation of natural muscles.11,53–59 Thus, the main difference between model materials and muscles is that the reversible reaction (i.e. reaction (2)) of the artificial material originates reversible volume variations while in natural muscles the irreversible reaction (1) only can drive the muscle contraction: symmetric (artificial) versus asymmetric (natural) volume variations. Artificial muscles give reversible movement by reversing the direct current flow (the reaction). Natural muscles need the actuation of an antagonistic muscle to recover the initial position by relaxation.Otherwise from the point of view of the reaction induced volume variations the cooperative actuation of the same artificial molecular motor is ambivalent: the oxidation of the polymer (e.g. polypyrrole, pPy) chains originates the expansion (reaction (2)) of the polymer film but the contraction of any polypyrrole-polyelectrolyte, or any polypyrrole–macroanion, (MA−), (e.g. pPy–DBS, dodecylbenzenesulphonate), blend by exchange of cations:31,35
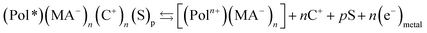 | (3) |
Model materials of the sarcomere functional reactions
As summary conducting polymers and other electroactive (in the sense that they follow reversible oxidation/reduction reactions in liquid electrolytes) materials as carbon nanotubes or graphenes can be taken as model materials of both, the basic chemical components of the sarcomere (macromolecular electro-chemical motors, ions and solvent) and the reaction-driven actuation (volume variation) in natural muscles.1Replication of the ectotherm muscular reactions and muscular actuation under different temperatures
In this context we can use both, films of conducting polymers coating metal electrodes or artificial muscles based on conducting polymers as either, model reactive materials of any functional sarcomere and model actuating devices of any natural muscle. Their investigation, physical–chemical characterization and theoretical description under different temperatures (Fig. 3) can help to describe the muscle's responses from cold-blooded animals.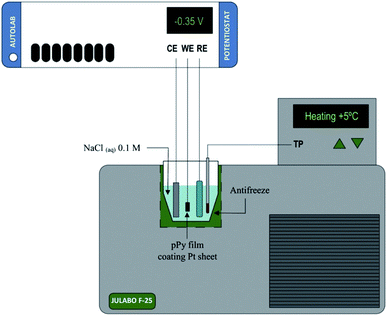 | ||
| Fig. 3 Schematic representation of the electrochemical system used during the characterization of both, the model materials, polypyrrole film here, coating a Pt electrode or the freestanding polymeric films (linear actuators); (CE, counterelectrode; WE, working electrode; RE, reference electrode; TP, temperature probe. This figure has been reproduced from ref. 60 with permission from Elsevier, copyright 2017. | ||
Here we will present the goals attained during the last years.
Films coating metals as model materials of the sarcomere functional reactions
Using films of conducting polymers coating a metal (inert) foil as the working electrode (Fig. 3) in liquid electrolytes the electrochemical responses to different potential or current stimulus were studied at different temperatures.60 The basic equations of the chemical and electrochemical kinetics will allow getting the quantitative equations describing the temperature influence on the reactions involving macromolecular motors checking those expressions with the attained experimental results.Stimulated by potential cycles the reversible reaction extension rises with temperature. The conducting polymer coating the metal electrode was submitted to consecutive potential cycles in a liquid electrolyte getting, after two or three cycles, stationary voltammetric responses. The procedure was repeated at different cell temperatures.60 Fig. 4 shows the attained stationary voltammetric (current/potential) and the concomitant coulovoltammetric (charge/potential) responses for increasing, and then for decreasing, temperatures. The closed coulovoltammetric loops guarantee the reaction reversibility (the charge consumed by the material oxidation equals the charge consumed by the material reduction) corroborating the absence of any simultaneous irreversible reaction occurring in the studied potential rage, e.g. solvent electrolysis, which should originate open coulovoltammetric loops.34,61
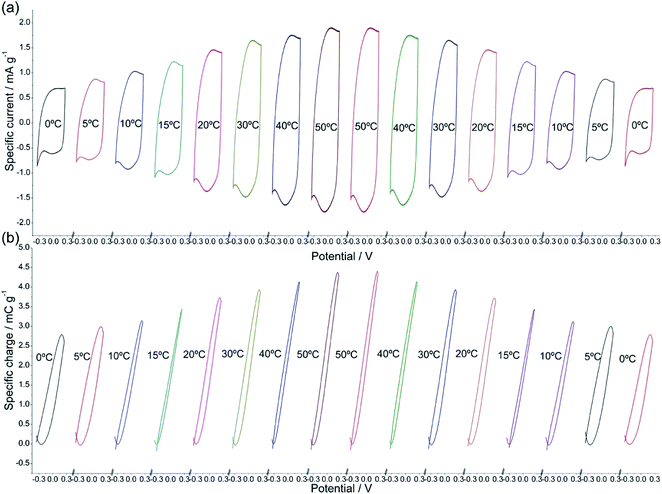 | ||
| Fig. 4 (a) Stationary voltammetric, or cyclovoltammetric (CV), responses from a polypyrrole film coating a Pt electrode obtained after application of three consecutive potential cycles performed between −0.35 and 0.25 V at 90 mV s−1 in 0.1 M NaCl aqueous solution at different experimental temperatures. (b) Stationary coulovoltammetric (QV) responses obtained by integration of the voltammetric responses presented in Fig. 1a, for different temperatures. This figure has been reproduced from ref. 60 with permission from Elsevier, copyright 2017. | ||
Voltammetric (CV) and coulovoltammetric (QV) responses illustrate the increase of both, the flowing currents and the consumed charges, during the film oxidation/reduction when the temperature rises. Here one of the reactants taking part in reaction (2) are large polymeric chains thus, rising available thermal energies promote, in addition to faster reaction rates (Arrhenius) either, larger conformational movements by relaxation of the film chains, the generation of more free volume in the film, the entrance from the electrolyte of a greater number of counterions and solvent to occupy that volume, and the required (reaction (2)) simultaneous extraction of a higher number of electrons from the chains giving rising currents on the voltammetric responses (Fig. 4a) and consuming higher coulovoltammetric charges (Fig. 4b). As conclusion rising redox charges, which mean rising reaction extensions, as responses to increasing reaction temperatures are linked to larger conformational movements of the reacting macromolecular electrochemical motors, Fig. 5, under the same voltammetric stimulus.
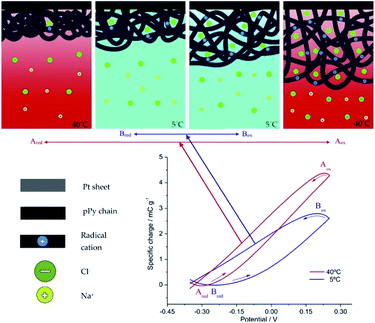 | ||
| Fig. 5 Top: Schemes presenting the extension of the electrochemically induced structural (volumetric) variations driven by cooperative actuation of the macromolecular motors (the film chains) during the reversible oxidation/reduction of the pPy film stimulated by potential cycling at 5 °C (blue arrows) and at 40 °C (red arrows). The sub-indexes mean: ox, oxidized; red, reduced. Bottom: the coulovoltammetric responses show the amplitude of the reactions (consumed oxidation charges equals the consumed reduction charges giving a closed loop)) at the working temperatures of 5 °C (blue line) and 40 °C (red line). This figure has been reproduced from ref. 60 with permission from Elsevier, copyright 2017. | ||
Theoretical description of the attained experimental results
From the basic equation of the reaction (2) rate:
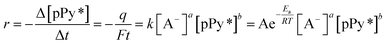 | (4) |
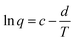 | (5) |
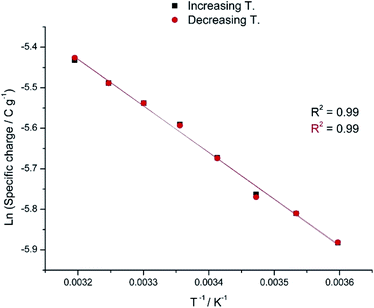 | ||
| Fig. 6 Semi logarithmic variation of the electrical specific charge consumed by the reversible oxidation/reduction of the polypyrrole film with the temperature obtained from coulovoltammograms in Fig. 4b. The specific charges obtained during the temperature increase series overlap those attained during the temperature decrease series. This figure has been reproduced from ref. 60 with permission from Elsevier, copyright 2017. | ||
A similar evolution of the reaction charge with the experimental temperature, described by the same theoretical equation were attained for different materials under stimulation by consecutive square potential waves.62,63
As a partial conclusion the stimulation of the model material by consecutive potential cycles or consecutive square potential waves reveals that rising temperatures influence the rate and amplitude of both, the reaction and the conformational movements of the reacting macromolecular motors. Now we will try to characterize the involved energetic transitions at different temperatures for a constant reaction extension.
Stimulation by square current waves
A different approach to our system is by exploring the temperature influence on the reaction involving macromolecular motors under constant amplitude of the model material reaction. The constant reaction extension in any electrochemical (faradaic) reaction is guaranteed by consuming a constant charge to move cyclically the material between the same reduced and oxidized states during every experiment. Any constant reaction extension should replicate parallel constant muscular displacements in ectotherm animals. Submitting the material to consecutive square current waves (Fig. 7a) guarantees that those constant oxidation and reduction charges [constant specific currents (i, mA g−1) are applied for a constant time (t, s) each imposing thus constant specific, anodic or cathodic, charges, q: q = it] drive the cooperative actuation of the macromolecular motors from the dense polymer gel between the same initial and final oxidized sates in a reversible way.62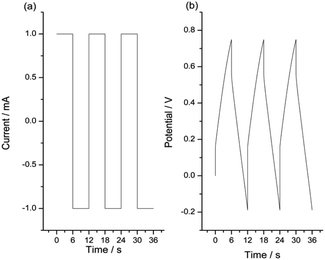 | ||
| Fig. 7 (a) Consecutive square current waves by flow of constant current of 1 mA and −1 mA applied during 6 s each. (b) Concomitant consecutive chronopotentiometric responses obtained from a pPy/Pt film in a 0.1 M NaCl aqueous solution at 40 °C. This figure has been reproduced from ref. 62 with permission from John Wiley and Sons, copyright 2017. | ||
The responses of the material potential to the square current waves are consecutive chronopotentiometric (potential/time) cycles (Fig. 7b). Usually after the second cycle stationary chronopotentiometric responses are attained.
For the same reaction extension the energy consumed at rising temperatures drops. The stationary chronopotentiometric (potential/time) responses during the oxidation of the model material and during the model material reduction attained at different experimental temperatures were overlapped in Fig. 8. They were normalized taking as origin of each potential transition (zero potential) the initial potential at the current transition time (from anodic to cathodic or from cathodic to anodic).
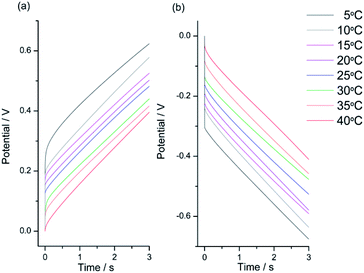 | ||
| Fig. 8 Stationary chronopotentiometric responses from a Pt/pPy film submitted to square current waves of (a) +1 mA (anodic response) for 6 s and (b) −1 mA (cathodic response) for 6 s at different temperatures. The potential origin was normalized to the potential at t = 0 s for every chronoamperometric response. Only the 3 initial seconds are represented here in order to see a clear evolution of the material potential. This figure has been reproduced from ref. 62 with permission from John Wiley and Sons, copyright 2017. | ||
The evolution of the material potential during the material reaction responds to the experimental temperature evolving at decreasing values when the temperature rises: the reaction resistance decreases at rising temperatures, as expected after Arrhenius. From the basic Buttler Volmer equation of the electrochemical kinetics by substituting the concentration of active species in the polymer (e.g. polypyrrole, pPy) at any time of the current flow: [pPy*] = [pPy*]in − (Q/ωF) = [pPy*]in – (It/ωF) = [pPy*]in − (it/F), we get the potential evolution during the anodic reaction driven by flow of a constant specific current, ia = Ia/ω:64
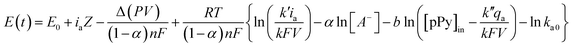 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔG0/RT) and k′ and k′′ are different mechanical constants that will be recovered below.2,64
exp(−ΔG0/RT) and k′ and k′′ are different mechanical constants that will be recovered below.2,64
Only the temperature is changing now between consecutive experiments thus the rest of the terms from eqn (6) remain constant and can be collected by two new constants: e and f. After any constant time of current flow for the different experiments, which means for any constant reaction extension or for the same oxidized state of the material, the material potential decreases linearly at increasing temperatures.
| E = e − fT | (7) |
Taking into account that we are interested to quantify the temperature influence on the energy consumed by the muscular action, the energy (U) consumed by the reaction of the model material under flow of a constant specific current, i, is:
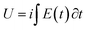 | (8) |
The integral is the area under each chronopotentiometric (Fig. 7) response. After substituting E(t) from eqn (6) and collecting the constant terms by two new constants (g and h) the energy consumed to drive the same reaction extension every time decreases at rising temperatures:62–65
| U = g − hT | (9) |
Eqn (7) and (9) indicate that both the material potential and the energy consumed by the material reaction respond to, adapt to and sense the material temperature. Taking into account that eqn (8) contains eqn (6) the reaction energy includes, at any reaction time, quantitative information about the thermal, mechanical and chemical reaction conditions.
Experimental results attained from Fig. 8 corroborate that the evolution of the material potential after any constant time of current flow follows, Fig. 9a, the temperature dependence described by eqn (7). Otherwise the evolution of the experimental consumed energy with the material temperature follows, Fig. 9b, the theoretical description by eqn (9). In order to guarantee that the attained results only describe the temperature influence experimental series were performed at increasing temperatures and then repeated at decreasing temperatures.
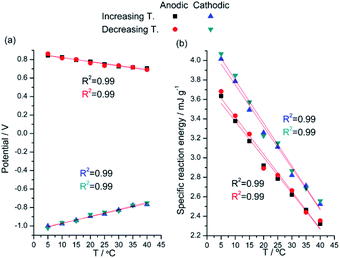 | ||
| Fig. 9 (a) Potential reached and (b) reaction energy consumed when a pPy/Pt film is submitted to square current waves of ±1 mA for 6 s at different temperatures. This figure has been reproduced from ref. 62 with permission from John Wiley and Sons, copyright 2017. | ||
The specific energy consumed for the same anodic (oxidation) reaction extension changes from 4 to 2.5 mJ g−1 when the reaction temperature moves from 5 °C to 40 °C: the increase of the muscle temperature saves 37.5% of the energy consumed when the reaction occurs at the lower temperature.
If those results can be translated to ectotherm muscles they indicate that using model materials we can attain some quantitative explanation of the energetic reasons behind the selection by nature of ectotherm animals: for the same reaction amplitude (same muscular displacement) they consume, as described by eqn (9), less chemical energy, which means that they save chemicals (ATP or glucose), by working at higher temperatures. In other words muscle’ reactions involving macromolecular motors as reactants harvest energy from the thermal environment consuming a smaller amount of chemical or electrochemical energy to perform the same reaction extension (the same muscular work) when the muscular temperature increases.
Higher thermal energies are available for the macromolecular motors at increasing temperatures of the model material giving faster and larger conformational movements of the reacting macromolecular motors (Fig. 1 and 5). The energy consumed by the reaction during every experiment to generate by cooperative actuation of the conformational movements the same variation of the free volume inside the material required to lodge balancing counterions and solvent decreases very fast when the material temperature rises. In electrochemical terms the reaction resistance decreases due to faster and easier conformational movements of the reacting macromolecular motors under rising temperatures. The macromolecular motors act as thermo-mechanical transducers: they transform thermal energy into mechanical energy through larger and faster conformational movements.
If translated to ectotherm muscles eqn (9) should describe the amount of chemical energy that the muscle saves after heating under the sunlight or by effect of any thermal source.
Artificial muscles (actuators) as model devices to get the temperature influence on reactions involving macromolecular motors
The conclusions attained in the previous sections from the study of the electrochemical reactions of model materials coating a metal electrode open the way to move towards model devices by exploring now the influence of the experimental temperature on linear66–73 and bending5,53,74–77 artificial muscles as experimental model devices of natural ectotherm muscles.The small volume variation driven by reversible electrochemical reactions of self-supported films of conducting polymers, carbon nanotubes or graphenes gives reversible linear variations of the film length: linear actuators or linear artificial muscles.66,68,69,71,71,72,78,79,79–84 Otherwise those small reversible variations of the film length can be transformed to large bending movements (up to ± 360°) by construction of bilayers, e.g. CP/tape or CP/metal foil, or triple layers as CP/tape/CP, getting bending artificial muscles.53,81,81,85,86,86–93 The resulting linear or bending artificial muscles are electro-chemo-mechanical transducers: they transform electrical energy into macroscopic mechanical (linear or bending) movements driven by electrochemical reactions through the cooperative actuation of their multi-step macromolecular or polymeric motors. Being electrochemical (faradaic) motors, when the reaction drives the exchange for charge balance of only one ionic specie from the electrolyte, the consumed specific (per unit of dry polymer mass) anodic charge, qa, controls, in absence of parallel reactions (e.g. solvent electrolysis), the amplitude of the bending movement, β, (β = k′′qa) and the flowing specific current (charge per unit of time and per unit of polymer mass), ia, controls the instantaneous movement rate, ω, (ω = k′ia).2 The presence of physical effects (electroosmosis and electrophoresis) controlling the exchange of solvent induces some minor deviations from the linearity of the movement.61 When those quantitative descriptions of the bending movement are substituted in eqn (6), the evolution of the muscle potential describes the influence of either, the thermal, the chemical and the mechanical (position, movement rate, movement direction and produced mechanical work) working conditions: eqn (6) describes artificial self-awareness and artificial mechanical proprioception.2,94
Being faradaic motors, by reversing the sense of the current flow (from anodic to cathodic, or vice versa) the reaction (2) changes from oxidation to reduction and the bending movement is instantaneously reversed. We have a good control of either, the angular displacement by the consumed specific charge, the direction and sense of the displacement by those of the flowing anodic or cathodic current, and the movement rate trough the flowing specific current.
Under those conditions we can use artificial muscles as model devices to characterize the behavior of natural muscles from ectotherm animals under different temperatures.
Freestanding films or bilayer muscles must be used as the working electrode (Fig. 3) of the electrochemical cell in the liquid electrolyte using a metal (Pt) plate as counterelectrode. A reference electrode (RE) must be used also if we like controlling, or following the evolution of, the muscle potential during the reaction driving the muscular movement.
The current flowing by the cell must go through the WE and the CE giving there the concomitant reactions, e.g. polymer oxidation at the WE and reduction of one of the electrolyte components at the CE. By using free standing films (linear muscles) or bilayer bending muscles most of the applied electrical energy is consumed by the reactions taking place at the metal counterelectrode during current flow, e.g. oxygen or hydrogen evolution in aqueous electrolytes. The energetic efficiency should increase by using triple layer artificial muscles (CP/tape/CP, Section 4.3.2). When one of the CP films is the anode of the electrochemical cell, expanding by oxidation and pushing the bending movement, the second CP film acts as the cell cathode, contracting by reduction the polymer film and trailing the bending movement. In a triple-layer artificial muscle both reactions, anodic and cathodic, are used to drive the muscular movement consuming less energy to produce the same angular displacement (the same reaction extension). In addition, the material oxidation and reduction reactions occurs (see Fig. 4a) inside the potential window of the water splitting: lower reaction overpotentials (anodic and cathodic) and lower muscle potentials will require, eqn (8), the consumption of lower amounts of energy to perform the same muscular displacement. If, as stated in previous sections, the reaction of the model materials harvest energy from the environment the higher harvesting efficiencies should be expected by using triple layer artificial muscles as model devices of ectotherm muscles.
Whatever the used device (monolayer, bilayer or triple layer) when submitted to consecutive square waves of current respond with a reproducible and reversible (oxidation charges equal reduction charges) linear or bending movement (go and back) describing a constant linear or angular, respectively, movement amplitude.
Lower energies are consumed at rising T to get the same reaction extension using freestanding films (linear artificial muscles)
We begin using a linear artificial muscle (a freestanding film) as the working electrode of the electrochemical cell in Fig. 3. Initiating the flow of a direct anodic current from a partially reduced state of the CP film acting as the working electrode the muscle potential steps (due to the electrolyte resistance plus the resistance of the film electrochemical reaction) to a more anodic value (Fig. 10a) where the oxidation reaction (reaction (2) forwards) starts. From there the material potential increases slowly with time following the material oxidation by extraction of consecutive electrons from each polymeric chain. When the current flow steps from anodic to cathodic the potential steps, instantaneously, to a more cathodic potential value (Fig. 10b) due to the electrolyte resistance plus the resistance to begin the reduction (reaction (2) backwards) of the oxidized film. There the injection of consecutive electrons to the oxidized chains gives a continuous increase of the muscle reduction potential. After getting stationary chronopotentiometric responses by application of 2–3 consecutive square current waves the cell temperature is changed to a new value. The experimental procedure was repeated at different temperatures and the attained results were overlapped (normalized) in Fig. 10.65,95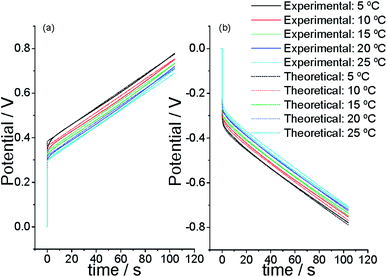 | ||
| Fig. 10 Experimental (straight line) and simulated from eqn (5) (dotted line) stationary chronopotentiometric responses obtained by flow of (a) 0.75 mA or (b) −0.75 mA through a polypyrrole film (10.77 mm × 5.09 mm x 19 μm), which dry mass after reduction is 1.6 mg, at different temperatures (5, 10, 15, 20, and 25 °C) in 1 M LiClO4 aqueous solution. Simulation constants: for n = 50; by flow of ± 0.75 mA; being the initial concentration of active centers [Pol*] = 2 mol L−1; electrolyte concentration [A−] = 1 M, assuming the electrochemical coefficient α = 0.5; for a polymeric film which length inside the electrolyte = 1 cm, width = 0.5 cm, polypyrrole mass = 1.6 mg; being the film density = 1540 g L−1. This figure has been reproduced from ref. 64 with permission from the ACS copyright 2012. | ||
The experimental results (full lines) presented in Fig. 10 show that the evolution of the muscle potential during the go and back bending muscular displacement shifts to lower anodic and lower cathodic, respectively, potentials when the muscular temperature rises. During any constant muscular displacement(by flow of a direct anodic or cathodic current for a constant time each) eqn (6) describes the evolution of the muscle potential during the reaction time as a function of the experimental temperature. The equation includes the mechanical description of the muscular movement: the movement rate, ω, (ω = k′ia) and the amplitude of the muscular movement, β, (β = k′′qa). The theoretical description from eqn (6) evolves at lower potentials when the experimental temperature raises fitting, dotted lines from Fig. 10, the experimental results (full lines).
Eqn (8) gives the energy consumed by the actuator to perform a constant displacement at each studied temperature. The integral is the area under every experimental chronopotentiometric response from Fig. 10. Fig. 11 depicts the evolution of the consumed energy as a function of the experimental temperature for different reaction extensions (different times of current flow in Fig. 10). The energy consumed to perform any constant muscular displacement decreases at rising muscular temperatures following eqn (9), which describes both, oxidation (anodic current flow) and reduction (cathodic current flow) processes: expansion and contraction linear displacements.
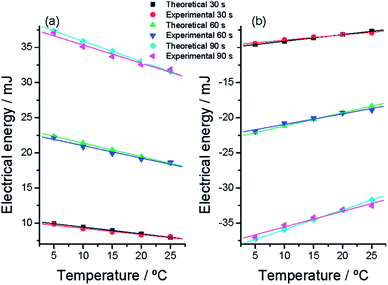 | ||
| Fig. 11 Evolution at different muscular temperatures of the electrical energy consumed (a) to oxidize or (b) to reduce the polymer film after different constant times (30, 60, and 90 s) of current (anodic or cathodic, respectively) flow. The experimental points were taken from Fig. 6. Theoretical points were calculated from eqn (9) and (6). Higher correlation coefficients than 0.98 were obtained from the experimental results. This figure has been reproduced from ref. 64 with permission from the ACS copyright 2012. | ||
Similar results, described by the same equations, were attained using films of conducting polymers exchanging cations96 and bending bilayer95 artificial muscles stimulated by consecutive square current waves.
Lower energies are consumed at rising T to describe the same angular displacement using bending triple-layer artificial muscles exchanging cations
In order to corroborate that any model device follows the above equations describing the temperature influence on the consumed muscular energy we will present now the results attained from reactions driving bending triple layer artificial muscles, CP/Tape/CP (Fig. 12A).65 The main different related to the previous section is the counterelectrode. There we used a metal electrode where most of the energy will be consumed by inefficient reactions. Now, for the characterization of the triple layer muscles the counterelectrode (CE) is also a conducting polymer film short-circuited (Fig. 12A) with the reference electrode (RE) exit from the potentiostat. Thus during application of consecutive square current waves the chronoamperometric responses depict the evolution of the muscle potential (working electrode versus counterelectrode) through the muscular displacement.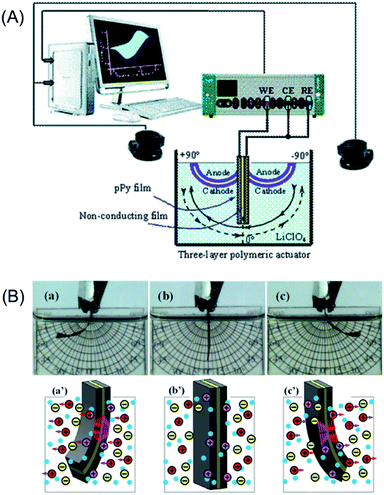 | ||
| Fig. 12 (A) Scheme of the electrochemical cell with the electrodic configuration (WE, working electrode; CE, counter electrode; RE, reference electrode) used to study the electrochemical actuation and energetic consumption of the triple-layer actuator (pPy–DBS/non-conducting tape/pPy–DBS). A vision system was used for video recording the angular displacement in aqueous electrolytes. (B) Bending movements (amplitude, ±60°) described by the triple layer in 0.1 M LiClO4 aqueous electrolyte. During anticlockwise movement, from (a) to (c), the left side pPy–DBS film swells by reduction (flow of cathodic current) and the right side pPy–DBS film shrinks by oxidation under anodic current flow: (c′) show both, the exchange of cations and the generated transversal stress gradients. By reversing the direction of the current flow, the left side film becomes the anode and the right side the cathode giving a clockwise movement from (c) to (a): ionic exchange and stress gradients are reversed (a′). This figure has been reproduced from ref. 65 with permission from the Royal Society of Chemistry copyright 2011. | ||
In addition, as a stress text for eqn (7) and (9), a chemical difference will be included now: if the previous sections involve conducting polymers exchanging anions (reaction (2)) during the driving reaction, now we will choose for the construction of the triple layer the polypyrrole–DBS (dodecylbenzenesulphonate) blend, a CP that exchanges cations with the electrolyte during electro-chemical reactions (reaction (3)).65 Fig. 12B presents the attained bending movements (a, b, c) and the concomitant ionic exchanges (a′, b′, c′).
Fig. 13 presents, overlapped and normalized, the attained chronopotentiometric responses at different temperatures, The energy consumed during the angular displacement follows the theoretical description by eqn (9) as depicted by Fig. 14.
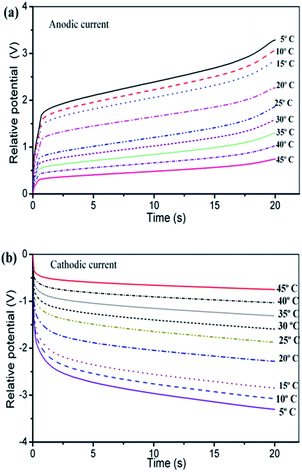 | ||
| Fig. 13 (a) Anodic and (b) cathodic chronopotentiometric responses attained when a triple layer artificial muscle polypyrrole–DBS/tape/polypyrrole–DBS was submitted to square current waves of ±3 mA at different temperatures indicated on the figure in 0.1 M LiClO4 aqueous solution driving a constant and reversible angular displacement of ±45 degrees of the triple layer actuator bottom. This figure has been reproduced from ref. 65 with permission from the Royal Society of Chemistry copyright 2011. | ||
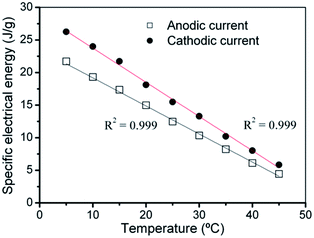 | ||
| Fig. 14 Linear evolution of the specific electrical energy consumed at different temperatures during the anodic and cathodic displacements of the triple-layer muscle corresponding to the experimental results shown in Fig. 13(a) and (b). The polypyrrole mass of the muscle reacting inside the electrolyte was 6.6 mg. R2 is the correlation coefficient of the linear fit. This figure has been reproduced from ref. 65 with permission from the Royal Society of Chemistry copyright 2011. | ||
As a partial conclusion eqn (9) describes the temperature influence on the energy consumed by those reactions involving macromolecular motors as reactants, does not matter if the polypyrrole oxidation originates the material expansion (reaction (2) forwards and Fig. 9b) or the material contraction (reaction (3) forwards and Fig. 14).
When the temperature increases from 5 to 45 °C the consumed anodic energy shifts from 27 to 9 J g−1: at 45 °C the energy consumed to perform every time the same angular displacement by the triple layer muscle drops up to 33,3% of the energy consumed to perform the same angular displacement (the same muscular work) at 5 °C. At 45 °C the muscle actuation saves, harvesting from the thermal environment, 66.6% of the energy consumed at 5 °C to perform the same muscular work.
Discussion
For any chemical or electrochemical reaction Arrhenius has stated the quantitative relationships between any reaction rate and the temperature (eqn (4)). In addition, the Electrochemically Stimulated Conformational Relaxation (ESCR) Model97–99 states that the reaction-driven actuation of compacted macromolecular motors involves two control processes: the initial conformational relaxation to open ionic channels through the material followed by the diffusion kinetic control of counterions from the solution inside the film.As for any other relaxation model (magnetic, mechanical or electrical) the conformational relaxation time (τ) of the macromolecular motors when the reaction of conducting polymer films begins is an exponential function of the molar reaction enthalpy (ΔH):
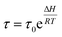 | (10) |
and the energy consumed by the reaction of one mole of polymeric segments (or macromolecular motors) involves three terms:
| ΔH = ΔH* + ΔHc − ΔHr = ΔH* + ηczc − ηrzr | (11) |
The ESCR model indicates that at rising temperatures the relaxation time decreases (eqn (10)) increasing the conformational relaxation rate. As a results the voltammetric oxidation peak (ηp = Ep − E0) shifts to lower overpotentials:99
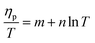 | (12) |
Faster conformational relaxation rates at rising temperatures means that the macromolecules act as thermo-mechanical transducers: they use increasing amounts of thermal energy from the environment to perform faster mechanical movements of the macromolecular motors. In addition, by reduction-compaction at the same cathodic potential for the same reduction time the empirical molar energy stored per by polymeric motors (ΔHc) increases linearly with the temperature, while zr remains constant.100
Otherwise for commodity polymers from the temperature influence on the diffusion, self-diffusion and reptation it was stated that, above the polymer glass transition temperature, Tg, the activation energy related to viscoelastic relaxation processes following the WLF (Williams–Landel–Ferry, which describes the temperature dependence of the diffusion coefficient) equation101 is a function of the experimental temperature:102
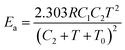 | (13) |
As conclusion, when any chemical or electrochemical reaction involves macromolecules as reactants the reaction rate and the reaction energy experience the synergic influence of three simultaneous effects: the Arrhenius law (eqn (4)), the increase of the conformational relaxation rate (eqn (12)) and the decrease of the diffusion coefficient (D) of the balancing counterions through the film (eqn (13)).
Conformational relaxation and diffusion processes can determine even if the reaction occurs or not. Whatever the electrical or chemical conditions the reaction does not occur at any temperature bellow the glass transition temperature of the macromolecular material: the total rigidity of the polymeric chains hinders either, the conformational movements of the chains, the cooperative actuation of the macromolecular motors, the generation inside the film of the free volume required to lodge balancing counterions and solvent, the penetration of balancing counterions and solvent from the solution to occupy that volume and the simultaneous extraction of electrons from the chains. The material acts below the Tg as a very high chemo-mechanical resistance becoming infinite the reaction resistance (the reaction activation energy, Ea → ∞).103 Otherwise reactions 2 and 3 are structural reactions linking free volume generation inside the film and counterion’ dimensions. Above the Tg very high chemo-mechanical resistances inhibit the reaction (2) forwards when the model material is checked in solutions of macro-anions, or polyelectrolytes where the anion is a polymer (polyanion).34 The emerging free volume that the actuation of the polymeric motors tries to generate in the film is not enough to lodge large macro-anions and the polymer oxidation is inhibited because the counterions cannot diffuse into the polymer (D → 0). The reversible oxidation/reduction of the polymer in its usual potential range is recovered as soon as the electrode is translated back to a solution with small counterions. Again the reaction resistance in a polyelectrolyte (only polymeric anions are present) solution is too high and the reaction is hindered inside the electrolyte potential window at any experimental temperature due to the counterion diffusion inhibition.
Thus, in presence of small counterions and above the Tg both, the conformational movements of the polymeric chains and the diffusion coefficient of the counterions are as faster as higher the working temperature is giving faster reaction rates (higher voltammetric currents) (Fig. 2a). Both, electrical (from the electrolyte) and chemical (form the film) resistances decrease very fast when the temperature rises by increase of either, the ionic mobility in the electrolyte, the conformational movement rate of the polymer chains in the film and the counterion diffusion flow through the swelling polymer film. Consequently, as in any parallel electric circuit, the reaction (driven by flow of a constant current) consumes decreasing energies to advance through the same reaction extension (flow of a constant charge by direct current flow for a constant time) when the involved resistances (electrical and chemical) drop, as depicted by Fig. 9b, 11 and 14.
Up to 60% of the energy consumed to produce a constant muscular displacement can be saved by increasing the temperature of the artificial muscle from 5 to 45° (Fig. 14). The cooperative actuation of: the Arrhenius effects, the conformational movements and the diffusion coefficient harvest from the thermal environment up to 60% of the energy required to perform the same muscular actuation when the temperature rises for 40 °C.
The macromolecular motors (natural or artificial) act, simultaneously, as electro-chemo-mechanical and thermo-mechanical transducers. They transform, simultaneously, electrical, chemical and thermal energy into mechanical energy.
Similar electrochemical responses to those here presented where attained at different temperatures using as model materials or model devices different conducting polymers (doesn't matter if exchanging anions95,104 or cations65 during the driving reaction), carbon nanotubes105 or graphenes.106
We can conclude that the electrochemical responses from model materials constituted by chemical macromolecular motors open the way for a quantitative description of the temperature-based efficiency gains observed in natural muscles from ectotherms bellow the efficiency maximum, as indicated at the introduction. In natural muscles higher efficiencies can be expected if we take into account that the mechanism of contraction involves a directional pulling on actin wile random conformational movements originate swelling/deswelling in model materials. Otherwise the entrance of calcium ions (ionic-electrical current) triggers the muscular actuation, which energy is provided by the ATP hydrolysis while the actuation of the model materials is initiated by the electric (electronic) current providing also the energy (electrical) required for the actuation of the macromolecular motors. Here counterions are required for the material charge balance during actuation of the macromolecular motors. Both calcium ions and counterions keep its charge during the muscular actuation. Model materials cannot reproduce the maximum of the temperature influence on the energetic efficiency of natural muscles, which could be related to the initiation of denaturation or degradation processes. Those differences between muscles and model materials indicate that a long scientific journey can drive, following the way open here, to improve the quantitative description of ectotherm muscular functions, and malfunctions, here initiated.
Technological perspectives
Electrochemical macromolecular motors from conducting polymers, carbon nanotubes, graphenes and other electroactive materials act as transducers between thermal, electrical, chemical and mechanical energies. The way is open now to translate those concepts attained form the temperature influence on both, the material reactions and the artificial muscles actuation to increase either, the energetic efficiencies, the transition times and the amplitude of the transient magnitude of any other electrical or electrochemical device working by cooperative actuation of macromolecular electrochemical motors: batteries and super-capacitors,107–118 smart windows,116,119–124 smart membranes,125–136 nervous interfaces or artificial chemical synapse,134,137–140 smart skins, smart drug delivery,141–146 ionic trapping,32,33,147 and so on.Thus, focusing on batteries, reaction (2) forwards indicates the charge of the positive electrode of a battery and reaction (2) backwards the discharge of the electrode constituted by macromolecular electrochemical motors. Fig. 6, 9b and 14 indicate that, whatever the charge/discharge methodology the magnitude of the charge stored and released increases very fast when the temperature of the electrode rises. That means that the time required to attain the same charged state (charge time) decreases very fast when performed at rising temperatures. Simultaneously the consumed energy (energy efficiency) decreases by 67%: the energy consumed to attain the same charged state decreases when the charge is performed at rising temperatures. The charging process stores energy from both sources: imposed electrical current and thermal environment. All those facts are of great technological interest in present days when the production and use of batteries is increasing exponentially. They are founded on the simultaneous actuation of the macromolecular motors from the electrodes as electro-chemo-mechanical and thermo-mechanical transducers, opening unexplored possibilities for batteries based on electrodes constituted by macromolecular electrochemical machines.
Similar reasons can be translated to the future development of any other of the above-mentioned bio-replicating devices based on materials constituted by macromolecular electrochemical motors. The attained results and theoretical descriptions can give back information to improve the description of natural muscles.
Biological perspectives
Translated to natural muscles from ectotherm animals the attained results indicate that coldblooded animals consume less chemical energy (ATP and glucose) to perform the same mechanical work (walking, running, digestion, and so on) when their body temperature is higher after heating by exposing to the sun light or to a thermal source. Eqn (4), (6) and (8) state an initial quantification of this influence under different experimental conditions. The different experimental methodologies applied to model materials and model devices can inspire different procedures to get the concomitant equation constants for natural muscle proteins. To do that scientist must attain a control enough of the natural macromolecular motor reactions with ATP to allow its physical chemical characterization under different experimental temperatures.14,19,21–28By using model materials the reaction saves between 40 and 60% of the consumed energy when the temperature rises from 5 to 40 °C (Fig. 9 and 14): the actuation of macromolecular motors at the higher temperature harvest up to 60% of the consumed energy from the thermal environment. We can hope that nature, which has been selecting and improving protein macromolecular motors for millions of years to get a directional pulling mechanism of contraction has attained still higher efficiencies than those here described from random conformational movements.
Natural muscles from coldblooded animals harvest thermal energy by the synergic actuation of three combined effects: the Arrhenius influence on the reaction rate (eqn (4)), the temperature influence on the rate of the conformational movements (eqn (12)) and the temperature influence on activation energy of counterions (ATP) diffusion coefficient (eqn (12)). From those equations and other basic concepts from Polymer Science, Electrochemical Kinetics and Mechanics a full theoretical description and quantification of the macroscopic and molecular events involving chemical and electrochemical biological macromolecular motors (ion channel proteins, generation and transmission of nervous pulses, electro-chemo-mechanical information storage, enzymatic reactions, respiration allosteric reactions, and so on) can be attained. Those theoretical descriptions and quantifications should pave the way for a theoretical electro-chemo-mechanical description of different biological functions, from muscular actuation with mechanical proprioception to brain functions.
As usual when the reactions involve macromolecular motors despite consuming equal anodic and cathodic charges (Fig. 4b) the consumed anodic and cathode energies are asymmetric, Fig. 9 and 14: the energy consumed to relax-swell the macromolecular motors is different than that required to shrink-contract them. Nature, using natural macromolecular motors has selected and improved the most efficient (reaction (1) forwards for muscles) to develop asymmetric muscular actuation: muscles only work by contraction, which means that the energy consumed by the antagonist muscle for the muscle relaxation is lower than that consumed by reaction (1) backwards.
In a similar way many other asymmetric biological functions involve the actuation of macromolecular (protein) motors: ionic pulses through ionic channels constituted by electro-chemo-mechanical proteins only allow one way ionic flow, nervous pulses always move from dendrites to axons or enzymatic allosteric reactions are irreversible reactions. As a fortunate exception despite this energetic asymmetry the hemoglobin-oxygen allosteric reaction is reversible in the sense that it takes oxygen from the lungs (or other respiration organs) when the oxygen concentration is high carrying it to any organ and liberating the oxygen to any cell where the oxygen concentration is low. Now the study of the energetic reasons behind biological asymmetric functions can be envisaged following experimental procedures inspired by those above described for model materials.
Otherwise, if the evolution of the muscular reaction energy includes, at any actuating time, quantitative information about the muscular temperature (eqn (6)–(9)) a fraction of this reaction energy can act on the temperature sensing ionic channel proteins (electro-chemical macromolecular motors) of the sensory neuron generating at the muscle/dendrite interface the nervous pulse transferring to the brain this quantitative thermal information. This hypothesis can open the way to clarify the origin of the nervous pulse carrying this information that still remains unknown.
Last but not least eqn (10) and (11) describe that those reactions involving macromolecular motors include quantitative information about the conformational electro-chemo-mechanical energy (zcηc) stored by the contracted state of the motor, e.g. quantitative information storage in ion channel proteins in neurons. This conformational energy stored by the conformational state defined by the specific electro-chemo-mechanical conditions at each channel protein generation time are read and carried by each generated ionic pulse during the channel opening and then restored during the channel closing for every opening/closing channel cycle. Those facts open a possible way to explore and quantify how brain can store, read and transfer quantitative information between neurons. The basic information unit should be stored by the conformational energetic state of the closed channel protein imposed by the specific physical chemical conditions at the channel formation time. The energy of each generated ionic pulse during the channel lifetime should read, carry this stored information, which is restored every time during the channel closing. If we corroborate the basic brain mechanism to store and read information a long and fascinating scientific way should be open to decipher how brain functions are generated from the concomitant information packages.
Conclusions
The electrochemistry of conducting polymers, carbon nanotubes, graphenes and other electroactive materials provides model materials of the functional biological reactions originating different biological functions: dense reactive gels constituted by multi-step macromolecular motors, ions and solvent.This reactive composition replicates the basic active components of the muscular sarcomere which reaction originates the muscular contraction.
Those reactive materials can be considered as model materials of the muscular actuation and its reactions as model reactions of those taking place in the muscle sarcomere. The artificial muscles constructed using those materials can be taken as model devices of natural muscles.
In order to attempt a replication of the physical chemical behavior of muscles from ectoderm animals both, model reactions and model devices have been used to determine the influence of the reaction temperature on both, the reaction extension and the energy consumed by the reaction.
The experimental study gives, using different electrochemical methodologies, the empirical equations quantifying the thermal influence on the cooperative actuation of the macromolecular electrochemical motors, whatever, artificial or natural. Those equations were theoretically attained from the basic principles of the chemical and electrochemical kinetics. The theoretical description fits the experimental results.
Rising temperatures decrease the reaction resistance, as described by the Arrhenius expression, with a synergic effect by the parallel faster conformational movements of the reacting macromolecular motors and the faster diffusion coefficients of the counterions. Macromolecular motors act, simultaneously, as electro-chemo-mechanical and thermo-mechanical transducers.
Under constant electro-chemical stimulus (cyclic voltammetry) the reaction extension described by the consumed charge increases under rising temperatures because either, the amplitude of the conformational movements, the free volume generated by cooperative actuation of the molecular motors, the number of counterions and solvent molecules lodged in this volume for charge compensation and osmotic balance and the concomitant number of electrons extracted from the chains increase when the temperature rises. The consumed charge responds to, adapts to and senses (eqn (6)) the working temperature.
Under a constant reaction extension, which means constant muscular displacement and constant muscular work, the consumed energy decreases for rising working temperatures. That means that under higher muscular temperature the reaction involving macromolecular motors in ectotherm animal muscles harvests rising amounts of thermal energy from the environment saving chemical energy.
Similar conclusions were attained using linear or bending artificial muscles as model devices which driving reactions exchange anions or cations during actuation.
Eqn (9) describes how the reaction energy adapts to, responds to and senses, at any reaction time (after any constant displacement of the muscular movement) the muscular temperature giving the harvesting energetic efficiency of muscular reactions in ectotherm animals.
If the evolution of the reaction energy includes, at any actuating time, quantitative information about the muscular temperature a fraction of this reaction energy can act on the temperature sensing ionic channel proteins (electro-chemical macromolecular motors) of the sensory neuron generating at the muscle/dendrite interface the nervous pulse (the origin still unknown) transferring to the brain this thermal information.
Those conclusions can be translated to any biological function originated by, and to any electrochemical device working by, electro-chemo-mechanical and/or thermo-mechanical actuation of macromolecular motors. Natural and artificial devices link chemical, electrical, thermal and mechanical energies.
Conflicts of interest
There are not conflicts to declare.Acknowledgements
We acknowledge the Universitat de Valencia for an invited professor grant, The Universidad Politécnica de Cartagena for a Sabbatical grant and the Spanish MCIU for the Unidad de Excelencia María de Maeztu CEX2019-000919 M.References
- T. F. Otero and J. G. Martinez, J. Mater. Chem. B, 2013, 1, 26–38 RSC.
- T. F. Otero, Electrochim. Acta, 2021, 368, 137576 CrossRef CAS.
- T. F. Otero, Conducting Polymers: Bioinspired Intelligent Materials and Devices, RSC, 2015 Search PubMed.
- Q. Pei and O. Inganas, Adv. Mater., 1992, 4, 277–278 CrossRef CAS.
- T. Otero, E. Angulo, J. Rodriguez and C. Santamaria, J. Electroanal. Chem., 1992, 341, 369–375 CrossRef CAS.
- R. H. Baughman, Synth. Met., 1996, 78, 339–353 CrossRef CAS.
- S. M. Mirvakili and I. W. Hunter, Adv. Mater., 2018, 30, 1704407 CrossRef PubMed.
- D. Melling, J. G. Martinez and E. W. H. Jager, Adv. Mater., 2019, 31, 1808210 CrossRef PubMed.
- M. Zou, S. Li, X. Hu, X. Leng, R. Wang, X. Zhou and Z. Liu, Adv. Funct. Mater., 2007437 Search PubMed.
- F. Hu, Y. Xue, J. Xu and B. Lu, Front. Robot. Ai, 2019, 6, 114 CrossRef PubMed.
- T. F. Otero, in Modern Aspects of Electrochemistry, ed. R. E. White, J. O. Bockris and B. E. Conway, Springer US, New York, 1999, pp. 307–434 Search PubMed.
- A. Huxley and R. Simmons, Nature, 1971, 233, 533 CrossRef CAS PubMed.
- J. Alvarado and G. H. Koenderink, in Building a Cell from Its Component Parts, ed. J. Ross and W. F. Marshall, Elsevier Academic Press Inc, San Diego, 2015, vol. 128, pp. 83–103 Search PubMed.
- A. Kakugo, K. Shikinaka, J. P. Gong and Y. Osada, Polymer, 2005, 46, 7759–7770 CrossRef CAS.
- M. J. Angilletta, P. H. Niewiarowski and C. A. Navas, J. Therm. Biol., 2002, 27, 249–268 CrossRef.
- R. Huey and J. Kingsolver, Trends Ecol. Evol., 1989, 4, 131–135 CrossRef CAS PubMed.
- W. I. Lutterschmidt and V. H. Hutchison, Can. J. Zool., 1997, 75, 1561–1574 CrossRef.
- T. Gleeson, I. Johnston, B. Sidell and W. Stephens, J. Physiol., 1984, 346, P65 Search PubMed.
- E. Lin and H. Cantiello, Biophys. J., 1993, 65, 1371–1378 CrossRef CAS PubMed.
- R. Rossi, M. Maffei, R. Bottinelli and M. Canepari, J. Appl. Physiol., 2005, 99, 2239–2245 CrossRef CAS PubMed.
- M. G. L. van den Heuvel and C. Dekker, Science, 2007, 317, 333–336 CrossRef CAS PubMed.
- P. Calvert, MRS Bull., 2008, 33, 207–212 CrossRef.
- J.-F. Joanny and J. Prost, HFSP J., 2009, 3, 94–104 CrossRef CAS PubMed.
- A. M. R. Kabir, A. Kakugo, J. P. Gong and Y. Osada, Macromol. Biosci., 2011, 11, 1314–1324 CrossRef CAS PubMed.
- Y. Osada and J. P. Gong, Polym. Sci., Ser. A, 2009, 51, 689–700 CrossRef.
- J. Alvarado and G. H. Koenderink, in Building a Cell from Its Component Parts, ed. J. Ross and W. F. Marshall, Elsevier Academic Press Inc, San Diego, 2015, vol. 128, pp. 83–103 Search PubMed.
- K. Okamoto, H. Ueda, T. Shimada, K. Tamura, T. Kato, M. Tasaka, M. T. Morita and I. Hara-Nishimura, Nat. Plants, 2015, 1, 15031 CrossRef CAS PubMed.
- M. A. Geeves, Biopolymers, 2016, 105, 483–491 CrossRef CAS PubMed.
- R. S. James, J. Comp. Physiol., B, 2013, 183, 723–733 CrossRef PubMed.
- T. F. Otero, Mod. Aspects Electrochem., 1999, 33, 307–434 CAS.
- T. F. Otero and J. G. Martinez, J. Mater. Chem. B, 2016, 4, 2069–2085 RSC.
- A. R. Hillman, S. J. Daisley and S. Bruckenstein, Electrochim. Acta, 2008, 53, 3763–3771 CrossRef CAS.
- J. Bisquert, Electrochim. Acta, 2002, 47, 2435–2449 CrossRef CAS.
- T. F. Otero, M. Alfaro, V. Martinez, M. A. Perez and J. G. Martinez, Adv. Funct. Mater., 2013, 23, 3929–3940 CrossRef CAS.
- T. F. Otero, Polym. Rev., 2013, 53, 311–351 CrossRef CAS.
- Y. Harima, F. Ogawa, R. Patil and X. Jiang, Electrochim. Acta, 2007, 52, 3615–3620 CrossRef CAS.
- X. Lin, J. Li, E. Smela and S. Yip, Int. J. Quantum Chem., 2005, 102, 980–985 CrossRef CAS.
- S. Stafstrom, J. Bredas, A. Epstein, H. Woo, D. Tanner, W. Huang and A. Macdiarmid, Phys. Rev. Lett., 1987, 59, 1464–1467 CrossRef CAS PubMed.
- O. Khatib, A. S. Mueller, H. T. Stinson, J. D. Yuen, A. J. Heeger and D. N. Basov, Phys. Rev. B, 2014, 90, 235307 CrossRef.
- The Nobel Prize in Chemistry, 2016, 2020, https://www.nobelprize.org/prizes/chemistry/2016/summary/ Search PubMed.
- J. P. Sauvage and P. Gaspard, From Non-Covalent Assemblies to Molecular Machines, John Wiley & Sons, Weinheim, 2011 Search PubMed.
- B. L. Feringa, Acc. Chem. Res., 2001, 34, 504–513 CrossRef CAS PubMed.
- V. Balzani, A. Credi, F. M. Raymo and J. F. Stoddart, Angew. Chem., Int. Ed., 2000, 39, 3348–3391 CrossRef CAS PubMed.
- Y. Liu, A. H. Flood, P. A. Bonvallett, S. A. Vignon, B. H. Northrop, H. R. Tseng, J. O. Jeppesen, T. J. Huang, B. Brough, M. Baller, S. Magonov, S. D. Solares, W. A. Goddard, C. M. Ho and J. F. Stoddart, J. Am. Chem. Soc., 2005, 127, 9745–9759 CrossRef CAS PubMed.
- M. Baroncini, L. Casimiro, C. de Vet, J. Groppi, S. Silvi and A. Credi, Chemistryopen, 2018, 7, 169–179 CrossRef CAS PubMed.
- K. Kinbara and T. Aida, Chem. Rev., 2005, 105, 1377–1400 CrossRef CAS PubMed.
- A. B. Kolomeisky, J. Phys.: Condens. Matter, 2013, 25, 463101 CrossRef PubMed.
- G. H. Lorimer, A. Horovitz and T. McLeish, Philos. Trans. R. Soc., B, 2018, 373, 20170173 CrossRef PubMed.
- T. F. Otero and J. G. Martinez, Adv. Funct. Mater., 2014, 24, 1259–1264 CrossRef CAS.
- T. Otero, I. Boyano, M. Cortes and G. Vázquez, Electrochim. Acta, 2004, 49, 3719–3726 CrossRef CAS.
- T. F. Otero and I. Boyano, Chemphyschem, 2003, 4, 868–872 CrossRef CAS PubMed.
- T. F. Otero, J. G. Martinez, M. Fuchiwaki and L. Valero, Adv. Funct. Mater., 2014, 24, 1265–1274 CrossRef CAS.
- Q. Pei and O. Inganas, J. Phys. Chem., 1992, 96, 10507–10514 CrossRef CAS.
- P. Chiarelli, D. Derossi, A. Dellasanta and A. Mazzoldi, Polym. Gels Networks, 1994, 2, 289–297 CrossRef CAS.
- E. Smela and N. Gadegaard, Adv. Mater., 1999, 11, 953 CrossRef CAS.
- D. S. H. Charrier, R. A. J. Janssen and M. Kemerink, Chem. Mater., 2010, 22, 3670–3677 CrossRef CAS.
- X. Chen and O. Inganas, Synth. Met., 1995, 74, 159–164 CrossRef CAS.
- E. M. Andrade, F. V. Molina, M. I. Florit and D. Posadas, Electrochem. Solid-State Lett., 2000, 3, 504–507 CrossRef CAS.
- M. F. Suarez and R. G. Compton, J. Electroanal. Chem., 1999, 462, 211–221 CrossRef CAS.
- T. F. Otero and S. Beaumont, Electrochim. Acta, 2017, 257, 403–411 CrossRef CAS.
- T. F. Otero, Electrochim. Acta, 2016, 212, 440–457 CrossRef CAS.
- S. Beaumont and T. F. Otero, Chemelectrochem, 2017, 4, 3091–3099 CrossRef CAS.
- Y. A. Ismail, J. G. Martinez, A. S. Al Harrasi, S. J. Kim and T. F. Otero, Sens. Actuators, B, 2011, 160, 1180–1190 CrossRef CAS.
- T. F. Otero, J. J. Sanchez and J. G. Martinez, J. Phys. Chem. B, 2012, 116, 5279–5290 CrossRef CAS PubMed.
- F. Garcia-Cordova, L. Valero, Y. A. Ismail and T. Fernandez Otero, J. Mater. Chem., 2011, 21, 17265–17272 RSC.
- A. DellaSanta, D. DeRossi and A. Mazzoldi, Synth. Met., 1997, 90, 93–100 CrossRef CAS.
- L. Bay, K. West, P. Sommer-Larsen, S. Skaarup and M. Benslimane, Adv. Mater., 2003, 15, 310–313 CrossRef CAS.
- K. Yamato and K. Kaneto, Anal. Chim. Acta, 2006, 568, 133–137 CrossRef CAS PubMed.
- F. Vidal, C. Plesse, G. Palaprat, A. Kheddar, J. Citerin, D. Teyssie and C. Chevrot, Synth. Met., 2006, 156, 1299–1304 CrossRef CAS.
- R. Kiefer, S. Y. Chu, P. A. Kilmartin, G. A. Bowmaker, R. P. Cooney and J. Travas-Sejdic, Electrochim. Acta, 2007, 52, 2386–2391 CrossRef CAS.
- S. J. Park, M. S. Cho, J. D. Nam, I. H. Kim, H. R. Choi, J. C. Koo and Y. Lee, Sens. Actuators, B, 2009, 135, 592–596 CrossRef CAS.
- H. Okuzaki, K. Hosaka, H. Suzuki and T. Ito, React. Funct. Polym., 2013, 73, 986–992 CrossRef CAS.
- N. Aydemir, P. A. Kilmartin, J. Travas-Sejdic, A. Kesküla, A.-L. Peikolainen, J. Parcell, M. Harjo, A. Aabloo and R. Kiefer, Sens. Actuators, B, 2015, 216, 24–32 CrossRef CAS.
- G. Alici, P. Metz and G. M. Spinks, in Ieee/Asme International Conference on Advanced Intelligent Mechatronics, Ieee, New York, 2005, vol. 1 and 2, pp. 1029–1034 Search PubMed.
- P. Du, X. Lin and X. Zhang, Sens. Actuators, A, 2010, 163, 240–246 CrossRef CAS.
- S. Maw, E. Smela, K. Yoshida, P. Sommer-Larsen and R. B. Stein, Sens. Actuators, A, 2001, 89, 175–184 CrossRef CAS.
- T. Okamoto, K. Tada and M. Onoda, Jpn. J. Appl. Phys., Part 1, 2000, 39, 2854–2858 CrossRef CAS.
- K. Asaka, K. Mukai, T. Sugino, H. Randriamahazaka and T. Fernandez Otero, Electroact. Polym. Actuators Devices Eapad, 2013, 2013, 8687 Search PubMed.
- R. H. Baughman, C. Cui, A. A. Zakhidov, Z. Iqbal, J. N. Barisci, G. M. Spinks, G. G. Wallace, A. Mazzoldi, D. De Rossi, A. G. Rinzler, O. Jaschinski, S. Roth and M. Kertesz, Science, 1999, 284, 1340–1344 CrossRef CAS PubMed.
- P. Giménez, K. Mukai, K. Asaka, K. Hata, H. Oike and T. Otero, Electrochim. Acta, 2012, 60, 177–183 CrossRef.
- L. Lu, J. Liu, Y. Hu, Y. Zhang, H. Randriamahazaka and W. Chen, Adv. Mater., 2012, 24, 4317–4321 CrossRef CAS PubMed.
- K. Mukai, K. Asaka, K. Hata, T. Fernandez Otero and H. Oike, Chem.–Eur. J., 2011, 17, 10965–10971 CrossRef CAS PubMed.
- J.-H. Jung, J.-H. Jeon, V. Sridhar and I.-K. Oh, Carbon, 2011, 49, 1279–1289 CrossRef CAS.
- L. Kong and W. Chen, Adv. Mater., 2014, 26, 1025–1043 CrossRef CAS PubMed.
- T. Otero, E. Angulo, J. Rodriguez and C. Santamaria, J. Electroanal. Chem., 1992, 341, 369–375 CrossRef CAS.
- Y. Wu, G. Alici, G. M. Spinks and G. G. Wallace, Synth. Met., 2006, 156, 1017–1022 CrossRef CAS.
- T. F. Otero and J. G. Martinez, Sens. Actuators, B, 2014, 199, 27–30 CrossRef CAS.
- T. F. Otero and M. T. Cortes, in Smart Structures and Materials 2000: Electroactive Polymer Actuators and Devices (eapad), ed. Y. BarCohen, 2000, vol. 3987, pp. 252–260 Search PubMed.
- T. F. Otero, M. T. Cortes and G. V. Arenas, Electrochim. Acta, 2007, 53, 1252–1258 CrossRef CAS.
- S. W. John, G. Alici and C. D. Cook, Ieee-Asme Trans. Mechatron., 2010, 15, 149–156 Search PubMed.
- C. V. Fengel, N. P. Bradshaw, S. Y. Severt, A. R. Murphy and J. M. Leger, Smart Mater. Struct., 2017, 26, 055004 CrossRef.
- J. G. Martinez and T. F. Otero, Electrochim. Acta, 2019, 294, 126–133 CrossRef CAS.
- U. L. Zainudeen, M. A. Careem and S. Skaarup, Sens. Actuators, B, 2008, 134, 467–470 CrossRef CAS.
- T. F. Otero and J. G. Martinez, Prog. Polym. Sci., 2015, 44, 62–78 CrossRef CAS.
- T. Otero and M. Cortes, Sens. Actuators, B, 2003, 96, 152–156 CrossRef CAS.
- L. Valero, J. Arias-Pardilia, M. Smit, J. Cauich-Rodriguez and T. F. Otero, Polym. Int., 2010, 59, 337–342 CrossRef CAS.
- T. F. Otero, H. J. Grande and J. Rodriguez, J. Phys. Chem. B, 1997, 101, 3688–3697 CrossRef CAS.
- T. F. Otero, H. Grande and J. Rodriguez, Electrochim. Acta, 1996, 41, 1863–1869 CrossRef CAS.
- T. F. Otero, H. Grande and J. Rodriguez, J. Phys. Chem. B, 1997, 101, 8525–8533 CrossRef CAS.
- T. F. Otero and H. Grande, J. Electroanal. Chem., 1996, 414, 171–176 Search PubMed.
- M. L. Williams, R. F. Landel and J. D. Ferry, J. Am. Chem. Soc., 1955, 77, 3701–3707 CrossRef CAS.
- R. Bachus and R. Kimmich, Polymer, 1983, 24, 964–970 CrossRef CAS.
- T. F. Otero, Phys. Chem. Chem. Phys., 2017, 19, 1718–1730 RSC.
- L. Valero Conzuelo, J. Arias-Pardilla, J. V. Cauich-Rodriguez, M. Afra Smit and T. Fernandez Otero, Sensors, 2010, 10, 2638–2674 CrossRef PubMed.
- J. G. Martinez, T. Sugino, K. Asaka and T. F. Otero, Chemphyschem, 2012, 13, 2108–2114 CrossRef CAS PubMed.
- J. G. Martinez, T. F. Otero, C. Bosch-Navarro, E. Coronado, C. Marti-Gastaldo and H. Prima-Garcia, Electrochim. Acta, 2012, 81, 49–57 CrossRef CAS.
- B. Conway, J. Electrochem. Soc., 1991, 138, 1539–1548 CrossRef CAS.
- T. Otero, C. Santamaria and J. Rodriguez, in Electrical, Optical, and Magnetic Properties of Organic Solid State Materials, ed. A. F. Garito, A. K. Y. Jen, C. Y. C. Lee and L. R. Dalton, 1994, vol. 328, pp. 805–810 Search PubMed.
- C. Barbero, M. C. Miras, R. Kötz and O. Haas, J. Electroanal. Chem., 1997, 437, 191–198 CrossRef CAS.
- J. A. Irvin, D. J. Irvin and J. D. Stenger-Smith, in Handbook of Conducting Polymers, ed. T. A. Skotheim, R. L. Elsenbaumer and J. R. Reynolds, CRC Press, Boca Raton, 2007, vol. 2 Search PubMed.
- J.-Z. Wang, S.-L. Chou, J. Chen, S.-Y. Chew, G.-X. Wang, K. Konstantinov, J. Wu, S.-X. Dou and H. K. Liu, Electrochem. Commun., 2008, 10, 1781–1784 CrossRef CAS.
- S. Biswas and L. T. Drzal, Chem. Mater., 2010, 22, 5667–5671 CrossRef CAS.
- Y. Fang, J. Liu, D. J. Yu, J. P. Wicksted, K. Kalkan, C. O. Topal, B. N. Flanders, J. Wu and J. Li, J. Power Sources, 2010, 195, 674–679 CrossRef CAS.
- I. Sultana, M. M. Rahman, J. Wang, C. Wang, G. G. Wallace and H.-K. Liu, Solid State Ionics, 2012, 215, 29–35 CrossRef CAS.
- G. Abellan, E. Coronado, C. Marti-Gastaldo, A. Ribera and T. F. Otero, Part. Part. Syst. Charact., 2013, 30, 853–863 CrossRef CAS.
- J. Wang, L. Zhang, L. Yu, Z. Jiao, H. Xie, X. W. (David) Lou and X. W. Sun, Nat. Commun., 2014, 5, ncomms5921 Search PubMed.
- K. D. Fong, T. Wang and S. K. Smoukov, Sustainable Energy Fuels, 2017, 1, 1857–1874 RSC.
- E. Gradzka, M. Wysocka-Zolopa and K. Winkler, Adv. Energy Mater., 2020, 10, 2001443 CrossRef CAS.
- D. Ofer, R. M. Crooks and M. S. Wrighton, J. Am. Chem. Soc., 1990, 112, 7869–7879 CrossRef CAS.
- V. Seshadri, J. Padilla, H. Bircan, B. Radmard, R. Draper, M. Wood, T. F. Otero and G. A. Sotzing, Org. Electron., 2007, 8, 367–381 CrossRef CAS.
- A. L. Dyer and J. R. Reynolds, in Handbook of Conducting Polymers, eds. T. A. Skotheim, R. M. Elsenbaumer and J. R. Reynolds, CRC Press, Boca Raton, 2007, vol. 1 Search PubMed.
- C. M. Amb, A. L. Dyer and J. R. Reynolds, Chem. Mater., 2011, 23, 397–415 CrossRef CAS.
- P. M. Beaujuge and J. R. Reynolds, Chem. Rev., 2010, 110, 268–320 CrossRef CAS.
- R. Celiesiute, A. Ramanaviciene, M. Gicevicius and A. Ramanavicius, Crit. Rev. Anal. Chem., 2019, 49, 195–208 CrossRef CAS PubMed.
- P. Burgmayer and R. Murray, J. Phys. Chem., 1984, 88, 2515–2521 CrossRef CAS.
- D. Feldheim and C. Elliott, J. Membr. Sci., 1992, 70, 9–15 CrossRef CAS.
- C. Ehrenbeck and K. Juttner, Electrochim. Acta, 1996, 41, 511–518 CrossRef CAS.
- C. Deslouis, T. E. Moustafid, M. M. Musiani, M. E. Orazem, V. Provost and B. Tribollet, Electrochim. Acta, 1999, 44, 2087–2093 CrossRef CAS.
- A. C. Partridge, C. B. Milestone, C. O. Too and G. G. Wallace, J. Membr. Sci., 1999, 152, 61–70 CrossRef CAS.
- J. Pellegrino, in Advanced Membrane Technology, ed. N. N. Li, E. Drioli, W. S. W. Ho and G. G. Lipscomb, New York Acad Sciences, New York, 2003, vol. 984, pp. 289–305 Search PubMed.
- M. J. Ariza and T. F. Otero, J. Membr. Sci., 2007, 290, 241–249 CrossRef CAS.
- F. D. R. Amado, M. A. S. Rodrigues, F. D. P. Morisso, A. M. Bernardes, J. Z. Ferreira and C. A. Ferreira, J. Colloid Interface Sci., 2008, 320, 52–61 CrossRef CAS PubMed.
- S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467, 190 CrossRef CAS PubMed.
- T. Otero, J. Martinez and J. Arias-Pardilla, Electrochim. Acta, 2012, 84, 112–128 CrossRef CAS.
- M. Miculescu, V. K. Thakur, F. Miculescu and S. I. Voicu, Polym. Adv. Technol., 2016, 27, 844–859 CrossRef CAS.
- S. Noh, J. Y. Jeon, S. Adhikari, Y. S. Kim and C. Bae, Acc. Chem. Res., 2019, 52, 2745–2755 CrossRef CAS PubMed.
- S. Y. Kim, K.-M. Kim, D. Hoffman-Kim, H.-K. Song and G. T. R. Pamore, ACS Appl. Mater. Interfaces, 2011, 3, 16–21 CrossRef CAS PubMed.
- P. Fattahi, G. Yang, G. Kim and M. R. Abidian, Adv. Mater., 2014, 26, 1846–1885 CrossRef CAS PubMed.
- Y. van de Burgt, E. Lubberman, E. J. Fuller, S. T. Keene, G. C. Faria, S. Agarwal, M. J. Marinella, A. A. Talin and A. Salleo, Nat. Mater., 2017, 16, 414–418 CrossRef CAS PubMed.
- C. Jiang, Y. Zhang, B. Tian, C. Luo, N. Zhong, J. Wang, X. Meng, H. Peng, C.-G. Duan and J. Chu, J. Mater. Chem. C, 2019, 7, 9933–9938 RSC.
- A. A. Entezami and B. Massoumi, Iran. Polym. J., 2006, 15, 13–30 CAS.
- S. Geetha, C. R. K. Rao, M. Vijayan and D. C. Trivedi, Anal. Chim. Acta, 2006, 568, 119–125 CrossRef CAS PubMed.
- S. Goenka, V. Sant and S. Sant, J. Controlled Release, 2014, 173, 75–88 CrossRef CAS PubMed.
- V. Pillay, T.-S. Tsai, Y. E. Choonara, L. C. du Toit, P. Kumar, G. Modi, D. Naidoo, L. K. Tomar, C. Tyagi and V. M. K. Ndesendo, J. Biomed. Mater. Res., Part A, 2014, 102, 2039–2054 CrossRef PubMed.
- K. Yang, L. Feng and Z. Liu, Adv. Drug Delivery Rev., 2016, 105, 228–241 CrossRef CAS PubMed.
- A. Puiggali-Jou, L. J. del Valle and C. Aleman, J. Controlled Release, 2019, 309, 244–264 CrossRef CAS PubMed.
- K. Borzutzki, D. Dong, C. Woelke, M. Kruteva, A. Stellhorn, M. Winter, D. Bedrov and G. Brunklaus, Iscience, 2020, 23, 101417 CrossRef CAS PubMed.
Footnote |
| † Present address: Instituto de Ciencia Molecular (ICMol), Universidad de Valencia, Catedrático José Beltrán 2, Paterna, 46980, Valencia, Spain. |
| This journal is © The Royal Society of Chemistry 2021 |


