Open Access Article
Open Access ArticleMeasurement of CO2 diffusion coefficients in both bulk liquids and carven filling porous media of fractured-vuggy carbonate reservoirs at 50 MPa and 393 K
Zhixing Wang ab and
Jirui Hou*ab
ab and
Jirui Hou*ab
aResearch Institute of Enhanced Oil Recovery, Unconventional Petroleum Research Institute, China University of Petroleum (Beijing), Beijing, 102249, China. E-mail: zhxwang0315@126.com; Tel: +86 13998768792
bKey Laboratory for Greenhouse Gas Sequestration and Oil Exploitation in Beijing, Unconventional Petroleum Research Institute, Beijing, 102249, China. E-mail: houjirui@126.com; Tel: +86 13718816146
First published on 1st June 2021
Abstract
Diffusion coefficients are necessary to describe the mass transfer and adsorption rate of CO2 in formation fluids. However, data is scarcely reported for actual reservoir conditions of high pressure and temperature, which are normal in most scenarios of the CO2-enhanced oil recovery process in China's fractured-vuggy reservoirs and carbon storage process. Accordingly, this work employed the pressure decay method (PD) and relevant mathematical models to determine the CO2 diffusion coefficient in both liquids and cavern filling porous media at 50 MPa and 393 K. The effects of the type of reservoir fluids, the properties of carven filling porous media, and water saturation on CO2 diffusion coefficients were investigated. Results in bulk reservoir liquids showed that the CO2 diffusion coefficient in the oil sample was 4.1243 × 10−8 m2 s−1, much higher than those in the pure alkane phase, pure water and brine sample from reservoirs. Results of CO2 diffusion in carven filling porous media saturated with oil demonstrated a significant dependence on properties such as porosity and permeability, and a correlation in the CO2 diffusion coefficients between the bulk oil phase and cavern filling porous media in the form of touristy was documented. CO2 diffusion in the fractured cavern porous media was much higher than that without fracture. An increase in water saturation reduced CO2 diffusion coefficients in the carven filling porous medium studied, herein. Thus, the CO2 diffusion coefficient is essentially related to the type of liquid and properties of the filling media.
1 Introduciton
Geological storage of CO2 gas in deep saline aquifers or depleted oil reservoirs is considered an efficient way to reduce the carbon emission. For petroleum industries, oil recovery can be increased by CO2 injection as a process fluid into a depleted reservoir. The Tahe oilfield has become the largest marine carbonate hydrocarbon reservoir in China with its equivalent oil–gas reserve at the billion-ton level.1–3 There are huge potentials for CO2 storage in this Ordovician carbonate reservoir given that fracture networks and cavities are abundant.4 Recently, gas injection has been applied in this reservoir.5,6 By injecting gas into the fracture-cavity production unit, gas contacts the formation fluid via diffusion, which causes the oil to swell, reduces the oil viscosity, extracts the light component, lowers the interfacial tension (IFT) and suppresses the water crest.7–11 Therefore, the volumetric sweeping and displacement efficiency are drastically improved.The diffusion coefficient is one of the most basic parameters to determine the mixing rate of the injection gas and reservoir liquids.12–14 A solution of gas in crude oil causes a series of property changes such as reduction in viscosity and volume expansion, which consequently improve the oil mobility and production capability.15 From the macroscopic point of view of oil stimulation, the gas diffusion process determines the sweeping efficiency, injection optimization and prediction of gas channeling. The gas diffusivity is also a key parameter to study the enhanced oil recovery mechanism in fractured reservoirs.16,17 Thus, it is of great importance to investigate the gas diffusivity under real reservoir conditions.
Extensive work has been carried out to determine the diffusion coefficients of carbon dioxide in formation liquids under reservoir conditions. For CO2 diffusivity in saline aquifers, Raad et al.18 studied the CO2 diffusivity in synthetic and saline aquifer solutions in the temperature range of 303–310 K and pressure range of 5.88–6.265 MPa. Values in an extended temperature range (268–473 K) at pressures up to 45 MPa were obtained by Lu et al.19 and a power-law relationship with temperature was derived. CO2 diffusion coefficients under similar conditions were also measured by Cadogan20 and correlated with the classical Stokes–Einstein equation. For engineering use, Renner21 introduced an empirical function simply considering the viscosity of solutions and CO2 to predict the CO2 diffusion coefficient for in water or brine. For CO2 diffusivity in hydrocarbon liquids, Schmidt et al.22 measured the CO2 diffusion coefficient in heavy oil at temperatures varying from 293 K to 473 K and pressure of up to 5 MPa, where the temperature was the first reported over 373 K. Values in pure alkanes were reported by Wang et al.23,24 and Cadogan et al.25 at temperatures between 298.15 and 423.15 K and pressures up to 69 MPa.
Due to confinement and tortuosity, the phase behaviors of CO2-alkane systems26 and mass transfer27 differ from that in the bulk phase, and studies on CO2 diffusivity in porous media were reported recently. Li and Dong28,29 calculated the effective CO2 diffusion coefficient in Berea cores saturated with n-hexadecane and concluded that the values were slightly dependent on the pressure variation from 2.3 to 6.3 MPa. The effects of oil saturation and tortuosity on CO2 diffusivity in porous media of low permeability were studied by Li et al.,30 and it was found that the diffusion coefficients were strongly dependent on the oil saturation and permeability of the porous media. Gao et al.31 correlated the CO2 diffusion coefficient with the permeability of porous media by tortuosity and found that high tortuosity retards the CO2 diffusivity by limiting the gas solubility.
However, the previous measurements of diffusion coefficients still need to be further extended. For CO2 diffusivity in bulk liquids, theoretical models can achieve high accuracy at a wide range of temperatures and pressures for carbon capture and storage (CCS), but the data of CO2 diffusion coefficients in alkane mixtures and crude oil is still deficient under real reservoir conditions. For example, the pressure in most reported data is below 10 MPa, which is critical for miscible flooding during gas flooding. For CO2 diffusivity in porous media, the existing data only covers a limited range of temperatures (<373 K) and pressures (<30 MPa), and the effects of properties such as permeability, porosity and tortuosity are briefly reported. The correlation between the bulk oil phase and porous media still lack experimental verification. These problems become more distinct in the case of CO2 injection under fracture-vuggy reservoirs, where the temperatures and pressures are extremely high, usually over 393 K and above 30 MPa. Besides, these reservoir characteristics are unique due to the complex fracture networks, discrete vugs and caverns partially filled with various sediments, and complicated oil–water contact. Measuring the CO2 diffusivity experimentally could facilitate mass transfer under these reservoir conditions.
Herein, the CO2 diffusion process in bulk crude oil and carven filling media saturated with reservoir fluids were studied at the temperature of 393 K and pressure of 50 MPa, corresponding to the common reservoir conditions of the fracture-vuggy carbonate studied. An improved pressure decay (PD) method was introduced to calculate the effective CO2 diffusion coefficient. The effects of reservoir fluids and carven filling medium properties, fractures and water saturation on the gas diffusion process were investigated. Several insights in the CO2 EOR mechanisms in fracture-vuggy carbonate reservoirs were facilitated, offering reference in gas injection optimization.
2 Experimental setup and procedures
2.1 Materials
The crude oil sample used in the experiment was collected from Tahe oilfield, China. The oil viscosity and density were 1.42 mPa s and 0.642 g cm−3 under reservoir conditions (413 K and 66.15 MPa), respectively. The saturate, aromatic, resin and asphaltene concentrations of the crude oil used in the experiments were tested, which were 67.14 wt%, 22.09 wt%, 7.72 wt% and 3.06 wt%, respectively. The minimum miscible pressure (MMP) of CO2 with the oil sample at 393 K was determined using the slim tube experiment, and the results are plotted in Fig. 1. The MMP at the experimental temperature is 52.49 MPa. Brine was also collected from the production well in the same reservoir, with a total mineralization of 2.2 × 105 mg L−1, CaCl2 type. The water viscosity and density were 0.4398 mPa s and 1.15 g cm−3 at 393 K and 50 MPa, respectively. The properties of the formation liquids were measured in a PVT cell (PVT240/1500FV, Sanchez Technologies). CO2 was provided by Jingao Gases with a purity of 99.99%.The carven filling porous media were made of outcrops corresponding to the formation. According to the statical data of cavern filling porous media from the fracture-vuggy reservoir studied, there were three main types of cavern fillings: breccia (porosity ∼20%, permeability ∼1000 mD), sedimentary rock represented by sandstone (porosity ∼15%, permeability ∼500 mD), and siltstone cemented by carbonate minerals (porosity ∼10%, permeability ∼50 mD). The physical properties of the carven filling porous media are listed in Table 1. All six cores were drilled at the same radius of 3.80 cm and similar length of 8.71–8.97 cm. Cores #1–3 had similar porosities (15.54–19.22%) and permeabilities (687.82–783.40 mD), but the oil saturations ranged from 0.00 to 69.97%. These 3 cores were used to investigate the effect of oil saturation on CO2 diffusivity. Cores #3–5 were used to study the effect of the cavern filling properties on the CO2 diffusivity. Their initial oil saturations (So) were similar (63.92–71.18%), but their porosities and permeabilities (air permeability, Kair, and brine permeability, Kbrine) were different. Core #6 was cut in half and used to study the effect of fracture media on CO2 diffusivity.
| Core no. | Core type | Length (cm) | Radius (cm) | Bulk volume (cm3) | Pore volume (cm3) | Porosity (%) | Kair (mD) | Kbrine (mD) | So (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Breccia | 8.84 | 3.802 | 100.31 | 16.3 | 16.25 | 1292 | 729 | 49.69 |
| 2 | Breccia | 8.96 | 3.802 | 101.67 | 15.8 | 15.54 | 1389 | 783 | 0 |
| 3 | Breccia | 8.71 | 3.802 | 98.83 | 19 | 19.22 | 1217 | 688 | 69.47 |
| 4 | Sandstone | 8.94 | 3.802 | 101.44 | 17 | 16.76 | 83 | 47 | 71.18 |
| 5 | Siltstone | 8.97 | 3.802 | 101.81 | 9.7 | 9.53 | 10 | 5 | 63.92 |
| 6 | Siltstone | 8.76 | 3.802 | 99.4 | 8.1 | 8.15 | 8 | 4 | 60.49 |
2.2 Experimental setup
A schematic diagram of the experimental setup for measuring the CO2 diffusion coefficients is shown in Fig. 2. It mainly consisted of four components, namely, diffusion cell, gas supply system, data acquisition system, and temperature maintenance system.A diffusion cell with an inner diameter of 5.5 cm and depth of 12.00 cm was used as a holder for the fluids and porous media. The diffusion cell was designed to sustain high pressure of up to 60 MPa and temperature of up to 423 K. The diffusion cell greatly improved the physical limitations of the experimental apparatus32 and it well covered the experimental condition of 50 MPa and 393 K in this work. As aforementioned, the gas diffusivity in both the bulk liquid and porous media can be studied in the same diffusion cell. Therefore, there are two scenarios in the diffusion cell, as can be seen in Fig. 3. For the gas diffusivity in the bulk liquid phase (scenario #1 in Fig. 3), the diffusion cell was filled with gas (CO2) and liquid (oil) with an adequate contact interface between the gas and liquid. Scenario #1 was designed to measure the diffusivity without the porous media, representing the condition when CO2 is injected into caverns without fillings. In the case of the gas diffusivity in porous media, an oil-saturated core was placed inside the diffusion cell, as can be seen in scenario #2 of Fig. 3. The size of the diffusion cell allowed a relatively large core sample to be placed, and thus there was an enlarged area for gas diffusion into the core through the annular space. Scenario #2 represents the condition when CO2 is injected to caverns with porous fillings saturated with formation liquids. Consequently, both scenarios covered the conditions when CO2 is injected to a carbonate reservoir with or without cavern fillings.
The data acquisition system was made of pressure transducers (±5 kPa accuracy, Model JYB, Collihigh Co., Ltd, China) and computers. The data for the pressure variations with time was monitored and recorded in the computer.
2.3 Experimental procedures
The pressure decay method has been widely accepted to determine the CO2 diffusion coefficient,28–31 and thus was applied in this work. The CO2 diffusion coefficient can be calculated by using the recorded real-time pressure data. The designed two scenarios share three main advantages: (1) the procedures are simple and it is easy to transfer liquid or porous media. (2) The improved diffusion flux area either by side surface or liquid surface reduces the sensitivity of the working environment and makes it easy to operate. (3) The pressure distribution in the system is homogeneous during the entire experimental process.Unlike previous studies, an improvement in the pressure build-up process was made in the experimental procedures. In the previous cases, the pressurization in the diffusion cell was built by directly pumping gas into the oil phase, and the initial pressure was obtained by continuous gas pressurization in the cell. However, the diffusion process took place at the moment when two phases contacted each other, and the pressure may not be accurate in the pressure decay method. In this study, an extra cylinder (CO2 cylinder-2 in Fig. 2) was added between the diffusion cell and the piston cylinder. It was used to generate the initial high pressure instantly in the diffusion cell. By pumping the gas via the pump and piston cylinder into cylinder-2, pressure higher than the initial pressure of CO2 was obtained with no contact between the two phases. The procedures for measuring the CO2 diffusion coefficients for the two scenarios are briefly described as follows:
(2) After CO2 cylinder-1, CO2 cylinder-2, and diffusion cell was vacuumed for 2 h, a desirable amount of oil was injected into the diffusion cell by the ISCO high-pressure pump from the oil cylinder.
(3) CO2 in cylinder-0 was transferred to cylinder-1 and cylinder-2. Then the valve on cylinder-0 was closed and the CO2 in cylinder-1 and cylinder-2 was pressurized by the ISCO pump to a desirable pressure.
(4) The system was maintained at 393 K for 4 h. Cylinder-1 and cylinder-2 were disconnected when the pressure stabilized at a certain pressure (over 50 MPa) prior to the gas diffusion test.
(5) At the beginning of the diffusion test, the pressurized CO2 was transferred from cylinder-2 to the diffusion cell. The real-time pressure in the diffusion cell was recorded by the transducer connected to the computer. The diffusion process be ceased when it reached the steady state.
(6) The CO2 in the diffusion cell was discharged. The liquid in the diffusion cell was removed and all the experimental devices were cleaned for the next measurement.
Once the core was well prepared, it was placed in the center of the diffusion cell (see scenario #2 in Fig. 3). The diffusion test was conducted as follows: the entire system was vacuumed, heated, and pressurized prior to the diffusion experiment similar to that for scenario #1. The pressure data in the diffusion cell was recorded. After the gas-porous media system reached the steady state, the pressure in the diffusion cell was released. The cell was disconnected, opened, and cleaned. A new sample was placed for the next measurement.
3 Mathematical models
As described above, the pressure decay method was used to calculate the CO2 diffusion coefficient in both scenarios. The mathematical models and solutions are briefly introduced below.3.1 Gas diffusion experiment in the bulk oil phase
The assumptions made for the mathematical model are as follows: (1) oil evaporation in the CO2 phase is negligible. The CO2 gas compressibility factor, Z, is constant. (2) No resistance to mass transfer exists at the CO2–liquid interface, namely, the concentration at the interface is the equilibrium concentration. (3) The change in the CO2 diffusion coefficient is not significant during the measurement process. (4) The temperature is constant during the measurement process. (5) Swelling of the liquid by dissolving CO2 is ignored.The molar flux of a gas diffusing into a liquid column can be expressed according to Fick's law.33 It can be simplified to an unsteady-state one-dimensional diffusion in a slab as follows:
 | (1) |
At the beginning of the diffusion test, the dead crude oil is free of CO2 and the initial amount of CO2 is assumed to be zero. The initial condition for eqn (1) can be expressed as:
| C(t,h) = 0,t = 0,(0 ≤ h < H) | (2) |
During the diffusion process, the molar concentration at the oil–gas interface varies with pressure and temperature. Considering that the gas diffusion process takes place under isothermal conditions, the CO2 concentration at equilibrium state, Ceq, is solely dependent on the pressure variations.
| C(t,h) = Ceq(P,t),h = H,(0 ≤ t) | (3) |
 | (4) |
 | (5) |
 | (6) |
P(t) = Peq + a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−b1t) + a2 exp(−b1t) + a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−b2t) exp(−b2t)
| (7) |
 | (8) |
3.2 Gas diffusion experiment in the filling porous media
The assumptions made for the mathematical model are as follows: (1) the cores used in the experiment are homogeneous and isotropic. Fluids are uniformly distributed within the cores. (2) The CO2 diffusion coefficients in the cores are constant during the measurement process. (3) The CO2 concentrations in the liquid phase on the core surface are constant during the measurement process. (4) Natural convection caused by the liquid density difference is ignored. (5) Evaporation of the liquid phase into CO2 is ignored. (6) There is still an interface between CO2 and the fluids within the porous media.According to the above-mentioned assumptions, the mathematical description of CO2 diffusion in porous media can be described as follows:29,30
 | (9) |
| C(r,t) = 0,(t = 0,0 < r < r0) | (10) |
| C(r, t) = 0,(0 ≤ t,r = r0) | (11) |
The analytical solution in an infinite series to diffusion eqn (9) subject to the initial condition boundary condition eqn (10) and (11) is similar to that in eqn (5):
 | (12) |
 | (13) |
When  the above equation can be simplified as:
the above equation can be simplified as:
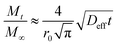 | (14) |
 | (15) |
 | (16) |
4 Results and discusion
4.1 CO2 diffusivity in bulk reservoir liquids
As mentioned above, vugs are the major storage space of formation liquids in fractured-vuggy reservoirs. Herein, for the first time, the CO2 diffusion coefficient of bulk oil and brine was first studied in the void space under high temperature and pressures.Fig. 4 shows the pressure data and fit results using eqn (7) for the CO2–oil system. The CO2 diffusion coefficient in the oil phase was 4.1243 × 10−8 m2 s−1 at 5.10 cm height in the diffusion cell according to eqn (8), and that in heptane was 1.17 × 10−8 m2 s−1 under similar conditions according to Cadogen et al.20 The diffusion coefficient of CO2 in the oil phase was higher than that in liquid heptane. The results presented here may contradict the theoretical Stokes–Einstein models, where the diffusivity of a solute decreases in an alkane with viscosity. This contradiction may be rationalized by considering three typical phenomena from the aspect of the gas enhanced oil recovery process: (1) the CO2 diffusion coefficient is calculated using the absorption law, where an increase in the difference between the equilibrium solubility and the solute concentration will result in a higher diffusion coefficient being observed. (2) A reduction in viscosity due to CO2 resolution, a pronounced mechanism for gas enhanced oil recovery, decreases the solution (oil phase) viscosity. (3) The oil density increases by the CO2 solubility in the oil phase, causing an unneglectable natural convection driven by density.
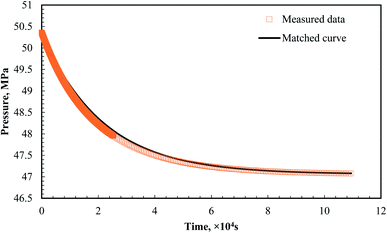 | ||
| Fig. 4 Measured data VS matched curve using eqn (7) (Peq = 47.06 MPa, a1 = 1.7153, a2 = 1.58300, b1 = 3.9193 × 10−5, and b2 = 4.1305 × 10−5). | ||
For the CO2-brine and CO2-pure water system, the diffusion coefficients in saline aquifer solution and pure water were 0.2083 × 10−8 m2 s−1 and 0.6824 × 10−8 m2 s−1, respectively (Table 2). The CO2 diffusivity in brine was lower than that in pure water. According to the statistical analysis by Renner,21 the diffusion coefficient is highly dependent on both solvent viscosity (water) and solute viscosity (CO2, in this case), which reflects the influence of temperature, pressure and salinity in water. The addition of salt will not increase the liquid density, where the liquid viscosity will increase,34,36 which results in a higher resistance for the movement of CO2 molecules through the water layers. Therefore, the CO2 diffusivity in the brine decreased compared to that in pure water.
| Liquid | Temperature (K) | Pressure (MPa) | Density (g cm−3) | Viscosity (mPa s) | Diffusion coefficient (×10−8 m2 s−1) |
|---|---|---|---|---|---|
| a Properties of pure components collected from NIST internet database. | |||||
| CO2a | 393 | 50 | 0.7637 | 0.0680 | — |
| Heptanea | 398 | 50 | 0.6555 | 0.2729 | 1.17 (ref. 20) |
| Oil | 403 | 66 | 0.6418 | 1.4200 | 4.1243 |
| Brine | 393 | 50 | 1.1500 | 0.4398 | 0.2083 |
| Watera | 393 | 50 | 0.9662 | 0.2448 | 0.6824 (ref. 35) |
4.2 CO2 diffusivity in carven-filling porous media with different properties
The vugs within the fractured-vuggy reservoirs are not only filled with liquids but sedimentary rocks due to packing transportation, deposition, and compaction and deformation.37–39 Over 70% of the void space is partially filled with limestone, sandstone and shale cemented by calcareous material.40–42 During the gas injection process, the properties of the porous media within the chamber cave are of great importance to analyze the gas sweeping efficiency. Therefore, effect of the cavern fillings properties on the gas diffusion process in fractured-vuggy reservoirs should be investigated. The CO2 diffusion process in carven fillings saturated with oil was studied in this section.Fig. 5 plots the pressure difference (delta P, pressure drop compared to the initial pressure, in MPa) vs. the square root of 100 s1/2. Unlike the dramatic drop in pressure, the decay curves of CO2 in the filling media demonstrated a gentle drop as the diffusion continued (Fig. 5). During the initial diffusion stage, the dimensionless pressure variation was irrelevant to the properties of the porous media, all demonstrating a linear decay pattern. CO2 penetrated the thin oil film first, and then dispersed in the oil in the pores and throats in the porous media. The pressure curves vary in the different porous media as the diffusion proceeded. For siltstone (core #5), with the assumed smallest averaged pore size and the most complicated pore-throat networks (Table 3), the pressure was the last to reach equilibrium and the pressure difference was 0.67 MPa, a 1.35% drop compared to the initial pressure. That in sandstone (core #4) was 0.72 MPa with a 1.58% drop. Also, that in breccias (core #3) was 0.94 MPa with a 1.85% drop. The CO2 pressure drop in breccia was greater than that in the other two types of cavern filling media, indicating a greater amount of gas was dissolved. The solubility of CO2 in the cavern filling porous media was calculated according to the equation of state of CO2 under constant volume condition (Table 4).
| Core no. | Lithology | Pint (MPa) | Pfnl (MPa) | ΔP (MPa) | ΔP/Pin (%) | CO2 dissolved (×10−5 mol) |
|---|---|---|---|---|---|---|
| 3 | Breccia | 50.64 | 49.70 | 0.94 | 1.8511 | 6.2610 |
| 4 | Sandstone | 50.00 | 49.28 | 0.72 | 1.5779 | 5.0902 |
| 5 | Siltstone | 50.25 | 49.58 | 0.67 | 1.3536 | 4.7295 |
The diffusion coefficients obtained using eqn (16) are demonstrated in Fig. 6. The effective diffusion coefficient of CO2 in breccias (core #3) was 2.55 × 10−9 m2 s−1, 1.91 × 10−9 m2 s−1 in sandstone (core #4), and 6.89 × 10−10 m2 s−1 in siltstone (core #5) respectively. Due to the complicated sedimentary conditions in carbonate reservoirs, the pores of various diameters are twisted and interconnected with each other, and the path for diffusion of a gas molecule within the pores is “tortuous”.43–45 For CO2 diffusion in siltstone, which has the highest tortuosity and smallest pore size, it would take the longest time to reach the inside porous media, corresponding to the pressure variations shown in Fig. 5.
In addition, the relationship of CO2 diffusion between bulk liquid and carven filling media can be described as the effective diffusion coefficient:
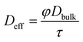 | (17) |
Compared to gas diffusion in the void space, the presence of porous media in the vug-cave space lowers the CO2 mass transfer in these reservoirs. Hence, the gas distribution within the production profile became more heterogeneous, and the property difference in the same production profile enhanced this nonuniformity.
4.3 CO2 diffusivity in the fractured carven-filling porous media
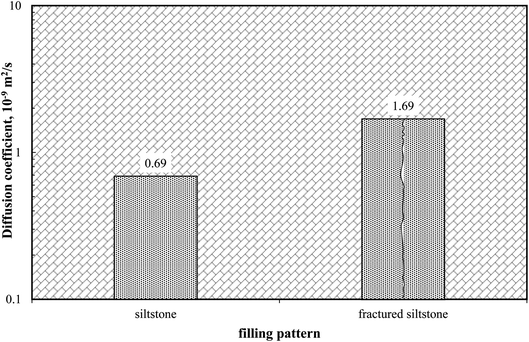
Besides collapse, breccias and cavern form at any scale, and the associated fracture networks drastically enhance the permeability beyond the matrix. Gas diffusion in the fracture is of great importance for gas injection.46 During the process of gas injection, CO2 is injected into the reservoir through the fractures and encompasses the matrix, and the concentration gradient drives CO2 into the matrix by diffusion. Oil expansion and viscosity reduction occur in the matrix due to the contact of CO2. Also, later flow back towards the production well occurs through fracture.47The effective CO2 diffusion coefficient in both siltstone and fractured siltstone are compared in Fig. 7. As demonstrated below, the CO2 diffusion coefficient in siltstone was 0.69 × 10−9 m2 s−1, which increased to 1.69 × 10−9 m2 s−1 in the fractured one, a 2.45-times increase. The existence of fracture significantly improved the gas diffusivity of the cavern siltstone samples. CO2 flows into the matrix via the fracture surface, enlarging the contact area for gas and matrix. Therefore, mass transfer between separate matrices is enhanced via fractures instead of tortuous pores and throats, allowing more CO2 to reach inside the porous media.
4.4 CO2 diffusivity in water-saturated carven-filling porous media
Carbonate materials are susceptible to dissolve in water, and hence splendid river terraces and deep gorges are carved by the subterranean river systems. Karst structures such as subsurface flow channels, solution cavities, sinkholes, pinnacles, and solution chimneys become the flow passages of not only hydrocarbons, but of the water from underground river systems and artificial injection. Production units made up of a single production well or multiple wells suffer excessive water production and reduced production lifetime. Thus, the injection of CO2 proved to be effective to stabilize oil and water contact, suppressing water cresting in experimental and practical cases. The CO2 diffusion process at different water saturations is analyzed in this part.The CO2 diffusion coefficients in breccias saturated with various water saturations are shown in Fig. 8. The diffusion coefficient decreased from 2.55 × 10−9 m2 s−1 to 1.59 × 10−10 m2 s−1 as the water saturation increased from 18% to 100%. The CO2 diffusivity declined to 93.76% as the water saturation in breccia increased from initially the connate state to complete saturation in this study.
 | ||
| Fig. 8 Diffusion coefficient of CO2 in breccias saturated with brine water (393 K, 50 MPa, light oil sample, brine). | ||
The measured data was also fit by an exponential decay equation (eqn (18)) and it was found that the CO2 diffusion coefficient is highly dependent on the water saturation, Sw, within the carven filling porous media.
| D = 1.21264 × 10−10 + 6.07504 × 10−9 × exp(−5.09441 × Sw) | (18) |
At connate water saturation, most of the oil is a continuous phase between the pore space, while water adheres to the pore body in the form of a film. CO2 can easily diffuse into pores and contact with the oil phase, and the diffusion coefficient is relatively high. However, in the water flooded area, a considerable amount of residual oil is isolated from being contacted by the subsequent CO2 due to water blocking. As listed in Table 2, CO2 in the oil phase is much higher than that in brine. CO2 contacts the brine first before dissolving in the oil phase. Considering the existence of torturous pores and throats within the breccia, this transfer process is further delayed. Consequently, the presence of water hinders the CO2 diffusion process in porous media due to the elevated water saturation (Fig. 9).
 | ||
| Fig. 9 Sketch of CO2 traces in breccias with various water saturations (left: innate state, middle: Sw = 50%; and right: Sw = 100%). | ||
5 Conclusion
For a better understanding of the mechanism of CO2 enhanced oil recovery in the fractured-vuggy carbonate reservoirs in China, the diffusion coefficients were measured using the pressure decay method under reservoir conditions (temperature = 393 K and pressure ≈ 50 MPa). The effects of fluid type, properties of the filling media, and water saturation in the filling media on the CO2 diffusion coefficients were discussed. The conclusions are as follows:(1) CO2 diffusivity in crude oil is almost 8 times higher than that in brine. A huge difference in the CO2 diffusion coefficients exists between the crude oil and brines under reservoir conditions. Therefore, the mass transfer of CO2 in the oil phase is more dominant than that in brine, giving priority to the interactions between CO2 and the oil phase.
(2) The existence of sedimentary rocks in the cavity space hinders the gas diffusion process in saturated oil. The increase in tortuosity in porous media increases the difficulty for CO2 to transport within fractured-vuggy reservoirs. The rock permeability, pore size, and tortuosity of the pore structures are the key factors that should be considered.
(3) The existence of fractures in sedimentary rock contributes to the CO2 diffusion process, where the diffusion coefficient increased by over 2 times in this study. Mass transfer is enhanced by the intervened fractures within the carven filling media.
(4) The CO2 diffusion coefficient shows a significant dependence on the water saturation of the carven filling media. Increasing the brine saturation retards the CO2 mass transfer in the carven filling media.
Nomenclature
| C | Molar concentration of gas, mol m−3 |
| Ceq | Molar concentration at equilibrium state, mol m−3 |
| D0 | Diffusion coefficient, m2 s−1 |
| DAB | Gas diffusion coefficient, m2 s−1 |
| DAB | Effective diffusion coefficient, m2 s−1 |
| h | Diffusion distance, m |
| H | Liquid depth, m |
| k | Slope of pressure difference vs. the square root of time, MPa t−0.5 |
| M∞ | Gas dissolved in the porous media, mol |
| P | Pressure, MPa |
| R | Gas constant, 8.314 J (mol K)−1 |
| r0 | Core radius, m |
| r | Diffusion radius, 0 < r < r0, m |
| t | Diffusion time, s |
| T | Temperature, K |
| V | CO2 volume in the annular space between the core and the diffusion cell, m3 |
| Z | Gas constant, dimensionless |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was financially supported by the China Scholarship Council (No. CSC201906440069).References
- Y. Li and Z. Fan, Developmental pattern and distribution rule of the fracture-cavity system of Ordovician carbonate reservoirs in the Tahe Oilfield, Acta Pet. Sin., 2011, 32(1), 101–106 Search PubMed.
- Z. Chen, Y. Dai and Z. Lang, Storage-percolation modes and production performance of the karst reservoirs in Tahe Oilfield, Petrol. Explor. Dev., 2005, 32(3), 101–105 Search PubMed.
- K. Zhang and D. Wang, Reservoir characterization of the Ordovician oil and gas pools in the Tahe Oilfield, Tarim Basin, Northwest China, Pet. Explor. Dev., 2004, 31(1), 123–126 Search PubMed.
- J. Allan and S. Sun, Recovery factor in fractured reservoirs: lessons learned from 100 fractured fields, Pet. Explor. Dev., 2003, 30(6), 129–136 Search PubMed.
- Y. Li, W. Pu and B. Wei, et al., The feasibility of CO2 and N2 injection for the Tahe fracture-cavity carbonate extra-heavy oil reservoir: An experimental study, Fuel, 2018, 226, 598–606 CrossRef CAS.
- X. Lyu, Z. Liu and J. Hou, et al., Mechanism and influencing factors of EOR by N2 injection in fractured-vuggy carbonate reservoirs, J. Nat. Gas Sci. Eng, 2017, 40, 226–235 CrossRef CAS.
- Y. Rong, J. Zhao and X. Lu, et al., Remaining oil distribution patterns and potential-tapping countermeasures in carbonate fracture-cavity reservoir, Acta Pet. Sin., 2014, 35(6), 1138–1146 Search PubMed.
- S. Zheng, M. Yang and Z. Kang, et al., Controlling factors of remaining oil distribution after water flooding and enhanced oil recovery methods for fracture-cavity reservoirs in Tahe Oilfield, Petrol. Explor. Dev., 2019, 46(4), 1–9 CrossRef.
- J. Hui, X. Liu and Y. Wang, et al., Mechanism and Practice of Nitrogen Injection for EOR in Fractured-Vuggy Carbonate Reservoir in Tahe Oilfield, Tarim Basin, Xinjiang Pet. Geol., 2015, 36(1), 75–77 Search PubMed.
- A. Sharbatian, A. Abedini and Z. Qi, et al., Full Characterization of CO2–Oil Properties On-Chip: Solubility, Diffusivity, Extraction Pressure, Miscibility, and Contact Angle, Anal. Chem., 2018, 90(4), 2461–2467 CrossRef CAS PubMed.
- L. Holm and V. Josendal, Mechanisms of oil displacement by carbon dioxide, J. Pet. Technol., 1974, 26(12), 1427–1438 CrossRef.
- E. L. Cussler, Diffusion-Mass transfer in fluid systems, Cambridge University Press, 3rd edn, 2007, vol. 16, DOI:10.1017/cbo9780511805134.001.
- P. Popov, Y. Efendiev and G. Qin, Multiscale. Modeling and simulations of flows in naturally fractured karst reservoirs, Commun. Comput. Phys, 2009, 6(1), 162 CrossRef.
- L. Rongy, K. Haugen and A. Firoozabadi, Mixing from Fickian diffusion and natural convection in binary non-equilibrium fluid phases, AIChE J., 2012, 58(5), 1336–1345 CrossRef CAS.
- M. E. Aguilera and A. López de Ramos, Effect of CO2 diffusion on wettability for hydrocarbon-water-CO2 systems in capillaries, Int. Commun. Heat Mass, 2004, 31, 1115–1122 CrossRef CAS.
- H. Hoteit, Modeling diffusion and gas–oil mass transfer in fractured reservoirs, J. Pet. Sci. Eng., 2013, 105, 1–17 CrossRef CAS.
- H. Hoteit and A. Firoozabadi, Numerical modeling of diffusion in fractured media for gas-injection and -recycling schemes, SPE J., 2009, 14(2), 323–337 CrossRef CAS.
- J. Raad, R. Azin and S. Osfouri, Measurement of CO2 diffusivity in synthetic and saline aquifer solutions at reservoir conditions: the role of ion interactions, Heat Mass Transfer, 2015, 51(11), 1587–1595 CrossRef.
- W. Lu, H. Guo and I. M. Chou, et al., Determination of diffusion coefficients of carbon dioxide in water between 268 and 473K in a high-pressure capillary optical cell with in situ Raman spectroscopic measurements, Geochim. Cosmochim. Acta, 2013, 115, 183–204 CrossRef CAS.
- S. P. Cadogan, Diffusion of CO2 in Fluids Relevant to Carbon Capture, Utilisation and Storage, Imperial College London, 2015 Search PubMed.
- T. A. Renner, Measurement and Correlation of Diffusion Coefficients for CO2 and Rich-Gas Applications, SPE Reservoir Eng., 1988, 3(2), 517–528 CrossRef CAS.
- T. Schmidt, T. Leshchyshyn and V. Puttagunta Diffusivity of Carbon Dioxide into Athabasca Bitumen, 33rd Annual Technical Meeting of the Petroleum Society of CIM, 1982, pp. 82−33 Search PubMed.
- L. Wang, Z. Lang and T. Guo, Measurement and Correlation of the Diffusion Coefficients of Carbon Dioxide in Liquid Hydrocarbons under Elevated Pressures, Fluid Phase Equilib., 1996, 117, 364–372 CrossRef CAS.
- L. Wang and C. Sun, Diffusion of Carbon Dioxide in Tetradecane, J. Chem. Eng. Data, 1997, 42, 1181–1186 CrossRef CAS.
- S. P. Cadogan, G. C. Maitland and J. P. Martin, Diffusion coefficients of CO2 and N2 in water at temperatures between 298.15 K and 423.15 K at pressures up to 45 MPa, J. Chem. Eng. Data, 2014, 59, 519–525 CrossRef CAS.
- G. Yang, Z. Fan and X. Li, Determination of Confined Fluid Phase Behavior Using Extended Peng-Robinson Equation of State, Chem. Eng. J., 2019, 378, 122032 CrossRef CAS.
- D. Chai, Z. Fan and X. Li, Gas Transport in Shale Matrix Coupling Multilayer Adsorption and Pore Confinement Effect, Chem. Eng. J., 2019, 370, 1534–1549 CrossRef CAS.
- Z. Li, M. Dong and E. Shirif, Transient natural convection induced by gas diffusion in liquid-saturated vertical porous columns, Ind. Eng. Chem. Res., 2006, 45, 3311–3319 CrossRef CAS.
- Z. Li and M. Dong, Experimental study of carbon dioxide diffusion in oil-saturated porous media under reservoir conditions, Ind. Eng. Chem. Res., 2009, 48, 9307–9317 CrossRef CAS.
- S. Li, Z. Li and Q. Dong, Diffusion coefficients of supercritical CO2 in oil-saturated cores under low permeability reservoir conditions, J. CO2 Util., 2016, 14, 47–60 CrossRef CAS.
- H. Gao, B. Zhang and L. Fan, et al., Study on Diffusivity of CO2 in Oil-Saturated Porous Media under High Pressure and Temperature, Energy Fuels, 2019, 33(11), 11364–11372 CrossRef CAS.
- M. Chordia and J. T. Japan, Diffusion in Naturally Fractured Reservoirs – A Review, Paper presented at the, SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Queensland, Australia, October 2010 Search PubMed.
- Y. Zhang, C. Hyndman and B. B. Maini, Measurement of gas diffusivity in heavy oils, J. Pet. Sci. Eng., 2000, 25(1), 37–47 CrossRef CAS.
- J. Crank, The Mathematics of Diffusion, Clarendon Press, 2nd edn, Oxford, 1975 Search PubMed.
- R. Azin and M. Mahmoudy, Measurement and modeling of CO2 diffusion coefficient in saline aquifer at reservoir conditions, Central Eur. J. Eng., 2013, 3(4), 585–594 CAS.
- W. Zhang, S. Wu, S. Ren and L. Zhang, et al., The modeling and experimental studies on the diffusion coefficient of CO2 in saline water, J. CO2 Utilization, 2015, 11, 49–53 CrossRef CAS.
- C. Mao, J. Zhong and Y. Li, et al., Ordovician carbonate rock matrix fractured-porous reservoirs in Tahe Oilfield, Pet. Explor. Dev., 2014, 41(6), 681–689 CAS.
- A. Sakhaee-Pour and H. Tran, The Permeability of a representative carbonate volume with a large vug, Transp. Porous Media, 2017, 120, 515–534 CrossRef CAS.
- P. Baud, U. Exner and M. Lommatzsch, et al., Mechanical behavior, failure mode, and transport properties in a porous carbonate, J. Geophys. Res.: Solid Earth, 2017, 122, 7363–7387 CrossRef.
- Q. Jin, F. Tian and X. Lu, et al., Characteristics of collapse breccias in caves of runoff zone in the Ordovician karst in Tahe oilfield, Tarim Basin, Oil Gas Geol., 2015, 36(5), 729–735+755 Search PubMed.
- Q. Jin, X. Kang and F. Tian, Genesis of chemical fillings in fracture-caves in paleo-karst runoff zone in Ordovician and their distributions in Tahe oilfield, Tarim Basin, Acta Pet. Sin., 2015, 36(7), 791–798+836 CrossRef CAS PubMed.
- Y. Li and Z. Fan, Developmental pattern and distribution rule of the fracture-cavity system of Ordovician carbonate reservoirs in the Tahe Oilfield, Acta Pet. Sin., 2011, 32(1), 101–106 Search PubMed.
- L. Zhang, J. Ba and L. Fu, et al., Estimation of pore microstructure by using the static and dynamic moduli, Int. J. Rock Mech. Min. Sci., 2019, 113, 24–30 CrossRef.
- B. Yu, J. Li and Z. Li, et al., Permeabilities of unsaturated fractal porous media, Int. J. Multiphase Flow, 2003, 29, 1625–1642 CrossRef CAS.
- J. Wu, D. Hu and J. Guo, et al., Study on the relationship between tortuosity and permeability in porous media, Journal of North China Institute and Technology, 2016, 13(4), 56–59 Search PubMed.
- B. Jia and J, R. Tsau, Barati. Role of molecular diffusion in heterogeneous, naturally fractured shale reservoirs during CO2 huff-n-puff, J. Pet. Sci. Eng., 2018, 164, 31–42 CrossRef CAS.
- S. B. Hawthorne, L. Jin and B. A. Kurz, et al., Integrating petrographic and petrophysical analyses with CO2 permeation and oil extraction and recovery in the Bakken tight oil formation, Paper Presented at the, SPE Unconventional Resources Conference, Calgary, Alberta, Canada, 15–16 February 2017 Search PubMed.
| This journal is © The Royal Society of Chemistry 2021 |